初中数学冀教版(2024)七年级上册期末 综合素质评价(含答案)
文档属性
| 名称 | 初中数学冀教版(2024)七年级上册期末 综合素质评价(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 86.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-14 00:00:00 | ||
图片预览




文档简介
冀教版七年级上册数学期末综合素质评价
一、选择题(每题3分,共36分)
1.如果水库水位上升记作,那么水库水位下降记作( )
A. B. C. D.
2.如图,还可以表示为( )
(第2题)
A. B. C. D.
3.已知是关于的一元一次方程,则的值为( )
A. B. C. D.
4.神舟十九号载人飞船回舱时拖着“长长的火焰”,我们用数学知识可解释为( )
A. 点动成线 B. 线动成面
C. 面动成体 D. 以上答案都不对
5.有理数,,在数轴上对应点的位置如图所示,如果,那么下列结论正确的是( )
(第5题)
A. B. C. D.
6.若和互为余角,与互补,且 ,则的度数为( )
A. B. C. D.
7.若,则代数式的值为( )
A. B. C. 7 D. 9
8.我国明代数学读本《算法统宗》中有一道题,其题意是:客人一起分银子,若每人7两,则剩4两;若每人9两,则差8两.设有人分银子,则可列方程为( )
A. B.
C. D.
9.如图,已知三角形是等边三角形,,,将三角形绕点按逆时针方向旋转,使得与重合,得到三角形,则旋转的角度是( )
(第9题)
A. B. C. D.
10.平面上有4个点,经过每两点画一条直线,所画直线条数不可能为( )
A. 1条 B. 3条 C. 4条 D. 6条
11.已知一件商品按成本价提高后标价,再打八折销售.小华在购买本商品时,打折后又使用支付宝红包抵扣了5元,最终付款139元.请问商家售出这件商品的盈利情况是( )
A. 盈利 B. 亏损 C. 不盈不亏 D. 盈亏不确定
12.将图①中的正方形剪开得到图②,图②中共有4个正方形;将图②中一个正方形剪开得到图③,图③中共有7个正方形;将图③中一个正方形剪开得到图④,图④中共有10个正方形, ,如此下去,则第2 025个图中共有正方形的个数为( )
A. 2 024 B. 2 025 C. 6 070 D. 6 073
二、填空题(每题3分,共12分)
13.有下列各数:,,,,,,其中正数有_ _ _ _ 个,负分数有_ _ _ _ 个,整数有_ _ _ _ 个.
14.若代数式的值与的取值无关,则的值为_ _ _ _ _ _ .
15.整理一批数据,由1人完成需要.先安排一些人整理,再增加4人一起整理,可完成这项工作的,假设这些人的工作效率相同,则先安排整理的人数为_ _ _ _ .
16.将一根绳子对折后用如图所示的线段表示,现从处将绳子剪断,测得剪断后的各段绳子中最长的一段长为,若,则这根绳子原来的长度为_____________ .
三、解答题(共72分)
17.(6分)计算:
(1) ;
(2) .
18.(6分) 解方程:
(1) ;
(2) .
19.(8分)已知,求的值.
20.(8分)某学习小组调查了一名外卖小哥一周的送餐情况,规定送餐量超过40单(送一次外卖称为一单)的部分记为“”,低于40单的部分记为“-”,如表是该外卖小哥一周的送餐量:
星期 一 二 三 四 五 六 日
送餐量(单位:单)
(1) 求该外卖小哥这一周平均每天送餐多少单.
(2) 外卖小哥每天的工资由底薪40元加上送单补贴构成.送单补贴的方案如下:每天送餐量不超过40单的部分,每单补贴4元;超过40单的部分,每单补贴8元.该外卖小哥这一周工资收入多少元?
21.(8分)如图,是直线上一点,以为顶点作 ,且,位于直线的两侧,平分.请你猜想和的数量关系,并说明理由.
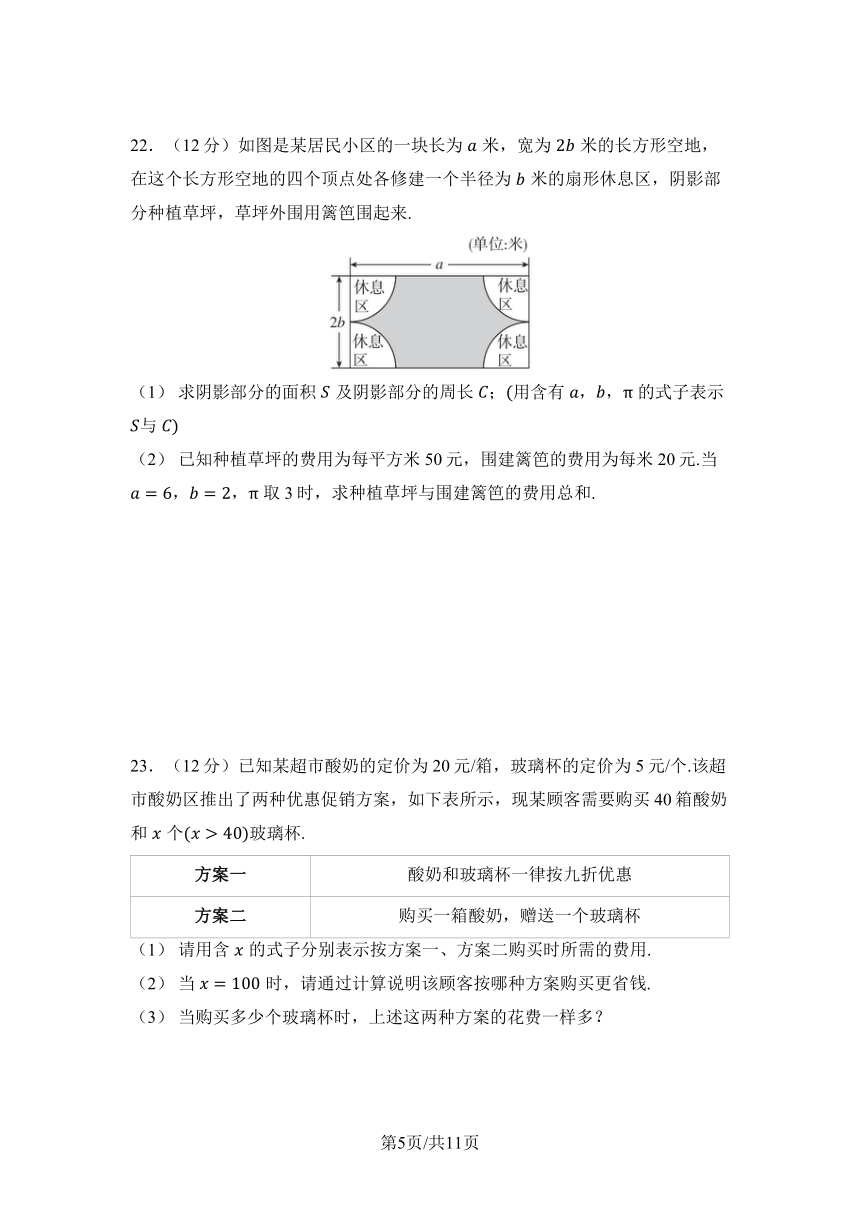
22.(12分)如图是某居民小区的一块长为米,宽为米的长方形空地,在这个长方形空地的四个顶点处各修建一个半径为米的扇形休息区,阴影部分种植草坪,草坪外围用篱笆围起来.
(1) 求阴影部分的面积及阴影部分的周长;用含有,, 的式子表示 与
(2) 已知种植草坪的费用为每平方米50元,围建篱笆的费用为每米20元.当,, 取3时,求种植草坪与围建篱笆的费用总和.
23.(12分)已知某超市酸奶的定价为20元/箱,玻璃杯的定价为5元/个.该超市酸奶区推出了两种优惠促销方案,如下表所示,现某顾客需要购买40箱酸奶和个玻璃杯.
方案一 酸奶和玻璃杯一律按九折优惠
方案二 购买一箱酸奶,赠送一个玻璃杯
(1) 请用含的式子分别表示按方案一、方案二购买时所需的费用.
(2) 当时,请通过计算说明该顾客按哪种方案购买更省钱.
(3) 当购买多少个玻璃杯时,上述这两种方案的花费一样多?
24.(12分)如图,,为数轴上的两个点,点对应的数记为,点对应的数记为,且,满足.解答下列问题:
(1) _ _ _ _ _ _ ,_ _ _ _ _ _ .
(2) 若数轴上点满足,求点对应的数.
(3) 点、点、点是数轴上的动点,点从点出发,沿数轴以5个单位/秒的速度向右移动,点从点出发,以3个单位/秒的速度沿数轴向右移动,同时点从点出发,沿数轴以1个单位/秒的速度向左移动,设运动时间为秒,在三个点移动的过程中,或是否会是定值 若会,求出的取值范围;若不会,请说明理由.
参考答案
1.C
2.C
3.C
4.A
5.C
6.B
7.B
【点拨】因为,所以,所以,故选.
8.B
9.A
10.B
【点拨】分以下三种情况:
①当有4个点在同一直线上时,如图①,故可以画1条直线;
②当有3个点在同一直线上时,如图②,故可以画4条直线;
③当有2个点在同一直线上时,如图③,可以画6条直线.
故选B.
11.B
【点拨】设该商品的成本价为元,根据题意得,解得.因为所以商家售出这件商品的盈利情况是亏损,故选.
12.D
【点拨】由题图可得,第①个图中共有1个正方形,第②个图中共有(个)正方形,第③个图中共有(个)正方形,第④个图中共有(个)正方形, ,则第2 025个图中共有(个)正方形.故选.
13.4; 3; 4
14.
【点拨】.由条件可知,,所以,,所以.
15.2
【点拨】设先安排整理的人数为,则易得,解方程,得,所以先安排整理的人数为2.
16.8或4
【点拨】根据题意,分两种情况:
①当对折点在点时,从处将绳子剪断,分成三段:,,.因为,所以,所以,即线段是最长的一段.因为最长的一段为,即,所以,解得,所以这根绳子原来的长度为;
②当对折点在点时,从处将绳子剪断,分成三段:,,.因为,所以是最长的一段,所以,解得,所以,所以这根绳子原来的长度为.
综上,这根绳子原来的长度为或.
,所以是最长的一段,所以,解得,所以,所以这根绳子原来的长度为.
综上,这根绳子原来的长度为或.
,所以是最长的一段,所以,解得,所以,所以这根绳子原来的长度为.
综上,这根绳子原来的长度为或.
17.(1) 【解】原式.
(2) 原式.
18.(1) 【解】去括号,得,
移项,得,
合并同类项,得,
将的系数化为1,得.
(2) 去分母,得,
去括号,得,
移项,得,
合并同类项,得,
将的系数化为1,得.
19.【解】由,
得,,解得,.
原式.
当,时,
原式.
20.(1) 【解】由题意,得(单),
所以该外卖小哥这一周平均每天送餐43单.
(2) 由题意,得(元),
答:该外卖小哥这一周工资收入1 632元.
21.【解】,理由如下:
因为 ,所以 ,
所以.
因为平分,
所以.
又因为 ,
所以 ,即 ,所以.
22.(1) 【解】平方米.
米.
(2) 把,,分别代入,,得
(平方米),
(米).
因为种植草坪的费用为每平方米50元,围建篱笆的费用为每米20元,
所以(元).
答:种植草坪与围建篱笆的费用总和为920元.
23.(1) 【解】根据题意,得按方案一购买时所需的费用为元.
按方案二购买时所需的费用为元.
(2) 当时,(元),
(元).
因为,所以该顾客按方案二购买更省钱.
(3) 根据题意,得,
解得.
答:当购买240个玻璃杯时,上述这两种方案的花费一样多.
24.(1) ;
(2) 【解】设点表示的数为.分两种情况:
①当点在线段上时,因为,
所以,解得;
②当点在线段的延长线上时,
因为,所以,
解得.
综上,点对应的数为7或22.
(3) 在三个点移动过程中,或会是定值.由题意得点表示的数为,点表示的数为,点表示的数为,
所以,.
①当时,,
此时,
所以是定值,
,
所以不是定值;
②当时,,
此时,
所以是定值,
,
所以不是定值;
综上,当时,是定值;当时,是定值.
第页/共页
一、选择题(每题3分,共36分)
1.如果水库水位上升记作,那么水库水位下降记作( )
A. B. C. D.
2.如图,还可以表示为( )
(第2题)
A. B. C. D.
3.已知是关于的一元一次方程,则的值为( )
A. B. C. D.
4.神舟十九号载人飞船回舱时拖着“长长的火焰”,我们用数学知识可解释为( )
A. 点动成线 B. 线动成面
C. 面动成体 D. 以上答案都不对
5.有理数,,在数轴上对应点的位置如图所示,如果,那么下列结论正确的是( )
(第5题)
A. B. C. D.
6.若和互为余角,与互补,且 ,则的度数为( )
A. B. C. D.
7.若,则代数式的值为( )
A. B. C. 7 D. 9
8.我国明代数学读本《算法统宗》中有一道题,其题意是:客人一起分银子,若每人7两,则剩4两;若每人9两,则差8两.设有人分银子,则可列方程为( )
A. B.
C. D.
9.如图,已知三角形是等边三角形,,,将三角形绕点按逆时针方向旋转,使得与重合,得到三角形,则旋转的角度是( )
(第9题)
A. B. C. D.
10.平面上有4个点,经过每两点画一条直线,所画直线条数不可能为( )
A. 1条 B. 3条 C. 4条 D. 6条
11.已知一件商品按成本价提高后标价,再打八折销售.小华在购买本商品时,打折后又使用支付宝红包抵扣了5元,最终付款139元.请问商家售出这件商品的盈利情况是( )
A. 盈利 B. 亏损 C. 不盈不亏 D. 盈亏不确定
12.将图①中的正方形剪开得到图②,图②中共有4个正方形;将图②中一个正方形剪开得到图③,图③中共有7个正方形;将图③中一个正方形剪开得到图④,图④中共有10个正方形, ,如此下去,则第2 025个图中共有正方形的个数为( )
A. 2 024 B. 2 025 C. 6 070 D. 6 073
二、填空题(每题3分,共12分)
13.有下列各数:,,,,,,其中正数有_ _ _ _ 个,负分数有_ _ _ _ 个,整数有_ _ _ _ 个.
14.若代数式的值与的取值无关,则的值为_ _ _ _ _ _ .
15.整理一批数据,由1人完成需要.先安排一些人整理,再增加4人一起整理,可完成这项工作的,假设这些人的工作效率相同,则先安排整理的人数为_ _ _ _ .
16.将一根绳子对折后用如图所示的线段表示,现从处将绳子剪断,测得剪断后的各段绳子中最长的一段长为,若,则这根绳子原来的长度为_____________ .
三、解答题(共72分)
17.(6分)计算:
(1) ;
(2) .
18.(6分) 解方程:
(1) ;
(2) .
19.(8分)已知,求的值.
20.(8分)某学习小组调查了一名外卖小哥一周的送餐情况,规定送餐量超过40单(送一次外卖称为一单)的部分记为“”,低于40单的部分记为“-”,如表是该外卖小哥一周的送餐量:
星期 一 二 三 四 五 六 日
送餐量(单位:单)
(1) 求该外卖小哥这一周平均每天送餐多少单.
(2) 外卖小哥每天的工资由底薪40元加上送单补贴构成.送单补贴的方案如下:每天送餐量不超过40单的部分,每单补贴4元;超过40单的部分,每单补贴8元.该外卖小哥这一周工资收入多少元?
21.(8分)如图,是直线上一点,以为顶点作 ,且,位于直线的两侧,平分.请你猜想和的数量关系,并说明理由.
22.(12分)如图是某居民小区的一块长为米,宽为米的长方形空地,在这个长方形空地的四个顶点处各修建一个半径为米的扇形休息区,阴影部分种植草坪,草坪外围用篱笆围起来.
(1) 求阴影部分的面积及阴影部分的周长;用含有,, 的式子表示 与
(2) 已知种植草坪的费用为每平方米50元,围建篱笆的费用为每米20元.当,, 取3时,求种植草坪与围建篱笆的费用总和.
23.(12分)已知某超市酸奶的定价为20元/箱,玻璃杯的定价为5元/个.该超市酸奶区推出了两种优惠促销方案,如下表所示,现某顾客需要购买40箱酸奶和个玻璃杯.
方案一 酸奶和玻璃杯一律按九折优惠
方案二 购买一箱酸奶,赠送一个玻璃杯
(1) 请用含的式子分别表示按方案一、方案二购买时所需的费用.
(2) 当时,请通过计算说明该顾客按哪种方案购买更省钱.
(3) 当购买多少个玻璃杯时,上述这两种方案的花费一样多?
24.(12分)如图,,为数轴上的两个点,点对应的数记为,点对应的数记为,且,满足.解答下列问题:
(1) _ _ _ _ _ _ ,_ _ _ _ _ _ .
(2) 若数轴上点满足,求点对应的数.
(3) 点、点、点是数轴上的动点,点从点出发,沿数轴以5个单位/秒的速度向右移动,点从点出发,以3个单位/秒的速度沿数轴向右移动,同时点从点出发,沿数轴以1个单位/秒的速度向左移动,设运动时间为秒,在三个点移动的过程中,或是否会是定值 若会,求出的取值范围;若不会,请说明理由.
参考答案
1.C
2.C
3.C
4.A
5.C
6.B
7.B
【点拨】因为,所以,所以,故选.
8.B
9.A
10.B
【点拨】分以下三种情况:
①当有4个点在同一直线上时,如图①,故可以画1条直线;
②当有3个点在同一直线上时,如图②,故可以画4条直线;
③当有2个点在同一直线上时,如图③,可以画6条直线.
故选B.
11.B
【点拨】设该商品的成本价为元,根据题意得,解得.因为所以商家售出这件商品的盈利情况是亏损,故选.
12.D
【点拨】由题图可得,第①个图中共有1个正方形,第②个图中共有(个)正方形,第③个图中共有(个)正方形,第④个图中共有(个)正方形, ,则第2 025个图中共有(个)正方形.故选.
13.4; 3; 4
14.
【点拨】.由条件可知,,所以,,所以.
15.2
【点拨】设先安排整理的人数为,则易得,解方程,得,所以先安排整理的人数为2.
16.8或4
【点拨】根据题意,分两种情况:
①当对折点在点时,从处将绳子剪断,分成三段:,,.因为,所以,所以,即线段是最长的一段.因为最长的一段为,即,所以,解得,所以这根绳子原来的长度为;
②当对折点在点时,从处将绳子剪断,分成三段:,,.因为,所以是最长的一段,所以,解得,所以,所以这根绳子原来的长度为.
综上,这根绳子原来的长度为或.
,所以是最长的一段,所以,解得,所以,所以这根绳子原来的长度为.
综上,这根绳子原来的长度为或.
,所以是最长的一段,所以,解得,所以,所以这根绳子原来的长度为.
综上,这根绳子原来的长度为或.
17.(1) 【解】原式.
(2) 原式.
18.(1) 【解】去括号,得,
移项,得,
合并同类项,得,
将的系数化为1,得.
(2) 去分母,得,
去括号,得,
移项,得,
合并同类项,得,
将的系数化为1,得.
19.【解】由,
得,,解得,.
原式.
当,时,
原式.
20.(1) 【解】由题意,得(单),
所以该外卖小哥这一周平均每天送餐43单.
(2) 由题意,得(元),
答:该外卖小哥这一周工资收入1 632元.
21.【解】,理由如下:
因为 ,所以 ,
所以.
因为平分,
所以.
又因为 ,
所以 ,即 ,所以.
22.(1) 【解】平方米.
米.
(2) 把,,分别代入,,得
(平方米),
(米).
因为种植草坪的费用为每平方米50元,围建篱笆的费用为每米20元,
所以(元).
答:种植草坪与围建篱笆的费用总和为920元.
23.(1) 【解】根据题意,得按方案一购买时所需的费用为元.
按方案二购买时所需的费用为元.
(2) 当时,(元),
(元).
因为,所以该顾客按方案二购买更省钱.
(3) 根据题意,得,
解得.
答:当购买240个玻璃杯时,上述这两种方案的花费一样多.
24.(1) ;
(2) 【解】设点表示的数为.分两种情况:
①当点在线段上时,因为,
所以,解得;
②当点在线段的延长线上时,
因为,所以,
解得.
综上,点对应的数为7或22.
(3) 在三个点移动过程中,或会是定值.由题意得点表示的数为,点表示的数为,点表示的数为,
所以,.
①当时,,
此时,
所以是定值,
,
所以不是定值;
②当时,,
此时,
所以是定值,
,
所以不是定值;
综上,当时,是定值;当时,是定值.
第页/共页
同课章节目录
