(期末拔高提分)期末综合素养培优卷-2024-2025学年五年级下学期数学西师大版(含解析)
文档属性
| 名称 | (期末拔高提分)期末综合素养培优卷-2024-2025学年五年级下学期数学西师大版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 130.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-14 11:36:17 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年五年级下学期数学期末综合素养培优卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题(共8小题,共8分)
1.把一张长方形纸对折,再对折……一共对折3次后,得到的小长方形纸的面积是a平方厘米,这张纸原来的面积是( )平方厘米。
A.4a B.8a C.12a D.16a
2.因为2+3=5,4+9=13,20+11=31,……,所以偶数与奇数的和一定是( )
A.质数 B.合数 C.奇数 D.偶数
3.《庄子 天下篇》中有一句话:“一尺之棰,日取其半,万世不竭。”意思就是:一根一尺长的木棒,第一天截取它的一半,第二天截取剩下的一半,第三天再截取剩下的一半……永远也截取不完。请问第三天截取的长度是这根木棒的( )
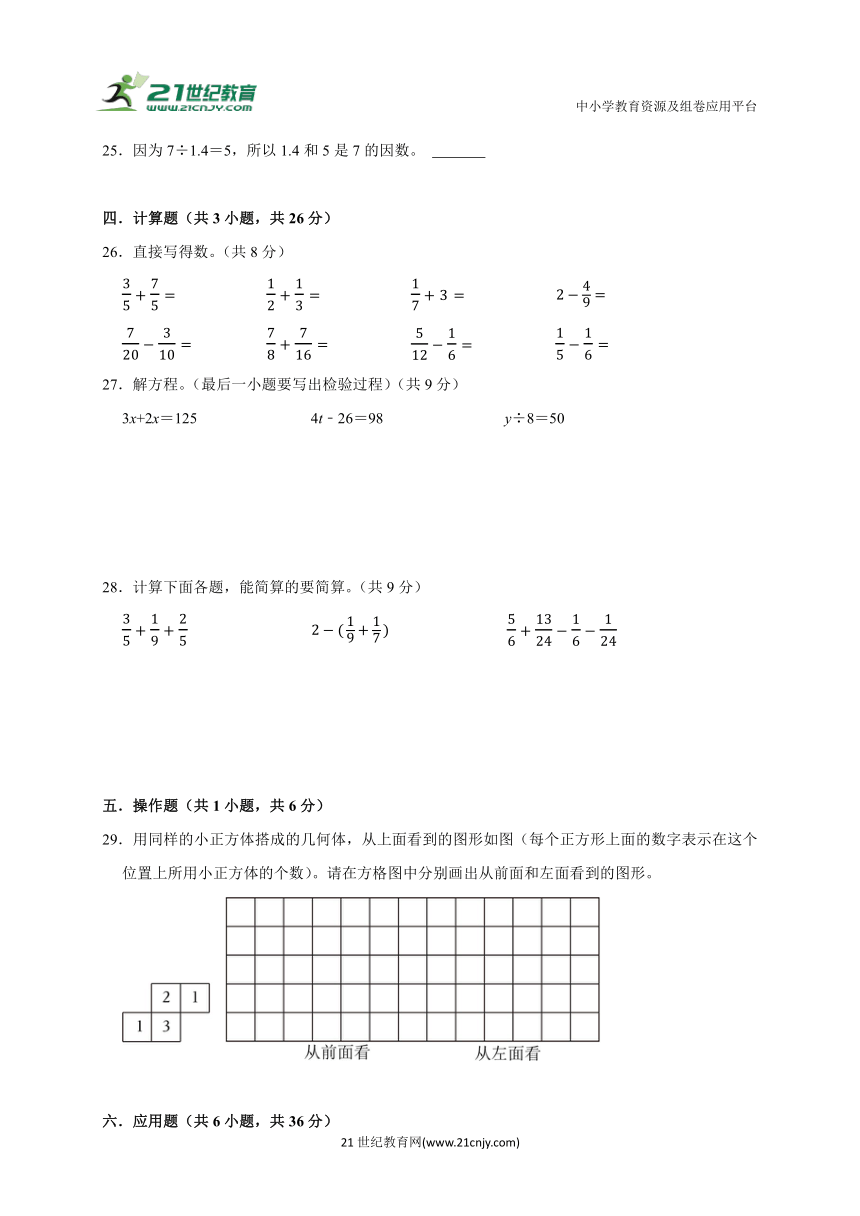
A. B. C. D.
4.王东用相同的小正方搭建几何体,如图是从上面看到的形状(上面的数字表示这个位置上小正方体的个数)。这个几何体正面看到的形状是( )
A. B. C. D.
5.在、、、、中,能化成有限小数或整数的有( )个。
A.2 B.3 C.4 D.5
6.小龙今年a岁,小飞今年(a﹣3)岁,再过b年,他们相差( )岁。
A.3 B.a﹣3 C.3b
7.把5克盐溶入50克水中,盐占盐水的( )
A. B. C. D.
8.下面的式子中,既不是方程,也不是等式的是( )
A.6x+5=17 B.x+6<27 C.46﹣9=37 D.5y=40
二.填空题(共12小题,共19分)
9.一个三位数的百位上是最小的质数,十位上是最小的合数,它还能同时被2,3,5整除,这个三位数是 。
10.如果自然数C是B的5倍,则B与C的最小公倍数是 .
11.把5m长的绳子平均分成8段,每段长 m,第三段占全长的 。
12.杯子中装满水, 的体积就是 的容积.(填“水”或“杯子”)
13.在括号里填上合适的单位。
一本数学书的体积约380 一桶食用油的容积约5
14.的分数单位是 ,它再添上 个这样的分数单位等于最小的合数.
15.一个两位数同时是2和3的倍数,十位上的数是最小的质数,这个两位数是 .
16.给的分子加上10,要使分数大小不变,分母应加上 .
17.临近期末,杨老师买来一些笔奖给优秀学生。如果每6支装一个盒子还剩3支,如果每4支装一个盒子也剩3支。杨老师至少买来了 支笔。
18.在1﹣30的自然数中,最小的合数是 ,最大的质数是 。 既是偶数又是质数。
19.把56写成质数相乘的形式是56= .
20.A=2×3×5,B=2×3×7.A和B的最大公因数是 ,最小公倍数是 .
三.判断题(共5小题,共5分)
21.约分会改变分子、分母的大小,但分数的大小不变。
22.和的意义不相同,但大小相等。
23.一根绳子剪成两段,第一段占全长的,第二段长m。两段绳子一样长。
24.表面积相等的两个正方体,它们的体积一定相等. .
25.因为7÷1.4=5,所以1.4和5是7的因数。
四.计算题(共3小题,共26分)
26.直接写得数。(共8分)
27.解方程。(最后一小题要写出检验过程)(共9分)
3x+2x=125 4t﹣26=98 y÷8=50
28.计算下面各题,能简算的要简算。(共9分)
五.操作题(共1小题,共6分)
29.用同样的小正方体搭成的几何体,从上面看到的图形如图(每个正方形上面的数字表示在这个位置上所用小正方体的个数)。请在方格图中分别画出从前面和左面看到的图形。
六.应用题(共6小题,共36分)
30.有一筐苹果,6个6个地数刚好数完,9个9个地数也刚好数完。这筐苹果至少有多少个?
31.一根蜡烛第一次烧掉全长的一半,第二次烧掉剩下的一半。两次一共烧掉了这根蜡烛的几分之几?
32.牛山寺公园新建的花卉园,要种菊花、樱花和梅花。菊花占总面积的,樱花占总面积的。梅花占总面积的几分之几?
33.甲、乙两地相距450km。一辆客车和一辆货车同时从甲、乙两地开出,相向而行,行驶3时两车相遇,这时客车行了270km。货车平均每时行多少千米?(用你喜欢的方法解)
34.我国上世纪60年代普通水稻亩产量是350kg,“杂交水稻之父”袁隆平在2015年培育成功的“超优千号”水稻,亩产量比普通水稻的3倍还多99kg,“超优千号”水稻亩产量是多少千克?
35.五(1)班买5个篮球和8副乒乓球拍,付出800元,找回65元。每个篮球75元,每副乒乓球拍多少元?(用你喜欢的方法解)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案与试题解析
一.选择题(共8小题,共8分)
1.B
【分析】把这张纸对折一次,每份是原来的,再对折,每份是原来的,对折三次,每份是原长的,就是这张纸的是a平方厘米,求这张纸的面积,是已知一个数的几分之几是多少,求这个数用除法计算。
【解析】解:a÷()
=a
=8a(平方厘米)
答:这张纸原来面积8a平方厘米。
故选:B。
【点评】解答此题的关键是明确:这张纸对折三次后的面积是原来的几分之几。
2.C
【分析】合数是在大于1的整数中,除了能被1和本身整除外,还能被其他数(0除外)整除的数;质数是一个自然数,只有1和它本身两个因数;偶数是在整数中,能被2整除的数;奇数是在整数中,不能被2整除的数。
【解析】解:设偶数为2a,奇数为2a+1。
2a+2a+1=4a+1,4a+1是奇数,所以偶数与奇数的和一定是奇数。
则因为2+3=5,4+9=13,20+11=31,……,所以偶数与奇数的和一定是奇数。
故选:C。
【点评】此题考查了奇数和偶数的初步认识,要求学生掌握。
3.D
【分析】把这根木棒的长度看作单位“1”,把它平均分成2份,每份是它的,取其中1份;再把取的这一份看作单位“1”,把它平均分成2份,每份是它的,取其中1份,这1份相当于原来这根木棒长度的的,即;再取其中1份,把它的长度看作单位“1”,把它平均分成2份,取其中1份,这1份相当于原来这根木棒长度的的,即。
【解析】解:如图:
第三天截取的长度是这根木棒的。
故选:D。
【点评】此题是考查分数的意义,把单位“1”平均分成若干份,用分数表示,分母是分成的份数,分子是要表示的份数。相当于把这根木棒平均分成2份、4份、8份……都取其中1份。
4.C
【分析】这个几何体正面看到的形状是三列小正方形,左面1个,中间合右面都是3个,下齐。
【解析】解:这个几何体正面看到的形状是。
故选:C。
【点评】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
5.C
【分析】首先,要把分数约分成最简分数,再根据一个最简分数,如果分母中除了2与5以外,不含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数。作出判断。
【解析】解:的分母中只含有质因数5,的分母中只含有质因数2,所以都能化成有限小数;
约分后是,可以化为整数3;约分后是,分母中含有质因数3,不能化成有限小数;
的分母中只含有质因数5,能化成有限小数。
所以能化成有限小数或整数的有一共有4个。
故选:C。
【点评】此题主要考查能化成有限小数的分数的特点。根据一个最简分数,如果分母中除了2与5以外,不含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数。就能很快作出判断。
6.A
【分析】两个人之间年龄差始终不变,因此直接求出今年他们相差多少岁,即可求出过b年他们相差多少岁。
【解析】解:a﹣(a﹣3)
=a﹣a+3
=3(岁)
答:再过b年,他们相差3岁。
故选:A。
【点评】此题主要考查了两个人之间年龄差始终不变的知识点,要熟练掌握。
7.C
【分析】先求出盐水的总重量,然后用盐的重量除以盐水的总重量,求出盐占盐水的几分之几即可.
【解析】解:盐占盐水的:5÷(5+50)
=5÷55
.
故选:C.
【点评】本题属于基本的分数除法应用题,只要找出单位“1”,问题不难解决.
8.B
【分析】表示两个数或两个代数式相等关系的式子叫做等式;含有未知数的等式叫方程。
【解析】解:A.6x+5=17,是等式,且含有未知数,所以是方程;
B.x+6<27,既不是方程,也不是等式;
C.46﹣9=37,是等式,但不是方程;
D.5y=40,含有未知数,且是等式,是方程。
故选:B。
【点评】熟练掌握等式与方程的意义是解题的关键。
二.填空题(共12小题,共19分)
9.见试题解答内容
【分析】最小的质数是2,所以百位上是2,最小的合数是4,所以十位上是4,又知这个数既是2的倍数,又有因数3和5,则这个数同时是2、3、5的倍数,据此分析解答即可。
【解析】解:最小的质数是2,最小的合数是4,既是2的倍数又是5的倍数,个位是0,所以这个三位数是240。
故答案为:240。
【点评】本题考查的是有关质数、合数以及2、3、5的倍数的特征,关键是要理解一个数同时是2和5的倍数,则这个数的个位一定是0。
10.见试题解答内容
【分析】根据最大公约数和最小公倍数的意义可知;最大公约数是两个数的公有的质因数的乘积,最小公倍数是两个数共有的质因数和各自独有的质因数的乘积,如果自然数C是B的5倍,B和C是倍数关系,据此解答.
【解析】解:自然数C是B的5倍,则B与C的最小公倍数是C.
故答案为:C.
【点评】主要考查倍数关系的最大公约数和最小公倍数的求法:较大的数是两个数的最小公倍数,较小的数是两个数的最大公约数.
11.,。
【分析】根据除法的意义,用5米除以8可得出每段的长度,把这根绳子的长度看作单位“1”,根据求一个数是另一个数的几分之几,用除法计算。
【解析】解:5÷8(米)
1÷8
答:每段长m,第三段占全长的。
故答案为:,。
【点评】本题考查的是分数意义的运用,找到题目中的单位“1”是解答本题的关键。
12.见试题解答内容
【分析】物体体积指物体所占空间的大小,物体容积指物体可以容纳物体的多少,所以只有杯子有容积,水不能说容积.这里杯子容纳的是水,所以杯子的容积等于杯中水的体积.
【解析】解:杯子中装满水,水的体积就是杯子的容积.
故答案为:水;杯子.
【点评】本题关键是了解物体体积和容积的区别与联系.
13.立方厘米,升。
【分析】根据生活经验以及数据的大小,选择合适的计量单位,即可解答。
【解析】解:一本数学书的体积约380立方厘米。
一桶食用油的容积约5升。
故答案为:立方厘米,升。
【点评】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
14.见试题解答内容
【分析】(1)根据分数的意义,分子是几,它的分数单位就是几分之一;
(2)最小的合数是4,求出4与的差,看差里含有几个,就是再添上 几个这样的分数单位等于最小的合数,据此解答.
【解析】解:(1)的分子是4,所以它的分数单位是;
(2)4,里含有24个;
故答案为:,24.
【点评】本题主要考查分数的意义和合数的意义,注意最小的合数是4.
15.见试题解答内容
【分析】最小的质数是2,同时是2和3的倍数,所以一个两位,这个数是24,据此解答.
【解析】解:一个两位数同时是2和3的倍数,十位上的数是最小的质数,这个两位数是24.
故答案为:24.
【点评】此题考查能同时被2、3整除的数的特征的运用及最小的质数.
16.见试题解答内容
【分析】先计算出分子增加10后,扩大了多少倍,再使分母扩大相同的倍数,得到新的分母,用新分母减去原分母,就是需要增加的.
【解析】解:因为的分子增加10,变成了10+5=15,
扩大了15÷5=3倍,
要使分数的大小不变,分母也应该扩大3倍,
即变成9×3=27,
分母应增加27﹣9=18;
故答案为:18.
【点评】此题主要考查分数的基本性质,即分数的分子和分母同时乘上或除以相同的数(0除外),分数的大小不变.
17.15。
【分析】每6支装一个盒子还剩3支,如果每4支装一个盒子也剩3支,可得这些笔的支数减3即是4和6的公倍数,要求至少买来了多少支,即是求4和6的最小公倍数再加3。
【解析】解:4=2×2
6=2×3
4和6的最小公倍数是2×2×3=12
12+3=15(支)
答:杨老师至少买来了15支笔。
故答案为:15。
【点评】本题主要考查了公倍数应用题,关键是得出4和6的最小公倍数。
18.4,29,2。
【分析】根据偶数与奇数,质数与合数的意义:是2的倍数的数叫做偶数;不是2的倍数的数叫做奇数;一个自然数,如果只有1和它本身两个因数,这样的数叫做质数;一个自然数,如果除了1和它本身还有别的因数,这样的数叫做合数;由此解答。
【解析】解:在1﹣30的自然数中,最小的合数是4,最大的质数是29。2既是偶数又是质数。
故答案为:4,29,2。
【点评】此题的解答关键是明确偶与奇数、质数与合数的概念及意义。
19.见试题解答内容
【分析】分解质因数就是把一个合数写成几个质数相乘的形式,一般先从较小的质数试着分解.
【解析】解:56=2×2×2×7
故答案为:2×2×2×7.
【点评】此题主要考查分解质因数的方法及其应用.一般先从较小的质数试着分解.
20.见试题解答内容
【分析】(1)根据最大公约数的意义,最大公约数就是A和B公约数中最大的一个,即最大公约数是A和B都含有的质因数的乘积,所得的积就是它们的最大公约数;
(2)根据最小公倍数的意义,最小公数就是A和B公倍数中最小的一个,即最小公倍数是A和B都含有的质因数的乘积,再乘上A和B独自含有的质因数,所得的积就是它们的最小公倍数.
【解析】解:(1)由A=2×3×5,B=2×3×7,可知A和B都含有的质因数是2和3,所以A和B的最大公约数是:2×3=6;
(2)由A=2×3×5,B=2×3×7,可知A和B都含有的质因数是2和3,A独自含有的质因数是5,B独自含有的质因数是7,所以A和B的最小公倍数是:2×7×3×5=210;
故答案为:6,210.
【点评】本题主要考查最大公因数和最小公倍数的意义.注意最大公约数是两个数都含有的约数的乘积,最小公倍数是两个数都含有的质因数的乘积,再乘上独自含有的质因数.
三.判断题(共5小题,共5分)
21.√
【分析】根据约分和通分的定义可以知道,它们都是利用了分数的基本性质将分数进行通分和约分的,所以没改变分数值的大小,由此判断即可。
【解析】解:根据分数的基本性质可知:约分只改变分数分子和分母的大小,没改变分数值的大小,所以原说法是正确的。
故答案为:√。
【点评】此题属于分数性质的运用,即通分和约分,都不会改变分数的大小。
22.√
【分析】表示把单位“1”平均分成4份,每份是,取其中的3份,表示把单位“1”平均分成8份,每份是,取其中的6份,二者意义不相同;根据分数的基本性质,的分子、分母都乘2就是,二者大小相等。
【解析】解:和的意义不相同,但大小相等。
原题说法正确。
故答案为:√。
【点评】此题考查的知识点:分数的意义、分数的大小比较、分数的基本性质。
23.×
【分析】把这条绳子的长度看作单位“1”,把它平均分成5份,每份占全长的,第一段占全长的,即占3份,第二段占2份,不论第二段有多长,这占的份数比第一段少,因此,这两段绳子相比,第一段绳子长。
【解析】解:第一段占全长的,即占3份,第二段占2份,
3份>2份
答:这两段绳子相比,第一段绳子长。
故答案为:×。
【点评】只比较两段绳子长各占全长的几分之几即可比较出哪段长,与第二段的长度无关。
24.√
【分析】正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,因为两个正方体的表面积相等,则每个面的面积相等,也就可以判定棱长相等,所以体积也相等.
【解析】解:因为两个正方体的表面积相等,
则每个面的面积相等,
也就可以判定棱长相等,
所以体积也相等,所以原题说法正确.
故答案为:√.
【点评】此题主要考查正方体表面积和体积公式的灵活应用以及正方体的特点.
25.×
【分析】要注意,只有在除法算式中,除数和被除数都是整数的情况下才能讨论倍数和约数的概念。
【解析】解:因为7÷1.4=5,所以1.4和5是7的因数,说法错误,因为1.4是小数。
故答案为:×。
【点评】此题是基本概念问题,主要考查约数与倍数的意义,倍数和约数两者都只能是整数,不能是小数。
四.计算题(共3小题,共26分)
26.2;;;;;;;。
【分析】根据异分母分数加减法的运算法则,先通分,再计算,结果化成最简分数或整数。
【解析】解:
2
【点评】本题主要考查分数加减法的运算,关键培养学生的运算能力。
27.x=25;t=31;y=400。
【分析】3x+2x=125合并未知数得5x=125,两边同时除以5,方程得解;
4t﹣26=98,等式两边同时加26再除以4,方程得解;
y÷8=50,等式两边同时乘8,方程得解。
【解析】解:3x+2x=125
5x=125
5x÷5=125÷5
x=25
4t﹣26=98
4t﹣26+26=98+26
4t÷4=124÷4
t=31
y÷8=50
y÷8×8=50×8
y=400
【点评】本题主要考查整数方程求解,关键利用等式的基本性质解答。
28.;;。
【分析】(1)利用加法交换律简便计算;
(2)先计算括号里面的分数加法,再计算括号外面的分数减法;
(3)利用加法交换律和加法结合律简便计算。
【解析】解:(1)
(2)
(3)
【点评】本题主要考查分数的四则混合运算。
五.操作题(共1小题,共6分)
29.
【分析】从前面看到3列小正方形,左右各1个,中间3个,下齐;从左面看到两列小正方形,左面2个,右面3个,下齐。
【解析】解:
【点评】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
六.应用题(共6小题,共36分)
30.18个。
【分析】要求这筐苹果至少有多少个,也就是求6和9的最小公倍数,即最小公倍数是6和9的公有质因数与独有质因数的连乘积。
【解析】解:6=2×3
9=3×3
所以6和9的最小公倍数是:2×3×3=18
答:这筐苹果至少有18个。
【点评】本题主要考查了利用求两个数的最小公倍数的方法解决生活中的实际问题。
31.。
【分析】根据题意可知,第一次烧掉全长的一半是把整根蜡烛看成单位“1”,则剩下的占整体的(1);第二次烧掉的是第一次剩下的一半,是把剩下的看成单位“1”,据此用乘法可求出第二次烧掉的分率;第一次烧掉的分率+第二次烧掉的分率=一共烧掉的分率,据此即可解答。
【解析】解:(1)
答:两次一共烧掉这根蜡烛的。
【点评】本题考查分数混合运算的应用,得到题目中的数量关系是关键。
32.。
【分析】根据题意,把这个花卉园的总面积看作“1”,用“1”减去种菊花占的分率,再减去种樱花占的分率,剩下的就是种梅花占的分率。
【解析】解:1
答:梅花占总面积的。
【点评】此题考查求剩余问题的应用题,用连减法计算;也可以用“1”减去种樱花与种菊花占的分率和。
33.60千米。
【分析】设客车每小时行x千米,依据货车的速度×相遇时间+相遇时客车行驶的路程=总路程,列方程解答即可。
【解析】解:设货车平均每小时行x千米。
3x+270=450
3x=180
x=60
答:货车平均每小时行60千米。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题。
34.1149千克。
【分析】根据倍数关系,先用350乘3求出普通水稻亩产量的3倍是多少,然后再加上99千克即可。
【解析】解:350×3+99
=1050+99
=1149(千克)
答:“超优千号”水稻亩产量是1149千克。
【点评】本题解答依据是:求一个数的几倍是多少,用乘法计算。
35.45元。
【分析】根据题意,这道题的等量关系是:每个篮球的钱数×5+每副乒乓球拍的钱数×8=付出的钱数﹣找回的钱数,根据这个等量关系,列方程解答。
【解析】解:设每副乒乓球拍x元。
75×5+8x=800﹣65
375+8x=735
8x=360
x=45
答:每副乒乓球拍45元。
【点评】本题考查列方程解应用题,解题关键是找出题目中的等量关系。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年五年级下学期数学期末综合素养培优卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题(共8小题,共8分)
1.把一张长方形纸对折,再对折……一共对折3次后,得到的小长方形纸的面积是a平方厘米,这张纸原来的面积是( )平方厘米。
A.4a B.8a C.12a D.16a
2.因为2+3=5,4+9=13,20+11=31,……,所以偶数与奇数的和一定是( )
A.质数 B.合数 C.奇数 D.偶数
3.《庄子 天下篇》中有一句话:“一尺之棰,日取其半,万世不竭。”意思就是:一根一尺长的木棒,第一天截取它的一半,第二天截取剩下的一半,第三天再截取剩下的一半……永远也截取不完。请问第三天截取的长度是这根木棒的( )
A. B. C. D.
4.王东用相同的小正方搭建几何体,如图是从上面看到的形状(上面的数字表示这个位置上小正方体的个数)。这个几何体正面看到的形状是( )
A. B. C. D.
5.在、、、、中,能化成有限小数或整数的有( )个。
A.2 B.3 C.4 D.5
6.小龙今年a岁,小飞今年(a﹣3)岁,再过b年,他们相差( )岁。
A.3 B.a﹣3 C.3b
7.把5克盐溶入50克水中,盐占盐水的( )
A. B. C. D.
8.下面的式子中,既不是方程,也不是等式的是( )
A.6x+5=17 B.x+6<27 C.46﹣9=37 D.5y=40
二.填空题(共12小题,共19分)
9.一个三位数的百位上是最小的质数,十位上是最小的合数,它还能同时被2,3,5整除,这个三位数是 。
10.如果自然数C是B的5倍,则B与C的最小公倍数是 .
11.把5m长的绳子平均分成8段,每段长 m,第三段占全长的 。
12.杯子中装满水, 的体积就是 的容积.(填“水”或“杯子”)
13.在括号里填上合适的单位。
一本数学书的体积约380 一桶食用油的容积约5
14.的分数单位是 ,它再添上 个这样的分数单位等于最小的合数.
15.一个两位数同时是2和3的倍数,十位上的数是最小的质数,这个两位数是 .
16.给的分子加上10,要使分数大小不变,分母应加上 .
17.临近期末,杨老师买来一些笔奖给优秀学生。如果每6支装一个盒子还剩3支,如果每4支装一个盒子也剩3支。杨老师至少买来了 支笔。
18.在1﹣30的自然数中,最小的合数是 ,最大的质数是 。 既是偶数又是质数。
19.把56写成质数相乘的形式是56= .
20.A=2×3×5,B=2×3×7.A和B的最大公因数是 ,最小公倍数是 .
三.判断题(共5小题,共5分)
21.约分会改变分子、分母的大小,但分数的大小不变。
22.和的意义不相同,但大小相等。
23.一根绳子剪成两段,第一段占全长的,第二段长m。两段绳子一样长。
24.表面积相等的两个正方体,它们的体积一定相等. .
25.因为7÷1.4=5,所以1.4和5是7的因数。
四.计算题(共3小题,共26分)
26.直接写得数。(共8分)
27.解方程。(最后一小题要写出检验过程)(共9分)
3x+2x=125 4t﹣26=98 y÷8=50
28.计算下面各题,能简算的要简算。(共9分)
五.操作题(共1小题,共6分)
29.用同样的小正方体搭成的几何体,从上面看到的图形如图(每个正方形上面的数字表示在这个位置上所用小正方体的个数)。请在方格图中分别画出从前面和左面看到的图形。
六.应用题(共6小题,共36分)
30.有一筐苹果,6个6个地数刚好数完,9个9个地数也刚好数完。这筐苹果至少有多少个?
31.一根蜡烛第一次烧掉全长的一半,第二次烧掉剩下的一半。两次一共烧掉了这根蜡烛的几分之几?
32.牛山寺公园新建的花卉园,要种菊花、樱花和梅花。菊花占总面积的,樱花占总面积的。梅花占总面积的几分之几?
33.甲、乙两地相距450km。一辆客车和一辆货车同时从甲、乙两地开出,相向而行,行驶3时两车相遇,这时客车行了270km。货车平均每时行多少千米?(用你喜欢的方法解)
34.我国上世纪60年代普通水稻亩产量是350kg,“杂交水稻之父”袁隆平在2015年培育成功的“超优千号”水稻,亩产量比普通水稻的3倍还多99kg,“超优千号”水稻亩产量是多少千克?
35.五(1)班买5个篮球和8副乒乓球拍,付出800元,找回65元。每个篮球75元,每副乒乓球拍多少元?(用你喜欢的方法解)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案与试题解析
一.选择题(共8小题,共8分)
1.B
【分析】把这张纸对折一次,每份是原来的,再对折,每份是原来的,对折三次,每份是原长的,就是这张纸的是a平方厘米,求这张纸的面积,是已知一个数的几分之几是多少,求这个数用除法计算。
【解析】解:a÷()
=a
=8a(平方厘米)
答:这张纸原来面积8a平方厘米。
故选:B。
【点评】解答此题的关键是明确:这张纸对折三次后的面积是原来的几分之几。
2.C
【分析】合数是在大于1的整数中,除了能被1和本身整除外,还能被其他数(0除外)整除的数;质数是一个自然数,只有1和它本身两个因数;偶数是在整数中,能被2整除的数;奇数是在整数中,不能被2整除的数。
【解析】解:设偶数为2a,奇数为2a+1。
2a+2a+1=4a+1,4a+1是奇数,所以偶数与奇数的和一定是奇数。
则因为2+3=5,4+9=13,20+11=31,……,所以偶数与奇数的和一定是奇数。
故选:C。
【点评】此题考查了奇数和偶数的初步认识,要求学生掌握。
3.D
【分析】把这根木棒的长度看作单位“1”,把它平均分成2份,每份是它的,取其中1份;再把取的这一份看作单位“1”,把它平均分成2份,每份是它的,取其中1份,这1份相当于原来这根木棒长度的的,即;再取其中1份,把它的长度看作单位“1”,把它平均分成2份,取其中1份,这1份相当于原来这根木棒长度的的,即。
【解析】解:如图:
第三天截取的长度是这根木棒的。
故选:D。
【点评】此题是考查分数的意义,把单位“1”平均分成若干份,用分数表示,分母是分成的份数,分子是要表示的份数。相当于把这根木棒平均分成2份、4份、8份……都取其中1份。
4.C
【分析】这个几何体正面看到的形状是三列小正方形,左面1个,中间合右面都是3个,下齐。
【解析】解:这个几何体正面看到的形状是。
故选:C。
【点评】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
5.C
【分析】首先,要把分数约分成最简分数,再根据一个最简分数,如果分母中除了2与5以外,不含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数。作出判断。
【解析】解:的分母中只含有质因数5,的分母中只含有质因数2,所以都能化成有限小数;
约分后是,可以化为整数3;约分后是,分母中含有质因数3,不能化成有限小数;
的分母中只含有质因数5,能化成有限小数。
所以能化成有限小数或整数的有一共有4个。
故选:C。
【点评】此题主要考查能化成有限小数的分数的特点。根据一个最简分数,如果分母中除了2与5以外,不含有其它的质因数,这个分数就能化成有限小数;如果分母中含有2与5以外的质因数,这个分数就不能化成有限小数。就能很快作出判断。
6.A
【分析】两个人之间年龄差始终不变,因此直接求出今年他们相差多少岁,即可求出过b年他们相差多少岁。
【解析】解:a﹣(a﹣3)
=a﹣a+3
=3(岁)
答:再过b年,他们相差3岁。
故选:A。
【点评】此题主要考查了两个人之间年龄差始终不变的知识点,要熟练掌握。
7.C
【分析】先求出盐水的总重量,然后用盐的重量除以盐水的总重量,求出盐占盐水的几分之几即可.
【解析】解:盐占盐水的:5÷(5+50)
=5÷55
.
故选:C.
【点评】本题属于基本的分数除法应用题,只要找出单位“1”,问题不难解决.
8.B
【分析】表示两个数或两个代数式相等关系的式子叫做等式;含有未知数的等式叫方程。
【解析】解:A.6x+5=17,是等式,且含有未知数,所以是方程;
B.x+6<27,既不是方程,也不是等式;
C.46﹣9=37,是等式,但不是方程;
D.5y=40,含有未知数,且是等式,是方程。
故选:B。
【点评】熟练掌握等式与方程的意义是解题的关键。
二.填空题(共12小题,共19分)
9.见试题解答内容
【分析】最小的质数是2,所以百位上是2,最小的合数是4,所以十位上是4,又知这个数既是2的倍数,又有因数3和5,则这个数同时是2、3、5的倍数,据此分析解答即可。
【解析】解:最小的质数是2,最小的合数是4,既是2的倍数又是5的倍数,个位是0,所以这个三位数是240。
故答案为:240。
【点评】本题考查的是有关质数、合数以及2、3、5的倍数的特征,关键是要理解一个数同时是2和5的倍数,则这个数的个位一定是0。
10.见试题解答内容
【分析】根据最大公约数和最小公倍数的意义可知;最大公约数是两个数的公有的质因数的乘积,最小公倍数是两个数共有的质因数和各自独有的质因数的乘积,如果自然数C是B的5倍,B和C是倍数关系,据此解答.
【解析】解:自然数C是B的5倍,则B与C的最小公倍数是C.
故答案为:C.
【点评】主要考查倍数关系的最大公约数和最小公倍数的求法:较大的数是两个数的最小公倍数,较小的数是两个数的最大公约数.
11.,。
【分析】根据除法的意义,用5米除以8可得出每段的长度,把这根绳子的长度看作单位“1”,根据求一个数是另一个数的几分之几,用除法计算。
【解析】解:5÷8(米)
1÷8
答:每段长m,第三段占全长的。
故答案为:,。
【点评】本题考查的是分数意义的运用,找到题目中的单位“1”是解答本题的关键。
12.见试题解答内容
【分析】物体体积指物体所占空间的大小,物体容积指物体可以容纳物体的多少,所以只有杯子有容积,水不能说容积.这里杯子容纳的是水,所以杯子的容积等于杯中水的体积.
【解析】解:杯子中装满水,水的体积就是杯子的容积.
故答案为:水;杯子.
【点评】本题关键是了解物体体积和容积的区别与联系.
13.立方厘米,升。
【分析】根据生活经验以及数据的大小,选择合适的计量单位,即可解答。
【解析】解:一本数学书的体积约380立方厘米。
一桶食用油的容积约5升。
故答案为:立方厘米,升。
【点评】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
14.见试题解答内容
【分析】(1)根据分数的意义,分子是几,它的分数单位就是几分之一;
(2)最小的合数是4,求出4与的差,看差里含有几个,就是再添上 几个这样的分数单位等于最小的合数,据此解答.
【解析】解:(1)的分子是4,所以它的分数单位是;
(2)4,里含有24个;
故答案为:,24.
【点评】本题主要考查分数的意义和合数的意义,注意最小的合数是4.
15.见试题解答内容
【分析】最小的质数是2,同时是2和3的倍数,所以一个两位,这个数是24,据此解答.
【解析】解:一个两位数同时是2和3的倍数,十位上的数是最小的质数,这个两位数是24.
故答案为:24.
【点评】此题考查能同时被2、3整除的数的特征的运用及最小的质数.
16.见试题解答内容
【分析】先计算出分子增加10后,扩大了多少倍,再使分母扩大相同的倍数,得到新的分母,用新分母减去原分母,就是需要增加的.
【解析】解:因为的分子增加10,变成了10+5=15,
扩大了15÷5=3倍,
要使分数的大小不变,分母也应该扩大3倍,
即变成9×3=27,
分母应增加27﹣9=18;
故答案为:18.
【点评】此题主要考查分数的基本性质,即分数的分子和分母同时乘上或除以相同的数(0除外),分数的大小不变.
17.15。
【分析】每6支装一个盒子还剩3支,如果每4支装一个盒子也剩3支,可得这些笔的支数减3即是4和6的公倍数,要求至少买来了多少支,即是求4和6的最小公倍数再加3。
【解析】解:4=2×2
6=2×3
4和6的最小公倍数是2×2×3=12
12+3=15(支)
答:杨老师至少买来了15支笔。
故答案为:15。
【点评】本题主要考查了公倍数应用题,关键是得出4和6的最小公倍数。
18.4,29,2。
【分析】根据偶数与奇数,质数与合数的意义:是2的倍数的数叫做偶数;不是2的倍数的数叫做奇数;一个自然数,如果只有1和它本身两个因数,这样的数叫做质数;一个自然数,如果除了1和它本身还有别的因数,这样的数叫做合数;由此解答。
【解析】解:在1﹣30的自然数中,最小的合数是4,最大的质数是29。2既是偶数又是质数。
故答案为:4,29,2。
【点评】此题的解答关键是明确偶与奇数、质数与合数的概念及意义。
19.见试题解答内容
【分析】分解质因数就是把一个合数写成几个质数相乘的形式,一般先从较小的质数试着分解.
【解析】解:56=2×2×2×7
故答案为:2×2×2×7.
【点评】此题主要考查分解质因数的方法及其应用.一般先从较小的质数试着分解.
20.见试题解答内容
【分析】(1)根据最大公约数的意义,最大公约数就是A和B公约数中最大的一个,即最大公约数是A和B都含有的质因数的乘积,所得的积就是它们的最大公约数;
(2)根据最小公倍数的意义,最小公数就是A和B公倍数中最小的一个,即最小公倍数是A和B都含有的质因数的乘积,再乘上A和B独自含有的质因数,所得的积就是它们的最小公倍数.
【解析】解:(1)由A=2×3×5,B=2×3×7,可知A和B都含有的质因数是2和3,所以A和B的最大公约数是:2×3=6;
(2)由A=2×3×5,B=2×3×7,可知A和B都含有的质因数是2和3,A独自含有的质因数是5,B独自含有的质因数是7,所以A和B的最小公倍数是:2×7×3×5=210;
故答案为:6,210.
【点评】本题主要考查最大公因数和最小公倍数的意义.注意最大公约数是两个数都含有的约数的乘积,最小公倍数是两个数都含有的质因数的乘积,再乘上独自含有的质因数.
三.判断题(共5小题,共5分)
21.√
【分析】根据约分和通分的定义可以知道,它们都是利用了分数的基本性质将分数进行通分和约分的,所以没改变分数值的大小,由此判断即可。
【解析】解:根据分数的基本性质可知:约分只改变分数分子和分母的大小,没改变分数值的大小,所以原说法是正确的。
故答案为:√。
【点评】此题属于分数性质的运用,即通分和约分,都不会改变分数的大小。
22.√
【分析】表示把单位“1”平均分成4份,每份是,取其中的3份,表示把单位“1”平均分成8份,每份是,取其中的6份,二者意义不相同;根据分数的基本性质,的分子、分母都乘2就是,二者大小相等。
【解析】解:和的意义不相同,但大小相等。
原题说法正确。
故答案为:√。
【点评】此题考查的知识点:分数的意义、分数的大小比较、分数的基本性质。
23.×
【分析】把这条绳子的长度看作单位“1”,把它平均分成5份,每份占全长的,第一段占全长的,即占3份,第二段占2份,不论第二段有多长,这占的份数比第一段少,因此,这两段绳子相比,第一段绳子长。
【解析】解:第一段占全长的,即占3份,第二段占2份,
3份>2份
答:这两段绳子相比,第一段绳子长。
故答案为:×。
【点评】只比较两段绳子长各占全长的几分之几即可比较出哪段长,与第二段的长度无关。
24.√
【分析】正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,因为两个正方体的表面积相等,则每个面的面积相等,也就可以判定棱长相等,所以体积也相等.
【解析】解:因为两个正方体的表面积相等,
则每个面的面积相等,
也就可以判定棱长相等,
所以体积也相等,所以原题说法正确.
故答案为:√.
【点评】此题主要考查正方体表面积和体积公式的灵活应用以及正方体的特点.
25.×
【分析】要注意,只有在除法算式中,除数和被除数都是整数的情况下才能讨论倍数和约数的概念。
【解析】解:因为7÷1.4=5,所以1.4和5是7的因数,说法错误,因为1.4是小数。
故答案为:×。
【点评】此题是基本概念问题,主要考查约数与倍数的意义,倍数和约数两者都只能是整数,不能是小数。
四.计算题(共3小题,共26分)
26.2;;;;;;;。
【分析】根据异分母分数加减法的运算法则,先通分,再计算,结果化成最简分数或整数。
【解析】解:
2
【点评】本题主要考查分数加减法的运算,关键培养学生的运算能力。
27.x=25;t=31;y=400。
【分析】3x+2x=125合并未知数得5x=125,两边同时除以5,方程得解;
4t﹣26=98,等式两边同时加26再除以4,方程得解;
y÷8=50,等式两边同时乘8,方程得解。
【解析】解:3x+2x=125
5x=125
5x÷5=125÷5
x=25
4t﹣26=98
4t﹣26+26=98+26
4t÷4=124÷4
t=31
y÷8=50
y÷8×8=50×8
y=400
【点评】本题主要考查整数方程求解,关键利用等式的基本性质解答。
28.;;。
【分析】(1)利用加法交换律简便计算;
(2)先计算括号里面的分数加法,再计算括号外面的分数减法;
(3)利用加法交换律和加法结合律简便计算。
【解析】解:(1)
(2)
(3)
【点评】本题主要考查分数的四则混合运算。
五.操作题(共1小题,共6分)
29.
【分析】从前面看到3列小正方形,左右各1个,中间3个,下齐;从左面看到两列小正方形,左面2个,右面3个,下齐。
【解析】解:
【点评】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
六.应用题(共6小题,共36分)
30.18个。
【分析】要求这筐苹果至少有多少个,也就是求6和9的最小公倍数,即最小公倍数是6和9的公有质因数与独有质因数的连乘积。
【解析】解:6=2×3
9=3×3
所以6和9的最小公倍数是:2×3×3=18
答:这筐苹果至少有18个。
【点评】本题主要考查了利用求两个数的最小公倍数的方法解决生活中的实际问题。
31.。
【分析】根据题意可知,第一次烧掉全长的一半是把整根蜡烛看成单位“1”,则剩下的占整体的(1);第二次烧掉的是第一次剩下的一半,是把剩下的看成单位“1”,据此用乘法可求出第二次烧掉的分率;第一次烧掉的分率+第二次烧掉的分率=一共烧掉的分率,据此即可解答。
【解析】解:(1)
答:两次一共烧掉这根蜡烛的。
【点评】本题考查分数混合运算的应用,得到题目中的数量关系是关键。
32.。
【分析】根据题意,把这个花卉园的总面积看作“1”,用“1”减去种菊花占的分率,再减去种樱花占的分率,剩下的就是种梅花占的分率。
【解析】解:1
答:梅花占总面积的。
【点评】此题考查求剩余问题的应用题,用连减法计算;也可以用“1”减去种樱花与种菊花占的分率和。
33.60千米。
【分析】设客车每小时行x千米,依据货车的速度×相遇时间+相遇时客车行驶的路程=总路程,列方程解答即可。
【解析】解:设货车平均每小时行x千米。
3x+270=450
3x=180
x=60
答:货车平均每小时行60千米。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题。
34.1149千克。
【分析】根据倍数关系,先用350乘3求出普通水稻亩产量的3倍是多少,然后再加上99千克即可。
【解析】解:350×3+99
=1050+99
=1149(千克)
答:“超优千号”水稻亩产量是1149千克。
【点评】本题解答依据是:求一个数的几倍是多少,用乘法计算。
35.45元。
【分析】根据题意,这道题的等量关系是:每个篮球的钱数×5+每副乒乓球拍的钱数×8=付出的钱数﹣找回的钱数,根据这个等量关系,列方程解答。
【解析】解:设每副乒乓球拍x元。
75×5+8x=800﹣65
375+8x=735
8x=360
x=45
答:每副乒乓球拍45元。
【点评】本题考查列方程解应用题,解题关键是找出题目中的等量关系。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
