人教版2025年小学四年级下学期数学期末复习专题分类强训:图形计算(附答案)
文档属性
| 名称 | 人教版2025年小学四年级下学期数学期末复习专题分类强训:图形计算(附答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 849.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-14 00:00:00 | ||
图片预览

文档简介
人教版2025年小学四年级下学期数学期末复习专题分类强训:图形计算(附答案)
学校:___________姓名:___________班级:___________
计算题
1.求图中阴影部分的面积。
2.计算下面图形中涂色部分的面积。(单位:厘米)
3.求出下面图形的周长。(单位:厘米)
4.分别计算下面每个三角形中未知角的度数。
5.计算下边这个图形的周长和面积。(每个小正方形的边长为1厘米、对角线长1.4厘米)
6.求出下面阴影部分图形的面积。
7.计算下面涂色部分的面积。
8.计算下面各图形的周长。(单位:cm)
9.求出阴影部分的面积。
10.求图中阴影部分的面积。(单位:米)
11.想一想,求出下面图形的周长。
12.计算图中涂色部分的面积。
13.计算正方形中阴影部分的面积。
14.计算如下图形的阴影部分面积。
15.如图,求出阴影部分图形的面积。
16.求下面图形的周长。
17.求三角形中∠1的度数。
18.如下图所示,求的度数。
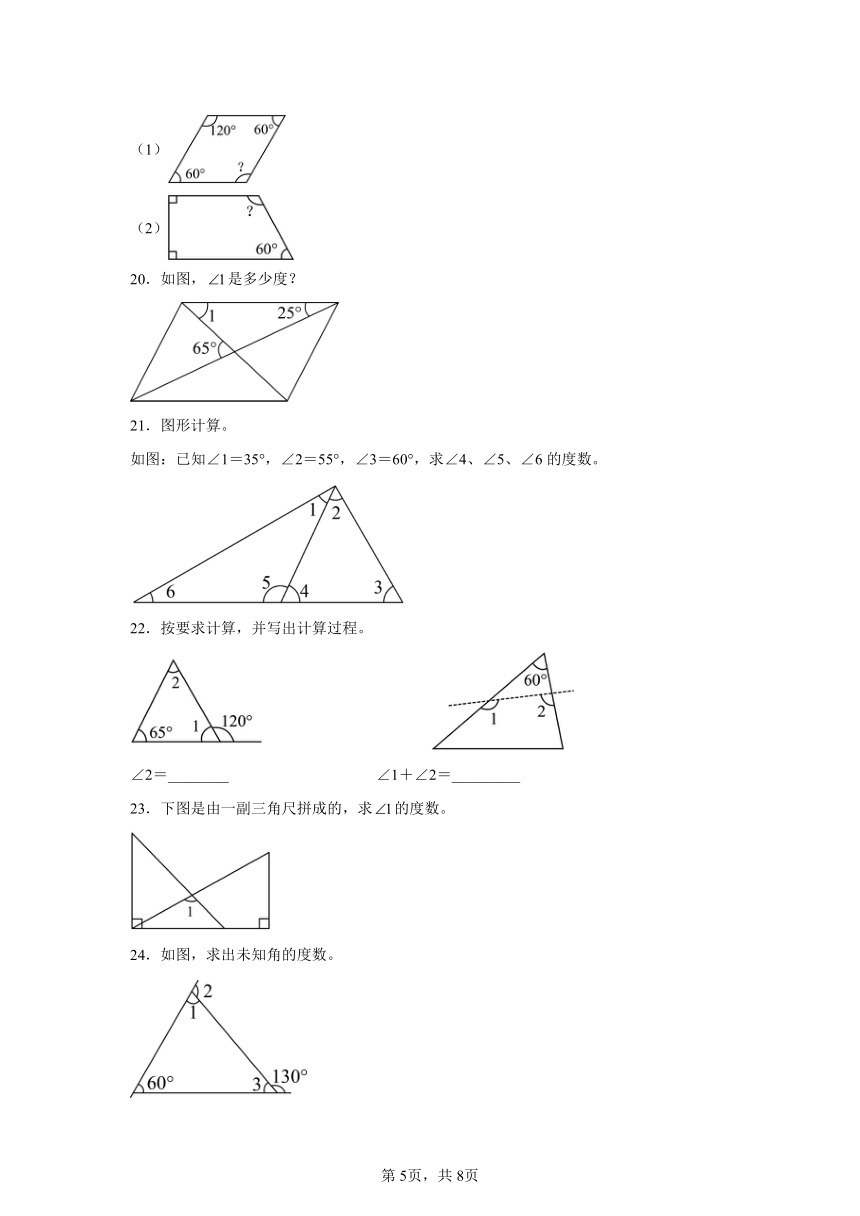
19.算出下面每个四边形中未知角的度数。
(1)
(2)
20.如图,是多少度?
21.图形计算。
如图:已知∠1=35°,∠2=55°,∠3=60°,求∠4、∠5、∠6的度数。
22.按要求计算,并写出计算过程。
∠2=________ ∠1+∠2=_________
23.下图是由一副三角尺拼成的,求的度数。
24.如图,求出未知角的度数。
25.求出下图中未知角的度数。
26.求的度数。
27.如图,,求,和的度数。
28.算一算。
已知,,,求,,。
29.如图,求∠1的度数。
30.如图所示,四边形ABCD中,∠A+∠C=160°,∠D是∠B的4倍,那么∠D和∠B分别是多少度?
31.列式计算算出下面各个未知角的度数。
32.如下图所示,一个等腰三角形,其中的一个底角∠1=45°,求顶角∠3=?
33.计算下面图形的周长。(单位:厘米)
(1) (2)
34.计算下面图形的周长和面积。
35.计算下面图形的周长。(单位:厘米)
36.求下边图形的面积。
37.计算如图形的面积。
38.用两种不同的方法计算下面图形的面积。
39.看图求面积。
第1页,共3页
第1页,共3页
参考答案
1.128平方厘米
【分析】
如图所示,将紫色线圈起来的阴影部分向下平移到空白半圆部分,此时阴影部分形成一个长方形,长方形的长是16厘米,宽8厘米,长方形面积=长×宽,据此解题。
【详解】16×8=128(平方厘米)
阴影部分的面积是128平方厘米。
2.16平方厘米
【分析】
涂色部分是4个直角三角形,如图所示,将其中的两个三角形进行平移,此时构成一个正方形,如图中红色正方形:正方形的边长是4个格子的长度,一个格子的长度是1厘米,正方形面积=边长×边长,据此解题。
【详解】4×4=16(平方厘米)
图形中涂色部分的面积是16平方厘米。
3.28厘米
【分析】
如图所示,按箭头所示将线段进行平移,此时图形可以变成一个边长是7厘米的长方形,长方形周长=边长×4,据此解题。
【详解】7×4=28(厘米)
图形的周长是28厘米。
4.38°;15°
【分析】根据三角形的内角和等于180°,第一个三角形为直角三角形,已知一个角的度数为52°,另一个角为直角,用180°减去这两个数,即可得到正确答案;第二个三角形为钝角三角形,且已知另外两个角的度数,用180°减去这两个数,即可解答此题。
【详解】180°-90°-52°
=90°-52°
=38°
180°-50°-115°
=130°-115°
=15°
5.周长19.6厘米;面积14平方厘米
【分析】图形周长是围这个图形一周的长度,有4条对角线和上下两条边围成,求和即可得出;面积是指这个图形表面大小,把这个图形右边的三角形平移到左边拼成一个长方形,根据长方形面积=长×宽计算,这里长是7厘米,宽是2厘米。
【详解】4×1.4+7×2
=5.6+14
=19.6(厘米)
7×2=14(平方厘米)
这个图形周长19.6厘米;面积14平方厘米。
6.8平方厘米
【分析】通过平移,将图中的一大一小两个阴影部分移到一个小正方形中,最终阴影部分合成了两个小正方形,面积是大正方形面积的一半,根据“正方形的面积=边长×边长”,再用大正方形的面积除以2,即可得到阴影部分图形的面积。
【详解】4×4÷2
=16÷2
=8(平方厘米)
阴影部分图形的面积为8平方厘米。
7.8 cm2
【分析】观察发现,图中4格的长度为4cm,那么每格的边长为1cm;将最右边两列中的阴影部分,平移到最左边,可以将阴影部分看作一个长4cm、宽2cm的长方形,长方形的面积=长×宽;据此解答。
【详解】4÷2=2(cm)
4×2=8(cm2)
所以涂色部分的面积为8 cm2。
8.左图:86厘米
右图:16厘米
【分析】封闭图形一周的长度叫做周长,左边的图是三角形,三角形周长就是围成三角形的三边的长度之和;右边的图形是不规则图形,我们可以将不规则图形通过边的平移转化为学过的规则图形,据此解答。
【详解】(1)
(厘米)
三角形的周长是86厘米。
(2)平移后转化为正方形:
(厘米)
图形的周长是16厘米。
9.24cm2
【分析】首先将左边阴影部分的半圆形进行切割,再通过平移的方法,将左边阴影部分的半圆形平移到右边空白部分的半圆形,这样不规则图形转化成了一个长6cm,宽4cm的长方形,根据长方形的面积=长×宽,代入数据计算即可解答。
【详解】6×4=24(cm2)
阴影部分的面积是24cm2。
10.4平方米
【分析】由图可知,阴影部分由两部分组成。直接将右下角的阴影部分平移到左上角即可得到一个边长为2米的正方形。正方形的面积=边长×边长,直接将数据代入即可求出它的面积。
【详解】2×2=4(平方米)
图中阴影部分的面积为4平方米。
11.30cm
【分析】如图:
通过平移可以将这个图形看作一个长10cm、宽5cm的长方形,长方形的周长=(长+宽)×2;据此解答。
【详解】(10+5)×2
=15×2
=30(cm)
所以图形的周长为30cm。
12.8平方厘米
【分析】通过观察图形可知,把上面的部分向下平移,拼成一个长4厘米,宽2厘米的长方形,根据长方形的面积=长×宽,把数据代入公式解答。
【详解】4×2=8(平方厘米)
图中涂色部分的面积是8平方厘米。
13.32平方分米
【分析】将上方的三角形平移到下方,这样就可以判断阴影部分所占的面积是正方形的一半,也就是下面长方形的面积,根据长方形的面积=长×宽,以此答题即可。
【详解】根据分析可知:
8×4=32(平方分米)
阴影部分的面积是32平方分米。
14.100cm2
【分析】如下图,把右边阴影向左平移到如箭头所示的空白处,这样阴影部分组合成一个边长为10cm的正方形;根据正方形的面积=边长×边长,代入数据计算,即可求出阴影部分的面积。
【详解】10×10=100(cm2)
阴影部分面积是100cm2。
15.8×2=16(cm2)
【分析】根据题意,仔细观察,通过平移,将图中的最右边的阴影半圆部分平移到最左边的半圆部分,把上面的阴影三角形平移到下边的三角形空白部分合成了1个长方形,数出长方形的长有8厘米,宽有2厘米,根据“长方形的面积=长×宽”,即可得到阴影部分图形的面积。以此答题即可。
【详解】根据分析可知:
8×2=16(平方厘米)
阴影部分图形的面积16平方厘米。
16.30米
【分析】图形的周长是由组成这个图形线段长度相加得到的,据此解答。如图是一个不规则图形,可利用平移法将它拼成一个长方形再利用长方形周长的计算公式解答。
【详解】
(7.1+2.2+5.7)×2
=15×2
=30(米)
答:这个图形的周长是30米。
【点睛】本题主要考查求不规则图形周长的简便方法以及小数加减法的计算,理解并熟练运用小数的加减法法则是解决本题的关键。
17.60°;15°;38°
【分析】三角形内角和为180°,据此解答。
(1)已知两个角分别为58°,62°,求第三个角,用减法计算;
(2)已知两个角分别为150°,15°,求第三个角,用减法计算;
(3)已知两个角分别为90°,52°,求第三个角,用减法计算;
【详解】(1)∠1=180°-58°-62°
=180°-120°
=60°
(2)∠1=180°-150°-15°
=30°-15°
=15°
(3)∠1=180°-90°-52°
=90°-52°
=38°
18.80°
【分析】四边形的内角和为360°。图中四边形一共有四个角,有1个直角,直角的度数为90°。可以先算出给出的三个角的度数之和,再用360°减去这三个角的度数之和即可得到剩下的那个角的度数,再用180°减去这个角度,就求出了∠1的度数。
【详解】90°+55°+115°=260°
360°-260°=100°
180°-100°=80°
∠1的度数是80°
19.(1)120°
(2)120°
【分析】根据四边形的内角和为360°,用360°分别减去另外的三个内角即可求出未知角的度数。
【详解】(1)360°-120°-60°-60°=120°
(2)360°-90°-90°-60°=120°
20.∠1=40°
【分析】1平角=180°,和65°相邻的右侧的钝角的度数是180°减65°的差,这个钝角是115°,三角形的内角和是180°,180°减115°,再减25°,即可求出∠1的度数。
【详解】180°-65°=115°
180°-115°-25°
=65°-25°
=40°
∠1=40°
21.∠4=65°;∠5=115°;∠6=30°
【分析】三角形的内角和是180°。
(1)∠2、∠3和∠4组成了一个三角形,所以∠4=180°-∠2-∠3。
(2)∠5和∠4组成了一个平角,1平角=180°,所以∠5=180°-∠4。
(3)∠1、∠5和∠6组成了一个三角形,所以∠6=180°-∠1-∠5,据此解答。
【详解】∠4=180°-∠2-∠3
=180°-55°-60°
=125°-60°
=65°
∠5=180°-∠4=180°-65°=115°
∠6=180°-∠1-∠5
=180°-35°-115°
=145°-115°
=30°
答:∠4的度数是65°,∠5的度数是115°,∠6的度数是30°。
22.55°;240°
【分析】
如图: ∠1和120°的角拼成一个平角,平角=180°,则∠1=180°-120°。三角形内角和等于180°,180°减去∠1的度数,再减去65°,即可算出∠2的度数;
如图:三角形内角和等于180°,则∠3+∠4=180°-60°。四边形的内角和是360°,则∠1+∠2=360°-(∠3+∠4)=360°-(180°-60°)。
【详解】∠2=180°-65°-(180°-120°)
=180°-65°-60°
=115°-60°
=55°
∠1+∠2=360°-(180°-60°)
=360°-120°
=240°
23.105°
【分析】一副三角板有两个三角尺,一个三角尺的三个角的度数分别为:90°、45°、45°,另一个三角尺的三个角的度数分别为:90°、30°、60°。图中∠1与一个45°角、一个30°角在同一个三角形内,根据三角形的内角和是180°,用180°减去45°再减去30°即可求解。
【详解】180°-45°-30°
=135°-30°
=105°
∠1的度数为105°。
24.∠1=70°;∠2=110°;∠3=50°
【分析】根据平角=180°,三角形三个内角度数和是180°;从图中可知:∠3与130°角组成平角,一共是180°,则用180°减130°即可求到∠3的度数;又因∠1、∠3和60°角是三角形的三个内角,三角形的内角和是180°,则用180°减去60°和∠3的度数,即可求到∠1的度数;又因∠1和∠2组成平角,一共是180°,则用180°减∠1的度数即可求到∠2的度数。据此解答。
【详解】∠3=180°-130°=50°
∠1=180°-60°-50°
=120°-50°
=70°
∠2=180°-70°=110°
所以,∠1=70°;∠2=110°;∠3=50°。
25.135°
【分析】四边形的内角和等于360°,已知四边形中三个角的度数,用四边形的内角和减去已知的三个角可得剩下的角的度数。
【详解】360°-90°-65°-70°
=270°-65°-70°
=205°-70°
=135°
即图中未知角的度数是135°。
26.
【分析】根据三角形内角和为,首先求出与相邻的角的度数,,再用平角减去这个角就是的度数。
【详解】
即的度数是。
27.60°;30°;60°
【分析】1直角=90°,三角形的内角和等于180°;
根据题意可知,如图:∠1和∠2组成一个直角,则∠2=90°-∠1;∠2、∠3和∠5在一个三角形内,则∠2+∠3+∠5=180°,所以∠3=180°-90°-∠2;∠3和∠4组成一个直角,则∠4=90°-∠3;据此解答。
【详解】∠2=90°-30°=60°;
∠3=180°-90°-60°=90°-60°=30°;
∠4=90°-30°=60°;
即∠2=60°,∠3=30°,∠4=60°。
28.∠4=105°;∠5=75°;∠6=95°
【分析】平角为180°,三角形内角和为180°,观察图可以发现,∠1、∠3和∠4组成三角形的内角和,用180°依次减去∠1、∠3,即可求出∠4。∠4和∠5组成平角,用180°减去∠4,即可求出∠5。∠5、∠2和∠6组成三角形的内角和,用180°依次减去∠2、∠5,即可求出∠6。
【详解】∠4=180°-30°-45°
=150°-45°
=105°
∠5=180°-105°=75°
∠6=180°-10°-75°
=170°-75°
=95°
即∠4=105°,∠5=75°,∠6=95°。
29.100°
【分析】
140°角和∠2组成1个平角,平角等于180°,用180°-140°=40°,求出∠2的度数,再根据三角形内角和等于180°,用180°-40°-40° ,即可求出∠1的度数。
【详解】180°-140°=40°
180°-40°-40°
=140°-40°
=100°
30.160°;40°
【分析】根据四边形内角和定理,四边形ABCD的内角和为360°,即∠A+∠B+∠C+∠ D=360°,已知∠A+∠C=160°,求∠B+∠D的度数用360°减去∠A和∠C的度数和;求∠B的度数,因为∠D是∠B的4倍,∠D的度数是4×∠B,∠B+∠D的度数和就是∠B度数的(1+4)倍,用除法可以算出∠B的度数,最后根据∠D是∠B的4倍,用乘法算出∠D的度数。
【详解】∠B=(360°-160°)÷(1+4)
=200°÷5
=40°
∠D=4×40°=160°
所以∠D=160°,∠B=40°。
31.78°;60°
【分析】根据三角形内角和是180°和图中给出的度数,用180°减去三角形的两个已知角度,可以求得未知角的度数。
【详解】根据分析可知:
180°-(65°+37°)
=180°-102°
= 78°
图一的未知角的度数是 78°。
180°-(90°+30°)
=180°-120°
= 60°
图二的未知角的度数是 60°。
32.90°
【分析】三角形的内角和为180°。在等腰三角形中,两个底角相等。由题意得,等腰三角形的一个底角是45°,那么另一个底角的度数也是45°,直接用180°减去两个底角的度数即可算出顶角的度数。
【详解】180°-45°-45°
=135°-45°
=90°
即顶角∠3=90°。
33.(1)131厘米
(2)170厘米
【详解】31+43+57
=31+(43+57)
=31+100
=131(厘米)
19+43+51+57
=(19+51)+(43+57)
=170(厘米)
34.276m,3800m2
【分析】周长就是封闭图形一周的长度,题图是一个不规则图形,通过观察不难发现这个不规则图形的周长与长、宽的长方形的周长相等,所以可以转换为求长方形的周长。不规则图形的面积没办法直接求,但是可以分割成两个长方形(一个长、宽,一个长、宽),把这两个长方形的面积相加即为所求。
【详解】周长:
(75+38+25)×2
=138×2
=276(m)
面积:
75×38+25×38
=(75+25)×38
=100×38
=3800(m2)
35.131厘米;170厘米;
【分析】封闭图形一周的长度是这个图形的周长,因此将每个图形中的每条边的长度加起来即可,依此列式并根据加法结合律的特点进行计算。
【详解】31+43+57
=31+(43+57)
=31+100
=131(厘米)
19+51+43+57
=(19+51)+(43+57)
=70+100
=170(厘米)
36.14平方厘米
【分析】长方形的面积=长×宽,因此可将这两个长方形的面积加起来即可解答,依此列式并根据乘法分配律的特点进行简算即可。
【详解】4×2+3×2
=(4+3)×2
=7×2
=14(平方厘米)
37.320平方米
【分析】通过切割法来求面积,即把一个不规则图形分割成几个规则图形,图形的面积等于长23m,宽8m的长方形面积加长17m,宽8m的长方形的面积,根据长方形的面积=长×宽,解答即可。
【详解】
(平方米)
图形的面积是320平方米。
38.360平方米;方法见详解
【分析】把这个图形分成两个长方形(不同的分法得到的两个长方形不同。),分别计算出两个长方形的面积,相加就是这个图形的面积。(方法不唯一)长方形的面积=长×宽。在计算过程中可用到乘法分配律使计算简便。
【详解】
方法一:21×9+19×9
=(21+19)×9
=40×9
=360(平方米)
方法二:(9+19)×9+(21-9)×9
=28×9+12×9
=(28+12)×9
=40×9
=360(平方米)
39.800cm2
【分析】首先用分割法把图形分割成两个长方形,一个长方形的长是20厘米,宽是10厘米,另一个长方形的长是20+10=30厘米,宽是20厘米,根据长方形的面积=长×宽,分别计算出所分割的图形的面积,再把分割图形的面积相加,即可解答。
【详解】20×10+(20+10)×20
=20×10+30×20
=200+30×20
=200+600
=800(cm2)
第1页,共2页
第1页,共2页
学校:___________姓名:___________班级:___________
计算题
1.求图中阴影部分的面积。
2.计算下面图形中涂色部分的面积。(单位:厘米)
3.求出下面图形的周长。(单位:厘米)
4.分别计算下面每个三角形中未知角的度数。
5.计算下边这个图形的周长和面积。(每个小正方形的边长为1厘米、对角线长1.4厘米)
6.求出下面阴影部分图形的面积。
7.计算下面涂色部分的面积。
8.计算下面各图形的周长。(单位:cm)
9.求出阴影部分的面积。
10.求图中阴影部分的面积。(单位:米)
11.想一想,求出下面图形的周长。
12.计算图中涂色部分的面积。
13.计算正方形中阴影部分的面积。
14.计算如下图形的阴影部分面积。
15.如图,求出阴影部分图形的面积。
16.求下面图形的周长。
17.求三角形中∠1的度数。
18.如下图所示,求的度数。
19.算出下面每个四边形中未知角的度数。
(1)
(2)
20.如图,是多少度?
21.图形计算。
如图:已知∠1=35°,∠2=55°,∠3=60°,求∠4、∠5、∠6的度数。
22.按要求计算,并写出计算过程。
∠2=________ ∠1+∠2=_________
23.下图是由一副三角尺拼成的,求的度数。
24.如图,求出未知角的度数。
25.求出下图中未知角的度数。
26.求的度数。
27.如图,,求,和的度数。
28.算一算。
已知,,,求,,。
29.如图,求∠1的度数。
30.如图所示,四边形ABCD中,∠A+∠C=160°,∠D是∠B的4倍,那么∠D和∠B分别是多少度?
31.列式计算算出下面各个未知角的度数。
32.如下图所示,一个等腰三角形,其中的一个底角∠1=45°,求顶角∠3=?
33.计算下面图形的周长。(单位:厘米)
(1) (2)
34.计算下面图形的周长和面积。
35.计算下面图形的周长。(单位:厘米)
36.求下边图形的面积。
37.计算如图形的面积。
38.用两种不同的方法计算下面图形的面积。
39.看图求面积。
第1页,共3页
第1页,共3页
参考答案
1.128平方厘米
【分析】
如图所示,将紫色线圈起来的阴影部分向下平移到空白半圆部分,此时阴影部分形成一个长方形,长方形的长是16厘米,宽8厘米,长方形面积=长×宽,据此解题。
【详解】16×8=128(平方厘米)
阴影部分的面积是128平方厘米。
2.16平方厘米
【分析】
涂色部分是4个直角三角形,如图所示,将其中的两个三角形进行平移,此时构成一个正方形,如图中红色正方形:正方形的边长是4个格子的长度,一个格子的长度是1厘米,正方形面积=边长×边长,据此解题。
【详解】4×4=16(平方厘米)
图形中涂色部分的面积是16平方厘米。
3.28厘米
【分析】
如图所示,按箭头所示将线段进行平移,此时图形可以变成一个边长是7厘米的长方形,长方形周长=边长×4,据此解题。
【详解】7×4=28(厘米)
图形的周长是28厘米。
4.38°;15°
【分析】根据三角形的内角和等于180°,第一个三角形为直角三角形,已知一个角的度数为52°,另一个角为直角,用180°减去这两个数,即可得到正确答案;第二个三角形为钝角三角形,且已知另外两个角的度数,用180°减去这两个数,即可解答此题。
【详解】180°-90°-52°
=90°-52°
=38°
180°-50°-115°
=130°-115°
=15°
5.周长19.6厘米;面积14平方厘米
【分析】图形周长是围这个图形一周的长度,有4条对角线和上下两条边围成,求和即可得出;面积是指这个图形表面大小,把这个图形右边的三角形平移到左边拼成一个长方形,根据长方形面积=长×宽计算,这里长是7厘米,宽是2厘米。
【详解】4×1.4+7×2
=5.6+14
=19.6(厘米)
7×2=14(平方厘米)
这个图形周长19.6厘米;面积14平方厘米。
6.8平方厘米
【分析】通过平移,将图中的一大一小两个阴影部分移到一个小正方形中,最终阴影部分合成了两个小正方形,面积是大正方形面积的一半,根据“正方形的面积=边长×边长”,再用大正方形的面积除以2,即可得到阴影部分图形的面积。
【详解】4×4÷2
=16÷2
=8(平方厘米)
阴影部分图形的面积为8平方厘米。
7.8 cm2
【分析】观察发现,图中4格的长度为4cm,那么每格的边长为1cm;将最右边两列中的阴影部分,平移到最左边,可以将阴影部分看作一个长4cm、宽2cm的长方形,长方形的面积=长×宽;据此解答。
【详解】4÷2=2(cm)
4×2=8(cm2)
所以涂色部分的面积为8 cm2。
8.左图:86厘米
右图:16厘米
【分析】封闭图形一周的长度叫做周长,左边的图是三角形,三角形周长就是围成三角形的三边的长度之和;右边的图形是不规则图形,我们可以将不规则图形通过边的平移转化为学过的规则图形,据此解答。
【详解】(1)
(厘米)
三角形的周长是86厘米。
(2)平移后转化为正方形:
(厘米)
图形的周长是16厘米。
9.24cm2
【分析】首先将左边阴影部分的半圆形进行切割,再通过平移的方法,将左边阴影部分的半圆形平移到右边空白部分的半圆形,这样不规则图形转化成了一个长6cm,宽4cm的长方形,根据长方形的面积=长×宽,代入数据计算即可解答。
【详解】6×4=24(cm2)
阴影部分的面积是24cm2。
10.4平方米
【分析】由图可知,阴影部分由两部分组成。直接将右下角的阴影部分平移到左上角即可得到一个边长为2米的正方形。正方形的面积=边长×边长,直接将数据代入即可求出它的面积。
【详解】2×2=4(平方米)
图中阴影部分的面积为4平方米。
11.30cm
【分析】如图:
通过平移可以将这个图形看作一个长10cm、宽5cm的长方形,长方形的周长=(长+宽)×2;据此解答。
【详解】(10+5)×2
=15×2
=30(cm)
所以图形的周长为30cm。
12.8平方厘米
【分析】通过观察图形可知,把上面的部分向下平移,拼成一个长4厘米,宽2厘米的长方形,根据长方形的面积=长×宽,把数据代入公式解答。
【详解】4×2=8(平方厘米)
图中涂色部分的面积是8平方厘米。
13.32平方分米
【分析】将上方的三角形平移到下方,这样就可以判断阴影部分所占的面积是正方形的一半,也就是下面长方形的面积,根据长方形的面积=长×宽,以此答题即可。
【详解】根据分析可知:
8×4=32(平方分米)
阴影部分的面积是32平方分米。
14.100cm2
【分析】如下图,把右边阴影向左平移到如箭头所示的空白处,这样阴影部分组合成一个边长为10cm的正方形;根据正方形的面积=边长×边长,代入数据计算,即可求出阴影部分的面积。
【详解】10×10=100(cm2)
阴影部分面积是100cm2。
15.8×2=16(cm2)
【分析】根据题意,仔细观察,通过平移,将图中的最右边的阴影半圆部分平移到最左边的半圆部分,把上面的阴影三角形平移到下边的三角形空白部分合成了1个长方形,数出长方形的长有8厘米,宽有2厘米,根据“长方形的面积=长×宽”,即可得到阴影部分图形的面积。以此答题即可。
【详解】根据分析可知:
8×2=16(平方厘米)
阴影部分图形的面积16平方厘米。
16.30米
【分析】图形的周长是由组成这个图形线段长度相加得到的,据此解答。如图是一个不规则图形,可利用平移法将它拼成一个长方形再利用长方形周长的计算公式解答。
【详解】
(7.1+2.2+5.7)×2
=15×2
=30(米)
答:这个图形的周长是30米。
【点睛】本题主要考查求不规则图形周长的简便方法以及小数加减法的计算,理解并熟练运用小数的加减法法则是解决本题的关键。
17.60°;15°;38°
【分析】三角形内角和为180°,据此解答。
(1)已知两个角分别为58°,62°,求第三个角,用减法计算;
(2)已知两个角分别为150°,15°,求第三个角,用减法计算;
(3)已知两个角分别为90°,52°,求第三个角,用减法计算;
【详解】(1)∠1=180°-58°-62°
=180°-120°
=60°
(2)∠1=180°-150°-15°
=30°-15°
=15°
(3)∠1=180°-90°-52°
=90°-52°
=38°
18.80°
【分析】四边形的内角和为360°。图中四边形一共有四个角,有1个直角,直角的度数为90°。可以先算出给出的三个角的度数之和,再用360°减去这三个角的度数之和即可得到剩下的那个角的度数,再用180°减去这个角度,就求出了∠1的度数。
【详解】90°+55°+115°=260°
360°-260°=100°
180°-100°=80°
∠1的度数是80°
19.(1)120°
(2)120°
【分析】根据四边形的内角和为360°,用360°分别减去另外的三个内角即可求出未知角的度数。
【详解】(1)360°-120°-60°-60°=120°
(2)360°-90°-90°-60°=120°
20.∠1=40°
【分析】1平角=180°,和65°相邻的右侧的钝角的度数是180°减65°的差,这个钝角是115°,三角形的内角和是180°,180°减115°,再减25°,即可求出∠1的度数。
【详解】180°-65°=115°
180°-115°-25°
=65°-25°
=40°
∠1=40°
21.∠4=65°;∠5=115°;∠6=30°
【分析】三角形的内角和是180°。
(1)∠2、∠3和∠4组成了一个三角形,所以∠4=180°-∠2-∠3。
(2)∠5和∠4组成了一个平角,1平角=180°,所以∠5=180°-∠4。
(3)∠1、∠5和∠6组成了一个三角形,所以∠6=180°-∠1-∠5,据此解答。
【详解】∠4=180°-∠2-∠3
=180°-55°-60°
=125°-60°
=65°
∠5=180°-∠4=180°-65°=115°
∠6=180°-∠1-∠5
=180°-35°-115°
=145°-115°
=30°
答:∠4的度数是65°,∠5的度数是115°,∠6的度数是30°。
22.55°;240°
【分析】
如图: ∠1和120°的角拼成一个平角,平角=180°,则∠1=180°-120°。三角形内角和等于180°,180°减去∠1的度数,再减去65°,即可算出∠2的度数;
如图:三角形内角和等于180°,则∠3+∠4=180°-60°。四边形的内角和是360°,则∠1+∠2=360°-(∠3+∠4)=360°-(180°-60°)。
【详解】∠2=180°-65°-(180°-120°)
=180°-65°-60°
=115°-60°
=55°
∠1+∠2=360°-(180°-60°)
=360°-120°
=240°
23.105°
【分析】一副三角板有两个三角尺,一个三角尺的三个角的度数分别为:90°、45°、45°,另一个三角尺的三个角的度数分别为:90°、30°、60°。图中∠1与一个45°角、一个30°角在同一个三角形内,根据三角形的内角和是180°,用180°减去45°再减去30°即可求解。
【详解】180°-45°-30°
=135°-30°
=105°
∠1的度数为105°。
24.∠1=70°;∠2=110°;∠3=50°
【分析】根据平角=180°,三角形三个内角度数和是180°;从图中可知:∠3与130°角组成平角,一共是180°,则用180°减130°即可求到∠3的度数;又因∠1、∠3和60°角是三角形的三个内角,三角形的内角和是180°,则用180°减去60°和∠3的度数,即可求到∠1的度数;又因∠1和∠2组成平角,一共是180°,则用180°减∠1的度数即可求到∠2的度数。据此解答。
【详解】∠3=180°-130°=50°
∠1=180°-60°-50°
=120°-50°
=70°
∠2=180°-70°=110°
所以,∠1=70°;∠2=110°;∠3=50°。
25.135°
【分析】四边形的内角和等于360°,已知四边形中三个角的度数,用四边形的内角和减去已知的三个角可得剩下的角的度数。
【详解】360°-90°-65°-70°
=270°-65°-70°
=205°-70°
=135°
即图中未知角的度数是135°。
26.
【分析】根据三角形内角和为,首先求出与相邻的角的度数,,再用平角减去这个角就是的度数。
【详解】
即的度数是。
27.60°;30°;60°
【分析】1直角=90°,三角形的内角和等于180°;
根据题意可知,如图:∠1和∠2组成一个直角,则∠2=90°-∠1;∠2、∠3和∠5在一个三角形内,则∠2+∠3+∠5=180°,所以∠3=180°-90°-∠2;∠3和∠4组成一个直角,则∠4=90°-∠3;据此解答。
【详解】∠2=90°-30°=60°;
∠3=180°-90°-60°=90°-60°=30°;
∠4=90°-30°=60°;
即∠2=60°,∠3=30°,∠4=60°。
28.∠4=105°;∠5=75°;∠6=95°
【分析】平角为180°,三角形内角和为180°,观察图可以发现,∠1、∠3和∠4组成三角形的内角和,用180°依次减去∠1、∠3,即可求出∠4。∠4和∠5组成平角,用180°减去∠4,即可求出∠5。∠5、∠2和∠6组成三角形的内角和,用180°依次减去∠2、∠5,即可求出∠6。
【详解】∠4=180°-30°-45°
=150°-45°
=105°
∠5=180°-105°=75°
∠6=180°-10°-75°
=170°-75°
=95°
即∠4=105°,∠5=75°,∠6=95°。
29.100°
【分析】
140°角和∠2组成1个平角,平角等于180°,用180°-140°=40°,求出∠2的度数,再根据三角形内角和等于180°,用180°-40°-40° ,即可求出∠1的度数。
【详解】180°-140°=40°
180°-40°-40°
=140°-40°
=100°
30.160°;40°
【分析】根据四边形内角和定理,四边形ABCD的内角和为360°,即∠A+∠B+∠C+∠ D=360°,已知∠A+∠C=160°,求∠B+∠D的度数用360°减去∠A和∠C的度数和;求∠B的度数,因为∠D是∠B的4倍,∠D的度数是4×∠B,∠B+∠D的度数和就是∠B度数的(1+4)倍,用除法可以算出∠B的度数,最后根据∠D是∠B的4倍,用乘法算出∠D的度数。
【详解】∠B=(360°-160°)÷(1+4)
=200°÷5
=40°
∠D=4×40°=160°
所以∠D=160°,∠B=40°。
31.78°;60°
【分析】根据三角形内角和是180°和图中给出的度数,用180°减去三角形的两个已知角度,可以求得未知角的度数。
【详解】根据分析可知:
180°-(65°+37°)
=180°-102°
= 78°
图一的未知角的度数是 78°。
180°-(90°+30°)
=180°-120°
= 60°
图二的未知角的度数是 60°。
32.90°
【分析】三角形的内角和为180°。在等腰三角形中,两个底角相等。由题意得,等腰三角形的一个底角是45°,那么另一个底角的度数也是45°,直接用180°减去两个底角的度数即可算出顶角的度数。
【详解】180°-45°-45°
=135°-45°
=90°
即顶角∠3=90°。
33.(1)131厘米
(2)170厘米
【详解】31+43+57
=31+(43+57)
=31+100
=131(厘米)
19+43+51+57
=(19+51)+(43+57)
=170(厘米)
34.276m,3800m2
【分析】周长就是封闭图形一周的长度,题图是一个不规则图形,通过观察不难发现这个不规则图形的周长与长、宽的长方形的周长相等,所以可以转换为求长方形的周长。不规则图形的面积没办法直接求,但是可以分割成两个长方形(一个长、宽,一个长、宽),把这两个长方形的面积相加即为所求。
【详解】周长:
(75+38+25)×2
=138×2
=276(m)
面积:
75×38+25×38
=(75+25)×38
=100×38
=3800(m2)
35.131厘米;170厘米;
【分析】封闭图形一周的长度是这个图形的周长,因此将每个图形中的每条边的长度加起来即可,依此列式并根据加法结合律的特点进行计算。
【详解】31+43+57
=31+(43+57)
=31+100
=131(厘米)
19+51+43+57
=(19+51)+(43+57)
=70+100
=170(厘米)
36.14平方厘米
【分析】长方形的面积=长×宽,因此可将这两个长方形的面积加起来即可解答,依此列式并根据乘法分配律的特点进行简算即可。
【详解】4×2+3×2
=(4+3)×2
=7×2
=14(平方厘米)
37.320平方米
【分析】通过切割法来求面积,即把一个不规则图形分割成几个规则图形,图形的面积等于长23m,宽8m的长方形面积加长17m,宽8m的长方形的面积,根据长方形的面积=长×宽,解答即可。
【详解】
(平方米)
图形的面积是320平方米。
38.360平方米;方法见详解
【分析】把这个图形分成两个长方形(不同的分法得到的两个长方形不同。),分别计算出两个长方形的面积,相加就是这个图形的面积。(方法不唯一)长方形的面积=长×宽。在计算过程中可用到乘法分配律使计算简便。
【详解】
方法一:21×9+19×9
=(21+19)×9
=40×9
=360(平方米)
方法二:(9+19)×9+(21-9)×9
=28×9+12×9
=(28+12)×9
=40×9
=360(平方米)
39.800cm2
【分析】首先用分割法把图形分割成两个长方形,一个长方形的长是20厘米,宽是10厘米,另一个长方形的长是20+10=30厘米,宽是20厘米,根据长方形的面积=长×宽,分别计算出所分割的图形的面积,再把分割图形的面积相加,即可解答。
【详解】20×10+(20+10)×20
=20×10+30×20
=200+30×20
=200+600
=800(cm2)
第1页,共2页
第1页,共2页
同课章节目录
