人教版2025年小学四年级下学期数学期末复习专题分类强训:作图题(附答案)
文档属性
| 名称 | 人教版2025年小学四年级下学期数学期末复习专题分类强训:作图题(附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-14 15:07:06 | ||
图片预览

文档简介
人教版2025年小学四年级下学期数学期末复习专题分类强训:作图题(附答案)
学校:___________姓名:___________班级:___________
作图题
1.在直线上标出下面各数的大致位置。
0.15 1.7 2.4 3.83 4.06 5.9
2.以直线l为对称轴,画出轴对称图形。
3.画出下面两个三角形指定底边上的高。
4.仙游动车站位于莆田市仙游县枫亭镇。由于枫亭镇是北宋著名书法家、文学家、政治家和茶学家蔡襄的故里,因此将站房设计为一个官帽的形状。从正面看,它是一个轴对称图形。
(1)方格纸中画出了主站房的一半,请根据对称轴补全这个轴对称图形。
(2)画出这个轴对称图形,先向右平移6格,再向上平移5格后的图形。
5.按要求在方格图中画三角形(每个小方格边长1cm)。
(1)以线段AB为底,画一个高3cm的三角形ABC,且AC=BC。
(2)以线段DE为底,画一个高3cm的直角三角形DEF。
6.画一画。(下图中每个小方格的边长均为1m)
(1)妙想用木条拼成一个底是4cm,高是3m的三角形,它可能是什么样子的呢?请你以BC为底在方格图中画一画。(至少画出3个)
(2)你有什么发现?
我发现:__________________________________。
7.在直线上标出下面各数的位置。
8.在原图形的基础上任选两个方格涂上颜色,使之成为轴对称图形。
(1)只有1条对称轴
(2)有2条对称轴
9.下图中涂色部分是由5个小正方形组成的,移动其中一个小正方形,使它变成轴对称图形,可以怎么移?画一画。(每次至少移1格)
10.给下图添上一个相同的小正方形,使这个图形成为轴对称图形。
11.在下面的正方形中,给其中的1个或几个圆涂色,使图形整体满足下面的要求。
12.在下面的直线上标出0.8、2.7和3.65的位置。
13.在小学我们学过三角形,三角形的内角和是180°,有两边相等的三角形叫等腰三角形,等腰三角形还是一个轴对称图形,由此可得到两条边所对的两个角也相等。比如图1,,。现有图 2,在中,,请画出一条直线,把这个三角形分割成两个等腰三角形。(请你选用下面给出的备用图,把所有不同的分割方法都画出来。只需要画图,不必说明理由,但要在图中标出相等两角的度数)
14.涂色表示下面各小数。
15.在直线上标出下列各数。
16.涂一涂,填一填。
分数: 小数:( )
分数:( ) 小数:0.47
17.下图中每个小正方形的边长都是1厘米。请在图中涂出2.5平方厘米。
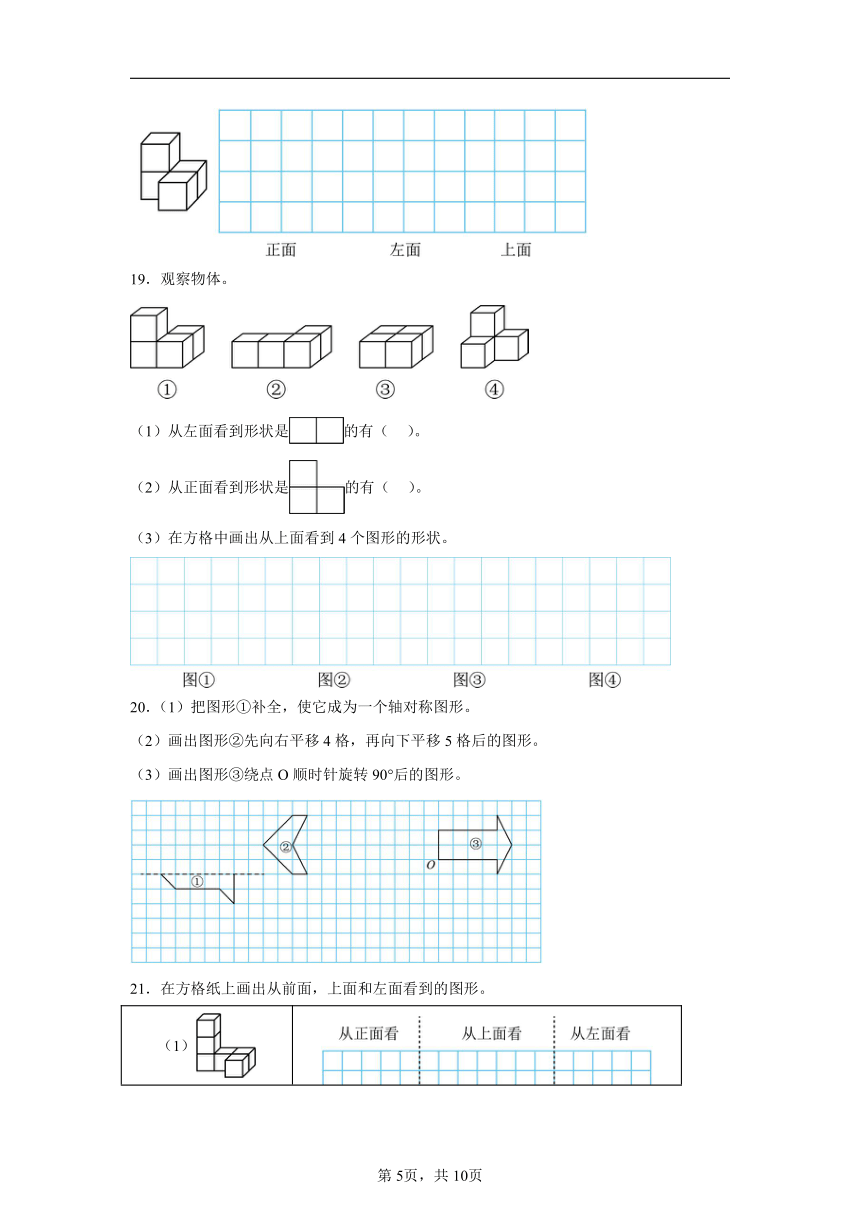
18.分别画出从前面、上面和左面看到的图形。
19.观察物体。
(1)从左面看到形状是的有( )。
(2)从正面看到形状是的有( )。
(3)在方格中画出从上面看到4个图形的形状。
20.(1)把图形①补全,使它成为一个轴对称图形。
(2)画出图形②先向右平移4格,再向下平移5格后的图形。
(3)画出图形③绕点O顺时针旋转90°后的图形。
21.在方格纸上画出从前面,上面和左面看到的图形。
(1)
(2)
22.画一画,填一填。
把平行四边形先向上平移2格,再向右平移3格。
23.如图,左面的几何是由一些相同的正方体拼搭而成的,正方体的一个面与方格纸上方格的大小相同,分别把从前面和右面看几何体得到的图形在方格纸上画出来。
24.画出下面图形向左平移4格后的图形。
25.在方格纸上画出图形的另一半,使它成为轴对称图形。
26.在直线上表示出下面数的位置。
27.在方格纸上分别画出下面物体从前面、上面和左面看到的图形。
28.学校篮球队球员的身高比较接近,都是两位小数,精确到十分位后都是1.6米。这些球员,最高是多少米?在下图中用↓标示出来。最矮是多少米?用▽标示出来。
29.按要求作图并填空。(每个方格的边长是1cm)
(1)作出三角形ABC底边AB上的高。
(2)画出三角形ABC 先向下平移3格,再向左平移2格后的图形。
(3)画出三角形ABC以虚线l为对称轴的轴对称图形。
30.(1)以虚线m为对称轴,画出这个轴对称图形(梯形ABCD)的另一半。
(2)画出三角形EFG底边EF上的高。
(3)三角形EFG先向( )平移( )cm,再向( )平移( )cm,与梯形ABCD组成一个长方形,这个长方形的面积是( )cm2。
31.如图所示,每个大正方形都表示整数“1”,涂色表示它下面的小数。
(1) (2)
32.观察下面的物体,分别画出从前面、上面和左面看到的图形。
33.画一画。
①根据对称轴补全这个轴对称图形。
②画出平行四边形先向右平移5格,再向下平移1格后的图形。
34.画一画。
在下面的图形中各画一条线段,按要求分一分。
35.涂色表示各小数。
36.迷宫挑战
想要把完整的移出出口,该怎样移动?(请在下面用文字表达移动过程)
37.涂色表示下面各小数。
38.操作。
(1)根据图中的对称轴l,画出这个轴对称图形的另一半。
(2)将补充完整的轴对称图形图形向右平移6格,画出平移后的图形。
39.涂色表示下面各小数。
40.在下面的直线上标出0.5、1.3、2.6、3.65的位置。
41.下面的物体从正面、上面、左面看到的图形分别是什么?画一画。
42.涂色表示如图各小数。
43.涂色表示下面各小数。
第1页,共3页
第1页,共3页
参考答案
1.见详解
【分析】图中每两个相邻数字间的线段是1大格,平均分成10份,每一小格表示0.1,那么每一小格的一半表示0.05。这里0.15表示1个0.1和1个0.05合起来;1.7表示1个1和7个0.1合起来;2.4表示2个1和4个0.1合起来;3.83表示3个1、8个0.1和3个0.01合起来;4.06表示4个1和6个0.01合起来;5.9表示5个1和9个0.1合起来。
【详解】如图:
2.见详解
【分析】根据轴对称图形的性质,各对称点到对称轴的距离相等,据此先描出各对称点的位置,然后顺次连接各点画出轴对称图形的另一半。据此解答。
【详解】如下图:
3.见详解
【分析】经过三角形的顶点(与底相对的点)向对边(底)作垂线,顶点和垂足之间的线段就是三角形的一条高,用三角板的直角可以画出三角形的高。
【详解】如图:
4.见详解
【分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
【详解】(1)、(2)如下图所示:
5.见详解
【分析】(1)要画一个以线段AB为底,高为3cm的三角形,且AC=BC的三角形,即画一个等腰三角形,先找到AB中点,再在中点距离AB所在直线3cm处确定顶点C,最后连接AC和BC;
(2)要画一个以线段DE为底,高为3cm的直角三角形,需要利用方格的直角特征,以DE为底边,在距离E点所在直线3cm处确定直角顶点F,使得两条直角边互相垂直,最后连接DF和EF即可。
【详解】根据分析画出图形:
(答案不唯一)
6.(1)见详解
(2)三角形的高的位置不同,画的三角形可能是直角三角形,可能是锐角三角,也可能是钝角三角形。
【分析】(1)从三角形一个顶点向它的对边作垂线,那么这个顶点和垂足间的线段叫做三角形的高。根据题意可知,三角形的底是4厘米,高是3厘米,每个小方格的边长是1厘米,以BC为底画三角形,要使高是3厘米,就是距离BC3格的地方点一点,过该点与B和C即可,由于距离BC3格的点不唯一,所以能画的三角形也不唯一。按角分类: 三角形按角分为锐角三角形(三个角均小于90°)、直角三角形(一个角为90°)和钝角三角形(一个角大于90°)。以此答题即可。
(2)根据题意经过分析,写出发现,合理即可。
【详解】根据分析可知:
(1)三角形可能是直角三角形,可能是锐角三角,也可能是钝角三角形。
画三角形如下:
(2)我发现:三角形的高的位置不同,画的三角形可能是直角三角形,可能是锐角三角,也可能是钝角三角形。
7.见详解
【分析】把0到0.5平均分成 5个单位长度,每个单位长度是0.1;再把每个单位长度平均分成10个小的单位长度,则每个小的单位长度是0.01。0.2位于从0数起的第二个较大单位长度处,0.02位于从0数起的第二个较小的单位长度处;0.45位于第四个较大的单位长度和0.5的正中间。
【详解】
8.(1)见详解
(2)见详解
【分析】一个图形沿着一条直线对折后两边能完全重合,这个图形就是轴对称图形,折痕所在的直线就是对称轴。根据对称轴的条数选择两个适当的方格涂色即可。
【详解】根据分析可知:
(1)只有1条对称轴
(2)有2条对称轴
(答案不唯一)
9.见详解
【分析】根据题意,平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这个图形就是轴对称图形;据此画一画。
【详解】根据分析画图如下:
10.见详解
【分析】如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形。第一幅可以在左上角左对齐添上一个相同的小正方形;第二幅图可以在右下角右对齐添上一个相同的小正方形;第三幅图在左下角左对齐添上一个相同的小正方形。
【详解】如图:
11.见详解
【分析】把一个平面图形沿一条直线对折,折痕两边的图形能够完全重合,这样的图形叫做轴对称图形,折痕所在的直线是轴对称图形的对称轴。正方形有4条对称轴,要使图形只有1条对称轴,需要打破其他3条对称轴的存在,可以选择不在正方形对称轴上的一排圆,涂出相对于正方形对称轴对称的两个圆;要使图形有2条对称轴,可以在正方形两边分别涂出两个圆形,注意不要涂在正方形顶点的圆上,以避免产生4条对称轴;要使图形保持4条对称轴,那么可以只涂色正方形中心的4个圆,据此解答即可。
【详解】如图:
12.见详解
【分析】根据题意,每两个数字之间一大格被平均分成10小格,每一小格就是0.1。8小格就是0.8。这样的27小格就是2.7。把一大格平均分成100小格,每一小格就是0.01。65小格就是0.65,再加上3大格,就是3.65。据此画出即可。
【详解】根据分析,各数的具体位置如下所示:
13.见详解
【分析】根据题意可知,通过画一条直线将给定的三角形分割成两个等腰三角形。等腰三角形两腰相等,三角形的内角和是180°,∠C=180°-∠A-∠B,也就是180°-90°-67.5°,结果是22.5°,所以可以分成22.5°、22.5°、135°和67.5°、67.5°、45°的两个等腰三角形;还可以分成22.5°、22.5°、135°和45°、45°、90°的两个等腰三角形;据此画图。
【详解】
14.涂色见详解
【分析】根据小数的意义,0.2表示把长方形平均分成10份,涂色部分占其中2份;1.3表示把一个正方形平均分成10份,涂色部分是13份,即先涂1个正方形,再把1个正方形平均分成10份,涂出其中3份;0.04m表示把1m平均分成100份,其中1份是0.01m,即1厘米,涂色部分占其中4份,也就是4cm。据此涂色。
【详解】根据分析,涂色如下:
15.见详解
【分析】图中从0到1,1到2都平均分成10小格,所以每小格表示0.1,0.5在0和1的中间,1.4在1的右边数第4小格的位置,2就在数字2所在的位置,2.85在2的右边,在2右边数第8和9小格的中间,据此解题。
【详解】
16.图见详解;0.7
图见详解;
【分析】把一个整体平均分成若干份,用分数表示,分母是分成的份数,分子是要表示的份数。小数的意义:分母是10、100、1000…的分数写成小数分别是一位小数、两位小数、三位小数……。
图一,把这个圆形的面积看成1,平均分成10份,每份是,表示7份涂色,用小数表示为0.7。
图二,把正方形的面积看成1,平均分成100份,其中的47份是,写成小数是0.47;由此解答即可。
【详解】涂色如下:
分数:;小数:0.7
分数:;小数:0.47
17.图见详解
【分析】已知每个小正方形的边长都是1厘米,根据正方形面积的计算方法:正方形面积=边长×边长,所以每个小正方形的面积为1×1=1平方厘米。因为要涂出2.5平方厘米,2个小正方形的面积是2平方厘米,还需半个小正方形的面积。所以总共要涂2个完整的小正方形和半个小正方形。
【详解】在图中选取2个小正方形全部涂满颜色,再选取另外一个小正方形,把它平均分成2份(可以沿着对角线分或者上下、左右平均分),涂其中的1份,这样就涂出了2.5平方厘米。(答案中给出的图片就是一种符合要求的涂色方式)
(答案不唯一)
18.见详解
【分析】从正面看,共有2行,上边1行1个小正方形,下面1行2个小正方形,左对齐;从左面看,共有2行,上边1行1个小正方形,下面1行2个小正方形,左对齐;从上面看,共有2行,上边1行2个小正方形,下面1行1个小正方形,右对齐;据此解答即可。
【详解】
19.(1)②③
(2)①④
(3)见详解
【分析】
(1)几何体①从左面看时,可以看见两排正方形。第一排只有一个正方形(靠右),第二排有两个正方形。几何体②从左面看时,可以看见两个正方形排成一排。几何体③从左面看时,可以看见两个正方形排成一排。几何体④从左面看时,可以看见两排正方形。第一排只有一个正方形(靠左),第二排有两个正方形。所以从左面看到形状是的几何体有②③。
(2)几何体①从正面看时,可以看见两排正方形。第一排只有一个正方形(靠左),第二排有两个正方形。几何体②从正面看时,可以看见三个正方形排成一排。几何体③从正面看时,可以看见两个正方形排成一排。几何体④从正面看时,可以看见两排正方形。第一排只有一个正方形(靠左),第二排有两个正方形。所以从正面看到形状是的有①④。
(3)几何体①从上面看时,可以看见两排正方形。第一排只有一个正方形(靠右),第二排有两个正方形。几何体②从上面看时,可以看见两排正方形。第一排只有一个正方形(靠右),第二排有三个正方形。几何体③从上面看时,可以看见两排正方形。第一排和第二排都有两个正方形且它们合起来组成一个大正方形。几何体④从上面看时,可以看见两排正方形。第一排有两个正方形,第二排只有一个正方形(靠左)。据此作图。
【详解】
(1)从左面看到形状是的有②③。
(2)从正面看到形状是的有①④。
(3)
20.(1)、(2)、(3)的画法见详解
【分析】(1)利用补全轴对称图形的方法:找出图①的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)根据平移的特征,将图②的各顶点分别向右平移4格,再向下平移5格,依次连接即可得到平移后的图形。
(3)根据旋转的特征,将图③绕O点顺时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
【详解】(1)、(2)、(3)的画法如下所示:
21.见详解
【分析】(1)从前面看可以看到3行,最下面一行3个小正方形,上面两行各1个小正方形,三行左对齐;从上面看可以看到2行,下面一行1个小正方形,上面一行3个小正方形,与下面一行右对齐;从左面看可以看到3行,最下面一行2个小正方形,上面两行各1个小正方形,三行左对齐;据此画图;
(2)从前面看可以看到2行,下面一行4个小正方形,上面一行1个小正方形放在下面一行从右往左数第2个小正方形上面;从上面看可以看到2行,下面一行1个小正方形,上面一行4个小正方形,下面的1个小正方形放在上面一行的从右往左数第3个小正方形下面;从左面看可以看到2行,下面一行2个小正方形,上面一行1个小正方形,左对齐;据此画图。
【详解】
22.见详解
【分析】作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
【详解】
23.见详解
【分析】根据题意,这个几何体,从前面看有三行,上面一行是一个小正方形左对齐,中间一行是两个小正方形左对齐,下面一行是三个小正方形排成一排。从右面看有三行,上面和中间一行都是一个小正方形右对齐。下面一行是两个小正方形排成一行。据此画出即可。
【详解】从前面和右面看几何体得到的图形如下所示:
24.见详解
【分析】根据平移的特征,把图中的图形的各顶点分别向左平移4个单位,依次连接即可。
【详解】如图:
25.见详解
【分析】补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【详解】如图:
26.见详解
【分析】根据小数的初步认识,0-1之间被平均分了10份,其中的1份是十分之一,即0.1,小数的整数部分是几就在刻度几的后面,十分位上是几就在第几小格。据此解答。
【详解】如图:
27.见详解
【分析】该立体图形,从前面看,可看到4个小正方形,分两层,上层1个,左对齐;下层3个;从上面看,可看到4个小正方形,分两层,上层1个,居中,下层3个;从左面看,可看到3个小正方形,分两层,上层1个,右对齐,下层2个;据此作图。
【详解】
28.见详解
【分析】一个小数,精确到十分位时,需要看百分位上数的大小,用“四舍五入”法求它的近似数;由题意得,两位小数精确到十分位是1.6。要使这个小数最大,说明它“四舍”后得到1.6,那么这个小数百分位上最大是4,即这个小数最大是1.64;要使这个小数最小,说明它“五入”后得到1.6。这个小数百分位上最小是5,十分位上是5,所以这个小数最小是1.55。由图可知,1.5米到1.6米之间,1.6米到1.7米之间都被平均分成了10小格,每小格表示0.1米。那么1.64米应该在1.6米之后的第4个小格处,1.55米应该在1.5米之后的第5个小格处。据此作图。
【详解】
29.(1)(2)(3)图见详解
【分析】(1)从三角形一个顶点向它的对边AB作一条垂线,三角形顶点和垂足之间的线段称三角形这条边上的高,据此画出AB边上的高即可;
(2)平移作图要注意:方向与距离。整个平移作图,就是把整个图案的每一个特征点按一定方向和一定的距离平行移动,找准特征点的对应点是作图的关键。将图形平移时,先找准平移后的对应点,然后再依次连线即可得到平移后的图形;据此画出三角形ABC 先向下平移3格,再向左平移2格后的图形即可;
(3)如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形;根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出关键对称点,依次连接即可。
【详解】(1)、(2)(3)作图如下:
30.(1)见详解
(2)见详解
(3)上;2;左;5;8
【分析】补全轴对称图形的方法:
(1)确定所给图形的关键点,也就是图形上每条线段的端点;
(2)确定关键点的对称点(对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出图形的关键对称点);
(3)把描出的对称点按顺序连线,得到轴对称图形的另一半。
三角形高是对确定的底而言,同一三角形所选底不同,高亦不同。经过三角形的顶点(与底相对的点)向对边(底)或者对边的延长线作垂线,顶点和垂足之间的线段就是三角形的一条高,用三角板的直角可以画出三角形的高(钝角三角形钝角边上的高在其反方向延长线上);直角三角形一条直角边就是以另一直角边为底的高。
通过观察图可知将直角三角形的斜边EF与梯形的一条腰CD重合,这两个图形可以组成一个长方形,通过把直角三角形向上后再向左平移(先向左再向上),可与梯形组成一个长方形,数出每次移动的格数(正方形的边长是1厘米)即可(答案不唯一)。边长是1厘米的正方形的面积是1平方厘米,数出这个长方形中有几个正方形就是几平方厘米。
【详解】(1)(2)
三角形EFG先向上平移2cm,再向左平移5cm,与梯形ABCD组成一个长方形,这个长方形的面积是8cm2。
31.(1)(2)见详解
【分析】(1)0.78表示把一个正方形平均分成100份,涂色部分占其中的78份。
(2)1.3可以分成1和0.3。1可以用一个完整的正方形(涂满色)表示,0.3表示把一个正方形平均分成10份,涂色部分占其中的3份。
【详解】
(1)
(2)
32.见详解
【分析】从前面看两行,下面一行3个小正方形,上面一行1个小正方形居中;
从上面看两行,下面一行3个小正方形,上面一行1个小正方形右对齐;
从左面看两列,左面一列1个小正方形,右面一列2个小正方形。
【详解】
33.(1)(2)图见详解
【分析】(1)如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形;根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的下边画出关键对称点,依次连接即可。
(2)平移作图要注意:方向与距离。整个平移作图,就是把整个图案的每一个特征点按一定方向和一定的距离平行移动,找准特征点的对应点是作图的关键。将图形平移时,先找准平移后的对应点,然后再依次连线即可得到平移后的图形;据此画出平行四边形先向右平移5格,再向下平移1格后的图形。
【详解】(1)、(2)作图如下:
34.见详解
【分析】有一个角是直角的三角形叫作直角三角形;有一个角是钝角的三角形叫作钝角三角形; 三个角都是锐角的三角形叫作锐角三角形。
(1)由题意得,要把这个三角形分成两个直角三角形。可以从上面的顶点出发,向它的对边作一条垂直线段。据此作图。
(2)由题意得,要把这个三角形分成一个直角三角形和一个钝角三角形。可以作一条线段把三角形最上面的钝角分为一个直角和一个钝角。据此作图。
(3)由题意得,要把这个三角形分成一个锐角三角形和一个钝角三角形。可以从三角形最上面的顶点出发,向它的对边斜着画一条线段。据此作图。
【详解】
35.见详解
【分析】0.44表示把一个整体平均分成100份,涂出其中的44份;
1.6表示把每把直尺的长平均分成10份,涂出其中的16份;
0.03米表示把1米平均分成100份,每份是1厘米,涂这样的3份,也就是3厘米。
【详解】如图:
36.见详解
【分析】在同一个平面内,如果一个图形上的所有点都按照某个直线方向做相同距离的移动,那么这样的图形运动就叫做图形的平移运动,简称平移;根据题意可知,通过合理规划三角形的移动路径,避开黑色方块的阻挡,最终到达出口。据此解答。
【详解】答:先让三角形向右移动4格,再向下移动1格,是为了绕过中间的黑色方块。接着向右移动6格,再向上移动2格,最后向右移动1格就成功到达出口。
37.见详解
【分析】(1)0.6表示把这个正方形平均分成10份,涂色部分占其中的6份。
(2)0.36表示把这个正方形平均分成100份,涂色部分占其中的36份。
(3)1.2表示一个完整的长方形和一个被平均分成10份,取其中的2份的长方形合在一起,以此涂色即可。
【详解】根据分析涂色如下:
38.见详解
【分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
【详解】
39.图见详解
【分析】左边的图形平均分成10份,其中的1份表示0.1,涂色其中的4份,表示0.4;
中间的图形平均分成100份,其中的1份表示0.01,涂色其中的29份,表示0.29;
右边的图形,一个正方形没有分,它表示整数部分1,另一个正方形平均分成10份,取其中的3份,就是0.3,把这两个部分加在一起就是1.3,据此涂色,即可解答。
【详解】
40.见详解
【分析】根据题意,0和1、1和2、2和3、3和4、4和5之间都平均分成了10格,则每格代表0.1,0.5在0和1之间第五格的位置;1.3在1和2之间第三格的位置;2.6在2和3之间第六格的位置;3.65在3和4之间第六格和第七格中间的位置,据此标出位置即可。
【详解】
41.见详解
【分析】根据题意,仔细观察图形,从正面看到是两层,下层3个小正方形,上层1个小正方形靠左;从上面看到两层,下层3个小正方形,上层3个小正方形并列排着;从左面看到是两层,下层2个小正方形,上层1个小正方形靠左;以此画图即可。
【详解】根据分析画图如下:
42.见详解
【分析】1.6中整数部分是1,则将最左边一个完整的尺涂满,十分位上是6,尺平均分为10格,每格代表0.1,涂其中6格即可;1米=1000毫米,0.045米则把1米平均分成1000份,每份是1毫米,取其中的45份,就是45毫米,据此涂色即可。
【详解】
如图:
43.见详解
【分析】根据小数的意义可知,0.6表示把整个圆平均分成10份,每一份是0.1,取其中的6份;1.58表示有一个完整的大正方形,再把另一个大正方形平均分成100份,取其中的58份。
【详解】
第1页,共2页
第1页,共2页
学校:___________姓名:___________班级:___________
作图题
1.在直线上标出下面各数的大致位置。
0.15 1.7 2.4 3.83 4.06 5.9
2.以直线l为对称轴,画出轴对称图形。
3.画出下面两个三角形指定底边上的高。
4.仙游动车站位于莆田市仙游县枫亭镇。由于枫亭镇是北宋著名书法家、文学家、政治家和茶学家蔡襄的故里,因此将站房设计为一个官帽的形状。从正面看,它是一个轴对称图形。
(1)方格纸中画出了主站房的一半,请根据对称轴补全这个轴对称图形。
(2)画出这个轴对称图形,先向右平移6格,再向上平移5格后的图形。
5.按要求在方格图中画三角形(每个小方格边长1cm)。
(1)以线段AB为底,画一个高3cm的三角形ABC,且AC=BC。
(2)以线段DE为底,画一个高3cm的直角三角形DEF。
6.画一画。(下图中每个小方格的边长均为1m)
(1)妙想用木条拼成一个底是4cm,高是3m的三角形,它可能是什么样子的呢?请你以BC为底在方格图中画一画。(至少画出3个)
(2)你有什么发现?
我发现:__________________________________。
7.在直线上标出下面各数的位置。
8.在原图形的基础上任选两个方格涂上颜色,使之成为轴对称图形。
(1)只有1条对称轴
(2)有2条对称轴
9.下图中涂色部分是由5个小正方形组成的,移动其中一个小正方形,使它变成轴对称图形,可以怎么移?画一画。(每次至少移1格)
10.给下图添上一个相同的小正方形,使这个图形成为轴对称图形。
11.在下面的正方形中,给其中的1个或几个圆涂色,使图形整体满足下面的要求。
12.在下面的直线上标出0.8、2.7和3.65的位置。
13.在小学我们学过三角形,三角形的内角和是180°,有两边相等的三角形叫等腰三角形,等腰三角形还是一个轴对称图形,由此可得到两条边所对的两个角也相等。比如图1,,。现有图 2,在中,,请画出一条直线,把这个三角形分割成两个等腰三角形。(请你选用下面给出的备用图,把所有不同的分割方法都画出来。只需要画图,不必说明理由,但要在图中标出相等两角的度数)
14.涂色表示下面各小数。
15.在直线上标出下列各数。
16.涂一涂,填一填。
分数: 小数:( )
分数:( ) 小数:0.47
17.下图中每个小正方形的边长都是1厘米。请在图中涂出2.5平方厘米。
18.分别画出从前面、上面和左面看到的图形。
19.观察物体。
(1)从左面看到形状是的有( )。
(2)从正面看到形状是的有( )。
(3)在方格中画出从上面看到4个图形的形状。
20.(1)把图形①补全,使它成为一个轴对称图形。
(2)画出图形②先向右平移4格,再向下平移5格后的图形。
(3)画出图形③绕点O顺时针旋转90°后的图形。
21.在方格纸上画出从前面,上面和左面看到的图形。
(1)
(2)
22.画一画,填一填。
把平行四边形先向上平移2格,再向右平移3格。
23.如图,左面的几何是由一些相同的正方体拼搭而成的,正方体的一个面与方格纸上方格的大小相同,分别把从前面和右面看几何体得到的图形在方格纸上画出来。
24.画出下面图形向左平移4格后的图形。
25.在方格纸上画出图形的另一半,使它成为轴对称图形。
26.在直线上表示出下面数的位置。
27.在方格纸上分别画出下面物体从前面、上面和左面看到的图形。
28.学校篮球队球员的身高比较接近,都是两位小数,精确到十分位后都是1.6米。这些球员,最高是多少米?在下图中用↓标示出来。最矮是多少米?用▽标示出来。
29.按要求作图并填空。(每个方格的边长是1cm)
(1)作出三角形ABC底边AB上的高。
(2)画出三角形ABC 先向下平移3格,再向左平移2格后的图形。
(3)画出三角形ABC以虚线l为对称轴的轴对称图形。
30.(1)以虚线m为对称轴,画出这个轴对称图形(梯形ABCD)的另一半。
(2)画出三角形EFG底边EF上的高。
(3)三角形EFG先向( )平移( )cm,再向( )平移( )cm,与梯形ABCD组成一个长方形,这个长方形的面积是( )cm2。
31.如图所示,每个大正方形都表示整数“1”,涂色表示它下面的小数。
(1) (2)
32.观察下面的物体,分别画出从前面、上面和左面看到的图形。
33.画一画。
①根据对称轴补全这个轴对称图形。
②画出平行四边形先向右平移5格,再向下平移1格后的图形。
34.画一画。
在下面的图形中各画一条线段,按要求分一分。
35.涂色表示各小数。
36.迷宫挑战
想要把完整的移出出口,该怎样移动?(请在下面用文字表达移动过程)
37.涂色表示下面各小数。
38.操作。
(1)根据图中的对称轴l,画出这个轴对称图形的另一半。
(2)将补充完整的轴对称图形图形向右平移6格,画出平移后的图形。
39.涂色表示下面各小数。
40.在下面的直线上标出0.5、1.3、2.6、3.65的位置。
41.下面的物体从正面、上面、左面看到的图形分别是什么?画一画。
42.涂色表示如图各小数。
43.涂色表示下面各小数。
第1页,共3页
第1页,共3页
参考答案
1.见详解
【分析】图中每两个相邻数字间的线段是1大格,平均分成10份,每一小格表示0.1,那么每一小格的一半表示0.05。这里0.15表示1个0.1和1个0.05合起来;1.7表示1个1和7个0.1合起来;2.4表示2个1和4个0.1合起来;3.83表示3个1、8个0.1和3个0.01合起来;4.06表示4个1和6个0.01合起来;5.9表示5个1和9个0.1合起来。
【详解】如图:
2.见详解
【分析】根据轴对称图形的性质,各对称点到对称轴的距离相等,据此先描出各对称点的位置,然后顺次连接各点画出轴对称图形的另一半。据此解答。
【详解】如下图:
3.见详解
【分析】经过三角形的顶点(与底相对的点)向对边(底)作垂线,顶点和垂足之间的线段就是三角形的一条高,用三角板的直角可以画出三角形的高。
【详解】如图:
4.见详解
【分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
【详解】(1)、(2)如下图所示:
5.见详解
【分析】(1)要画一个以线段AB为底,高为3cm的三角形,且AC=BC的三角形,即画一个等腰三角形,先找到AB中点,再在中点距离AB所在直线3cm处确定顶点C,最后连接AC和BC;
(2)要画一个以线段DE为底,高为3cm的直角三角形,需要利用方格的直角特征,以DE为底边,在距离E点所在直线3cm处确定直角顶点F,使得两条直角边互相垂直,最后连接DF和EF即可。
【详解】根据分析画出图形:
(答案不唯一)
6.(1)见详解
(2)三角形的高的位置不同,画的三角形可能是直角三角形,可能是锐角三角,也可能是钝角三角形。
【分析】(1)从三角形一个顶点向它的对边作垂线,那么这个顶点和垂足间的线段叫做三角形的高。根据题意可知,三角形的底是4厘米,高是3厘米,每个小方格的边长是1厘米,以BC为底画三角形,要使高是3厘米,就是距离BC3格的地方点一点,过该点与B和C即可,由于距离BC3格的点不唯一,所以能画的三角形也不唯一。按角分类: 三角形按角分为锐角三角形(三个角均小于90°)、直角三角形(一个角为90°)和钝角三角形(一个角大于90°)。以此答题即可。
(2)根据题意经过分析,写出发现,合理即可。
【详解】根据分析可知:
(1)三角形可能是直角三角形,可能是锐角三角,也可能是钝角三角形。
画三角形如下:
(2)我发现:三角形的高的位置不同,画的三角形可能是直角三角形,可能是锐角三角,也可能是钝角三角形。
7.见详解
【分析】把0到0.5平均分成 5个单位长度,每个单位长度是0.1;再把每个单位长度平均分成10个小的单位长度,则每个小的单位长度是0.01。0.2位于从0数起的第二个较大单位长度处,0.02位于从0数起的第二个较小的单位长度处;0.45位于第四个较大的单位长度和0.5的正中间。
【详解】
8.(1)见详解
(2)见详解
【分析】一个图形沿着一条直线对折后两边能完全重合,这个图形就是轴对称图形,折痕所在的直线就是对称轴。根据对称轴的条数选择两个适当的方格涂色即可。
【详解】根据分析可知:
(1)只有1条对称轴
(2)有2条对称轴
(答案不唯一)
9.见详解
【分析】根据题意,平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这个图形就是轴对称图形;据此画一画。
【详解】根据分析画图如下:
10.见详解
【分析】如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形。第一幅可以在左上角左对齐添上一个相同的小正方形;第二幅图可以在右下角右对齐添上一个相同的小正方形;第三幅图在左下角左对齐添上一个相同的小正方形。
【详解】如图:
11.见详解
【分析】把一个平面图形沿一条直线对折,折痕两边的图形能够完全重合,这样的图形叫做轴对称图形,折痕所在的直线是轴对称图形的对称轴。正方形有4条对称轴,要使图形只有1条对称轴,需要打破其他3条对称轴的存在,可以选择不在正方形对称轴上的一排圆,涂出相对于正方形对称轴对称的两个圆;要使图形有2条对称轴,可以在正方形两边分别涂出两个圆形,注意不要涂在正方形顶点的圆上,以避免产生4条对称轴;要使图形保持4条对称轴,那么可以只涂色正方形中心的4个圆,据此解答即可。
【详解】如图:
12.见详解
【分析】根据题意,每两个数字之间一大格被平均分成10小格,每一小格就是0.1。8小格就是0.8。这样的27小格就是2.7。把一大格平均分成100小格,每一小格就是0.01。65小格就是0.65,再加上3大格,就是3.65。据此画出即可。
【详解】根据分析,各数的具体位置如下所示:
13.见详解
【分析】根据题意可知,通过画一条直线将给定的三角形分割成两个等腰三角形。等腰三角形两腰相等,三角形的内角和是180°,∠C=180°-∠A-∠B,也就是180°-90°-67.5°,结果是22.5°,所以可以分成22.5°、22.5°、135°和67.5°、67.5°、45°的两个等腰三角形;还可以分成22.5°、22.5°、135°和45°、45°、90°的两个等腰三角形;据此画图。
【详解】
14.涂色见详解
【分析】根据小数的意义,0.2表示把长方形平均分成10份,涂色部分占其中2份;1.3表示把一个正方形平均分成10份,涂色部分是13份,即先涂1个正方形,再把1个正方形平均分成10份,涂出其中3份;0.04m表示把1m平均分成100份,其中1份是0.01m,即1厘米,涂色部分占其中4份,也就是4cm。据此涂色。
【详解】根据分析,涂色如下:
15.见详解
【分析】图中从0到1,1到2都平均分成10小格,所以每小格表示0.1,0.5在0和1的中间,1.4在1的右边数第4小格的位置,2就在数字2所在的位置,2.85在2的右边,在2右边数第8和9小格的中间,据此解题。
【详解】
16.图见详解;0.7
图见详解;
【分析】把一个整体平均分成若干份,用分数表示,分母是分成的份数,分子是要表示的份数。小数的意义:分母是10、100、1000…的分数写成小数分别是一位小数、两位小数、三位小数……。
图一,把这个圆形的面积看成1,平均分成10份,每份是,表示7份涂色,用小数表示为0.7。
图二,把正方形的面积看成1,平均分成100份,其中的47份是,写成小数是0.47;由此解答即可。
【详解】涂色如下:
分数:;小数:0.7
分数:;小数:0.47
17.图见详解
【分析】已知每个小正方形的边长都是1厘米,根据正方形面积的计算方法:正方形面积=边长×边长,所以每个小正方形的面积为1×1=1平方厘米。因为要涂出2.5平方厘米,2个小正方形的面积是2平方厘米,还需半个小正方形的面积。所以总共要涂2个完整的小正方形和半个小正方形。
【详解】在图中选取2个小正方形全部涂满颜色,再选取另外一个小正方形,把它平均分成2份(可以沿着对角线分或者上下、左右平均分),涂其中的1份,这样就涂出了2.5平方厘米。(答案中给出的图片就是一种符合要求的涂色方式)
(答案不唯一)
18.见详解
【分析】从正面看,共有2行,上边1行1个小正方形,下面1行2个小正方形,左对齐;从左面看,共有2行,上边1行1个小正方形,下面1行2个小正方形,左对齐;从上面看,共有2行,上边1行2个小正方形,下面1行1个小正方形,右对齐;据此解答即可。
【详解】
19.(1)②③
(2)①④
(3)见详解
【分析】
(1)几何体①从左面看时,可以看见两排正方形。第一排只有一个正方形(靠右),第二排有两个正方形。几何体②从左面看时,可以看见两个正方形排成一排。几何体③从左面看时,可以看见两个正方形排成一排。几何体④从左面看时,可以看见两排正方形。第一排只有一个正方形(靠左),第二排有两个正方形。所以从左面看到形状是的几何体有②③。
(2)几何体①从正面看时,可以看见两排正方形。第一排只有一个正方形(靠左),第二排有两个正方形。几何体②从正面看时,可以看见三个正方形排成一排。几何体③从正面看时,可以看见两个正方形排成一排。几何体④从正面看时,可以看见两排正方形。第一排只有一个正方形(靠左),第二排有两个正方形。所以从正面看到形状是的有①④。
(3)几何体①从上面看时,可以看见两排正方形。第一排只有一个正方形(靠右),第二排有两个正方形。几何体②从上面看时,可以看见两排正方形。第一排只有一个正方形(靠右),第二排有三个正方形。几何体③从上面看时,可以看见两排正方形。第一排和第二排都有两个正方形且它们合起来组成一个大正方形。几何体④从上面看时,可以看见两排正方形。第一排有两个正方形,第二排只有一个正方形(靠左)。据此作图。
【详解】
(1)从左面看到形状是的有②③。
(2)从正面看到形状是的有①④。
(3)
20.(1)、(2)、(3)的画法见详解
【分析】(1)利用补全轴对称图形的方法:找出图①的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)根据平移的特征,将图②的各顶点分别向右平移4格,再向下平移5格,依次连接即可得到平移后的图形。
(3)根据旋转的特征,将图③绕O点顺时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
【详解】(1)、(2)、(3)的画法如下所示:
21.见详解
【分析】(1)从前面看可以看到3行,最下面一行3个小正方形,上面两行各1个小正方形,三行左对齐;从上面看可以看到2行,下面一行1个小正方形,上面一行3个小正方形,与下面一行右对齐;从左面看可以看到3行,最下面一行2个小正方形,上面两行各1个小正方形,三行左对齐;据此画图;
(2)从前面看可以看到2行,下面一行4个小正方形,上面一行1个小正方形放在下面一行从右往左数第2个小正方形上面;从上面看可以看到2行,下面一行1个小正方形,上面一行4个小正方形,下面的1个小正方形放在上面一行的从右往左数第3个小正方形下面;从左面看可以看到2行,下面一行2个小正方形,上面一行1个小正方形,左对齐;据此画图。
【详解】
22.见详解
【分析】作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
【详解】
23.见详解
【分析】根据题意,这个几何体,从前面看有三行,上面一行是一个小正方形左对齐,中间一行是两个小正方形左对齐,下面一行是三个小正方形排成一排。从右面看有三行,上面和中间一行都是一个小正方形右对齐。下面一行是两个小正方形排成一行。据此画出即可。
【详解】从前面和右面看几何体得到的图形如下所示:
24.见详解
【分析】根据平移的特征,把图中的图形的各顶点分别向左平移4个单位,依次连接即可。
【详解】如图:
25.见详解
【分析】补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【详解】如图:
26.见详解
【分析】根据小数的初步认识,0-1之间被平均分了10份,其中的1份是十分之一,即0.1,小数的整数部分是几就在刻度几的后面,十分位上是几就在第几小格。据此解答。
【详解】如图:
27.见详解
【分析】该立体图形,从前面看,可看到4个小正方形,分两层,上层1个,左对齐;下层3个;从上面看,可看到4个小正方形,分两层,上层1个,居中,下层3个;从左面看,可看到3个小正方形,分两层,上层1个,右对齐,下层2个;据此作图。
【详解】
28.见详解
【分析】一个小数,精确到十分位时,需要看百分位上数的大小,用“四舍五入”法求它的近似数;由题意得,两位小数精确到十分位是1.6。要使这个小数最大,说明它“四舍”后得到1.6,那么这个小数百分位上最大是4,即这个小数最大是1.64;要使这个小数最小,说明它“五入”后得到1.6。这个小数百分位上最小是5,十分位上是5,所以这个小数最小是1.55。由图可知,1.5米到1.6米之间,1.6米到1.7米之间都被平均分成了10小格,每小格表示0.1米。那么1.64米应该在1.6米之后的第4个小格处,1.55米应该在1.5米之后的第5个小格处。据此作图。
【详解】
29.(1)(2)(3)图见详解
【分析】(1)从三角形一个顶点向它的对边AB作一条垂线,三角形顶点和垂足之间的线段称三角形这条边上的高,据此画出AB边上的高即可;
(2)平移作图要注意:方向与距离。整个平移作图,就是把整个图案的每一个特征点按一定方向和一定的距离平行移动,找准特征点的对应点是作图的关键。将图形平移时,先找准平移后的对应点,然后再依次连线即可得到平移后的图形;据此画出三角形ABC 先向下平移3格,再向左平移2格后的图形即可;
(3)如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形;根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出关键对称点,依次连接即可。
【详解】(1)、(2)(3)作图如下:
30.(1)见详解
(2)见详解
(3)上;2;左;5;8
【分析】补全轴对称图形的方法:
(1)确定所给图形的关键点,也就是图形上每条线段的端点;
(2)确定关键点的对称点(对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出图形的关键对称点);
(3)把描出的对称点按顺序连线,得到轴对称图形的另一半。
三角形高是对确定的底而言,同一三角形所选底不同,高亦不同。经过三角形的顶点(与底相对的点)向对边(底)或者对边的延长线作垂线,顶点和垂足之间的线段就是三角形的一条高,用三角板的直角可以画出三角形的高(钝角三角形钝角边上的高在其反方向延长线上);直角三角形一条直角边就是以另一直角边为底的高。
通过观察图可知将直角三角形的斜边EF与梯形的一条腰CD重合,这两个图形可以组成一个长方形,通过把直角三角形向上后再向左平移(先向左再向上),可与梯形组成一个长方形,数出每次移动的格数(正方形的边长是1厘米)即可(答案不唯一)。边长是1厘米的正方形的面积是1平方厘米,数出这个长方形中有几个正方形就是几平方厘米。
【详解】(1)(2)
三角形EFG先向上平移2cm,再向左平移5cm,与梯形ABCD组成一个长方形,这个长方形的面积是8cm2。
31.(1)(2)见详解
【分析】(1)0.78表示把一个正方形平均分成100份,涂色部分占其中的78份。
(2)1.3可以分成1和0.3。1可以用一个完整的正方形(涂满色)表示,0.3表示把一个正方形平均分成10份,涂色部分占其中的3份。
【详解】
(1)
(2)
32.见详解
【分析】从前面看两行,下面一行3个小正方形,上面一行1个小正方形居中;
从上面看两行,下面一行3个小正方形,上面一行1个小正方形右对齐;
从左面看两列,左面一列1个小正方形,右面一列2个小正方形。
【详解】
33.(1)(2)图见详解
【分析】(1)如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形;根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的下边画出关键对称点,依次连接即可。
(2)平移作图要注意:方向与距离。整个平移作图,就是把整个图案的每一个特征点按一定方向和一定的距离平行移动,找准特征点的对应点是作图的关键。将图形平移时,先找准平移后的对应点,然后再依次连线即可得到平移后的图形;据此画出平行四边形先向右平移5格,再向下平移1格后的图形。
【详解】(1)、(2)作图如下:
34.见详解
【分析】有一个角是直角的三角形叫作直角三角形;有一个角是钝角的三角形叫作钝角三角形; 三个角都是锐角的三角形叫作锐角三角形。
(1)由题意得,要把这个三角形分成两个直角三角形。可以从上面的顶点出发,向它的对边作一条垂直线段。据此作图。
(2)由题意得,要把这个三角形分成一个直角三角形和一个钝角三角形。可以作一条线段把三角形最上面的钝角分为一个直角和一个钝角。据此作图。
(3)由题意得,要把这个三角形分成一个锐角三角形和一个钝角三角形。可以从三角形最上面的顶点出发,向它的对边斜着画一条线段。据此作图。
【详解】
35.见详解
【分析】0.44表示把一个整体平均分成100份,涂出其中的44份;
1.6表示把每把直尺的长平均分成10份,涂出其中的16份;
0.03米表示把1米平均分成100份,每份是1厘米,涂这样的3份,也就是3厘米。
【详解】如图:
36.见详解
【分析】在同一个平面内,如果一个图形上的所有点都按照某个直线方向做相同距离的移动,那么这样的图形运动就叫做图形的平移运动,简称平移;根据题意可知,通过合理规划三角形的移动路径,避开黑色方块的阻挡,最终到达出口。据此解答。
【详解】答:先让三角形向右移动4格,再向下移动1格,是为了绕过中间的黑色方块。接着向右移动6格,再向上移动2格,最后向右移动1格就成功到达出口。
37.见详解
【分析】(1)0.6表示把这个正方形平均分成10份,涂色部分占其中的6份。
(2)0.36表示把这个正方形平均分成100份,涂色部分占其中的36份。
(3)1.2表示一个完整的长方形和一个被平均分成10份,取其中的2份的长方形合在一起,以此涂色即可。
【详解】根据分析涂色如下:
38.见详解
【分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
【详解】
39.图见详解
【分析】左边的图形平均分成10份,其中的1份表示0.1,涂色其中的4份,表示0.4;
中间的图形平均分成100份,其中的1份表示0.01,涂色其中的29份,表示0.29;
右边的图形,一个正方形没有分,它表示整数部分1,另一个正方形平均分成10份,取其中的3份,就是0.3,把这两个部分加在一起就是1.3,据此涂色,即可解答。
【详解】
40.见详解
【分析】根据题意,0和1、1和2、2和3、3和4、4和5之间都平均分成了10格,则每格代表0.1,0.5在0和1之间第五格的位置;1.3在1和2之间第三格的位置;2.6在2和3之间第六格的位置;3.65在3和4之间第六格和第七格中间的位置,据此标出位置即可。
【详解】
41.见详解
【分析】根据题意,仔细观察图形,从正面看到是两层,下层3个小正方形,上层1个小正方形靠左;从上面看到两层,下层3个小正方形,上层3个小正方形并列排着;从左面看到是两层,下层2个小正方形,上层1个小正方形靠左;以此画图即可。
【详解】根据分析画图如下:
42.见详解
【分析】1.6中整数部分是1,则将最左边一个完整的尺涂满,十分位上是6,尺平均分为10格,每格代表0.1,涂其中6格即可;1米=1000毫米,0.045米则把1米平均分成1000份,每份是1毫米,取其中的45份,就是45毫米,据此涂色即可。
【详解】
如图:
43.见详解
【分析】根据小数的意义可知,0.6表示把整个圆平均分成10份,每一份是0.1,取其中的6份;1.58表示有一个完整的大正方形,再把另一个大正方形平均分成100份,取其中的58份。
【详解】
第1页,共2页
第1页,共2页
同课章节目录
