华东师大版九年级数学上册第25章随机事件的概率复习课件
文档属性
| 名称 | 华东师大版九年级数学上册第25章随机事件的概率复习课件 |
|
|
| 格式 | ppt | ||
| 文件大小 | 363.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 00:00:00 | ||
图片预览







文档简介
(共16张PPT)
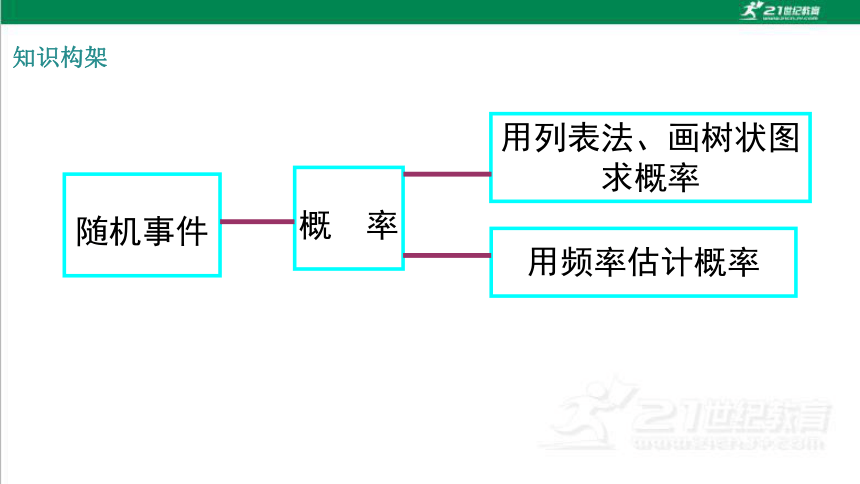
随机事件
概 率
用列表法、画树状图求概率
用频率估计概率
知识构架
1.确定事件
(2)在每次试验中都一定不会发生的事件叫做
2.随机事件
无法预先确定在一次试验中会不会发生的事件,叫做随机事件.
3.事件发生的概率与事件发生的频率有什么关系?
必然事件.
(1)无需通过试验就能预先确定它们在每次
试验中都一定会发生叫做
不可能事件.
考点分类
在多次试验中,某个事件出现的次数叫 ,某个事件出现的次数与试验总次数的比,叫做这个事件出现的 ,一个事件在多次试验中发生的可能性叫做这个事件发生的 .
频数
频率
概率
4. 频数、频率、概率
(1)一般地,在大量重复试验中,如果事件 A 发生的频率会稳定在某个常数 P 附近,那么,这个常数 P 就叫作事件 A 的概率,事件 A 发生的频率是:在 n 次试验中,事件 A 发生的频数 m 与 n 的比.
(2)求一个事件的概率的基本方法是:进行大量的重复试验,用这个事件发生的频率近似地作为它的概率.
(3)对于某些随机事件也可以不通过重复试验,而只通过一次试验中可能出现的结果的分析来计算概率.例如:掷两枚硬币,求两枚硬币正面向上的概率.
一般地,如果在一次试验中,有 n 种可能的结果,并且它们发生的可能性都相等,事件 A 包含其中 m 种结果,那么事件 A 发生的概率为:
5.在什么条件下适用 P(A)= 得到事件的概率?
6.如何用列举法求概率?
当事件要经过一步完成时列举出所有可能情况,当事件要经过两步完成时用列表法,当事件要经过三步及以上完成时用树状图法.
随堂练习
1.下面是两个可以自由转动的转盘,每个转盘被分成了三个相等的扇形,小明和小亮用它们做配紫色(红色与蓝色能配成紫色)游戏,你认为配成紫色与配不成紫色的概率相同吗?
A
B
一共有 9 种结果,每种结果出现的可能性相同,(红,蓝)能配紫色的有 5 种,概率为 ;不能配紫色的有 4 种,概率为 ,它们的概率不相同.
解:所有可能出现的结果如下:
红 红 蓝A
(红,红) (蓝,红) (蓝,红)
(红,红) (蓝,红) (蓝,红)
(红,蓝) (蓝,蓝) (蓝,蓝)
红 蓝 蓝 B
2.一个桶里有 60 个弹珠,一些是红色的,一些是蓝色的,一些是白色的.拿出红色弹珠的概率是 35%,拿出蓝色弹珠的概率是 25%,桶里每种颜色的弹珠各有多少?
解:60×35% = 21(个),
60×25% = 15(个),
60 - 21 - 15 = 24(个).
答:桶内有红色弹珠 21 个,蓝色弹珠 15 个,白色弹珠 24 个.
3.将一枚硬币连掷 3 次,出现“两反,一正”的概率是多少?
开始
正
反
正
反
正
反
正
反
正
反
正
反
正
反
解:根据题意,画出如下树状图,记出现“两反,一正”为事件 A,
故 P(A) = .
4.某校决定从三名男生和两名女生中选出两名同学担任校艺术节文艺演出专场的主持人,请用列表法或树状图法,求选出的恰为一男一女的概率.
解:列表如下:
男1 男2 男3 女1 女2
男1 ﹣﹣﹣ (男2,男1) (男3,男1) (女1,男1) (女2,男1)
男2 (男1,男2) ﹣﹣﹣ (男3,男1) (女1,男2) (女2,男2)
男3 (男1,男3) (男2,男3) ﹣﹣﹣ (女1,男3) (女2,男3)
女1 (男1,女1) (男2,女1) (男3,女1) ﹣﹣﹣ (女2,女1)
女2 (男1,女2) (男2,女2) (男3,女2) (女1,女2) ﹣﹣﹣
所有等可能的情况有 20 种,其中一男一女的情况有12 种,则 P(一男一女) = .
1.概率的定义及基本性质
如果在一次试验中,有 n 种可能的结果,并且他们
发生的可能性都相等,事件 A 包含其中的 m 种结果,那么事件 A 发生的概率 P(A) = .
0≤m≤n,有 0≤ ≤1 .
课堂小结
2.必然事件 A,则 P(A)=1;
不可能事件 B,则 P(B)=0;
随机事件 C,则 0<P(C)<1.
当事件经过一步完成时,列举出所有可能情况;
当事件要经过两步完成时,用列表法;
当事件要经过三步以上完成时,用树状图法.
当试验的所有可能结果不是有限个或各种可能结果发生的可能性不相等时,常常通过统计频率来估计概率,即在同样条件下,大量重复试验所得到的随机事件发生的频率的稳定值来估计这个事件发生概率.
随机事件
概 率
用列表法、画树状图求概率
用频率估计概率
知识构架
1.确定事件
(2)在每次试验中都一定不会发生的事件叫做
2.随机事件
无法预先确定在一次试验中会不会发生的事件,叫做随机事件.
3.事件发生的概率与事件发生的频率有什么关系?
必然事件.
(1)无需通过试验就能预先确定它们在每次
试验中都一定会发生叫做
不可能事件.
考点分类
在多次试验中,某个事件出现的次数叫 ,某个事件出现的次数与试验总次数的比,叫做这个事件出现的 ,一个事件在多次试验中发生的可能性叫做这个事件发生的 .
频数
频率
概率
4. 频数、频率、概率
(1)一般地,在大量重复试验中,如果事件 A 发生的频率会稳定在某个常数 P 附近,那么,这个常数 P 就叫作事件 A 的概率,事件 A 发生的频率是:在 n 次试验中,事件 A 发生的频数 m 与 n 的比.
(2)求一个事件的概率的基本方法是:进行大量的重复试验,用这个事件发生的频率近似地作为它的概率.
(3)对于某些随机事件也可以不通过重复试验,而只通过一次试验中可能出现的结果的分析来计算概率.例如:掷两枚硬币,求两枚硬币正面向上的概率.
一般地,如果在一次试验中,有 n 种可能的结果,并且它们发生的可能性都相等,事件 A 包含其中 m 种结果,那么事件 A 发生的概率为:
5.在什么条件下适用 P(A)= 得到事件的概率?
6.如何用列举法求概率?
当事件要经过一步完成时列举出所有可能情况,当事件要经过两步完成时用列表法,当事件要经过三步及以上完成时用树状图法.
随堂练习
1.下面是两个可以自由转动的转盘,每个转盘被分成了三个相等的扇形,小明和小亮用它们做配紫色(红色与蓝色能配成紫色)游戏,你认为配成紫色与配不成紫色的概率相同吗?
A
B
一共有 9 种结果,每种结果出现的可能性相同,(红,蓝)能配紫色的有 5 种,概率为 ;不能配紫色的有 4 种,概率为 ,它们的概率不相同.
解:所有可能出现的结果如下:
红 红 蓝A
(红,红) (蓝,红) (蓝,红)
(红,红) (蓝,红) (蓝,红)
(红,蓝) (蓝,蓝) (蓝,蓝)
红 蓝 蓝 B
2.一个桶里有 60 个弹珠,一些是红色的,一些是蓝色的,一些是白色的.拿出红色弹珠的概率是 35%,拿出蓝色弹珠的概率是 25%,桶里每种颜色的弹珠各有多少?
解:60×35% = 21(个),
60×25% = 15(个),
60 - 21 - 15 = 24(个).
答:桶内有红色弹珠 21 个,蓝色弹珠 15 个,白色弹珠 24 个.
3.将一枚硬币连掷 3 次,出现“两反,一正”的概率是多少?
开始
正
反
正
反
正
反
正
反
正
反
正
反
正
反
解:根据题意,画出如下树状图,记出现“两反,一正”为事件 A,
故 P(A) = .
4.某校决定从三名男生和两名女生中选出两名同学担任校艺术节文艺演出专场的主持人,请用列表法或树状图法,求选出的恰为一男一女的概率.
解:列表如下:
男1 男2 男3 女1 女2
男1 ﹣﹣﹣ (男2,男1) (男3,男1) (女1,男1) (女2,男1)
男2 (男1,男2) ﹣﹣﹣ (男3,男1) (女1,男2) (女2,男2)
男3 (男1,男3) (男2,男3) ﹣﹣﹣ (女1,男3) (女2,男3)
女1 (男1,女1) (男2,女1) (男3,女1) ﹣﹣﹣ (女2,女1)
女2 (男1,女2) (男2,女2) (男3,女2) (女1,女2) ﹣﹣﹣
所有等可能的情况有 20 种,其中一男一女的情况有12 种,则 P(一男一女) = .
1.概率的定义及基本性质
如果在一次试验中,有 n 种可能的结果,并且他们
发生的可能性都相等,事件 A 包含其中的 m 种结果,那么事件 A 发生的概率 P(A) = .
0≤m≤n,有 0≤ ≤1 .
课堂小结
2.必然事件 A,则 P(A)=1;
不可能事件 B,则 P(B)=0;
随机事件 C,则 0<P(C)<1.
当事件经过一步完成时,列举出所有可能情况;
当事件要经过两步完成时,用列表法;
当事件要经过三步以上完成时,用树状图法.
当试验的所有可能结果不是有限个或各种可能结果发生的可能性不相等时,常常通过统计频率来估计概率,即在同样条件下,大量重复试验所得到的随机事件发生的频率的稳定值来估计这个事件发生概率.
