华东师大版九年级数学上册22.2一元二次方程的解法第5课时一元二次方程的根与系数的关系课件
文档属性
| 名称 | 华东师大版九年级数学上册22.2一元二次方程的解法第5课时一元二次方程的根与系数的关系课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 499.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 07:43:07 | ||
图片预览





文档简介
(共19张PPT)
1. 了解一元二次方程根与系数的关系;(重点)
2. 会应用一元二次方程根与系数的关系. (难点)
学习目标
2.求根公式是什么?根的个数怎么确定的?
1.一元二次方程的解法有哪些,步骤呢?
知识回顾
导入新课
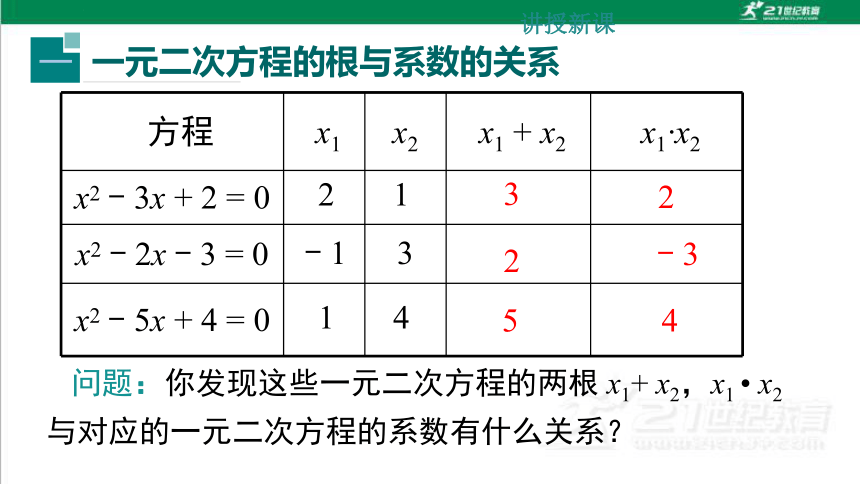
方程 x1 x2 x1 + x2 x1 x2
x2 - 3x + 2 = 0
x2 - 2x - 3 = 0
x2 - 5x + 4 = 0
问题:你发现这些一元二次方程的两根 x1+ x2,x1 x2 与对应的一元二次方程的系数有什么关系?
2 1
3
2
- 1 3
2
- 3
1 4
5
4
一元二次方程的根与系数的关系
一
讲授新课
方 程
- 2
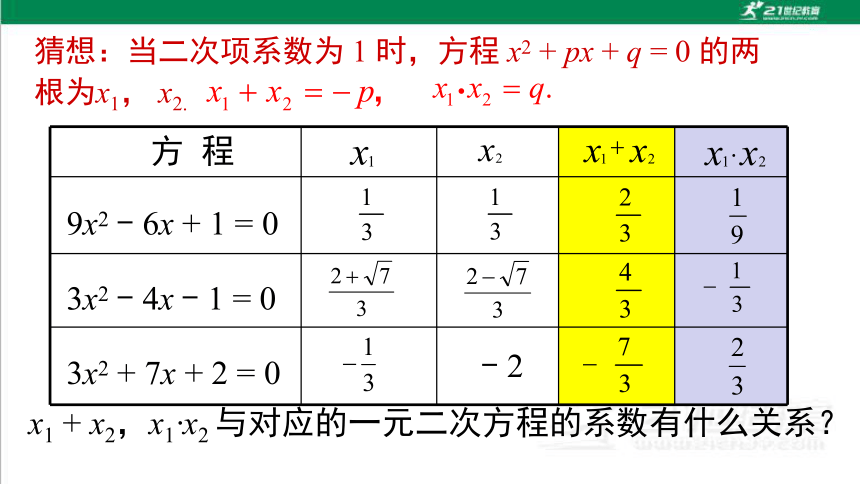
x1 + x2,x1 x2 与对应的一元二次方程的系数有什么关系?
猜想:当二次项系数为 1 时,方程 x2 + px + q = 0 的两根为x1, x2.
9x2 - 6x + 1 = 0
3x2 - 4x - 1 = 0
3x2 + 7x + 2 = 0
如果 ax2 + bx + c = 0 ( a、b、c 是常数,a ≠ 0) 的两个根为 x1, x2,则
b2 - 4ac≥0.
由二次项系数为1的一元二次方程根与系数的关系,可得
猜想
解:
任何一个一元二次方程的根与系数的关系:
如果方程 ax2 + bx + c = 0 (a ≠ 0) 的两个根是 x1,x2,
那么
(韦达定理)
注:能用根与系数的关系的前提条件为 b2 - 4ac≥0.
一、直接运用根与系数的关系
例1 不解方程,求下列方程两根的和与积.
利用一元二次方程的根与系数的关系解决问题
二
在使用根与系数的关系时,应注意:
(1)不是一般式的要先化成一般式;
(2)在使用 时,注意“- ”不要漏写.
二、求关于两根的代数式的值
例2 设 x1,x2 是方程 2x + 4x - 3 = 0 的两个根,利用根与系数的关系,求下列各式的值.
解:由题意知
三、构造新方程
例3 求一个一元二次方程,使它的两个根是 2 和 3,且二次项系数为 1.
解:(x - 2)(x - 3)=0,
x2 - 5x + 6 = 0.
例4 方程 的两根的和为 6,一根为 2,求 p、q 的值.
四、求方程中的待定系数
解:若方程的另一个根为 x1,由题意得
2 + x1 = - p = 6,2x1 = q,
即 x1 = 4,p = - 6,q = 8.
1.关于 x 的方程 有一个正根,一个负根,求 m 的取值范围.
解:由已知得
即
m>0
m - 1<0
∴0<m<1
当堂练习
2. 求一个一元二次方程,使它的两个根是 2 和 3,且二次项系数为 5.
解: 5(x - 2)(x - 3) = 0,
5x2 - 25x + 30 = 0.
一元二次方程的根与系数的关系
如果 ax2 + bx + c = 0 (a ≠ 0) 的两个根为 x1, x2,那么
注意
满足上述关系的前提条件
b2 - 4ac≥0.
课堂小结
一正根,一负根
Δ >0
x1x2<0
两个正根
Δ ≥0
x1x2>0
x1+x2>0
两个负根
Δ ≥0
x1x2>0
x1+x2<0
1. 了解一元二次方程根与系数的关系;(重点)
2. 会应用一元二次方程根与系数的关系. (难点)
学习目标
2.求根公式是什么?根的个数怎么确定的?
1.一元二次方程的解法有哪些,步骤呢?
知识回顾
导入新课
方程 x1 x2 x1 + x2 x1 x2
x2 - 3x + 2 = 0
x2 - 2x - 3 = 0
x2 - 5x + 4 = 0
问题:你发现这些一元二次方程的两根 x1+ x2,x1 x2 与对应的一元二次方程的系数有什么关系?
2 1
3
2
- 1 3
2
- 3
1 4
5
4
一元二次方程的根与系数的关系
一
讲授新课
方 程
- 2
x1 + x2,x1 x2 与对应的一元二次方程的系数有什么关系?
猜想:当二次项系数为 1 时,方程 x2 + px + q = 0 的两根为x1, x2.
9x2 - 6x + 1 = 0
3x2 - 4x - 1 = 0
3x2 + 7x + 2 = 0
如果 ax2 + bx + c = 0 ( a、b、c 是常数,a ≠ 0) 的两个根为 x1, x2,则
b2 - 4ac≥0.
由二次项系数为1的一元二次方程根与系数的关系,可得
猜想
解:
任何一个一元二次方程的根与系数的关系:
如果方程 ax2 + bx + c = 0 (a ≠ 0) 的两个根是 x1,x2,
那么
(韦达定理)
注:能用根与系数的关系的前提条件为 b2 - 4ac≥0.
一、直接运用根与系数的关系
例1 不解方程,求下列方程两根的和与积.
利用一元二次方程的根与系数的关系解决问题
二
在使用根与系数的关系时,应注意:
(1)不是一般式的要先化成一般式;
(2)在使用 时,注意“- ”不要漏写.
二、求关于两根的代数式的值
例2 设 x1,x2 是方程 2x + 4x - 3 = 0 的两个根,利用根与系数的关系,求下列各式的值.
解:由题意知
三、构造新方程
例3 求一个一元二次方程,使它的两个根是 2 和 3,且二次项系数为 1.
解:(x - 2)(x - 3)=0,
x2 - 5x + 6 = 0.
例4 方程 的两根的和为 6,一根为 2,求 p、q 的值.
四、求方程中的待定系数
解:若方程的另一个根为 x1,由题意得
2 + x1 = - p = 6,2x1 = q,
即 x1 = 4,p = - 6,q = 8.
1.关于 x 的方程 有一个正根,一个负根,求 m 的取值范围.
解:由已知得
即
m>0
m - 1<0
∴0<m<1
当堂练习
2. 求一个一元二次方程,使它的两个根是 2 和 3,且二次项系数为 5.
解: 5(x - 2)(x - 3) = 0,
5x2 - 25x + 30 = 0.
一元二次方程的根与系数的关系
如果 ax2 + bx + c = 0 (a ≠ 0) 的两个根为 x1, x2,那么
注意
满足上述关系的前提条件
b2 - 4ac≥0.
课堂小结
一正根,一负根
Δ >0
x1x2<0
两个正根
Δ ≥0
x1x2>0
x1+x2>0
两个负根
Δ ≥0
x1x2>0
x1+x2<0
