华东师大版九年级数学上册23.1成比例线段第1课时成比例线段课件
文档属性
| 名称 | 华东师大版九年级数学上册23.1成比例线段第1课时成比例线段课件 |

|
|
| 格式 | ppt | ||
| 文件大小 | 731.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
1. 掌握相似图形的概念;(重点)
2. 了解成比例线段,比例的基本性质; (重点)
3. 能根据比例的基本性质解决相关问题.(难点)
学习目标
问题1 下面两张邮票有什么特点?有什么关系?
导入新课
情境引入
问题2 多啦 A 梦的 2 寸照片和 4 寸照片,它的形状改变了吗?大小呢?
下面图形有什么相同和不同的地方?
讲授新课
相似图形的概念
一
观察与思考
相同点:形状相同
不同点:大小不相同
相同形状的图形称为相似图形.
相似图形的大小不一定相同.
归纳:
线段的比和成比例线段
二
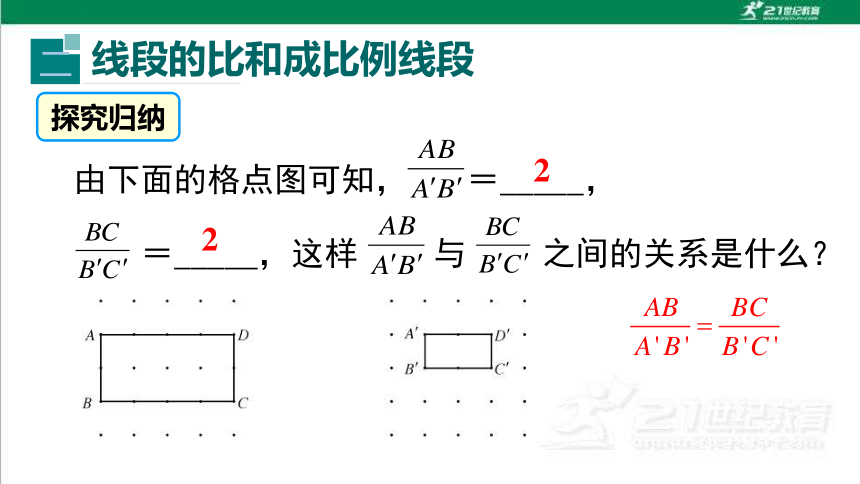
探究归纳
由下面的格点图可知, =_____,
=_____,这样 与 之间的关系是什么?
2
2
四条线段 a,b,c,d 中,如果其中两条线段的长度之比等于另外两条线段的长度比,如 (或 a : b = c : d ),那么这四条线段叫做成比例线段,简称比例线段.此时,也称这四条线段成比例.
归纳总结
两条线段的比就是它们长度的比;
、
2.已知 ,那么 各等于多少?
1.已知线段 a、b、c 满足关系式 ,
且 b = 4,那么 ac =______.
练一练
16
例 判断下列线段 a、b、c、d 是否是成比例线段:
(1)a=4,b=6,c=5,d=10;
解:(1)∵
∴ 线段 a、b、c、d 不是成比例线段.
,
∴
,
典例精析
(2)a=2,b=
,c=
,d=
.
(2) ∵
∴
∴ 线段 a、b、c、d 是成比例线段.
注意:
1. 若 a : b = k,说明 a 是 b 的 k 倍;
2. 两条线段的比与所采用的长度单位无关,但求比时两条线段的长度单位必须一致;
3. 两条线段的比值是一个没有单位的正数;
4. 除了 a = b 外,a : b ≠ b : a,
互为倒数.
如果 ,那么 ad=bc.如果 ad=bc (a、b、c、d 都不等于 0),那么 .
对于成比例线段,我们有下面的结论:
你还可以得到其他的等比例式吗?
比例的基本性质
三
例 证明:(1)如果 ,那么
;
证明:(1)∵
典例精析
∴在等式两边同加上 1.
证明:∵
∴ ad=bc.
∴ -ad = -bc. 等式两边同加上 ac
∴ ac-ad=ac-bc,
∴ a(c-d)=(a-b)c. 两边同除以(a-b)(c-d)
∴
(2)如果 ,那么 ( 其中 a ≠ b,c ≠ d ).
合比性质:
等比性质:
(b + d +···+ m ≠ 0)
拓展归纳
1.下列各组数中一定成比例的是( )
A. 2,3,4,5 B. -1,2,-2,4
C. -2,1,2,0 D. a,2b,c,2d
B
当堂练习
解:根据题意可知, ,
AB = 15, AC = 10,BD = 6.
则 AD = AB - BD =15 - 6 = 9.
则
3.已知 ,AB = 15,AC = 10,BD = 6.求 AE.
A
B
C
D
E
1. 比例的基本性质:
2. 常用方法:设元法,即设一份为 k.
3. 若线段 a,b,c,d 满足 ,则 a,b,c,d 叫做成比例线段,简称比例线段.
课堂小结
4. 比例线段的等价变形:
a : b = c : d
1. 掌握相似图形的概念;(重点)
2. 了解成比例线段,比例的基本性质; (重点)
3. 能根据比例的基本性质解决相关问题.(难点)
学习目标
问题1 下面两张邮票有什么特点?有什么关系?
导入新课
情境引入
问题2 多啦 A 梦的 2 寸照片和 4 寸照片,它的形状改变了吗?大小呢?
下面图形有什么相同和不同的地方?
讲授新课
相似图形的概念
一
观察与思考
相同点:形状相同
不同点:大小不相同
相同形状的图形称为相似图形.
相似图形的大小不一定相同.
归纳:
线段的比和成比例线段
二
探究归纳
由下面的格点图可知, =_____,
=_____,这样 与 之间的关系是什么?
2
2
四条线段 a,b,c,d 中,如果其中两条线段的长度之比等于另外两条线段的长度比,如 (或 a : b = c : d ),那么这四条线段叫做成比例线段,简称比例线段.此时,也称这四条线段成比例.
归纳总结
两条线段的比就是它们长度的比;
、
2.已知 ,那么 各等于多少?
1.已知线段 a、b、c 满足关系式 ,
且 b = 4,那么 ac =______.
练一练
16
例 判断下列线段 a、b、c、d 是否是成比例线段:
(1)a=4,b=6,c=5,d=10;
解:(1)∵
∴ 线段 a、b、c、d 不是成比例线段.
,
∴
,
典例精析
(2)a=2,b=
,c=
,d=
.
(2) ∵
∴
∴ 线段 a、b、c、d 是成比例线段.
注意:
1. 若 a : b = k,说明 a 是 b 的 k 倍;
2. 两条线段的比与所采用的长度单位无关,但求比时两条线段的长度单位必须一致;
3. 两条线段的比值是一个没有单位的正数;
4. 除了 a = b 外,a : b ≠ b : a,
互为倒数.
如果 ,那么 ad=bc.如果 ad=bc (a、b、c、d 都不等于 0),那么 .
对于成比例线段,我们有下面的结论:
你还可以得到其他的等比例式吗?
比例的基本性质
三
例 证明:(1)如果 ,那么
;
证明:(1)∵
典例精析
∴在等式两边同加上 1.
证明:∵
∴ ad=bc.
∴ -ad = -bc. 等式两边同加上 ac
∴ ac-ad=ac-bc,
∴ a(c-d)=(a-b)c. 两边同除以(a-b)(c-d)
∴
(2)如果 ,那么 ( 其中 a ≠ b,c ≠ d ).
合比性质:
等比性质:
(b + d +···+ m ≠ 0)
拓展归纳
1.下列各组数中一定成比例的是( )
A. 2,3,4,5 B. -1,2,-2,4
C. -2,1,2,0 D. a,2b,c,2d
B
当堂练习
解:根据题意可知, ,
AB = 15, AC = 10,BD = 6.
则 AD = AB - BD =15 - 6 = 9.
则
3.已知 ,AB = 15,AC = 10,BD = 6.求 AE.
A
B
C
D
E
1. 比例的基本性质:
2. 常用方法:设元法,即设一份为 k.
3. 若线段 a,b,c,d 满足 ,则 a,b,c,d 叫做成比例线段,简称比例线段.
课堂小结
4. 比例线段的等价变形:
a : b = c : d
