【期末押题卷】期末核心考点 应用题-2024-2025学年六年级下学期数学苏教版(含解析)
文档属性
| 名称 | 【期末押题卷】期末核心考点 应用题-2024-2025学年六年级下学期数学苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-14 15:56:13 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末核心考点 应用题
1.欣欣水果店运进10箱橘子,以每箱25kg为标准,超过的记为正数,不足的记为负数,称重记录如下:+1.5,﹣3.2,+2.5,﹣1.8,0,+1,﹣2,﹣1.4,+2,+2.4,将这10箱橘子的实际质量按由重到轻的顺序进行排列.(单位:kg)
2.小小百货店每个月的营业成本是12万元。下表是这家店今年上半年收入情况统计表,请你用正、负数表示盈亏情况。(盈利用正数表示,亏损用负数表示)请你想办法计算一下小小百货店上半年是盈利了还是亏损了?盈利或亏损多少万元?
一月份 二月份 三月份 四月份 五月份 六月份
14万元 15万元 11万元 12万元 16万元 11万元
3.8名学生进行仰卧起坐达标检测,1分钟满30个则为达标,超过的记为正,不足的记为负,8名学生在30个达标的基础上的记录分别为:3、﹣2、0、1、﹣4、5、2、﹣3。这些同学中有几名达标?这8名同学一共做了多少个仰卧起坐?
4.一只梅花鹿从起点向前跳5米,再向后跳4米,又朝前跳7米,朝后跳10米,然后停下休息。你知道梅花鹿停在起点前还是起点后?与起点相距几米?
5.王钢把50000元人民币存入银行,定期2年,年利率是2.7%.到期时,王钢应得本金和利息一共多少元?
6.个人所得税法规定:从2008年3月1日起公民每月工资(薪金)所得未超过2000元的部分不纳税,超过2000元的部分为本月应纳税所得额.此项纳税按如表累进计算:
全月应纳税所得额 税率
不超过500元的部分 5%
超过500元至2000元的部分 10%
超过2000元至5000元的部分 15%
超过5000元至20000元的部分 20%
(1)姚老师3月份工资收入3400元,交纳税款后实际收入多少元?
(2)薛老师是一位名校长,3月份工资收入5800元,应交纳税款多少元?
7.某商场用“满300送100”的办法来促销,即购物满300元,赠送100元“礼券”,超过但不足300元的部分略去不计。如购买720元商品,可获是两张100元“礼券”,多余120元略去不计。“礼券”在下次购物时代替现金,但“礼券”部分不能再享受“满300送100”的优惠。一位顾客先用1000元购了A商品,得到“礼券”后,又用这些“礼券”和200元现金购了B商品,那么这位顾客购买A、B两种商品相当于几折优惠?
8.李欣按九折的优惠价格购买了2张足球赛门票,共用去540元。每张门票的原价是多少元?
9.一个数,添上百分号后减少了29.7,这个数原来是多少?
10.某公司进行年终分红,规定按下面的规则将钱平均分给每个人,第一个人先取1元,再取余下的;接着第二人先取2元,再取余下的;如此继续下去,第k个人先取k元,再取余下奖金的,最后奖金被分完,则公司有多少人参与分红?
11.工厂计划本月用电100度,实际用了80度电,实际比计划节约了百分之几?
12.中小学生营养午餐蛋白质摄入标准如表1,部分食物的蛋白质含量如表2。
表1:
年龄/岁 6~8 9~11 12~15
营养午餐蛋白质摄入标准/g 24 28 32
表2:
食物 鸡肉 鸡蛋 黄豆 胡萝卜 番茄 米饭
蛋白质含量 20% 13% 36% 0.6% 0.9% 3%
请你根据上述信息,给自己设计一份午餐食品清单,并写出你的思考过程。
13.把一个底面直径是20厘米,高是3厘米的圆柱形钢坯锻造成底面半径是5厘米的圆锥形钢坯,这个圆锥形钢坯的高是几厘米?(用方程解)
14.王师傅想利用下面的铁皮做一个底面直径40厘米、高40厘米的油桶,请你画出做这个油桶的示意图(接头处忽略不计),再计算出这个油桶的容积是多少升?(厚度忽略不计)
15.一个圆柱形容器,里面盛有一些水,有一个底面积为157平方厘米的圆锥形铁块浸没在容器内,把铁块从容器中拿出来后,水面下降了2厘米。如果这个容器底面半径是10厘米,那么这个圆锥形铁块的高是多少厘米?
16.工厂要加工一批无盖的圆柱形铁皮水桶,底面直径是40厘米,高是45厘米。做一个这样的水桶至少要用多少平方厘米铁皮?(不考虑接缝处面积)
17.在一张长方形彩纸上摆满小正方形,每个小正方形面积与所需小正方形的数量如表:
每个小正方形的面积/cm2 4 9 16
所需小正方形的数量/个 216 96 54
(1)每个小正方形的面积与所需小正方形的数量成 比例关系。
(2)如果采用面积是36cm2的小正方形来摆满这张长方形彩纸,需要多少个小正方形?(用比例方法解答)
18.某工厂生产一批零件,原计划每天生产25件,18天完成任务。实际每天多生产20%,可提前几天完成任务?(用比例知识解答)
19.甲、乙两车间原有人数的比为4:3,从甲车间调12人到乙车间后,甲、乙两车间的人数比变为2:3,甲车间原有多少人?
20.今年三毛和二毛的年龄比是7:5,五年后,三毛与二毛的年龄比是13:10,问两人今年各几岁?
21.一间教室要用方砖铺地,用面积是64平方分米的方砖要90块,如果改用6分米的方砖,需要多少块?(用比例解)
22.王爷爷家新建了一座房。王奶奶对王爷爷说:“咱们家的客厅用边长为0.6米的方砖铺地,正好需要128块。”王爷爷不同意,坚持用边长8dm的方砖铺。请你用比例算一下,按王爷爷的想法,客厅需要多少块方砖?
23.用96厘米长的铁丝围成一个长方体,长、宽、高的比是5:3:4,这个长方体的体积是多少立方厘米?
24.一间教室,用面积是25平方分米的地砖铺地,需要320块.如果用面积是16平方分米的地砖铺,需要多少块?(用比例解)
25.把43颗玻璃球放入下面的盒子中,一定有一个盒子中至少放入多少颗玻璃球?
26.袋子里有4只红手套,2只黑手套,2只紫手套。一次摸出几只手套才能保证至少有一只红手套?
27.如图所示,盒子中有4种不同颜色的球,小华蒙着眼睛往外摸球,至少要摸出多少个,才能保证摸出的球至少有3种不同的颜色?
28.把若干个苹果放进9个抽屉里,不管怎么放,要保证总有一个抽屉里至少放进3个苹果,苹果的总数至少有多少个?
29.滑雪场上共有1200人,滑雪运动员占;其中女滑雪运动员占滑雪运动员总人数的,滑雪场上有多少名女滑雪运动员?
30.果果用铁丝做了一个棱长是dm的正方体框架,一共用了多少厘米铁丝?(接头处忽略不计)
30.玲玲把一些一元的硬币如图摆放.
(1)照这样摆下去,摆6层用了多少枚硬币?
(2)如果用了45枚硬币摆成,这个等边三角形每条边上摆几枚硬币?
31.一串数:,,,,,,,,,,……
(1)第800个数是多少?
(2)是第几个数?
(3)前552个数的和是多少?
(4)前n个数的和能否等于106,如果能,试求出n的值,如果不能,试说明理由.
33.画出1路公共汽车的行走路线。
1路公共汽车从起点站向东偏北25°方向行驶2千米,接着向东行驶3千米,又向西偏北40°方向行驶2千米,又向北行驶1千米,最后向东偏南30°方向行驶4千米到终点上。
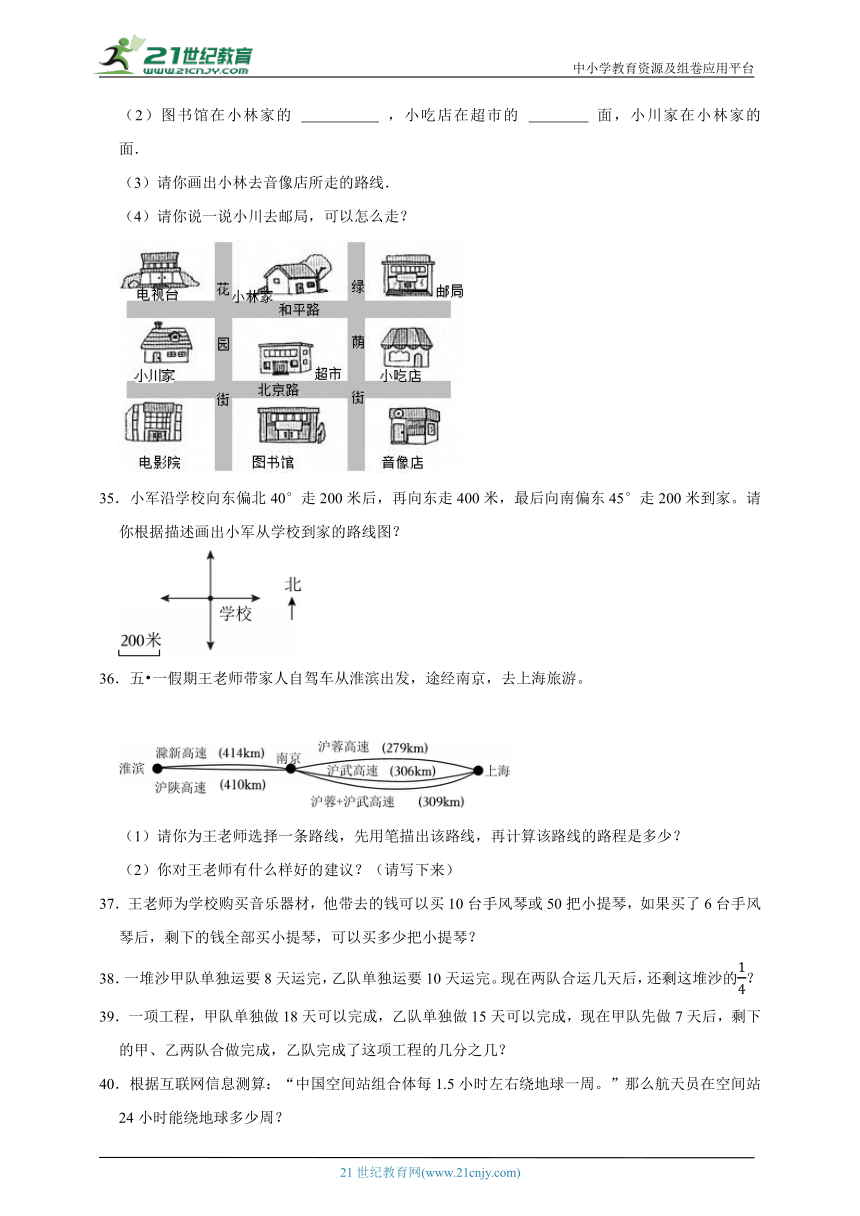
34.(1)花园街的西面有 、 、 .
(2)图书馆在小林家的 ,小吃店在超市的 面,小川家在小林家的 面.
(3)请你画出小林去音像店所走的路线.
(4)请你说一说小川去邮局,可以怎么走?
35.小军沿学校向东偏北40°走200米后,再向东走400米,最后向南偏东45°走200米到家。请你根据描述画出小军从学校到家的路线图?
36.五 一假期王老师带家人自驾车从淮滨出发,途经南京,去上海旅游。
(1)请你为王老师选择一条路线,先用笔描出该路线,再计算该路线的路程是多少?
(2)你对王老师有什么样好的建议?(请写下来)
37.王老师为学校购买音乐器材,他带去的钱可以买10台手风琴或50把小提琴,如果买了6台手风琴后,剩下的钱全部买小提琴,可以买多少把小提琴?
38.一堆沙甲队单独运要8天运完,乙队单独运要10天运完。现在两队合运几天后,还剩这堆沙的?
39.一项工程,甲队单独做18天可以完成,乙队单独做15天可以完成,现在甲队先做7天后,剩下的甲、乙两队合做完成,乙队完成了这项工程的几分之几?
40.根据互联网信息测算:“中国空间站组合体每1.5小时左右绕地球一周。”那么航天员在空间站24小时能绕地球多少周?
41.某市交警部门开展“一盔一带”安全守护行动,呼吁骑电动车的市民佩戴头盔。政策颁布后,头盔的销售量火爆。某商店第二天卖出108顶头盔,比第一天多卖出。商店第一天卖出多少顶头盔?(列方程解答)
42.如图,窗户比门高出了多少米?
43.一个圆形花坛的周长是62.8米,在它的周围铺一条宽为2米的小路,这条小路的面积是多少平方米?
44.一个环形砂轮,外圆半径是0.4米,环宽10厘米,这个环形砂轮的面积是多少?
45.有一个圆形花坛,半径是50米,王叔叔每天早晨绕花坛跑4圈,他每天早晨跑多少米?
46.一根7米长的绳子,绕树一周还余下0.72米,树的直径是多少米?
47.钟面上时针长6厘米,时针尖端走一天的距离是多少厘米?
48.原产非洲的“猴面包树”,它的树干非常粗,其中一棵“猴面包树”的直径为15.7m,如果用绳子绕它的树干一周,至少需要准备多长的绳子?
49.填表:
分数
小数 0.2 0.6
百分数 8% 12.5%
50.说一说下面百分数的具体含义。
(1)我国人口约占世界人口的22%。
(2)我国耕地面积约占世界耕地面积的7%。
(3)某发电厂4月份完成计划发电任务的115%。
51.某修路队上半年修路6400米,比原计划多修了1600米,这支修路队多修了百分之几?
52.近年来,各地“广场舞”噪音干扰的问题倍受关注。相关人员对本地区15~65岁年龄段的市民进行了随机调查,并制作了如下相应的统计图。市民对“广场舞”噪音干扰的态度有以下五种:A.没影响B.影响不大C.有影响,建议做无声运动D.影响很大,建议取缔E.不关心这个问题。
根据以上信息解答下列问题:
(1)根据统计图填空:m= 。
(2)在此次调查中,“不关心这个问题”的有25人,请问一共调查了 人。
(3)在此次调查中,持“影响不大”态度的人比持“没影响”态度的人多百分之 。
53.聪聪家2009年11月支出情况统计如图.聪聪家2009年11月的总支出是3600元.请你回答问题.
(1)这个月哪项支出最多?支出了多少元?
(2)文化教育支出了多少元?购买衣物支出了多少元?
(3)购买衣物的支出比文化教育支出少百分之几?
54.如图是我国国土各种地形所占百分比情况统计图。
(1)盆地占我国国土面积的 %。
(2)山地占我国国土面积的 %。
(3)高原所占面积与丘陵所占面积的最简单的整数比是 。
(4)我国国土面积约960万平方千米,平原的面积约是 万平方千米。
55.某小学参加兴趣小组情况如图:已知参加体育的有136人,参加“其它”兴趣小组的共有多少人?
56.每年的4月23日是“世界读书日”,为深入推进全民阅读,培育良好的阅读习惯。实验小学新进一批图书,情况统计如图。已知科技书和童话故事的本数比是3:5。
(1)实验小学新进的这批图书共有多少本?
(2)儿童文学有多少本?
57.如图是1班和2班的男生和女生的人数统计图,已知两个班的人数都不少于30,也不多于40,则1班有多少名学生,2班有多少名学生?
期末核心考点 应用题
参考答案与试题解析
1.欣欣水果店运进10箱橘子,以每箱25kg为标准,超过的记为正数,不足的记为负数,称重记录如下:+1.5,﹣3.2,+2.5,﹣1.8,0,+1,﹣2,﹣1.4,+2,+2.4,将这10箱橘子的实际质量按由重到轻的顺序进行排列.(单位:kg)
【答案】见试题解答内容
【分析】(1)正数>0>负数;
(2)负数大小比较就是看负号后面的数字,数字越大的反而越小,跟正数恰好相反;
由此比较出这些数据,即可求解.
【解答】解:比较可得:
+2.5>+2.4>+2>+1.5>+1>0>﹣1.4>﹣1.8>﹣2>﹣3.2.
【要点】此题考查正负数的大小比较的方法,要熟练掌握.
2.小小百货店每个月的营业成本是12万元。下表是这家店今年上半年收入情况统计表,请你用正、负数表示盈亏情况。(盈利用正数表示,亏损用负数表示)请你想办法计算一下小小百货店上半年是盈利了还是亏损了?盈利或亏损多少万元?
一月份 二月份 三月份 四月份 五月份 六月份
14万元 15万元 11万元 12万元 16万元 11万元
【答案】+2、+3、﹣1、0、+4、﹣1。盈利,7万元。
【分析】用正负数表示意义相反的两种量:高于营业成本记作正,则低于营业成本就记作负。由此得解。正负数相加,看最后是正数还是负数即可。
【解答】解:
一月份 二月份 三月份 四月份 五月份 六月份
14万元 15万元 11万元 12万元 16万元 11万元
+2 +3 ﹣1 0 +4 ﹣1
+2+3﹣1+0+4﹣1=+7(万元)
答:盈利7万元。
【要点】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
3.8名学生进行仰卧起坐达标检测,1分钟满30个则为达标,超过的记为正,不足的记为负,8名学生在30个达标的基础上的记录分别为:3、﹣2、0、1、﹣4、5、2、﹣3。这些同学中有几名达标?这8名同学一共做了多少个仰卧起坐?
【答案】5名;242个。
【分析】正数和0共有5个,也就是这些同学中有5名达标;求出3、﹣2、0、1、﹣4、5、2、﹣3的和,再加上30×8就是这8名同学一共做了多少个仰卧起坐。
【解答】解:3﹣2+0+1﹣4+5+2﹣3+30×8
=2+240
=242(个)
答:这些同学中有5名达标,这8名同学一共做了242个仰卧起坐。
【要点】根据正、负数的意义,解答此题即可。
4.一只梅花鹿从起点向前跳5米,再向后跳4米,又朝前跳7米,朝后跳10米,然后停下休息。你知道梅花鹿停在起点前还是起点后?与起点相距几米?
【答案】起点后,2米。
【分析】用正负数表示意义相反的两种量:向前跳记作正,则向后跳就记作负。把所有数据用正负数表示并相加,求出最后位置即可。
【解答】解:+5﹣4+7﹣10=﹣2(米)
答:梅花鹿停在起点后,与起点相距2米。
【要点】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
5.王钢把50000元人民币存入银行,定期2年,年利率是2.7%.到期时,王钢应得本金和利息一共多少元?
【答案】见试题解答内容
【分析】在此题中,本金是50000元,时间是2年,利率是2.7%,求本息,运用关系式:本息=本金+本金×年利率×时间,解决问题.
【解答】解:50000+50000×2.7%×2
=50000+2700
=52700(元)
答:王钢应得本金和利息一共52700元.
【要点】这种类型属于利息问题,运用关系式“本息=本金+本金×年利率×时间”,代入数据,解决问题.
6.个人所得税法规定:从2008年3月1日起公民每月工资(薪金)所得未超过2000元的部分不纳税,超过2000元的部分为本月应纳税所得额.此项纳税按如表累进计算:
全月应纳税所得额 税率
不超过500元的部分 5%
超过500元至2000元的部分 10%
超过2000元至5000元的部分 15%
超过5000元至20000元的部分 20%
(1)姚老师3月份工资收入3400元,交纳税款后实际收入多少元?
(2)薛老师是一位名校长,3月份工资收入5800元,应交纳税款多少元?
【答案】见试题解答内容
【分析】(1)根据题意,姚老师3月份工资收入3400元,超过2000元的部分为1400元,这1400元当中的500元按5%纳税,其余的900元按10%纳税,用工资收入3400元分别减去交纳的税款即得实际收入;
(2)此题应分类交税,工资收入5800元,超过2000元的部分为3800元,先求不超过500元的部分应交税500×5%=25(元),超过500元至2000元的部分应交税(2000﹣500)×10%=130(元),剩余部分应缴纳(3800﹣500﹣1500)×15%,把这三部分加起来,即为所求.
【解答】解:(1)3400﹣2000=1400(元)
500×5%=25(元)
(1400﹣500)×10%
=900×10%
=90(元)
3400﹣25﹣90=3285(元)
答:交纳税款后实际收入3285元.
(2)5800﹣2000=3800(元)
不超过500元的部分应交税:
500×5%=25(元)
超过500元至2000元的部分应交税:
(2000﹣500)×10%
=1500×10%
=150(元)
剩余部分应缴纳:
(3800﹣500﹣1500)×15%
=1800×15%
=270(元)
25+150+270=445(元)
答:应交纳税款445元.
【要点】(1)先求出应交税多少元,再求交纳税款后实际收入多少元;
(2)解答这一题应注意分类交税.
7.某商场用“满300送100”的办法来促销,即购物满300元,赠送100元“礼券”,超过但不足300元的部分略去不计。如购买720元商品,可获是两张100元“礼券”,多余120元略去不计。“礼券”在下次购物时代替现金,但“礼券”部分不能再享受“满300送100”的优惠。一位顾客先用1000元购了A商品,得到“礼券”后,又用这些“礼券”和200元现金购了B商品,那么这位顾客购买A、B两种商品相当于几折优惠?
【答案】这位顾客购买A、B两种商品相当于8折优惠。
【分析】1000÷300=3……100,则可知一位顾客先用1000元购了A商品,得到“礼券”为3张,又用这些“礼券”和200元现金购了B商品,则可知B产品价格为300+200=500(元),所以A、B两种商品的价格和为1000+500=1500(元),实际顾客花了1000+200=1200(元)。据此运算即可获得实际几折优惠。
【解答】解:1000÷300=3……100
3×100=300(元)
300+200=500(元)
1000+500=1500(元)
1000+200=1200(元)
1200÷1500×100%
=0.8×100%
=80%
答:这位顾客购买A、B两种商品相当于8折优惠。
【要点】本题考查折扣问题。购买金额÷原价金额×100%=折扣。
8.李欣按九折的优惠价格购买了2张足球赛门票,共用去540元。每张门票的原价是多少元?
【答案】300元。
【分析】九折是指现价是原价的90%,把原价看成单位“1”,它的90%就是现价540元,用540除以这个分率求出原来2张的原价,再除以2即可求出每张门票的原价是多少元。
【解答】解:540÷90%=600(元)
600÷2=300(元)
答:每张门票的原价是300元。
【要点】本题关键是理解打折的含义:打几折,现价就是原价的百分之几十;打几几折,现价就是原价的百分之几十几。
9.一个数,添上百分号后减少了29.7,这个数原来是多少?
【答案】30。
【分析】在一个数(这个数不等于0)的后面添上百分号,相当于把这个数的小数点向移动2位,这个数缩小到原来的,由此可知:这个数的(1﹣1%)是29.7,根据已知一个数的几分之几是多少,求这个数,用除法解答即可。
【解答】解:29.7÷(1﹣1%)
=29.7÷0.99
=30
答:这个数原来是30。
【要点】此题考查百分数的意义,在一个数(这个数不等于0)的后面添上百分号相当于小数点向左移动2位,这个数缩小到原来的,据此解答即可。
10.某公司进行年终分红,规定按下面的规则将钱平均分给每个人,第一个人先取1元,再取余下的;接着第二人先取2元,再取余下的;如此继续下去,第k个人先取k元,再取余下奖金的,最后奖金被分完,则公司有多少人参与分红?
【答案】2020人。
【分析】根据题目中描述的分红规则来建立方程解答,首先设总钱数为一个未知数x,然后根据每个人取钱的规则列出方程,最后通过解方程求出总钱数,再根据总钱数求出每人分到的钱数,进而得出参与分红的人数。
【解答】解:设总钱数为x元。
第一个人先取1元,此时剩下(x﹣1)元,再取余下的,即(x﹣1)(元)
所以第1个人共取钱数为:1(元)
第二个人先取2元,此时剩下(x2)元,再取余下的,即(x2)(元)
所以第2个人共取钱数为:2(元)
因为最后奖金被分完,即第一个人分的钱和第二个分的钱相等(这里假设只有2个人先进行分析,实际对于任意相邻的人分的钱数是相等的),即列方程为:
解得:x=4080400
所以每人分得钱数为:(4080400+2020)÷2021=2020(元)
即参与分红的人数为4080400÷2020=2020(人)
答:公司有2020人参与分红。
【要点】解答此题的关键是通过设未知数,根据每人分红金额相同的求出一共分红的金额。
11.工厂计划本月用电100度,实际用了80度电,实际比计划节约了百分之几?
【答案】见试题解答内容
【分析】先求出节约了多少度,然后把计划用电的度数看作单位“1”,求节约的度数占计划投资的百分之几,根据求一个数是另一个数的百分之几,用除法解答.
【解答】解:(100﹣80)÷100
=20÷100
=20%;
答:实际比计划节约了20%.
【要点】解答此题的关键是:先求出节约了多少度,再判断出单位“1”,然后根据求一个数是另一个数的百分之几,用除法解答.
12.中小学生营养午餐蛋白质摄入标准如表1,部分食物的蛋白质含量如表2。
表1:
年龄/岁 6~8 9~11 12~15
营养午餐蛋白质摄入标准/g 24 28 32
表2:
食物 鸡肉 鸡蛋 黄豆 胡萝卜 番茄 米饭
蛋白质含量 20% 13% 36% 0.6% 0.9% 3%
请你根据上述信息,给自己设计一份午餐食品清单,并写出你的思考过程。
【答案】蛋白质32克;我的午餐食品清单:100克米饭;74克鸡肉;50克胡萝卜;100克番茄;100克鸡蛋。(答案不唯一)
【分析】根据题意,先根据人物的年龄,找出午餐应摄入蛋白质的重量。然后用食物的重量乘食物的蛋白质含量的百分比,求出食物中蛋白质的重量,然后将各种食物的蛋白质的重量相加,如果和等于午餐应摄入蛋白质的重量,即可解答。
【解答】解:米饭:100×3%=3(克)
鸡肉:74×20%=14.8(克)
胡萝卜:50×0.6%=0.3(克)
番茄:100×0.9%=0.9(克)
鸡蛋:100×13%=13(克)
3+14.8+0.3+0.9+13
=17.8+0.3+0.9+13
=18.1+0.9+13
=19+13
=32(克)
答:我今年12岁,午餐应摄入蛋白质32克。
我的午餐食品清单:100克米饭;74克鸡肉;50克胡萝卜;100克番茄;100克鸡蛋。(答案不唯一)
【要点】此题考查了百分数的意义及应用,要求学生掌握。
13.把一个底面直径是20厘米,高是3厘米的圆柱形钢坯锻造成底面半径是5厘米的圆锥形钢坯,这个圆锥形钢坯的高是几厘米?(用方程解)
【答案】36厘米。
【分析】圆柱形钢坯锻造成圆锥形钢坯,说明它们的体积相等,根据圆柱的体积公式:V=πr2h,圆锥的体积公式:VSh,分别表示出二者体积,根据体积相等列方程解答即可。
【解答】解:设这个圆锥形钢坯的高是x厘米。
3.14×52×x3.14×(20÷2)2×3
3.14×25×x3.14×100×3
25x=900
x=36
答:这个圆锥形钢坯的高是36厘米。
【要点】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式。
14.王师傅想利用下面的铁皮做一个底面直径40厘米、高40厘米的油桶,请你画出做这个油桶的示意图(接头处忽略不计),再计算出这个油桶的容积是多少升?(厚度忽略不计)
【答案】50.24升。
【分析】根据题意,要制作底面直径40厘米、高40厘米的油桶,先画出两个直径40厘米的圆作油桶的上下底,再画出一个直径40厘米圆的周长作长方形的长,宽为40厘米的长方形,即可制作这个油桶;再根据圆柱的体积(容积)公式V=Sh,即可解答。
【解答】解:3.14×40=125.6(厘米)
3.14×(40÷2)2×40
=3.14×202×40
=3.14×400×40
=50240(立方厘米)
50240立方厘米=50.24立方分米=50.24升
答:这个油桶的容积是50.24升。
【要点】此题考查的目的是理解掌握圆柱的特征,以及圆柱体积(容积)公式的灵活运用。
15.一个圆柱形容器,里面盛有一些水,有一个底面积为157平方厘米的圆锥形铁块浸没在容器内,把铁块从容器中拿出来后,水面下降了2厘米。如果这个容器底面半径是10厘米,那么这个圆锥形铁块的高是多少厘米?
【答案】12厘米。
【分析】圆锥体铁块浸没在容器中,从容器中拿出来后,水面下降了2厘米,则圆锥的体积即下降的水的体积,根据圆柱的体积公式:V=πr2h,求出上升水的体积,再根据圆锥的体积公式:VSh,变式求高:h=3V÷S,代入数值计算即可。
【解答】解:下降的水的体积为:
3.14×10×10×2
=31.4×10×2
=314×2
=628(立方厘米)
圆锥铁块的高为:
628×3÷157
=1884÷157
=12(cm)
答:这个圆锥体的高是12厘米。
【要点】本题主要考查了圆柱和圆锥的体积公式,需要学生灵活运用,并能正确辨别出题目中的有用数据及无用数据。
16.工厂要加工一批无盖的圆柱形铁皮水桶,底面直径是40厘米,高是45厘米。做一个这样的水桶至少要用多少平方厘米铁皮?(不考虑接缝处面积)
【答案】6908平方厘米。
【分析】先分清制作没有盖的圆柱形铁皮水桶,需要计算几个面的面积:侧面面积与底面圆的面积两个面,由圆柱体侧面积和圆的面积计算方法列式解答即可。
【解答】解:水桶的侧面积:3.14×40×45=5652(平方厘米)
水桶的底面积:
3.14×(40÷2)2
=3.14×202
=1256(平方厘米)
水桶的表面积:5652+1256=6908(平方厘米)
答:做一个这样的水桶要用6908平方厘米铁皮。
【要点】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
17.在一张长方形彩纸上摆满小正方形,每个小正方形面积与所需小正方形的数量如表:
每个小正方形的面积/cm2 4 9 16
所需小正方形的数量/个 216 96 54
(1)每个小正方形的面积与所需小正方形的数量成 反 比例关系。
(2)如果采用面积是36cm2的小正方形来摆满这张长方形彩纸,需要多少个小正方形?(用比例方法解答)
【答案】见试题解答内容
【分析】(1)每个小正方形的面积×小正方形的数量=长方形彩纸的面积;长方形彩纸的面积一定,每个小正方形的面积与所需小正方形的数量成反比例关系。
(2)长方形彩纸的面积=36×需要小正方形个数,由此解答。
【解答】解:(1)长方形彩纸的面积一定,每个小正方形的面积与所需小正方形的数量成反比例关系。
(2)设需要多x个小正方形。
36x=216×4
36x÷36=216×4÷36
x=24
答:(1)每个小正方形的面积与所需小正方形的数量成反比例关系。
(2)需要24个小正方形。
故答案为:反,24。
【要点】解决此题关键是根据比值一定或乘积一定,先列出比例,进而根据比例的性质先把比例式转化为乘积式来解比例得解;注意等号要对齐。
18.某工厂生产一批零件,原计划每天生产25件,18天完成任务。实际每天多生产20%,可提前几天完成任务?(用比例知识解答)
【答案】3天。
【分析】把一批零件的总数看作单位“1“,批零件的总数一定,所以每天生产的件数与天数成反比例,设出未知数,列出比例计算即可。
【解答】解:设可提前x天完成任务。
25×18=25×(1+20%)×(18﹣x)
25×1.2×(18﹣x)=450
30×(18﹣x)=450
18﹣x=15
x=3
答:可提前3天完成任务。
【要点】本题考查了比较复杂的百分数和比例的问题。首先需要求出实际每天生产的件数。
19.甲、乙两车间原有人数的比为4:3,从甲车间调12人到乙车间后,甲、乙两车间的人数比变为2:3,甲车间原有多少人?
【答案】40人。
【分析】甲、乙两车间原有人数的比为4:3,则甲车间的人数占总人数的4÷(4+3),从甲车间调12人到乙车间后,甲、乙两车间的人数比变为2:3,这时甲车间的人数占总人数的2÷(2+3),则这12人占总人数的(),根据分数除法的意义,用12除以()求出总人数,再用总人数乘即可求出甲车间原有多少人。
【解答】解:4÷(4+3)
2÷(2+3)
12÷()
=12
=70(人)
7040(人)
答:甲车间原有40人。
【要点】本题考查了比较复杂的有关比和问题和分数的除法问题。
20.今年三毛和二毛的年龄比是7:5,五年后,三毛与二毛的年龄比是13:10,问两人今年各几岁?
【答案】21岁,15岁。
【分析】根据题意,设三毛和二毛今年的年龄分别是7x岁和5x岁,五年后,两个人的年龄分别是(7x+5)岁和(5x+5)岁,又知道5年后,三毛与二毛的年龄比是13:10,所以(7x+5)岁比上(5x+5)岁等于13:10,求出x,再分别求出两个人今年的年龄。
【解答】解:设三毛和二毛今年的年龄分别是7x岁和5x岁,
(7x+5):(5x+5)=13:10
10(7x+5)=13(5x+5)
70x+50=65x+65
70x﹣65x=65﹣50
5x=15
x=3
7x=7×3=21(岁)
5x=5×3=15(岁)
答:三毛今年是21岁,二毛今年是15岁。
【要点】本题考查了有关比的问题,关键是根据比的意义解答。
21.一间教室要用方砖铺地,用面积是64平方分米的方砖要90块,如果改用6分米的方砖,需要多少块?(用比例解)
【答案】160块。
【分析】这块地的面积是一定的,每块砖的面积与所需要的块数成反比例,设出未知数,列出比例式解答即可。
【解答】解:设需要方砖x块,由题意得:
6×6×x=64×90
36x=5760
x=160
答:需要方砖160块。
【要点】此题主要考查对反比例的意义的运用:两种相关联的量,一种量变化,另一种量也随着变化,但两种量的乘积一定,这两种量成反比例。
22.王爷爷家新建了一座房。王奶奶对王爷爷说:“咱们家的客厅用边长为0.6米的方砖铺地,正好需要128块。”王爷爷不同意,坚持用边长8dm的方砖铺。请你用比例算一下,按王爷爷的想法,客厅需要多少块方砖?
【答案】72块。
【分析】方砖的面积是边长乘边长,客厅地面的面积一定的,正方形方砖的面积乘块数就是客厅的面积,即正方形方砖的面积和块数的乘积是一定的,所以正方形方砖的面积和块数成反比例;列出比例式,即可得解。
【解答】解:设客厅需要x块方砖。
8dm=0.8m
0.6×0.6×128=0.8×0.8×x
46.08=0.64x
x=72
答:客厅需要72块方砖。
【要点】本题考查了正比例、反比例的应用。
23.用96厘米长的铁丝围成一个长方体,长、宽、高的比是5:3:4,这个长方体的体积是多少立方厘米?
【答案】480立方厘米。
【分析】用96除以4,求出长方体的长加宽加高的和,再把这个和按5:3:4进行分配,求出长方体的长、宽、高,再根据长方体体积=长×宽×高,即可解答。
【解答】解:96÷4=24(厘米)
2410(厘米)
246(厘米)
248(厘米)
10×6×8
=60×8
=480(立方厘米)
答;这个长方体的体积是480立方厘米。
【要点】本题考查的是按比例分配应用题,掌握按比例分配的方法是解答关键。
24.一间教室,用面积是25平方分米的地砖铺地,需要320块.如果用面积是16平方分米的地砖铺,需要多少块?(用比例解)
【答案】见试题解答内容
【分析】根据题意知道一间教室的面积,地砖的面积×地砖的块数=一间教室的面积(一定),所以地砖的面积与地砖的块数成反比例,设出未知数,列出比例解答即可.
【解答】解:设需要x块,
16x=25×320,
x,
x=500,
答:需要500块.
【要点】解答此题的关键是,根据题意,先判断哪两种相关联的量成何比例,即两个量的乘积一定则成反比例,两个量的比值一定则成正比例;再列出比例解答即可.
25.把43颗玻璃球放入下面的盒子中,一定有一个盒子中至少放入多少颗玻璃球?
【答案】见试题解答内容
【分析】把4个盒子看作4个抽屉,把43颗玻璃球看作43个元素,43÷4=10(颗)…3(颗),从最不利情况考虑,每个抽屉先放10颗,余下的这3颗无论放在那些抽屉里,总有一个抽屉里的有10+1=11(颗),据此解答.
【解答】解:43÷4=10(颗)…3(颗)
10+1=11(颗)
答:一定有一个盒子中至少放入11颗玻璃球.
【要点】此题考查了利用抽屉原理解决实际问题的灵活应用,关键是从最差情况考虑.
26.袋子里有4只红手套,2只黑手套,2只紫手套。一次摸出几只手套才能保证至少有一只红手套?
【答案】5只。
【分析】根据题干,最坏的情况是取出4只手套:2只黑手套,2只紫手套,此时剩下的全是红色手套,再任意取出1只,就能保证至少有一只红手套。
【解答】解:2+2+1=5(只)
答:一次摸出5只手套,才能保证至少有一只红手套。
【要点】此题主要考查了抽屉原理的灵活应用,要注意考虑最不利情况。
27.如图所示,盒子中有4种不同颜色的球,小华蒙着眼睛往外摸球,至少要摸出多少个,才能保证摸出的球至少有3种不同的颜色?
【答案】见试题解答内容
【分析】此题要从最差情况考虑:摸出5个红球、4个黑球共9个球,只有2种颜色的球,此时再摸出任意一个都会出现3种不同颜色的球,据此即可解答.
【解答】解:5+4+1
=9+1
=10(个)
答:至少要摸出10个球,才能保证摸出的球至少有3种不同的颜色.
【要点】此题考查抽屉原理的应用,注意考虑最差情况.
28.把若干个苹果放进9个抽屉里,不管怎么放,要保证总有一个抽屉里至少放进3个苹果,苹果的总数至少有多少个?
【答案】见试题解答内容
【分析】要保证总有一个抽屉里至少放进3个苹果,考虑最差情况:每个抽屉先都有2个苹果,此时苹果数最少是2×9=18个,再加上1个,即可出现一个抽屉里至少放进3个苹果,据此即可求出苹果最少有18+1=19个.
【解答】解:9×(3﹣1)+1
=18+1
=19(个)
答:苹果的总数至少有19个.
【要点】此题考查了利用抽屉原理解决实际问题的灵活应用,关键是从最差情况考虑.
29.滑雪场上共有1200人,滑雪运动员占;其中女滑雪运动员占滑雪运动员总人数的,滑雪场上有多少名女滑雪运动员?
【答案】24名。
【分析】根据题意,利用滑雪场上共有的人数滑雪运动员的人数,再利用滑雪运动员的人数女滑雪运动员的人数,据此计算解答。
【解答】解:1200
=60
=24(名)
答:滑雪场上有24名女滑雪运动员。
【要点】解答此题的关键是找准两个不同的单位“1”,利用求一个数的几分之几的计算方法解答。
30.玲玲把一些一元的硬币如图摆放.
(1)照这样摆下去,摆6层用了多少枚硬币?
(2)如果用了45枚硬币摆成,这个等边三角形每条边上摆几枚硬币?
【答案】(1)21;
(2)9。
【分析】观察图形可知,硬币的数量是从1开始的连续整数的和,整数得个数等于层数,而连续整数得和,等于整数的个数,乘第一个数与最后一个数的和,再除以2,据此规律计算即可。
【解答】解:(1)第六层有:
1+2+3+4+5+6
=6×(1+6)÷2
=6×7÷2
=42÷2
=21(个)
答:摆6层用了21个硬币。
(2)因为,45×2=90=9×10=9×(9+1)
所以,这个等边三角形有9层,也就是每个边上摆9个硬币。
答:这个等边三角形每条边上摆9枚硬币。
【要点】本题主要考查了数与形结合的规律,根据图形找出数的计算方法,再根据总数与层数的关系,确定有多少层,是本题解题的关键。
31.一串数:,,,,,,,,,,……
(1)第800个数是多少?
(2)是第几个数?
(3)前552个数的和是多少?
(4)前n个数的和能否等于106,如果能,试求出n的值,如果不能,试说明理由.
【答案】(1);(2)第261个数或第285个数;(3)287.5;(4)存在前n个数的和等于106,此时n的值是201。
【分析】观察数列,,,,,,,,,,……,可发现:分母为1的分数有1个,分母为2的数有3个,分母为3的数有5个,所以可得出:分母为n的分数有2n﹣1个;分子都是从1开始到与分母的数字相同连续的自然数,再倒数回到1,由此规律解决问题:
(1)首先要计算第800个数之前最大的平方是:当n=28时,n2=784,第784个数是分母为28的最后一个数,所以可以找到第800个数;
(2)先找出分母是16的最后一个数,是第162个数,162=256,再向右数5个即可,因为同一个分母的数除中间为1的数是出现一次外,其余都是出现2次,所以倒数第5个数也是,得出结论;
(3)同(1)同理,先计算第552个数之前最大的平方数:当n=23时,n2=529,先计算分母为1至23的所有分数之和:1+2+3+……+23的值,再确定第529到552之间数的和,最后相加即可;
(4)因为分母为n的分数有2n﹣1个,且这2n﹣1个分数相加和为n;所以分母为n时,前n2个数的和为,确定当n为最大时,最接近106时的n=14,即前196个数的和为105,与106还相差1,分母为15的分数能否达到几个分数和为1,来判断。
【解答】解:观察数列,,,,,,,,,,……,可发现:分母为1的分数有1个,分母为2的数有3个,分母为3的数有5个,所以可得出:分母为n的分数有2n﹣1个;且这2n﹣1个分数相加和为n.;第12个是分母为1的最后一个,第22个是分母为2的最后一个……,第n2个是分母为n的最后一个;
(1)因为1+3+5+…+2n﹣1=n2,
所以令n2≤800,
解得:n≤28,
当n=28时,n2=784,
所以第784个数是分母为28的最后一个数,
所以800个数的分母为29,分子为800﹣784=16,所以第800个数为;
(2)因为162+5=256+5=261,
172﹣4=289﹣4=285,
所以是第261个数或第285个数;
(3)令n2≤552,
解得:n≤23,
当n=23时,n2=529,
即前529个数的和为:1+2+3+……+23=24×11+12=276,
第530至第552个数之间一共有:
552﹣530+1=23个数,
第530至第552个数的和为:
11.5,
所以前552个数的和是:276+11.5=287.5;
(4)分母为n时,前n2个数的和为,当n=14时,前142=196个数的和为:
105,
第197个数开始为分母是15的数:
1,
105+1=106,
所以存在前n个数的和等于106,此时n=196+5=201。
故答案为:(1);(2)第261个数或第285个数;(3)287.5;(4)存在前n个数的和等于106,此时n的值是201。
【要点】解决本题的关键是找出规律,解决问题。
32.在下图中用阴影表示出平方米.
【答案】见试题解答内容
【分析】根据:4,把4平方米平均分成6份,每份就是平方米.
【解答】解:4
.
【要点】此题主要考查了分数除法的运算方法,以及分数的意义和应用,要熟练掌握.
33.画出1路公共汽车的行走路线。
1路公共汽车从起点站向东偏北25°方向行驶2千米,接着向东行驶3千米,又向西偏北40°方向行驶2千米,又向北行驶1千米,最后向东偏南30°方向行驶4千米到终点上。
【答案】
【分析】利用实际距离÷1即可求出图上距离;根据对地图上方向的规定,结合距离和角度求解,据此解答。
【解答】解:图上距离=实际距离÷比例尺
2÷1=2(厘米)
3÷1=3(厘米)
4÷1=4(厘米)
作图如下:
【要点】本题是一道关于确定位置方面的题目,可依据角度、方向与距离求解。
34.(1)花园街的西面有 电视台 、 小川家 、 电影院 .
(2)图书馆在小林家的 南面 ,小吃店在超市的 东 面,小川家在小林家的 西南 面.
(3)请你画出小林去音像店所走的路线.
(4)请你说一说小川去邮局,可以怎么走?
【答案】见试题解答内容
【分析】依据地图上的方向辨别方法,即“上北下南,左西右东”,以及图上标注的其他信息,即可进行解答.
【解答】解:(1)花园街的西面有 电视台、小川家、电影院.
(2)图书馆在小林家的 南面,小吃店在超市的 东面,小川家在小林家的 西南面.
(3)小林去音像店所走的路线如图所示:
(4)小川去邮局先沿北京路向东走,到达绿荫路后再向北走,
到达和平路后再向东走即可.
故答案为:电视台、小川家、电影院;南面、东、西南.
【要点】此题主要考查地图上的方向辨别方法的灵活应用.
35.小军沿学校向东偏北40°走200米后,再向东走400米,最后向南偏东45°走200米到家。请你根据描述画出小军从学校到家的路线图?
【答案】。
【分析】依据图示可知,图上1厘米代表实际距离200米,由此计算出向东走的图上距离,利用平面图上方向规定:上北下南,左西右东,依据题意结合图示去作图。
【解答】解:依据图示可知,图上1厘米代表实际距离200米,400÷200=2(厘米)
【要点】本题考查的是根据方向和距离确定物体的位置的应用。
36.五 一假期王老师带家人自驾车从淮滨出发,途经南京,去上海旅游。
(1)请你为王老师选择一条路线,先用笔描出该路线,再计算该路线的路程是多少?
(2)你对王老师有什么样好的建议?(请写下来)
【答案】(1),689千米;(2)言之有理即可,答案不唯一:节能减排,选择路程最短的线路。即从淮滨出发,选择沪陕高速,经410km到达南京,经停南京后选择沪蓉高速离开南京驶往上海,经279km到达上海。
【分析】(1)从淮滨到南京有2条线路,从南京到上海有3条线路,根据乘法原理可知,从淮滨到上海合计有(2×3)条线路,找一条线路画一画并根据加法的意义计算路程即可;
(2)言之有理即可,答案不唯一,比如本着节能减耗的目的,选择路线最短的。
【解答】解:(1)从淮滨出发,选择沪陕高速,经410km到达南京,经停南京后选择沪蓉高速离开南京驶往上海,经279km到达上海,如下图红色线路所示:
410+279=689(km)
答:该路线的路程是689千米。
(2)言之有理即可,答案不唯一:节能减排,选择路程最短的线路。即从淮滨出发,选择沪陕高速,经410km到达南京,经停南京后选择沪蓉高速离开南京驶往上海,经279km到达上海。
【要点】本题考查了千以内加法计算的应用以及路线图的应用。
37.王老师为学校购买音乐器材,他带去的钱可以买10台手风琴或50把小提琴,如果买了6台手风琴后,剩下的钱全部买小提琴,可以买多少把小提琴?
【答案】20把。
【分析】根据他带去的钱可以买10台手风琴或50把小提琴,可知买手风琴的钱数是买小提琴钱数的50÷10=5倍,如果买了6台手风琴后,剩下的钱数能买10﹣6=4(台)手风琴,剩下的钱全部买4×5=20(台)小提琴,据此解答。
【解答】解:50÷10=5
10﹣6=4(台)
4×5=20(台)
答:可以买20把小提琴。
【要点】本题考查的是工程问题,求出买手风琴的钱数是买小提琴钱数的50÷10=5倍是解答关键。
38.一堆沙甲队单独运要8天运完,乙队单独运要10天运完。现在两队合运几天后,还剩这堆沙的?
【答案】天。
【分析】把这堆沙子的重量看作单位“1”,甲队单独运要8天运完,可知甲车的工效是,乙队单独运要10天运完,可知,乙车的工效是,要求几天后还剩下这堆沙子的,依据工作时间=工作总量÷工作效率即可解答。
【解答】解:(1)÷()
(天)
答:现在两队合运天后,还剩这堆沙的。
【要点】解答本题的关键是明确等量关系式:工作时间=工作总量÷工作效率。
39.一项工程,甲队单独做18天可以完成,乙队单独做15天可以完成,现在甲队先做7天后,剩下的甲、乙两队合做完成,乙队完成了这项工程的几分之几?
【答案】。
【分析】已知甲队单独做18天可以完成,乙队单独做15天可以完成,把一项工程看作单位“1”,根据工作效率=工作总量÷工作时间,甲队的工作效率为,乙队的工作效率为;甲队工作7天工作量为,剩下工作量为1;根据工作量÷效率和=甲乙两队完成剩下工作量的时间;用所求时间×乙队的工作效率=乙队的工作量,据此解答。
【解答】解:(1﹣7)÷()
=5
答:乙队完成了这项工程的。
【要点】理清题中数量关系是解答关键。
40.根据互联网信息测算:“中国空间站组合体每1.5小时左右绕地球一周。”那么航天员在空间站24小时能绕地球多少周?
【答案】16周。
【分析】用24小时除以中国空间站组合体绕地球一周的时间即可。
【解答】解:24÷1.5=16(周)
答:航天员在空间站24小时能绕地球16周。
【要点】本题主要考查小数除法的应用。
41.某市交警部门开展“一盔一带”安全守护行动,呼吁骑电动车的市民佩戴头盔。政策颁布后,头盔的销售量火爆。某商店第二天卖出108顶头盔,比第一天多卖出。商店第一天卖出多少顶头盔?(列方程解答)
【答案】60顶。
【分析】首先根据题意,设商店第一天卖出x顶头盔;然后根据:第一天卖出头盔的数量×(1)=第二天卖出头盔的数量,列出方程,求出商店第一天卖出多少顶头盔即可。
【解答】解:设商店第一天卖出x顶头盔。
(1)x=108
x=108
x108
x=60
答:商店第一天卖出60顶头盔。
【要点】此题主要考查了一元一次方程的应用,弄清题意,找出合适的等量关系,进而列出方程是解答此类问题的关键。
42.如图,窗户比门高出了多少米?
【答案】见试题解答内容
【分析】先用窗户距离低面的高度加上窗户的高度,求出窗户的最高处距离地面多少米,再减去门的高度(门的最高处距离地面的长度),即可求出窗户比门高出了多少米?
【解答】解:1.63+0.75﹣2
=2.38﹣2
=0.38(米)
答:窗户比门高出了0.38米.
【要点】解答此题,首先观察图,弄清题意,分清已知与所求,再找出基本数量关系,由此列式解答.
43.一个圆形花坛的周长是62.8米,在它的周围铺一条宽为2米的小路,这条小路的面积是多少平方米?
【答案】138.16平方米。
【分析】根据环形面积=外圆面积﹣内圆面积,先求出花坛的半径,花坛的半径加上路宽就是外圆半径,然后把数据代入公式解答。
【解答】解:62.8÷3.14÷2=10(米)
3.14×[(10+2)2﹣102]
=3.14×[144﹣100]
=3.14×44
=138.16(平方米)
答:这条小路的面积是138.16平方米。
【要点】此题主要考查环形面积公式在实际生活中的应用,关键是熟记公式。
44.一个环形砂轮,外圆半径是0.4米,环宽10厘米,这个环形砂轮的面积是多少?
【答案】2198平方厘米。
【分析】先求出环形砂轮内圆的半径,则内、外圆的半径确定,要求圆环的面积,可直接利用公式S圆环=π(R2﹣r2)列式解答即可。
【解答】解:0.4米=40厘米
40﹣10=30(厘米)
3.14×(402﹣302)
=3.14×(1600﹣900)
=3.14×700
=2198(平方厘米)
答:这个环形砂轮的面积是2198平方厘米。
【要点】此题考查了圆环的面积计算,要先知道各自的半径,再利用公式进行计算。
45.有一个圆形花坛,半径是50米,王叔叔每天早晨绕花坛跑4圈,他每天早晨跑多少米?
【答案】见试题解答内容
【分析】根据圆的周长公式:C=2πr,把数据代入公式求出花坛的周长,然后乘4即可.
【解答】解:2×3.14×50×4
=314×4
=1256(米)
答:他每天早晨跑1256米.
【要点】此题主要考查圆的周长公式C=2πr在实际生活中的应用.
46.一根7米长的绳子,绕树一周还余下0.72米,树的直径是多少米?
【答案】见试题解答内容
【分析】先根据题目条件得到这棵树的周长,再根据圆的周长可求这棵树的直径..
【解答】解:(7﹣0.72)÷3.14
=6.28÷3.14
=2(米)
答:树的直径是2米.
【要点】考查了圆的周长在实际生活中的应用,本题关键是得到这棵树的周长.
47.钟面上时针长6厘米,时针尖端走一天的距离是多少厘米?
【答案】75.36厘米。
【分析】2×π×半径=圆的周长,圆的周长×2=时针尖端走一天的距离。
【解答】解:2×3.14×6×2
=37.68×2
=75.36(厘米)
答:时针尖端走一天的距离是75.36厘米。
【要点】本题主要考查圆的周公式的应用。
48.原产非洲的“猴面包树”,它的树干非常粗,其中一棵“猴面包树”的直径为15.7m,如果用绳子绕它的树干一周,至少需要准备多长的绳子?
【答案】见试题解答内容
【分析】根据圆的周长公式:C=πd,把数据代入公式求出树干的周长即可.
【解答】解:3.14×15.7=49.298(m)
答:至少需要准备49.298m长的绳子.
【要点】此题主要考查圆的周长公式在实际生活中的应用,关键是熟记公式.
49.填表:
分数
小数 0.2 0.6
百分数 8% 12.5%
【答案】见试题解答内容
【分析】百分数化小数的方法:去掉百分号,把小数点向左移动两位;
百分数化分数的方法:先写成分数的形式,再进一步化简成最简分数;
分数化成小数,用分数的分子除以分数的分母,如果不能化成有限小数,根据需要取近似值,一般保留一位小数;
分数化百数,分母是100的分数,直接改写成百分数号即可,即去掉分母,添上百分号(%);一般分数化百分数,首先把分数化成小数,再把小数点向右移动两位,添上百分号(%)即可,如果不能化成有限小数,根据需要取近似值,一般百分号前保留一位小数;
小数化百分数只要把小数点向右移动两位,添上百分号即可;把百分数化成小数时,把百分数去掉百分号,同时把小数点向左移动两位即可;
小数化分数的方法:一位小数表示十分之几,两位小数表示百分之几,三位小数表示千分之几…先写成分数的形式,再进一步化简成最简分数;据此解答.
【解答】解:
分数
小数 0.2 0.25 0.08 0.625 0.6 0.125
百分数 20% 25% 8% 62.5% 60% 12.5%
【要点】解答本题关键是明确百分数、小数和分数三者之间互化的方法.
50.说一说下面百分数的具体含义。
(1)我国人口约占世界人口的22%。
(2)我国耕地面积约占世界耕地面积的7%。
(3)某发电厂4月份完成计划发电任务的115%。
【答案】(1)世界上每100个人里有22个是中国人口;(2)把世界耕地总面积平均分成100份,我国的耕地面积大约占其中的7份;(3)发电的任务看成“1”,4月份完成了1.15。
【分析】根据百分数的意义:百分数是“表示一个数是另一个数百分之几的数,”由此解答即可。
【解答】解:(1)我国人口约占世界人口的22%,这句话可以理解为世界上每100个人里有22个是中国人口;
(2)中国耕地面积约是世界耕地面积的7%,表示表示把世界耕地总面积平均分成100份,我国的耕地面积大约占其中的7份;
(3)某发电厂4月份完成计划发电任务的115%,表示把发电的任务看成“1”,4月份完成了1.15。
【要点】本题主要考查了百分数的意义,属于基础知识。
51.某修路队上半年修路6400米,比原计划多修了1600米,这支修路队多修了百分之几?
【答案】33.33%。
【分析】根据百分数的意义,用这支修路队多修的长度除以原计划修的长度,就是这支修路队多修的路是原计划的百分之几。
【解答】解:1600÷(6400﹣1600)×100%
=1600÷4800×100%
≈33.33%
答:这支修路队大约多修了33.33%。
【要点】本题是求一个数是另一个数的百分之几,关键是看把谁当成了单位“1”,单位“1”的量为除数。
52.近年来,各地“广场舞”噪音干扰的问题倍受关注。相关人员对本地区15~65岁年龄段的市民进行了随机调查,并制作了如下相应的统计图。市民对“广场舞”噪音干扰的态度有以下五种:A.没影响B.影响不大C.有影响,建议做无声运动D.影响很大,建议取缔E.不关心这个问题。
根据以上信息解答下列问题:
(1)根据统计图填空:m= 32% 。
(2)在此次调查中,“不关心这个问题”的有25人,请问一共调查了 500 人。
(3)在此次调查中,持“影响不大”态度的人比持“没影响”态度的人多百分之 六十五 。
【答案】(1)32%;
(2)500;
(3)六十五。
【分析】(1)调查的总人数看作单位“1”,根据减法的意义,用减法解答。
(2)调查的总人数看作单位“1”,“不关心这个问题”的有25人,占调查总人数的5%,根据已知一个数的百分之几是多少,求这个数,用除法解答。
(3)把持“没影响”态度的人数看作单位“1”,先用减法求出持“影响不大”态度的人比持“没影响”态度的人多占总人数百分之几,然后根据求一个数是另一个数的百分之几,用除法解答。
【解答】解:1﹣(10%+5%+20%+33%)
=1﹣68%
=32%
答:m=32%。
(2)25÷5%
=25÷0.05
=500(人)
答:一共调查了500人。
(3)(33%﹣20%)÷20%
=0.13÷0.2
=0.65
=65%
答:持“影响不大”态度的人比持“没影响”态度的人多65%。
故答案为:32%;500;六十五。
【要点】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
53.聪聪家2009年11月支出情况统计如图.聪聪家2009年11月的总支出是3600元.请你回答问题.
(1)这个月哪项支出最多?支出了多少元?
(2)文化教育支出了多少元?购买衣物支出了多少元?
(3)购买衣物的支出比文化教育支出少百分之几?
【答案】见试题解答内容
【分析】(1)通过观察扇形统计图可知:这个月伙食费支出最多,根据一个数乘百分数的意义,用乘法解答;
(2)把总支出看作单位“1”,根据一个数乘百分数的意义,用乘法解答;
(3)把文化教育支出看作单位“1”,根据求一个数是另一个数的百分之几,用除法解答.
【解答】解:(1)3600×35%
=3600×0.35
=1260(元);
答:这个月伙食费支出最多,支出了1260元.
(2)3600×25%
=3600×0.25
=900(元);
3600×20%
=3600×0.2
=720(元);
答:文化教育支出900元,购买衣物支出720元.
(3)(900﹣720)÷900
=180÷900
=0.2
=20%;
答:购买衣物的支出比文化教育支出少20%.
【要点】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
54.如图是我国国土各种地形所占百分比情况统计图。
(1)盆地占我国国土面积的 19 %。
(2)山地占我国国土面积的 33 %。
(3)高原所占面积与丘陵所占面积的最简单的整数比是 13:5 。
(4)我国国土面积约960万平方千米,平原的面积约是 115.2 万平方千米。
【答案】(1)19;
(2)33;
(3)13:5;
(4)115.2。
【分析】(1)通过观察统计图直接回答问题。
(2)把我国国土总面积看作单位“1”,根据减法的意义,用减法解答。
(3)根据比的意义、比的化简方法解答即可。
(4)把我国国土总面积看作单位“1”,根据求一个数的百分之几是多少,用乘法解答。
【解答】解:(1)盆地占我国国土面积的19%。
(2)1﹣12%﹣19%﹣10%﹣26%=33%
答:山地占我国国土面积的33%。
(3)26%:10%=13:5
答:高原所占面积与丘陵所占面积的最简单的整数比是13:5。
(4)960×12%
=960×0.12
=115.2(万平方千米)
答:平原的面积约是115.2万平方千米。
故答案为:19;33;13:5;115.2。
【要点】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
55.某小学参加兴趣小组情况如图:已知参加体育的有136人,参加“其它”兴趣小组的共有多少人?
【答案】见试题解答内容
【分析】根据扇形统计图可知,把总人数看作单位“1”,总人数的34%是136人,根据“已知一个数的百分之几是多少,求这个数用除法计算”,用136除以34%可求出总人数;然后求出参加“其它”兴趣小组占了总人数的百分比:1﹣34%﹣18%﹣26%,再根据百分数乘法的意义解答即可.
【解答】解:136÷34%=400(人)
400×(1﹣34%﹣18%﹣26%)
=400×22%
=88(人)
答:参加“其它”兴趣小组的共有88人.
【要点】本题主要考查了学生根据扇形统计图分析数量关系解答问题的能力.
56.每年的4月23日是“世界读书日”,为深入推进全民阅读,培育良好的阅读习惯。实验小学新进一批图书,情况统计如图。已知科技书和童话故事的本数比是3:5。
(1)实验小学新进的这批图书共有多少本?
(2)儿童文学有多少本?
【答案】(1)2000本;(2)640本。
【分析】(1)已知科技书有300本,科技书和童话故事的本数比是3:5。也就是科技书的本数是童话故事的,根据已知一个数的几分之几是多少,求这个数,用除法解答得出童话故事的本数,再除以它占的百分率,即可得实验小学新进的这批图书共有多少本。
(2)用乘法计算得出其他的本数,再用减法计算即可得儿童文学的本数。
【解答】解:(1)300500(本)
500÷25%=2000(本)
答:实验小学新进的这批图书共有2000本。
(2)2000×28%=560(本)
2000﹣300﹣500﹣560=640(本)
答:儿童文学有640本。
【要点】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
57.如图是1班和2班的男生和女生的人数统计图,已知两个班的人数都不少于30,也不多于40,则1班有多少名学生,2班有多少名学生?
【答案】见试题解答内容
【分析】(1)利用圆心角的度数之比,可以求得各班的女生与男生人数之比.①1班180:180=1:1,所以:女:男=1:1=2:2;②2班144:(360﹣144)=2:3,所以:女:男=2:3;③1班和2班之和160:(360﹣160)=4:5,女:男=4:5;由此可得:4+5=9,总人数可分为9份,其中1班占:2+2=4份;2班占:2+3=5份.
(2)根据题干已知两个班的人数都不少于30,也不多于40.可得:两个班的总人数应在60~80之间(包括两端),而总人数为(4+5=9)份,那么总人数应是9的倍数,因此有2种可能:总人数为63人或72人,由此展开分析讨论即可解决问题.
【解答】解:根据题干分析可得:①1班:180:360=12,所以:女:男=1:1=2:2;
②2班:144:(360﹣144)=2:3,所以:女:男=2:3;
③1班和2班之和:160:(360﹣160)=4:5,所以:女:男=4:5;
由此可得:4+5=9,总人数可分为9份,其中1班占:2+2=4(份),2班占:2+3=5(份);
(1)若总人数为63人:则每份有:63÷9=7(人),
则1班人数为:7×(2+2)=28(人),不符合题意;
(2)若总人数为72人,则每份有:72÷9=8(人),
则1班人数为:8×(2+2)=32(人),
2班人数为:8×(2+3)=40(人),
答:1班人数为32人,2班人数为40人.
故答案为:32;40.
【要点】根据统计图求出各班女生与男生的比,和女生总人数与男生总人数的比的关系,把总人数分成9份,确定出1班人数占4份,2班人数占5份是解答本题的关键,也是一个难点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末核心考点 应用题
1.欣欣水果店运进10箱橘子,以每箱25kg为标准,超过的记为正数,不足的记为负数,称重记录如下:+1.5,﹣3.2,+2.5,﹣1.8,0,+1,﹣2,﹣1.4,+2,+2.4,将这10箱橘子的实际质量按由重到轻的顺序进行排列.(单位:kg)
2.小小百货店每个月的营业成本是12万元。下表是这家店今年上半年收入情况统计表,请你用正、负数表示盈亏情况。(盈利用正数表示,亏损用负数表示)请你想办法计算一下小小百货店上半年是盈利了还是亏损了?盈利或亏损多少万元?
一月份 二月份 三月份 四月份 五月份 六月份
14万元 15万元 11万元 12万元 16万元 11万元
3.8名学生进行仰卧起坐达标检测,1分钟满30个则为达标,超过的记为正,不足的记为负,8名学生在30个达标的基础上的记录分别为:3、﹣2、0、1、﹣4、5、2、﹣3。这些同学中有几名达标?这8名同学一共做了多少个仰卧起坐?
4.一只梅花鹿从起点向前跳5米,再向后跳4米,又朝前跳7米,朝后跳10米,然后停下休息。你知道梅花鹿停在起点前还是起点后?与起点相距几米?
5.王钢把50000元人民币存入银行,定期2年,年利率是2.7%.到期时,王钢应得本金和利息一共多少元?
6.个人所得税法规定:从2008年3月1日起公民每月工资(薪金)所得未超过2000元的部分不纳税,超过2000元的部分为本月应纳税所得额.此项纳税按如表累进计算:
全月应纳税所得额 税率
不超过500元的部分 5%
超过500元至2000元的部分 10%
超过2000元至5000元的部分 15%
超过5000元至20000元的部分 20%
(1)姚老师3月份工资收入3400元,交纳税款后实际收入多少元?
(2)薛老师是一位名校长,3月份工资收入5800元,应交纳税款多少元?
7.某商场用“满300送100”的办法来促销,即购物满300元,赠送100元“礼券”,超过但不足300元的部分略去不计。如购买720元商品,可获是两张100元“礼券”,多余120元略去不计。“礼券”在下次购物时代替现金,但“礼券”部分不能再享受“满300送100”的优惠。一位顾客先用1000元购了A商品,得到“礼券”后,又用这些“礼券”和200元现金购了B商品,那么这位顾客购买A、B两种商品相当于几折优惠?
8.李欣按九折的优惠价格购买了2张足球赛门票,共用去540元。每张门票的原价是多少元?
9.一个数,添上百分号后减少了29.7,这个数原来是多少?
10.某公司进行年终分红,规定按下面的规则将钱平均分给每个人,第一个人先取1元,再取余下的;接着第二人先取2元,再取余下的;如此继续下去,第k个人先取k元,再取余下奖金的,最后奖金被分完,则公司有多少人参与分红?
11.工厂计划本月用电100度,实际用了80度电,实际比计划节约了百分之几?
12.中小学生营养午餐蛋白质摄入标准如表1,部分食物的蛋白质含量如表2。
表1:
年龄/岁 6~8 9~11 12~15
营养午餐蛋白质摄入标准/g 24 28 32
表2:
食物 鸡肉 鸡蛋 黄豆 胡萝卜 番茄 米饭
蛋白质含量 20% 13% 36% 0.6% 0.9% 3%
请你根据上述信息,给自己设计一份午餐食品清单,并写出你的思考过程。
13.把一个底面直径是20厘米,高是3厘米的圆柱形钢坯锻造成底面半径是5厘米的圆锥形钢坯,这个圆锥形钢坯的高是几厘米?(用方程解)
14.王师傅想利用下面的铁皮做一个底面直径40厘米、高40厘米的油桶,请你画出做这个油桶的示意图(接头处忽略不计),再计算出这个油桶的容积是多少升?(厚度忽略不计)
15.一个圆柱形容器,里面盛有一些水,有一个底面积为157平方厘米的圆锥形铁块浸没在容器内,把铁块从容器中拿出来后,水面下降了2厘米。如果这个容器底面半径是10厘米,那么这个圆锥形铁块的高是多少厘米?
16.工厂要加工一批无盖的圆柱形铁皮水桶,底面直径是40厘米,高是45厘米。做一个这样的水桶至少要用多少平方厘米铁皮?(不考虑接缝处面积)
17.在一张长方形彩纸上摆满小正方形,每个小正方形面积与所需小正方形的数量如表:
每个小正方形的面积/cm2 4 9 16
所需小正方形的数量/个 216 96 54
(1)每个小正方形的面积与所需小正方形的数量成 比例关系。
(2)如果采用面积是36cm2的小正方形来摆满这张长方形彩纸,需要多少个小正方形?(用比例方法解答)
18.某工厂生产一批零件,原计划每天生产25件,18天完成任务。实际每天多生产20%,可提前几天完成任务?(用比例知识解答)
19.甲、乙两车间原有人数的比为4:3,从甲车间调12人到乙车间后,甲、乙两车间的人数比变为2:3,甲车间原有多少人?
20.今年三毛和二毛的年龄比是7:5,五年后,三毛与二毛的年龄比是13:10,问两人今年各几岁?
21.一间教室要用方砖铺地,用面积是64平方分米的方砖要90块,如果改用6分米的方砖,需要多少块?(用比例解)
22.王爷爷家新建了一座房。王奶奶对王爷爷说:“咱们家的客厅用边长为0.6米的方砖铺地,正好需要128块。”王爷爷不同意,坚持用边长8dm的方砖铺。请你用比例算一下,按王爷爷的想法,客厅需要多少块方砖?
23.用96厘米长的铁丝围成一个长方体,长、宽、高的比是5:3:4,这个长方体的体积是多少立方厘米?
24.一间教室,用面积是25平方分米的地砖铺地,需要320块.如果用面积是16平方分米的地砖铺,需要多少块?(用比例解)
25.把43颗玻璃球放入下面的盒子中,一定有一个盒子中至少放入多少颗玻璃球?
26.袋子里有4只红手套,2只黑手套,2只紫手套。一次摸出几只手套才能保证至少有一只红手套?
27.如图所示,盒子中有4种不同颜色的球,小华蒙着眼睛往外摸球,至少要摸出多少个,才能保证摸出的球至少有3种不同的颜色?
28.把若干个苹果放进9个抽屉里,不管怎么放,要保证总有一个抽屉里至少放进3个苹果,苹果的总数至少有多少个?
29.滑雪场上共有1200人,滑雪运动员占;其中女滑雪运动员占滑雪运动员总人数的,滑雪场上有多少名女滑雪运动员?
30.果果用铁丝做了一个棱长是dm的正方体框架,一共用了多少厘米铁丝?(接头处忽略不计)
30.玲玲把一些一元的硬币如图摆放.
(1)照这样摆下去,摆6层用了多少枚硬币?
(2)如果用了45枚硬币摆成,这个等边三角形每条边上摆几枚硬币?
31.一串数:,,,,,,,,,,……
(1)第800个数是多少?
(2)是第几个数?
(3)前552个数的和是多少?
(4)前n个数的和能否等于106,如果能,试求出n的值,如果不能,试说明理由.
33.画出1路公共汽车的行走路线。
1路公共汽车从起点站向东偏北25°方向行驶2千米,接着向东行驶3千米,又向西偏北40°方向行驶2千米,又向北行驶1千米,最后向东偏南30°方向行驶4千米到终点上。
34.(1)花园街的西面有 、 、 .
(2)图书馆在小林家的 ,小吃店在超市的 面,小川家在小林家的 面.
(3)请你画出小林去音像店所走的路线.
(4)请你说一说小川去邮局,可以怎么走?
35.小军沿学校向东偏北40°走200米后,再向东走400米,最后向南偏东45°走200米到家。请你根据描述画出小军从学校到家的路线图?
36.五 一假期王老师带家人自驾车从淮滨出发,途经南京,去上海旅游。
(1)请你为王老师选择一条路线,先用笔描出该路线,再计算该路线的路程是多少?
(2)你对王老师有什么样好的建议?(请写下来)
37.王老师为学校购买音乐器材,他带去的钱可以买10台手风琴或50把小提琴,如果买了6台手风琴后,剩下的钱全部买小提琴,可以买多少把小提琴?
38.一堆沙甲队单独运要8天运完,乙队单独运要10天运完。现在两队合运几天后,还剩这堆沙的?
39.一项工程,甲队单独做18天可以完成,乙队单独做15天可以完成,现在甲队先做7天后,剩下的甲、乙两队合做完成,乙队完成了这项工程的几分之几?
40.根据互联网信息测算:“中国空间站组合体每1.5小时左右绕地球一周。”那么航天员在空间站24小时能绕地球多少周?
41.某市交警部门开展“一盔一带”安全守护行动,呼吁骑电动车的市民佩戴头盔。政策颁布后,头盔的销售量火爆。某商店第二天卖出108顶头盔,比第一天多卖出。商店第一天卖出多少顶头盔?(列方程解答)
42.如图,窗户比门高出了多少米?
43.一个圆形花坛的周长是62.8米,在它的周围铺一条宽为2米的小路,这条小路的面积是多少平方米?
44.一个环形砂轮,外圆半径是0.4米,环宽10厘米,这个环形砂轮的面积是多少?
45.有一个圆形花坛,半径是50米,王叔叔每天早晨绕花坛跑4圈,他每天早晨跑多少米?
46.一根7米长的绳子,绕树一周还余下0.72米,树的直径是多少米?
47.钟面上时针长6厘米,时针尖端走一天的距离是多少厘米?
48.原产非洲的“猴面包树”,它的树干非常粗,其中一棵“猴面包树”的直径为15.7m,如果用绳子绕它的树干一周,至少需要准备多长的绳子?
49.填表:
分数
小数 0.2 0.6
百分数 8% 12.5%
50.说一说下面百分数的具体含义。
(1)我国人口约占世界人口的22%。
(2)我国耕地面积约占世界耕地面积的7%。
(3)某发电厂4月份完成计划发电任务的115%。
51.某修路队上半年修路6400米,比原计划多修了1600米,这支修路队多修了百分之几?
52.近年来,各地“广场舞”噪音干扰的问题倍受关注。相关人员对本地区15~65岁年龄段的市民进行了随机调查,并制作了如下相应的统计图。市民对“广场舞”噪音干扰的态度有以下五种:A.没影响B.影响不大C.有影响,建议做无声运动D.影响很大,建议取缔E.不关心这个问题。
根据以上信息解答下列问题:
(1)根据统计图填空:m= 。
(2)在此次调查中,“不关心这个问题”的有25人,请问一共调查了 人。
(3)在此次调查中,持“影响不大”态度的人比持“没影响”态度的人多百分之 。
53.聪聪家2009年11月支出情况统计如图.聪聪家2009年11月的总支出是3600元.请你回答问题.
(1)这个月哪项支出最多?支出了多少元?
(2)文化教育支出了多少元?购买衣物支出了多少元?
(3)购买衣物的支出比文化教育支出少百分之几?
54.如图是我国国土各种地形所占百分比情况统计图。
(1)盆地占我国国土面积的 %。
(2)山地占我国国土面积的 %。
(3)高原所占面积与丘陵所占面积的最简单的整数比是 。
(4)我国国土面积约960万平方千米,平原的面积约是 万平方千米。
55.某小学参加兴趣小组情况如图:已知参加体育的有136人,参加“其它”兴趣小组的共有多少人?
56.每年的4月23日是“世界读书日”,为深入推进全民阅读,培育良好的阅读习惯。实验小学新进一批图书,情况统计如图。已知科技书和童话故事的本数比是3:5。
(1)实验小学新进的这批图书共有多少本?
(2)儿童文学有多少本?
57.如图是1班和2班的男生和女生的人数统计图,已知两个班的人数都不少于30,也不多于40,则1班有多少名学生,2班有多少名学生?
期末核心考点 应用题
参考答案与试题解析
1.欣欣水果店运进10箱橘子,以每箱25kg为标准,超过的记为正数,不足的记为负数,称重记录如下:+1.5,﹣3.2,+2.5,﹣1.8,0,+1,﹣2,﹣1.4,+2,+2.4,将这10箱橘子的实际质量按由重到轻的顺序进行排列.(单位:kg)
【答案】见试题解答内容
【分析】(1)正数>0>负数;
(2)负数大小比较就是看负号后面的数字,数字越大的反而越小,跟正数恰好相反;
由此比较出这些数据,即可求解.
【解答】解:比较可得:
+2.5>+2.4>+2>+1.5>+1>0>﹣1.4>﹣1.8>﹣2>﹣3.2.
【要点】此题考查正负数的大小比较的方法,要熟练掌握.
2.小小百货店每个月的营业成本是12万元。下表是这家店今年上半年收入情况统计表,请你用正、负数表示盈亏情况。(盈利用正数表示,亏损用负数表示)请你想办法计算一下小小百货店上半年是盈利了还是亏损了?盈利或亏损多少万元?
一月份 二月份 三月份 四月份 五月份 六月份
14万元 15万元 11万元 12万元 16万元 11万元
【答案】+2、+3、﹣1、0、+4、﹣1。盈利,7万元。
【分析】用正负数表示意义相反的两种量:高于营业成本记作正,则低于营业成本就记作负。由此得解。正负数相加,看最后是正数还是负数即可。
【解答】解:
一月份 二月份 三月份 四月份 五月份 六月份
14万元 15万元 11万元 12万元 16万元 11万元
+2 +3 ﹣1 0 +4 ﹣1
+2+3﹣1+0+4﹣1=+7(万元)
答:盈利7万元。
【要点】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
3.8名学生进行仰卧起坐达标检测,1分钟满30个则为达标,超过的记为正,不足的记为负,8名学生在30个达标的基础上的记录分别为:3、﹣2、0、1、﹣4、5、2、﹣3。这些同学中有几名达标?这8名同学一共做了多少个仰卧起坐?
【答案】5名;242个。
【分析】正数和0共有5个,也就是这些同学中有5名达标;求出3、﹣2、0、1、﹣4、5、2、﹣3的和,再加上30×8就是这8名同学一共做了多少个仰卧起坐。
【解答】解:3﹣2+0+1﹣4+5+2﹣3+30×8
=2+240
=242(个)
答:这些同学中有5名达标,这8名同学一共做了242个仰卧起坐。
【要点】根据正、负数的意义,解答此题即可。
4.一只梅花鹿从起点向前跳5米,再向后跳4米,又朝前跳7米,朝后跳10米,然后停下休息。你知道梅花鹿停在起点前还是起点后?与起点相距几米?
【答案】起点后,2米。
【分析】用正负数表示意义相反的两种量:向前跳记作正,则向后跳就记作负。把所有数据用正负数表示并相加,求出最后位置即可。
【解答】解:+5﹣4+7﹣10=﹣2(米)
答:梅花鹿停在起点后,与起点相距2米。
【要点】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
5.王钢把50000元人民币存入银行,定期2年,年利率是2.7%.到期时,王钢应得本金和利息一共多少元?
【答案】见试题解答内容
【分析】在此题中,本金是50000元,时间是2年,利率是2.7%,求本息,运用关系式:本息=本金+本金×年利率×时间,解决问题.
【解答】解:50000+50000×2.7%×2
=50000+2700
=52700(元)
答:王钢应得本金和利息一共52700元.
【要点】这种类型属于利息问题,运用关系式“本息=本金+本金×年利率×时间”,代入数据,解决问题.
6.个人所得税法规定:从2008年3月1日起公民每月工资(薪金)所得未超过2000元的部分不纳税,超过2000元的部分为本月应纳税所得额.此项纳税按如表累进计算:
全月应纳税所得额 税率
不超过500元的部分 5%
超过500元至2000元的部分 10%
超过2000元至5000元的部分 15%
超过5000元至20000元的部分 20%
(1)姚老师3月份工资收入3400元,交纳税款后实际收入多少元?
(2)薛老师是一位名校长,3月份工资收入5800元,应交纳税款多少元?
【答案】见试题解答内容
【分析】(1)根据题意,姚老师3月份工资收入3400元,超过2000元的部分为1400元,这1400元当中的500元按5%纳税,其余的900元按10%纳税,用工资收入3400元分别减去交纳的税款即得实际收入;
(2)此题应分类交税,工资收入5800元,超过2000元的部分为3800元,先求不超过500元的部分应交税500×5%=25(元),超过500元至2000元的部分应交税(2000﹣500)×10%=130(元),剩余部分应缴纳(3800﹣500﹣1500)×15%,把这三部分加起来,即为所求.
【解答】解:(1)3400﹣2000=1400(元)
500×5%=25(元)
(1400﹣500)×10%
=900×10%
=90(元)
3400﹣25﹣90=3285(元)
答:交纳税款后实际收入3285元.
(2)5800﹣2000=3800(元)
不超过500元的部分应交税:
500×5%=25(元)
超过500元至2000元的部分应交税:
(2000﹣500)×10%
=1500×10%
=150(元)
剩余部分应缴纳:
(3800﹣500﹣1500)×15%
=1800×15%
=270(元)
25+150+270=445(元)
答:应交纳税款445元.
【要点】(1)先求出应交税多少元,再求交纳税款后实际收入多少元;
(2)解答这一题应注意分类交税.
7.某商场用“满300送100”的办法来促销,即购物满300元,赠送100元“礼券”,超过但不足300元的部分略去不计。如购买720元商品,可获是两张100元“礼券”,多余120元略去不计。“礼券”在下次购物时代替现金,但“礼券”部分不能再享受“满300送100”的优惠。一位顾客先用1000元购了A商品,得到“礼券”后,又用这些“礼券”和200元现金购了B商品,那么这位顾客购买A、B两种商品相当于几折优惠?
【答案】这位顾客购买A、B两种商品相当于8折优惠。
【分析】1000÷300=3……100,则可知一位顾客先用1000元购了A商品,得到“礼券”为3张,又用这些“礼券”和200元现金购了B商品,则可知B产品价格为300+200=500(元),所以A、B两种商品的价格和为1000+500=1500(元),实际顾客花了1000+200=1200(元)。据此运算即可获得实际几折优惠。
【解答】解:1000÷300=3……100
3×100=300(元)
300+200=500(元)
1000+500=1500(元)
1000+200=1200(元)
1200÷1500×100%
=0.8×100%
=80%
答:这位顾客购买A、B两种商品相当于8折优惠。
【要点】本题考查折扣问题。购买金额÷原价金额×100%=折扣。
8.李欣按九折的优惠价格购买了2张足球赛门票,共用去540元。每张门票的原价是多少元?
【答案】300元。
【分析】九折是指现价是原价的90%,把原价看成单位“1”,它的90%就是现价540元,用540除以这个分率求出原来2张的原价,再除以2即可求出每张门票的原价是多少元。
【解答】解:540÷90%=600(元)
600÷2=300(元)
答:每张门票的原价是300元。
【要点】本题关键是理解打折的含义:打几折,现价就是原价的百分之几十;打几几折,现价就是原价的百分之几十几。
9.一个数,添上百分号后减少了29.7,这个数原来是多少?
【答案】30。
【分析】在一个数(这个数不等于0)的后面添上百分号,相当于把这个数的小数点向移动2位,这个数缩小到原来的,由此可知:这个数的(1﹣1%)是29.7,根据已知一个数的几分之几是多少,求这个数,用除法解答即可。
【解答】解:29.7÷(1﹣1%)
=29.7÷0.99
=30
答:这个数原来是30。
【要点】此题考查百分数的意义,在一个数(这个数不等于0)的后面添上百分号相当于小数点向左移动2位,这个数缩小到原来的,据此解答即可。
10.某公司进行年终分红,规定按下面的规则将钱平均分给每个人,第一个人先取1元,再取余下的;接着第二人先取2元,再取余下的;如此继续下去,第k个人先取k元,再取余下奖金的,最后奖金被分完,则公司有多少人参与分红?
【答案】2020人。
【分析】根据题目中描述的分红规则来建立方程解答,首先设总钱数为一个未知数x,然后根据每个人取钱的规则列出方程,最后通过解方程求出总钱数,再根据总钱数求出每人分到的钱数,进而得出参与分红的人数。
【解答】解:设总钱数为x元。
第一个人先取1元,此时剩下(x﹣1)元,再取余下的,即(x﹣1)(元)
所以第1个人共取钱数为:1(元)
第二个人先取2元,此时剩下(x2)元,再取余下的,即(x2)(元)
所以第2个人共取钱数为:2(元)
因为最后奖金被分完,即第一个人分的钱和第二个分的钱相等(这里假设只有2个人先进行分析,实际对于任意相邻的人分的钱数是相等的),即列方程为:
解得:x=4080400
所以每人分得钱数为:(4080400+2020)÷2021=2020(元)
即参与分红的人数为4080400÷2020=2020(人)
答:公司有2020人参与分红。
【要点】解答此题的关键是通过设未知数,根据每人分红金额相同的求出一共分红的金额。
11.工厂计划本月用电100度,实际用了80度电,实际比计划节约了百分之几?
【答案】见试题解答内容
【分析】先求出节约了多少度,然后把计划用电的度数看作单位“1”,求节约的度数占计划投资的百分之几,根据求一个数是另一个数的百分之几,用除法解答.
【解答】解:(100﹣80)÷100
=20÷100
=20%;
答:实际比计划节约了20%.
【要点】解答此题的关键是:先求出节约了多少度,再判断出单位“1”,然后根据求一个数是另一个数的百分之几,用除法解答.
12.中小学生营养午餐蛋白质摄入标准如表1,部分食物的蛋白质含量如表2。
表1:
年龄/岁 6~8 9~11 12~15
营养午餐蛋白质摄入标准/g 24 28 32
表2:
食物 鸡肉 鸡蛋 黄豆 胡萝卜 番茄 米饭
蛋白质含量 20% 13% 36% 0.6% 0.9% 3%
请你根据上述信息,给自己设计一份午餐食品清单,并写出你的思考过程。
【答案】蛋白质32克;我的午餐食品清单:100克米饭;74克鸡肉;50克胡萝卜;100克番茄;100克鸡蛋。(答案不唯一)
【分析】根据题意,先根据人物的年龄,找出午餐应摄入蛋白质的重量。然后用食物的重量乘食物的蛋白质含量的百分比,求出食物中蛋白质的重量,然后将各种食物的蛋白质的重量相加,如果和等于午餐应摄入蛋白质的重量,即可解答。
【解答】解:米饭:100×3%=3(克)
鸡肉:74×20%=14.8(克)
胡萝卜:50×0.6%=0.3(克)
番茄:100×0.9%=0.9(克)
鸡蛋:100×13%=13(克)
3+14.8+0.3+0.9+13
=17.8+0.3+0.9+13
=18.1+0.9+13
=19+13
=32(克)
答:我今年12岁,午餐应摄入蛋白质32克。
我的午餐食品清单:100克米饭;74克鸡肉;50克胡萝卜;100克番茄;100克鸡蛋。(答案不唯一)
【要点】此题考查了百分数的意义及应用,要求学生掌握。
13.把一个底面直径是20厘米,高是3厘米的圆柱形钢坯锻造成底面半径是5厘米的圆锥形钢坯,这个圆锥形钢坯的高是几厘米?(用方程解)
【答案】36厘米。
【分析】圆柱形钢坯锻造成圆锥形钢坯,说明它们的体积相等,根据圆柱的体积公式:V=πr2h,圆锥的体积公式:VSh,分别表示出二者体积,根据体积相等列方程解答即可。
【解答】解:设这个圆锥形钢坯的高是x厘米。
3.14×52×x3.14×(20÷2)2×3
3.14×25×x3.14×100×3
25x=900
x=36
答:这个圆锥形钢坯的高是36厘米。
【要点】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式。
14.王师傅想利用下面的铁皮做一个底面直径40厘米、高40厘米的油桶,请你画出做这个油桶的示意图(接头处忽略不计),再计算出这个油桶的容积是多少升?(厚度忽略不计)
【答案】50.24升。
【分析】根据题意,要制作底面直径40厘米、高40厘米的油桶,先画出两个直径40厘米的圆作油桶的上下底,再画出一个直径40厘米圆的周长作长方形的长,宽为40厘米的长方形,即可制作这个油桶;再根据圆柱的体积(容积)公式V=Sh,即可解答。
【解答】解:3.14×40=125.6(厘米)
3.14×(40÷2)2×40
=3.14×202×40
=3.14×400×40
=50240(立方厘米)
50240立方厘米=50.24立方分米=50.24升
答:这个油桶的容积是50.24升。
【要点】此题考查的目的是理解掌握圆柱的特征,以及圆柱体积(容积)公式的灵活运用。
15.一个圆柱形容器,里面盛有一些水,有一个底面积为157平方厘米的圆锥形铁块浸没在容器内,把铁块从容器中拿出来后,水面下降了2厘米。如果这个容器底面半径是10厘米,那么这个圆锥形铁块的高是多少厘米?
【答案】12厘米。
【分析】圆锥体铁块浸没在容器中,从容器中拿出来后,水面下降了2厘米,则圆锥的体积即下降的水的体积,根据圆柱的体积公式:V=πr2h,求出上升水的体积,再根据圆锥的体积公式:VSh,变式求高:h=3V÷S,代入数值计算即可。
【解答】解:下降的水的体积为:
3.14×10×10×2
=31.4×10×2
=314×2
=628(立方厘米)
圆锥铁块的高为:
628×3÷157
=1884÷157
=12(cm)
答:这个圆锥体的高是12厘米。
【要点】本题主要考查了圆柱和圆锥的体积公式,需要学生灵活运用,并能正确辨别出题目中的有用数据及无用数据。
16.工厂要加工一批无盖的圆柱形铁皮水桶,底面直径是40厘米,高是45厘米。做一个这样的水桶至少要用多少平方厘米铁皮?(不考虑接缝处面积)
【答案】6908平方厘米。
【分析】先分清制作没有盖的圆柱形铁皮水桶,需要计算几个面的面积:侧面面积与底面圆的面积两个面,由圆柱体侧面积和圆的面积计算方法列式解答即可。
【解答】解:水桶的侧面积:3.14×40×45=5652(平方厘米)
水桶的底面积:
3.14×(40÷2)2
=3.14×202
=1256(平方厘米)
水桶的表面积:5652+1256=6908(平方厘米)
答:做一个这样的水桶要用6908平方厘米铁皮。
【要点】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
17.在一张长方形彩纸上摆满小正方形,每个小正方形面积与所需小正方形的数量如表:
每个小正方形的面积/cm2 4 9 16
所需小正方形的数量/个 216 96 54
(1)每个小正方形的面积与所需小正方形的数量成 反 比例关系。
(2)如果采用面积是36cm2的小正方形来摆满这张长方形彩纸,需要多少个小正方形?(用比例方法解答)
【答案】见试题解答内容
【分析】(1)每个小正方形的面积×小正方形的数量=长方形彩纸的面积;长方形彩纸的面积一定,每个小正方形的面积与所需小正方形的数量成反比例关系。
(2)长方形彩纸的面积=36×需要小正方形个数,由此解答。
【解答】解:(1)长方形彩纸的面积一定,每个小正方形的面积与所需小正方形的数量成反比例关系。
(2)设需要多x个小正方形。
36x=216×4
36x÷36=216×4÷36
x=24
答:(1)每个小正方形的面积与所需小正方形的数量成反比例关系。
(2)需要24个小正方形。
故答案为:反,24。
【要点】解决此题关键是根据比值一定或乘积一定,先列出比例,进而根据比例的性质先把比例式转化为乘积式来解比例得解;注意等号要对齐。
18.某工厂生产一批零件,原计划每天生产25件,18天完成任务。实际每天多生产20%,可提前几天完成任务?(用比例知识解答)
【答案】3天。
【分析】把一批零件的总数看作单位“1“,批零件的总数一定,所以每天生产的件数与天数成反比例,设出未知数,列出比例计算即可。
【解答】解:设可提前x天完成任务。
25×18=25×(1+20%)×(18﹣x)
25×1.2×(18﹣x)=450
30×(18﹣x)=450
18﹣x=15
x=3
答:可提前3天完成任务。
【要点】本题考查了比较复杂的百分数和比例的问题。首先需要求出实际每天生产的件数。
19.甲、乙两车间原有人数的比为4:3,从甲车间调12人到乙车间后,甲、乙两车间的人数比变为2:3,甲车间原有多少人?
【答案】40人。
【分析】甲、乙两车间原有人数的比为4:3,则甲车间的人数占总人数的4÷(4+3),从甲车间调12人到乙车间后,甲、乙两车间的人数比变为2:3,这时甲车间的人数占总人数的2÷(2+3),则这12人占总人数的(),根据分数除法的意义,用12除以()求出总人数,再用总人数乘即可求出甲车间原有多少人。
【解答】解:4÷(4+3)
2÷(2+3)
12÷()
=12
=70(人)
7040(人)
答:甲车间原有40人。
【要点】本题考查了比较复杂的有关比和问题和分数的除法问题。
20.今年三毛和二毛的年龄比是7:5,五年后,三毛与二毛的年龄比是13:10,问两人今年各几岁?
【答案】21岁,15岁。
【分析】根据题意,设三毛和二毛今年的年龄分别是7x岁和5x岁,五年后,两个人的年龄分别是(7x+5)岁和(5x+5)岁,又知道5年后,三毛与二毛的年龄比是13:10,所以(7x+5)岁比上(5x+5)岁等于13:10,求出x,再分别求出两个人今年的年龄。
【解答】解:设三毛和二毛今年的年龄分别是7x岁和5x岁,
(7x+5):(5x+5)=13:10
10(7x+5)=13(5x+5)
70x+50=65x+65
70x﹣65x=65﹣50
5x=15
x=3
7x=7×3=21(岁)
5x=5×3=15(岁)
答:三毛今年是21岁,二毛今年是15岁。
【要点】本题考查了有关比的问题,关键是根据比的意义解答。
21.一间教室要用方砖铺地,用面积是64平方分米的方砖要90块,如果改用6分米的方砖,需要多少块?(用比例解)
【答案】160块。
【分析】这块地的面积是一定的,每块砖的面积与所需要的块数成反比例,设出未知数,列出比例式解答即可。
【解答】解:设需要方砖x块,由题意得:
6×6×x=64×90
36x=5760
x=160
答:需要方砖160块。
【要点】此题主要考查对反比例的意义的运用:两种相关联的量,一种量变化,另一种量也随着变化,但两种量的乘积一定,这两种量成反比例。
22.王爷爷家新建了一座房。王奶奶对王爷爷说:“咱们家的客厅用边长为0.6米的方砖铺地,正好需要128块。”王爷爷不同意,坚持用边长8dm的方砖铺。请你用比例算一下,按王爷爷的想法,客厅需要多少块方砖?
【答案】72块。
【分析】方砖的面积是边长乘边长,客厅地面的面积一定的,正方形方砖的面积乘块数就是客厅的面积,即正方形方砖的面积和块数的乘积是一定的,所以正方形方砖的面积和块数成反比例;列出比例式,即可得解。
【解答】解:设客厅需要x块方砖。
8dm=0.8m
0.6×0.6×128=0.8×0.8×x
46.08=0.64x
x=72
答:客厅需要72块方砖。
【要点】本题考查了正比例、反比例的应用。
23.用96厘米长的铁丝围成一个长方体,长、宽、高的比是5:3:4,这个长方体的体积是多少立方厘米?
【答案】480立方厘米。
【分析】用96除以4,求出长方体的长加宽加高的和,再把这个和按5:3:4进行分配,求出长方体的长、宽、高,再根据长方体体积=长×宽×高,即可解答。
【解答】解:96÷4=24(厘米)
2410(厘米)
246(厘米)
248(厘米)
10×6×8
=60×8
=480(立方厘米)
答;这个长方体的体积是480立方厘米。
【要点】本题考查的是按比例分配应用题,掌握按比例分配的方法是解答关键。
24.一间教室,用面积是25平方分米的地砖铺地,需要320块.如果用面积是16平方分米的地砖铺,需要多少块?(用比例解)
【答案】见试题解答内容
【分析】根据题意知道一间教室的面积,地砖的面积×地砖的块数=一间教室的面积(一定),所以地砖的面积与地砖的块数成反比例,设出未知数,列出比例解答即可.
【解答】解:设需要x块,
16x=25×320,
x,
x=500,
答:需要500块.
【要点】解答此题的关键是,根据题意,先判断哪两种相关联的量成何比例,即两个量的乘积一定则成反比例,两个量的比值一定则成正比例;再列出比例解答即可.
25.把43颗玻璃球放入下面的盒子中,一定有一个盒子中至少放入多少颗玻璃球?
【答案】见试题解答内容
【分析】把4个盒子看作4个抽屉,把43颗玻璃球看作43个元素,43÷4=10(颗)…3(颗),从最不利情况考虑,每个抽屉先放10颗,余下的这3颗无论放在那些抽屉里,总有一个抽屉里的有10+1=11(颗),据此解答.
【解答】解:43÷4=10(颗)…3(颗)
10+1=11(颗)
答:一定有一个盒子中至少放入11颗玻璃球.
【要点】此题考查了利用抽屉原理解决实际问题的灵活应用,关键是从最差情况考虑.
26.袋子里有4只红手套,2只黑手套,2只紫手套。一次摸出几只手套才能保证至少有一只红手套?
【答案】5只。
【分析】根据题干,最坏的情况是取出4只手套:2只黑手套,2只紫手套,此时剩下的全是红色手套,再任意取出1只,就能保证至少有一只红手套。
【解答】解:2+2+1=5(只)
答:一次摸出5只手套,才能保证至少有一只红手套。
【要点】此题主要考查了抽屉原理的灵活应用,要注意考虑最不利情况。
27.如图所示,盒子中有4种不同颜色的球,小华蒙着眼睛往外摸球,至少要摸出多少个,才能保证摸出的球至少有3种不同的颜色?
【答案】见试题解答内容
【分析】此题要从最差情况考虑:摸出5个红球、4个黑球共9个球,只有2种颜色的球,此时再摸出任意一个都会出现3种不同颜色的球,据此即可解答.
【解答】解:5+4+1
=9+1
=10(个)
答:至少要摸出10个球,才能保证摸出的球至少有3种不同的颜色.
【要点】此题考查抽屉原理的应用,注意考虑最差情况.
28.把若干个苹果放进9个抽屉里,不管怎么放,要保证总有一个抽屉里至少放进3个苹果,苹果的总数至少有多少个?
【答案】见试题解答内容
【分析】要保证总有一个抽屉里至少放进3个苹果,考虑最差情况:每个抽屉先都有2个苹果,此时苹果数最少是2×9=18个,再加上1个,即可出现一个抽屉里至少放进3个苹果,据此即可求出苹果最少有18+1=19个.
【解答】解:9×(3﹣1)+1
=18+1
=19(个)
答:苹果的总数至少有19个.
【要点】此题考查了利用抽屉原理解决实际问题的灵活应用,关键是从最差情况考虑.
29.滑雪场上共有1200人,滑雪运动员占;其中女滑雪运动员占滑雪运动员总人数的,滑雪场上有多少名女滑雪运动员?
【答案】24名。
【分析】根据题意,利用滑雪场上共有的人数滑雪运动员的人数,再利用滑雪运动员的人数女滑雪运动员的人数,据此计算解答。
【解答】解:1200
=60
=24(名)
答:滑雪场上有24名女滑雪运动员。
【要点】解答此题的关键是找准两个不同的单位“1”,利用求一个数的几分之几的计算方法解答。
30.玲玲把一些一元的硬币如图摆放.
(1)照这样摆下去,摆6层用了多少枚硬币?
(2)如果用了45枚硬币摆成,这个等边三角形每条边上摆几枚硬币?
【答案】(1)21;
(2)9。
【分析】观察图形可知,硬币的数量是从1开始的连续整数的和,整数得个数等于层数,而连续整数得和,等于整数的个数,乘第一个数与最后一个数的和,再除以2,据此规律计算即可。
【解答】解:(1)第六层有:
1+2+3+4+5+6
=6×(1+6)÷2
=6×7÷2
=42÷2
=21(个)
答:摆6层用了21个硬币。
(2)因为,45×2=90=9×10=9×(9+1)
所以,这个等边三角形有9层,也就是每个边上摆9个硬币。
答:这个等边三角形每条边上摆9枚硬币。
【要点】本题主要考查了数与形结合的规律,根据图形找出数的计算方法,再根据总数与层数的关系,确定有多少层,是本题解题的关键。
31.一串数:,,,,,,,,,,……
(1)第800个数是多少?
(2)是第几个数?
(3)前552个数的和是多少?
(4)前n个数的和能否等于106,如果能,试求出n的值,如果不能,试说明理由.
【答案】(1);(2)第261个数或第285个数;(3)287.5;(4)存在前n个数的和等于106,此时n的值是201。
【分析】观察数列,,,,,,,,,,……,可发现:分母为1的分数有1个,分母为2的数有3个,分母为3的数有5个,所以可得出:分母为n的分数有2n﹣1个;分子都是从1开始到与分母的数字相同连续的自然数,再倒数回到1,由此规律解决问题:
(1)首先要计算第800个数之前最大的平方是:当n=28时,n2=784,第784个数是分母为28的最后一个数,所以可以找到第800个数;
(2)先找出分母是16的最后一个数,是第162个数,162=256,再向右数5个即可,因为同一个分母的数除中间为1的数是出现一次外,其余都是出现2次,所以倒数第5个数也是,得出结论;
(3)同(1)同理,先计算第552个数之前最大的平方数:当n=23时,n2=529,先计算分母为1至23的所有分数之和:1+2+3+……+23的值,再确定第529到552之间数的和,最后相加即可;
(4)因为分母为n的分数有2n﹣1个,且这2n﹣1个分数相加和为n;所以分母为n时,前n2个数的和为,确定当n为最大时,最接近106时的n=14,即前196个数的和为105,与106还相差1,分母为15的分数能否达到几个分数和为1,来判断。
【解答】解:观察数列,,,,,,,,,,……,可发现:分母为1的分数有1个,分母为2的数有3个,分母为3的数有5个,所以可得出:分母为n的分数有2n﹣1个;且这2n﹣1个分数相加和为n.;第12个是分母为1的最后一个,第22个是分母为2的最后一个……,第n2个是分母为n的最后一个;
(1)因为1+3+5+…+2n﹣1=n2,
所以令n2≤800,
解得:n≤28,
当n=28时,n2=784,
所以第784个数是分母为28的最后一个数,
所以800个数的分母为29,分子为800﹣784=16,所以第800个数为;
(2)因为162+5=256+5=261,
172﹣4=289﹣4=285,
所以是第261个数或第285个数;
(3)令n2≤552,
解得:n≤23,
当n=23时,n2=529,
即前529个数的和为:1+2+3+……+23=24×11+12=276,
第530至第552个数之间一共有:
552﹣530+1=23个数,
第530至第552个数的和为:
11.5,
所以前552个数的和是:276+11.5=287.5;
(4)分母为n时,前n2个数的和为,当n=14时,前142=196个数的和为:
105,
第197个数开始为分母是15的数:
1,
105+1=106,
所以存在前n个数的和等于106,此时n=196+5=201。
故答案为:(1);(2)第261个数或第285个数;(3)287.5;(4)存在前n个数的和等于106,此时n的值是201。
【要点】解决本题的关键是找出规律,解决问题。
32.在下图中用阴影表示出平方米.
【答案】见试题解答内容
【分析】根据:4,把4平方米平均分成6份,每份就是平方米.
【解答】解:4
.
【要点】此题主要考查了分数除法的运算方法,以及分数的意义和应用,要熟练掌握.
33.画出1路公共汽车的行走路线。
1路公共汽车从起点站向东偏北25°方向行驶2千米,接着向东行驶3千米,又向西偏北40°方向行驶2千米,又向北行驶1千米,最后向东偏南30°方向行驶4千米到终点上。
【答案】
【分析】利用实际距离÷1即可求出图上距离;根据对地图上方向的规定,结合距离和角度求解,据此解答。
【解答】解:图上距离=实际距离÷比例尺
2÷1=2(厘米)
3÷1=3(厘米)
4÷1=4(厘米)
作图如下:
【要点】本题是一道关于确定位置方面的题目,可依据角度、方向与距离求解。
34.(1)花园街的西面有 电视台 、 小川家 、 电影院 .
(2)图书馆在小林家的 南面 ,小吃店在超市的 东 面,小川家在小林家的 西南 面.
(3)请你画出小林去音像店所走的路线.
(4)请你说一说小川去邮局,可以怎么走?
【答案】见试题解答内容
【分析】依据地图上的方向辨别方法,即“上北下南,左西右东”,以及图上标注的其他信息,即可进行解答.
【解答】解:(1)花园街的西面有 电视台、小川家、电影院.
(2)图书馆在小林家的 南面,小吃店在超市的 东面,小川家在小林家的 西南面.
(3)小林去音像店所走的路线如图所示:
(4)小川去邮局先沿北京路向东走,到达绿荫路后再向北走,
到达和平路后再向东走即可.
故答案为:电视台、小川家、电影院;南面、东、西南.
【要点】此题主要考查地图上的方向辨别方法的灵活应用.
35.小军沿学校向东偏北40°走200米后,再向东走400米,最后向南偏东45°走200米到家。请你根据描述画出小军从学校到家的路线图?
【答案】。
【分析】依据图示可知,图上1厘米代表实际距离200米,由此计算出向东走的图上距离,利用平面图上方向规定:上北下南,左西右东,依据题意结合图示去作图。
【解答】解:依据图示可知,图上1厘米代表实际距离200米,400÷200=2(厘米)
【要点】本题考查的是根据方向和距离确定物体的位置的应用。
36.五 一假期王老师带家人自驾车从淮滨出发,途经南京,去上海旅游。
(1)请你为王老师选择一条路线,先用笔描出该路线,再计算该路线的路程是多少?
(2)你对王老师有什么样好的建议?(请写下来)
【答案】(1),689千米;(2)言之有理即可,答案不唯一:节能减排,选择路程最短的线路。即从淮滨出发,选择沪陕高速,经410km到达南京,经停南京后选择沪蓉高速离开南京驶往上海,经279km到达上海。
【分析】(1)从淮滨到南京有2条线路,从南京到上海有3条线路,根据乘法原理可知,从淮滨到上海合计有(2×3)条线路,找一条线路画一画并根据加法的意义计算路程即可;
(2)言之有理即可,答案不唯一,比如本着节能减耗的目的,选择路线最短的。
【解答】解:(1)从淮滨出发,选择沪陕高速,经410km到达南京,经停南京后选择沪蓉高速离开南京驶往上海,经279km到达上海,如下图红色线路所示:
410+279=689(km)
答:该路线的路程是689千米。
(2)言之有理即可,答案不唯一:节能减排,选择路程最短的线路。即从淮滨出发,选择沪陕高速,经410km到达南京,经停南京后选择沪蓉高速离开南京驶往上海,经279km到达上海。
【要点】本题考查了千以内加法计算的应用以及路线图的应用。
37.王老师为学校购买音乐器材,他带去的钱可以买10台手风琴或50把小提琴,如果买了6台手风琴后,剩下的钱全部买小提琴,可以买多少把小提琴?
【答案】20把。
【分析】根据他带去的钱可以买10台手风琴或50把小提琴,可知买手风琴的钱数是买小提琴钱数的50÷10=5倍,如果买了6台手风琴后,剩下的钱数能买10﹣6=4(台)手风琴,剩下的钱全部买4×5=20(台)小提琴,据此解答。
【解答】解:50÷10=5
10﹣6=4(台)
4×5=20(台)
答:可以买20把小提琴。
【要点】本题考查的是工程问题,求出买手风琴的钱数是买小提琴钱数的50÷10=5倍是解答关键。
38.一堆沙甲队单独运要8天运完,乙队单独运要10天运完。现在两队合运几天后,还剩这堆沙的?
【答案】天。
【分析】把这堆沙子的重量看作单位“1”,甲队单独运要8天运完,可知甲车的工效是,乙队单独运要10天运完,可知,乙车的工效是,要求几天后还剩下这堆沙子的,依据工作时间=工作总量÷工作效率即可解答。
【解答】解:(1)÷()
(天)
答:现在两队合运天后,还剩这堆沙的。
【要点】解答本题的关键是明确等量关系式:工作时间=工作总量÷工作效率。
39.一项工程,甲队单独做18天可以完成,乙队单独做15天可以完成,现在甲队先做7天后,剩下的甲、乙两队合做完成,乙队完成了这项工程的几分之几?
【答案】。
【分析】已知甲队单独做18天可以完成,乙队单独做15天可以完成,把一项工程看作单位“1”,根据工作效率=工作总量÷工作时间,甲队的工作效率为,乙队的工作效率为;甲队工作7天工作量为,剩下工作量为1;根据工作量÷效率和=甲乙两队完成剩下工作量的时间;用所求时间×乙队的工作效率=乙队的工作量,据此解答。
【解答】解:(1﹣7)÷()
=5
答:乙队完成了这项工程的。
【要点】理清题中数量关系是解答关键。
40.根据互联网信息测算:“中国空间站组合体每1.5小时左右绕地球一周。”那么航天员在空间站24小时能绕地球多少周?
【答案】16周。
【分析】用24小时除以中国空间站组合体绕地球一周的时间即可。
【解答】解:24÷1.5=16(周)
答:航天员在空间站24小时能绕地球16周。
【要点】本题主要考查小数除法的应用。
41.某市交警部门开展“一盔一带”安全守护行动,呼吁骑电动车的市民佩戴头盔。政策颁布后,头盔的销售量火爆。某商店第二天卖出108顶头盔,比第一天多卖出。商店第一天卖出多少顶头盔?(列方程解答)
【答案】60顶。
【分析】首先根据题意,设商店第一天卖出x顶头盔;然后根据:第一天卖出头盔的数量×(1)=第二天卖出头盔的数量,列出方程,求出商店第一天卖出多少顶头盔即可。
【解答】解:设商店第一天卖出x顶头盔。
(1)x=108
x=108
x108
x=60
答:商店第一天卖出60顶头盔。
【要点】此题主要考查了一元一次方程的应用,弄清题意,找出合适的等量关系,进而列出方程是解答此类问题的关键。
42.如图,窗户比门高出了多少米?
【答案】见试题解答内容
【分析】先用窗户距离低面的高度加上窗户的高度,求出窗户的最高处距离地面多少米,再减去门的高度(门的最高处距离地面的长度),即可求出窗户比门高出了多少米?
【解答】解:1.63+0.75﹣2
=2.38﹣2
=0.38(米)
答:窗户比门高出了0.38米.
【要点】解答此题,首先观察图,弄清题意,分清已知与所求,再找出基本数量关系,由此列式解答.
43.一个圆形花坛的周长是62.8米,在它的周围铺一条宽为2米的小路,这条小路的面积是多少平方米?
【答案】138.16平方米。
【分析】根据环形面积=外圆面积﹣内圆面积,先求出花坛的半径,花坛的半径加上路宽就是外圆半径,然后把数据代入公式解答。
【解答】解:62.8÷3.14÷2=10(米)
3.14×[(10+2)2﹣102]
=3.14×[144﹣100]
=3.14×44
=138.16(平方米)
答:这条小路的面积是138.16平方米。
【要点】此题主要考查环形面积公式在实际生活中的应用,关键是熟记公式。
44.一个环形砂轮,外圆半径是0.4米,环宽10厘米,这个环形砂轮的面积是多少?
【答案】2198平方厘米。
【分析】先求出环形砂轮内圆的半径,则内、外圆的半径确定,要求圆环的面积,可直接利用公式S圆环=π(R2﹣r2)列式解答即可。
【解答】解:0.4米=40厘米
40﹣10=30(厘米)
3.14×(402﹣302)
=3.14×(1600﹣900)
=3.14×700
=2198(平方厘米)
答:这个环形砂轮的面积是2198平方厘米。
【要点】此题考查了圆环的面积计算,要先知道各自的半径,再利用公式进行计算。
45.有一个圆形花坛,半径是50米,王叔叔每天早晨绕花坛跑4圈,他每天早晨跑多少米?
【答案】见试题解答内容
【分析】根据圆的周长公式:C=2πr,把数据代入公式求出花坛的周长,然后乘4即可.
【解答】解:2×3.14×50×4
=314×4
=1256(米)
答:他每天早晨跑1256米.
【要点】此题主要考查圆的周长公式C=2πr在实际生活中的应用.
46.一根7米长的绳子,绕树一周还余下0.72米,树的直径是多少米?
【答案】见试题解答内容
【分析】先根据题目条件得到这棵树的周长,再根据圆的周长可求这棵树的直径..
【解答】解:(7﹣0.72)÷3.14
=6.28÷3.14
=2(米)
答:树的直径是2米.
【要点】考查了圆的周长在实际生活中的应用,本题关键是得到这棵树的周长.
47.钟面上时针长6厘米,时针尖端走一天的距离是多少厘米?
【答案】75.36厘米。
【分析】2×π×半径=圆的周长,圆的周长×2=时针尖端走一天的距离。
【解答】解:2×3.14×6×2
=37.68×2
=75.36(厘米)
答:时针尖端走一天的距离是75.36厘米。
【要点】本题主要考查圆的周公式的应用。
48.原产非洲的“猴面包树”,它的树干非常粗,其中一棵“猴面包树”的直径为15.7m,如果用绳子绕它的树干一周,至少需要准备多长的绳子?
【答案】见试题解答内容
【分析】根据圆的周长公式:C=πd,把数据代入公式求出树干的周长即可.
【解答】解:3.14×15.7=49.298(m)
答:至少需要准备49.298m长的绳子.
【要点】此题主要考查圆的周长公式在实际生活中的应用,关键是熟记公式.
49.填表:
分数
小数 0.2 0.6
百分数 8% 12.5%
【答案】见试题解答内容
【分析】百分数化小数的方法:去掉百分号,把小数点向左移动两位;
百分数化分数的方法:先写成分数的形式,再进一步化简成最简分数;
分数化成小数,用分数的分子除以分数的分母,如果不能化成有限小数,根据需要取近似值,一般保留一位小数;
分数化百数,分母是100的分数,直接改写成百分数号即可,即去掉分母,添上百分号(%);一般分数化百分数,首先把分数化成小数,再把小数点向右移动两位,添上百分号(%)即可,如果不能化成有限小数,根据需要取近似值,一般百分号前保留一位小数;
小数化百分数只要把小数点向右移动两位,添上百分号即可;把百分数化成小数时,把百分数去掉百分号,同时把小数点向左移动两位即可;
小数化分数的方法:一位小数表示十分之几,两位小数表示百分之几,三位小数表示千分之几…先写成分数的形式,再进一步化简成最简分数;据此解答.
【解答】解:
分数
小数 0.2 0.25 0.08 0.625 0.6 0.125
百分数 20% 25% 8% 62.5% 60% 12.5%
【要点】解答本题关键是明确百分数、小数和分数三者之间互化的方法.
50.说一说下面百分数的具体含义。
(1)我国人口约占世界人口的22%。
(2)我国耕地面积约占世界耕地面积的7%。
(3)某发电厂4月份完成计划发电任务的115%。
【答案】(1)世界上每100个人里有22个是中国人口;(2)把世界耕地总面积平均分成100份,我国的耕地面积大约占其中的7份;(3)发电的任务看成“1”,4月份完成了1.15。
【分析】根据百分数的意义:百分数是“表示一个数是另一个数百分之几的数,”由此解答即可。
【解答】解:(1)我国人口约占世界人口的22%,这句话可以理解为世界上每100个人里有22个是中国人口;
(2)中国耕地面积约是世界耕地面积的7%,表示表示把世界耕地总面积平均分成100份,我国的耕地面积大约占其中的7份;
(3)某发电厂4月份完成计划发电任务的115%,表示把发电的任务看成“1”,4月份完成了1.15。
【要点】本题主要考查了百分数的意义,属于基础知识。
51.某修路队上半年修路6400米,比原计划多修了1600米,这支修路队多修了百分之几?
【答案】33.33%。
【分析】根据百分数的意义,用这支修路队多修的长度除以原计划修的长度,就是这支修路队多修的路是原计划的百分之几。
【解答】解:1600÷(6400﹣1600)×100%
=1600÷4800×100%
≈33.33%
答:这支修路队大约多修了33.33%。
【要点】本题是求一个数是另一个数的百分之几,关键是看把谁当成了单位“1”,单位“1”的量为除数。
52.近年来,各地“广场舞”噪音干扰的问题倍受关注。相关人员对本地区15~65岁年龄段的市民进行了随机调查,并制作了如下相应的统计图。市民对“广场舞”噪音干扰的态度有以下五种:A.没影响B.影响不大C.有影响,建议做无声运动D.影响很大,建议取缔E.不关心这个问题。
根据以上信息解答下列问题:
(1)根据统计图填空:m= 32% 。
(2)在此次调查中,“不关心这个问题”的有25人,请问一共调查了 500 人。
(3)在此次调查中,持“影响不大”态度的人比持“没影响”态度的人多百分之 六十五 。
【答案】(1)32%;
(2)500;
(3)六十五。
【分析】(1)调查的总人数看作单位“1”,根据减法的意义,用减法解答。
(2)调查的总人数看作单位“1”,“不关心这个问题”的有25人,占调查总人数的5%,根据已知一个数的百分之几是多少,求这个数,用除法解答。
(3)把持“没影响”态度的人数看作单位“1”,先用减法求出持“影响不大”态度的人比持“没影响”态度的人多占总人数百分之几,然后根据求一个数是另一个数的百分之几,用除法解答。
【解答】解:1﹣(10%+5%+20%+33%)
=1﹣68%
=32%
答:m=32%。
(2)25÷5%
=25÷0.05
=500(人)
答:一共调查了500人。
(3)(33%﹣20%)÷20%
=0.13÷0.2
=0.65
=65%
答:持“影响不大”态度的人比持“没影响”态度的人多65%。
故答案为:32%;500;六十五。
【要点】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
53.聪聪家2009年11月支出情况统计如图.聪聪家2009年11月的总支出是3600元.请你回答问题.
(1)这个月哪项支出最多?支出了多少元?
(2)文化教育支出了多少元?购买衣物支出了多少元?
(3)购买衣物的支出比文化教育支出少百分之几?
【答案】见试题解答内容
【分析】(1)通过观察扇形统计图可知:这个月伙食费支出最多,根据一个数乘百分数的意义,用乘法解答;
(2)把总支出看作单位“1”,根据一个数乘百分数的意义,用乘法解答;
(3)把文化教育支出看作单位“1”,根据求一个数是另一个数的百分之几,用除法解答.
【解答】解:(1)3600×35%
=3600×0.35
=1260(元);
答:这个月伙食费支出最多,支出了1260元.
(2)3600×25%
=3600×0.25
=900(元);
3600×20%
=3600×0.2
=720(元);
答:文化教育支出900元,购买衣物支出720元.
(3)(900﹣720)÷900
=180÷900
=0.2
=20%;
答:购买衣物的支出比文化教育支出少20%.
【要点】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
54.如图是我国国土各种地形所占百分比情况统计图。
(1)盆地占我国国土面积的 19 %。
(2)山地占我国国土面积的 33 %。
(3)高原所占面积与丘陵所占面积的最简单的整数比是 13:5 。
(4)我国国土面积约960万平方千米,平原的面积约是 115.2 万平方千米。
【答案】(1)19;
(2)33;
(3)13:5;
(4)115.2。
【分析】(1)通过观察统计图直接回答问题。
(2)把我国国土总面积看作单位“1”,根据减法的意义,用减法解答。
(3)根据比的意义、比的化简方法解答即可。
(4)把我国国土总面积看作单位“1”,根据求一个数的百分之几是多少,用乘法解答。
【解答】解:(1)盆地占我国国土面积的19%。
(2)1﹣12%﹣19%﹣10%﹣26%=33%
答:山地占我国国土面积的33%。
(3)26%:10%=13:5
答:高原所占面积与丘陵所占面积的最简单的整数比是13:5。
(4)960×12%
=960×0.12
=115.2(万平方千米)
答:平原的面积约是115.2万平方千米。
故答案为:19;33;13:5;115.2。
【要点】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
55.某小学参加兴趣小组情况如图:已知参加体育的有136人,参加“其它”兴趣小组的共有多少人?
【答案】见试题解答内容
【分析】根据扇形统计图可知,把总人数看作单位“1”,总人数的34%是136人,根据“已知一个数的百分之几是多少,求这个数用除法计算”,用136除以34%可求出总人数;然后求出参加“其它”兴趣小组占了总人数的百分比:1﹣34%﹣18%﹣26%,再根据百分数乘法的意义解答即可.
【解答】解:136÷34%=400(人)
400×(1﹣34%﹣18%﹣26%)
=400×22%
=88(人)
答:参加“其它”兴趣小组的共有88人.
【要点】本题主要考查了学生根据扇形统计图分析数量关系解答问题的能力.
56.每年的4月23日是“世界读书日”,为深入推进全民阅读,培育良好的阅读习惯。实验小学新进一批图书,情况统计如图。已知科技书和童话故事的本数比是3:5。
(1)实验小学新进的这批图书共有多少本?
(2)儿童文学有多少本?
【答案】(1)2000本;(2)640本。
【分析】(1)已知科技书有300本,科技书和童话故事的本数比是3:5。也就是科技书的本数是童话故事的,根据已知一个数的几分之几是多少,求这个数,用除法解答得出童话故事的本数,再除以它占的百分率,即可得实验小学新进的这批图书共有多少本。
(2)用乘法计算得出其他的本数,再用减法计算即可得儿童文学的本数。
【解答】解:(1)300500(本)
500÷25%=2000(本)
答:实验小学新进的这批图书共有2000本。
(2)2000×28%=560(本)
2000﹣300﹣500﹣560=640(本)
答:儿童文学有640本。
【要点】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
57.如图是1班和2班的男生和女生的人数统计图,已知两个班的人数都不少于30,也不多于40,则1班有多少名学生,2班有多少名学生?
【答案】见试题解答内容
【分析】(1)利用圆心角的度数之比,可以求得各班的女生与男生人数之比.①1班180:180=1:1,所以:女:男=1:1=2:2;②2班144:(360﹣144)=2:3,所以:女:男=2:3;③1班和2班之和160:(360﹣160)=4:5,女:男=4:5;由此可得:4+5=9,总人数可分为9份,其中1班占:2+2=4份;2班占:2+3=5份.
(2)根据题干已知两个班的人数都不少于30,也不多于40.可得:两个班的总人数应在60~80之间(包括两端),而总人数为(4+5=9)份,那么总人数应是9的倍数,因此有2种可能:总人数为63人或72人,由此展开分析讨论即可解决问题.
【解答】解:根据题干分析可得:①1班:180:360=12,所以:女:男=1:1=2:2;
②2班:144:(360﹣144)=2:3,所以:女:男=2:3;
③1班和2班之和:160:(360﹣160)=4:5,所以:女:男=4:5;
由此可得:4+5=9,总人数可分为9份,其中1班占:2+2=4(份),2班占:2+3=5(份);
(1)若总人数为63人:则每份有:63÷9=7(人),
则1班人数为:7×(2+2)=28(人),不符合题意;
(2)若总人数为72人,则每份有:72÷9=8(人),
则1班人数为:8×(2+2)=32(人),
2班人数为:8×(2+3)=40(人),
答:1班人数为32人,2班人数为40人.
故答案为:32;40.
【要点】根据统计图求出各班女生与男生的比,和女生总人数与男生总人数的比的关系,把总人数分成9份,确定出1班人数占4份,2班人数占5份是解答本题的关键,也是一个难点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
