(期末拔高提分)期末核心素养培优卷-2024-2025学年五年级下学期数学青岛版(六三制)(含答案解析)
文档属性
| 名称 | (期末拔高提分)期末核心素养培优卷-2024-2025学年五年级下学期数学青岛版(六三制)(含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 100.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-14 00:00:00 | ||
图片预览


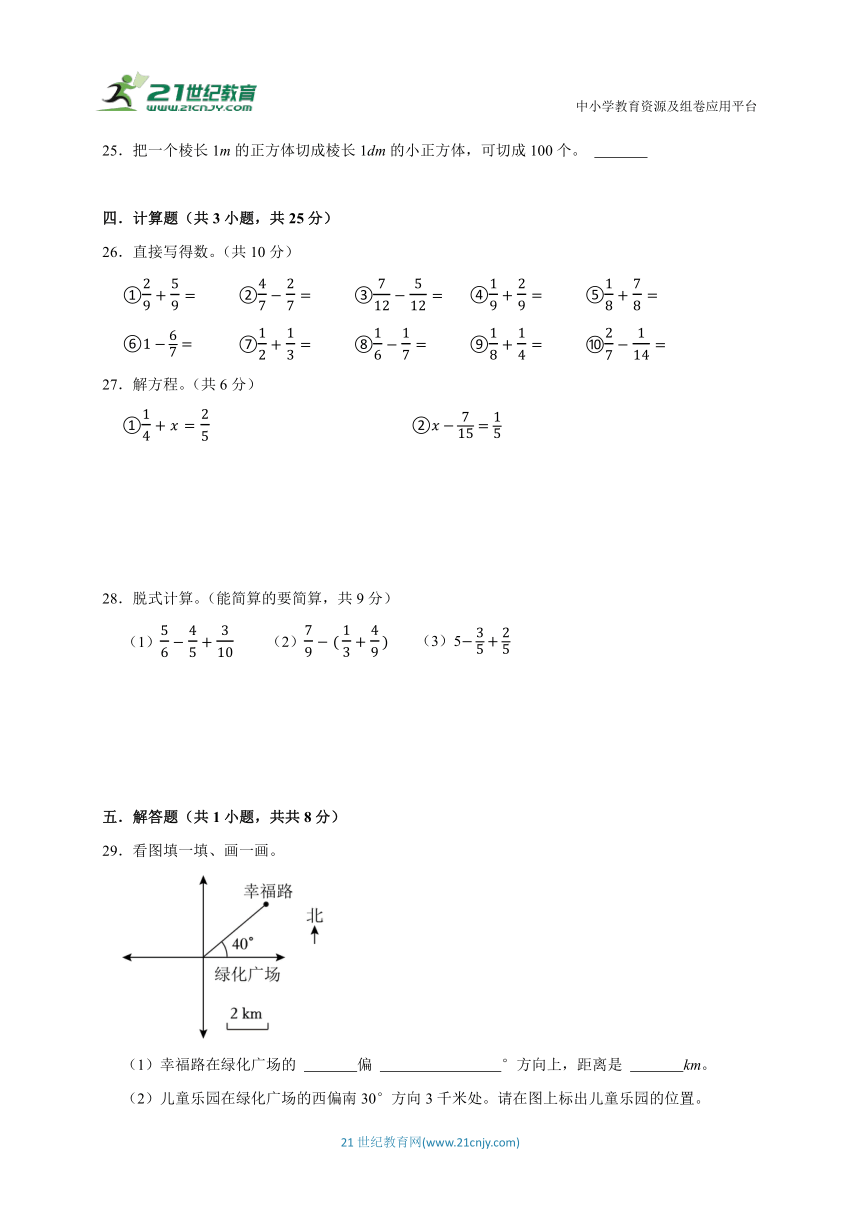


文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年五年级下学期数学期末核心素养培优卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题(共8小题,共8分)
1.A点的位置记为0,A点东面10m记作+10m,现在小刚从A点先向东行8m,再向西行6m,这时小刚的位置记作( )
A.+2m B.﹣2m C.+14m
2.a÷b=7(a、b都为非0自然数),a和b的最小公倍数是( )
A.a B.b C.ab
3.下列算式中,数字“6”和“4”可以直接相加减的是( )
A.567+432 B. C.3.67+2.04
4.10克盐完全溶解在100克水中,盐与盐水的比是( )
A.1:10 B.1:9 C.1:11
5.平平和凡凡进行800米跑步比赛,相同时间内,平平跑了全程的,凡凡跑了全程的,( )跑得快。
A.平平 B.凡凡 C.无法判断
6.一项工作,甲单独完成需要8小时,乙单独完成需要10小时,甲、乙的工作效率比是( )
A.4:5 B.5:4 C.8:10
7.一堆煤两天运完,第一天运走吨,第二天运走这堆煤的,( )运得多。
A.第一天 B.第二天 C.无法确定
8.“一去二三里,烟村四五家,亭台六七座,八九十枝花。”这首诗中表示数的字占总字数的( )
A. B. C.
二.填空题(共12小题,共18分)
9.一个方便袋里有30多个苹果,如果4个一盘或者6个一盘,正好分完.这个方便袋里一共有 个苹果.
10.1里有 个,再添上 个等于2.
11.一段方钢长1.5米,横截面是正方形,把它锯成相等的两段后表面积比原来增加18平方厘米,每段钢材的体积是 .
12.五年级一班要从5名候选人中选两名担任本班“六一”联欢会的主持人,有 种不同的选法。
13.0.54m3= L; 5050cm3= dm3.
14.小明、小李和小凯三人读同一篇文章,小明用了小时,小李用了小时,小凯用了0.2小时, 的速度最快.
15.把两个棱长是10厘米的正方体粘合成一个长方体,这个长方体的表面积是 平方厘米,体积是 立方厘米.
16.四个小朋友进行乒乓球比赛,每两人都要赛一场,他们一共要赛 场.
17.把的分母加上10,要使分数的大小不变,分子应加上 .
18.如图折成正方体后,与5号相对的面是 号, 号与6号是相对的面。
19.把一个棱长为3分米的正方体木块,切成棱长为1分米的小正方体,可以切成 块。
20.六月份,学校食堂报表学生吃了大米总数的,把 看做单位“1”,平均分成 份,吃了的占这样的 份。
三.判断题(共5小题,共5分)
21.把的分子加上6,要使分数的大小不变,分母也要加上6。
22.两个小正方体拼成一个长方体,长方体的体积等于两个小正方体的体积之和. .
23.假分数一定大于1,真分数一定小于1.
24.盐溶解于水后,盐水的体积正好等于盐的体积与水的体积之和。
25.把一个棱长1m的正方体切成棱长1dm的小正方体,可切成100个。
四.计算题(共3小题,共25分)
26.直接写得数。(共10分)
① ② ③ ④ ⑤
⑥ ⑦ ⑧ ⑨ ⑩
27.解方程。(共6分)
① ②
28.脱式计算。(能简算的要简算,共9分)
(1) (2) (3)5
五.解答题(共1小题,共共8分)
29.看图填一填、画一画。
(1)幸福路在绿化广场的 偏 °方向上,距离是 km。
(2)儿童乐园在绿化广场的西偏南30°方向3千米处。请在图上标出儿童乐园的位置。
六.应用题(共6小题,共36分)
30.一块棱长为40cm的正方体冰块,如果每立方厘米冰的质量是0.9g,那么这块冰的质量一共是多少千克?
31.一本故事书共120页,小欣第一周看了全书的,第二周看了40页,两周共看了书的几分之几?
32.爸爸买了一个长80厘米,宽60厘米的鱼缸,水深50厘米,妈妈为点缀鱼缸,买了12立方分米的假山放进鱼缸完全浸没在水中,这时水面升高了多少厘米?
33.一辆货车的油箱是一个长方体,长、宽、高分别是0.8米、0.8米、0.5米(箱壁厚度忽略不计)。
①做这样一个油箱3平方米的铁皮够吗?
②如果这辆货车每行驶100千米耗油50升,加满油后可以行驶多少千米?
34.一个长方体和一个正方体的棱长总和相等。已知长方体的长是4cm、宽是3cm、高是5cm。
(1)正方体的棱长是多少厘米?
(2)正方体的表面积是多少平方厘米?
(3)正方体的体积是多少立方厘米?
35.一个棱长4分米的正方体形状的无盖玻璃鱼缸。
(1)做这个鱼缸至少需要多少平方分米的玻璃?
(2)这个鱼缸最多能盛水多少升?( 玻璃的厚度忽略不计)
(3)鱼缸里原来有50升水,往水里放入一些鹅卵石,水面上升到33厘米。这些鹅石的体积是多少立方厘米?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案与试题解析
一.选择题(共8小题,共8分)
1.A
【分析】在数轴上,A点的位置记为0,A点东面10m记作+10m,现在小刚从A点先向东行8m,记作+8m,再向西行6m,8﹣6=2m,相当于小刚从A点先向东走了2m,记作+2m。
【解析】解:由分析得知,A点的位置记为0,A点东面10m记作+10m,现在小刚从A点先向东行8m,再向西行6m,这时小刚的位置记作+2m。
故选:A。
【点评】此题考查了负数的意义及其应用,要求学生掌握。
2.A
【分析】因为a÷b=7(a、b都为非0的自然数),所以a和b是倍数关系,当两个数是倍数关系时,较大的数是它们的最小公倍数,较小的数是它们的最大公因数,据此解答.
【解析】解:因为a÷b=7(a、b都为非0的自然数),
所以a和b的最小公倍数是:a.
故选:A.
【点评】本题考查:当两个数是倍数关系时,较大的数是它们的最小公倍数,较小的数是它们的最大公因数.
3.B
【分析】根据“只有计数单位相同的数才能直接相加减”直接判断。
【解析】解:选项A,567的“6”在十位上,432的“4”在百位上,计数单位不同,不能直接相加减;
选项B,表示6个,表示4个,两个分数的计算单位相同,可以直接相加减;
选项C,3.67的“6”在十分位上,2.04的“4”在百分位上,计数单位不同,不能直接相加减。
故选:B。
【点评】解答本题需明确:只有计数单位相同的数才能直接相加减。
4.C
【分析】把10克盐完全溶解在100克水中,就形成了10+100=110克的盐水,要求盐与盐水的重量比,也就是求10克与110克的比.
【解析】解:10:(10+100)
=10:110
=1:11.
故选:C.
【点评】此题考查比的意义,要注意:求的是盐与盐水对应的重量比,所以要先求出形成的盐水的重量是解题关键.
5.A
【分析】将800米看作单位“1”,比较出和的大小,即可确定谁跑得快。
【解析】解:
答:平平跑得快。
故选:A。
【点评】本题考查了利用比较分数的大小解决问题,需准确理解题意。
6.B
【分析】根据工作总量一定,工作效率和时间成反比例进行求解。
【解析】解:10:8
=(10÷2):(8÷2)
=5:4
答:甲、乙的工作效率比是5:4。
故选:B。
【点评】熟练掌握工作总量一定,工作效率的比等于时间的反比是解题的关键。
7.A
【分析】一堆煤两天运完,第二天运了这堆煤的,那么第一天运了这堆煤的多少呢?把这堆煤看做“1”,用减法,然后比较分数的大小,即可得解。
【解析】解:1
答:第一天运得多。
故选:A。
【点评】此题所给的吨可以看作是一个干扰数据,进行分数的减法计算和分数大小比较,即可得解。
8.A
【分析】这首诗一共有20字,其中表示数的有一、二、三、四、五、六、七、八、九、十共10个,求这首诗中表示数的字占总字数的几分之几,用表示数的字数除以总字数。
【解析】解:10÷20
答:这首诗中表示数的字占总字数的。
故选:A。
【点评】求一个数是另一个数的几分之几,用这个数除以另一个数。
二.填空题(共12小题,共18分)
9.见试题解答内容
【分析】先求出4、6的最小公倍数,再找到4、6的公倍数在30左右的数即为所求.
【解析】解:4、6的最小公倍数是3×2×2=12,
因为12×3=36,苹果总数在30左右,
所以这个方便袋里一共有 36个苹果;
答:这个方便袋里一共有 36个苹果;
故答案为:36.
【点评】此题考查了公倍数问题,解答该题关键是会求两个数的最小公倍数,并用它解决实际问题.
10.见试题解答内容
【分析】首先用1除以,判断出1里有多少个;然后用2减去1,求出2比1多多少,即可判断出再添上个等于2.
【解析】解:因为1,
所以1里有多10个;
因为2﹣1,
所以2比1多,1再添上4个等于2.
故答案为:10、4.
【点评】此题主要考查了分数除法的运算方法,要熟练掌握.
11.见试题解答内容
【分析】由题意可知:把一根长1.5米的方钢截成两段,表面积增加了2个横截面的面积,由此可以求得这个方钢的横截面的面积为:18÷2=9平方厘米,再利用长方体的体积公式:v=sh,把数据代入公式解答即可.
【解析】解:1.5米=150厘米,
18÷2×150÷2,
=9×150÷2,
=1350÷2,
=675(立方厘米);
答:每段钢材的体积是765立方厘米.
故答案为:675立方厘米.
【点评】根据切割特点,利用增加部分的表面积求出长方体钢材的横截面的面积是解决本题的关键.
12.10。
【分析】从5名候选人中选两名,相当于两两组合,根据握手问题的公式n(n﹣1)÷2解答即可。
【解析】解:5×(5﹣1)÷2
=20÷2
=10(种)
答:有10种不同的选法。
故答案为:10。
【点评】本题考查了握手问题的实际应用,要注意去掉重复计算的情况,如果数量比较少可以用枚举法解答,如果数量比较多可以用公式n(n﹣1)÷2解答。
13.见试题解答内容
【分析】(1)高级单位立方米化低级单位升乘进率1000.
(2)低级单位立方厘米化高级单位立方分米除以进率1000.
【解析】解:(1)0.54m3=540L;
(2)5050cm3=5.05dm3.
故答案为:540,5.05.
【点评】本题是考查体积、容积的单位换算.单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率.
14.见试题解答内容
【分析】同样一篇文章,谁用的时间少,谁的速度就快;利用异分母分数大小的比较方法先将它们化成同分母分数,再比较大小即可.
【解析】解:因为,
,
0.2,
且,
即0.2,
所以小明的速度最快;
故答案为:小明.
【点评】解答此题的关键是将这几个数化成同分母分数,再比较大小.
15.见试题解答内容
【分析】根据题意可知:把两个棱长是10厘米的正方体粘合成一个长方体,这个长方体的表面积比两个正方体的表面积和减少了正方体的两个面的面积,长方体的体积等于两个正方体的体积和,根据正方体的表面积公式:s=6a2,体积公式:v=a3,把数据分别代入公式解答即可.
【解析】解:10×10×6×2﹣10×10×2
=100×6×2﹣100×2
=1200﹣200
=1000(平方厘米);
10×10×10×2
=100×10×2
=1000×2
=2000(立方厘米);
答:这个长方体的表面积是1000平方厘米,体积是2000立方厘米.
故答案为:1000,2000.
【点评】此题主要考查正方体、长方体的表面积公式、体积公式的灵活运用,关键是熟记公式.
16.见试题解答内容
【分析】因为每一个小朋友都和其他人三个小朋友比赛,每小朋友比赛三场,一共比赛3×4=12场,但两个小朋友之间重复了一次,因此需比赛12÷2=6场.
【解析】解:4×3÷2=6(场);
答:一共要赛6场.
故答案为:6.
【点评】此题考查单循环比赛,计算方法为n(n﹣1)场,如果为双循环为n(n﹣1)场(n是指参加的人数或队数).
17.见试题解答内容
【分析】首先分析分母之间的变化,原来分母是5,由5变成(5+10)=15,扩大了3倍,要使分数的大小不变,分子也应该扩大3倍,据此解答.
【解析】解:原来的分母是5,现在的分母是(5+10)=15,扩大了3倍,
原来的分子是3,要使分数的大小不变,分子也应该扩大3倍,3×3=9,9﹣3=6,
答:分子应加上6.
故答案为:6.
【点评】此题主要利用分数的基本性质解答问题,先观察分子或分母之间的变化,发现规律,再进一步通过计算解答问题.
18.2;4。
【分析】如图,根据正方体展开图的11种特征,属于正方体展开图的“1﹣3﹣2”型,折成正方体后,1号面与3号面相对,2号面与5号面相对,4号面与6号面相对。
【解析】解:如图:
折成正方体后,1号面与3号面相对,5号面与2号面相对,4号面与6号面相对.
故答案为:2;4。
【点评】正方体展开图分四种类型,11种情况,每种情况折成正方体后哪些面相对是有规律的,可自己动手操作一下并记住,能快速解答此类题。
19.27。
【分析】根据正方体的体积公式:V=a3,分别求出棱长3分米、棱长1分米的正方体的体积,然后根据“包含”除法的意义,用除法解答。
【解析】解:3×3×3÷(1×1×1)
=27÷1
=27(块)
答:可以切成27块。
故答案为:27。
【点评】此题主要考查正方体体积公式的灵活运用,关键是熟记公式。
20.7,4。
【分析】“比”“占”“是”“相当于”后面的、“的”前面的通常看作单位“1”,据此解答即可。
【解析】解:六月份,学校食堂报表学生吃了大米总数的,把大米总数看做单位“1”,平均分成7份,吃了的占这样的4份。
故答案为:大米总数,7,4。
【点评】此题主要考查了单位“1”的确定方法,要熟练掌握。
三.判断题(共5小题,共5分)
21.×
【分析】的分子加上6,扩大了3倍,关键分数的基本性质,要使分数的大小不变,分母也应扩大3倍,变成12,即加上8,据此解答即可.
【解析】解:3+6=9,9÷3=3
分子变成9,扩大了3倍,
要使分数的大小不变,分母应扩大3倍;
4×3=12,12﹣4=8
即分母应加上8。
故答案为:×。
【点评】此题主要考查了分数的基本性质的应用。
22.见试题解答内容
【分析】由题意可知:两个小长方体在拼接的过程中,所占空间的大小不变,即它们的体积不变,所以长方体的体积等于两个小正方体的体积之和.
【解析】解:两个小正方体拼成一个长方体,长方体的体积等于两个小正方体的体积之和.
故答案为:√.
【点评】解答此题的主要依据是:长方体和正方体的体积的意义.
23.见试题解答内容
【分析】首先根据分子大于或者等于分母的分数是假分数,可得假分数不一定大于1,也可能等于1,然后根据分子比分母小的分数是真分数,可得真分数一定小于1,据此判断即可.
【解析】解:根据假分数、真分数的特征,可得
假分数不一定大于1,也可能等于1,真分数一定小于1,
所以题中说法不正确.
故答案为:×.
【点评】此题主要考查了真分数、假分数的特征和应用,要熟练掌握.
24.×
【分析】查资料可知:盐溶解于水后,盐离子和水分子互相进入了之间的间隙,盐水的体积小于盐和水的体积之和。
【解析】解:分析可知,盐溶解于水后,盐离子和水分子互相进入了之间的间隙,盐水的体积小于盐和水的体积之和。所以原题说法错误。
故答案为:×。
【点评】一种固体或液体物质溶于另一种液体物质时,两种物质的体积之和小于溶液的体积。
25.×
【分析】根据正方体的体积公式:V=a3,再根据体积单位相邻单位之间的进率,1立方米=1000立方分米,据此判断。
【解析】解:因为1立方米=1000立方分米,所以把一个棱长1m的正方体切成棱长1dm的小正方体,可切成1000个。
因此题干中的结论是错误的。
故答案为:×。
【点评】此题考查的目的是理解掌握正方体的体积公式、体积单位相邻单位之间的进率及换算。
四.计算题(共3小题,共25分)
26.①;②;③;④;⑤1;⑥;⑦;⑧;⑨;⑩。
【分析】根据分数加减法的计算方法直接进行口算即可。
【解析】解:
① ② ③ ④ ⑤1
⑥ ⑦ ⑧ ⑨ ⑩
【点评】本题考查了基本的运算,注意运算数据和运算符号,细心计算即可。
27.①x;②x。
【分析】①方程两边同时减去;
②方程两边同时加上。
【解析】解:①
x
x
②
x
【点评】熟练掌握等式的基本性质是解题的关键。
28.(1);(2)0;(3)4;(4)2。
【分析】(1)、(3)按从左到右的运算顺序依次计算。
(2)根据减法的性质简算即可。
(4)根据加法的交换律与结合律简算即可。
【解析】解:(1)
(2)
=0
(3)5
=4
=4
(4)
=()+()
=1+1
=2
【点评】计算混合运算时,要注意按照运算顺序计算;能简算的要简算,不要错用运算定律。
五.解答题(共1小题,共8分)
29.(1)东,北,40,4;
(2)。
【分析】由图可知,图上1厘米代表实际距离2千米,(1)计算出幸福路到绿化广场的实际距离,利用平面图上方向规定:上北下南左西右东,依据题意结合图示去解答;
(2)儿童乐园到绿化广场的图上距离,利用平面图上方向规定:上北下南左西右东,依据题意结合图示去作图。
【解析】解:(1)2×2=4(千米),幸福路在绿化广场的东偏北40°方向上,距离是4千米。
(2)3÷2=1.5(厘米)
故答案为:东,北,40,4。
【点评】本题考查的是根据方向和距离确定物体位置的应用。
六.应用题(共6小题,共36分)
30.57.6千克。
【分析】先利用正方体的体积=棱长3,求出这块冰块的体积,再乘0.9克即可解答问题。
【解析】解:40×40×40×0.9
=64000×0.9
=57600(克)
57600克=57.6千克
答:这块冰的质量一共是57.6千克。
【点评】此题主要考查正方体的体积公式的实际应用,注意单位的换算。
31.。
【分析】先用第二周看的页数除以总页数,求出第二周看的页数占总页数的几分之几,再把第一周、第二周看的页数所占的分率相加。
【解析】解:40÷120
答:两周共看了书的。
【点评】求一个数是另一个数的几分之几,用这个数除以另一个数;把两个分数合并成一个分数,用加法计算。
32.2.5厘米。
【分析】根据题意可知,用假山的体积除以鱼缸的底面积就是水面上升的高度。据此解答即可。
【解析】解:12立方分米=12000立方厘米
12000÷(80×60)
=12000÷4800
=2.5(厘米)
答:这时水面升高了2.5厘米。
【点评】此题主要考查长方体体积公式的灵活运用,关键是熟记公式。
33.①够;
②640千米。
【分析】①长方体的表面积=(长×宽+长×高+宽×高)×2,把数据代入公式求出做这个油箱需要铁皮的面积,然后与3平方米进行比较即可。
②首先根据“等分”除法的意义,用除法求出行驶1千米平均耗油多少升,然后根据“包含”除法的意义,用油的体积除以每千米的耗油量即可。
【解析】解:①(0.8×0.8+0.8×0.5+0.8×0.5)×2
=(0.64+0.4+0.4)×2
=1.44×2
=2.88(平方米)
3平方米>2.88平方米
答:做这样一个油箱3平方米的铁皮够。
②0.8×0.8×0.5=0.32(立方米)
0.32立方米=320升
320÷(50÷100)
=320÷0.5
=640(千米)
答:加满油后可以行驶640千米。
【点评】此题主要考查长方体的表面积公式、体积(容积)公式的灵活运用,关键是熟记公式。
34.(1)4厘米;
(2)96平方厘米;
(3)64立方厘米。
【分析】(1)根据长方体的棱长总和=(长+宽+高)×4,正方体的棱长总和=棱长×12,那么棱长=棱长总和÷12,把数据代入公式解答。
(2)根据正方体的表面积公式:S=6a2,把数据代入公式解答。
(3)根据正方体的体积公式:V=a3,把数据代入公式解答。
【解析】解:(4+3+5)×4÷12
=12×4÷12
=4(厘米)
答:正方体的棱长是4厘米。
(2)4×4×6
=16×6
=96(平方厘米)
答:正方体的表面积是96平方厘米。
(3)4×4×4
=16×4
=64(立方厘米)
答:正方体的体积是64立方厘米。
【点评】此题主要考查长方体的棱长总和公式、正方体的棱长总和公式、表面积公式、体积公式的灵活运用,关键是熟记公式。
35.(1)80平方分米;
(2)64升;
(3)2800立方厘米。
【分析】(1)根据正方体的表面积公式:S=6a2,因为这个玻璃缸无盖,所以只求它的5个面的总面积即可。
(2)根据正方体的容积(体积)公式:V=a3,把数据代入公式解答。
(3)根据题意可知,这些鹅石的体积等于水与这些鹅石的体积减去水的体积,根据长方体的体积公式:V=abh,把数据代入公式解答。
【解析】解:(1)4×4×5=80(平方分米)
答:做这个鱼缸至少需要80平方分米的玻璃。
(2)4×4×4=64(立方分米)
64立方分米=64升
答:这个鱼缸最多能盛水64升。
(3)50升=50000立方厘米
4分米=40厘米
40×40×33﹣50000
=52800﹣50000
=2800(立方厘米)
答:这些鹅石的体积是2800立方厘米。
【点评】此题主要考查正方体、长方体的表面积公式、容积(体积)公式的灵活运用,关键是熟记公式。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年五年级下学期数学期末核心素养培优卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题(共8小题,共8分)
1.A点的位置记为0,A点东面10m记作+10m,现在小刚从A点先向东行8m,再向西行6m,这时小刚的位置记作( )
A.+2m B.﹣2m C.+14m
2.a÷b=7(a、b都为非0自然数),a和b的最小公倍数是( )
A.a B.b C.ab
3.下列算式中,数字“6”和“4”可以直接相加减的是( )
A.567+432 B. C.3.67+2.04
4.10克盐完全溶解在100克水中,盐与盐水的比是( )
A.1:10 B.1:9 C.1:11
5.平平和凡凡进行800米跑步比赛,相同时间内,平平跑了全程的,凡凡跑了全程的,( )跑得快。
A.平平 B.凡凡 C.无法判断
6.一项工作,甲单独完成需要8小时,乙单独完成需要10小时,甲、乙的工作效率比是( )
A.4:5 B.5:4 C.8:10
7.一堆煤两天运完,第一天运走吨,第二天运走这堆煤的,( )运得多。
A.第一天 B.第二天 C.无法确定
8.“一去二三里,烟村四五家,亭台六七座,八九十枝花。”这首诗中表示数的字占总字数的( )
A. B. C.
二.填空题(共12小题,共18分)
9.一个方便袋里有30多个苹果,如果4个一盘或者6个一盘,正好分完.这个方便袋里一共有 个苹果.
10.1里有 个,再添上 个等于2.
11.一段方钢长1.5米,横截面是正方形,把它锯成相等的两段后表面积比原来增加18平方厘米,每段钢材的体积是 .
12.五年级一班要从5名候选人中选两名担任本班“六一”联欢会的主持人,有 种不同的选法。
13.0.54m3= L; 5050cm3= dm3.
14.小明、小李和小凯三人读同一篇文章,小明用了小时,小李用了小时,小凯用了0.2小时, 的速度最快.
15.把两个棱长是10厘米的正方体粘合成一个长方体,这个长方体的表面积是 平方厘米,体积是 立方厘米.
16.四个小朋友进行乒乓球比赛,每两人都要赛一场,他们一共要赛 场.
17.把的分母加上10,要使分数的大小不变,分子应加上 .
18.如图折成正方体后,与5号相对的面是 号, 号与6号是相对的面。
19.把一个棱长为3分米的正方体木块,切成棱长为1分米的小正方体,可以切成 块。
20.六月份,学校食堂报表学生吃了大米总数的,把 看做单位“1”,平均分成 份,吃了的占这样的 份。
三.判断题(共5小题,共5分)
21.把的分子加上6,要使分数的大小不变,分母也要加上6。
22.两个小正方体拼成一个长方体,长方体的体积等于两个小正方体的体积之和. .
23.假分数一定大于1,真分数一定小于1.
24.盐溶解于水后,盐水的体积正好等于盐的体积与水的体积之和。
25.把一个棱长1m的正方体切成棱长1dm的小正方体,可切成100个。
四.计算题(共3小题,共25分)
26.直接写得数。(共10分)
① ② ③ ④ ⑤
⑥ ⑦ ⑧ ⑨ ⑩
27.解方程。(共6分)
① ②
28.脱式计算。(能简算的要简算,共9分)
(1) (2) (3)5
五.解答题(共1小题,共共8分)
29.看图填一填、画一画。
(1)幸福路在绿化广场的 偏 °方向上,距离是 km。
(2)儿童乐园在绿化广场的西偏南30°方向3千米处。请在图上标出儿童乐园的位置。
六.应用题(共6小题,共36分)
30.一块棱长为40cm的正方体冰块,如果每立方厘米冰的质量是0.9g,那么这块冰的质量一共是多少千克?
31.一本故事书共120页,小欣第一周看了全书的,第二周看了40页,两周共看了书的几分之几?
32.爸爸买了一个长80厘米,宽60厘米的鱼缸,水深50厘米,妈妈为点缀鱼缸,买了12立方分米的假山放进鱼缸完全浸没在水中,这时水面升高了多少厘米?
33.一辆货车的油箱是一个长方体,长、宽、高分别是0.8米、0.8米、0.5米(箱壁厚度忽略不计)。
①做这样一个油箱3平方米的铁皮够吗?
②如果这辆货车每行驶100千米耗油50升,加满油后可以行驶多少千米?
34.一个长方体和一个正方体的棱长总和相等。已知长方体的长是4cm、宽是3cm、高是5cm。
(1)正方体的棱长是多少厘米?
(2)正方体的表面积是多少平方厘米?
(3)正方体的体积是多少立方厘米?
35.一个棱长4分米的正方体形状的无盖玻璃鱼缸。
(1)做这个鱼缸至少需要多少平方分米的玻璃?
(2)这个鱼缸最多能盛水多少升?( 玻璃的厚度忽略不计)
(3)鱼缸里原来有50升水,往水里放入一些鹅卵石,水面上升到33厘米。这些鹅石的体积是多少立方厘米?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案与试题解析
一.选择题(共8小题,共8分)
1.A
【分析】在数轴上,A点的位置记为0,A点东面10m记作+10m,现在小刚从A点先向东行8m,记作+8m,再向西行6m,8﹣6=2m,相当于小刚从A点先向东走了2m,记作+2m。
【解析】解:由分析得知,A点的位置记为0,A点东面10m记作+10m,现在小刚从A点先向东行8m,再向西行6m,这时小刚的位置记作+2m。
故选:A。
【点评】此题考查了负数的意义及其应用,要求学生掌握。
2.A
【分析】因为a÷b=7(a、b都为非0的自然数),所以a和b是倍数关系,当两个数是倍数关系时,较大的数是它们的最小公倍数,较小的数是它们的最大公因数,据此解答.
【解析】解:因为a÷b=7(a、b都为非0的自然数),
所以a和b的最小公倍数是:a.
故选:A.
【点评】本题考查:当两个数是倍数关系时,较大的数是它们的最小公倍数,较小的数是它们的最大公因数.
3.B
【分析】根据“只有计数单位相同的数才能直接相加减”直接判断。
【解析】解:选项A,567的“6”在十位上,432的“4”在百位上,计数单位不同,不能直接相加减;
选项B,表示6个,表示4个,两个分数的计算单位相同,可以直接相加减;
选项C,3.67的“6”在十分位上,2.04的“4”在百分位上,计数单位不同,不能直接相加减。
故选:B。
【点评】解答本题需明确:只有计数单位相同的数才能直接相加减。
4.C
【分析】把10克盐完全溶解在100克水中,就形成了10+100=110克的盐水,要求盐与盐水的重量比,也就是求10克与110克的比.
【解析】解:10:(10+100)
=10:110
=1:11.
故选:C.
【点评】此题考查比的意义,要注意:求的是盐与盐水对应的重量比,所以要先求出形成的盐水的重量是解题关键.
5.A
【分析】将800米看作单位“1”,比较出和的大小,即可确定谁跑得快。
【解析】解:
答:平平跑得快。
故选:A。
【点评】本题考查了利用比较分数的大小解决问题,需准确理解题意。
6.B
【分析】根据工作总量一定,工作效率和时间成反比例进行求解。
【解析】解:10:8
=(10÷2):(8÷2)
=5:4
答:甲、乙的工作效率比是5:4。
故选:B。
【点评】熟练掌握工作总量一定,工作效率的比等于时间的反比是解题的关键。
7.A
【分析】一堆煤两天运完,第二天运了这堆煤的,那么第一天运了这堆煤的多少呢?把这堆煤看做“1”,用减法,然后比较分数的大小,即可得解。
【解析】解:1
答:第一天运得多。
故选:A。
【点评】此题所给的吨可以看作是一个干扰数据,进行分数的减法计算和分数大小比较,即可得解。
8.A
【分析】这首诗一共有20字,其中表示数的有一、二、三、四、五、六、七、八、九、十共10个,求这首诗中表示数的字占总字数的几分之几,用表示数的字数除以总字数。
【解析】解:10÷20
答:这首诗中表示数的字占总字数的。
故选:A。
【点评】求一个数是另一个数的几分之几,用这个数除以另一个数。
二.填空题(共12小题,共18分)
9.见试题解答内容
【分析】先求出4、6的最小公倍数,再找到4、6的公倍数在30左右的数即为所求.
【解析】解:4、6的最小公倍数是3×2×2=12,
因为12×3=36,苹果总数在30左右,
所以这个方便袋里一共有 36个苹果;
答:这个方便袋里一共有 36个苹果;
故答案为:36.
【点评】此题考查了公倍数问题,解答该题关键是会求两个数的最小公倍数,并用它解决实际问题.
10.见试题解答内容
【分析】首先用1除以,判断出1里有多少个;然后用2减去1,求出2比1多多少,即可判断出再添上个等于2.
【解析】解:因为1,
所以1里有多10个;
因为2﹣1,
所以2比1多,1再添上4个等于2.
故答案为:10、4.
【点评】此题主要考查了分数除法的运算方法,要熟练掌握.
11.见试题解答内容
【分析】由题意可知:把一根长1.5米的方钢截成两段,表面积增加了2个横截面的面积,由此可以求得这个方钢的横截面的面积为:18÷2=9平方厘米,再利用长方体的体积公式:v=sh,把数据代入公式解答即可.
【解析】解:1.5米=150厘米,
18÷2×150÷2,
=9×150÷2,
=1350÷2,
=675(立方厘米);
答:每段钢材的体积是765立方厘米.
故答案为:675立方厘米.
【点评】根据切割特点,利用增加部分的表面积求出长方体钢材的横截面的面积是解决本题的关键.
12.10。
【分析】从5名候选人中选两名,相当于两两组合,根据握手问题的公式n(n﹣1)÷2解答即可。
【解析】解:5×(5﹣1)÷2
=20÷2
=10(种)
答:有10种不同的选法。
故答案为:10。
【点评】本题考查了握手问题的实际应用,要注意去掉重复计算的情况,如果数量比较少可以用枚举法解答,如果数量比较多可以用公式n(n﹣1)÷2解答。
13.见试题解答内容
【分析】(1)高级单位立方米化低级单位升乘进率1000.
(2)低级单位立方厘米化高级单位立方分米除以进率1000.
【解析】解:(1)0.54m3=540L;
(2)5050cm3=5.05dm3.
故答案为:540,5.05.
【点评】本题是考查体积、容积的单位换算.单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率.
14.见试题解答内容
【分析】同样一篇文章,谁用的时间少,谁的速度就快;利用异分母分数大小的比较方法先将它们化成同分母分数,再比较大小即可.
【解析】解:因为,
,
0.2,
且,
即0.2,
所以小明的速度最快;
故答案为:小明.
【点评】解答此题的关键是将这几个数化成同分母分数,再比较大小.
15.见试题解答内容
【分析】根据题意可知:把两个棱长是10厘米的正方体粘合成一个长方体,这个长方体的表面积比两个正方体的表面积和减少了正方体的两个面的面积,长方体的体积等于两个正方体的体积和,根据正方体的表面积公式:s=6a2,体积公式:v=a3,把数据分别代入公式解答即可.
【解析】解:10×10×6×2﹣10×10×2
=100×6×2﹣100×2
=1200﹣200
=1000(平方厘米);
10×10×10×2
=100×10×2
=1000×2
=2000(立方厘米);
答:这个长方体的表面积是1000平方厘米,体积是2000立方厘米.
故答案为:1000,2000.
【点评】此题主要考查正方体、长方体的表面积公式、体积公式的灵活运用,关键是熟记公式.
16.见试题解答内容
【分析】因为每一个小朋友都和其他人三个小朋友比赛,每小朋友比赛三场,一共比赛3×4=12场,但两个小朋友之间重复了一次,因此需比赛12÷2=6场.
【解析】解:4×3÷2=6(场);
答:一共要赛6场.
故答案为:6.
【点评】此题考查单循环比赛,计算方法为n(n﹣1)场,如果为双循环为n(n﹣1)场(n是指参加的人数或队数).
17.见试题解答内容
【分析】首先分析分母之间的变化,原来分母是5,由5变成(5+10)=15,扩大了3倍,要使分数的大小不变,分子也应该扩大3倍,据此解答.
【解析】解:原来的分母是5,现在的分母是(5+10)=15,扩大了3倍,
原来的分子是3,要使分数的大小不变,分子也应该扩大3倍,3×3=9,9﹣3=6,
答:分子应加上6.
故答案为:6.
【点评】此题主要利用分数的基本性质解答问题,先观察分子或分母之间的变化,发现规律,再进一步通过计算解答问题.
18.2;4。
【分析】如图,根据正方体展开图的11种特征,属于正方体展开图的“1﹣3﹣2”型,折成正方体后,1号面与3号面相对,2号面与5号面相对,4号面与6号面相对。
【解析】解:如图:
折成正方体后,1号面与3号面相对,5号面与2号面相对,4号面与6号面相对.
故答案为:2;4。
【点评】正方体展开图分四种类型,11种情况,每种情况折成正方体后哪些面相对是有规律的,可自己动手操作一下并记住,能快速解答此类题。
19.27。
【分析】根据正方体的体积公式:V=a3,分别求出棱长3分米、棱长1分米的正方体的体积,然后根据“包含”除法的意义,用除法解答。
【解析】解:3×3×3÷(1×1×1)
=27÷1
=27(块)
答:可以切成27块。
故答案为:27。
【点评】此题主要考查正方体体积公式的灵活运用,关键是熟记公式。
20.7,4。
【分析】“比”“占”“是”“相当于”后面的、“的”前面的通常看作单位“1”,据此解答即可。
【解析】解:六月份,学校食堂报表学生吃了大米总数的,把大米总数看做单位“1”,平均分成7份,吃了的占这样的4份。
故答案为:大米总数,7,4。
【点评】此题主要考查了单位“1”的确定方法,要熟练掌握。
三.判断题(共5小题,共5分)
21.×
【分析】的分子加上6,扩大了3倍,关键分数的基本性质,要使分数的大小不变,分母也应扩大3倍,变成12,即加上8,据此解答即可.
【解析】解:3+6=9,9÷3=3
分子变成9,扩大了3倍,
要使分数的大小不变,分母应扩大3倍;
4×3=12,12﹣4=8
即分母应加上8。
故答案为:×。
【点评】此题主要考查了分数的基本性质的应用。
22.见试题解答内容
【分析】由题意可知:两个小长方体在拼接的过程中,所占空间的大小不变,即它们的体积不变,所以长方体的体积等于两个小正方体的体积之和.
【解析】解:两个小正方体拼成一个长方体,长方体的体积等于两个小正方体的体积之和.
故答案为:√.
【点评】解答此题的主要依据是:长方体和正方体的体积的意义.
23.见试题解答内容
【分析】首先根据分子大于或者等于分母的分数是假分数,可得假分数不一定大于1,也可能等于1,然后根据分子比分母小的分数是真分数,可得真分数一定小于1,据此判断即可.
【解析】解:根据假分数、真分数的特征,可得
假分数不一定大于1,也可能等于1,真分数一定小于1,
所以题中说法不正确.
故答案为:×.
【点评】此题主要考查了真分数、假分数的特征和应用,要熟练掌握.
24.×
【分析】查资料可知:盐溶解于水后,盐离子和水分子互相进入了之间的间隙,盐水的体积小于盐和水的体积之和。
【解析】解:分析可知,盐溶解于水后,盐离子和水分子互相进入了之间的间隙,盐水的体积小于盐和水的体积之和。所以原题说法错误。
故答案为:×。
【点评】一种固体或液体物质溶于另一种液体物质时,两种物质的体积之和小于溶液的体积。
25.×
【分析】根据正方体的体积公式:V=a3,再根据体积单位相邻单位之间的进率,1立方米=1000立方分米,据此判断。
【解析】解:因为1立方米=1000立方分米,所以把一个棱长1m的正方体切成棱长1dm的小正方体,可切成1000个。
因此题干中的结论是错误的。
故答案为:×。
【点评】此题考查的目的是理解掌握正方体的体积公式、体积单位相邻单位之间的进率及换算。
四.计算题(共3小题,共25分)
26.①;②;③;④;⑤1;⑥;⑦;⑧;⑨;⑩。
【分析】根据分数加减法的计算方法直接进行口算即可。
【解析】解:
① ② ③ ④ ⑤1
⑥ ⑦ ⑧ ⑨ ⑩
【点评】本题考查了基本的运算,注意运算数据和运算符号,细心计算即可。
27.①x;②x。
【分析】①方程两边同时减去;
②方程两边同时加上。
【解析】解:①
x
x
②
x
【点评】熟练掌握等式的基本性质是解题的关键。
28.(1);(2)0;(3)4;(4)2。
【分析】(1)、(3)按从左到右的运算顺序依次计算。
(2)根据减法的性质简算即可。
(4)根据加法的交换律与结合律简算即可。
【解析】解:(1)
(2)
=0
(3)5
=4
=4
(4)
=()+()
=1+1
=2
【点评】计算混合运算时,要注意按照运算顺序计算;能简算的要简算,不要错用运算定律。
五.解答题(共1小题,共8分)
29.(1)东,北,40,4;
(2)。
【分析】由图可知,图上1厘米代表实际距离2千米,(1)计算出幸福路到绿化广场的实际距离,利用平面图上方向规定:上北下南左西右东,依据题意结合图示去解答;
(2)儿童乐园到绿化广场的图上距离,利用平面图上方向规定:上北下南左西右东,依据题意结合图示去作图。
【解析】解:(1)2×2=4(千米),幸福路在绿化广场的东偏北40°方向上,距离是4千米。
(2)3÷2=1.5(厘米)
故答案为:东,北,40,4。
【点评】本题考查的是根据方向和距离确定物体位置的应用。
六.应用题(共6小题,共36分)
30.57.6千克。
【分析】先利用正方体的体积=棱长3,求出这块冰块的体积,再乘0.9克即可解答问题。
【解析】解:40×40×40×0.9
=64000×0.9
=57600(克)
57600克=57.6千克
答:这块冰的质量一共是57.6千克。
【点评】此题主要考查正方体的体积公式的实际应用,注意单位的换算。
31.。
【分析】先用第二周看的页数除以总页数,求出第二周看的页数占总页数的几分之几,再把第一周、第二周看的页数所占的分率相加。
【解析】解:40÷120
答:两周共看了书的。
【点评】求一个数是另一个数的几分之几,用这个数除以另一个数;把两个分数合并成一个分数,用加法计算。
32.2.5厘米。
【分析】根据题意可知,用假山的体积除以鱼缸的底面积就是水面上升的高度。据此解答即可。
【解析】解:12立方分米=12000立方厘米
12000÷(80×60)
=12000÷4800
=2.5(厘米)
答:这时水面升高了2.5厘米。
【点评】此题主要考查长方体体积公式的灵活运用,关键是熟记公式。
33.①够;
②640千米。
【分析】①长方体的表面积=(长×宽+长×高+宽×高)×2,把数据代入公式求出做这个油箱需要铁皮的面积,然后与3平方米进行比较即可。
②首先根据“等分”除法的意义,用除法求出行驶1千米平均耗油多少升,然后根据“包含”除法的意义,用油的体积除以每千米的耗油量即可。
【解析】解:①(0.8×0.8+0.8×0.5+0.8×0.5)×2
=(0.64+0.4+0.4)×2
=1.44×2
=2.88(平方米)
3平方米>2.88平方米
答:做这样一个油箱3平方米的铁皮够。
②0.8×0.8×0.5=0.32(立方米)
0.32立方米=320升
320÷(50÷100)
=320÷0.5
=640(千米)
答:加满油后可以行驶640千米。
【点评】此题主要考查长方体的表面积公式、体积(容积)公式的灵活运用,关键是熟记公式。
34.(1)4厘米;
(2)96平方厘米;
(3)64立方厘米。
【分析】(1)根据长方体的棱长总和=(长+宽+高)×4,正方体的棱长总和=棱长×12,那么棱长=棱长总和÷12,把数据代入公式解答。
(2)根据正方体的表面积公式:S=6a2,把数据代入公式解答。
(3)根据正方体的体积公式:V=a3,把数据代入公式解答。
【解析】解:(4+3+5)×4÷12
=12×4÷12
=4(厘米)
答:正方体的棱长是4厘米。
(2)4×4×6
=16×6
=96(平方厘米)
答:正方体的表面积是96平方厘米。
(3)4×4×4
=16×4
=64(立方厘米)
答:正方体的体积是64立方厘米。
【点评】此题主要考查长方体的棱长总和公式、正方体的棱长总和公式、表面积公式、体积公式的灵活运用,关键是熟记公式。
35.(1)80平方分米;
(2)64升;
(3)2800立方厘米。
【分析】(1)根据正方体的表面积公式:S=6a2,因为这个玻璃缸无盖,所以只求它的5个面的总面积即可。
(2)根据正方体的容积(体积)公式:V=a3,把数据代入公式解答。
(3)根据题意可知,这些鹅石的体积等于水与这些鹅石的体积减去水的体积,根据长方体的体积公式:V=abh,把数据代入公式解答。
【解析】解:(1)4×4×5=80(平方分米)
答:做这个鱼缸至少需要80平方分米的玻璃。
(2)4×4×4=64(立方分米)
64立方分米=64升
答:这个鱼缸最多能盛水64升。
(3)50升=50000立方厘米
4分米=40厘米
40×40×33﹣50000
=52800﹣50000
=2800(立方厘米)
答:这些鹅石的体积是2800立方厘米。
【点评】此题主要考查正方体、长方体的表面积公式、容积(体积)公式的灵活运用,关键是熟记公式。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
