2025年辽宁省葫芦岛市中考数学二模试卷(含详解)
文档属性
| 名称 | 2025年辽宁省葫芦岛市中考数学二模试卷(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 254.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-14 00:00:00 | ||
图片预览




文档简介
2025年辽宁省葫芦岛市中考数学二模试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.一个由圆柱和半圆柱组成的几何体如图水平放置,其俯视图为( )
A.
B.
C.
D.
2.在实数;;;;;中,其中无理数有( )
A. 个 B. 个 C. 个 D. 个
3.广东省年计划新增电源装机万千瓦,完善绿电市场交易机制,加紧经济社会发展全面绿色转型其中数据万用科学记数法表示为( )
A. B. C. D.
4.如图,在 中,交对角线于点若,则的度数为( )
A.
B.
C.
D.
5.下列计算正确的是( )
A. B.
C. D.
6.如图,甲、乙、丙三位球员分别站在足球门前的点,,处射门,点,,都在同一个以为弦的圆上,若球员面对足球门的视角越大踢进足球的可能性越大,则下列说法正确的是( )
A. 甲踢进足球的可能性最大
B. 乙踢进足球的可能性最大
C. 丙踢进足球的可能性最大
D. 三位球员踢进足球的可能性一样大
7.下列交通标志牌中,是中心对称图形的是( )
A. B. C. D.
8.我国古代数学著作九章算术中有如下问题:“今有二马、牛价过一万,如半马之价;一马、二牛价不满一万,如半牛之价,问牛、马价各几何?”其翻译成现代文为“现在两匹马和一头牛的价格超过一万,其超出的钱数相当于半匹马的价格,一匹马和两头牛的价格不足一万,所差的钱数相当于半头牛的价格问每头牛、每匹马的价格各是多少?”若设每匹马的价格为,每头牛的价格为,则根据题意,可列方程组( )
A. B.
C. D.
9.如图,在中,,,,将绕点沿逆时针方向旋转得到,的对应边交于点,则的面积为( )
A.
B.
C.
D.
10.矩形在平面直角坐标系中的位置如图所示,反比例函数的图象与边交于点,与边交于点,与交于点,,若四边形的面积为,则的值是( )
A. B. C. D.
二、填空题:本题共5小题,每小题3分,共15分。
11.分式方程的解是 .
12.因式分解: .
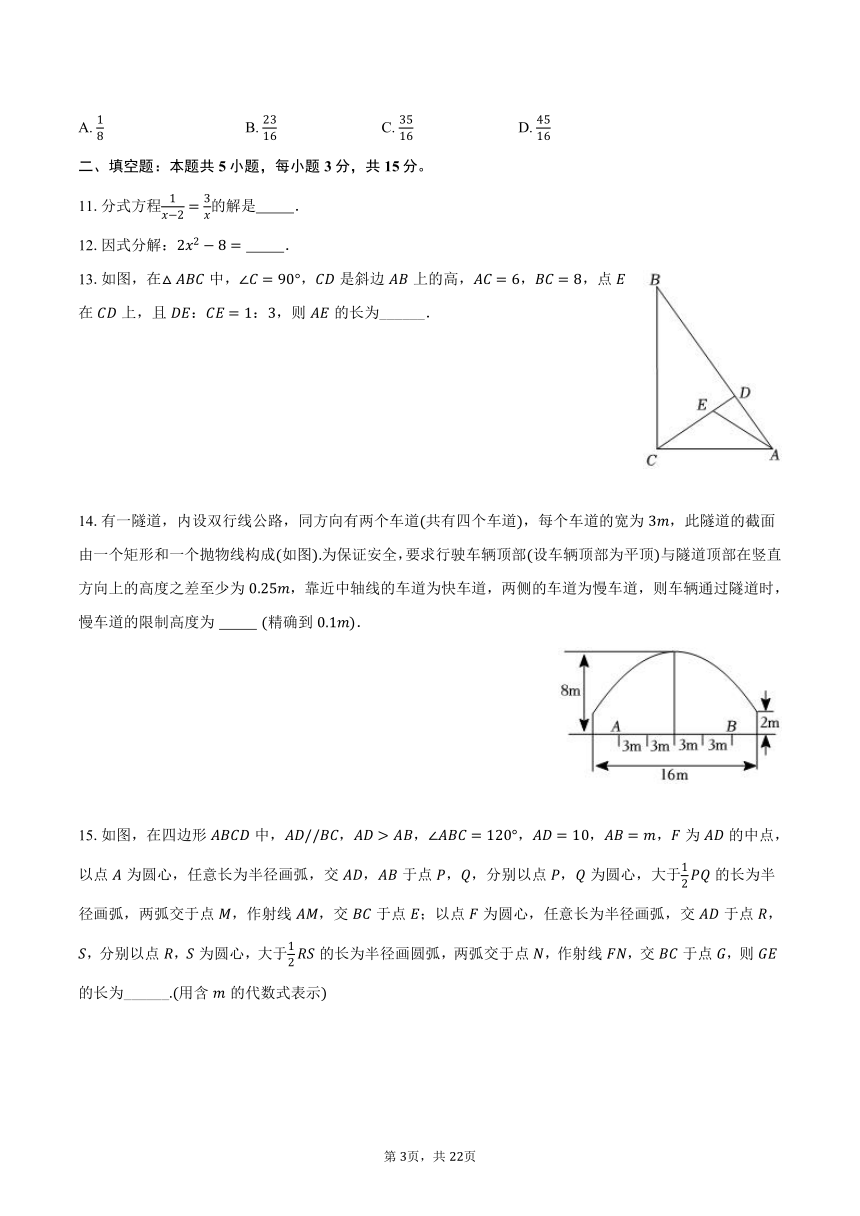
13.如图,在中,,是斜边上的高,,,点在上,且::,则的长为______.
14.有一隧道,内设双行线公路,同方向有两个车道共有四个车道,每个车道的宽为,此隧道的截面由一个矩形和一个抛物线构成如图为保证安全,要求行驶车辆顶部设车辆顶部为平顶与隧道顶部在竖直方向上的高度之差至少为,靠近中轴线的车道为快车道,两侧的车道为慢车道,则车辆通过隧道时,慢车道的限制高度为 精确到.
15.如图,在四边形中,,,,,,为的中点,以点为圆心,任意长为半径画弧,交,于点,,分别以点,为圆心,大于的长为半径画弧,两弧交于点,作射线,交于点;以点为圆心,任意长为半径画弧,交于点,,分别以点,为圆心,大于的长为半径画圆弧,两弧交于点,作射线,交于点,则的长为______用含的代数式表示
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:.
先化简,再从,,,中选择一个合适的的值代入求值.
17.本小题分
某工厂有甲、乙两个车间,甲车间生产产品,乙车间生产产品已知销售产品件,产品件,共收入元;销售产品件,产品件,共收入元.
求,两种产品的销售单价.
若该工厂销售,两种产品共件,总收入不超过元,则最少要销售产品多少件?
18.本小题分
为确保师生“吃得安全,吃得健康”,某学校切实履行监督职责,随机抽取名教师和名家长做评委,对甲配餐公司提供的饭菜质量进行评分评分用表示,单位:分,并对他们的评分结果进行整理、描述、分析,得到如下部分信息:
教师评分:
家长评分的数据整理后分成组,组:,组:,组:,组:,组:,并绘制成如图的频数分布直方图和扇形统计图.
评委评分平均数、中位数、众数如表:
平均数 中位数 众数
教师评分
家长评分
根据以上信息,回答下列问题:
的值为______,的值为______;
的值位于家长评分数据分组的______组,请补全频数分布直方图;
在扇形统计图中,组所对应的扇形圆心角的度数为______;
新学期即将开始,为了让家长对配餐公司有更多的了解,该校再组织这名教师和名家长考察乙配餐公司,并按教师打分平均数占,家长打分平均数占,确定配餐公司的最终得分,已知教师和家长评委对乙配餐公司打分的平均数分别为分,分,如果只比较两家配餐公司的最终得分,请通过计算说明学校下学期还会继续让甲配餐公司为师生提供服务吗?
19.本小题分
某校与部队联合开展红色之旅研学活动,上午:,部队官兵乘坐军车从营地出发,同时学校师生乘坐大巴车从学校出发,沿公路如图到爱国主义教育基地进行研学上午:,军车在离营地的地方追上大巴车并继续前行,到达仓库后,部队官兵下车领取研学物资,然后乘坐军车按原速前行,最后和学校师生同时到达基地军车和大巴车离营地的路程与所用时间之间的函数关系如图所示.
军车的速度为______,的值为______;
求大巴车离营地的路程与所用时间之间的函数表达式;
部队官兵在仓库领取物资期间,直接写出大巴车离仓库的路程的取值范围.
20.本小题分
美丽的凤栖湖畔坐落着恢弘的圣寿寺塔,小明与同学借助工具测量塔高如图,在点处用距离地面高度为的测角器测出塔顶端的仰角为,然后沿方向走到达点,用同样高度的测角器测出塔顶端的仰角为根据小明的测量数据求塔高精确到
参考数据:,,,,,
21.本小题分
如图,内接于,是的直径,为上一点,过点作的切线交的延长线于点,且,连接.
求证:;
若,,求的长.
22.本小题分
如图,在中,,点在上,连接,并延长至点,使得,,连接,,是上的一点,连接.
如图,求证:四边形是菱形.
如图,将沿折叠,使点的对应点落在上,若,猜想与的数量关系,并加以证明.
如图,将沿折叠,点的对应点落在的延长线上,与交于点.
求证:.
若,,求的值.
23.本小题分
如图,抛物线和轴相交于点、两点,交轴于点,顶点为点,点是点关于抛物线对称轴的对称点,过点作轴于点.
求抛物线的解析式;
如图,点是线段上方抛物线上一点,过点作轴交轴于点,交线段与点,当四边形的面积最大时,在线段上有一动点,在线段上有一动点,在轴上有一动点,且满足,连接,,,,求的最小值.
将抛物线沿射线方向平移个单位得到新抛物线点为新抛物线对称轴上一动点,连接,,当时,在平面内找到一点,使得四边形是平行四边形,请写出所有符合条件的点的坐标,并写出一个点的求解过程.
答案和解析
1.【答案】
【解析】解:这个几何体的俯视图为:
故选:.
2.【答案】
【解析】解:根据无理数定义及无理数有三种形式可得:
是整数,不是无理数;是无理数;是分数,不是无理数;
是整数,不是无理数;是整数,不是无理数;是小数,不是无理数;
即无理数有个,
故选:.
3.【答案】
【解析】解:万.
故选:.
4.【答案】
【解析】解:,
,
四边形是平行四边形,
,
两直线平行,内错角相等,
三角形外角和定理,
等量代换,
,
即的度数为,
故选:.
5.【答案】
【解析】解:根据积的乘方、同底数幂的乘法法则、完全平方公式、同类项的定义逐项分析判断如下:
A、,故原选项计算错误,不符合题意;
B、,故原选项计算正确,符合题意;
C、,故原选项计算错误,不符合题意;
D、与非同类项,无法计算,故原选项计算错误,不符合题意.
故选:.
6.【答案】
【解析】解:如图,分别连接,,三点与、两点的线段,
,
;
球员面对足球门的视角越大踢进足球的可能性越大,
三位球员踢进足球的可能性一样大,
故选:.
7.【答案】
【解析】解:、图形不是中心对称图形,不符合题意;
B、图形不是中心对称图形,不符合题意;
C、图形是中心对称图形,符合题意;
D、图形不是中心对称图形,不符合题意,
故选:.
8.【答案】
【解析】解:依题意得:,
故选:.
9.【答案】
【解析】解:将绕点沿逆时针方向旋转得到,过点作,垂足为,
,,,
,
,,
,
,
,
,
,
解得,
的面积,
故选:.
10.【答案】
【解析】解:设点的坐标为,
,
,
,
四边形的面积为,
,
,解得.
故选:.
11.【答案】
【解析】解:去分母得:,
去括号得:,
解得:,
经检验是分式方程的解.
12.【答案】
【解析】解:
.
故答案为:.
13.【答案】
【解析】解:由题意可得:,
,
,
,即,
,
::,且,
,
在中,,
在中,.
故答案为:.
14.【答案】
【解析】解:如图所示,建立平面直角坐标系,
抛物线顶点的坐标是,
设抛物线的解析式为:,
又点在此抛物线上,
,
得,
,
将代入,得,
又行驶车辆顶部设为平顶与隧道顶部在竖直方向上高度之差至少要有,
车辆经过隧道时的限制高度是:,
由实际情况可得车辆经过隧道时的限制高度约为,
即车辆经过隧道时的限制高度是.
故答案为:.
15.【答案】
【解析】解:在四边形中,,,则,
由题意可知,平分,则,
,
,
,
过点作,如图所示:
由题意可知,,
由条件可知,
,
,
,
,则四边形是矩形,
,
由中点定义可知,则,
,
故答案为:.
16.【解析】
;
,
,,,
,,,
当时,原式.
17.【解析】解:设产品的销售单价为元,产品的销售单价为元,
根据题意得:,
解得:.
答:产品的销售单价为元,产品的销售单价为元;
设销售产品件,则销售产品件,
根据题意得:,
解得:,
的最小值为.
答:最少要销售产品件.
18.【解析】,教师评分的众数,
故答案为:、;
家长评分的中位数是第、个数据的平均数,而这个数据均落在组:,
所以的值位于家长评分数据分组的组,
的人数为人,
补全图形如下:
故答案为:;
在扇形统计图中,组所对应的扇形圆心角的度数为,
故答案为:;
甲公司最终得分:分,
乙公司最终得分:分,
,
学校下学期还会继续让甲配餐公司为师生提供服务.
19.【解析】军车的速度为,
根据图象,得,
解得.
故答案为:,.
大巴车的速度为,
,
当时,解得,
大巴车离营地的路程与所用时间之间的函数表达式为.
由知,,
根据图象,得,即,
解得,
当时,两车之间的距离为,
当时,两车之间的距离为,
部队官兵在仓库领取物资期间,大巴车离仓库的路程的取值范围为.
20.【答案】米.
【解析】解:连接并延长,交于点,
,,
,
,
,
,
,
,
,
,
米,
塔高约为米.
21.【解析】证明:如图,连接.
由题意可得:,
,
.
,
.
又
,
.
解:如图,连接.
,
,.
由得,
,
.
,
,
.
又,
∽,
.
,
,
.
设,则,,.
,即,
,
,,,
.
,
.
,
.
22.【解析】证明:由条件可知是的垂直平分线,
,.
,
,
四边形是菱形.
证明如下:
证明:如图,延长,交于点.
由折叠的性质,可得,.
由菱形的性质可知,,
.
,
,
,
设,则,,
,
,
,
∽,
,
,
.
证明:由折叠的性质,可得,
,
四边形是菱形,
,
,
,
.
如图,延长,交的延长线于点.
,.
,
,
∽,
,
.
由折叠的性质,可得,.
由菱形性质可知:,,
,
,
,
,
由平行线可知∽,
,
,
,
.
23.【解析】抛物线和轴相交于点、两点,将点,点的坐标分别代入得:
解得:
抛物线的解析式为;
抛物线的解析式为,
对称轴为直线,
抛物线交轴于点,
当时,得:,
,
点是点关于抛物线对称轴的对称点,
点,
设直线的解析式为,将,分别代入得:
,
解得:,
直线的解析式为,
设点的坐标为,则点的坐标为,
,
,
,
当时,有最大值,
此时点的坐标为,
,
将点向右平移个单位得到,
连接,可得四边形是平行四边形,如图,
,
作点关于轴的对称点,连接,
当点、、共线时,有最小值,
此时,
的最小值为;
点的坐标是或理由如下:
将抛物线沿射线方向平移个单位,相当于将抛物线先向左平移个单位,再向下平移个单位,
所得新抛物线解析式为,所得新抛物线的对称轴为直线.
点为新抛物线对称轴上一动点,
设点的坐标为,
由题意可知,
,
方法一:过点作交于点,如图,
则为等腰直角三角形,且.
再过点作轴于点,
过点作轴于点易得≌.
,,
,
,
由∽,可得,
,
,
,
解得或,
点的坐标是或.
设点的坐标为,
四边形是平行四边形,
且,
,
,
点的坐标是或;
方法二:由定边对定角得,
点是在以点为圆心,以为半径的圆上.
,
或,
点的坐标是或.
设点的坐标为,
四边形是平行四边形,
且,
,
,
点的坐标是或.
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.一个由圆柱和半圆柱组成的几何体如图水平放置,其俯视图为( )
A.
B.
C.
D.
2.在实数;;;;;中,其中无理数有( )
A. 个 B. 个 C. 个 D. 个
3.广东省年计划新增电源装机万千瓦,完善绿电市场交易机制,加紧经济社会发展全面绿色转型其中数据万用科学记数法表示为( )
A. B. C. D.
4.如图,在 中,交对角线于点若,则的度数为( )
A.
B.
C.
D.
5.下列计算正确的是( )
A. B.
C. D.
6.如图,甲、乙、丙三位球员分别站在足球门前的点,,处射门,点,,都在同一个以为弦的圆上,若球员面对足球门的视角越大踢进足球的可能性越大,则下列说法正确的是( )
A. 甲踢进足球的可能性最大
B. 乙踢进足球的可能性最大
C. 丙踢进足球的可能性最大
D. 三位球员踢进足球的可能性一样大
7.下列交通标志牌中,是中心对称图形的是( )
A. B. C. D.
8.我国古代数学著作九章算术中有如下问题:“今有二马、牛价过一万,如半马之价;一马、二牛价不满一万,如半牛之价,问牛、马价各几何?”其翻译成现代文为“现在两匹马和一头牛的价格超过一万,其超出的钱数相当于半匹马的价格,一匹马和两头牛的价格不足一万,所差的钱数相当于半头牛的价格问每头牛、每匹马的价格各是多少?”若设每匹马的价格为,每头牛的价格为,则根据题意,可列方程组( )
A. B.
C. D.
9.如图,在中,,,,将绕点沿逆时针方向旋转得到,的对应边交于点,则的面积为( )
A.
B.
C.
D.
10.矩形在平面直角坐标系中的位置如图所示,反比例函数的图象与边交于点,与边交于点,与交于点,,若四边形的面积为,则的值是( )
A. B. C. D.
二、填空题:本题共5小题,每小题3分,共15分。
11.分式方程的解是 .
12.因式分解: .
13.如图,在中,,是斜边上的高,,,点在上,且::,则的长为______.
14.有一隧道,内设双行线公路,同方向有两个车道共有四个车道,每个车道的宽为,此隧道的截面由一个矩形和一个抛物线构成如图为保证安全,要求行驶车辆顶部设车辆顶部为平顶与隧道顶部在竖直方向上的高度之差至少为,靠近中轴线的车道为快车道,两侧的车道为慢车道,则车辆通过隧道时,慢车道的限制高度为 精确到.
15.如图,在四边形中,,,,,,为的中点,以点为圆心,任意长为半径画弧,交,于点,,分别以点,为圆心,大于的长为半径画弧,两弧交于点,作射线,交于点;以点为圆心,任意长为半径画弧,交于点,,分别以点,为圆心,大于的长为半径画圆弧,两弧交于点,作射线,交于点,则的长为______用含的代数式表示
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:.
先化简,再从,,,中选择一个合适的的值代入求值.
17.本小题分
某工厂有甲、乙两个车间,甲车间生产产品,乙车间生产产品已知销售产品件,产品件,共收入元;销售产品件,产品件,共收入元.
求,两种产品的销售单价.
若该工厂销售,两种产品共件,总收入不超过元,则最少要销售产品多少件?
18.本小题分
为确保师生“吃得安全,吃得健康”,某学校切实履行监督职责,随机抽取名教师和名家长做评委,对甲配餐公司提供的饭菜质量进行评分评分用表示,单位:分,并对他们的评分结果进行整理、描述、分析,得到如下部分信息:
教师评分:
家长评分的数据整理后分成组,组:,组:,组:,组:,组:,并绘制成如图的频数分布直方图和扇形统计图.
评委评分平均数、中位数、众数如表:
平均数 中位数 众数
教师评分
家长评分
根据以上信息,回答下列问题:
的值为______,的值为______;
的值位于家长评分数据分组的______组,请补全频数分布直方图;
在扇形统计图中,组所对应的扇形圆心角的度数为______;
新学期即将开始,为了让家长对配餐公司有更多的了解,该校再组织这名教师和名家长考察乙配餐公司,并按教师打分平均数占,家长打分平均数占,确定配餐公司的最终得分,已知教师和家长评委对乙配餐公司打分的平均数分别为分,分,如果只比较两家配餐公司的最终得分,请通过计算说明学校下学期还会继续让甲配餐公司为师生提供服务吗?
19.本小题分
某校与部队联合开展红色之旅研学活动,上午:,部队官兵乘坐军车从营地出发,同时学校师生乘坐大巴车从学校出发,沿公路如图到爱国主义教育基地进行研学上午:,军车在离营地的地方追上大巴车并继续前行,到达仓库后,部队官兵下车领取研学物资,然后乘坐军车按原速前行,最后和学校师生同时到达基地军车和大巴车离营地的路程与所用时间之间的函数关系如图所示.
军车的速度为______,的值为______;
求大巴车离营地的路程与所用时间之间的函数表达式;
部队官兵在仓库领取物资期间,直接写出大巴车离仓库的路程的取值范围.
20.本小题分
美丽的凤栖湖畔坐落着恢弘的圣寿寺塔,小明与同学借助工具测量塔高如图,在点处用距离地面高度为的测角器测出塔顶端的仰角为,然后沿方向走到达点,用同样高度的测角器测出塔顶端的仰角为根据小明的测量数据求塔高精确到
参考数据:,,,,,
21.本小题分
如图,内接于,是的直径,为上一点,过点作的切线交的延长线于点,且,连接.
求证:;
若,,求的长.
22.本小题分
如图,在中,,点在上,连接,并延长至点,使得,,连接,,是上的一点,连接.
如图,求证:四边形是菱形.
如图,将沿折叠,使点的对应点落在上,若,猜想与的数量关系,并加以证明.
如图,将沿折叠,点的对应点落在的延长线上,与交于点.
求证:.
若,,求的值.
23.本小题分
如图,抛物线和轴相交于点、两点,交轴于点,顶点为点,点是点关于抛物线对称轴的对称点,过点作轴于点.
求抛物线的解析式;
如图,点是线段上方抛物线上一点,过点作轴交轴于点,交线段与点,当四边形的面积最大时,在线段上有一动点,在线段上有一动点,在轴上有一动点,且满足,连接,,,,求的最小值.
将抛物线沿射线方向平移个单位得到新抛物线点为新抛物线对称轴上一动点,连接,,当时,在平面内找到一点,使得四边形是平行四边形,请写出所有符合条件的点的坐标,并写出一个点的求解过程.
答案和解析
1.【答案】
【解析】解:这个几何体的俯视图为:
故选:.
2.【答案】
【解析】解:根据无理数定义及无理数有三种形式可得:
是整数,不是无理数;是无理数;是分数,不是无理数;
是整数,不是无理数;是整数,不是无理数;是小数,不是无理数;
即无理数有个,
故选:.
3.【答案】
【解析】解:万.
故选:.
4.【答案】
【解析】解:,
,
四边形是平行四边形,
,
两直线平行,内错角相等,
三角形外角和定理,
等量代换,
,
即的度数为,
故选:.
5.【答案】
【解析】解:根据积的乘方、同底数幂的乘法法则、完全平方公式、同类项的定义逐项分析判断如下:
A、,故原选项计算错误,不符合题意;
B、,故原选项计算正确,符合题意;
C、,故原选项计算错误,不符合题意;
D、与非同类项,无法计算,故原选项计算错误,不符合题意.
故选:.
6.【答案】
【解析】解:如图,分别连接,,三点与、两点的线段,
,
;
球员面对足球门的视角越大踢进足球的可能性越大,
三位球员踢进足球的可能性一样大,
故选:.
7.【答案】
【解析】解:、图形不是中心对称图形,不符合题意;
B、图形不是中心对称图形,不符合题意;
C、图形是中心对称图形,符合题意;
D、图形不是中心对称图形,不符合题意,
故选:.
8.【答案】
【解析】解:依题意得:,
故选:.
9.【答案】
【解析】解:将绕点沿逆时针方向旋转得到,过点作,垂足为,
,,,
,
,,
,
,
,
,
,
解得,
的面积,
故选:.
10.【答案】
【解析】解:设点的坐标为,
,
,
,
四边形的面积为,
,
,解得.
故选:.
11.【答案】
【解析】解:去分母得:,
去括号得:,
解得:,
经检验是分式方程的解.
12.【答案】
【解析】解:
.
故答案为:.
13.【答案】
【解析】解:由题意可得:,
,
,
,即,
,
::,且,
,
在中,,
在中,.
故答案为:.
14.【答案】
【解析】解:如图所示,建立平面直角坐标系,
抛物线顶点的坐标是,
设抛物线的解析式为:,
又点在此抛物线上,
,
得,
,
将代入,得,
又行驶车辆顶部设为平顶与隧道顶部在竖直方向上高度之差至少要有,
车辆经过隧道时的限制高度是:,
由实际情况可得车辆经过隧道时的限制高度约为,
即车辆经过隧道时的限制高度是.
故答案为:.
15.【答案】
【解析】解:在四边形中,,,则,
由题意可知,平分,则,
,
,
,
过点作,如图所示:
由题意可知,,
由条件可知,
,
,
,
,则四边形是矩形,
,
由中点定义可知,则,
,
故答案为:.
16.【解析】
;
,
,,,
,,,
当时,原式.
17.【解析】解:设产品的销售单价为元,产品的销售单价为元,
根据题意得:,
解得:.
答:产品的销售单价为元,产品的销售单价为元;
设销售产品件,则销售产品件,
根据题意得:,
解得:,
的最小值为.
答:最少要销售产品件.
18.【解析】,教师评分的众数,
故答案为:、;
家长评分的中位数是第、个数据的平均数,而这个数据均落在组:,
所以的值位于家长评分数据分组的组,
的人数为人,
补全图形如下:
故答案为:;
在扇形统计图中,组所对应的扇形圆心角的度数为,
故答案为:;
甲公司最终得分:分,
乙公司最终得分:分,
,
学校下学期还会继续让甲配餐公司为师生提供服务.
19.【解析】军车的速度为,
根据图象,得,
解得.
故答案为:,.
大巴车的速度为,
,
当时,解得,
大巴车离营地的路程与所用时间之间的函数表达式为.
由知,,
根据图象,得,即,
解得,
当时,两车之间的距离为,
当时,两车之间的距离为,
部队官兵在仓库领取物资期间,大巴车离仓库的路程的取值范围为.
20.【答案】米.
【解析】解:连接并延长,交于点,
,,
,
,
,
,
,
,
,
,
米,
塔高约为米.
21.【解析】证明:如图,连接.
由题意可得:,
,
.
,
.
又
,
.
解:如图,连接.
,
,.
由得,
,
.
,
,
.
又,
∽,
.
,
,
.
设,则,,.
,即,
,
,,,
.
,
.
,
.
22.【解析】证明:由条件可知是的垂直平分线,
,.
,
,
四边形是菱形.
证明如下:
证明:如图,延长,交于点.
由折叠的性质,可得,.
由菱形的性质可知,,
.
,
,
,
设,则,,
,
,
,
∽,
,
,
.
证明:由折叠的性质,可得,
,
四边形是菱形,
,
,
,
.
如图,延长,交的延长线于点.
,.
,
,
∽,
,
.
由折叠的性质,可得,.
由菱形性质可知:,,
,
,
,
,
由平行线可知∽,
,
,
,
.
23.【解析】抛物线和轴相交于点、两点,将点,点的坐标分别代入得:
解得:
抛物线的解析式为;
抛物线的解析式为,
对称轴为直线,
抛物线交轴于点,
当时,得:,
,
点是点关于抛物线对称轴的对称点,
点,
设直线的解析式为,将,分别代入得:
,
解得:,
直线的解析式为,
设点的坐标为,则点的坐标为,
,
,
,
当时,有最大值,
此时点的坐标为,
,
将点向右平移个单位得到,
连接,可得四边形是平行四边形,如图,
,
作点关于轴的对称点,连接,
当点、、共线时,有最小值,
此时,
的最小值为;
点的坐标是或理由如下:
将抛物线沿射线方向平移个单位,相当于将抛物线先向左平移个单位,再向下平移个单位,
所得新抛物线解析式为,所得新抛物线的对称轴为直线.
点为新抛物线对称轴上一动点,
设点的坐标为,
由题意可知,
,
方法一:过点作交于点,如图,
则为等腰直角三角形,且.
再过点作轴于点,
过点作轴于点易得≌.
,,
,
,
由∽,可得,
,
,
,
解得或,
点的坐标是或.
设点的坐标为,
四边形是平行四边形,
且,
,
,
点的坐标是或;
方法二:由定边对定角得,
点是在以点为圆心,以为半径的圆上.
,
或,
点的坐标是或.
设点的坐标为,
四边形是平行四边形,
且,
,
,
点的坐标是或.
第1页,共1页
同课章节目录
