2025年广东省中考数学冲刺模拟试卷(含详解)
文档属性
| 名称 | 2025年广东省中考数学冲刺模拟试卷(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 545.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 00:00:00 | ||
图片预览




文档简介
2025年广东省中考数学冲刺模拟试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.我们在生活中经常会遇到各种相反意义的量,如在课堂抢答活动中,若把加分记作分,则扣分记作( )
A. 分 B. 分 C. 分 D. 分
2.下列倡导环保的图案中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.广东省年计划新增电源装机万千瓦,完善绿电市场交易机制,加紧经济社会发展全面绿色转型其中数据万用科学记数法表示为( )
A. B. C. D.
4.已知单项式与的乘积为,则单项式是( )
A. B. C. D.
5.汽车前灯是由灯泡、反光镜和配光镜三部分组成,光源位于焦点处,光线经反射后互相平行射出如图为其侧面示意图,已知,,则的度数为( )
A.
B.
C.
D.
6.“十二生肖纪年法”是我国历法的一种传统纪年法,又称天干地支纪年法,给十二地支配上相应的十二兽名,以十二年为一循环的纪年法小明购买了一套十二生肖邮票共张,从中任意抽一张邮票送给小玲,恰好抽到“蛇”的邮票的概率是( )
A. B. C. D.
7.计算的结果是( )
A. B. C. D.
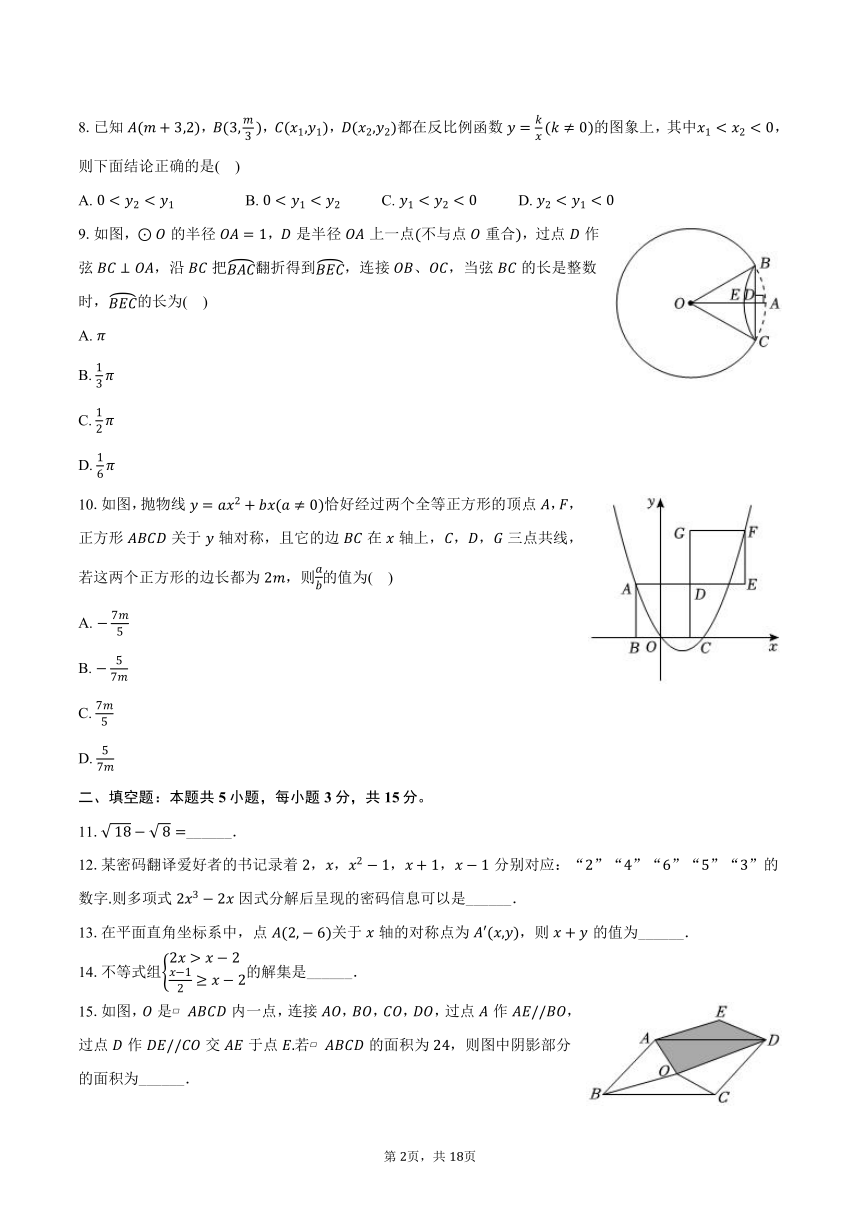
8.已知,,,都在反比例函数的图象上,其中,则下面结论正确的是( )
A. B. C. D.
9.如图,的半径,是半径上一点不与点重合,过点作弦,沿把翻折得到,连接、,当弦的长是整数时,的长为( )
A.
B.
C.
D.
10.如图,抛物线恰好经过两个全等正方形的顶点,,正方形关于轴对称,且它的边在轴上,,,三点共线,若这两个正方形的边长都为,则的值为( )
A.
B.
C.
D.
二、填空题:本题共5小题,每小题3分,共15分。
11.______.
12.某密码翻译爱好者的书记录着,,,,分别对应:“”“”“”“”“”的数字则多项式因式分解后呈现的密码信息可以是______.
13.在平面直角坐标系中,点关于轴的对称点为,则的值为______.
14.不等式组的解集是______.
15.如图,是 内一点,连接,,,,过点作,过点作交于点若 的面积为,则图中阴影部分的面积为______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:.
17.本小题分
如图,在 中,是边上的高.
实践与操作:用尺规作图法在和边上分别作,,使得四边形是菱形;保留作图痕迹,不要求写作法
应用与计算:在的条件下,连接,,若,分别求菱形两条对角线的长.
18.本小题分
如图是珠江纵队司令部旧址的红色雕塑实物图,为宣扬红色精神,某红色文化主题公园要复刻一座置于园内,将其抽象成如图所示的示意图,在底座中,,底座上沿到地面的距离为,雕塑主体,,点,的连线平行于,,,,图中所有点均在同一平面内.
求的度数;
求点到地面的距离结果精确到,参考数据:,,
19.本小题分
某农业试验基地在相同环境条件下,研究甲、乙两种小麦的苗高分布,以评估其生长稳定性和产量潜力,为优化种植方案提供依据从两种小麦试验田各随机抽取株麦苗,测量苗高单位:,将数据分组整理,分别得到了如下统计表表内方差保留整数和不完整的统计图注:将苗高共分为,,,四组,分别用,,,表示
其中甲种小麦苗高的具体数据如下:,,,,,,,,,,,,,,,.
甲、乙两种小麦苗高情况统计表
统计量 中位数 众数 方差
甲种小麦
乙种小麦
根据以上信息解答下列问题:
将条形统计图补充完整;
______, ______;
请结合稳定性优先和产量潜力优质麦苗占比更高的品种潜力大两个要求,给出种植建议并说明理由.
20.本小题分
如图,佛山的龙狮文化是中华传统文化的重要组成部分,象征着吉祥和祈福为宣传龙狮文化,某学校计划购买龙和狮的摆件放于学校的宣传栏已知龙摆件比狮摆件的单价多元,用元购买龙摆件与用元购买狮摆件的数量相同.
求龙、狮摆件的单价分别是多少?
若计划购买龙、狮摆件共个,且狮摆件的数量不超过龙摆件数量的倍,则该校至少要花费多少钱购买龙、狮摆件?
21.本小题分
综合与实践
【主题】用竹棒搭建鲁班桥.
【背景】鲁班桥是一种自承式结构桥梁,依靠桥梁自身的结构间的力来维持稳固,是我国古代劳动人民智慧的结晶.
【素材】宽为的长方体竹棒、底面圆直径为的圆柱竹棒各若干、尺子、小刀等.
【实践操作】
步骤:如图:长方体竹棒上下共刻出个半径为的半圆凹槽,圆心分别为,,,其中是竹棒中点,,到竹棒两端的距离均为;
步骤:用两个长方体竹棒夹住一个圆柱竹棒,其侧面示意图如图,以此类推重复拼搭即可搭建出如图的鲁班桥.
【实践探索】
步骤图中,个长方体竹棒搭建,,为竹棒与地面的交点,若竹棒长,跨度为,则凹槽圆心到的距离为多少?
将鲁班桥首尾相连绕成环,图为其侧面示意图,形状为两个完全相同的正方形,则需要准备长方体竹棒的长为多少厘米?
22.本小题分
分类讨论思想是当问题所给的对象不能进行统一研究时,需要对研究对象按某标准进行分类,然后研究得出每一类别的结论,最后综合解答.
如图,已知是的外接圆,是的直径,,点在上连接,,,过作的垂线交直线于点.
【构建联系】
试说明的形状,并说明理由;
【发现问题】
当是的中点时,求的值;
【深入探究】
当,,中任意一个点恰好是另外两点所连线段的中点时,求的值注:的值不存在
23.本小题分
【问题背景】在矩形中,沿对角线翻折得到,连接,,与交于点.
如图,求证:;
如图,当时,求的值;
【构建联系】
如图,当点从点往上运动时,若,设的度数为,表示点运动的路径长.
求与的函数关系式;
当中有一个角是时,求的值.
答案和解析
1.【答案】
【解析】解:根据题意可知,扣分记作分.
故选:.
2.【答案】
【解析】解:选项图形不是中心对称图形,也不是轴对称图形,不符合题意;
B.选项图形不是中心对称图形,不是轴对称图形,不符合题意;
C.选项图形是中心对称图形,是轴对称图形,符合题意;
D.选项图形是轴对称图形,不是中心对称图形,不符合题意.
故选:.
3.【答案】
【解析】解:万.
故选:.
4.【答案】
【解析】解:单项式与的乘积为,
,
故单项式是.
故选:.
5.【答案】
【解析】解:由题意可得,如图,
两直线平行,同位角相等,
,
,
故选:.
6.【答案】
【解析】解:邮票共张,“蛇”的邮票共张,
从中任意抽一张邮票送给小玲,恰好抽到“蛇”的邮票的概率是,
故选:.
7.【答案】
【解析】解:根据同分母分式减法运算法则可得:
,
故选:.
8.【答案】
【解析】解:由条件可知,
,
解得:,
反比例函数图象位于第二、四象限,且在第二象限内,随的增大而增大,
,都在反比例函数的图象上,且,
,
故选:.
9.【答案】
【解析】解:由条件可知,
是半径上一点不与点重合,
,
弦的长是整数,
弦,
是等边三角形,
,
的长,
的长为,
故选:.
10.【答案】
【解析】解:由题意,可知:,
,,
由题意可得:,
,
,
;
故选:.
11.【答案】
【解析】解:原式,
故答案为:.
12.【答案】答案不唯一
【解析】解:原式,
,
13.【答案】
【解析】解:根据题意可知,,,
.
故答案为:.
14.【答案】
【解析】解:解不等式得:,
解不等式得:,
不等式组的解集为:.
15.【答案】
【解析】解:四边形是平行四边形,
,,
,
,
,
,
同理,
在和中,
,
≌,
作 的高,的高,的高,
由平行线间的距离处处相等,
,
,
图中阴影部分的面积为,
故答案为:.
16.【答案】.
【解析】解:原式
.
17.【解析】如图,四边形即为所求;
根据作图可得,,
,
又四边形是平行四边形,
,
,
四边形是平行四边形,
,
四边形是菱形;
如图,过点作于点,则四边形是矩形,
由条件可知,
四边形是菱形,
,
,
由勾股定理可得,
,
,
又,
中,.
18.【解析】由题意可得:四边形是矩形,
,,
,
;
过点作的垂线,交延长线于点,
,
,
,
,
,
,
点到地面的距离.
19.【解析】甲种小麦苗高在内的个,内的个,
补全条形统计图,
甲种顺序排列:,,,,,,,,,,,,,,,.
,,
故答案为:,;
由方差可知甲种小麦的稳定性更优,
甲种小麦的优质麦苗占比为,
乙种小麦的优质麦苗占比为,
甲种小麦的产量潜力更高,
故建议种植甲种小麦.
20.【解析】设龙、狮摆件的单价分别是元、元,
由题意得,
整理得,,
解得,
经检验,是原方程的解,
则,
答:龙摆件的单价是元、狮摆件的单价是元;
设购进龙摆件个,则狮摆件个,总费用为,
由题意可得,
整理得,,
解得,
总费用为:,
,
当时,费用最小,最小为,
答:该校至少要花费元钱购买龙、狮摆件.
21.【解析】如图,作于点,
由题意得,,,
,
,,
.
答:凹槽圆心到的距离为.
如图,作于点,
由题意得,,,
是等腰直角三角形,,
,长方体竹棒的宽为,
,,
是等腰直角三角形,,,
由条件可知四边形是平行四边形,
长方体竹棒的宽度相等,
每条边上的高相等,
由条件可知 每条边相等,
是菱形,
,
由中点性质可知长方体竹棒的长为厘米.
答:需要准备长方体竹棒的长为厘米.
22.【解析】是等腰直角三角形,理由如下:
已知是的外接圆,是的直径,,
,
,
,
,
又,
,
,
,
是等腰直角三角形;
如图,过点作于点,
,
设,
,
是的中点,
,
,,
,
,
;
由可得当是的中点时,;
当是的中点时,则,如图,过点作于点,
是等腰直角三角形,
,
四边形是的内接四边形,
,
,
又,
是等腰直角三角形;
,
,
,
,
设,
在直角三角形中,由勾股定理得:,
在直角三角形中,由勾股定理得:,
,
,
,
,
如图,当是的中点时,如图,点与重合,此时,的值不存在,
综上所述,当,,中任意一个点恰好是另外两点所连线段的中点时,的值为.
23.【解析】证明:沿对角线翻折得到,
,,,
是的垂直平分线,
,,
如图,记,的交点为,
四边形是矩形,
,,
,
,
,,
,
,
,
,
,
,
;
解:如图,记,的交点为,连接交于,
四边形是矩形,
,
,,
,
,
,
设,
在直角三角形中,由勾股定理得:,
,
;
如图,由对折可得,
在以为圆心,为半径的圆上运动,运动路径为,
当点从点往上运动时,设的度数为,
,
,
,
,
,
;
当时,
结合得:,
,
;
当时,如图,
,由对折可得,结合矩形可得,
,
解得:,
;
当时,不合题意,舍去;
综上所述,的值为或.
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.我们在生活中经常会遇到各种相反意义的量,如在课堂抢答活动中,若把加分记作分,则扣分记作( )
A. 分 B. 分 C. 分 D. 分
2.下列倡导环保的图案中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.广东省年计划新增电源装机万千瓦,完善绿电市场交易机制,加紧经济社会发展全面绿色转型其中数据万用科学记数法表示为( )
A. B. C. D.
4.已知单项式与的乘积为,则单项式是( )
A. B. C. D.
5.汽车前灯是由灯泡、反光镜和配光镜三部分组成,光源位于焦点处,光线经反射后互相平行射出如图为其侧面示意图,已知,,则的度数为( )
A.
B.
C.
D.
6.“十二生肖纪年法”是我国历法的一种传统纪年法,又称天干地支纪年法,给十二地支配上相应的十二兽名,以十二年为一循环的纪年法小明购买了一套十二生肖邮票共张,从中任意抽一张邮票送给小玲,恰好抽到“蛇”的邮票的概率是( )
A. B. C. D.
7.计算的结果是( )
A. B. C. D.
8.已知,,,都在反比例函数的图象上,其中,则下面结论正确的是( )
A. B. C. D.
9.如图,的半径,是半径上一点不与点重合,过点作弦,沿把翻折得到,连接、,当弦的长是整数时,的长为( )
A.
B.
C.
D.
10.如图,抛物线恰好经过两个全等正方形的顶点,,正方形关于轴对称,且它的边在轴上,,,三点共线,若这两个正方形的边长都为,则的值为( )
A.
B.
C.
D.
二、填空题:本题共5小题,每小题3分,共15分。
11.______.
12.某密码翻译爱好者的书记录着,,,,分别对应:“”“”“”“”“”的数字则多项式因式分解后呈现的密码信息可以是______.
13.在平面直角坐标系中,点关于轴的对称点为,则的值为______.
14.不等式组的解集是______.
15.如图,是 内一点,连接,,,,过点作,过点作交于点若 的面积为,则图中阴影部分的面积为______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:.
17.本小题分
如图,在 中,是边上的高.
实践与操作:用尺规作图法在和边上分别作,,使得四边形是菱形;保留作图痕迹,不要求写作法
应用与计算:在的条件下,连接,,若,分别求菱形两条对角线的长.
18.本小题分
如图是珠江纵队司令部旧址的红色雕塑实物图,为宣扬红色精神,某红色文化主题公园要复刻一座置于园内,将其抽象成如图所示的示意图,在底座中,,底座上沿到地面的距离为,雕塑主体,,点,的连线平行于,,,,图中所有点均在同一平面内.
求的度数;
求点到地面的距离结果精确到,参考数据:,,
19.本小题分
某农业试验基地在相同环境条件下,研究甲、乙两种小麦的苗高分布,以评估其生长稳定性和产量潜力,为优化种植方案提供依据从两种小麦试验田各随机抽取株麦苗,测量苗高单位:,将数据分组整理,分别得到了如下统计表表内方差保留整数和不完整的统计图注:将苗高共分为,,,四组,分别用,,,表示
其中甲种小麦苗高的具体数据如下:,,,,,,,,,,,,,,,.
甲、乙两种小麦苗高情况统计表
统计量 中位数 众数 方差
甲种小麦
乙种小麦
根据以上信息解答下列问题:
将条形统计图补充完整;
______, ______;
请结合稳定性优先和产量潜力优质麦苗占比更高的品种潜力大两个要求,给出种植建议并说明理由.
20.本小题分
如图,佛山的龙狮文化是中华传统文化的重要组成部分,象征着吉祥和祈福为宣传龙狮文化,某学校计划购买龙和狮的摆件放于学校的宣传栏已知龙摆件比狮摆件的单价多元,用元购买龙摆件与用元购买狮摆件的数量相同.
求龙、狮摆件的单价分别是多少?
若计划购买龙、狮摆件共个,且狮摆件的数量不超过龙摆件数量的倍,则该校至少要花费多少钱购买龙、狮摆件?
21.本小题分
综合与实践
【主题】用竹棒搭建鲁班桥.
【背景】鲁班桥是一种自承式结构桥梁,依靠桥梁自身的结构间的力来维持稳固,是我国古代劳动人民智慧的结晶.
【素材】宽为的长方体竹棒、底面圆直径为的圆柱竹棒各若干、尺子、小刀等.
【实践操作】
步骤:如图:长方体竹棒上下共刻出个半径为的半圆凹槽,圆心分别为,,,其中是竹棒中点,,到竹棒两端的距离均为;
步骤:用两个长方体竹棒夹住一个圆柱竹棒,其侧面示意图如图,以此类推重复拼搭即可搭建出如图的鲁班桥.
【实践探索】
步骤图中,个长方体竹棒搭建,,为竹棒与地面的交点,若竹棒长,跨度为,则凹槽圆心到的距离为多少?
将鲁班桥首尾相连绕成环,图为其侧面示意图,形状为两个完全相同的正方形,则需要准备长方体竹棒的长为多少厘米?
22.本小题分
分类讨论思想是当问题所给的对象不能进行统一研究时,需要对研究对象按某标准进行分类,然后研究得出每一类别的结论,最后综合解答.
如图,已知是的外接圆,是的直径,,点在上连接,,,过作的垂线交直线于点.
【构建联系】
试说明的形状,并说明理由;
【发现问题】
当是的中点时,求的值;
【深入探究】
当,,中任意一个点恰好是另外两点所连线段的中点时,求的值注:的值不存在
23.本小题分
【问题背景】在矩形中,沿对角线翻折得到,连接,,与交于点.
如图,求证:;
如图,当时,求的值;
【构建联系】
如图,当点从点往上运动时,若,设的度数为,表示点运动的路径长.
求与的函数关系式;
当中有一个角是时,求的值.
答案和解析
1.【答案】
【解析】解:根据题意可知,扣分记作分.
故选:.
2.【答案】
【解析】解:选项图形不是中心对称图形,也不是轴对称图形,不符合题意;
B.选项图形不是中心对称图形,不是轴对称图形,不符合题意;
C.选项图形是中心对称图形,是轴对称图形,符合题意;
D.选项图形是轴对称图形,不是中心对称图形,不符合题意.
故选:.
3.【答案】
【解析】解:万.
故选:.
4.【答案】
【解析】解:单项式与的乘积为,
,
故单项式是.
故选:.
5.【答案】
【解析】解:由题意可得,如图,
两直线平行,同位角相等,
,
,
故选:.
6.【答案】
【解析】解:邮票共张,“蛇”的邮票共张,
从中任意抽一张邮票送给小玲,恰好抽到“蛇”的邮票的概率是,
故选:.
7.【答案】
【解析】解:根据同分母分式减法运算法则可得:
,
故选:.
8.【答案】
【解析】解:由条件可知,
,
解得:,
反比例函数图象位于第二、四象限,且在第二象限内,随的增大而增大,
,都在反比例函数的图象上,且,
,
故选:.
9.【答案】
【解析】解:由条件可知,
是半径上一点不与点重合,
,
弦的长是整数,
弦,
是等边三角形,
,
的长,
的长为,
故选:.
10.【答案】
【解析】解:由题意,可知:,
,,
由题意可得:,
,
,
;
故选:.
11.【答案】
【解析】解:原式,
故答案为:.
12.【答案】答案不唯一
【解析】解:原式,
,
13.【答案】
【解析】解:根据题意可知,,,
.
故答案为:.
14.【答案】
【解析】解:解不等式得:,
解不等式得:,
不等式组的解集为:.
15.【答案】
【解析】解:四边形是平行四边形,
,,
,
,
,
,
同理,
在和中,
,
≌,
作 的高,的高,的高,
由平行线间的距离处处相等,
,
,
图中阴影部分的面积为,
故答案为:.
16.【答案】.
【解析】解:原式
.
17.【解析】如图,四边形即为所求;
根据作图可得,,
,
又四边形是平行四边形,
,
,
四边形是平行四边形,
,
四边形是菱形;
如图,过点作于点,则四边形是矩形,
由条件可知,
四边形是菱形,
,
,
由勾股定理可得,
,
,
又,
中,.
18.【解析】由题意可得:四边形是矩形,
,,
,
;
过点作的垂线,交延长线于点,
,
,
,
,
,
,
点到地面的距离.
19.【解析】甲种小麦苗高在内的个,内的个,
补全条形统计图,
甲种顺序排列:,,,,,,,,,,,,,,,.
,,
故答案为:,;
由方差可知甲种小麦的稳定性更优,
甲种小麦的优质麦苗占比为,
乙种小麦的优质麦苗占比为,
甲种小麦的产量潜力更高,
故建议种植甲种小麦.
20.【解析】设龙、狮摆件的单价分别是元、元,
由题意得,
整理得,,
解得,
经检验,是原方程的解,
则,
答:龙摆件的单价是元、狮摆件的单价是元;
设购进龙摆件个,则狮摆件个,总费用为,
由题意可得,
整理得,,
解得,
总费用为:,
,
当时,费用最小,最小为,
答:该校至少要花费元钱购买龙、狮摆件.
21.【解析】如图,作于点,
由题意得,,,
,
,,
.
答:凹槽圆心到的距离为.
如图,作于点,
由题意得,,,
是等腰直角三角形,,
,长方体竹棒的宽为,
,,
是等腰直角三角形,,,
由条件可知四边形是平行四边形,
长方体竹棒的宽度相等,
每条边上的高相等,
由条件可知 每条边相等,
是菱形,
,
由中点性质可知长方体竹棒的长为厘米.
答:需要准备长方体竹棒的长为厘米.
22.【解析】是等腰直角三角形,理由如下:
已知是的外接圆,是的直径,,
,
,
,
,
又,
,
,
,
是等腰直角三角形;
如图,过点作于点,
,
设,
,
是的中点,
,
,,
,
,
;
由可得当是的中点时,;
当是的中点时,则,如图,过点作于点,
是等腰直角三角形,
,
四边形是的内接四边形,
,
,
又,
是等腰直角三角形;
,
,
,
,
设,
在直角三角形中,由勾股定理得:,
在直角三角形中,由勾股定理得:,
,
,
,
,
如图,当是的中点时,如图,点与重合,此时,的值不存在,
综上所述,当,,中任意一个点恰好是另外两点所连线段的中点时,的值为.
23.【解析】证明:沿对角线翻折得到,
,,,
是的垂直平分线,
,,
如图,记,的交点为,
四边形是矩形,
,,
,
,
,,
,
,
,
,
,
,
;
解:如图,记,的交点为,连接交于,
四边形是矩形,
,
,,
,
,
,
设,
在直角三角形中,由勾股定理得:,
,
;
如图,由对折可得,
在以为圆心,为半径的圆上运动,运动路径为,
当点从点往上运动时,设的度数为,
,
,
,
,
,
;
当时,
结合得:,
,
;
当时,如图,
,由对折可得,结合矩形可得,
,
解得:,
;
当时,不合题意,舍去;
综上所述,的值为或.
第1页,共1页
同课章节目录
