【期末核心考点】平行四边形的判定(含解析)2024-2025学年八年级下册数学华东师大版
文档属性
| 名称 | 【期末核心考点】平行四边形的判定(含解析)2024-2025学年八年级下册数学华东师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-14 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末核心考点 平行四边形的判定
一.选择题(共7小题)
1.(2024秋 林州市期末)四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AC⊥BD,∠A=∠C B.AB=DC,AD=BC
C.AB∥DC,AD∥BC D.AB∥DC,AB=DC
2.(2025 长安区一模)根据所标数据,不能判断下列四边形是平行四边形的是( )
A. B.
C. D.
3.(2025春 阳东区期中)如图,在△ABC中,∠B=49°,分别以点A,C为圆心,BC,AB长为半径作弧,两弧相交于点D,连接AD,CD,则∠ADC的度数为( )
A.41° B.49° C.51° D.59°
4.(2025春 宿迁期中)汽车雨刮器是扫除车窗玻璃上妨碍视线的雨雪和尘土的重要工具,通常两个雨刮器的刷片长度相同,即AB=CD.某时刻汽车雨刮器的位置如图所示,此时∠ABE=∠C,则下列说法错误的是( )
A.四边形ABCD是平行四边形
B.∠A=∠D
C.AD=BC
D.AD∥BC
5.(2025春 西山区校级期中)下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,能判定四边形ABCD是平行四边形的是( )
A.1:2:3:4 B.2:3:2:3 C.2:3:3:2 D.1:2:2:3
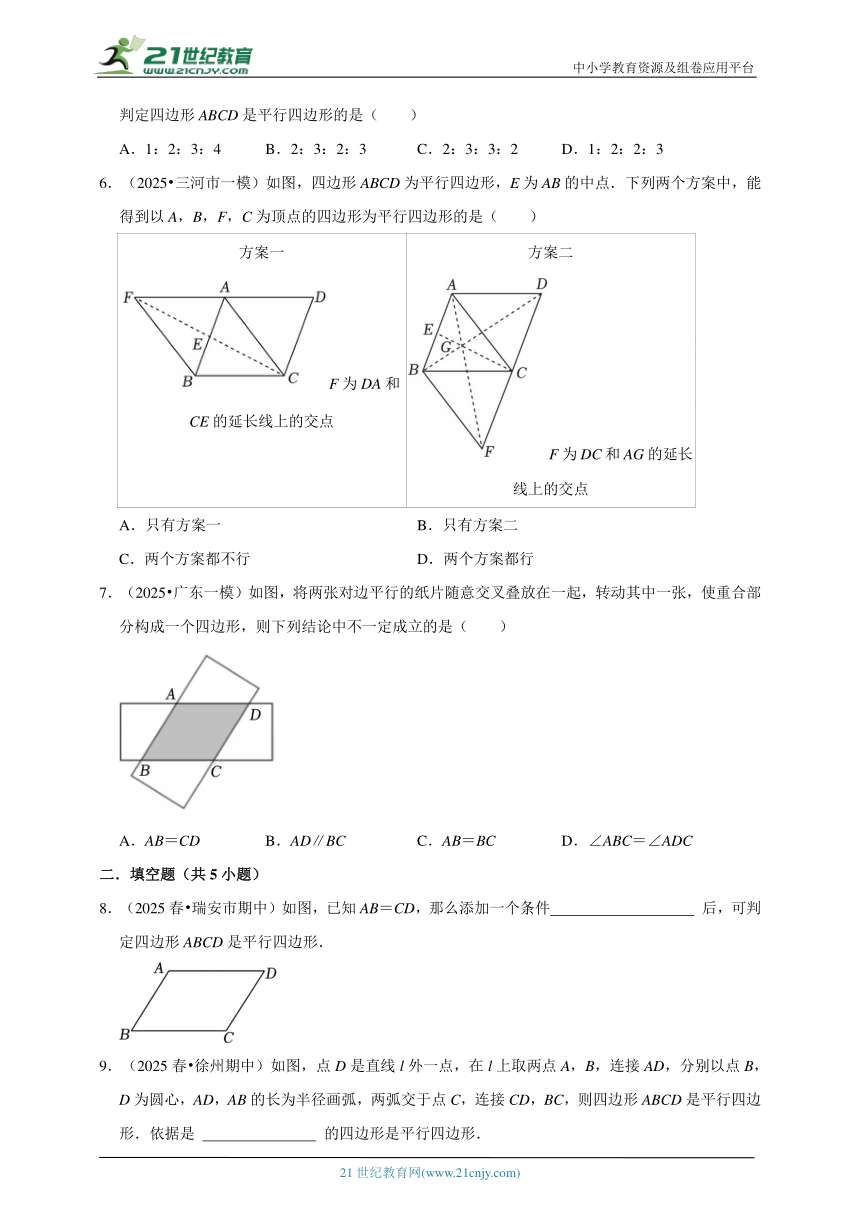
6.(2025 三河市一模)如图,四边形ABCD为平行四边形,E为AB的中点.下列两个方案中,能得到以A,B,F,C为顶点的四边形为平行四边形的是( )
方案一 F为DA和CE的延长线上的交点 方案二 F为DC和AG的延长线上的交点
A.只有方案一 B.只有方案二
C.两个方案都不行 D.两个方案都行
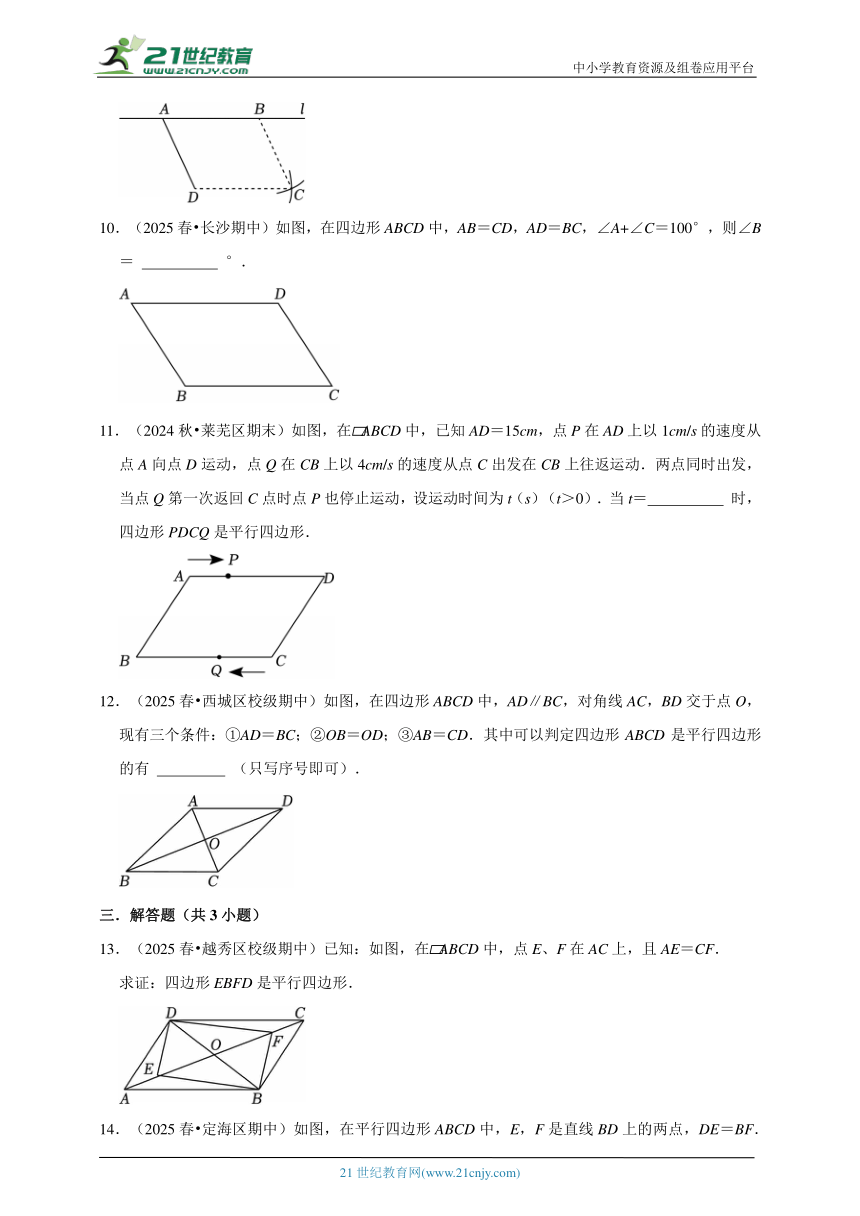
7.(2025 广东一模)如图,将两张对边平行的纸片随意交叉叠放在一起,转动其中一张,使重合部分构成一个四边形,则下列结论中不一定成立的是( )
A.AB=CD B.AD∥BC C.AB=BC D.∠ABC=∠ADC
二.填空题(共5小题)
8.(2025春 瑞安市期中)如图,已知AB=CD,那么添加一个条件 后,可判定四边形ABCD是平行四边形.
9.(2025春 徐州期中)如图,点D是直线l外一点,在l上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形.依据是 的四边形是平行四边形.
10.(2025春 长沙期中)如图,在四边形ABCD中,AB=CD,AD=BC,∠A+∠C=100°,则∠B= °.
11.(2024秋 莱芜区期末)如图,在 ABCD中,已知AD=15cm,点P在AD上以1cm/s的速度从点A向点D运动,点Q在CB上以4cm/s的速度从点C出发在CB上往返运动.两点同时出发,当点Q第一次返回C点时点P也停止运动,设运动时间为t(s)(t>0).当t= 时,四边形PDCQ是平行四边形.
12.(2025春 西城区校级期中)如图,在四边形ABCD中,AD∥BC,对角线AC,BD交于点O,现有三个条件:①AD=BC;②OB=OD;③AB=CD.其中可以判定四边形ABCD是平行四边形的有 (只写序号即可).
三.解答题(共3小题)
13.(2025春 越秀区校级期中)已知:如图,在 ABCD中,点E、F在AC上,且AE=CF.
求证:四边形EBFD是平行四边形.
14.(2025春 定海区期中)如图,在平行四边形ABCD中,E,F是直线BD上的两点,DE=BF.
(1)求证:四边形AECF是平行四边形;
(2)若AD⊥BD,AB=10,BC=6,且EF﹣AF=4,求DE的长.
15.(2025 防城港一模)如图,在△ABF中,AB=BF,BE⊥AF于点E,过点A作AD∥BF,连接DE并延长,交BF于点C.
(1)求证:AE=EF.
(2)连接AC,DF,求证:四边形ACFD是平行四边形.
期末核心考点 平行四边形的判定
参考答案与试题解析
一.选择题(共7小题)
1.(2024秋 林州市期末)四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AC⊥BD,∠A=∠C B.AB=DC,AD=BC
C.AB∥DC,AD∥BC D.AB∥DC,AB=DC
【考点】平行四边形的判定.
【专题】多边形与平行四边形;推理能力.
【分析】利用平行四边形的判定方法依次判断可求解.
【解答】解:A、若AC⊥BD,∠A=∠C,无法判断四边形ABCD是平行四边形,故选项A符合题意;
B、若AB=DC,AD=BC,由两组对边相等的四边形是平行四边形,可判断四边形ABCD是平行四边形,故选项B不符合题意;
C、若AB∥DC,AD∥BC,由两组对边平行的四边形是平行四边形,可判断四边形ABCD是平行四边形,故选项C不符合题意;
D、若AB∥DC,AB=DC,由一组对边平行且相等的四边形是平行四边形,可判断四边形ABCD是平行四边形,故选项D不符合题意;
故选:A.
【点评】本题考查了平行四边形的判定,掌握平行四边形的判定方法是解题的关键.
2.(2025 长安区一模)根据所标数据,不能判断下列四边形是平行四边形的是( )
A. B.
C. D.
【考点】平行四边形的判定.
【专题】多边形与平行四边形;推理能力.
【分析】依据题意,根据平行四边形的判定定理逐个进行分析可以判断得解.
【解答】解:A、∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,故不符合题意;
B、∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,故不符合题意;
C、∵∠ACB=∠DAC=40°,
∴AD∥BC,
∵AB=CD,
∴不能判定四边形ABCD是平行四边形,故符合题意;
D、∠ACB=∠CAD=40°,
∴AD∥BC,
∵∠ABD=∠BDC=35°,
∴AB∥CD,
∴四边形ABCD是平行四边形,故不符合题意;
故选:C.
【点评】本题主要考查了平行四边形的判定,解题时要熟练掌握平行四边形的判定定理是关键.
3.(2025春 阳东区期中)如图,在△ABC中,∠B=49°,分别以点A,C为圆心,BC,AB长为半径作弧,两弧相交于点D,连接AD,CD,则∠ADC的度数为( )
A.41° B.49° C.51° D.59°
【考点】平行四边形的判定与性质.
【专题】多边形与平行四边形;推理能力.
【分析】判定四边形ABCD是平行四边形,推出∠ADC=∠B=49°.
【解答】解:由题意得到:AD=BC,CD=AB,
∴四边形ABCD是平行四边形,
∴∠ADC=∠B=49°.
故选:B.
【点评】本题考查平行四边形的判定和性质,关键是掌握两组对边分别相等的四边形是平行四边形,平行四边形的对角相等.
4.(2025春 宿迁期中)汽车雨刮器是扫除车窗玻璃上妨碍视线的雨雪和尘土的重要工具,通常两个雨刮器的刷片长度相同,即AB=CD.某时刻汽车雨刮器的位置如图所示,此时∠ABE=∠C,则下列说法错误的是( )
A.四边形ABCD是平行四边形
B.∠A=∠D
C.AD=BC
D.AD∥BC
【考点】平行四边形的判定与性质.
【专题】多边形与平行四边形;推理能力.
【分析】先根据一组对边平行且相等的四边形是平行四边形可得:四边形ABCD是平行四边形,然后利用平行四边形的性质即可解答.
【解答】解:∵∠ABE=∠C,
∴AB∥CD,
又∵AB=CD,
∴四边形ABCD是平行四边形,
∴∠A+∠D=180°,AD=BC,AD∥BC,
故选项B错误,符合题意;
故选:B.
【点评】本题考查了平行四边形的判定与性质,熟练掌握平行四边形的判定与性质是解题的关键.
5.(2025春 西山区校级期中)下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,能判定四边形ABCD是平行四边形的是( )
A.1:2:3:4 B.2:3:2:3 C.2:3:3:2 D.1:2:2:3
【考点】平行四边形的判定.
【专题】多边形与平行四边形;推理能力.
【分析】两组对角分别相等的四边形是平行四边形,由此即可判断.
【解答】解:A、C、D中的条件不能推出四边形ABCD的两组对角分别相等,故A、C、D不符合题意;
B、由条件推出∠A=∠C,∠B=∠D,判定四边形ABCD是平行四边形,故B符合题意.
故选:B.
【点评】本题考查平行四边形的判定,关键是掌握两组对角分别相等的四边形是平行四边形.
6.(2025 三河市一模)如图,四边形ABCD为平行四边形,E为AB的中点.下列两个方案中,能得到以A,B,F,C为顶点的四边形为平行四边形的是( )
方案一 F为DA和CE的延长线上的交点 方案二 F为DC和AG的延长线上的交点
A.只有方案一 B.只有方案二
C.两个方案都不行 D.两个方案都行
【考点】平行四边形的判定与性质.
【专题】多边形与平行四边形;推理能力.
【分析】方案一证明△AFE≌△BCE(AAS)可得AF=BC,AF∥BC,即可判断四边形ABFC是平行四边形;方案二通过证明△ABI≌△FCI(AAS)可得AB=CF,AB∥CF,即可判断四边形ABFC是平行四边形,从而可得结论.
【解答】解:方案一:由题意可得:AD∥BC,AE=BE,
∴∠FAE=∠CBE,∠AFE=∠BCE,
在△AFE和△BCE中,
,
∴△AFE≌△BCE(AAS),
∴AF=BC,
又AF∥BC,
∴四边形ABFC是平行四边形,
方案二:由题意可得:
∴AB∥CD,AC,BD互相平分于点H,如图,
又E为AB的中点,
∴G为△ABC的重心,
∴AI为BC边上的中线,I为BC边的中点,
∵AB∥CF,
∴∠BAI=∠CFI,∠ABI=∠FCI,
又BI=CI,
∴△ABI≌△FCI(AAS),
∴AB=CF,
又AB∥CF,
∴四边形ABFC是平行四边形,
综上,方案一和方案二都正确,
故选:D.
【点评】本题主要考查平行四边形的判定和全等三角形的判定与性质,正确记忆相关知识点是解题关键.
7.(2025 广东一模)如图,将两张对边平行的纸片随意交叉叠放在一起,转动其中一张,使重合部分构成一个四边形,则下列结论中不一定成立的是( )
A.AB=CD B.AD∥BC C.AB=BC D.∠ABC=∠ADC
【考点】平行四边形的判定与性质.
【专题】多边形与平行四边形;几何直观;推理能力.
【分析】根据题意证得四边形ABCD是平行四边形,再逐项判断即可.
【解答】解:∵将两张对边平行的纸片随意交叉叠放在一起,
∴AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形.
∴AB=CD,∠ABC=∠ADC,
∴A、B、D一定成立,不符合题意;
∴AB不一定等于BC,与两张纸片的宽度有关,
故C不一定成立,符合题意;
故选:C.
【点评】本题考查平行四边形的判定和性质,掌握平行四边形的判定方法和其性质是解答本题的关键.
二.填空题(共5小题)
8.(2025春 瑞安市期中)如图,已知AB=CD,那么添加一个条件 AB∥CD(答案不唯一) 后,可判定四边形ABCD是平行四边形.
【考点】平行四边形的判定.
【专题】多边形与平行四边形;推理能力.
【分析】由平行四边形的判定方法即可得出结论.
【解答】解:添加条件为:AB∥CD,理由如下:
∵AB=CD,AB∥CD,
∴四边形ABCD是平行四边形,
故答案为:AB∥CD(答案不唯一).
【点评】本题考查了平行四边形的判定,熟练掌握平行四边形的判定方法是解题的关键.
9.(2025春 徐州期中)如图,点D是直线l外一点,在l上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形.依据是 两组对边分别相等 的四边形是平行四边形.
【考点】平行四边形的判定.
【专题】多边形与平行四边形;推理能力.
【分析】根据两组对边分别相等的四边形是平行四边形进行判定即可.
【解答】解:由作图可知,BC=AD,CD=AB,
∴四边形ABCD是平行四边形,
依据是:两组对边分别相等的四边形是平行四边形,
故答案为:两组对边分别相等.
【点评】本题考查了平行四边形的判定,熟记两组对边分别相等的四边形为平行四边形是解题的关键.
10.(2025春 长沙期中)如图,在四边形ABCD中,AB=CD,AD=BC,∠A+∠C=100°,则∠B= 130 °.
【考点】平行四边形的判定与性质.
【专题】多边形与平行四边形;运算能力;推理能力.
【分析】由平行四边形的性质等∠C=∠A,AD∥BC,得∠A+∠B=180°,再求出∠A=50°,即可解决问题.
【解答】解:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴∠C=∠A,AD∥BC,
∴∠A+∠B=180°,
∵∠A+∠C=100°,
∴∠A=50°,
∴∠B=180°﹣50°=130°,
故答案为:130.
【点评】本题考查了平行四边形的判定与性质,熟练掌握平行四边形的判定与性质是解题的关键.
11.(2024秋 莱芜区期末)如图,在 ABCD中,已知AD=15cm,点P在AD上以1cm/s的速度从点A向点D运动,点Q在CB上以4cm/s的速度从点C出发在CB上往返运动.两点同时出发,当点Q第一次返回C点时点P也停止运动,设运动时间为t(s)(t>0).当t= 3或5 时,四边形PDCQ是平行四边形.
【考点】平行四边形的判定与性质.
【专题】分类讨论;多边形与平行四边形;推理能力.
【分析】根据平行四边形的性质得出DP=CQ,分情况讨论,再列出方程,求出方程的解即可.
【解答】解:设经过t秒,四边形PDCQ是平行四边形,
∵P在AD上运动,
∴t7.5,即0<t≤7.5,
∵四边形PDCQ是平行四边形,
∴DP=CQ,
分为以下情况:①点Q的运动路线是C﹣B,方程为4t=15﹣t,
解得t=3,
②点Q的运动路线是C﹣B﹣C,方程为15﹣415﹣t,
解得:t=5;
故答案为:3或5.
【点评】本题考查了平行四边形的判定与性质,能求出符合的所有情况是解此题的关键,用了分类讨论思想.
12.(2025春 西城区校级期中)如图,在四边形ABCD中,AD∥BC,对角线AC,BD交于点O,现有三个条件:①AD=BC;②OB=OD;③AB=CD.其中可以判定四边形ABCD是平行四边形的有 ①② (只写序号即可).
【考点】平行四边形的判定;全等三角形的判定与性质.
【专题】图形的全等;多边形与平行四边形;推理能力.
【分析】根据平行四边形的判定方法分别对各个条件进行判断即可.
【解答】解:①∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,故①符合题意;
②∵AD∥BC,
∴∠OBC=∠ODA,
又∵OB=OD,∠BOC=∠DOA,
∴△OBC≌△ODA(ASA),
∴OA=OC,
∴四边形ABCD是平行四边形,故②符合题意;
③由AD∥BC,AB=CD,不能判定四边形ABCD是平行四边形,故③不符合题意;
故答案为:①②.
【点评】本题考查了平行四边形的判定以及全等三角形的判定与性质等知识,熟练掌握平行四边形的判定方法是解题的关键.
三.解答题(共3小题)
13.(2025春 越秀区校级期中)已知:如图,在 ABCD中,点E、F在AC上,且AE=CF.
求证:四边形EBFD是平行四边形.
【考点】平行四边形的判定与性质.
【专题】多边形与平行四边形;几何直观;推理能力.
【分析】由平行四边形可知OB=OD,OA=OC,又AE=CF,所以OE=OF,然后依据对角线互相平分的四边形是平行四边形即可证明.
【解答】证明:∵四边形ABCD是平行四边形,AE=CF,
∴AO=CO,BO=DO,
∴AO﹣AE=CO﹣CF,
∴OE=OF.
∴四边形EBFD为平行四边形.
【点评】本题主要考查了平行四边形的判定与性质,解答本题的关键要明确:对角线互相平分的四边形是平行四边形.
14.(2025春 定海区期中)如图,在平行四边形ABCD中,E,F是直线BD上的两点,DE=BF.
(1)求证:四边形AECF是平行四边形;
(2)若AD⊥BD,AB=10,BC=6,且EF﹣AF=4,求DE的长.
【考点】平行四边形的判定与性质;平行线的判定与性质;全等三角形的判定与性质;勾股定理.
【专题】线段、角、相交线与平行线;图形的全等;等腰三角形与直角三角形;多边形与平行四边形.
【分析】(1)由平行四边形的性质得出AD∥BC,AD=BC,再证△ADE≌△CBF(SAS),得出AE=CF,∠AED=∠CFB,则AE∥CF,即可得出结论;
(2)由勾股定理得求出BD=8,设DE=BF=x,则EF=2x+8,DF=8+x,推出AF=2x+4,然后由勾股定理求出x=2,即可得出结果.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ADB=∠CBD,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS),
∴AE=CF,∠AED=∠CFB,
∴AE∥CF,
∴四边形AECF是平行四边形;
(2)解:∵四边形ABCD是平行四边形,
∴BC=AD=6,
在Rt△ADB中,由勾股定理得:BD8,
设DE=BF=x,
∴EF=2x+8,DF=8+x,
∵EF﹣AF=4,
∴AF=2x+4,
在Rt△ADF中,由勾股定理得:AF2=AD2+DF2,
即(2x+4)2=62+(8+x)2,
解得:x=2(负值已舍去),
∴DE的长为2.
【点评】本题考查了平行四边形的判定与性质、勾股定理以及全等三角形的判定与性质等知识,熟练掌握平行四边形的判定与性质是解题的关键.
15.(2025 防城港一模)如图,在△ABF中,AB=BF,BE⊥AF于点E,过点A作AD∥BF,连接DE并延长,交BF于点C.
(1)求证:AE=EF.
(2)连接AC,DF,求证:四边形ACFD是平行四边形.
【考点】平行四边形的判定;全等三角形的判定与性质;等腰三角形的性质.
【专题】图形的全等;矩形 菱形 正方形;推理能力.
【分析】(1)由等腰三角形的性质可求解;
(2)由AAS可证△ADE≌△FCE,可得AD=CF,即可求解.
【解答】证明:(1)∵AB=BF,BE⊥AF,
∴AE=EF;
(2)∵AD∥BF,
∴∠ADE=∠FCE,
在△ADE和△FCE中,
∴△ADE≌△FCE(AAS),
∴AD=CF.
∵AD∥BF,
∴四边形ACFD是平行四边形.
【点评】本题考查了平行四边形的判定,全等三角形的判定和性质,等腰三角形的性质,灵活运用这些性质解决问题是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末核心考点 平行四边形的判定
一.选择题(共7小题)
1.(2024秋 林州市期末)四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AC⊥BD,∠A=∠C B.AB=DC,AD=BC
C.AB∥DC,AD∥BC D.AB∥DC,AB=DC
2.(2025 长安区一模)根据所标数据,不能判断下列四边形是平行四边形的是( )
A. B.
C. D.
3.(2025春 阳东区期中)如图,在△ABC中,∠B=49°,分别以点A,C为圆心,BC,AB长为半径作弧,两弧相交于点D,连接AD,CD,则∠ADC的度数为( )
A.41° B.49° C.51° D.59°
4.(2025春 宿迁期中)汽车雨刮器是扫除车窗玻璃上妨碍视线的雨雪和尘土的重要工具,通常两个雨刮器的刷片长度相同,即AB=CD.某时刻汽车雨刮器的位置如图所示,此时∠ABE=∠C,则下列说法错误的是( )
A.四边形ABCD是平行四边形
B.∠A=∠D
C.AD=BC
D.AD∥BC
5.(2025春 西山区校级期中)下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,能判定四边形ABCD是平行四边形的是( )
A.1:2:3:4 B.2:3:2:3 C.2:3:3:2 D.1:2:2:3
6.(2025 三河市一模)如图,四边形ABCD为平行四边形,E为AB的中点.下列两个方案中,能得到以A,B,F,C为顶点的四边形为平行四边形的是( )
方案一 F为DA和CE的延长线上的交点 方案二 F为DC和AG的延长线上的交点
A.只有方案一 B.只有方案二
C.两个方案都不行 D.两个方案都行
7.(2025 广东一模)如图,将两张对边平行的纸片随意交叉叠放在一起,转动其中一张,使重合部分构成一个四边形,则下列结论中不一定成立的是( )
A.AB=CD B.AD∥BC C.AB=BC D.∠ABC=∠ADC
二.填空题(共5小题)
8.(2025春 瑞安市期中)如图,已知AB=CD,那么添加一个条件 后,可判定四边形ABCD是平行四边形.
9.(2025春 徐州期中)如图,点D是直线l外一点,在l上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形.依据是 的四边形是平行四边形.
10.(2025春 长沙期中)如图,在四边形ABCD中,AB=CD,AD=BC,∠A+∠C=100°,则∠B= °.
11.(2024秋 莱芜区期末)如图,在 ABCD中,已知AD=15cm,点P在AD上以1cm/s的速度从点A向点D运动,点Q在CB上以4cm/s的速度从点C出发在CB上往返运动.两点同时出发,当点Q第一次返回C点时点P也停止运动,设运动时间为t(s)(t>0).当t= 时,四边形PDCQ是平行四边形.
12.(2025春 西城区校级期中)如图,在四边形ABCD中,AD∥BC,对角线AC,BD交于点O,现有三个条件:①AD=BC;②OB=OD;③AB=CD.其中可以判定四边形ABCD是平行四边形的有 (只写序号即可).
三.解答题(共3小题)
13.(2025春 越秀区校级期中)已知:如图,在 ABCD中,点E、F在AC上,且AE=CF.
求证:四边形EBFD是平行四边形.
14.(2025春 定海区期中)如图,在平行四边形ABCD中,E,F是直线BD上的两点,DE=BF.
(1)求证:四边形AECF是平行四边形;
(2)若AD⊥BD,AB=10,BC=6,且EF﹣AF=4,求DE的长.
15.(2025 防城港一模)如图,在△ABF中,AB=BF,BE⊥AF于点E,过点A作AD∥BF,连接DE并延长,交BF于点C.
(1)求证:AE=EF.
(2)连接AC,DF,求证:四边形ACFD是平行四边形.
期末核心考点 平行四边形的判定
参考答案与试题解析
一.选择题(共7小题)
1.(2024秋 林州市期末)四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AC⊥BD,∠A=∠C B.AB=DC,AD=BC
C.AB∥DC,AD∥BC D.AB∥DC,AB=DC
【考点】平行四边形的判定.
【专题】多边形与平行四边形;推理能力.
【分析】利用平行四边形的判定方法依次判断可求解.
【解答】解:A、若AC⊥BD,∠A=∠C,无法判断四边形ABCD是平行四边形,故选项A符合题意;
B、若AB=DC,AD=BC,由两组对边相等的四边形是平行四边形,可判断四边形ABCD是平行四边形,故选项B不符合题意;
C、若AB∥DC,AD∥BC,由两组对边平行的四边形是平行四边形,可判断四边形ABCD是平行四边形,故选项C不符合题意;
D、若AB∥DC,AB=DC,由一组对边平行且相等的四边形是平行四边形,可判断四边形ABCD是平行四边形,故选项D不符合题意;
故选:A.
【点评】本题考查了平行四边形的判定,掌握平行四边形的判定方法是解题的关键.
2.(2025 长安区一模)根据所标数据,不能判断下列四边形是平行四边形的是( )
A. B.
C. D.
【考点】平行四边形的判定.
【专题】多边形与平行四边形;推理能力.
【分析】依据题意,根据平行四边形的判定定理逐个进行分析可以判断得解.
【解答】解:A、∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,故不符合题意;
B、∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,故不符合题意;
C、∵∠ACB=∠DAC=40°,
∴AD∥BC,
∵AB=CD,
∴不能判定四边形ABCD是平行四边形,故符合题意;
D、∠ACB=∠CAD=40°,
∴AD∥BC,
∵∠ABD=∠BDC=35°,
∴AB∥CD,
∴四边形ABCD是平行四边形,故不符合题意;
故选:C.
【点评】本题主要考查了平行四边形的判定,解题时要熟练掌握平行四边形的判定定理是关键.
3.(2025春 阳东区期中)如图,在△ABC中,∠B=49°,分别以点A,C为圆心,BC,AB长为半径作弧,两弧相交于点D,连接AD,CD,则∠ADC的度数为( )
A.41° B.49° C.51° D.59°
【考点】平行四边形的判定与性质.
【专题】多边形与平行四边形;推理能力.
【分析】判定四边形ABCD是平行四边形,推出∠ADC=∠B=49°.
【解答】解:由题意得到:AD=BC,CD=AB,
∴四边形ABCD是平行四边形,
∴∠ADC=∠B=49°.
故选:B.
【点评】本题考查平行四边形的判定和性质,关键是掌握两组对边分别相等的四边形是平行四边形,平行四边形的对角相等.
4.(2025春 宿迁期中)汽车雨刮器是扫除车窗玻璃上妨碍视线的雨雪和尘土的重要工具,通常两个雨刮器的刷片长度相同,即AB=CD.某时刻汽车雨刮器的位置如图所示,此时∠ABE=∠C,则下列说法错误的是( )
A.四边形ABCD是平行四边形
B.∠A=∠D
C.AD=BC
D.AD∥BC
【考点】平行四边形的判定与性质.
【专题】多边形与平行四边形;推理能力.
【分析】先根据一组对边平行且相等的四边形是平行四边形可得:四边形ABCD是平行四边形,然后利用平行四边形的性质即可解答.
【解答】解:∵∠ABE=∠C,
∴AB∥CD,
又∵AB=CD,
∴四边形ABCD是平行四边形,
∴∠A+∠D=180°,AD=BC,AD∥BC,
故选项B错误,符合题意;
故选:B.
【点评】本题考查了平行四边形的判定与性质,熟练掌握平行四边形的判定与性质是解题的关键.
5.(2025春 西山区校级期中)下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,能判定四边形ABCD是平行四边形的是( )
A.1:2:3:4 B.2:3:2:3 C.2:3:3:2 D.1:2:2:3
【考点】平行四边形的判定.
【专题】多边形与平行四边形;推理能力.
【分析】两组对角分别相等的四边形是平行四边形,由此即可判断.
【解答】解:A、C、D中的条件不能推出四边形ABCD的两组对角分别相等,故A、C、D不符合题意;
B、由条件推出∠A=∠C,∠B=∠D,判定四边形ABCD是平行四边形,故B符合题意.
故选:B.
【点评】本题考查平行四边形的判定,关键是掌握两组对角分别相等的四边形是平行四边形.
6.(2025 三河市一模)如图,四边形ABCD为平行四边形,E为AB的中点.下列两个方案中,能得到以A,B,F,C为顶点的四边形为平行四边形的是( )
方案一 F为DA和CE的延长线上的交点 方案二 F为DC和AG的延长线上的交点
A.只有方案一 B.只有方案二
C.两个方案都不行 D.两个方案都行
【考点】平行四边形的判定与性质.
【专题】多边形与平行四边形;推理能力.
【分析】方案一证明△AFE≌△BCE(AAS)可得AF=BC,AF∥BC,即可判断四边形ABFC是平行四边形;方案二通过证明△ABI≌△FCI(AAS)可得AB=CF,AB∥CF,即可判断四边形ABFC是平行四边形,从而可得结论.
【解答】解:方案一:由题意可得:AD∥BC,AE=BE,
∴∠FAE=∠CBE,∠AFE=∠BCE,
在△AFE和△BCE中,
,
∴△AFE≌△BCE(AAS),
∴AF=BC,
又AF∥BC,
∴四边形ABFC是平行四边形,
方案二:由题意可得:
∴AB∥CD,AC,BD互相平分于点H,如图,
又E为AB的中点,
∴G为△ABC的重心,
∴AI为BC边上的中线,I为BC边的中点,
∵AB∥CF,
∴∠BAI=∠CFI,∠ABI=∠FCI,
又BI=CI,
∴△ABI≌△FCI(AAS),
∴AB=CF,
又AB∥CF,
∴四边形ABFC是平行四边形,
综上,方案一和方案二都正确,
故选:D.
【点评】本题主要考查平行四边形的判定和全等三角形的判定与性质,正确记忆相关知识点是解题关键.
7.(2025 广东一模)如图,将两张对边平行的纸片随意交叉叠放在一起,转动其中一张,使重合部分构成一个四边形,则下列结论中不一定成立的是( )
A.AB=CD B.AD∥BC C.AB=BC D.∠ABC=∠ADC
【考点】平行四边形的判定与性质.
【专题】多边形与平行四边形;几何直观;推理能力.
【分析】根据题意证得四边形ABCD是平行四边形,再逐项判断即可.
【解答】解:∵将两张对边平行的纸片随意交叉叠放在一起,
∴AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形.
∴AB=CD,∠ABC=∠ADC,
∴A、B、D一定成立,不符合题意;
∴AB不一定等于BC,与两张纸片的宽度有关,
故C不一定成立,符合题意;
故选:C.
【点评】本题考查平行四边形的判定和性质,掌握平行四边形的判定方法和其性质是解答本题的关键.
二.填空题(共5小题)
8.(2025春 瑞安市期中)如图,已知AB=CD,那么添加一个条件 AB∥CD(答案不唯一) 后,可判定四边形ABCD是平行四边形.
【考点】平行四边形的判定.
【专题】多边形与平行四边形;推理能力.
【分析】由平行四边形的判定方法即可得出结论.
【解答】解:添加条件为:AB∥CD,理由如下:
∵AB=CD,AB∥CD,
∴四边形ABCD是平行四边形,
故答案为:AB∥CD(答案不唯一).
【点评】本题考查了平行四边形的判定,熟练掌握平行四边形的判定方法是解题的关键.
9.(2025春 徐州期中)如图,点D是直线l外一点,在l上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形.依据是 两组对边分别相等 的四边形是平行四边形.
【考点】平行四边形的判定.
【专题】多边形与平行四边形;推理能力.
【分析】根据两组对边分别相等的四边形是平行四边形进行判定即可.
【解答】解:由作图可知,BC=AD,CD=AB,
∴四边形ABCD是平行四边形,
依据是:两组对边分别相等的四边形是平行四边形,
故答案为:两组对边分别相等.
【点评】本题考查了平行四边形的判定,熟记两组对边分别相等的四边形为平行四边形是解题的关键.
10.(2025春 长沙期中)如图,在四边形ABCD中,AB=CD,AD=BC,∠A+∠C=100°,则∠B= 130 °.
【考点】平行四边形的判定与性质.
【专题】多边形与平行四边形;运算能力;推理能力.
【分析】由平行四边形的性质等∠C=∠A,AD∥BC,得∠A+∠B=180°,再求出∠A=50°,即可解决问题.
【解答】解:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴∠C=∠A,AD∥BC,
∴∠A+∠B=180°,
∵∠A+∠C=100°,
∴∠A=50°,
∴∠B=180°﹣50°=130°,
故答案为:130.
【点评】本题考查了平行四边形的判定与性质,熟练掌握平行四边形的判定与性质是解题的关键.
11.(2024秋 莱芜区期末)如图,在 ABCD中,已知AD=15cm,点P在AD上以1cm/s的速度从点A向点D运动,点Q在CB上以4cm/s的速度从点C出发在CB上往返运动.两点同时出发,当点Q第一次返回C点时点P也停止运动,设运动时间为t(s)(t>0).当t= 3或5 时,四边形PDCQ是平行四边形.
【考点】平行四边形的判定与性质.
【专题】分类讨论;多边形与平行四边形;推理能力.
【分析】根据平行四边形的性质得出DP=CQ,分情况讨论,再列出方程,求出方程的解即可.
【解答】解:设经过t秒,四边形PDCQ是平行四边形,
∵P在AD上运动,
∴t7.5,即0<t≤7.5,
∵四边形PDCQ是平行四边形,
∴DP=CQ,
分为以下情况:①点Q的运动路线是C﹣B,方程为4t=15﹣t,
解得t=3,
②点Q的运动路线是C﹣B﹣C,方程为15﹣415﹣t,
解得:t=5;
故答案为:3或5.
【点评】本题考查了平行四边形的判定与性质,能求出符合的所有情况是解此题的关键,用了分类讨论思想.
12.(2025春 西城区校级期中)如图,在四边形ABCD中,AD∥BC,对角线AC,BD交于点O,现有三个条件:①AD=BC;②OB=OD;③AB=CD.其中可以判定四边形ABCD是平行四边形的有 ①② (只写序号即可).
【考点】平行四边形的判定;全等三角形的判定与性质.
【专题】图形的全等;多边形与平行四边形;推理能力.
【分析】根据平行四边形的判定方法分别对各个条件进行判断即可.
【解答】解:①∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,故①符合题意;
②∵AD∥BC,
∴∠OBC=∠ODA,
又∵OB=OD,∠BOC=∠DOA,
∴△OBC≌△ODA(ASA),
∴OA=OC,
∴四边形ABCD是平行四边形,故②符合题意;
③由AD∥BC,AB=CD,不能判定四边形ABCD是平行四边形,故③不符合题意;
故答案为:①②.
【点评】本题考查了平行四边形的判定以及全等三角形的判定与性质等知识,熟练掌握平行四边形的判定方法是解题的关键.
三.解答题(共3小题)
13.(2025春 越秀区校级期中)已知:如图,在 ABCD中,点E、F在AC上,且AE=CF.
求证:四边形EBFD是平行四边形.
【考点】平行四边形的判定与性质.
【专题】多边形与平行四边形;几何直观;推理能力.
【分析】由平行四边形可知OB=OD,OA=OC,又AE=CF,所以OE=OF,然后依据对角线互相平分的四边形是平行四边形即可证明.
【解答】证明:∵四边形ABCD是平行四边形,AE=CF,
∴AO=CO,BO=DO,
∴AO﹣AE=CO﹣CF,
∴OE=OF.
∴四边形EBFD为平行四边形.
【点评】本题主要考查了平行四边形的判定与性质,解答本题的关键要明确:对角线互相平分的四边形是平行四边形.
14.(2025春 定海区期中)如图,在平行四边形ABCD中,E,F是直线BD上的两点,DE=BF.
(1)求证:四边形AECF是平行四边形;
(2)若AD⊥BD,AB=10,BC=6,且EF﹣AF=4,求DE的长.
【考点】平行四边形的判定与性质;平行线的判定与性质;全等三角形的判定与性质;勾股定理.
【专题】线段、角、相交线与平行线;图形的全等;等腰三角形与直角三角形;多边形与平行四边形.
【分析】(1)由平行四边形的性质得出AD∥BC,AD=BC,再证△ADE≌△CBF(SAS),得出AE=CF,∠AED=∠CFB,则AE∥CF,即可得出结论;
(2)由勾股定理得求出BD=8,设DE=BF=x,则EF=2x+8,DF=8+x,推出AF=2x+4,然后由勾股定理求出x=2,即可得出结果.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ADB=∠CBD,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS),
∴AE=CF,∠AED=∠CFB,
∴AE∥CF,
∴四边形AECF是平行四边形;
(2)解:∵四边形ABCD是平行四边形,
∴BC=AD=6,
在Rt△ADB中,由勾股定理得:BD8,
设DE=BF=x,
∴EF=2x+8,DF=8+x,
∵EF﹣AF=4,
∴AF=2x+4,
在Rt△ADF中,由勾股定理得:AF2=AD2+DF2,
即(2x+4)2=62+(8+x)2,
解得:x=2(负值已舍去),
∴DE的长为2.
【点评】本题考查了平行四边形的判定与性质、勾股定理以及全等三角形的判定与性质等知识,熟练掌握平行四边形的判定与性质是解题的关键.
15.(2025 防城港一模)如图,在△ABF中,AB=BF,BE⊥AF于点E,过点A作AD∥BF,连接DE并延长,交BF于点C.
(1)求证:AE=EF.
(2)连接AC,DF,求证:四边形ACFD是平行四边形.
【考点】平行四边形的判定;全等三角形的判定与性质;等腰三角形的性质.
【专题】图形的全等;矩形 菱形 正方形;推理能力.
【分析】(1)由等腰三角形的性质可求解;
(2)由AAS可证△ADE≌△FCE,可得AD=CF,即可求解.
【解答】证明:(1)∵AB=BF,BE⊥AF,
∴AE=EF;
(2)∵AD∥BF,
∴∠ADE=∠FCE,
在△ADE和△FCE中,
∴△ADE≌△FCE(AAS),
∴AD=CF.
∵AD∥BF,
∴四边形ACFD是平行四边形.
【点评】本题考查了平行四边形的判定,全等三角形的判定和性质,等腰三角形的性质,灵活运用这些性质解决问题是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
