【期末核心考点】平行四边形的性质(含解析)2024-2025学年八年级下册数学华东师大版
文档属性
| 名称 | 【期末核心考点】平行四边形的性质(含解析)2024-2025学年八年级下册数学华东师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 805.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-14 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末核心考点 平行四边形的性质
一.选择题(共7小题)
1.(2025 浙江模拟)如图,在 ABCD中,对角线AC,BD相交于点O,AC⊥BC.若BD=8,AO=2,则AB的长为( )
A. B.2 C. D.2
2.(2025春 北京校级期中)如图,平行四边形ABCD中,AD=7,AB=3,AE平分∠BAD交BC边于点E,则EC等于( )
A.1 B.2 C.3 D.4
3.(2024秋 任城区期末)如图,在平行四边形ABCD中,∠A+∠C=120°,则∠C的度数为( )
A.50° B.60° C.70° D.120°
4.(2025春 温州期中)如图,已知在 ABCD中,∠A+∠C=200°,则∠B的度数为( )
A.70° B.75° C.80° D.85°
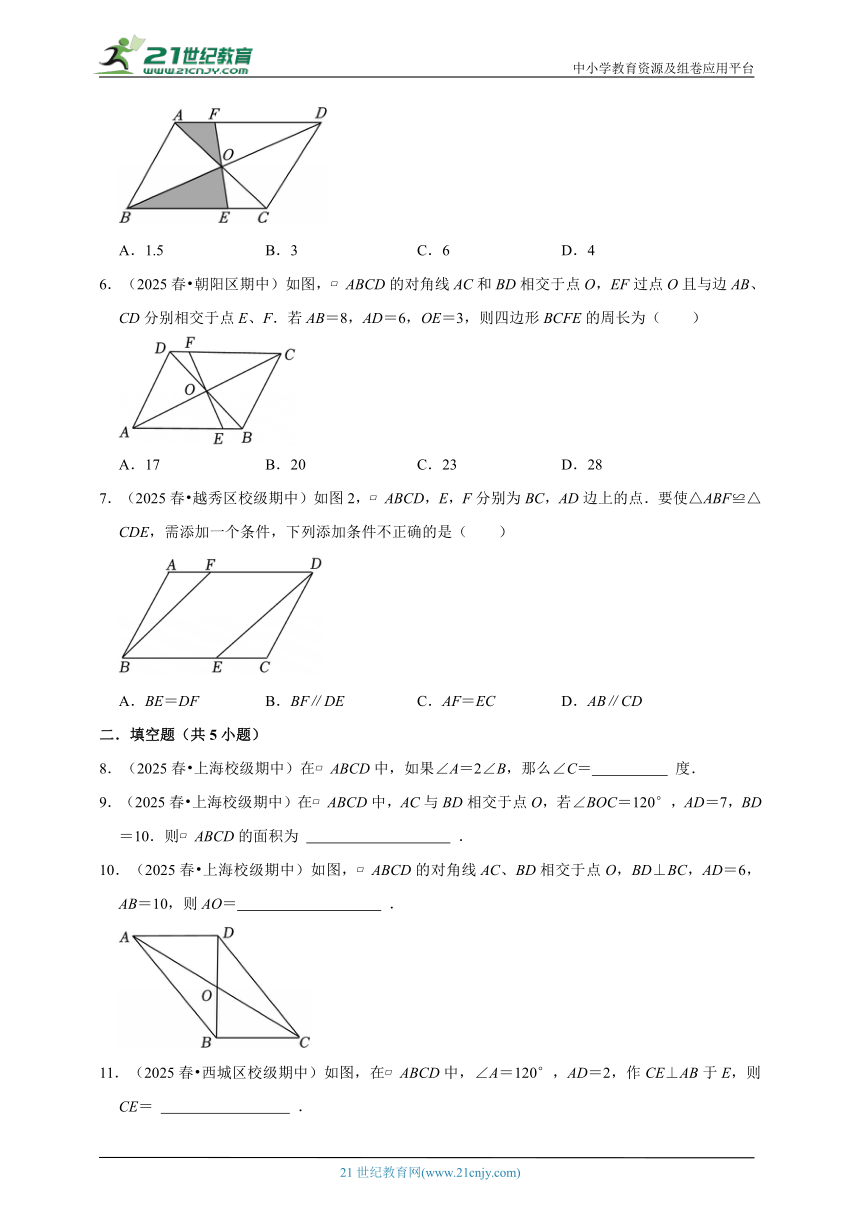
5.(2025 清城区校级模拟)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,EF过点O,交AD于点F,交BC于点E.若AB=3,AC=4,AD=5,则图中阴影部分的面积是( )
A.1.5 B.3 C.6 D.4
6.(2025春 朝阳区期中)如图, ABCD的对角线AC和BD相交于点O,EF过点O且与边AB、CD分别相交于点E、F.若AB=8,AD=6,OE=3,则四边形BCFE的周长为( )
A.17 B.20 C.23 D.28
7.(2025春 越秀区校级期中)如图2, ABCD,E,F分别为BC,AD边上的点.要使△ABF≌△CDE,需添加一个条件,下列添加条件不正确的是( )
A.BE=DF B.BF∥DE C.AF=EC D.AB∥CD
二.填空题(共5小题)
8.(2025春 上海校级期中)在 ABCD中,如果∠A=2∠B,那么∠C= 度.
9.(2025春 上海校级期中)在 ABCD中,AC与BD相交于点O,若∠BOC=120°,AD=7,BD=10.则 ABCD的面积为 .
10.(2025春 上海校级期中)如图, ABCD的对角线AC、BD相交于点O,BD⊥BC,AD=6,AB=10,则AO= .
11.(2025春 西城区校级期中)如图,在 ABCD中,∠A=120°,AD=2,作CE⊥AB于E,则CE= .
12.(2025春 姜堰区期中)如图,在 ABCD中,对角线AC,BD相交于点O,AB⊥AC,垂足为点A,EF过点O,交AD于点F,交BC于点E.若AB=6,BC=10,则图中阴影部分的面积是 .
三.解答题(共3小题)
13.(2025春 博罗县期中)如图,四边形ABCD是平行四边形,AC与BD相交于点O,已知AD=8,AB=10,BD=6.
(1)求OB、OA的长;
(2)求平行四边形ABCD的面积.
14.(2025春 天津校级期中)如图,BD为平行四边形ABCD的对角线,AE⊥BD,CF⊥BD,垂足分别为E、F.求证:BE=DF.
15.(2025春 江阴市校级月考)如图,点E是 ABCD的边CD的中点,连结AE并延长,交BC的延长线于点F.
(1)求证:BC=CF.
(2)若∠BAF=90°,AD=2,AE,求AB的长.
期末核心考点 平行四边形的性质
参考答案与试题解析
一.选择题(共7小题)
1.(2025 浙江模拟)如图,在 ABCD中,对角线AC,BD相交于点O,AC⊥BC.若BD=8,AO=2,则AB的长为( )
A. B.2 C. D.2
【考点】平行四边形的性质;勾股定理.
【专题】等腰三角形与直角三角形;多边形与平行四边形;运算能力.
【答案】B
【分析】根据题意得到,则AC=2OA=4,由勾股定理得,,由此即可求解.
【解答】解:∵四边形ABCD是平行四边形,
∴OB=ODBD8=4,OA=OC=2,则AC=2OA=2×2=4,
∵AC⊥BC,
∴,
∴,
故选:B.
【点评】本题考查了平行四边形的性质,勾股定理的运用,掌握平行四边形的性质是关键.
2.(2025春 北京校级期中)如图,平行四边形ABCD中,AD=7,AB=3,AE平分∠BAD交BC边于点E,则EC等于( )
A.1 B.2 C.3 D.4
【考点】平行四边形的性质;角平分线的定义.
【专题】多边形与平行四边形;几何直观;推理能力.
【答案】D
【分析】先根据平行四边形的性质得到AD∥BC,BC=AD=7,进一步证明∠BAE=∠BEA,得到BE=AB=3,则CE=BC﹣BE=4.
【解答】解:在平行四边形ABCD中,AD=7,AB=3,AE平分∠BAD交BC边于点E,
∴AD∥BC,BC=AD=7,∠BAE=∠DAE,
∴∠AEB=∠DAE,
∴∠BAE=∠BEA,
∴BE=AB=3,
∴CE=BC﹣BE=4,
故选:D.
【点评】本题主要考查了平行四边形的性质,角平分线的定义,证明∠BAE=∠BEA,得到BE=AB=3是解题的关键.
3.(2024秋 任城区期末)如图,在平行四边形ABCD中,∠A+∠C=120°,则∠C的度数为( )
A.50° B.60° C.70° D.120°
【考点】平行四边形的性质.
【专题】多边形与平行四边形;推理能力.
【答案】B
【分析】根据平行四边形的性质进行解答即可.
【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵∠A+∠C=120°,
∴∠C=60°,
故选:B.
【点评】此题主要考查了平行四边形的性质,关键是掌握:
(1)平行四边形的概念:有两组对边分别平行的四边形叫做平行四边形.
(2)平行四边形的性质:①边:平行四边形的对边相等. ②角:平行四边形的对角相等. ③对角线:平行四边形的对角线互相平分.
4.(2025春 温州期中)如图,已知在 ABCD中,∠A+∠C=200°,则∠B的度数为( )
A.70° B.75° C.80° D.85°
【考点】平行四边形的性质.
【专题】多边形与平行四边形;推理能力.
【答案】C
【分析】由四边形ABCD是平行四边形,可得∠A=∠C,AD∥BC,又由∠A+∠C=200°,即可求得∠A的度数,继而求得答案.
【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD∥BC,
∵∠A+∠C=200°,
∴∠A=100°,
∴∠B=180°﹣∠A=80°.
故选:C.
【点评】此题考查了平行四边形的性质,掌握平行四边形的对角相等、邻角互补是解题的关键.
5.(2025 清城区校级模拟)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,EF过点O,交AD于点F,交BC于点E.若AB=3,AC=4,AD=5,则图中阴影部分的面积是( )
A.1.5 B.3 C.6 D.4
【考点】平行四边形的性质;全等三角形的判定与性质;勾股定理的逆定理.
【专题】三角形;图形的全等;多边形与平行四边形;解直角三角形及其应用;运算能力;推理能力.
【答案】B
【分析】先利用勾股定理的逆定理求出△ABC是直角三角形,再利用AAS定理证出△COE≌△AOF,根据全等三角 形的性质可得S△COE=S△AOF,从而可得阴影部 分的面积等于S△BOC,然后根据平行四边形的性质求解即可得.
【解答】解:∵四边形ABCD是平行四边形,且AD=5,
∴BC=AD=5,AD∥BC,OC=OA,,
∵AB=3,AC=4,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,且∠BAC=90°,
∴ AC=6,
∴,
又∵AD∥BC,
∴∠OCE=∠OAF,∠OEC=∠OFA,
在△COE和△AOF中,
,
∴△COE≌△AOF(AAS),
∴S△COE=S△AOF,
则图中阴影部分的面积是=S△BOE+S△AOF=S△BOE+S△COE=S△BOC=3,
故选:B.
【点评】本题考查了勾股定理的逆定理、平行四边形的性质、三角形全等的判定与性质等知识点,熟练掌握平行四边形的性质是解题关键.
6.(2025春 朝阳区期中)如图, ABCD的对角线AC和BD相交于点O,EF过点O且与边AB、CD分别相交于点E、F.若AB=8,AD=6,OE=3,则四边形BCFE的周长为( )
A.17 B.20 C.23 D.28
【考点】平行四边形的性质;全等三角形的判定与性质.
【专题】图形的全等;多边形与平行四边形;推理能力.
【答案】B
【分析】由四边形ABCD是平行四边形,可得OA=OC,AB∥CD,则可证得△AOE≌△COF(ASA),继而证得OE=OF,进而可得EF=2OE,BE+CF=AB,继而求出四边形的周长.
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,OA=OC,BC=AD=6,
∴∠OCF=∠OAE,
在△AOE和△COF,
,
∴△AOE≌△COF(ASA),
∴AE=CF,OE=OF,
∴EF=2OE=2×3=6,
∴四边形BCFE的周长为:EF+CF+BC+BE=EF+BC+AE+BE=EF+BC+AB=6+6+8=20.
故选:B.
【点评】此题考查了平行四边形的性质以及全等三角形的判定与性质,判定△AOE与△COF全等是解此题的关键.
7.(2025春 越秀区校级期中)如图2, ABCD,E,F分别为BC,AD边上的点.要使△ABF≌△CDE,需添加一个条件,下列添加条件不正确的是( )
A.BE=DF B.BF∥DE C.AF=EC D.AB∥CD
【考点】平行四边形的性质;全等三角形的判定.
【专题】多边形与平行四边形;推理能力.
【答案】D
【分析】根据平行四边形的性质和全等三角形的判定推出即可.
【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,∠A=∠C,AD∥BC,AD=BC,
∴∠AFB=∠FBE,
添加BE=DF,∴AF=EC,利用SAS使△ABF≌△CDE,故A不符合题意;
添加BF∥DE,∴∠FBE=∠DEC,∴∠AFB=∠DEC,利用AAS使△ABF≌△CDE,故B不符合题意;
添加AF=EC,利用SAS使△ABF≌△CDE,故C不符合题意;
添加AB∥CD,不能使△ABF≌△CDE,故D符合题意;
故选:D.
【点评】此题考查平行四边形的性质,关键是根据平行四边形的性质和全等三角形的判定解答.
二.填空题(共5小题)
8.(2025春 上海校级期中)在 ABCD中,如果∠A=2∠B,那么∠C= 120 度.
【考点】平行四边形的性质.
【专题】多边形与平行四边形;推理能力.
【答案】120.
【分析】平行四边形中,利用邻角互补和∠A=2∠B求出∠B=60°,∠A=120°,利用对角相等,即可得∠C的值.
【解答】解:∵在 ABCD中,
∴∠A+∠B=180°,
如果∠A=2∠B,
∴2∠B+∠B=180°
解得∠B=60°,
∴∠A=2×60°=120°
∴∠C=∠A=120°,所以∠C的度数为120°.
故答案为:120.
【点评】本题考查了行四边形的性质,解题的关键是掌握平行四边形的邻角互补和对角相等结论.
9.(2025春 上海校级期中)在 ABCD中,AC与BD相交于点O,若∠BOC=120°,AD=7,BD=10.则 ABCD的面积为 .
【考点】平行四边形的性质;勾股定理.
【专题】等腰三角形与直角三角形;多边形与平行四边形;运算能力.
【答案】.
【分析】过点A作AE⊥BD于E,设OE=a,则OA=2a,,在直角三角形ADE中,利用勾股定理可得DE2+AE2=AD2,进而可求出a的值,由平行四边形的性质可知: ABCD的面积=2S△ABD,即可求解.
【解答】解:过点A作AE⊥BD于E,
∵四边形ABCD是平行四边形,
∴,
∵∠BOC=120°,
∴∠AOE=60°,
设OE=a,则OA=2a,,
∴DE=5+a,
在直角三角形ADE中,由勾股定理可得DE2+AE2=AD2,
∴,
解得:(负数已舍),
∴,
∴ ABCD的面积.
故答案为:.
【点评】本题考查了平行四边形的性质以及勾股定理,含30°角直角三角形的性质,解题关键是掌握数形结合思想与方程思想的应用.
10.(2025春 上海校级期中)如图, ABCD的对角线AC、BD相交于点O,BD⊥BC,AD=6,AB=10,则AO= .
【考点】平行四边形的性质;勾股定理.
【专题】等腰三角形与直角三角形;多边形与平行四边形;推理能力.
【答案】.
【分析】根据平行四边形的性质得:,再由BD⊥BC,得出BD⊥AD,结合勾股定理求出BD,再根据勾股定理求出AO.
【解答】解:∵四边形ABCD是平行四边形,
∴,
∵BD⊥BC,
∴BD⊥AD,
∵BD⊥BC,AD=6,AB=10,
∴,
∵四边形ABCD是平行四边形,
∴BO=DOBD8=4,
∴,即AO的长为.
故答案为:.
【点评】本题考查平行四边形的性质,勾股定理,属于基础题,关键是勾股定理的熟练掌握.
11.(2025春 西城区校级期中)如图,在 ABCD中,∠A=120°,AD=2,作CE⊥AB于E,则CE= .
【考点】平行四边形的性质.
【专题】等腰三角形与直角三角形;多边形与平行四边形;运算能力;推理能力.
【答案】.
【分析】由平行四边形的性质推出BC=AD=2,BC∥AD,由平行线的性质推出∠B+∠A=180°,求出∠B=60°,由直角三角形的性质得到∠BCE=30°,由含30度角的直角三角形的性质得到BEBC=1,由勾股定理求出CE.
【解答】解:∵四边形ABCD是平行四边形,
∴BC=AD=2,BC∥AD,
∴∠B+∠A=180°,
∵∠A=120°,
∴∠B=60°,
∵CE⊥AB,
∴∠BEC=90°,
∴∠BCE=90°﹣60°=30°,
∴BEBC=1,
∴CE.
故答案为:.
【点评】本题考查平行四边形的性质,含30度角的直角三角形,勾股定理,关键是由含30度角的直角三角形的性质得到BEBC.
12.(2025春 姜堰区期中)如图,在 ABCD中,对角线AC,BD相交于点O,AB⊥AC,垂足为点A,EF过点O,交AD于点F,交BC于点E.若AB=6,BC=10,则图中阴影部分的面积是 24 .
【考点】平行四边形的性质;全等三角形的判定与性质.
【专题】图形的全等;多边形与平行四边形;推理能力.
【答案】24.
【分析】由平行四边形的性质推出AO=CO,AD∥BC,AB∥CD,AB=CD,得到∠OAF=∠OCE,∠AFO=∠CEO,判定△AOF≌△COE(AAS),得到阴影部分的面积=△DBC的面积,由勾股定理求出AC=8,得到△ABC的面积AB AC=24,由△DBC的面积=△ABC的面积=24,即可得到图中阴影部分的面积.
【解答】解:∵四边形ABCD是平行四边形,
∴AO=CO,AD∥BC,AB∥CD,AB=CD,
∴∠OAF=∠OCE,∠AFO=∠CEO,
∴△AOF≌△COE(AAS),
∴△AOF的面积=△COE的面积,
∴阴影部分的面积=△DBC的面积,
∵AB⊥AC,
∴∠BAC=90°,
∵AB=6,BC=10,
∴AC8,
∴△ABC的面积AB AC6×8=24,
∵AB∥DC,AB=DC,
∴△DBC的面积=△ABC的面积=24.
∴图中阴影部分的面积=24.
故答案为:24.
【点评】本题考查平行四边形的性质,全等三角形的判定和性质,关键是由平行四边形的性质推出△AOF≌△COE(AAS),得到阴影部分的面积=△DBC的面积.
三.解答题(共3小题)
13.(2025春 博罗县期中)如图,四边形ABCD是平行四边形,AC与BD相交于点O,已知AD=8,AB=10,BD=6.
(1)求OB、OA的长;
(2)求平行四边形ABCD的面积.
【考点】平行四边形的性质;勾股定理的逆定理.
【专题】等腰三角形与直角三角形;多边形与平行四边形;运算能力;推理能力.
【答案】(1)OB=3,OA;
(2)48.
【分析】(1)由勾股定理的逆定理推出∠ADB=90°,由平行四边形的性质推出OB=ODBD=3,由勾股定理求出OA;
(2)由平行四边形的面积公式,即可求出平行四边形ABCD的面积.
【解答】解:(1)∵AD=8,AB=10,BD=6,
∴AD2+BD2=AB2,
∴∠ADB=90°,
∵四边形ABCD是平行四边形,
∴OB=ODBD=3,
∴OA;
(2)由(1)知AD⊥DB,
∴平行四边形ABCD的面积=AD DB=8×6=48.
【点评】本题考查平行四边形的性质,勾股定理的逆定理,关键是由勾股定理的逆定理推出∠ADB=90°,由平行四边形的性质推出OB=OD,掌握平行四边形的面积公式.
14.(2025春 天津校级期中)如图,BD为平行四边形ABCD的对角线,AE⊥BD,CF⊥BD,垂足分别为E、F.求证:BE=DF.
【考点】平行四边形的性质;全等三角形的判定与性质.
【专题】图形的全等;多边形与平行四边形;推理能力.
【答案】见解析.
【分析】由平行四边形的性质可知AB∥CD,AB=CD,即得出∠ABE=∠CDF.再根据AE⊥BD,CF⊥BD,即得出∠AEB=∠CFD=90°,从而可利用“AAS”证明△ABE≌△CDF,即证明出BE=DF.
【解答】证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠ABD=∠CDB,即∠ABE=∠CDF.
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS).
∴BE=DF.
【点评】本题主要考查平行四边形的性质,全等三角形的判定和性质.结合平行四边形的性质找出使三角形全等的条件是解题关键.
15.(2025春 江阴市校级月考)如图,点E是 ABCD的边CD的中点,连结AE并延长,交BC的延长线于点F.
(1)求证:BC=CF.
(2)若∠BAF=90°,AD=2,AE,求AB的长.
【考点】平行四边形的性质.
【专题】多边形与平行四边形;运算能力.
【答案】(1)证明见解析;
(2)AB=2.
【分析】(1)先证明△ADE≌△FCE,可得AE=EF,再由AB∥CD,可得,从而可得结论;
(2)先求解,BF=4,再利用勾股定理可得答案.
【解答】(1)证明:∵点E是平行四边形ABCD的边CD的中点,
∴AB∥CD,AD∥BC,AD=BC,CE=DE,
∴∠D=∠DCF,∠DAE=∠F,
∴△ADE≌△FCE,
∴AE=EF,
∵AB∥CD,
∴,
∴BC=CF;
(2)解:由(1)得:AE=EF,AD=BC=CF,
∴,AD=BC=CF=2,
∴,BF=4,
∵∠BAF=90°,
∴.
【点评】本题考查的是勾股定理的应用,全等三角形的判定与性质,平行四边形的性质,平行线分线段成比例,熟练的利用平行四边形的性质解题是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末核心考点 平行四边形的性质
一.选择题(共7小题)
1.(2025 浙江模拟)如图,在 ABCD中,对角线AC,BD相交于点O,AC⊥BC.若BD=8,AO=2,则AB的长为( )
A. B.2 C. D.2
2.(2025春 北京校级期中)如图,平行四边形ABCD中,AD=7,AB=3,AE平分∠BAD交BC边于点E,则EC等于( )
A.1 B.2 C.3 D.4
3.(2024秋 任城区期末)如图,在平行四边形ABCD中,∠A+∠C=120°,则∠C的度数为( )
A.50° B.60° C.70° D.120°
4.(2025春 温州期中)如图,已知在 ABCD中,∠A+∠C=200°,则∠B的度数为( )
A.70° B.75° C.80° D.85°
5.(2025 清城区校级模拟)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,EF过点O,交AD于点F,交BC于点E.若AB=3,AC=4,AD=5,则图中阴影部分的面积是( )
A.1.5 B.3 C.6 D.4
6.(2025春 朝阳区期中)如图, ABCD的对角线AC和BD相交于点O,EF过点O且与边AB、CD分别相交于点E、F.若AB=8,AD=6,OE=3,则四边形BCFE的周长为( )
A.17 B.20 C.23 D.28
7.(2025春 越秀区校级期中)如图2, ABCD,E,F分别为BC,AD边上的点.要使△ABF≌△CDE,需添加一个条件,下列添加条件不正确的是( )
A.BE=DF B.BF∥DE C.AF=EC D.AB∥CD
二.填空题(共5小题)
8.(2025春 上海校级期中)在 ABCD中,如果∠A=2∠B,那么∠C= 度.
9.(2025春 上海校级期中)在 ABCD中,AC与BD相交于点O,若∠BOC=120°,AD=7,BD=10.则 ABCD的面积为 .
10.(2025春 上海校级期中)如图, ABCD的对角线AC、BD相交于点O,BD⊥BC,AD=6,AB=10,则AO= .
11.(2025春 西城区校级期中)如图,在 ABCD中,∠A=120°,AD=2,作CE⊥AB于E,则CE= .
12.(2025春 姜堰区期中)如图,在 ABCD中,对角线AC,BD相交于点O,AB⊥AC,垂足为点A,EF过点O,交AD于点F,交BC于点E.若AB=6,BC=10,则图中阴影部分的面积是 .
三.解答题(共3小题)
13.(2025春 博罗县期中)如图,四边形ABCD是平行四边形,AC与BD相交于点O,已知AD=8,AB=10,BD=6.
(1)求OB、OA的长;
(2)求平行四边形ABCD的面积.
14.(2025春 天津校级期中)如图,BD为平行四边形ABCD的对角线,AE⊥BD,CF⊥BD,垂足分别为E、F.求证:BE=DF.
15.(2025春 江阴市校级月考)如图,点E是 ABCD的边CD的中点,连结AE并延长,交BC的延长线于点F.
(1)求证:BC=CF.
(2)若∠BAF=90°,AD=2,AE,求AB的长.
期末核心考点 平行四边形的性质
参考答案与试题解析
一.选择题(共7小题)
1.(2025 浙江模拟)如图,在 ABCD中,对角线AC,BD相交于点O,AC⊥BC.若BD=8,AO=2,则AB的长为( )
A. B.2 C. D.2
【考点】平行四边形的性质;勾股定理.
【专题】等腰三角形与直角三角形;多边形与平行四边形;运算能力.
【答案】B
【分析】根据题意得到,则AC=2OA=4,由勾股定理得,,由此即可求解.
【解答】解:∵四边形ABCD是平行四边形,
∴OB=ODBD8=4,OA=OC=2,则AC=2OA=2×2=4,
∵AC⊥BC,
∴,
∴,
故选:B.
【点评】本题考查了平行四边形的性质,勾股定理的运用,掌握平行四边形的性质是关键.
2.(2025春 北京校级期中)如图,平行四边形ABCD中,AD=7,AB=3,AE平分∠BAD交BC边于点E,则EC等于( )
A.1 B.2 C.3 D.4
【考点】平行四边形的性质;角平分线的定义.
【专题】多边形与平行四边形;几何直观;推理能力.
【答案】D
【分析】先根据平行四边形的性质得到AD∥BC,BC=AD=7,进一步证明∠BAE=∠BEA,得到BE=AB=3,则CE=BC﹣BE=4.
【解答】解:在平行四边形ABCD中,AD=7,AB=3,AE平分∠BAD交BC边于点E,
∴AD∥BC,BC=AD=7,∠BAE=∠DAE,
∴∠AEB=∠DAE,
∴∠BAE=∠BEA,
∴BE=AB=3,
∴CE=BC﹣BE=4,
故选:D.
【点评】本题主要考查了平行四边形的性质,角平分线的定义,证明∠BAE=∠BEA,得到BE=AB=3是解题的关键.
3.(2024秋 任城区期末)如图,在平行四边形ABCD中,∠A+∠C=120°,则∠C的度数为( )
A.50° B.60° C.70° D.120°
【考点】平行四边形的性质.
【专题】多边形与平行四边形;推理能力.
【答案】B
【分析】根据平行四边形的性质进行解答即可.
【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵∠A+∠C=120°,
∴∠C=60°,
故选:B.
【点评】此题主要考查了平行四边形的性质,关键是掌握:
(1)平行四边形的概念:有两组对边分别平行的四边形叫做平行四边形.
(2)平行四边形的性质:①边:平行四边形的对边相等. ②角:平行四边形的对角相等. ③对角线:平行四边形的对角线互相平分.
4.(2025春 温州期中)如图,已知在 ABCD中,∠A+∠C=200°,则∠B的度数为( )
A.70° B.75° C.80° D.85°
【考点】平行四边形的性质.
【专题】多边形与平行四边形;推理能力.
【答案】C
【分析】由四边形ABCD是平行四边形,可得∠A=∠C,AD∥BC,又由∠A+∠C=200°,即可求得∠A的度数,继而求得答案.
【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD∥BC,
∵∠A+∠C=200°,
∴∠A=100°,
∴∠B=180°﹣∠A=80°.
故选:C.
【点评】此题考查了平行四边形的性质,掌握平行四边形的对角相等、邻角互补是解题的关键.
5.(2025 清城区校级模拟)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,EF过点O,交AD于点F,交BC于点E.若AB=3,AC=4,AD=5,则图中阴影部分的面积是( )
A.1.5 B.3 C.6 D.4
【考点】平行四边形的性质;全等三角形的判定与性质;勾股定理的逆定理.
【专题】三角形;图形的全等;多边形与平行四边形;解直角三角形及其应用;运算能力;推理能力.
【答案】B
【分析】先利用勾股定理的逆定理求出△ABC是直角三角形,再利用AAS定理证出△COE≌△AOF,根据全等三角 形的性质可得S△COE=S△AOF,从而可得阴影部 分的面积等于S△BOC,然后根据平行四边形的性质求解即可得.
【解答】解:∵四边形ABCD是平行四边形,且AD=5,
∴BC=AD=5,AD∥BC,OC=OA,,
∵AB=3,AC=4,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,且∠BAC=90°,
∴ AC=6,
∴,
又∵AD∥BC,
∴∠OCE=∠OAF,∠OEC=∠OFA,
在△COE和△AOF中,
,
∴△COE≌△AOF(AAS),
∴S△COE=S△AOF,
则图中阴影部分的面积是=S△BOE+S△AOF=S△BOE+S△COE=S△BOC=3,
故选:B.
【点评】本题考查了勾股定理的逆定理、平行四边形的性质、三角形全等的判定与性质等知识点,熟练掌握平行四边形的性质是解题关键.
6.(2025春 朝阳区期中)如图, ABCD的对角线AC和BD相交于点O,EF过点O且与边AB、CD分别相交于点E、F.若AB=8,AD=6,OE=3,则四边形BCFE的周长为( )
A.17 B.20 C.23 D.28
【考点】平行四边形的性质;全等三角形的判定与性质.
【专题】图形的全等;多边形与平行四边形;推理能力.
【答案】B
【分析】由四边形ABCD是平行四边形,可得OA=OC,AB∥CD,则可证得△AOE≌△COF(ASA),继而证得OE=OF,进而可得EF=2OE,BE+CF=AB,继而求出四边形的周长.
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,OA=OC,BC=AD=6,
∴∠OCF=∠OAE,
在△AOE和△COF,
,
∴△AOE≌△COF(ASA),
∴AE=CF,OE=OF,
∴EF=2OE=2×3=6,
∴四边形BCFE的周长为:EF+CF+BC+BE=EF+BC+AE+BE=EF+BC+AB=6+6+8=20.
故选:B.
【点评】此题考查了平行四边形的性质以及全等三角形的判定与性质,判定△AOE与△COF全等是解此题的关键.
7.(2025春 越秀区校级期中)如图2, ABCD,E,F分别为BC,AD边上的点.要使△ABF≌△CDE,需添加一个条件,下列添加条件不正确的是( )
A.BE=DF B.BF∥DE C.AF=EC D.AB∥CD
【考点】平行四边形的性质;全等三角形的判定.
【专题】多边形与平行四边形;推理能力.
【答案】D
【分析】根据平行四边形的性质和全等三角形的判定推出即可.
【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,∠A=∠C,AD∥BC,AD=BC,
∴∠AFB=∠FBE,
添加BE=DF,∴AF=EC,利用SAS使△ABF≌△CDE,故A不符合题意;
添加BF∥DE,∴∠FBE=∠DEC,∴∠AFB=∠DEC,利用AAS使△ABF≌△CDE,故B不符合题意;
添加AF=EC,利用SAS使△ABF≌△CDE,故C不符合题意;
添加AB∥CD,不能使△ABF≌△CDE,故D符合题意;
故选:D.
【点评】此题考查平行四边形的性质,关键是根据平行四边形的性质和全等三角形的判定解答.
二.填空题(共5小题)
8.(2025春 上海校级期中)在 ABCD中,如果∠A=2∠B,那么∠C= 120 度.
【考点】平行四边形的性质.
【专题】多边形与平行四边形;推理能力.
【答案】120.
【分析】平行四边形中,利用邻角互补和∠A=2∠B求出∠B=60°,∠A=120°,利用对角相等,即可得∠C的值.
【解答】解:∵在 ABCD中,
∴∠A+∠B=180°,
如果∠A=2∠B,
∴2∠B+∠B=180°
解得∠B=60°,
∴∠A=2×60°=120°
∴∠C=∠A=120°,所以∠C的度数为120°.
故答案为:120.
【点评】本题考查了行四边形的性质,解题的关键是掌握平行四边形的邻角互补和对角相等结论.
9.(2025春 上海校级期中)在 ABCD中,AC与BD相交于点O,若∠BOC=120°,AD=7,BD=10.则 ABCD的面积为 .
【考点】平行四边形的性质;勾股定理.
【专题】等腰三角形与直角三角形;多边形与平行四边形;运算能力.
【答案】.
【分析】过点A作AE⊥BD于E,设OE=a,则OA=2a,,在直角三角形ADE中,利用勾股定理可得DE2+AE2=AD2,进而可求出a的值,由平行四边形的性质可知: ABCD的面积=2S△ABD,即可求解.
【解答】解:过点A作AE⊥BD于E,
∵四边形ABCD是平行四边形,
∴,
∵∠BOC=120°,
∴∠AOE=60°,
设OE=a,则OA=2a,,
∴DE=5+a,
在直角三角形ADE中,由勾股定理可得DE2+AE2=AD2,
∴,
解得:(负数已舍),
∴,
∴ ABCD的面积.
故答案为:.
【点评】本题考查了平行四边形的性质以及勾股定理,含30°角直角三角形的性质,解题关键是掌握数形结合思想与方程思想的应用.
10.(2025春 上海校级期中)如图, ABCD的对角线AC、BD相交于点O,BD⊥BC,AD=6,AB=10,则AO= .
【考点】平行四边形的性质;勾股定理.
【专题】等腰三角形与直角三角形;多边形与平行四边形;推理能力.
【答案】.
【分析】根据平行四边形的性质得:,再由BD⊥BC,得出BD⊥AD,结合勾股定理求出BD,再根据勾股定理求出AO.
【解答】解:∵四边形ABCD是平行四边形,
∴,
∵BD⊥BC,
∴BD⊥AD,
∵BD⊥BC,AD=6,AB=10,
∴,
∵四边形ABCD是平行四边形,
∴BO=DOBD8=4,
∴,即AO的长为.
故答案为:.
【点评】本题考查平行四边形的性质,勾股定理,属于基础题,关键是勾股定理的熟练掌握.
11.(2025春 西城区校级期中)如图,在 ABCD中,∠A=120°,AD=2,作CE⊥AB于E,则CE= .
【考点】平行四边形的性质.
【专题】等腰三角形与直角三角形;多边形与平行四边形;运算能力;推理能力.
【答案】.
【分析】由平行四边形的性质推出BC=AD=2,BC∥AD,由平行线的性质推出∠B+∠A=180°,求出∠B=60°,由直角三角形的性质得到∠BCE=30°,由含30度角的直角三角形的性质得到BEBC=1,由勾股定理求出CE.
【解答】解:∵四边形ABCD是平行四边形,
∴BC=AD=2,BC∥AD,
∴∠B+∠A=180°,
∵∠A=120°,
∴∠B=60°,
∵CE⊥AB,
∴∠BEC=90°,
∴∠BCE=90°﹣60°=30°,
∴BEBC=1,
∴CE.
故答案为:.
【点评】本题考查平行四边形的性质,含30度角的直角三角形,勾股定理,关键是由含30度角的直角三角形的性质得到BEBC.
12.(2025春 姜堰区期中)如图,在 ABCD中,对角线AC,BD相交于点O,AB⊥AC,垂足为点A,EF过点O,交AD于点F,交BC于点E.若AB=6,BC=10,则图中阴影部分的面积是 24 .
【考点】平行四边形的性质;全等三角形的判定与性质.
【专题】图形的全等;多边形与平行四边形;推理能力.
【答案】24.
【分析】由平行四边形的性质推出AO=CO,AD∥BC,AB∥CD,AB=CD,得到∠OAF=∠OCE,∠AFO=∠CEO,判定△AOF≌△COE(AAS),得到阴影部分的面积=△DBC的面积,由勾股定理求出AC=8,得到△ABC的面积AB AC=24,由△DBC的面积=△ABC的面积=24,即可得到图中阴影部分的面积.
【解答】解:∵四边形ABCD是平行四边形,
∴AO=CO,AD∥BC,AB∥CD,AB=CD,
∴∠OAF=∠OCE,∠AFO=∠CEO,
∴△AOF≌△COE(AAS),
∴△AOF的面积=△COE的面积,
∴阴影部分的面积=△DBC的面积,
∵AB⊥AC,
∴∠BAC=90°,
∵AB=6,BC=10,
∴AC8,
∴△ABC的面积AB AC6×8=24,
∵AB∥DC,AB=DC,
∴△DBC的面积=△ABC的面积=24.
∴图中阴影部分的面积=24.
故答案为:24.
【点评】本题考查平行四边形的性质,全等三角形的判定和性质,关键是由平行四边形的性质推出△AOF≌△COE(AAS),得到阴影部分的面积=△DBC的面积.
三.解答题(共3小题)
13.(2025春 博罗县期中)如图,四边形ABCD是平行四边形,AC与BD相交于点O,已知AD=8,AB=10,BD=6.
(1)求OB、OA的长;
(2)求平行四边形ABCD的面积.
【考点】平行四边形的性质;勾股定理的逆定理.
【专题】等腰三角形与直角三角形;多边形与平行四边形;运算能力;推理能力.
【答案】(1)OB=3,OA;
(2)48.
【分析】(1)由勾股定理的逆定理推出∠ADB=90°,由平行四边形的性质推出OB=ODBD=3,由勾股定理求出OA;
(2)由平行四边形的面积公式,即可求出平行四边形ABCD的面积.
【解答】解:(1)∵AD=8,AB=10,BD=6,
∴AD2+BD2=AB2,
∴∠ADB=90°,
∵四边形ABCD是平行四边形,
∴OB=ODBD=3,
∴OA;
(2)由(1)知AD⊥DB,
∴平行四边形ABCD的面积=AD DB=8×6=48.
【点评】本题考查平行四边形的性质,勾股定理的逆定理,关键是由勾股定理的逆定理推出∠ADB=90°,由平行四边形的性质推出OB=OD,掌握平行四边形的面积公式.
14.(2025春 天津校级期中)如图,BD为平行四边形ABCD的对角线,AE⊥BD,CF⊥BD,垂足分别为E、F.求证:BE=DF.
【考点】平行四边形的性质;全等三角形的判定与性质.
【专题】图形的全等;多边形与平行四边形;推理能力.
【答案】见解析.
【分析】由平行四边形的性质可知AB∥CD,AB=CD,即得出∠ABE=∠CDF.再根据AE⊥BD,CF⊥BD,即得出∠AEB=∠CFD=90°,从而可利用“AAS”证明△ABE≌△CDF,即证明出BE=DF.
【解答】证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠ABD=∠CDB,即∠ABE=∠CDF.
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS).
∴BE=DF.
【点评】本题主要考查平行四边形的性质,全等三角形的判定和性质.结合平行四边形的性质找出使三角形全等的条件是解题关键.
15.(2025春 江阴市校级月考)如图,点E是 ABCD的边CD的中点,连结AE并延长,交BC的延长线于点F.
(1)求证:BC=CF.
(2)若∠BAF=90°,AD=2,AE,求AB的长.
【考点】平行四边形的性质.
【专题】多边形与平行四边形;运算能力.
【答案】(1)证明见解析;
(2)AB=2.
【分析】(1)先证明△ADE≌△FCE,可得AE=EF,再由AB∥CD,可得,从而可得结论;
(2)先求解,BF=4,再利用勾股定理可得答案.
【解答】(1)证明:∵点E是平行四边形ABCD的边CD的中点,
∴AB∥CD,AD∥BC,AD=BC,CE=DE,
∴∠D=∠DCF,∠DAE=∠F,
∴△ADE≌△FCE,
∴AE=EF,
∵AB∥CD,
∴,
∴BC=CF;
(2)解:由(1)得:AE=EF,AD=BC=CF,
∴,AD=BC=CF=2,
∴,BF=4,
∵∠BAF=90°,
∴.
【点评】本题考查的是勾股定理的应用,全等三角形的判定与性质,平行四边形的性质,平行线分线段成比例,熟练的利用平行四边形的性质解题是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
