【期末核心考点】数据的集中趋势(含解析)2024-2025学年八年级下册数学华东师大版
文档属性
| 名称 | 【期末核心考点】数据的集中趋势(含解析)2024-2025学年八年级下册数学华东师大版 |
|
|
| 格式 | docx | ||
| 文件大小 | 928.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-14 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末核心考点 数据的集中趋势
一.选择题(共7小题)
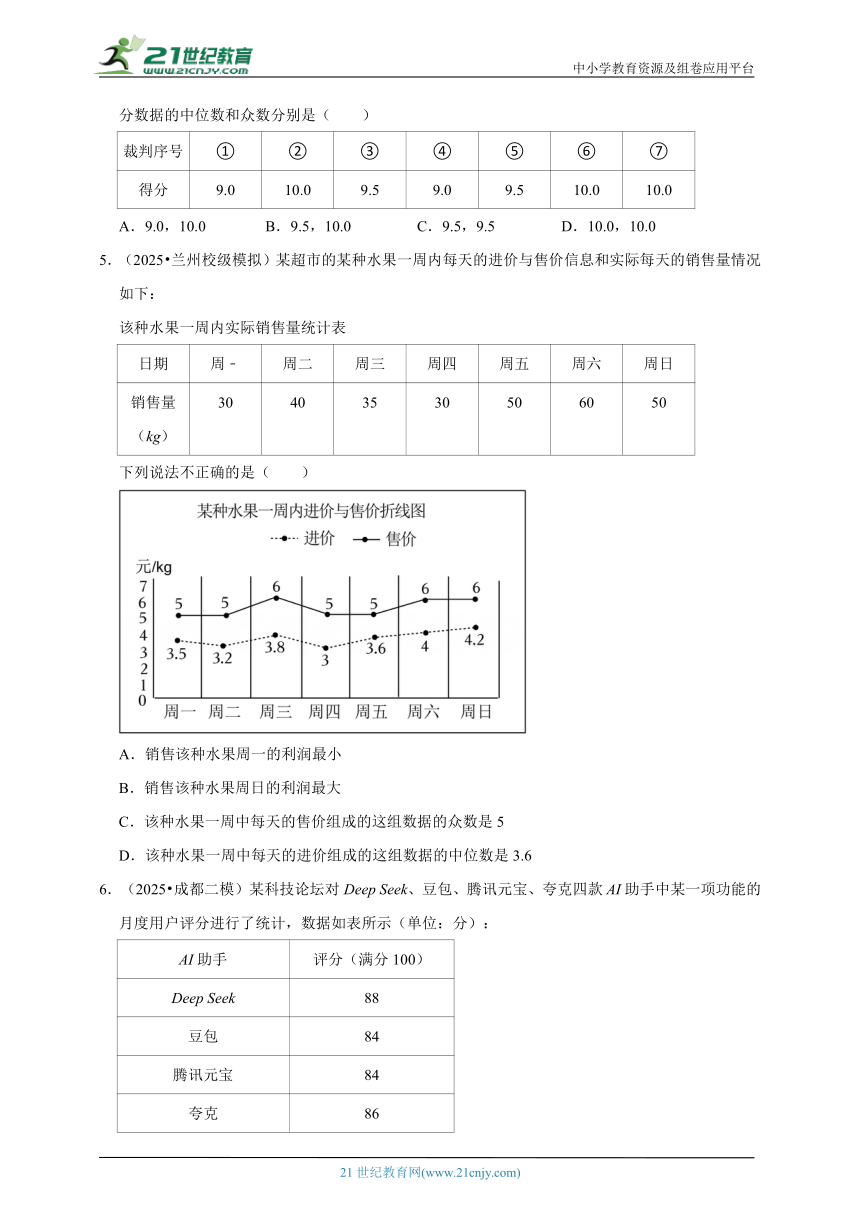
1.(2025 永春县模拟)保险公司汽车保险中,继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数有关,该公司随机调查了该险种的300名续保人在一年内的出险情况,得到如下统计图:则出险次数的中位数为( )
A.1 B.2 C.3 D.4
2.(2025 西山区校级模拟)“樱云织诗笺 少年拾春行”,2025年3月,昆明市第三中学举办“樱”为有你春日校园创意文化活动.小明随机调查了学校30名初中同学制作书笺的数量,数据如表所示:
人数 7 8 10 5
书笺数量(张) 1 2 4 5
则制作书笺数量的中位数和众数分别是( )
A.4,10 B.2,4 C.4,4 D.3,4
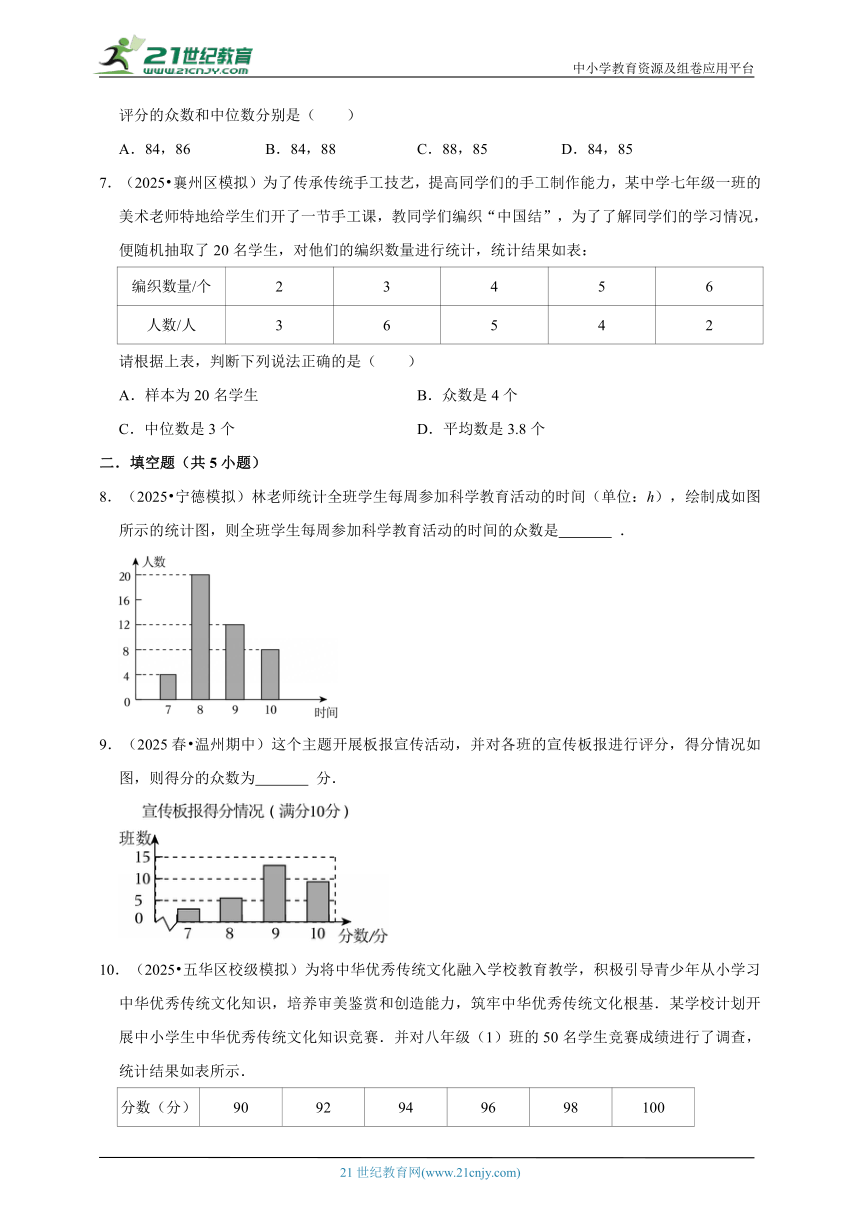
3.(2025 乌鲁木齐模拟)小明调查了班里40名同学一周的体育锻炼情况,结果如图所示.该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A.16小时、15小时 B.8小时、9小时
C.10小时、8.5小时 D.8小时、8.5小时
4.(2025 官渡区一模)2025年4月6日中国跳水队员陈芋汐以419.35分的成绩夺得跳水世界杯女子10米台冠军.她在第二跳中展现极高水准,如表为第二跳七位裁判给出的评分情况,则这组得分数据的中位数和众数分别是( )
裁判序号 ① ② ③ ④ ⑤ ⑥ ⑦
得分 9.0 10.0 9.5 9.0 9.5 10.0 10.0
A.9.0,10.0 B.9.5,10.0 C.9.5,9.5 D.10.0,10.0
5.(2025 兰州校级模拟)某超市的某种水果一周内每天的进价与售价信息和实际每天的销售量情况如下:
该种水果一周内实际销售量统计表
日期 周﹣ 周二 周三 周四 周五 周六 周日
销售量(kg) 30 40 35 30 50 60 50
下列说法不正确的是( )
A.销售该种水果周一的利润最小
B.销售该种水果周日的利润最大
C.该种水果一周中每天的售价组成的这组数据的众数是5
D.该种水果一周中每天的进价组成的这组数据的中位数是3.6
6.(2025 成都二模)某科技论坛对Deep Seek、豆包、腾讯元宝、夸克四款AI助手中某一项功能的月度用户评分进行了统计,数据如表所示(单位:分):
AI助手 评分(满分100)
Deep Seek 88
豆包 84
腾讯元宝 84
夸克 86
评分的众数和中位数分别是( )
A.84,86 B.84,88 C.88,85 D.84,85
7.(2025 襄州区模拟)为了传承传统手工技艺,提高同学们的手工制作能力,某中学七年级一班的美术老师特地给学生们开了一节手工课,教同学们编织“中国结”,为了了解同学们的学习情况,便随机抽取了20名学生,对他们的编织数量进行统计,统计结果如表:
编织数量/个 2 3 4 5 6
人数/人 3 6 5 4 2
请根据上表,判断下列说法正确的是( )
A.样本为20名学生 B.众数是4个
C.中位数是3个 D.平均数是3.8个
二.填空题(共5小题)
8.(2025 宁德模拟)林老师统计全班学生每周参加科学教育活动的时间(单位:h),绘制成如图所示的统计图,则全班学生每周参加科学教育活动的时间的众数是 .
9.(2025春 温州期中)这个主题开展板报宣传活动,并对各班的宣传板报进行评分,得分情况如图,则得分的众数为 分.
10.(2025 五华区校级模拟)为将中华优秀传统文化融入学校教育教学,积极引导青少年从小学习中华优秀传统文化知识,培养审美鉴赏和创造能力,筑牢中华优秀传统文化根基.某学校计划开展中小学生中华优秀传统文化知识竞赛.并对八年级(1)班的50名学生竞赛成绩进行了调查,统计结果如表所示.
分数(分) 90 92 94 96 98 100
人数(人) 4 10 11 13 9 3
在本次调查中,八年级(1)班这50名学生竞赛成绩的中位数是 分.
11.(2025 汕尾模拟)2024年12月17日,农业农村部农产品质量安全中心公示了“2024年第三批全国名特优新农产品名录”,汕尾市4个农产品入选,分别是凤山红灯笼荔枝、华侨红杨桃、陆河油柑和陆丰莲藕.“凤山红灯笼”是汕尾的名优荔枝,是糯米糍与怀枝自然杂交的优良品种.现抽查出7个单果,质量(单位:克)分别为27,24,28,27,26,25,25.这些数据的中位数是 .
12.(2025春 浙江期中)已知一组数据:4,5,a,6,7的平均数为6,则这组数据的中位数是 .
三.解答题(共3小题)
13.(2025 沙坪坝区校级一模)为加快智慧校园建设,学校举行了趣味数学答题机解题比赛,现从七、八年级参加比赛的学生中各随机抽取20名同学的成绩进行收集、整理、描述、分析.成绩共分为四组(成绩用x表示:A.x≤70;B.70<x≤80;C.80<x≤90:D.90<x≤100:单位:分)
七年级20名同学的成绩为:62,63,65,66,72,72,75,76,82,83,85,87,88,88,88,89,92,96,97,99.
八年级20名同学成绩在C组的数据是:83,84,84,84,85,87,88.
七、八年级所抽学生比赛成绩统计表
年级 平均数 中位数 众数
七年级 81.25 84.5 b
八年级 81.25 a 84
根据以上信息,解答下列问题:
(1)上述图表中a= ,b= ,m= ;
(2)根据以上数据分析,你认为该校七、八年级中哪个年级学生解题比赛的成绩较好?请说明理由(写出一条理由即可);
(3)该校七年级有1200名学生、八年级有1100名同学参加了此次趣味数学答题机解题比赛,估计该校七、八年级参加解题比赛的成绩为优秀(x>90)的学生人数一共是多少?
14.(2025 新兴县一模)为了深入学习贯彻党的二十届三中全会精神,某校举行了“学三中全会精神,做新时代好少年”为主题的知识竞赛.现从八、九年级学生中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩用x表示,共分成四组:A.80<x≤85;B.85<x≤90;C.90<x≤95;D.95<x≤100),现在给出了部分信息如下:
八年级10名学生的竞赛成绩在C组中的数据:93,94,95.
九年级10名学生的竞赛成绩:81,83,85,89,90,95,99,99,99,100.
抽取的八、九年级学生竞赛成绩统计表
年级 八年级 九年级
平均数 92 92
中位数 b 92.5
众数 100 c
根据以上信息,解答下列问题.
(1)填空:a= ,b= ,c= .
(2)根据以上数据,你认为该校八、九年级中抽取的哪个年级的学生对三中全会知识的掌握程度更好?请说明理由.(写出一条即可)
(3)若该校八、九年级各有300名学生参加了此次竞赛,请估计该校参加此次竞赛成绩(x>95)为优秀的学生总人数.
15.(2025 文成县二模)九年级(1)(2)两个班各40人参加垃圾分类知识竞赛,规则如图.已知比赛中,所有同学均按要求一对一连线,无多连、少连.两个班的得分信息如表:
九(1)班成绩统计表
得分 0 5 10 15 20
人数 2 4 a b c
九(2)班成绩统计表
平均分 中位数 众数 满分率
14.25 10 10 45%
(1)分数10,15,20中,每人得分不可能是 分.
(2)已知九(1)班成绩的中位数是15分,求a和c的值.
(3)在(2)的情况下,你认为哪个班级成绩更优秀?请从平均分、中位数、众数和满分率四个方面作出评价.
期末核心考点 数据的集中趋势
参考答案与试题解析
一.选择题(共7小题)
1.(2025 永春县模拟)保险公司汽车保险中,继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数有关,该公司随机调查了该险种的300名续保人在一年内的出险情况,得到如下统计图:则出险次数的中位数为( )
A.1 B.2 C.3 D.4
【考点】中位数;频数(率)分布直方图.
【专题】统计的应用;应用意识.
【答案】A
【分析】根据中位数的定义进行计算即可.
【解答】解:将数据按从小到大排列后,
位于第150和第151的两个数为:1,1.
中位数为:1.
故选:A.
【点评】本题考查了中位数,解题的关键是根据中位数的意义来解答.
2.(2025 西山区校级模拟)“樱云织诗笺 少年拾春行”,2025年3月,昆明市第三中学举办“樱”为有你春日校园创意文化活动.小明随机调查了学校30名初中同学制作书笺的数量,数据如表所示:
人数 7 8 10 5
书笺数量(张) 1 2 4 5
则制作书笺数量的中位数和众数分别是( )
A.4,10 B.2,4 C.4,4 D.3,4
【考点】众数;中位数.
【专题】数据的收集与整理;数据分析观念.
【答案】D
【分析】根据中位数:“将数据按照顺序排列后,中间一位或中间两位的平均数即为中位数”,众数:“出现次数最多的数据”,进行判断即可.
【解答】解:数据排序后,第15个和第16个数据为2和4,
∴中位数为(2+4)÷2=3,
∵4出现的次数最多,
∴众数为4.
故选:D.
【点评】本题考查中位数和众数,熟练掌握中位数和众数的定义是解答本题的关键.
3.(2025 乌鲁木齐模拟)小明调查了班里40名同学一周的体育锻炼情况,结果如图所示.该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A.16小时、15小时 B.8小时、9小时
C.10小时、8.5小时 D.8小时、8.5小时
【考点】众数;中位数.
【专题】统计的应用;运算能力.
【答案】B
【分析】根据众数、中位数的概念即可求出答案.
【解答】解:众数是一组数据中出现次数最多的数,即8;
而将这组数据从小到大的顺序排列后,处于20,21两个数的平均数,由中位数的定义可知,这组数据的中位数是9.
故选:B.
【点评】本题考查了中位数、众数的概念,本题为统计题,考查众数与中位数的意义,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会错误地将这组数据最中间的那个数当作中位数.
4.(2025 官渡区一模)2025年4月6日中国跳水队员陈芋汐以419.35分的成绩夺得跳水世界杯女子10米台冠军.她在第二跳中展现极高水准,如表为第二跳七位裁判给出的评分情况,则这组得分数据的中位数和众数分别是( )
裁判序号 ① ② ③ ④ ⑤ ⑥ ⑦
得分 9.0 10.0 9.5 9.0 9.5 10.0 10.0
A.9.0,10.0 B.9.5,10.0 C.9.5,9.5 D.10.0,10.0
【考点】众数;中位数.
【专题】统计的应用;数据分析观念.
【答案】B
【分析】将题目中的数据,按照从小到大排列,即可得到这组数据的众数和中位数.
【解答】解:按照从小到大排列是:9.0,9.0,9.5,9.5,10.0,10.0,10.0,
根据众数、中位数的定义可得:这组数据的众数是10.0,中位数是9.5,
故选:B.
【点评】本题考查众数、中位数,解答本题的关键是明确众数和中位数的含义,找出相应的众数和中位数.
5.(2025 兰州校级模拟)某超市的某种水果一周内每天的进价与售价信息和实际每天的销售量情况如下:
该种水果一周内实际销售量统计表
日期 周﹣ 周二 周三 周四 周五 周六 周日
销售量(kg) 30 40 35 30 50 60 50
下列说法不正确的是( )
A.销售该种水果周一的利润最小
B.销售该种水果周日的利润最大
C.该种水果一周中每天的售价组成的这组数据的众数是5
D.该种水果一周中每天的进价组成的这组数据的中位数是3.6
【考点】众数;中位数.
【专题】统计的应用;数据分析观念.
【答案】B
【分析】根据折线图得出信息进行判断即可.
【解答】解:该商品周一的利润为45元,周二的利润为72元,周三的利润为77元,周四的利润为60元,周五的利润为70元,周六的利润为120元,周日的利润为90元,
A.该商品周一的利润45元,最小,原说法正确,不符合题意;
B.该商品周六的利润120元,最大,原说法错误,符合题意;
C.一周中该商品每天售价组成的这组数据的众数是5,原说法正确,不符合题意;
D.一周中的该商品每天进价组成的这组数据的中位数是3.6,原说法正确,不符合题意.
故选:B.
【点评】此题考查折线统计图,关键是根据折线图得出信息进行解答.
6.(2025 成都二模)某科技论坛对Deep Seek、豆包、腾讯元宝、夸克四款AI助手中某一项功能的月度用户评分进行了统计,数据如表所示(单位:分):
AI助手 评分(满分100)
Deep Seek 88
豆包 84
腾讯元宝 84
夸克 86
评分的众数和中位数分别是( )
A.84,86 B.84,88 C.88,85 D.84,85
【考点】众数;中位数.
【专题】统计的应用;运算能力.
【答案】D
【分析】将题目中4个数据按照从小到大的顺序排列,即可得到这组数据的众数与中位数.
【解答】解:数据按照从小到大排列是:84,84,86,88,
84出现次数最多,
故众数是84,中位数是,
故选:D.
【点评】本题考查众数和中位数,掌握众数和中位数,会求众数与中位数,特别注意中位数除排序外还要根据数据的个数是奇与偶来计算是关键.
7.(2025 襄州区模拟)为了传承传统手工技艺,提高同学们的手工制作能力,某中学七年级一班的美术老师特地给学生们开了一节手工课,教同学们编织“中国结”,为了了解同学们的学习情况,便随机抽取了20名学生,对他们的编织数量进行统计,统计结果如表:
编织数量/个 2 3 4 5 6
人数/人 3 6 5 4 2
请根据上表,判断下列说法正确的是( )
A.样本为20名学生 B.众数是4个
C.中位数是3个 D.平均数是3.8个
【考点】众数;加权平均数;中位数.
【专题】数据的收集与整理;数据分析观念.
【答案】D
【分析】根据样本的概念、众数、中位数及加权平均数的定义分别求解即可.
【解答】解:A.样本为20名学生的编织数量,此选项错误,不符合题意;
B.众数是3,此选项错误,不符合题意;
C.共20个数据,从小到大排列后位于第10个和第11个的数据分别是4和4,
∴中位数为4,此选项错误,不符合题意;
D.平均数为(2×3+3×6+4×5+5×4+6×2)=3.8(个),此选项正确,符合题意;
故选:D.
【点评】本题主要考查众数、中位数、加权平均数,解题的关键是掌握众数、中位数及加权平均数的定义.
二.填空题(共5小题)
8.(2025 宁德模拟)林老师统计全班学生每周参加科学教育活动的时间(单位:h),绘制成如图所示的统计图,则全班学生每周参加科学教育活动的时间的众数是 8 .
【考点】众数.
【专题】统计的应用;数据分析观念.
【答案】8.
【分析】根据“众数就是一组数据中出现次数最多的那个数据”解答即可.
【解答】解:根据“众数就是一组数据中出现次数最多的那个数据”可得:
每周参加科学教育活动的时间为8h的人数最多,
∴全班学生每周参加科学教育活动的时间的众数是8,
故答案为:8.
【点评】本题考查了众数,熟知众数的定义是解题的关键.
9.(2025春 温州期中)这个主题开展板报宣传活动,并对各班的宣传板报进行评分,得分情况如图,则得分的众数为 9 分.
【考点】众数;条形统计图.
【专题】数据的收集与整理;数据分析观念.
【答案】9.
【分析】根据众数的概念求解即可.
【解答】解:根据条形统计图可知9分的班数最多为13,即众数为9分,
故答案为:9.
【点评】本题考查众数的概念,解题的关键是熟知相关概念,出现次数最多的数为众数.
10.(2025 五华区校级模拟)为将中华优秀传统文化融入学校教育教学,积极引导青少年从小学习中华优秀传统文化知识,培养审美鉴赏和创造能力,筑牢中华优秀传统文化根基.某学校计划开展中小学生中华优秀传统文化知识竞赛.并对八年级(1)班的50名学生竞赛成绩进行了调查,统计结果如表所示.
分数(分) 90 92 94 96 98 100
人数(人) 4 10 11 13 9 3
在本次调查中,八年级(1)班这50名学生竞赛成绩的中位数是 95 分.
【考点】中位数.
【专题】统计的应用;运算能力.
【答案】95.
【分析】根据中位数的定义即可得出答案.
【解答】解:∵一共有50名学生竞赛成绩,成绩从低到高排列后第25和26个成绩分别是94分和96分,
∴八年级(1)班这50名学生竞赛成绩的中位数是95(分).
故答案为:95.
【点评】本题考查了中位数,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数).
11.(2025 汕尾模拟)2024年12月17日,农业农村部农产品质量安全中心公示了“2024年第三批全国名特优新农产品名录”,汕尾市4个农产品入选,分别是凤山红灯笼荔枝、华侨红杨桃、陆河油柑和陆丰莲藕.“凤山红灯笼”是汕尾的名优荔枝,是糯米糍与怀枝自然杂交的优良品种.现抽查出7个单果,质量(单位:克)分别为27,24,28,27,26,25,25.这些数据的中位数是 26 .
【考点】中位数.
【专题】统计的应用;应用意识.
【答案】26.
【分析】根据中位数的定义进行解答.
【解答】解:将数据从小到大排列:24,25,25,26,27,27,28.
所以中位数为:26,
故答案为:26.
【点评】本题考查了中位数,解题的关键是掌握中位数的定义.
12.(2025春 浙江期中)已知一组数据:4,5,a,6,7的平均数为6,则这组数据的中位数是 6 .
【考点】中位数;算术平均数.
【专题】实数;运算能力.
【答案】6.
【分析】根据平均数的定义先算出a的值,再把数据按从小到大的顺序排列,找出最中间的数,即为中位数.
【解答】解:∵一组数据:4,5,a,6,7的平均数为6,
∴,
解得:a=8,
将这组数据从小到大重新排列为:4,5,6,7,8,中间的数是6,
∴中位数是6.
故答案为:6.
【点评】本题考查了平均数和中位数,熟知中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),叫做这组数据的中位数是解题的关键.
三.解答题(共3小题)
13.(2025 沙坪坝区校级一模)为加快智慧校园建设,学校举行了趣味数学答题机解题比赛,现从七、八年级参加比赛的学生中各随机抽取20名同学的成绩进行收集、整理、描述、分析.成绩共分为四组(成绩用x表示:A.x≤70;B.70<x≤80;C.80<x≤90:D.90<x≤100:单位:分)
七年级20名同学的成绩为:62,63,65,66,72,72,75,76,82,83,85,87,88,88,88,89,92,96,97,99.
八年级20名同学成绩在C组的数据是:83,84,84,84,85,87,88.
七、八年级所抽学生比赛成绩统计表
年级 平均数 中位数 众数
七年级 81.25 84.5 b
八年级 81.25 a 84
根据以上信息,解答下列问题:
(1)上述图表中a= 84 ,b= 88 ,m= 10 ;
(2)根据以上数据分析,你认为该校七、八年级中哪个年级学生解题比赛的成绩较好?请说明理由(写出一条理由即可);
(3)该校七年级有1200名学生、八年级有1100名同学参加了此次趣味数学答题机解题比赛,估计该校七、八年级参加解题比赛的成绩为优秀(x>90)的学生人数一共是多少?
【考点】众数;中位数.
【专题】数据的收集与整理;数据分析观念.
【答案】(1)84,88,10;(2)见解答(答案不唯一);(3)515名.
【分析】(1)分别根据中位数、众数的意义求解即可求出a、b,用“1”分别减去其它组所占百分比可得m的值;
(2)从平均数、中位数、众数的角度比较得出结论;
(3)用总人数乘七、八年级优秀(x>90)人数所占百分比即可.
【解答】解:(1)由题意可知,m%=1﹣30%﹣25%10%,即m=10.
八年级A组有:20×30%=6(人),B组有:20×10%=2(人),
故八年级的中位数a84;
在被抽取的七年级20名学生的解题比赛成绩中,88分8出现的次数最多,故众数b=88;
故答案为:84,88,10;
(2)七年级学生解题比赛的成绩较好,理由:
虽然两个年级的平均数相同,但七年级学生成绩的中位数和众数均比八年级的高,所以七年级学生解题比赛的成绩较好.(答案不唯一);
(3)12001100×25%=240+275=515(名),
答:估计该校七、八年级参加解题比赛的成绩为优秀(x>90)的学生人数一共是515名.
【点评】本题考查了用样本估计总体,算术平均数,中位数,众数,掌握相关知识是解题的关键.
14.(2025 新兴县一模)为了深入学习贯彻党的二十届三中全会精神,某校举行了“学三中全会精神,做新时代好少年”为主题的知识竞赛.现从八、九年级学生中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩用x表示,共分成四组:A.80<x≤85;B.85<x≤90;C.90<x≤95;D.95<x≤100),现在给出了部分信息如下:
八年级10名学生的竞赛成绩在C组中的数据:93,94,95.
九年级10名学生的竞赛成绩:81,83,85,89,90,95,99,99,99,100.
抽取的八、九年级学生竞赛成绩统计表
年级 八年级 九年级
平均数 92 92
中位数 b 92.5
众数 100 c
根据以上信息,解答下列问题.
(1)填空:a= 40 ,b= 94.5 ,c= 99 .
(2)根据以上数据,你认为该校八、九年级中抽取的哪个年级的学生对三中全会知识的掌握程度更好?请说明理由.(写出一条即可)
(3)若该校八、九年级各有300名学生参加了此次竞赛,请估计该校参加此次竞赛成绩(x>95)为优秀的学生总人数.
【考点】众数;用样本估计总体;中位数.
【专题】数据的收集与整理;数据分析观念.
【答案】(1)40,94.5,99;(2)八年级学生对三中全会知识的掌握程度更好,理由见解答;(3)240人.
【分析】(1)用“1”分别减去其它三组所占百分比即可求出a,再根据中位数和众数的定义即可求解;
(2)比较平均数,众数和中位数,即可求解;
(3)用样本估计总体,即可求解.
【解答】解:(1)由题意得,a%=1﹣10%﹣20%100%=40%,即a=40;
将八年级10名学生的竞赛成绩从小到大排列,排在中间的两个数分别是94,95,故中位数b94.5;
在九年级10名学生的竞赛成绩中,99出现的次数最多,故众数c=99.
故答案为:40,94.5,99;
(2)八年级学生对三中全会知识的掌握程度更好,理由如下:
虽然两个年级的平均数相同,但八年级学生的中位数和众数均高于九年级,所以八年级学生对三中全会知识的掌握程度更好;
(3)300×40%+300240(人),
答:估计该校参加此次竞赛成绩(x>95)为优秀的学生总人数为240人.
【点评】本题考查扇形统计图,中位数,众数,掌握平均数、中位数、众数的意义和计算方法是解答本题的关键.
15.(2025 文成县二模)九年级(1)(2)两个班各40人参加垃圾分类知识竞赛,规则如图.已知比赛中,所有同学均按要求一对一连线,无多连、少连.两个班的得分信息如表:
九(1)班成绩统计表
得分 0 5 10 15 20
人数 2 4 a b c
九(2)班成绩统计表
平均分 中位数 众数 满分率
14.25 10 10 45%
(1)分数10,15,20中,每人得分不可能是 15 分.
(2)已知九(1)班成绩的中位数是15分,求a和c的值.
(3)在(2)的情况下,你认为哪个班级成绩更优秀?请从平均分、中位数、众数和满分率四个方面作出评价.
【考点】众数;算术平均数;中位数.
【专题】数据的收集与整理;数据分析观念.
【答案】(1)15;(2)a=14,c=20;(3)见解答(答案不唯一).
【分析】(1)根据得分规则课判断出不可能得的分数;
(2)由(1)可知b的值,再根据中位数的定义可得a与c的值;
(3)分别求出九(1)班的平均分和满分率,再结合平均数,中位数,众数和满分率的定义解答即可.
【解答】解:(1)∵共有4条线,
可能全部连错,得0分,
可能1条线对,3条线错,得5分,
可能2条线对,2条线错,得10分,
可能3条线对,则第4条也对,得20分,
∴每人得分不可能是15分;
故答案为:15.
故答案为:15;
(2)由(1)可知b=0,因为中位数是15分,所以2+4+a=c=20,
所以a=14,c=20;
(3)九(1)班的成绩更优秀,理由如下:
九(1)班的平均分为分,中位数为15分,众数为20分,满分率为,
九(2)班的平均分为14.25分,中位数为10分,众数为10分,满分率为45%,
可见九(1)班的中位数、众数和满分率都高于九(2)班,所以我认为九(1)班的成绩更优秀.(答案不唯一).
【点评】本题考查了中位数、众数以及用样本估计总体,理解中位数、众数的意义是正确解答的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末核心考点 数据的集中趋势
一.选择题(共7小题)
1.(2025 永春县模拟)保险公司汽车保险中,继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数有关,该公司随机调查了该险种的300名续保人在一年内的出险情况,得到如下统计图:则出险次数的中位数为( )
A.1 B.2 C.3 D.4
2.(2025 西山区校级模拟)“樱云织诗笺 少年拾春行”,2025年3月,昆明市第三中学举办“樱”为有你春日校园创意文化活动.小明随机调查了学校30名初中同学制作书笺的数量,数据如表所示:
人数 7 8 10 5
书笺数量(张) 1 2 4 5
则制作书笺数量的中位数和众数分别是( )
A.4,10 B.2,4 C.4,4 D.3,4
3.(2025 乌鲁木齐模拟)小明调查了班里40名同学一周的体育锻炼情况,结果如图所示.该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A.16小时、15小时 B.8小时、9小时
C.10小时、8.5小时 D.8小时、8.5小时
4.(2025 官渡区一模)2025年4月6日中国跳水队员陈芋汐以419.35分的成绩夺得跳水世界杯女子10米台冠军.她在第二跳中展现极高水准,如表为第二跳七位裁判给出的评分情况,则这组得分数据的中位数和众数分别是( )
裁判序号 ① ② ③ ④ ⑤ ⑥ ⑦
得分 9.0 10.0 9.5 9.0 9.5 10.0 10.0
A.9.0,10.0 B.9.5,10.0 C.9.5,9.5 D.10.0,10.0
5.(2025 兰州校级模拟)某超市的某种水果一周内每天的进价与售价信息和实际每天的销售量情况如下:
该种水果一周内实际销售量统计表
日期 周﹣ 周二 周三 周四 周五 周六 周日
销售量(kg) 30 40 35 30 50 60 50
下列说法不正确的是( )
A.销售该种水果周一的利润最小
B.销售该种水果周日的利润最大
C.该种水果一周中每天的售价组成的这组数据的众数是5
D.该种水果一周中每天的进价组成的这组数据的中位数是3.6
6.(2025 成都二模)某科技论坛对Deep Seek、豆包、腾讯元宝、夸克四款AI助手中某一项功能的月度用户评分进行了统计,数据如表所示(单位:分):
AI助手 评分(满分100)
Deep Seek 88
豆包 84
腾讯元宝 84
夸克 86
评分的众数和中位数分别是( )
A.84,86 B.84,88 C.88,85 D.84,85
7.(2025 襄州区模拟)为了传承传统手工技艺,提高同学们的手工制作能力,某中学七年级一班的美术老师特地给学生们开了一节手工课,教同学们编织“中国结”,为了了解同学们的学习情况,便随机抽取了20名学生,对他们的编织数量进行统计,统计结果如表:
编织数量/个 2 3 4 5 6
人数/人 3 6 5 4 2
请根据上表,判断下列说法正确的是( )
A.样本为20名学生 B.众数是4个
C.中位数是3个 D.平均数是3.8个
二.填空题(共5小题)
8.(2025 宁德模拟)林老师统计全班学生每周参加科学教育活动的时间(单位:h),绘制成如图所示的统计图,则全班学生每周参加科学教育活动的时间的众数是 .
9.(2025春 温州期中)这个主题开展板报宣传活动,并对各班的宣传板报进行评分,得分情况如图,则得分的众数为 分.
10.(2025 五华区校级模拟)为将中华优秀传统文化融入学校教育教学,积极引导青少年从小学习中华优秀传统文化知识,培养审美鉴赏和创造能力,筑牢中华优秀传统文化根基.某学校计划开展中小学生中华优秀传统文化知识竞赛.并对八年级(1)班的50名学生竞赛成绩进行了调查,统计结果如表所示.
分数(分) 90 92 94 96 98 100
人数(人) 4 10 11 13 9 3
在本次调查中,八年级(1)班这50名学生竞赛成绩的中位数是 分.
11.(2025 汕尾模拟)2024年12月17日,农业农村部农产品质量安全中心公示了“2024年第三批全国名特优新农产品名录”,汕尾市4个农产品入选,分别是凤山红灯笼荔枝、华侨红杨桃、陆河油柑和陆丰莲藕.“凤山红灯笼”是汕尾的名优荔枝,是糯米糍与怀枝自然杂交的优良品种.现抽查出7个单果,质量(单位:克)分别为27,24,28,27,26,25,25.这些数据的中位数是 .
12.(2025春 浙江期中)已知一组数据:4,5,a,6,7的平均数为6,则这组数据的中位数是 .
三.解答题(共3小题)
13.(2025 沙坪坝区校级一模)为加快智慧校园建设,学校举行了趣味数学答题机解题比赛,现从七、八年级参加比赛的学生中各随机抽取20名同学的成绩进行收集、整理、描述、分析.成绩共分为四组(成绩用x表示:A.x≤70;B.70<x≤80;C.80<x≤90:D.90<x≤100:单位:分)
七年级20名同学的成绩为:62,63,65,66,72,72,75,76,82,83,85,87,88,88,88,89,92,96,97,99.
八年级20名同学成绩在C组的数据是:83,84,84,84,85,87,88.
七、八年级所抽学生比赛成绩统计表
年级 平均数 中位数 众数
七年级 81.25 84.5 b
八年级 81.25 a 84
根据以上信息,解答下列问题:
(1)上述图表中a= ,b= ,m= ;
(2)根据以上数据分析,你认为该校七、八年级中哪个年级学生解题比赛的成绩较好?请说明理由(写出一条理由即可);
(3)该校七年级有1200名学生、八年级有1100名同学参加了此次趣味数学答题机解题比赛,估计该校七、八年级参加解题比赛的成绩为优秀(x>90)的学生人数一共是多少?
14.(2025 新兴县一模)为了深入学习贯彻党的二十届三中全会精神,某校举行了“学三中全会精神,做新时代好少年”为主题的知识竞赛.现从八、九年级学生中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩用x表示,共分成四组:A.80<x≤85;B.85<x≤90;C.90<x≤95;D.95<x≤100),现在给出了部分信息如下:
八年级10名学生的竞赛成绩在C组中的数据:93,94,95.
九年级10名学生的竞赛成绩:81,83,85,89,90,95,99,99,99,100.
抽取的八、九年级学生竞赛成绩统计表
年级 八年级 九年级
平均数 92 92
中位数 b 92.5
众数 100 c
根据以上信息,解答下列问题.
(1)填空:a= ,b= ,c= .
(2)根据以上数据,你认为该校八、九年级中抽取的哪个年级的学生对三中全会知识的掌握程度更好?请说明理由.(写出一条即可)
(3)若该校八、九年级各有300名学生参加了此次竞赛,请估计该校参加此次竞赛成绩(x>95)为优秀的学生总人数.
15.(2025 文成县二模)九年级(1)(2)两个班各40人参加垃圾分类知识竞赛,规则如图.已知比赛中,所有同学均按要求一对一连线,无多连、少连.两个班的得分信息如表:
九(1)班成绩统计表
得分 0 5 10 15 20
人数 2 4 a b c
九(2)班成绩统计表
平均分 中位数 众数 满分率
14.25 10 10 45%
(1)分数10,15,20中,每人得分不可能是 分.
(2)已知九(1)班成绩的中位数是15分,求a和c的值.
(3)在(2)的情况下,你认为哪个班级成绩更优秀?请从平均分、中位数、众数和满分率四个方面作出评价.
期末核心考点 数据的集中趋势
参考答案与试题解析
一.选择题(共7小题)
1.(2025 永春县模拟)保险公司汽车保险中,继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数有关,该公司随机调查了该险种的300名续保人在一年内的出险情况,得到如下统计图:则出险次数的中位数为( )
A.1 B.2 C.3 D.4
【考点】中位数;频数(率)分布直方图.
【专题】统计的应用;应用意识.
【答案】A
【分析】根据中位数的定义进行计算即可.
【解答】解:将数据按从小到大排列后,
位于第150和第151的两个数为:1,1.
中位数为:1.
故选:A.
【点评】本题考查了中位数,解题的关键是根据中位数的意义来解答.
2.(2025 西山区校级模拟)“樱云织诗笺 少年拾春行”,2025年3月,昆明市第三中学举办“樱”为有你春日校园创意文化活动.小明随机调查了学校30名初中同学制作书笺的数量,数据如表所示:
人数 7 8 10 5
书笺数量(张) 1 2 4 5
则制作书笺数量的中位数和众数分别是( )
A.4,10 B.2,4 C.4,4 D.3,4
【考点】众数;中位数.
【专题】数据的收集与整理;数据分析观念.
【答案】D
【分析】根据中位数:“将数据按照顺序排列后,中间一位或中间两位的平均数即为中位数”,众数:“出现次数最多的数据”,进行判断即可.
【解答】解:数据排序后,第15个和第16个数据为2和4,
∴中位数为(2+4)÷2=3,
∵4出现的次数最多,
∴众数为4.
故选:D.
【点评】本题考查中位数和众数,熟练掌握中位数和众数的定义是解答本题的关键.
3.(2025 乌鲁木齐模拟)小明调查了班里40名同学一周的体育锻炼情况,结果如图所示.该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A.16小时、15小时 B.8小时、9小时
C.10小时、8.5小时 D.8小时、8.5小时
【考点】众数;中位数.
【专题】统计的应用;运算能力.
【答案】B
【分析】根据众数、中位数的概念即可求出答案.
【解答】解:众数是一组数据中出现次数最多的数,即8;
而将这组数据从小到大的顺序排列后,处于20,21两个数的平均数,由中位数的定义可知,这组数据的中位数是9.
故选:B.
【点评】本题考查了中位数、众数的概念,本题为统计题,考查众数与中位数的意义,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会错误地将这组数据最中间的那个数当作中位数.
4.(2025 官渡区一模)2025年4月6日中国跳水队员陈芋汐以419.35分的成绩夺得跳水世界杯女子10米台冠军.她在第二跳中展现极高水准,如表为第二跳七位裁判给出的评分情况,则这组得分数据的中位数和众数分别是( )
裁判序号 ① ② ③ ④ ⑤ ⑥ ⑦
得分 9.0 10.0 9.5 9.0 9.5 10.0 10.0
A.9.0,10.0 B.9.5,10.0 C.9.5,9.5 D.10.0,10.0
【考点】众数;中位数.
【专题】统计的应用;数据分析观念.
【答案】B
【分析】将题目中的数据,按照从小到大排列,即可得到这组数据的众数和中位数.
【解答】解:按照从小到大排列是:9.0,9.0,9.5,9.5,10.0,10.0,10.0,
根据众数、中位数的定义可得:这组数据的众数是10.0,中位数是9.5,
故选:B.
【点评】本题考查众数、中位数,解答本题的关键是明确众数和中位数的含义,找出相应的众数和中位数.
5.(2025 兰州校级模拟)某超市的某种水果一周内每天的进价与售价信息和实际每天的销售量情况如下:
该种水果一周内实际销售量统计表
日期 周﹣ 周二 周三 周四 周五 周六 周日
销售量(kg) 30 40 35 30 50 60 50
下列说法不正确的是( )
A.销售该种水果周一的利润最小
B.销售该种水果周日的利润最大
C.该种水果一周中每天的售价组成的这组数据的众数是5
D.该种水果一周中每天的进价组成的这组数据的中位数是3.6
【考点】众数;中位数.
【专题】统计的应用;数据分析观念.
【答案】B
【分析】根据折线图得出信息进行判断即可.
【解答】解:该商品周一的利润为45元,周二的利润为72元,周三的利润为77元,周四的利润为60元,周五的利润为70元,周六的利润为120元,周日的利润为90元,
A.该商品周一的利润45元,最小,原说法正确,不符合题意;
B.该商品周六的利润120元,最大,原说法错误,符合题意;
C.一周中该商品每天售价组成的这组数据的众数是5,原说法正确,不符合题意;
D.一周中的该商品每天进价组成的这组数据的中位数是3.6,原说法正确,不符合题意.
故选:B.
【点评】此题考查折线统计图,关键是根据折线图得出信息进行解答.
6.(2025 成都二模)某科技论坛对Deep Seek、豆包、腾讯元宝、夸克四款AI助手中某一项功能的月度用户评分进行了统计,数据如表所示(单位:分):
AI助手 评分(满分100)
Deep Seek 88
豆包 84
腾讯元宝 84
夸克 86
评分的众数和中位数分别是( )
A.84,86 B.84,88 C.88,85 D.84,85
【考点】众数;中位数.
【专题】统计的应用;运算能力.
【答案】D
【分析】将题目中4个数据按照从小到大的顺序排列,即可得到这组数据的众数与中位数.
【解答】解:数据按照从小到大排列是:84,84,86,88,
84出现次数最多,
故众数是84,中位数是,
故选:D.
【点评】本题考查众数和中位数,掌握众数和中位数,会求众数与中位数,特别注意中位数除排序外还要根据数据的个数是奇与偶来计算是关键.
7.(2025 襄州区模拟)为了传承传统手工技艺,提高同学们的手工制作能力,某中学七年级一班的美术老师特地给学生们开了一节手工课,教同学们编织“中国结”,为了了解同学们的学习情况,便随机抽取了20名学生,对他们的编织数量进行统计,统计结果如表:
编织数量/个 2 3 4 5 6
人数/人 3 6 5 4 2
请根据上表,判断下列说法正确的是( )
A.样本为20名学生 B.众数是4个
C.中位数是3个 D.平均数是3.8个
【考点】众数;加权平均数;中位数.
【专题】数据的收集与整理;数据分析观念.
【答案】D
【分析】根据样本的概念、众数、中位数及加权平均数的定义分别求解即可.
【解答】解:A.样本为20名学生的编织数量,此选项错误,不符合题意;
B.众数是3,此选项错误,不符合题意;
C.共20个数据,从小到大排列后位于第10个和第11个的数据分别是4和4,
∴中位数为4,此选项错误,不符合题意;
D.平均数为(2×3+3×6+4×5+5×4+6×2)=3.8(个),此选项正确,符合题意;
故选:D.
【点评】本题主要考查众数、中位数、加权平均数,解题的关键是掌握众数、中位数及加权平均数的定义.
二.填空题(共5小题)
8.(2025 宁德模拟)林老师统计全班学生每周参加科学教育活动的时间(单位:h),绘制成如图所示的统计图,则全班学生每周参加科学教育活动的时间的众数是 8 .
【考点】众数.
【专题】统计的应用;数据分析观念.
【答案】8.
【分析】根据“众数就是一组数据中出现次数最多的那个数据”解答即可.
【解答】解:根据“众数就是一组数据中出现次数最多的那个数据”可得:
每周参加科学教育活动的时间为8h的人数最多,
∴全班学生每周参加科学教育活动的时间的众数是8,
故答案为:8.
【点评】本题考查了众数,熟知众数的定义是解题的关键.
9.(2025春 温州期中)这个主题开展板报宣传活动,并对各班的宣传板报进行评分,得分情况如图,则得分的众数为 9 分.
【考点】众数;条形统计图.
【专题】数据的收集与整理;数据分析观念.
【答案】9.
【分析】根据众数的概念求解即可.
【解答】解:根据条形统计图可知9分的班数最多为13,即众数为9分,
故答案为:9.
【点评】本题考查众数的概念,解题的关键是熟知相关概念,出现次数最多的数为众数.
10.(2025 五华区校级模拟)为将中华优秀传统文化融入学校教育教学,积极引导青少年从小学习中华优秀传统文化知识,培养审美鉴赏和创造能力,筑牢中华优秀传统文化根基.某学校计划开展中小学生中华优秀传统文化知识竞赛.并对八年级(1)班的50名学生竞赛成绩进行了调查,统计结果如表所示.
分数(分) 90 92 94 96 98 100
人数(人) 4 10 11 13 9 3
在本次调查中,八年级(1)班这50名学生竞赛成绩的中位数是 95 分.
【考点】中位数.
【专题】统计的应用;运算能力.
【答案】95.
【分析】根据中位数的定义即可得出答案.
【解答】解:∵一共有50名学生竞赛成绩,成绩从低到高排列后第25和26个成绩分别是94分和96分,
∴八年级(1)班这50名学生竞赛成绩的中位数是95(分).
故答案为:95.
【点评】本题考查了中位数,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数).
11.(2025 汕尾模拟)2024年12月17日,农业农村部农产品质量安全中心公示了“2024年第三批全国名特优新农产品名录”,汕尾市4个农产品入选,分别是凤山红灯笼荔枝、华侨红杨桃、陆河油柑和陆丰莲藕.“凤山红灯笼”是汕尾的名优荔枝,是糯米糍与怀枝自然杂交的优良品种.现抽查出7个单果,质量(单位:克)分别为27,24,28,27,26,25,25.这些数据的中位数是 26 .
【考点】中位数.
【专题】统计的应用;应用意识.
【答案】26.
【分析】根据中位数的定义进行解答.
【解答】解:将数据从小到大排列:24,25,25,26,27,27,28.
所以中位数为:26,
故答案为:26.
【点评】本题考查了中位数,解题的关键是掌握中位数的定义.
12.(2025春 浙江期中)已知一组数据:4,5,a,6,7的平均数为6,则这组数据的中位数是 6 .
【考点】中位数;算术平均数.
【专题】实数;运算能力.
【答案】6.
【分析】根据平均数的定义先算出a的值,再把数据按从小到大的顺序排列,找出最中间的数,即为中位数.
【解答】解:∵一组数据:4,5,a,6,7的平均数为6,
∴,
解得:a=8,
将这组数据从小到大重新排列为:4,5,6,7,8,中间的数是6,
∴中位数是6.
故答案为:6.
【点评】本题考查了平均数和中位数,熟知中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),叫做这组数据的中位数是解题的关键.
三.解答题(共3小题)
13.(2025 沙坪坝区校级一模)为加快智慧校园建设,学校举行了趣味数学答题机解题比赛,现从七、八年级参加比赛的学生中各随机抽取20名同学的成绩进行收集、整理、描述、分析.成绩共分为四组(成绩用x表示:A.x≤70;B.70<x≤80;C.80<x≤90:D.90<x≤100:单位:分)
七年级20名同学的成绩为:62,63,65,66,72,72,75,76,82,83,85,87,88,88,88,89,92,96,97,99.
八年级20名同学成绩在C组的数据是:83,84,84,84,85,87,88.
七、八年级所抽学生比赛成绩统计表
年级 平均数 中位数 众数
七年级 81.25 84.5 b
八年级 81.25 a 84
根据以上信息,解答下列问题:
(1)上述图表中a= 84 ,b= 88 ,m= 10 ;
(2)根据以上数据分析,你认为该校七、八年级中哪个年级学生解题比赛的成绩较好?请说明理由(写出一条理由即可);
(3)该校七年级有1200名学生、八年级有1100名同学参加了此次趣味数学答题机解题比赛,估计该校七、八年级参加解题比赛的成绩为优秀(x>90)的学生人数一共是多少?
【考点】众数;中位数.
【专题】数据的收集与整理;数据分析观念.
【答案】(1)84,88,10;(2)见解答(答案不唯一);(3)515名.
【分析】(1)分别根据中位数、众数的意义求解即可求出a、b,用“1”分别减去其它组所占百分比可得m的值;
(2)从平均数、中位数、众数的角度比较得出结论;
(3)用总人数乘七、八年级优秀(x>90)人数所占百分比即可.
【解答】解:(1)由题意可知,m%=1﹣30%﹣25%10%,即m=10.
八年级A组有:20×30%=6(人),B组有:20×10%=2(人),
故八年级的中位数a84;
在被抽取的七年级20名学生的解题比赛成绩中,88分8出现的次数最多,故众数b=88;
故答案为:84,88,10;
(2)七年级学生解题比赛的成绩较好,理由:
虽然两个年级的平均数相同,但七年级学生成绩的中位数和众数均比八年级的高,所以七年级学生解题比赛的成绩较好.(答案不唯一);
(3)12001100×25%=240+275=515(名),
答:估计该校七、八年级参加解题比赛的成绩为优秀(x>90)的学生人数一共是515名.
【点评】本题考查了用样本估计总体,算术平均数,中位数,众数,掌握相关知识是解题的关键.
14.(2025 新兴县一模)为了深入学习贯彻党的二十届三中全会精神,某校举行了“学三中全会精神,做新时代好少年”为主题的知识竞赛.现从八、九年级学生中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩用x表示,共分成四组:A.80<x≤85;B.85<x≤90;C.90<x≤95;D.95<x≤100),现在给出了部分信息如下:
八年级10名学生的竞赛成绩在C组中的数据:93,94,95.
九年级10名学生的竞赛成绩:81,83,85,89,90,95,99,99,99,100.
抽取的八、九年级学生竞赛成绩统计表
年级 八年级 九年级
平均数 92 92
中位数 b 92.5
众数 100 c
根据以上信息,解答下列问题.
(1)填空:a= 40 ,b= 94.5 ,c= 99 .
(2)根据以上数据,你认为该校八、九年级中抽取的哪个年级的学生对三中全会知识的掌握程度更好?请说明理由.(写出一条即可)
(3)若该校八、九年级各有300名学生参加了此次竞赛,请估计该校参加此次竞赛成绩(x>95)为优秀的学生总人数.
【考点】众数;用样本估计总体;中位数.
【专题】数据的收集与整理;数据分析观念.
【答案】(1)40,94.5,99;(2)八年级学生对三中全会知识的掌握程度更好,理由见解答;(3)240人.
【分析】(1)用“1”分别减去其它三组所占百分比即可求出a,再根据中位数和众数的定义即可求解;
(2)比较平均数,众数和中位数,即可求解;
(3)用样本估计总体,即可求解.
【解答】解:(1)由题意得,a%=1﹣10%﹣20%100%=40%,即a=40;
将八年级10名学生的竞赛成绩从小到大排列,排在中间的两个数分别是94,95,故中位数b94.5;
在九年级10名学生的竞赛成绩中,99出现的次数最多,故众数c=99.
故答案为:40,94.5,99;
(2)八年级学生对三中全会知识的掌握程度更好,理由如下:
虽然两个年级的平均数相同,但八年级学生的中位数和众数均高于九年级,所以八年级学生对三中全会知识的掌握程度更好;
(3)300×40%+300240(人),
答:估计该校参加此次竞赛成绩(x>95)为优秀的学生总人数为240人.
【点评】本题考查扇形统计图,中位数,众数,掌握平均数、中位数、众数的意义和计算方法是解答本题的关键.
15.(2025 文成县二模)九年级(1)(2)两个班各40人参加垃圾分类知识竞赛,规则如图.已知比赛中,所有同学均按要求一对一连线,无多连、少连.两个班的得分信息如表:
九(1)班成绩统计表
得分 0 5 10 15 20
人数 2 4 a b c
九(2)班成绩统计表
平均分 中位数 众数 满分率
14.25 10 10 45%
(1)分数10,15,20中,每人得分不可能是 15 分.
(2)已知九(1)班成绩的中位数是15分,求a和c的值.
(3)在(2)的情况下,你认为哪个班级成绩更优秀?请从平均分、中位数、众数和满分率四个方面作出评价.
【考点】众数;算术平均数;中位数.
【专题】数据的收集与整理;数据分析观念.
【答案】(1)15;(2)a=14,c=20;(3)见解答(答案不唯一).
【分析】(1)根据得分规则课判断出不可能得的分数;
(2)由(1)可知b的值,再根据中位数的定义可得a与c的值;
(3)分别求出九(1)班的平均分和满分率,再结合平均数,中位数,众数和满分率的定义解答即可.
【解答】解:(1)∵共有4条线,
可能全部连错,得0分,
可能1条线对,3条线错,得5分,
可能2条线对,2条线错,得10分,
可能3条线对,则第4条也对,得20分,
∴每人得分不可能是15分;
故答案为:15.
故答案为:15;
(2)由(1)可知b=0,因为中位数是15分,所以2+4+a=c=20,
所以a=14,c=20;
(3)九(1)班的成绩更优秀,理由如下:
九(1)班的平均分为分,中位数为15分,众数为20分,满分率为,
九(2)班的平均分为14.25分,中位数为10分,众数为10分,满分率为45%,
可见九(1)班的中位数、众数和满分率都高于九(2)班,所以我认为九(1)班的成绩更优秀.(答案不唯一).
【点评】本题考查了中位数、众数以及用样本估计总体,理解中位数、众数的意义是正确解答的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
