【期末核心考点】数据的离散程度(含解析)2024-2025学年八年级下册数学华东师大版
文档属性
| 名称 | 【期末核心考点】数据的离散程度(含解析)2024-2025学年八年级下册数学华东师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 569.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-14 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末核心考点 数据的离散程度
一.选择题(共7小题)
1.(2025 兰州模拟)已知一组数据x1,x2,x3,x4,x5的平均数为4,方差是3.2,则另一组数据2x1+2,2x2+2,2x3+2,2x4+2,2x5+2的平均数和方差分别是( )
A.4,5.2 B.8,6.4 C.10,12.8 D.12,16
2.(2025 南明区一模)投壶是中国古代一种传统礼仪和宴饮游戏.某校2025年迎新活动中,九年级(1)班5名同学参加投壶游戏体验传统民俗,每人有10支箭进行投壶,投进去的箭数分别为:6,8,5,9,7(单位:支),某同学求得这组数据的平均数为7支,则这组数据的方差是( )
A.2 B.3 C.4 D.5
3.(2025 濠江区一模)科学家记录了四种花卉的平均开花天数(天数越短开花越快)和方差(方差越小开花越稳定),数据如表.
种类 甲种类 乙种类 丙种类 丁种类
平均数 2.3 2.3 2.8 3.1
方差 1.05 0.78 1.05 0.78
开花最快且最稳定的是( )
A.甲种类 B.乙种类 C.丙种类 D.丁种类
4.(2025春 定海区期中)某社团统计成员一周的活动时间情况,列出了方差的计算公式:,则的值是( )
A.4 B.3 C.3.6 D.4.25
5.(2025 崇左二模)某班30位同学的安全知识测试成绩统计如表,其中有两个数据被遮盖,不影响下列关于成绩的统计量的是( )
成绩 24 25 26 27 28 29 30
人数 □ □ 3 3 6 7 9
A.平均数,众数 B.中位数,众数
C.平均数,方差 D.中位数,方差
6.(2025春 高州市期中)体育锻炼是学生健康成长的重要组成部分,为此学校开展了丰富的体育活动.甲乙两位同学积极参加学校举办的1分钟跳绳比赛,训练期间甲乙两名同学各进行10次跳绳练均成绩均为195下,他们成绩的方差分别是:,,根据方差的意义可知( )
A.甲的成绩波动比乙大
B.乙的成绩波动比甲大
C.甲、乙两人成绩波动一样大
D.无法比较甲、乙两人成绩波动大小
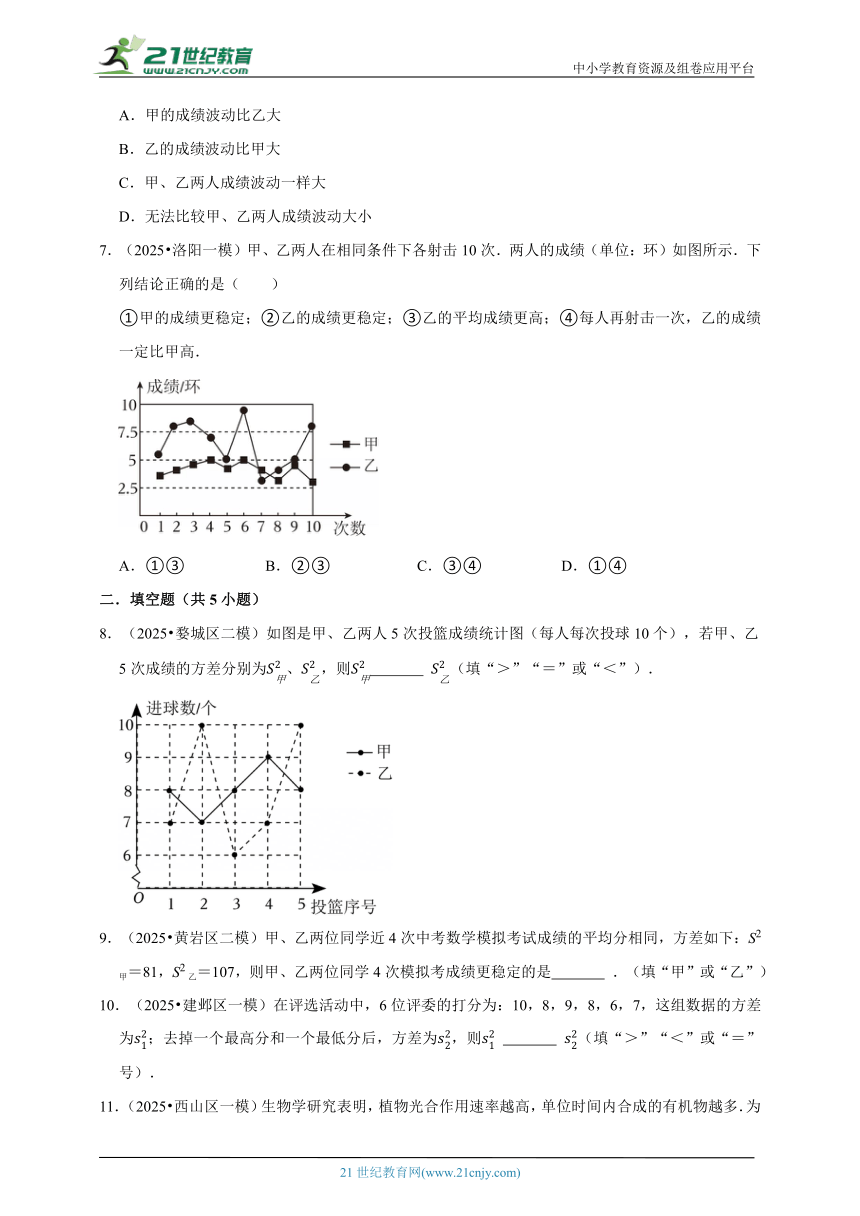
7.(2025 洛阳一模)甲、乙两人在相同条件下各射击10次.两人的成绩(单位:环)如图所示.下列结论正确的是( )
①甲的成绩更稳定;②乙的成绩更稳定;③乙的平均成绩更高;④每人再射击一次,乙的成绩一定比甲高.
A.①③ B.②③ C.③④ D.①④
二.填空题(共5小题)
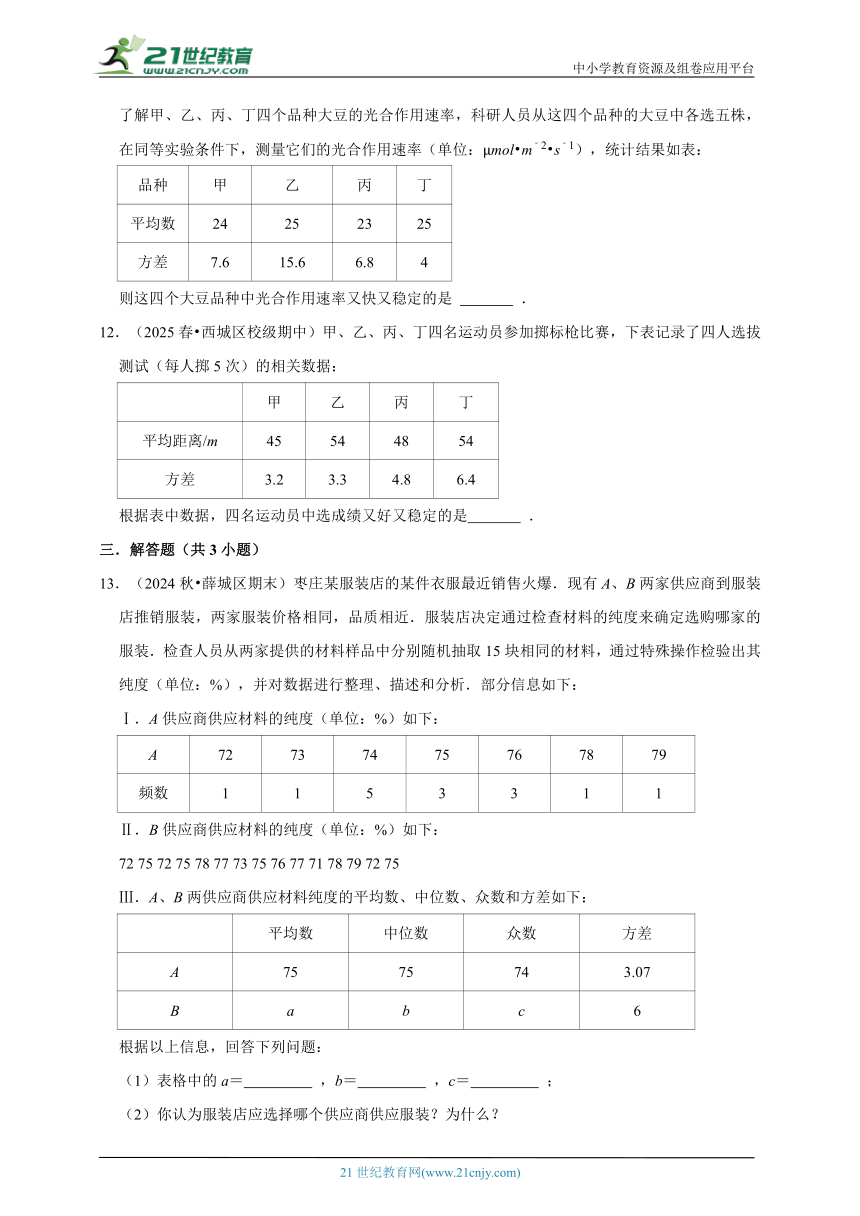
8.(2025 婺城区二模)如图是甲、乙两人5次投篮成绩统计图(每人每次投球10个),若甲、乙5次成绩的方差分别为、,则 (填“>”“=”或“<”).
9.(2025 黄岩区二模)甲、乙两位同学近4次中考数学模拟考试成绩的平均分相同,方差如下:S2甲=81,S2乙=107,则甲、乙两位同学4次模拟考成绩更稳定的是 .(填“甲”或“乙”)
10.(2025 建邺区一模)在评选活动中,6位评委的打分为:10,8,9,8,6,7,这组数据的方差为;去掉一个最高分和一个最低分后,方差为,则 (填“>”“<”或“=”号).
11.(2025 西山区一模)生物学研究表明,植物光合作用速率越高,单位时间内合成的有机物越多.为了解甲、乙、丙、丁四个品种大豆的光合作用速率,科研人员从这四个品种的大豆中各选五株,在同等实验条件下,测量它们的光合作用速率(单位:μmol m﹣2 s﹣1),统计结果如表:
品种 甲 乙 丙 丁
平均数 24 25 23 25
方差 7.6 15.6 6.8 4
则这四个大豆品种中光合作用速率又快又稳定的是 .
12.(2025春 西城区校级期中)甲、乙、丙、丁四名运动员参加掷标枪比赛,下表记录了四人选拔测试(每人掷5次)的相关数据:
甲 乙 丙 丁
平均距离/m 45 54 48 54
方差 3.2 3.3 4.8 6.4
根据表中数据,四名运动员中选成绩又好又稳定的是 .
三.解答题(共3小题)
13.(2024秋 薛城区期末)枣庄某服装店的某件衣服最近销售火爆.现有A、B两家供应商到服装店推销服装,两家服装价格相同,品质相近.服装店决定通过检查材料的纯度来确定选购哪家的服装.检查人员从两家提供的材料样品中分别随机抽取15块相同的材料,通过特殊操作检验出其纯度(单位:%),并对数据进行整理、描述和分析.部分信息如下:
Ⅰ.A供应商供应材料的纯度(单位:%)如下:
A 72 73 74 75 76 78 79
频数 1 1 5 3 3 1 1
Ⅱ.B供应商供应材料的纯度(单位:%)如下:
72 75 72 75 78 77 73 75 76 77 71 78 79 72 75
Ⅲ.A、B两供应商供应材料纯度的平均数、中位数、众数和方差如下:
平均数 中位数 众数 方差
A 75 75 74 3.07
B a b c 6
根据以上信息,回答下列问题:
(1)表格中的a= ,b= ,c= ;
(2)你认为服装店应选择哪个供应商供应服装?为什么?
14.(2025 江阴市二模)某班以小组为单位开展知识竞赛,规定满分为10分,9分及以上为优秀.
有甲、乙两组同学,每组各8人,按照1﹣8号进行编号,他们的成绩统计图如下:
小夏对这两个小组的成绩进行了如下分析:
平均数(分) 中位数(分) 众数(分) 方差 优秀率
甲组 7.625 a 7 4.48 37.5%
乙组 7.625 7 b 0.73 c
请阅读上述信息,回答下列问题:
(1)填空:a= ,b= ,c= ;
(2)根据所学的统计知识,请你利用数据,从不同角度对甲、乙两组的成绩进行比较与评价.
15.(2025 东莞市二模)2023年6月5日是世界环境日,某学校举办了以“生态文明与环境保护”为主题的相关知识测试.为了了解学生对“生态文明与环境保护”相关知识的掌握情况,现从七年级和八年级参与竞赛的学生中各随机选出20名同学的成绩进行分析(单位:分,满分100分),将学生竞赛成绩分为A,B,C,D四个等级,分别是:
A:x<70,B:70≤x<80,C:80≤x<90,D:90≤x≤100.
其中,七年级学生的竞赛成绩为:
66,75,76,78,79,81,82,83,84,86,
86,88,88,88,91,92,94,95,96,96;
八年级等级C的学生成绩为:81,82,83,86,87,88,89.
两组数据的平均数、中位数、众数、方差如下表:
学生 平均数 中位数 众数 方差
七年级 85.2 86 b 59.66
八年级 85.2 a 91 91.76
根据以上信息,解答下列问题;
(1)填空:a= ,b= ,m= ;
(2)根据以上数据,你认为在此次知识竞赛中,哪个年级的成绩更好?请说明理由;(一条理由即可)
(3)若七年级有500名学生参赛,八年级有700名学生参赛,请估计两个年级参赛学生中成绩优秀(大于或等于90分)的学生共有多少人?
期末核心考点 数据的离散程度
参考答案与试题解析
一.选择题(共7小题)
1.(2025 兰州模拟)已知一组数据x1,x2,x3,x4,x5的平均数为4,方差是3.2,则另一组数据2x1+2,2x2+2,2x3+2,2x4+2,2x5+2的平均数和方差分别是( )
A.4,5.2 B.8,6.4 C.10,12.8 D.12,16
【考点】方差;算术平均数.
【专题】统计的应用.
【答案】C
【分析】根据平均数的定义和方差的定义解答即可.
【解答】解:∵一组数据x1,x2,x3,x4,x5的平均数为4,
∴x1+x2+x3+x4+x5=20,
∴
=10,
∵一组数据x1,x2,x3,x4,x5的平均数为4,方差是3.2,
∴,
∴另一组数据的方差为
=4×3.2
=12.8,
故选:C.
【点评】本题主要考查了确定一组数据的方差和平均数,理解方差和平均数的意义是解题的关键.
2.(2025 南明区一模)投壶是中国古代一种传统礼仪和宴饮游戏.某校2025年迎新活动中,九年级(1)班5名同学参加投壶游戏体验传统民俗,每人有10支箭进行投壶,投进去的箭数分别为:6,8,5,9,7(单位:支),某同学求得这组数据的平均数为7支,则这组数据的方差是( )
A.2 B.3 C.4 D.5
【考点】方差;算术平均数.
【专题】数据的收集与整理;数据分析观念.
【答案】A
【分析】根据方差的公式计算即可.
【解答】解:这组数据的方差为:[(6﹣7)2+(8﹣7)2+(5﹣7)2+(9﹣7)2+(7﹣7)2]=2.
故选:A.
【点评】本题考查了方差,方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
3.(2025 濠江区一模)科学家记录了四种花卉的平均开花天数(天数越短开花越快)和方差(方差越小开花越稳定),数据如表.
种类 甲种类 乙种类 丙种类 丁种类
平均数 2.3 2.3 2.8 3.1
方差 1.05 0.78 1.05 0.78
开花最快且最稳定的是( )
A.甲种类 B.乙种类 C.丙种类 D.丁种类
【考点】方差.
【专题】数据的收集与整理;数据分析观念.
【答案】B
【分析】先比较平均数,再比较方差;方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.据此只要比较方差大小即可求解.
【解答】解:甲种类和乙种类的平均数相同,且比丙种类与丁种类的小,所以甲种类和乙种类开花最快;
又因为乙种类的方差比甲小,所以开花最快且最稳定的是乙种类.
故选:B.
【点评】本题考查方差的意义,正确记忆相关知识点是解题关键.
4.(2025春 定海区期中)某社团统计成员一周的活动时间情况,列出了方差的计算公式:,则的值是( )
A.4 B.3 C.3.6 D.4.25
【考点】方差;算术平均数.
【专题】统计的应用;运算能力.
【答案】C
【分析】根据方差的计算算式得出这组数据为2、2、3、3、3、3、4、4、4、8,再根据平均数的定义列式计算即可.
【解答】解:由题意知,这组数据为2、2、3、3、3、3、4、4、4、8,
所以这组数据的平均数为(2×2+3×4+4×3+8)=3.6,
故选:C.
【点评】本题主要考查方差与平均数,解题的关键是掌握方差与算术平均数的定义.
5.(2025 崇左二模)某班30位同学的安全知识测试成绩统计如表,其中有两个数据被遮盖,不影响下列关于成绩的统计量的是( )
成绩 24 25 26 27 28 29 30
人数 □ □ 3 3 6 7 9
A.平均数,众数 B.中位数,众数
C.平均数,方差 D.中位数,方差
【考点】方差;加权平均数;中位数;众数.
【专题】数据的收集与整理;数据分析观念.
【答案】B
【分析】先计算成绩在24、25的学生数,再根据平均数、众数、中位数、方差的定义进行判断即可.
【解答】解:成绩24、25的学生数共:30﹣3﹣3﹣6﹣7﹣9=2(位).
成绩在24、25的学生数会影响该组数据的平均数,也会影响该组数据的方差.
由于成绩在第十五、第十六的两个数都是29,其它各个成绩出现次数都大于3,
所以成绩在24、25的学生数,不会影响该组数据的中位数和众数.
故选:B.
【点评】本题考查了统计的有关概念,掌握平均数、众数、中位数、方差的定义和计算方法是解决本题的关键.
6.(2025春 高州市期中)体育锻炼是学生健康成长的重要组成部分,为此学校开展了丰富的体育活动.甲乙两位同学积极参加学校举办的1分钟跳绳比赛,训练期间甲乙两名同学各进行10次跳绳练均成绩均为195下,他们成绩的方差分别是:,,根据方差的意义可知( )
A.甲的成绩波动比乙大
B.乙的成绩波动比甲大
C.甲、乙两人成绩波动一样大
D.无法比较甲、乙两人成绩波动大小
【考点】方差.
【专题】统计与概率;数据分析观念.
【答案】A
【分析】根据方差的意义解答即可.
【解答】解:∵平均成绩均为195下,,
∴甲的成绩波动比乙大,
故选:A.
【点评】本题考查方差的意义.方差反映了一组数据的波动大小,熟练掌握方差越小,波动性越小是解本题的关键.
7.(2025 洛阳一模)甲、乙两人在相同条件下各射击10次.两人的成绩(单位:环)如图所示.下列结论正确的是( )
①甲的成绩更稳定;②乙的成绩更稳定;③乙的平均成绩更高;④每人再射击一次,乙的成绩一定比甲高.
A.①③ B.②③ C.③④ D.①④
【考点】方差.
【专题】统计的应用.
【答案】A
【分析】方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定,根据方差、平均数的意义进行判断即可求出答案.
【解答】解:根据图象可知甲的波动比乙小,则甲的成绩更加稳定,故①正确,②错误;
根据图象可知甲的平均成绩稳定在5以下,而乙的平均成绩稳定在7.5左右,则乙的平均成绩更高,故③正确;
如果每人再射击一次,但乙的成绩不一定比甲高,只能是可能性较大,因为乙的平均成绩更高,但是波动较大,故④错误;
故选:A.
【点评】本题考查了平均数、方差的意义、解答本题的关键是掌握它们的定义.
二.填空题(共5小题)
8.(2025 婺城区二模)如图是甲、乙两人5次投篮成绩统计图(每人每次投球10个),若甲、乙5次成绩的方差分别为、,则 < (填“>”“=”或“<”).
【考点】方差.
【专题】统计的应用.
【答案】<.
【分析】先分别求出甲、乙的平均数和方差,进行比较即可得到结论.
【解答】解:甲的平均成绩为,
,
乙的平均成绩为,
,
∴.
故答案为:<.
【点评】此题主要考查了求方差,熟练掌握方差的计算方法是解题的关键.
9.(2025 黄岩区二模)甲、乙两位同学近4次中考数学模拟考试成绩的平均分相同,方差如下:S2甲=81,S2乙=107,则甲、乙两位同学4次模拟考成绩更稳定的是 甲 .(填“甲”或“乙”)
【考点】方差.
【专题】数据的收集与整理;数据分析观念.
【答案】甲.
【分析】根据方差的意义解答即可.
【解答】解:∵S2甲=81,S2乙=107,
∴S2<S2乙,
∴甲、乙两位同学4次模考成绩更稳定的是甲.
故答案为:甲.
【点评】本题主要考查方差,方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越差;反之,则它与其平均值的离散程度越小,稳定性越好.
10.(2025 建邺区一模)在评选活动中,6位评委的打分为:10,8,9,8,6,7,这组数据的方差为;去掉一个最高分和一个最低分后,方差为,则 > (填“>”“<”或“=”号).
【考点】方差;算术平均数.
【专题】统计的应用;运算能力.
【答案】>.
【分析】分别根据方差公式计算出方差,然后判断即可.
【解答】解:6位评委的打分的平均数为8,
这组数据的方差s[(10﹣8)2+(8﹣8)2+(9﹣8)2+(8﹣8)2+(6﹣8)2+(7﹣8)2],
去掉一个最高分和一个最低分后平均数为8,
方差s[(8﹣8)2+(9﹣8)2+(8﹣8)2+(7﹣8)2],
∵,
∴ss.
故答案为:>.
【点评】本题主要考查了方差和算术平均数,熟记方差公式是解题的关键.
11.(2025 西山区一模)生物学研究表明,植物光合作用速率越高,单位时间内合成的有机物越多.为了解甲、乙、丙、丁四个品种大豆的光合作用速率,科研人员从这四个品种的大豆中各选五株,在同等实验条件下,测量它们的光合作用速率(单位:μmol m﹣2 s﹣1),统计结果如表:
品种 甲 乙 丙 丁
平均数 24 25 23 25
方差 7.6 15.6 6.8 4
则这四个大豆品种中光合作用速率又快又稳定的是 丁 .
【考点】方差;负整数指数幂.
【专题】概率及其应用;数据分析观念.
【答案】见试题解答内容
【分析】先比较平均数得到乙和丁光合作用速率较高,然后比较方差得到丁比较稳定.
【解答】解:因为乙和丁光合作用速率的平均数较高,所以从乙和丁中选取,
又丁的方差比乙小,所以丁的光合作用速率比较稳定,
所以应选择的优良大豆品种是丁.
故答案为:丁.
【点评】本题考查了方差:一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差.方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.也考查了平均数的意义.
12.(2025春 西城区校级期中)甲、乙、丙、丁四名运动员参加掷标枪比赛,下表记录了四人选拔测试(每人掷5次)的相关数据:
甲 乙 丙 丁
平均距离/m 45 54 48 54
方差 3.2 3.3 4.8 6.4
根据表中数据,四名运动员中选成绩又好又稳定的是 乙 .
【考点】方差.
【专题】数据的收集与整理;数据分析观念.
【答案】乙.
【分析】首先比较平均数,平均数相同时选择方差较小的参加比赛.
【解答】解:由表知乙、丁平均数相等,大于甲、丙射击成绩的平均数,
∴从乙、丁中选择一人参加竞赛,
∵乙的方差较小,
∴四名运动员中选成绩又好又稳定的是乙.
故答案为:乙.
【点评】此题考查了平均数和方差,解答本题的关键是明确方差的定义:方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
三.解答题(共3小题)
13.(2024秋 薛城区期末)枣庄某服装店的某件衣服最近销售火爆.现有A、B两家供应商到服装店推销服装,两家服装价格相同,品质相近.服装店决定通过检查材料的纯度来确定选购哪家的服装.检查人员从两家提供的材料样品中分别随机抽取15块相同的材料,通过特殊操作检验出其纯度(单位:%),并对数据进行整理、描述和分析.部分信息如下:
Ⅰ.A供应商供应材料的纯度(单位:%)如下:
A 72 73 74 75 76 78 79
频数 1 1 5 3 3 1 1
Ⅱ.B供应商供应材料的纯度(单位:%)如下:
72 75 72 75 78 77 73 75 76 77 71 78 79 72 75
Ⅲ.A、B两供应商供应材料纯度的平均数、中位数、众数和方差如下:
平均数 中位数 众数 方差
A 75 75 74 3.07
B a b c 6
根据以上信息,回答下列问题:
(1)表格中的a= 75 ,b= 75 ,c= 75 ;
(2)你认为服装店应选择哪个供应商供应服装?为什么?
【考点】方差;算术平均数;中位数;众数.
【专题】统计的应用;数据分析观念.
【答案】(1)75;75;75;
(2)选A供应商供应服装,理由见解析.
【分析】(1)根据平均数,众数和方差的计算公式分别进行解答即可;
(2)根据方差的定义,方差越小数据越稳定即可得出答案.
【解答】解:(1)根据平均数,众数和方差的计算公式分别进行可得:
,
将数据按从小到大排列,可确定中位数b=75,
∵75出现的次数最多,
∴众数c=75,
故答案为:75;75;75;
(2)选A供应商供应服装,理由如下:
∵B的方差比A的大,A更稳定,
∴选A供应商供应服装.
【点评】本题主要考查了方差、平均数、中位数、众数等知识点,熟悉相关统计量的计算公式和意义是解决此题的关键.
14.(2025 江阴市二模)某班以小组为单位开展知识竞赛,规定满分为10分,9分及以上为优秀.
有甲、乙两组同学,每组各8人,按照1﹣8号进行编号,他们的成绩统计图如下:
小夏对这两个小组的成绩进行了如下分析:
平均数(分) 中位数(分) 众数(分) 方差 优秀率
甲组 7.625 a 7 4.48 37.5%
乙组 7.625 7 b 0.73 c
请阅读上述信息,回答下列问题:
(1)填空:a= 7.5 ,b= 7 ,c= 25% ;
(2)根据所学的统计知识,请你利用数据,从不同角度对甲、乙两组的成绩进行比较与评价.
【考点】方差;中位数;众数.
【专题】统计的应用.
【答案】(1)7.5;7;25%;
(2)见解析.
【分析】(1)根据中位数、众数、优秀率的定义即可求解;
(2)从优秀率、中位数和方差等角度进行分析即可.
【解答】解:(1)将甲组的成绩从小到大顺序排列,中位数为第4位和第5位的平均数,
∴,
乙组的成绩出现次数最多的是7分,共5次,
∴b=7,
乙组的成绩9分及以上有2人,
∴优秀率,
故答案为:7.5;7;25%;
(2)①甲组成绩的优秀率为37.5%,乙组成绩的优秀率为25%,
∴从优秀率的角度来看,甲组的成绩比乙组的成绩好;
②甲组成绩的中位数为7.5,乙组成绩的中位数为7,
∴从中位数的角度来看,甲组的成绩比乙组的成绩好;
③甲组成绩的方差为4.48,乙组成绩的方差为0.73,
∴从方差的角度来看,乙组的成绩比甲组的成绩更稳定.
【点评】本题考查了求中位数、求众数、方差的意义,熟练掌握相关知识点是解题的关键.
15.(2025 东莞市二模)2023年6月5日是世界环境日,某学校举办了以“生态文明与环境保护”为主题的相关知识测试.为了了解学生对“生态文明与环境保护”相关知识的掌握情况,现从七年级和八年级参与竞赛的学生中各随机选出20名同学的成绩进行分析(单位:分,满分100分),将学生竞赛成绩分为A,B,C,D四个等级,分别是:
A:x<70,B:70≤x<80,C:80≤x<90,D:90≤x≤100.
其中,七年级学生的竞赛成绩为:
66,75,76,78,79,81,82,83,84,86,
86,88,88,88,91,92,94,95,96,96;
八年级等级C的学生成绩为:81,82,83,86,87,88,89.
两组数据的平均数、中位数、众数、方差如下表:
学生 平均数 中位数 众数 方差
七年级 85.2 86 b 59.66
八年级 85.2 a 91 91.76
根据以上信息,解答下列问题;
(1)填空:a= 87.5 ,b= 88 ,m= 35 ;
(2)根据以上数据,你认为在此次知识竞赛中,哪个年级的成绩更好?请说明理由;(一条理由即可)
(3)若七年级有500名学生参赛,八年级有700名学生参赛,请估计两个年级参赛学生中成绩优秀(大于或等于90分)的学生共有多少人?
【考点】方差;用样本估计总体;算术平均数;中位数;众数.
【专题】统计的应用;数据分析观念;运算能力.
【答案】(1)87.5,88,35;
(2)八年级的成绩更好,理由见解析;
(3)430人.
【分析】(1)利用中位数和众数的定义即可求出a和b的值;利用八年级C组的频数除以20即可得m的值;
(2)根据平均数、中位数和众数的角度进行分析即可得;
(3)分别利用500和800乘以七、八年级的优秀率即可得.
【解答】解:(1)八年级A、B组的频数和为20×(10%+15%)=5,
所以将八年级20名学生的成绩按从大到小排序后,第10个数和第11个数在C组,分别为87,88,
则其中位数a87.5,
七年级D组的人数为10%×20=2(人),
根据七年级成绩可知88分的最多有3人,所以众数为b=88,
∵m%=7÷20×100%=35%,
所以m=35;
故答案为:87.5,88,35;
(2)八年级的成绩更好,理由如下:
七、八年级的平均数相同,但八年级成绩的中位数和众数都比七年级的大,所以八年级的更好;
(3)500700×(1﹣10%﹣15%﹣35%)=150+280=430(人),
答:估计两个年级参赛学生中成绩优秀(大于或等于90分)的学生共有430人.
【点评】本题考查频数分布直方图,用样本估算总体,加权平均数,中位数,掌握相关知识是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末核心考点 数据的离散程度
一.选择题(共7小题)
1.(2025 兰州模拟)已知一组数据x1,x2,x3,x4,x5的平均数为4,方差是3.2,则另一组数据2x1+2,2x2+2,2x3+2,2x4+2,2x5+2的平均数和方差分别是( )
A.4,5.2 B.8,6.4 C.10,12.8 D.12,16
2.(2025 南明区一模)投壶是中国古代一种传统礼仪和宴饮游戏.某校2025年迎新活动中,九年级(1)班5名同学参加投壶游戏体验传统民俗,每人有10支箭进行投壶,投进去的箭数分别为:6,8,5,9,7(单位:支),某同学求得这组数据的平均数为7支,则这组数据的方差是( )
A.2 B.3 C.4 D.5
3.(2025 濠江区一模)科学家记录了四种花卉的平均开花天数(天数越短开花越快)和方差(方差越小开花越稳定),数据如表.
种类 甲种类 乙种类 丙种类 丁种类
平均数 2.3 2.3 2.8 3.1
方差 1.05 0.78 1.05 0.78
开花最快且最稳定的是( )
A.甲种类 B.乙种类 C.丙种类 D.丁种类
4.(2025春 定海区期中)某社团统计成员一周的活动时间情况,列出了方差的计算公式:,则的值是( )
A.4 B.3 C.3.6 D.4.25
5.(2025 崇左二模)某班30位同学的安全知识测试成绩统计如表,其中有两个数据被遮盖,不影响下列关于成绩的统计量的是( )
成绩 24 25 26 27 28 29 30
人数 □ □ 3 3 6 7 9
A.平均数,众数 B.中位数,众数
C.平均数,方差 D.中位数,方差
6.(2025春 高州市期中)体育锻炼是学生健康成长的重要组成部分,为此学校开展了丰富的体育活动.甲乙两位同学积极参加学校举办的1分钟跳绳比赛,训练期间甲乙两名同学各进行10次跳绳练均成绩均为195下,他们成绩的方差分别是:,,根据方差的意义可知( )
A.甲的成绩波动比乙大
B.乙的成绩波动比甲大
C.甲、乙两人成绩波动一样大
D.无法比较甲、乙两人成绩波动大小
7.(2025 洛阳一模)甲、乙两人在相同条件下各射击10次.两人的成绩(单位:环)如图所示.下列结论正确的是( )
①甲的成绩更稳定;②乙的成绩更稳定;③乙的平均成绩更高;④每人再射击一次,乙的成绩一定比甲高.
A.①③ B.②③ C.③④ D.①④
二.填空题(共5小题)
8.(2025 婺城区二模)如图是甲、乙两人5次投篮成绩统计图(每人每次投球10个),若甲、乙5次成绩的方差分别为、,则 (填“>”“=”或“<”).
9.(2025 黄岩区二模)甲、乙两位同学近4次中考数学模拟考试成绩的平均分相同,方差如下:S2甲=81,S2乙=107,则甲、乙两位同学4次模拟考成绩更稳定的是 .(填“甲”或“乙”)
10.(2025 建邺区一模)在评选活动中,6位评委的打分为:10,8,9,8,6,7,这组数据的方差为;去掉一个最高分和一个最低分后,方差为,则 (填“>”“<”或“=”号).
11.(2025 西山区一模)生物学研究表明,植物光合作用速率越高,单位时间内合成的有机物越多.为了解甲、乙、丙、丁四个品种大豆的光合作用速率,科研人员从这四个品种的大豆中各选五株,在同等实验条件下,测量它们的光合作用速率(单位:μmol m﹣2 s﹣1),统计结果如表:
品种 甲 乙 丙 丁
平均数 24 25 23 25
方差 7.6 15.6 6.8 4
则这四个大豆品种中光合作用速率又快又稳定的是 .
12.(2025春 西城区校级期中)甲、乙、丙、丁四名运动员参加掷标枪比赛,下表记录了四人选拔测试(每人掷5次)的相关数据:
甲 乙 丙 丁
平均距离/m 45 54 48 54
方差 3.2 3.3 4.8 6.4
根据表中数据,四名运动员中选成绩又好又稳定的是 .
三.解答题(共3小题)
13.(2024秋 薛城区期末)枣庄某服装店的某件衣服最近销售火爆.现有A、B两家供应商到服装店推销服装,两家服装价格相同,品质相近.服装店决定通过检查材料的纯度来确定选购哪家的服装.检查人员从两家提供的材料样品中分别随机抽取15块相同的材料,通过特殊操作检验出其纯度(单位:%),并对数据进行整理、描述和分析.部分信息如下:
Ⅰ.A供应商供应材料的纯度(单位:%)如下:
A 72 73 74 75 76 78 79
频数 1 1 5 3 3 1 1
Ⅱ.B供应商供应材料的纯度(单位:%)如下:
72 75 72 75 78 77 73 75 76 77 71 78 79 72 75
Ⅲ.A、B两供应商供应材料纯度的平均数、中位数、众数和方差如下:
平均数 中位数 众数 方差
A 75 75 74 3.07
B a b c 6
根据以上信息,回答下列问题:
(1)表格中的a= ,b= ,c= ;
(2)你认为服装店应选择哪个供应商供应服装?为什么?
14.(2025 江阴市二模)某班以小组为单位开展知识竞赛,规定满分为10分,9分及以上为优秀.
有甲、乙两组同学,每组各8人,按照1﹣8号进行编号,他们的成绩统计图如下:
小夏对这两个小组的成绩进行了如下分析:
平均数(分) 中位数(分) 众数(分) 方差 优秀率
甲组 7.625 a 7 4.48 37.5%
乙组 7.625 7 b 0.73 c
请阅读上述信息,回答下列问题:
(1)填空:a= ,b= ,c= ;
(2)根据所学的统计知识,请你利用数据,从不同角度对甲、乙两组的成绩进行比较与评价.
15.(2025 东莞市二模)2023年6月5日是世界环境日,某学校举办了以“生态文明与环境保护”为主题的相关知识测试.为了了解学生对“生态文明与环境保护”相关知识的掌握情况,现从七年级和八年级参与竞赛的学生中各随机选出20名同学的成绩进行分析(单位:分,满分100分),将学生竞赛成绩分为A,B,C,D四个等级,分别是:
A:x<70,B:70≤x<80,C:80≤x<90,D:90≤x≤100.
其中,七年级学生的竞赛成绩为:
66,75,76,78,79,81,82,83,84,86,
86,88,88,88,91,92,94,95,96,96;
八年级等级C的学生成绩为:81,82,83,86,87,88,89.
两组数据的平均数、中位数、众数、方差如下表:
学生 平均数 中位数 众数 方差
七年级 85.2 86 b 59.66
八年级 85.2 a 91 91.76
根据以上信息,解答下列问题;
(1)填空:a= ,b= ,m= ;
(2)根据以上数据,你认为在此次知识竞赛中,哪个年级的成绩更好?请说明理由;(一条理由即可)
(3)若七年级有500名学生参赛,八年级有700名学生参赛,请估计两个年级参赛学生中成绩优秀(大于或等于90分)的学生共有多少人?
期末核心考点 数据的离散程度
参考答案与试题解析
一.选择题(共7小题)
1.(2025 兰州模拟)已知一组数据x1,x2,x3,x4,x5的平均数为4,方差是3.2,则另一组数据2x1+2,2x2+2,2x3+2,2x4+2,2x5+2的平均数和方差分别是( )
A.4,5.2 B.8,6.4 C.10,12.8 D.12,16
【考点】方差;算术平均数.
【专题】统计的应用.
【答案】C
【分析】根据平均数的定义和方差的定义解答即可.
【解答】解:∵一组数据x1,x2,x3,x4,x5的平均数为4,
∴x1+x2+x3+x4+x5=20,
∴
=10,
∵一组数据x1,x2,x3,x4,x5的平均数为4,方差是3.2,
∴,
∴另一组数据的方差为
=4×3.2
=12.8,
故选:C.
【点评】本题主要考查了确定一组数据的方差和平均数,理解方差和平均数的意义是解题的关键.
2.(2025 南明区一模)投壶是中国古代一种传统礼仪和宴饮游戏.某校2025年迎新活动中,九年级(1)班5名同学参加投壶游戏体验传统民俗,每人有10支箭进行投壶,投进去的箭数分别为:6,8,5,9,7(单位:支),某同学求得这组数据的平均数为7支,则这组数据的方差是( )
A.2 B.3 C.4 D.5
【考点】方差;算术平均数.
【专题】数据的收集与整理;数据分析观念.
【答案】A
【分析】根据方差的公式计算即可.
【解答】解:这组数据的方差为:[(6﹣7)2+(8﹣7)2+(5﹣7)2+(9﹣7)2+(7﹣7)2]=2.
故选:A.
【点评】本题考查了方差,方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
3.(2025 濠江区一模)科学家记录了四种花卉的平均开花天数(天数越短开花越快)和方差(方差越小开花越稳定),数据如表.
种类 甲种类 乙种类 丙种类 丁种类
平均数 2.3 2.3 2.8 3.1
方差 1.05 0.78 1.05 0.78
开花最快且最稳定的是( )
A.甲种类 B.乙种类 C.丙种类 D.丁种类
【考点】方差.
【专题】数据的收集与整理;数据分析观念.
【答案】B
【分析】先比较平均数,再比较方差;方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.据此只要比较方差大小即可求解.
【解答】解:甲种类和乙种类的平均数相同,且比丙种类与丁种类的小,所以甲种类和乙种类开花最快;
又因为乙种类的方差比甲小,所以开花最快且最稳定的是乙种类.
故选:B.
【点评】本题考查方差的意义,正确记忆相关知识点是解题关键.
4.(2025春 定海区期中)某社团统计成员一周的活动时间情况,列出了方差的计算公式:,则的值是( )
A.4 B.3 C.3.6 D.4.25
【考点】方差;算术平均数.
【专题】统计的应用;运算能力.
【答案】C
【分析】根据方差的计算算式得出这组数据为2、2、3、3、3、3、4、4、4、8,再根据平均数的定义列式计算即可.
【解答】解:由题意知,这组数据为2、2、3、3、3、3、4、4、4、8,
所以这组数据的平均数为(2×2+3×4+4×3+8)=3.6,
故选:C.
【点评】本题主要考查方差与平均数,解题的关键是掌握方差与算术平均数的定义.
5.(2025 崇左二模)某班30位同学的安全知识测试成绩统计如表,其中有两个数据被遮盖,不影响下列关于成绩的统计量的是( )
成绩 24 25 26 27 28 29 30
人数 □ □ 3 3 6 7 9
A.平均数,众数 B.中位数,众数
C.平均数,方差 D.中位数,方差
【考点】方差;加权平均数;中位数;众数.
【专题】数据的收集与整理;数据分析观念.
【答案】B
【分析】先计算成绩在24、25的学生数,再根据平均数、众数、中位数、方差的定义进行判断即可.
【解答】解:成绩24、25的学生数共:30﹣3﹣3﹣6﹣7﹣9=2(位).
成绩在24、25的学生数会影响该组数据的平均数,也会影响该组数据的方差.
由于成绩在第十五、第十六的两个数都是29,其它各个成绩出现次数都大于3,
所以成绩在24、25的学生数,不会影响该组数据的中位数和众数.
故选:B.
【点评】本题考查了统计的有关概念,掌握平均数、众数、中位数、方差的定义和计算方法是解决本题的关键.
6.(2025春 高州市期中)体育锻炼是学生健康成长的重要组成部分,为此学校开展了丰富的体育活动.甲乙两位同学积极参加学校举办的1分钟跳绳比赛,训练期间甲乙两名同学各进行10次跳绳练均成绩均为195下,他们成绩的方差分别是:,,根据方差的意义可知( )
A.甲的成绩波动比乙大
B.乙的成绩波动比甲大
C.甲、乙两人成绩波动一样大
D.无法比较甲、乙两人成绩波动大小
【考点】方差.
【专题】统计与概率;数据分析观念.
【答案】A
【分析】根据方差的意义解答即可.
【解答】解:∵平均成绩均为195下,,
∴甲的成绩波动比乙大,
故选:A.
【点评】本题考查方差的意义.方差反映了一组数据的波动大小,熟练掌握方差越小,波动性越小是解本题的关键.
7.(2025 洛阳一模)甲、乙两人在相同条件下各射击10次.两人的成绩(单位:环)如图所示.下列结论正确的是( )
①甲的成绩更稳定;②乙的成绩更稳定;③乙的平均成绩更高;④每人再射击一次,乙的成绩一定比甲高.
A.①③ B.②③ C.③④ D.①④
【考点】方差.
【专题】统计的应用.
【答案】A
【分析】方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定,根据方差、平均数的意义进行判断即可求出答案.
【解答】解:根据图象可知甲的波动比乙小,则甲的成绩更加稳定,故①正确,②错误;
根据图象可知甲的平均成绩稳定在5以下,而乙的平均成绩稳定在7.5左右,则乙的平均成绩更高,故③正确;
如果每人再射击一次,但乙的成绩不一定比甲高,只能是可能性较大,因为乙的平均成绩更高,但是波动较大,故④错误;
故选:A.
【点评】本题考查了平均数、方差的意义、解答本题的关键是掌握它们的定义.
二.填空题(共5小题)
8.(2025 婺城区二模)如图是甲、乙两人5次投篮成绩统计图(每人每次投球10个),若甲、乙5次成绩的方差分别为、,则 < (填“>”“=”或“<”).
【考点】方差.
【专题】统计的应用.
【答案】<.
【分析】先分别求出甲、乙的平均数和方差,进行比较即可得到结论.
【解答】解:甲的平均成绩为,
,
乙的平均成绩为,
,
∴.
故答案为:<.
【点评】此题主要考查了求方差,熟练掌握方差的计算方法是解题的关键.
9.(2025 黄岩区二模)甲、乙两位同学近4次中考数学模拟考试成绩的平均分相同,方差如下:S2甲=81,S2乙=107,则甲、乙两位同学4次模拟考成绩更稳定的是 甲 .(填“甲”或“乙”)
【考点】方差.
【专题】数据的收集与整理;数据分析观念.
【答案】甲.
【分析】根据方差的意义解答即可.
【解答】解:∵S2甲=81,S2乙=107,
∴S2<S2乙,
∴甲、乙两位同学4次模考成绩更稳定的是甲.
故答案为:甲.
【点评】本题主要考查方差,方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越差;反之,则它与其平均值的离散程度越小,稳定性越好.
10.(2025 建邺区一模)在评选活动中,6位评委的打分为:10,8,9,8,6,7,这组数据的方差为;去掉一个最高分和一个最低分后,方差为,则 > (填“>”“<”或“=”号).
【考点】方差;算术平均数.
【专题】统计的应用;运算能力.
【答案】>.
【分析】分别根据方差公式计算出方差,然后判断即可.
【解答】解:6位评委的打分的平均数为8,
这组数据的方差s[(10﹣8)2+(8﹣8)2+(9﹣8)2+(8﹣8)2+(6﹣8)2+(7﹣8)2],
去掉一个最高分和一个最低分后平均数为8,
方差s[(8﹣8)2+(9﹣8)2+(8﹣8)2+(7﹣8)2],
∵,
∴ss.
故答案为:>.
【点评】本题主要考查了方差和算术平均数,熟记方差公式是解题的关键.
11.(2025 西山区一模)生物学研究表明,植物光合作用速率越高,单位时间内合成的有机物越多.为了解甲、乙、丙、丁四个品种大豆的光合作用速率,科研人员从这四个品种的大豆中各选五株,在同等实验条件下,测量它们的光合作用速率(单位:μmol m﹣2 s﹣1),统计结果如表:
品种 甲 乙 丙 丁
平均数 24 25 23 25
方差 7.6 15.6 6.8 4
则这四个大豆品种中光合作用速率又快又稳定的是 丁 .
【考点】方差;负整数指数幂.
【专题】概率及其应用;数据分析观念.
【答案】见试题解答内容
【分析】先比较平均数得到乙和丁光合作用速率较高,然后比较方差得到丁比较稳定.
【解答】解:因为乙和丁光合作用速率的平均数较高,所以从乙和丁中选取,
又丁的方差比乙小,所以丁的光合作用速率比较稳定,
所以应选择的优良大豆品种是丁.
故答案为:丁.
【点评】本题考查了方差:一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差.方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.也考查了平均数的意义.
12.(2025春 西城区校级期中)甲、乙、丙、丁四名运动员参加掷标枪比赛,下表记录了四人选拔测试(每人掷5次)的相关数据:
甲 乙 丙 丁
平均距离/m 45 54 48 54
方差 3.2 3.3 4.8 6.4
根据表中数据,四名运动员中选成绩又好又稳定的是 乙 .
【考点】方差.
【专题】数据的收集与整理;数据分析观念.
【答案】乙.
【分析】首先比较平均数,平均数相同时选择方差较小的参加比赛.
【解答】解:由表知乙、丁平均数相等,大于甲、丙射击成绩的平均数,
∴从乙、丁中选择一人参加竞赛,
∵乙的方差较小,
∴四名运动员中选成绩又好又稳定的是乙.
故答案为:乙.
【点评】此题考查了平均数和方差,解答本题的关键是明确方差的定义:方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
三.解答题(共3小题)
13.(2024秋 薛城区期末)枣庄某服装店的某件衣服最近销售火爆.现有A、B两家供应商到服装店推销服装,两家服装价格相同,品质相近.服装店决定通过检查材料的纯度来确定选购哪家的服装.检查人员从两家提供的材料样品中分别随机抽取15块相同的材料,通过特殊操作检验出其纯度(单位:%),并对数据进行整理、描述和分析.部分信息如下:
Ⅰ.A供应商供应材料的纯度(单位:%)如下:
A 72 73 74 75 76 78 79
频数 1 1 5 3 3 1 1
Ⅱ.B供应商供应材料的纯度(单位:%)如下:
72 75 72 75 78 77 73 75 76 77 71 78 79 72 75
Ⅲ.A、B两供应商供应材料纯度的平均数、中位数、众数和方差如下:
平均数 中位数 众数 方差
A 75 75 74 3.07
B a b c 6
根据以上信息,回答下列问题:
(1)表格中的a= 75 ,b= 75 ,c= 75 ;
(2)你认为服装店应选择哪个供应商供应服装?为什么?
【考点】方差;算术平均数;中位数;众数.
【专题】统计的应用;数据分析观念.
【答案】(1)75;75;75;
(2)选A供应商供应服装,理由见解析.
【分析】(1)根据平均数,众数和方差的计算公式分别进行解答即可;
(2)根据方差的定义,方差越小数据越稳定即可得出答案.
【解答】解:(1)根据平均数,众数和方差的计算公式分别进行可得:
,
将数据按从小到大排列,可确定中位数b=75,
∵75出现的次数最多,
∴众数c=75,
故答案为:75;75;75;
(2)选A供应商供应服装,理由如下:
∵B的方差比A的大,A更稳定,
∴选A供应商供应服装.
【点评】本题主要考查了方差、平均数、中位数、众数等知识点,熟悉相关统计量的计算公式和意义是解决此题的关键.
14.(2025 江阴市二模)某班以小组为单位开展知识竞赛,规定满分为10分,9分及以上为优秀.
有甲、乙两组同学,每组各8人,按照1﹣8号进行编号,他们的成绩统计图如下:
小夏对这两个小组的成绩进行了如下分析:
平均数(分) 中位数(分) 众数(分) 方差 优秀率
甲组 7.625 a 7 4.48 37.5%
乙组 7.625 7 b 0.73 c
请阅读上述信息,回答下列问题:
(1)填空:a= 7.5 ,b= 7 ,c= 25% ;
(2)根据所学的统计知识,请你利用数据,从不同角度对甲、乙两组的成绩进行比较与评价.
【考点】方差;中位数;众数.
【专题】统计的应用.
【答案】(1)7.5;7;25%;
(2)见解析.
【分析】(1)根据中位数、众数、优秀率的定义即可求解;
(2)从优秀率、中位数和方差等角度进行分析即可.
【解答】解:(1)将甲组的成绩从小到大顺序排列,中位数为第4位和第5位的平均数,
∴,
乙组的成绩出现次数最多的是7分,共5次,
∴b=7,
乙组的成绩9分及以上有2人,
∴优秀率,
故答案为:7.5;7;25%;
(2)①甲组成绩的优秀率为37.5%,乙组成绩的优秀率为25%,
∴从优秀率的角度来看,甲组的成绩比乙组的成绩好;
②甲组成绩的中位数为7.5,乙组成绩的中位数为7,
∴从中位数的角度来看,甲组的成绩比乙组的成绩好;
③甲组成绩的方差为4.48,乙组成绩的方差为0.73,
∴从方差的角度来看,乙组的成绩比甲组的成绩更稳定.
【点评】本题考查了求中位数、求众数、方差的意义,熟练掌握相关知识点是解题的关键.
15.(2025 东莞市二模)2023年6月5日是世界环境日,某学校举办了以“生态文明与环境保护”为主题的相关知识测试.为了了解学生对“生态文明与环境保护”相关知识的掌握情况,现从七年级和八年级参与竞赛的学生中各随机选出20名同学的成绩进行分析(单位:分,满分100分),将学生竞赛成绩分为A,B,C,D四个等级,分别是:
A:x<70,B:70≤x<80,C:80≤x<90,D:90≤x≤100.
其中,七年级学生的竞赛成绩为:
66,75,76,78,79,81,82,83,84,86,
86,88,88,88,91,92,94,95,96,96;
八年级等级C的学生成绩为:81,82,83,86,87,88,89.
两组数据的平均数、中位数、众数、方差如下表:
学生 平均数 中位数 众数 方差
七年级 85.2 86 b 59.66
八年级 85.2 a 91 91.76
根据以上信息,解答下列问题;
(1)填空:a= 87.5 ,b= 88 ,m= 35 ;
(2)根据以上数据,你认为在此次知识竞赛中,哪个年级的成绩更好?请说明理由;(一条理由即可)
(3)若七年级有500名学生参赛,八年级有700名学生参赛,请估计两个年级参赛学生中成绩优秀(大于或等于90分)的学生共有多少人?
【考点】方差;用样本估计总体;算术平均数;中位数;众数.
【专题】统计的应用;数据分析观念;运算能力.
【答案】(1)87.5,88,35;
(2)八年级的成绩更好,理由见解析;
(3)430人.
【分析】(1)利用中位数和众数的定义即可求出a和b的值;利用八年级C组的频数除以20即可得m的值;
(2)根据平均数、中位数和众数的角度进行分析即可得;
(3)分别利用500和800乘以七、八年级的优秀率即可得.
【解答】解:(1)八年级A、B组的频数和为20×(10%+15%)=5,
所以将八年级20名学生的成绩按从大到小排序后,第10个数和第11个数在C组,分别为87,88,
则其中位数a87.5,
七年级D组的人数为10%×20=2(人),
根据七年级成绩可知88分的最多有3人,所以众数为b=88,
∵m%=7÷20×100%=35%,
所以m=35;
故答案为:87.5,88,35;
(2)八年级的成绩更好,理由如下:
七、八年级的平均数相同,但八年级成绩的中位数和众数都比七年级的大,所以八年级的更好;
(3)500700×(1﹣10%﹣15%﹣35%)=150+280=430(人),
答:估计两个年级参赛学生中成绩优秀(大于或等于90分)的学生共有430人.
【点评】本题考查频数分布直方图,用样本估算总体,加权平均数,中位数,掌握相关知识是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
