【期末核心考点】与三角形有关的边和角(含解析)2024-2025学年七年级下册数学华东师大版(2024)
文档属性
| 名称 | 【期末核心考点】与三角形有关的边和角(含解析)2024-2025学年七年级下册数学华东师大版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 852.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-14 19:16:21 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
期末核心考点 与三角形有关的边和角
一.选择题(共7小题)
1.(2024秋 贵池区期末)△ABC中,AB=6,BC=2,若边AC的长为偶数,则△ABC的周长为( )
A.12 B.14 C.15 D.16
2.(2024秋 砀山县期末)如图,△ABC缺了一个角∠C,若∠A=76°,∠B=20°,则∠C的度数是( )
A.96° B.86° C.84° D.66°
3.(2025 茂名一模)如图,△ABC和△DEF都是直角三角形,∠C=∠F=90°,∠B=45°,∠D=30°,点A在DE上.若DF∥AB,则∠CAD的度数为( )
A.60° B.45° C.30° D.15°
4.(2024秋 醴陵市期末)如图,在△ABC中,线段BE表示△ABC的边AC上的高的图是( )
A. B.
C. D.
5.(2024秋 武陟县期末)将一副三角板按照如图方式摆放,点C、B、E共线,∠FEB=62°,则∠EDB的度数为( )
A.12° B.13° C.17° D.18°
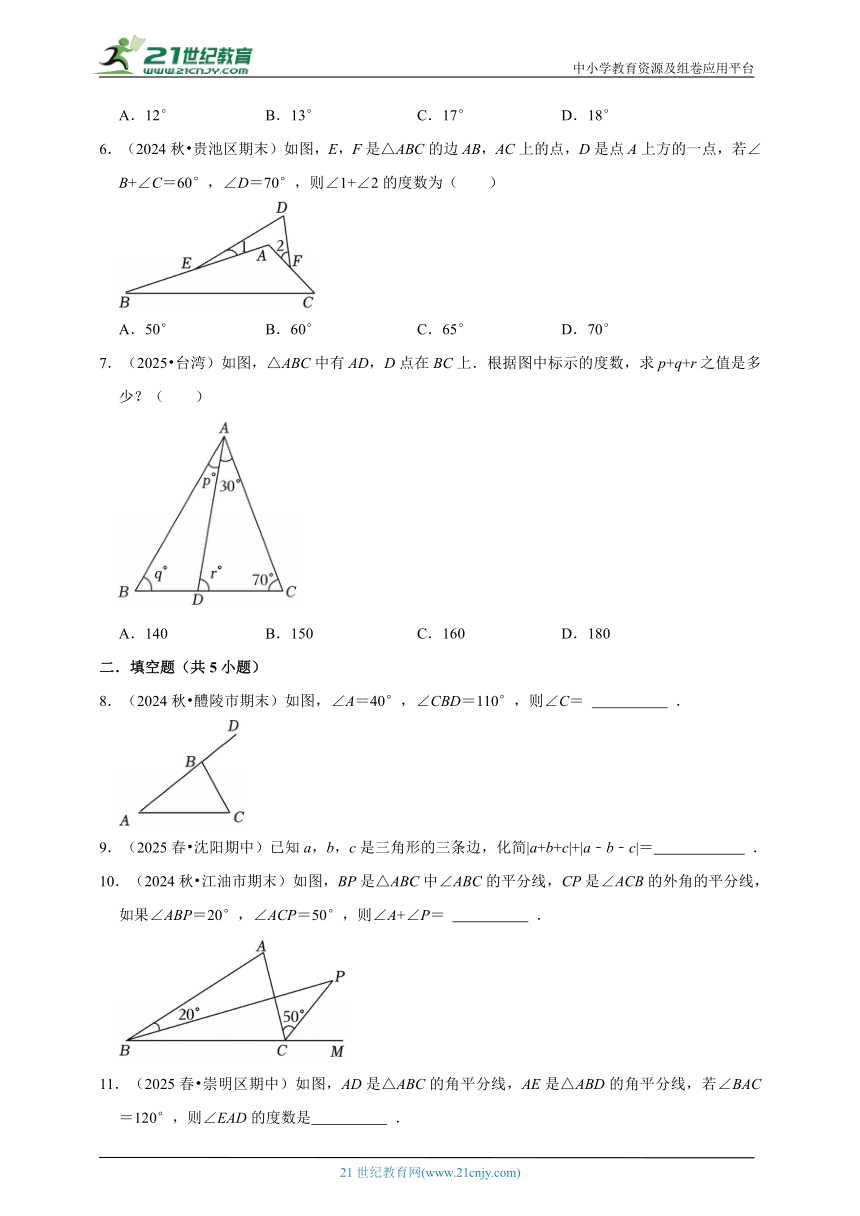
6.(2024秋 贵池区期末)如图,E,F是△ABC的边AB,AC上的点,D是点A上方的一点,若∠B+∠C=60°,∠D=70°,则∠1+∠2的度数为( )
A.50° B.60° C.65° D.70°
7.(2025 台湾)如图,△ABC中有AD,D点在BC上.根据图中标示的度数,求p+q+r之值是多少?( )
A.140 B.150 C.160 D.180
二.填空题(共5小题)
8.(2024秋 醴陵市期末)如图,∠A=40°,∠CBD=110°,则∠C= .
9.(2025春 沈阳期中)已知a,b,c是三角形的三条边,化简|a+b+c|+|a﹣b﹣c|= .
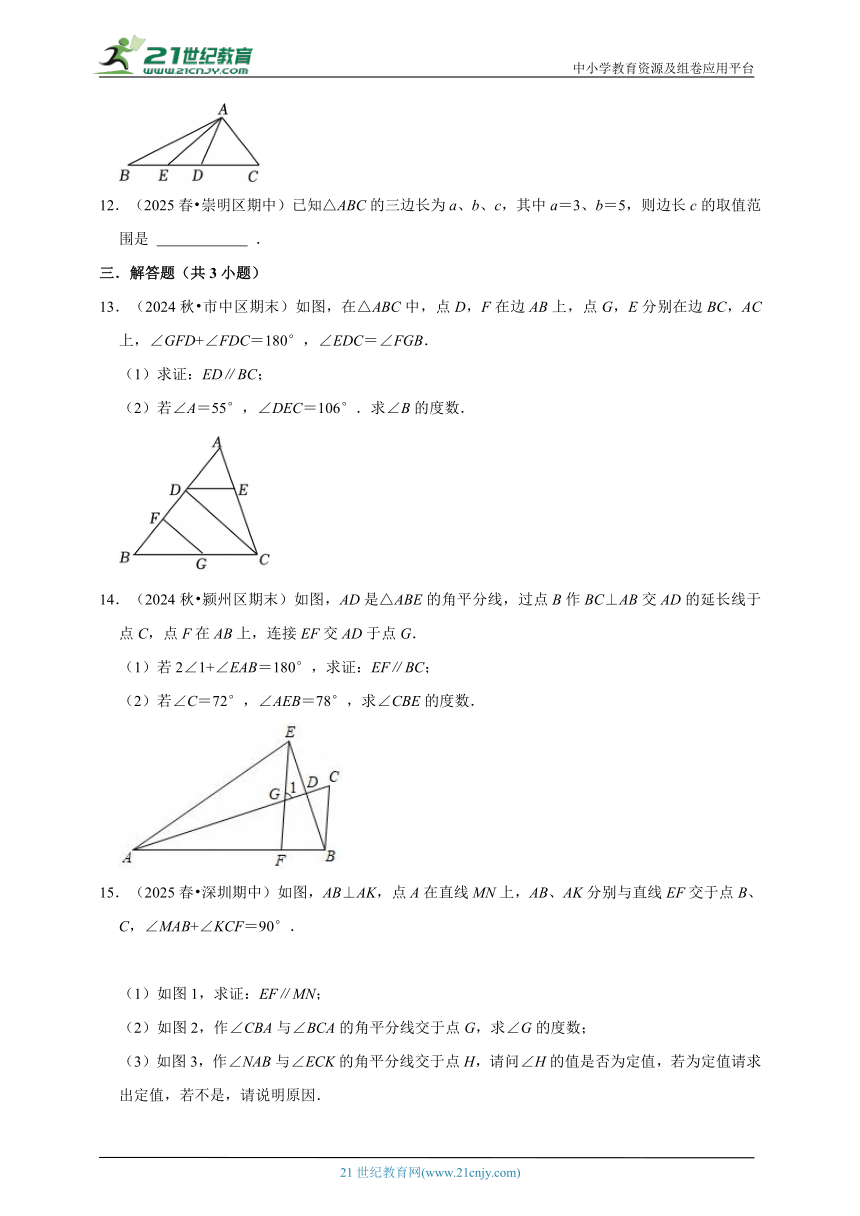
10.(2024秋 江油市期末)如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P= .
11.(2025春 崇明区期中)如图,AD是△ABC的角平分线,AE是△ABD的角平分线,若∠BAC=120°,则∠EAD的度数是 .
12.(2025春 崇明区期中)已知△ABC的三边长为a、b、c,其中a=3、b=5,则边长c的取值范围是 .
三.解答题(共3小题)
13.(2024秋 市中区期末)如图,在△ABC中,点D,F在边AB上,点G,E分别在边BC,AC上,∠GFD+∠FDC=180°,∠EDC=∠FGB.
(1)求证:ED∥BC;
(2)若∠A=55°,∠DEC=106°.求∠B的度数.
14.(2024秋 颍州区期末)如图,AD是△ABE的角平分线,过点B作BC⊥AB交AD的延长线于点C,点F在AB上,连接EF交AD于点G.
(1)若2∠1+∠EAB=180°,求证:EF∥BC;
(2)若∠C=72°,∠AEB=78°,求∠CBE的度数.
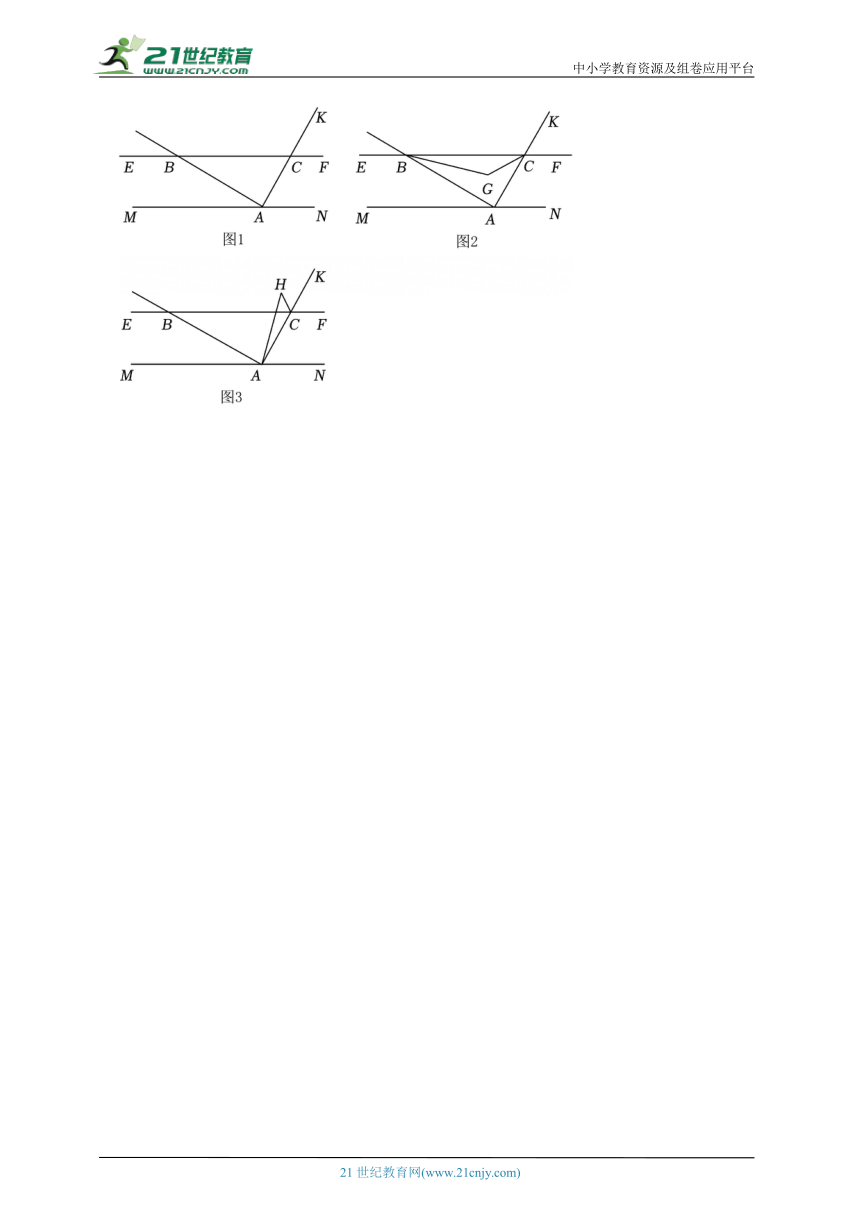
15.(2025春 深圳期中)如图,AB⊥AK,点A在直线MN上,AB、AK分别与直线EF交于点B、C,∠MAB+∠KCF=90°.
(1)如图1,求证:EF∥MN;
(2)如图2,作∠CBA与∠BCA的角平分线交于点G,求∠G的度数;
(3)如图3,作∠NAB与∠ECK的角平分线交于点H,请问∠H的值是否为定值,若为定值请求出定值,若不是,请说明原因.
期末核心考点 与三角形有关的边和角
参考答案与试题解析
一.选择题(共7小题)
1.(2024秋 贵池区期末)△ABC中,AB=6,BC=2,若边AC的长为偶数,则△ABC的周长为( )
A.12 B.14 C.15 D.16
【考点】三角形三边关系.
【专题】三角形;推理能力.
【答案】B
【分析】三角形任意两边之和大于第三边,任意两边之差小于第三边.根据三角形的三边关系求得第三边的取值范围;再根据第三边是偶数,确定第三边的值,从而求得三角形的周长.
【解答】解:∵AB=6,BC=2,
∴6﹣2<AC<6+2,
即4<AC<8,
∵AC为偶数,
∴AC=6,
∴△ABC的周长为:6+2+6=14,
故选:B.
【点评】本题考查了三角形三条边的关系,熟练掌握三角形三条边的关系是解答本题的关键.
2.(2024秋 砀山县期末)如图,△ABC缺了一个角∠C,若∠A=76°,∠B=20°,则∠C的度数是( )
A.96° B.86° C.84° D.66°
【考点】三角形内角和定理.
【专题】线段、角、相交线与平行线;三角形;推理能力.
【答案】C
【分析】根据三角形内角和定理可得∠C=180°﹣∠A﹣∠B,由此即可求出答案.
【解答】解:根据三角形内角和定理可得:∠C=180°﹣76°﹣20°=84°,
故选:C.
【点评】本题考查了三角形内角和定理,熟练掌握该知识点是关键.
3.(2025 茂名一模)如图,△ABC和△DEF都是直角三角形,∠C=∠F=90°,∠B=45°,∠D=30°,点A在DE上.若DF∥AB,则∠CAD的度数为( )
A.60° B.45° C.30° D.15°
【考点】三角形内角和定理;平行线的性质.
【专题】线段、角、相交线与平行线;三角形;运算能力.
【答案】D
【分析】在△ABC中,利用三角形内角和定理,可求出∠BAC的度数,由DF∥AB,利用“两直线平行,内错角相等”,可求出∠BAD的度数,再结合∠CAD=∠BAC﹣∠BAD,即可求出∠CAD的度数.
【解答】解:在△ABC中,∠C=90°,∠B=45°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣45°﹣90°=45°.
∵DF∥AB,
∴∠BAD=∠D=30°,
∴∠CAD=∠BAC﹣∠BAD=45°﹣30°=15°.
故选:D.
【点评】本题考查了平行线的性质以及三角形内角和定理,牢记“两直线平行,内错角相等”及“三角形的内角和等于180°”是解题的关键.
4.(2024秋 醴陵市期末)如图,在△ABC中,线段BE表示△ABC的边AC上的高的图是( )
A. B.
C. D.
【考点】三角形的角平分线、中线和高.
【专题】三角形;应用意识.
【答案】D
【分析】根据三角形高的定义判断即可.
【解答】解:过点B作AC的垂线,且垂足在直线AC上,
所以正确画出AC边上的高的是D选项,
故选:D.
【点评】本题主要考查了三角形高线的定义,熟练掌握从三角形的一个顶点向对边所在直线作垂线,顶点与垂足间的线段叫做三角形的高是解题的关键.
5.(2024秋 武陟县期末)将一副三角板按照如图方式摆放,点C、B、E共线,∠FEB=62°,则∠EDB的度数为( )
A.12° B.13° C.17° D.18°
【考点】三角形内角和定理.
【专题】三角形;推理能力.
【答案】B
【分析】由三角板的特征得出∠DEF=45°,∠ABC=30°,即可求出∠BED、∠ABE的度数,在△BED中根据三角形内角和定理即可求出∠EDB的度数.
【解答】解:根据题意得,∠DEF=45°,∠ABC=30°,
∵∠FEB=62°,
∴∠BED=∠FEB﹣∠DEF=62°﹣45°=17°,
∵∠ABC=30°,
∴∠ABE=180°﹣∠ABC=180°﹣30°=150°,
∴∠EDB=180°﹣∠ABE﹣∠BED=180°﹣150°﹣17°=13°,
故选:B.
【点评】本题考查了三角形内角和定理,一副三角板的特征,熟练掌握三角形内角和定理是解题的关键.
6.(2024秋 贵池区期末)如图,E,F是△ABC的边AB,AC上的点,D是点A上方的一点,若∠B+∠C=60°,∠D=70°,则∠1+∠2的度数为( )
A.50° B.60° C.65° D.70°
【考点】三角形内角和定理.
【专题】三角形;推理能力.
【答案】A
【分析】连接EF,利用三角形的内角和定理结合整体思想即可解决问题.
【解答】解:如图,连接EF,
∵∠B+∠C=60°,
∴∠A=180°﹣(∠B+∠C)=120°,
∴∠AEF+∠AFE=180°﹣∠A=60°.
∵∠D=70°,
∴∠DEF+∠DFE=180°﹣∠D=110°,
∵∠1+∠AEF=∠DEF,∠2+∠AFE=∠DFE,
∴∠1+∠2=∠DEF+∠DFE﹣(∠AEF+∠AFE)=110°﹣60°=50°.
故选:A.
【点评】本题考查三角形内角和定理,熟知三角形的内角和定理及巧用整体思想是解题的关键.
7.(2025 台湾)如图,△ABC中有AD,D点在BC上.根据图中标示的度数,求p+q+r之值是多少?( )
A.140 B.150 C.160 D.180
【考点】三角形的外角性质.
【专题】三角形;几何直观;运算能力.
【答案】C
【分析】先由三角形内角和定理得r=80,再根据三角形外角性质得p+q=80,由此即可得出p+q+r的值.
【解答】解:在△ACD中,∠DAC=30°,∠C=70°,∠ADC=r°,
由三角形内角和定理得:∠DAC+∠C+∠ADC=180°,
∴30°+70°+r°=180°,
∴r=80,
∴∠ADC=r°=80°,
∵∠ADC是△ABD的外角,∠B=q°,∠BAD=p°,
∴∠ADC=∠B+∠BAD=p°+q°,
∴p°+q°=80°,
∴p+q=80,
∴p+q+r=80+80=160.
故选:C.
【点评】此题主要考查了三角形的外角性质,三角形的内角和定理,熟练掌握三角形的外角性质,三角形的内角和定理是解决问题的关键.
二.填空题(共5小题)
8.(2024秋 醴陵市期末)如图,∠A=40°,∠CBD=110°,则∠C= 70° .
【考点】三角形的外角性质.
【专题】三角形;运算能力.
【答案】70°.
【分析】根据∠CBD=∠C+∠A,即可求解.
【解答】解:由条件可知∠CBD=∠C+∠A,
∵∠A=40°,∠CBD=110°,
∴∠C=70°,
故答案为:70°.
【点评】本题考查了三角形外角的性质,三角形的一个外角等于与它不相邻的两个内角的和是关键.
9.(2025春 沈阳期中)已知a,b,c是三角形的三条边,化简|a+b+c|+|a﹣b﹣c|= 2b+2c .
【考点】三角形三边关系;绝对值.
【专题】三角形;推理能力.
【答案】2b+2c.
【分析】先根据三角形的三边关系可得a>0,b>0,c>0,b+c>a,然后根据绝对值的性质,即可求解.
【解答】解:∵a,b,c是三角形的三条边,
∴a+b+c>0,a﹣(b+c)<0,
原式=|a+b+c|+|a﹣(b+c)|
=a+b+c+b+c﹣a
=2b+2c,
故答案为:2b+2c.
【点评】本题主要考查了三角形的三边关系,绝对值,熟知三角形两边之和大于第三边;三角形的两边差小于第三边是解题的关键.
10.(2024秋 江油市期末)如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P= 90° .
【考点】三角形的外角性质;三角形内角和定理.
【专题】三角形;推理能力.
【答案】见试题解答内容
【分析】根据角平分线的定义以及一个三角形的外角等于与它不相邻的两个内角和,可求出∠A的度数,根据补角的定义求出∠ACB的度数,根据三角形的内角和即可求出∠P的度数,即可求出结果.
【解答】解:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,
又∵∠ABP=20°,∠ACP=50°,
∴∠ABC=2∠ABP=40°,∠ACM=2∠ACP=100°,
∴∠A=∠ACM﹣∠ABC=60°,
∠ACB=180°﹣∠ACM=80°,
∴∠BCP=∠ACB+∠ACP=130°,
∵∠PBC=20°,
∴∠P=180°﹣∠PBC﹣∠BCP=30°,
∴∠A+∠P=90°,
故答案为:90°.
【点评】本题考查了三角形的外角性质,三角形的内角和定理,解答的关键是明确:一个三角形的外角等于与它不相邻的两个内角和以及补角的定义以及三角形的内角和为180°.
11.(2025春 崇明区期中)如图,AD是△ABC的角平分线,AE是△ABD的角平分线,若∠BAC=120°,则∠EAD的度数是 30° .
【考点】三角形内角和定理.
【专题】三角形.
【答案】30°.
【分析】根据∠BAC=120°,AD是△ABC 的角平分线,得出,根据AE是△ABD的角平分线,即可得出.
【解答】解:∵AD是△ABC的角平分线,∠BAC=120°,
∴∠DAC=∠DAB=60°,
∵AE是△ABD的角平分线,
∴,
故答案为:30°.
【点评】本题主要考查了三角形的角平分线,掌握其性质是解题的关键.
12.(2025春 崇明区期中)已知△ABC的三边长为a、b、c,其中a=3、b=5,则边长c的取值范围是 2<c<8 .
【考点】三角形三边关系.
【专题】三角形;推理能力.
【答案】2<c<8.
【分析】三角形两边之和大于第三边,三角形两边的差小于第三边,由此即可得到答案.
【解答】解:由三角形三边关系定理得到:5﹣3<c<5+3,
∴2<c<8.
故答案为:2<c<8.
【点评】本题考查三角形三边关系,关键是掌握三角形三边关系定理.
三.解答题(共3小题)
13.(2024秋 市中区期末)如图,在△ABC中,点D,F在边AB上,点G,E分别在边BC,AC上,∠GFD+∠FDC=180°,∠EDC=∠FGB.
(1)求证:ED∥BC;
(2)若∠A=55°,∠DEC=106°.求∠B的度数.
【考点】三角形内角和定理;平行线的判定与性质.
【专题】三角形;运算能力.
【答案】(1)见解析;
(2)51°.
【分析】(1)先证明FG∥CD得到∠FGB=∠DCB,等量代换得∠EDC=∠DCB,进而可得ED∥BC;
(2)根据三角形外角的性质,可以得到∠ADE=51°,然后根据平行线的性质可以求解.
【解答】(1)证明:∵∠GFD+∠FDC=180°,
∴FG∥CD.
∴∠FGB=∠DCB.
∵∠EDC=∠FGB,
∴∠EDC=∠DCB,
∴DE∥BC.
(2)解:由条件可知∠ADE=∠DEC﹣∠A=106°﹣55°=51°.
∵DE∥BC,
∴∠B=∠ADE=51°.
【点评】本题主要考查了平行线的性质与判定,三角形外角的性质,解题的关键在于能够熟练掌握相关知识进行求解.
14.(2024秋 颍州区期末)如图,AD是△ABE的角平分线,过点B作BC⊥AB交AD的延长线于点C,点F在AB上,连接EF交AD于点G.
(1)若2∠1+∠EAB=180°,求证:EF∥BC;
(2)若∠C=72°,∠AEB=78°,求∠CBE的度数.
【考点】三角形内角和定理;平行线的判定与性质.
【专题】三角形;推理能力.
【答案】见试题解答内容
【分析】(1)先根据垂直等于得到∠ABC=90°,则∠C+∠BAC=90°,再证明2∠C+∠EAB=180°,加上2∠1+∠EAB=180°,则∠1=∠C,然后根据平行线的判定方法得到结论;
(2)先根据三角形内角和定理可计算出计算出∠BAC=18°,则∠EAD=18°,根据三角形内角和定理得到∠EAD+∠AED=∠C+∠CBE,即18°+78°=72°+∠CBE,从而可求出∠CBE的度数.
【解答】(1)证明:∵BC⊥AB,
∴∠ABC=90°,
∴∠C+∠BAC=90°,
∵AD是△ABE的角平分线,
∴∠BAC∠EAB,
∴∠C∠EAB=90°,
即2∠C+∠EAB=180°,
∵2∠1+∠EAB=180°,
∴∠1=∠C,
∴EF∥BC;
(2)解:∵∠ABC=90°,∠C=72°,
∴∠BAC=18°,
∴∠EAD=∠BAC=18°,
∵∠ADE=∠BDC,
∴∠EAD+∠AED=∠C+∠CBE,
即18°+78°=72°+∠CBE,
∴∠CBE=24°.
【点评】本题考查了三角形内角和定理:运用三角形内角和定理可根据两已知角求第三个角.也考查了平行线的性质.
15.(2025春 深圳期中)如图,AB⊥AK,点A在直线MN上,AB、AK分别与直线EF交于点B、C,∠MAB+∠KCF=90°.
(1)如图1,求证:EF∥MN;
(2)如图2,作∠CBA与∠BCA的角平分线交于点G,求∠G的度数;
(3)如图3,作∠NAB与∠ECK的角平分线交于点H,请问∠H的值是否为定值,若为定值请求出定值,若不是,请说明原因.
【考点】三角形内角和定理;平行线的判定与性质.
【专题】三角形;推理能力.
【答案】(1)见解析;
(2)∠BGC=135°;
(3)∠H的值是为定值,∠H=45°.
【分析】(1)由垂直定义可得∠MAB+∠KCF=90°,然后根据同角的余角相等可得∠NAC=∠KCF,从而判定两直线平行.
(2)根据角平分线的性质和直角三角形两个锐角互余,可得出∠CBG+∠BCG=45°,再利用三角形内角和180°即可求解.
(3)设∠MAB=∠ABC=x,则∠KCF=90﹣x,再结合角平分线的性质和平行线的性质即可求解.
【解答】(1)证明:∵AB⊥AK,
∴∠MAB+∠NAC=90°,
又∵∠MAB+∠KCF=90°,
∴∠NAC=∠KCF,
∴MN∥EF.
(2)解:∵AB⊥AK,
∴∠BAC=90°,
∴∠CBA+∠ACB=90°,
∵BG平分∠CBA,
∴,
同理,
∴,
∴∠BGC=180°﹣(∠CBG+∠BCG)=135°.
(3)解:∠H的值是为定值.
设∠MAB=x,
则∠ABC=x,∠KCF=90﹣x,
∵AH平分∠BAN,
∴,
∴,
同理,
∴∠H=45°.
【点评】本题考查了角平分线的性质、平行线的判定及性质、直角三角形两锐角互余知识,解决本题的关键是熟练掌握知识点,找到角的关系,列出等式求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末核心考点 与三角形有关的边和角
一.选择题(共7小题)
1.(2024秋 贵池区期末)△ABC中,AB=6,BC=2,若边AC的长为偶数,则△ABC的周长为( )
A.12 B.14 C.15 D.16
2.(2024秋 砀山县期末)如图,△ABC缺了一个角∠C,若∠A=76°,∠B=20°,则∠C的度数是( )
A.96° B.86° C.84° D.66°
3.(2025 茂名一模)如图,△ABC和△DEF都是直角三角形,∠C=∠F=90°,∠B=45°,∠D=30°,点A在DE上.若DF∥AB,则∠CAD的度数为( )
A.60° B.45° C.30° D.15°
4.(2024秋 醴陵市期末)如图,在△ABC中,线段BE表示△ABC的边AC上的高的图是( )
A. B.
C. D.
5.(2024秋 武陟县期末)将一副三角板按照如图方式摆放,点C、B、E共线,∠FEB=62°,则∠EDB的度数为( )
A.12° B.13° C.17° D.18°
6.(2024秋 贵池区期末)如图,E,F是△ABC的边AB,AC上的点,D是点A上方的一点,若∠B+∠C=60°,∠D=70°,则∠1+∠2的度数为( )
A.50° B.60° C.65° D.70°
7.(2025 台湾)如图,△ABC中有AD,D点在BC上.根据图中标示的度数,求p+q+r之值是多少?( )
A.140 B.150 C.160 D.180
二.填空题(共5小题)
8.(2024秋 醴陵市期末)如图,∠A=40°,∠CBD=110°,则∠C= .
9.(2025春 沈阳期中)已知a,b,c是三角形的三条边,化简|a+b+c|+|a﹣b﹣c|= .
10.(2024秋 江油市期末)如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P= .
11.(2025春 崇明区期中)如图,AD是△ABC的角平分线,AE是△ABD的角平分线,若∠BAC=120°,则∠EAD的度数是 .
12.(2025春 崇明区期中)已知△ABC的三边长为a、b、c,其中a=3、b=5,则边长c的取值范围是 .
三.解答题(共3小题)
13.(2024秋 市中区期末)如图,在△ABC中,点D,F在边AB上,点G,E分别在边BC,AC上,∠GFD+∠FDC=180°,∠EDC=∠FGB.
(1)求证:ED∥BC;
(2)若∠A=55°,∠DEC=106°.求∠B的度数.
14.(2024秋 颍州区期末)如图,AD是△ABE的角平分线,过点B作BC⊥AB交AD的延长线于点C,点F在AB上,连接EF交AD于点G.
(1)若2∠1+∠EAB=180°,求证:EF∥BC;
(2)若∠C=72°,∠AEB=78°,求∠CBE的度数.
15.(2025春 深圳期中)如图,AB⊥AK,点A在直线MN上,AB、AK分别与直线EF交于点B、C,∠MAB+∠KCF=90°.
(1)如图1,求证:EF∥MN;
(2)如图2,作∠CBA与∠BCA的角平分线交于点G,求∠G的度数;
(3)如图3,作∠NAB与∠ECK的角平分线交于点H,请问∠H的值是否为定值,若为定值请求出定值,若不是,请说明原因.
期末核心考点 与三角形有关的边和角
参考答案与试题解析
一.选择题(共7小题)
1.(2024秋 贵池区期末)△ABC中,AB=6,BC=2,若边AC的长为偶数,则△ABC的周长为( )
A.12 B.14 C.15 D.16
【考点】三角形三边关系.
【专题】三角形;推理能力.
【答案】B
【分析】三角形任意两边之和大于第三边,任意两边之差小于第三边.根据三角形的三边关系求得第三边的取值范围;再根据第三边是偶数,确定第三边的值,从而求得三角形的周长.
【解答】解:∵AB=6,BC=2,
∴6﹣2<AC<6+2,
即4<AC<8,
∵AC为偶数,
∴AC=6,
∴△ABC的周长为:6+2+6=14,
故选:B.
【点评】本题考查了三角形三条边的关系,熟练掌握三角形三条边的关系是解答本题的关键.
2.(2024秋 砀山县期末)如图,△ABC缺了一个角∠C,若∠A=76°,∠B=20°,则∠C的度数是( )
A.96° B.86° C.84° D.66°
【考点】三角形内角和定理.
【专题】线段、角、相交线与平行线;三角形;推理能力.
【答案】C
【分析】根据三角形内角和定理可得∠C=180°﹣∠A﹣∠B,由此即可求出答案.
【解答】解:根据三角形内角和定理可得:∠C=180°﹣76°﹣20°=84°,
故选:C.
【点评】本题考查了三角形内角和定理,熟练掌握该知识点是关键.
3.(2025 茂名一模)如图,△ABC和△DEF都是直角三角形,∠C=∠F=90°,∠B=45°,∠D=30°,点A在DE上.若DF∥AB,则∠CAD的度数为( )
A.60° B.45° C.30° D.15°
【考点】三角形内角和定理;平行线的性质.
【专题】线段、角、相交线与平行线;三角形;运算能力.
【答案】D
【分析】在△ABC中,利用三角形内角和定理,可求出∠BAC的度数,由DF∥AB,利用“两直线平行,内错角相等”,可求出∠BAD的度数,再结合∠CAD=∠BAC﹣∠BAD,即可求出∠CAD的度数.
【解答】解:在△ABC中,∠C=90°,∠B=45°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣45°﹣90°=45°.
∵DF∥AB,
∴∠BAD=∠D=30°,
∴∠CAD=∠BAC﹣∠BAD=45°﹣30°=15°.
故选:D.
【点评】本题考查了平行线的性质以及三角形内角和定理,牢记“两直线平行,内错角相等”及“三角形的内角和等于180°”是解题的关键.
4.(2024秋 醴陵市期末)如图,在△ABC中,线段BE表示△ABC的边AC上的高的图是( )
A. B.
C. D.
【考点】三角形的角平分线、中线和高.
【专题】三角形;应用意识.
【答案】D
【分析】根据三角形高的定义判断即可.
【解答】解:过点B作AC的垂线,且垂足在直线AC上,
所以正确画出AC边上的高的是D选项,
故选:D.
【点评】本题主要考查了三角形高线的定义,熟练掌握从三角形的一个顶点向对边所在直线作垂线,顶点与垂足间的线段叫做三角形的高是解题的关键.
5.(2024秋 武陟县期末)将一副三角板按照如图方式摆放,点C、B、E共线,∠FEB=62°,则∠EDB的度数为( )
A.12° B.13° C.17° D.18°
【考点】三角形内角和定理.
【专题】三角形;推理能力.
【答案】B
【分析】由三角板的特征得出∠DEF=45°,∠ABC=30°,即可求出∠BED、∠ABE的度数,在△BED中根据三角形内角和定理即可求出∠EDB的度数.
【解答】解:根据题意得,∠DEF=45°,∠ABC=30°,
∵∠FEB=62°,
∴∠BED=∠FEB﹣∠DEF=62°﹣45°=17°,
∵∠ABC=30°,
∴∠ABE=180°﹣∠ABC=180°﹣30°=150°,
∴∠EDB=180°﹣∠ABE﹣∠BED=180°﹣150°﹣17°=13°,
故选:B.
【点评】本题考查了三角形内角和定理,一副三角板的特征,熟练掌握三角形内角和定理是解题的关键.
6.(2024秋 贵池区期末)如图,E,F是△ABC的边AB,AC上的点,D是点A上方的一点,若∠B+∠C=60°,∠D=70°,则∠1+∠2的度数为( )
A.50° B.60° C.65° D.70°
【考点】三角形内角和定理.
【专题】三角形;推理能力.
【答案】A
【分析】连接EF,利用三角形的内角和定理结合整体思想即可解决问题.
【解答】解:如图,连接EF,
∵∠B+∠C=60°,
∴∠A=180°﹣(∠B+∠C)=120°,
∴∠AEF+∠AFE=180°﹣∠A=60°.
∵∠D=70°,
∴∠DEF+∠DFE=180°﹣∠D=110°,
∵∠1+∠AEF=∠DEF,∠2+∠AFE=∠DFE,
∴∠1+∠2=∠DEF+∠DFE﹣(∠AEF+∠AFE)=110°﹣60°=50°.
故选:A.
【点评】本题考查三角形内角和定理,熟知三角形的内角和定理及巧用整体思想是解题的关键.
7.(2025 台湾)如图,△ABC中有AD,D点在BC上.根据图中标示的度数,求p+q+r之值是多少?( )
A.140 B.150 C.160 D.180
【考点】三角形的外角性质.
【专题】三角形;几何直观;运算能力.
【答案】C
【分析】先由三角形内角和定理得r=80,再根据三角形外角性质得p+q=80,由此即可得出p+q+r的值.
【解答】解:在△ACD中,∠DAC=30°,∠C=70°,∠ADC=r°,
由三角形内角和定理得:∠DAC+∠C+∠ADC=180°,
∴30°+70°+r°=180°,
∴r=80,
∴∠ADC=r°=80°,
∵∠ADC是△ABD的外角,∠B=q°,∠BAD=p°,
∴∠ADC=∠B+∠BAD=p°+q°,
∴p°+q°=80°,
∴p+q=80,
∴p+q+r=80+80=160.
故选:C.
【点评】此题主要考查了三角形的外角性质,三角形的内角和定理,熟练掌握三角形的外角性质,三角形的内角和定理是解决问题的关键.
二.填空题(共5小题)
8.(2024秋 醴陵市期末)如图,∠A=40°,∠CBD=110°,则∠C= 70° .
【考点】三角形的外角性质.
【专题】三角形;运算能力.
【答案】70°.
【分析】根据∠CBD=∠C+∠A,即可求解.
【解答】解:由条件可知∠CBD=∠C+∠A,
∵∠A=40°,∠CBD=110°,
∴∠C=70°,
故答案为:70°.
【点评】本题考查了三角形外角的性质,三角形的一个外角等于与它不相邻的两个内角的和是关键.
9.(2025春 沈阳期中)已知a,b,c是三角形的三条边,化简|a+b+c|+|a﹣b﹣c|= 2b+2c .
【考点】三角形三边关系;绝对值.
【专题】三角形;推理能力.
【答案】2b+2c.
【分析】先根据三角形的三边关系可得a>0,b>0,c>0,b+c>a,然后根据绝对值的性质,即可求解.
【解答】解:∵a,b,c是三角形的三条边,
∴a+b+c>0,a﹣(b+c)<0,
原式=|a+b+c|+|a﹣(b+c)|
=a+b+c+b+c﹣a
=2b+2c,
故答案为:2b+2c.
【点评】本题主要考查了三角形的三边关系,绝对值,熟知三角形两边之和大于第三边;三角形的两边差小于第三边是解题的关键.
10.(2024秋 江油市期末)如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P= 90° .
【考点】三角形的外角性质;三角形内角和定理.
【专题】三角形;推理能力.
【答案】见试题解答内容
【分析】根据角平分线的定义以及一个三角形的外角等于与它不相邻的两个内角和,可求出∠A的度数,根据补角的定义求出∠ACB的度数,根据三角形的内角和即可求出∠P的度数,即可求出结果.
【解答】解:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,
又∵∠ABP=20°,∠ACP=50°,
∴∠ABC=2∠ABP=40°,∠ACM=2∠ACP=100°,
∴∠A=∠ACM﹣∠ABC=60°,
∠ACB=180°﹣∠ACM=80°,
∴∠BCP=∠ACB+∠ACP=130°,
∵∠PBC=20°,
∴∠P=180°﹣∠PBC﹣∠BCP=30°,
∴∠A+∠P=90°,
故答案为:90°.
【点评】本题考查了三角形的外角性质,三角形的内角和定理,解答的关键是明确:一个三角形的外角等于与它不相邻的两个内角和以及补角的定义以及三角形的内角和为180°.
11.(2025春 崇明区期中)如图,AD是△ABC的角平分线,AE是△ABD的角平分线,若∠BAC=120°,则∠EAD的度数是 30° .
【考点】三角形内角和定理.
【专题】三角形.
【答案】30°.
【分析】根据∠BAC=120°,AD是△ABC 的角平分线,得出,根据AE是△ABD的角平分线,即可得出.
【解答】解:∵AD是△ABC的角平分线,∠BAC=120°,
∴∠DAC=∠DAB=60°,
∵AE是△ABD的角平分线,
∴,
故答案为:30°.
【点评】本题主要考查了三角形的角平分线,掌握其性质是解题的关键.
12.(2025春 崇明区期中)已知△ABC的三边长为a、b、c,其中a=3、b=5,则边长c的取值范围是 2<c<8 .
【考点】三角形三边关系.
【专题】三角形;推理能力.
【答案】2<c<8.
【分析】三角形两边之和大于第三边,三角形两边的差小于第三边,由此即可得到答案.
【解答】解:由三角形三边关系定理得到:5﹣3<c<5+3,
∴2<c<8.
故答案为:2<c<8.
【点评】本题考查三角形三边关系,关键是掌握三角形三边关系定理.
三.解答题(共3小题)
13.(2024秋 市中区期末)如图,在△ABC中,点D,F在边AB上,点G,E分别在边BC,AC上,∠GFD+∠FDC=180°,∠EDC=∠FGB.
(1)求证:ED∥BC;
(2)若∠A=55°,∠DEC=106°.求∠B的度数.
【考点】三角形内角和定理;平行线的判定与性质.
【专题】三角形;运算能力.
【答案】(1)见解析;
(2)51°.
【分析】(1)先证明FG∥CD得到∠FGB=∠DCB,等量代换得∠EDC=∠DCB,进而可得ED∥BC;
(2)根据三角形外角的性质,可以得到∠ADE=51°,然后根据平行线的性质可以求解.
【解答】(1)证明:∵∠GFD+∠FDC=180°,
∴FG∥CD.
∴∠FGB=∠DCB.
∵∠EDC=∠FGB,
∴∠EDC=∠DCB,
∴DE∥BC.
(2)解:由条件可知∠ADE=∠DEC﹣∠A=106°﹣55°=51°.
∵DE∥BC,
∴∠B=∠ADE=51°.
【点评】本题主要考查了平行线的性质与判定,三角形外角的性质,解题的关键在于能够熟练掌握相关知识进行求解.
14.(2024秋 颍州区期末)如图,AD是△ABE的角平分线,过点B作BC⊥AB交AD的延长线于点C,点F在AB上,连接EF交AD于点G.
(1)若2∠1+∠EAB=180°,求证:EF∥BC;
(2)若∠C=72°,∠AEB=78°,求∠CBE的度数.
【考点】三角形内角和定理;平行线的判定与性质.
【专题】三角形;推理能力.
【答案】见试题解答内容
【分析】(1)先根据垂直等于得到∠ABC=90°,则∠C+∠BAC=90°,再证明2∠C+∠EAB=180°,加上2∠1+∠EAB=180°,则∠1=∠C,然后根据平行线的判定方法得到结论;
(2)先根据三角形内角和定理可计算出计算出∠BAC=18°,则∠EAD=18°,根据三角形内角和定理得到∠EAD+∠AED=∠C+∠CBE,即18°+78°=72°+∠CBE,从而可求出∠CBE的度数.
【解答】(1)证明:∵BC⊥AB,
∴∠ABC=90°,
∴∠C+∠BAC=90°,
∵AD是△ABE的角平分线,
∴∠BAC∠EAB,
∴∠C∠EAB=90°,
即2∠C+∠EAB=180°,
∵2∠1+∠EAB=180°,
∴∠1=∠C,
∴EF∥BC;
(2)解:∵∠ABC=90°,∠C=72°,
∴∠BAC=18°,
∴∠EAD=∠BAC=18°,
∵∠ADE=∠BDC,
∴∠EAD+∠AED=∠C+∠CBE,
即18°+78°=72°+∠CBE,
∴∠CBE=24°.
【点评】本题考查了三角形内角和定理:运用三角形内角和定理可根据两已知角求第三个角.也考查了平行线的性质.
15.(2025春 深圳期中)如图,AB⊥AK,点A在直线MN上,AB、AK分别与直线EF交于点B、C,∠MAB+∠KCF=90°.
(1)如图1,求证:EF∥MN;
(2)如图2,作∠CBA与∠BCA的角平分线交于点G,求∠G的度数;
(3)如图3,作∠NAB与∠ECK的角平分线交于点H,请问∠H的值是否为定值,若为定值请求出定值,若不是,请说明原因.
【考点】三角形内角和定理;平行线的判定与性质.
【专题】三角形;推理能力.
【答案】(1)见解析;
(2)∠BGC=135°;
(3)∠H的值是为定值,∠H=45°.
【分析】(1)由垂直定义可得∠MAB+∠KCF=90°,然后根据同角的余角相等可得∠NAC=∠KCF,从而判定两直线平行.
(2)根据角平分线的性质和直角三角形两个锐角互余,可得出∠CBG+∠BCG=45°,再利用三角形内角和180°即可求解.
(3)设∠MAB=∠ABC=x,则∠KCF=90﹣x,再结合角平分线的性质和平行线的性质即可求解.
【解答】(1)证明:∵AB⊥AK,
∴∠MAB+∠NAC=90°,
又∵∠MAB+∠KCF=90°,
∴∠NAC=∠KCF,
∴MN∥EF.
(2)解:∵AB⊥AK,
∴∠BAC=90°,
∴∠CBA+∠ACB=90°,
∵BG平分∠CBA,
∴,
同理,
∴,
∴∠BGC=180°﹣(∠CBG+∠BCG)=135°.
(3)解:∠H的值是为定值.
设∠MAB=x,
则∠ABC=x,∠KCF=90﹣x,
∵AH平分∠BAN,
∴,
∴,
同理,
∴∠H=45°.
【点评】本题考查了角平分线的性质、平行线的判定及性质、直角三角形两锐角互余知识,解决本题的关键是熟练掌握知识点,找到角的关系,列出等式求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
