【期末核心考点】轴对称(含解析)2024-2025学年七年级下册数学华东师大版(2024)
文档属性
| 名称 | 【期末核心考点】轴对称(含解析)2024-2025学年七年级下册数学华东师大版(2024) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-14 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末核心考点 轴对称
一.选择题(共8小题)
1.(2024秋 醴陵市期末)如图,直线DE是△BAC的边AB的垂直平分线,已知AC=5cm,△ADC的周长为18cm,则BC的长为( )
A.4cm B.10cm C.12cm D.13cm
2.(2025 淮安区校级一模)下列生肖图案中,是轴对称图形的为( )
A. B.
C. D.
3.(2025 罗湖区校级模拟)如图,在△ABC中,∠A=90°,AB=2,BC=5,BD是∠ABC的平分线,设△ABD和△BDC的面积分别是S1,S2,则S1:S2的值为( )
A.5:2 B.2:5 C.1:2 D.1:5
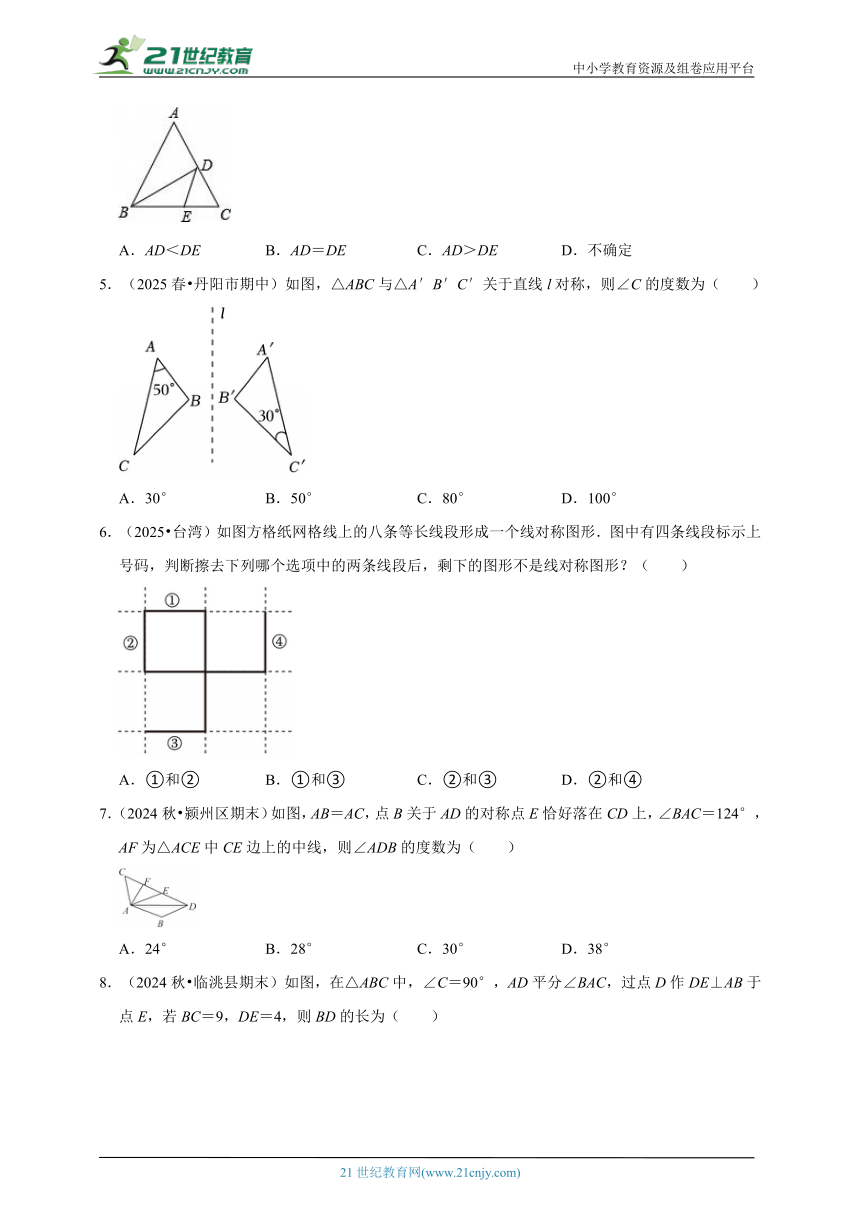
4.(2024秋 太康县期末)如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为( )
A.AD<DE B.AD=DE C.AD>DE D.不确定
5.(2025春 丹阳市期中)如图,△ABC与△A′B′C′关于直线l对称,则∠C的度数为( )
A.30° B.50° C.80° D.100°
6.(2025 台湾)如图方格纸网格线上的八条等长线段形成一个线对称图形.图中有四条线段标示上号码,判断擦去下列哪个选项中的两条线段后,剩下的图形不是线对称图形?( )
A.①和② B.①和③ C.②和③ D.②和④
7.(2024秋 颍州区期末)如图,AB=AC,点B关于AD的对称点E恰好落在CD上,∠BAC=124°,AF为△ACE中CE边上的中线,则∠ADB的度数为( )
A.24° B.28° C.30° D.38°
8.(2024秋 临洮县期末)如图,在△ABC中,∠C=90°,AD平分∠BAC,过点D作DE⊥AB于点E,若BC=9,DE=4,则BD的长为( )
A.4 B.5 C.6 D.7
二.填空题(共4小题)
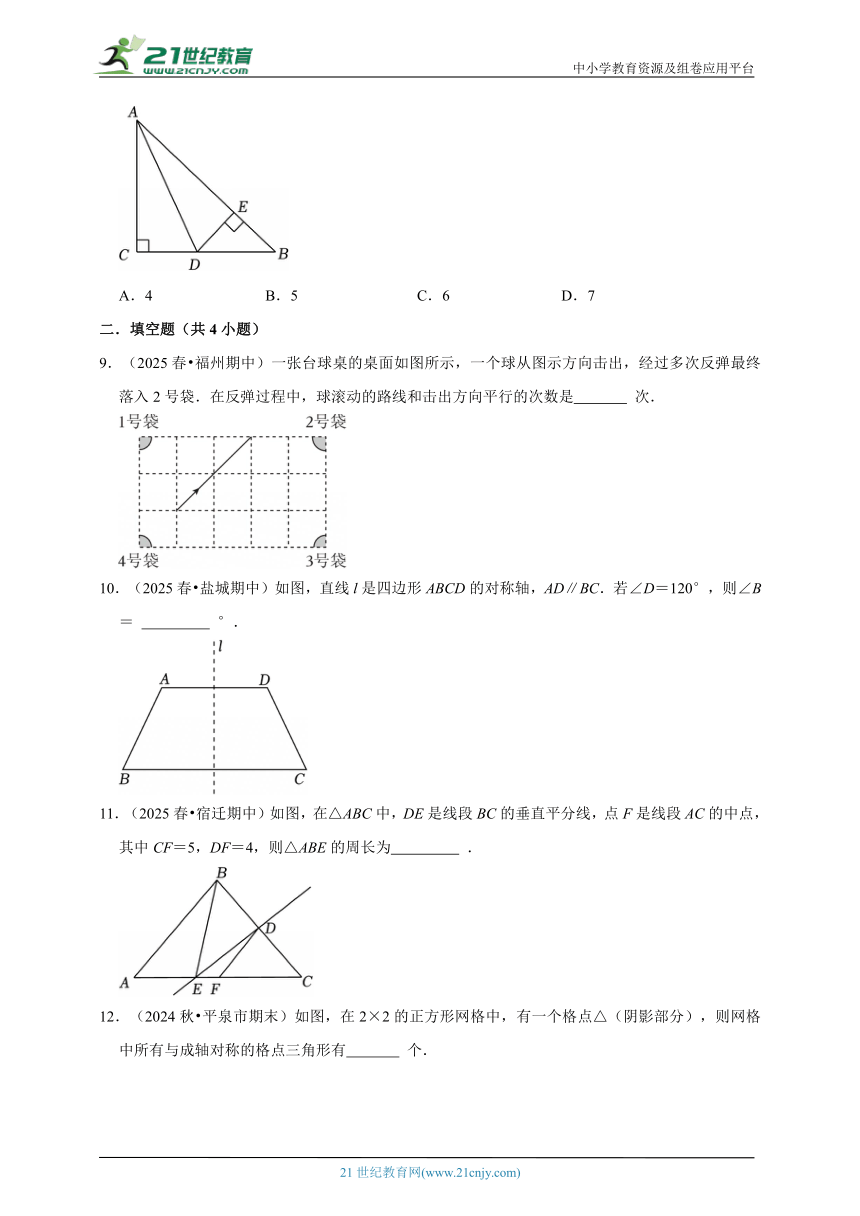
9.(2025春 福州期中)一张台球桌的桌面如图所示,一个球从图示方向击出,经过多次反弹最终落入2号袋.在反弹过程中,球滚动的路线和击出方向平行的次数是 次.
10.(2025春 盐城期中)如图,直线l是四边形ABCD的对称轴,AD∥BC.若∠D=120°,则∠B= °.
11.(2025春 宿迁期中)如图,在△ABC中,DE是线段BC的垂直平分线,点F是线段AC的中点,其中CF=5,DF=4,则△ABE的周长为 .
12.(2024秋 平泉市期末)如图,在2×2的正方形网格中,有一个格点△(阴影部分),则网格中所有与成轴对称的格点三角形有 个.
三.解答题(共3小题)
13.(2024秋 萧县期末)如图,已知直线l和直线外A,B,C三点,按下列要求画图:
(1)画射线AB;
(2)连接BC,延长BC至点D使得CD=BC;
(3)在直线l上确定点E,使得点E到点A,点C的距离之和最短.
14.(2025春 白云区期中)如图,请按要求画图.
(1)过点C画出点C到AB的最短路径CM;
(2)过点D画出DN⊥FC,垂足为N;
(3)过点E画出EP∥FC,交直线DF于点P.
15.(2025 武汉模拟)如图是由小正方形组成的7×7网格,△ABC的顶点A,B,C都是格点,仅用无刻度的直尺在给定网格中完成下列画图.
(1)在图1中,先画△ABC的高CP,再在AC上画一点Q,使得∠AQB=∠ABC;
(2)在图2中,D是AB与网格线的交点,先画线段AD关于AC对称的线段AE,再在AC上画点F,使得EF=AE.
期末核心考点 轴对称
参考答案与试题解析
一.选择题(共8小题)
1.(2024秋 醴陵市期末)如图,直线DE是△BAC的边AB的垂直平分线,已知AC=5cm,△ADC的周长为18cm,则BC的长为( )
A.4cm B.10cm C.12cm D.13cm
【考点】线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】D
【分析】根据线段垂直平分线的性质得到DA=DB,再根据三角形周长公式计算,得到答案.
【解答】解:∵直线DE是AB的垂直平分线,
∴DA=DB,
由条件可知AC+CD+DA=18cm,
∴AC+CD+DB=18cm,
∵AC=5cm,
∴BC=13cm,
故选:D.
【点评】本题考查的是线段的垂直平分线的性质,熟记线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
2.(2025 淮安区校级一模)下列生肖图案中,是轴对称图形的为( )
A. B.
C. D.
【考点】轴对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】A
【分析】如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,据此进行判断即可.
【解答】解:根据轴对称图形的概念逐项分析判断如下:
A.它是轴对称图形,符合题意;
B.它不是轴对称图形,不符合题意;
C.它不是轴对称图形,不符合题意;
D.它不是轴对称图形,不符合题意;
故选:A.
【点评】本题考查轴对称图形的概念,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线成轴对称,熟练掌握此知识点是解题的关键.
3.(2025 罗湖区校级模拟)如图,在△ABC中,∠A=90°,AB=2,BC=5,BD是∠ABC的平分线,设△ABD和△BDC的面积分别是S1,S2,则S1:S2的值为( )
A.5:2 B.2:5 C.1:2 D.1:5
【考点】角平分线的性质.
【专题】线段、角、相交线与平行线;运算能力.
【答案】B
【分析】过D点作DE⊥BC于E,根据角平分线的性质得到DE=DA,然后利用三角形的面积公式求S1:S2的值.
【解答】解:过D点作DE⊥BC于E,如图,
∵BD是∠ABC的平分线,DE⊥BC,DA⊥AB,
∴DE=DA,
∴.
故选:B.
【点评】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.
4.(2024秋 太康县期末)如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为( )
A.AD<DE B.AD=DE C.AD>DE D.不确定
【考点】角平分线的性质.
【答案】D
【分析】根据角平分线上的点到角的两边距离相等可得点D到AB、BC的距离相等,AD、BE都不是点D到AB、BC的距离,大小不确定.
【解答】解:∵BD平分∠ABC,
∴点D到AB、BC的距离相等,
∵AD不是点D到AB的距离,点E是BC上一点,
∴AD、DE的大小不确定.
故选:D.
【点评】本题考查了角平分线上的点到角的两边距离相等的性质,熟记性质并准确识图判断出AD、BE都不是点D到AB、BC的距离是解题的关键.
5.(2025春 丹阳市期中)如图,△ABC与△A′B′C′关于直线l对称,则∠C的度数为( )
A.30° B.50° C.80° D.100°
【考点】轴对称的性质.
【专题】平移、旋转与对称;推理能力.
【答案】A
【分析】根据成轴对称的两条图形的对应角相等,进行求解即可.
【解答】解:由题意,得:∠C=∠C′=30.
故选:A.
【点评】本题考查成轴对称的性质,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.
6.(2025 台湾)如图方格纸网格线上的八条等长线段形成一个线对称图形.图中有四条线段标示上号码,判断擦去下列哪个选项中的两条线段后,剩下的图形不是线对称图形?( )
A.①和② B.①和③ C.②和③ D.②和④
【考点】轴对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】C
【分析】根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,进行分析即可.
【解答】解:擦去①和②,①和③,②和④,剩下的图形是线对称图形;
擦去②和③,剩下的图形不是线对称图形;
故选:C.
【点评】此题主要考查了轴对称图形,轴对称图形是针对一个图形而言的,是一种具有特殊性质图形,被一条直线分割成的两部分沿着对称轴折叠时,互相重合;轴对称图形的对称轴可以是一条,也可以是多条甚至无数条.
7.(2024秋 颍州区期末)如图,AB=AC,点B关于AD的对称点E恰好落在CD上,∠BAC=124°,AF为△ACE中CE边上的中线,则∠ADB的度数为( )
A.24° B.28° C.30° D.38°
【考点】轴对称的性质.
【专题】平移、旋转与对称;推理能力.
【答案】B
【分析】证明AC=AE,利用等腰三角形的三线合一的性质证明∠AFD=90°,求出∠DAF,即可解决问题.
【解答】解:如图,∵△AED与△ABD关于AD对称,
∴AB=AE,∠ADB=∠ADE,∠BAD=∠DAE,
∵AC=AB,
∴AC=AE,
∵AF是△ACE的中线,
∴∠CAF=∠EAF,AF⊥CE,
∴∠DAF∠BAC=62°,
∵∠AFD=90°,
∴∠ADF=90°﹣62°=28°,
∴∠ADB=∠ADF=28°,
故选:B.
【点评】本题考查轴对称的性质,等腰三角形的性质,三角形内角和定理等知识,解题的关键是证明AC=AE,利用等腰三角形的三线合一的性质解决问题.
8.(2024秋 临洮县期末)如图,在△ABC中,∠C=90°,AD平分∠BAC,过点D作DE⊥AB于点E,若BC=9,DE=4,则BD的长为( )
A.4 B.5 C.6 D.7
【考点】角平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】B
【分析】由角平分线的性质推出CD=ED=4,即可求出BD的长.
【解答】解:∵∠C=90°,
∴DC⊥AC,
∵AD平分∠BAC,DE⊥AB,
∴CD=ED=4,
∴BD=BC﹣CD=9﹣4=5.
故选:B.
【点评】本题考查角平分线的性质,关键是由角平分线的性质推出CD=DE.
二.填空题(共4小题)
9.(2025春 福州期中)一张台球桌的桌面如图所示,一个球从图示方向击出,经过多次反弹最终落入2号袋.在反弹过程中,球滚动的路线和击出方向平行的次数是 3 次.
【考点】生活中的轴对称现象;平行线的判定.
【专题】平移、旋转与对称;推理能力.
【答案】3.
【分析】利用轴对称画出图形即可求解.
【解答】解:利用轴对称画出图形可知球的运动路线如图:
∴经过多次反弹最终落入2号袋.在反弹过程中,球滚动的路线和击出方向平行的次数是3次;
故答案为:3.
【点评】本题主要考查了生活中的轴对称现象,关键是正确画出图形.
10.(2025春 盐城期中)如图,直线l是四边形ABCD的对称轴,AD∥BC.若∠D=120°,则∠B= 60 °.
【考点】轴对称的性质;平行线的性质.
【专题】平移、旋转与对称;推理能力.
【答案】60.
【分析】先由平行线的性质求出∠C的度数,再由轴对称图形的性质即可得到答案.
【解答】解:∵AD∥BC,
∴∠D+∠C=180°,
∵∠D=120°,
∴∠C=180°﹣∠D=180°﹣120°=60°,
∵直线l是四边形ABCD的对称轴,
∴∠B=∠C=60°,
故答案为:60.
【点评】本题主要考查了轴对称的性质,平行线的性质,熟知如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线是解题的关键.
11.(2025春 宿迁期中)如图,在△ABC中,DE是线段BC的垂直平分线,点F是线段AC的中点,其中CF=5,DF=4,则△ABE的周长为 18 .
【考点】线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;运算能力.
【答案】18.
【分析】根据垂直平分线的性质得到CE=BE,BD=CD,根据中位线的性质可得AB=2DF=8,AC=2CF=10,进而求解即可.
【解答】解:有条件可知CE=BE,BD=CD,AB=2DF=8,AC=2CF=10,
∴△ABE的周长=AB+AE+BE=AB+AE+CE=AB+AC=18.
故答案为:18.
【点评】本题主要考查了线段垂直平分线的性质及三角形中位线的性质,熟练掌握线段垂直平分线的性质及三角形中位线的性质是解题的关键.
12.(2024秋 平泉市期末)如图,在2×2的正方形网格中,有一个格点△(阴影部分),则网格中所有与成轴对称的格点三角形有 5 个.
【考点】轴对称图形.
【专题】平移、旋转与对称.
【答案】5.
【分析】因为对称图形是全等的,所以面积相等,据此连接矩形的对角线,观察得到的三角形即可解答.
【解答】解:如图,与△ABC成轴对称的格点三角形有△ACF、△ACD、△DBC,△HEG,△HBG共5个,
故答案为:5.
【点评】此题考查轴对称图形,掌握轴对称图形的定义是解答本题的关键.
三.解答题(共3小题)
13.(2024秋 萧县期末)如图,已知直线l和直线外A,B,C三点,按下列要求画图:
(1)画射线AB;
(2)连接BC,延长BC至点D使得CD=BC;
(3)在直线l上确定点E,使得点E到点A,点C的距离之和最短.
【考点】作图—复杂作图;直线、射线、线段;线段的性质:两点之间线段最短;两点间的距离.
【专题】作图题;几何直观.
【答案】(1)(2)(3)作图见解析部分.
【分析】(1)根据射线的定义画出图形.
(2)根据线段的定义画出图形即可.
(3)连接AC交直线l于点E,点E即为所求.
【解答】解:(1)如图,射线AB即为所求.
(2)如图,线段BC,线段CD即为所求.
(3)如图,点E即为所求.
【点评】本题考查作图﹣复杂作图,直线,射线,线段的定义,两点之间线段最短等知识,解题的关键是掌握直线,射线,线段的定义,属于中考常考题型.
14.(2025春 白云区期中)如图,请按要求画图.
(1)过点C画出点C到AB的最短路径CM;
(2)过点D画出DN⊥FC,垂足为N;
(3)过点E画出EP∥FC,交直线DF于点P.
【考点】作图—复杂作图.
【专题】作图题;几何直观.
【答案】见解析.
【分析】(1)根据垂线段的定义画出图形;
(2)根据垂线的定义画出图形;
(3)根据平行线的定义画出图形.
【解答】解:(1)如图,线段CM即为所求;
(2)如图,直线DN即为所求;
(3)如图,直线PE即为所求.
【点评】本题考查作图﹣复杂作图,解题的关键是理解题意,正确画出图形.
15.(2025 武汉模拟)如图是由小正方形组成的7×7网格,△ABC的顶点A,B,C都是格点,仅用无刻度的直尺在给定网格中完成下列画图.
(1)在图1中,先画△ABC的高CP,再在AC上画一点Q,使得∠AQB=∠ABC;
(2)在图2中,D是AB与网格线的交点,先画线段AD关于AC对称的线段AE,再在AC上画点F,使得EF=AE.
【考点】作图﹣轴对称变换.
【专题】几何直观;推理能力.
【答案】(1)图见解析;
(2)图见解析.
【分析】(1)取格点D、E,延长AB交CE于P,连接BD交AC于Q,则点P和点Q即为所求;
(2)如图所示,取格点L、M,连接AM,BL分别交格线于E,R,连接ER交AC于F,则线段AE和点F即为所求.
【解答】解:(1)如图,取格点D、E,延长AB交CE于P,连接BD交AC于Q,则点P和点Q即为所求;
可证明CE⊥AB,即CP⊥AB,则CP即为△ABC的高;
可证明△ABD是等腰直角三角形,则∠ABD=45°,
根据网格的特点可证明∠ACB=45°,
由∠QAB=∠BAC,∠QBA=∠BCA,可得∠AQB=∠ABC;
(2)如图,取格点L、M,连接AM,BL分别交格线于E,R,连接ER交AC于F,则线段AE和点F即为所求;
【点评】本题考查作图—轴对称变换,掌握轴对称变换的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末核心考点 轴对称
一.选择题(共8小题)
1.(2024秋 醴陵市期末)如图,直线DE是△BAC的边AB的垂直平分线,已知AC=5cm,△ADC的周长为18cm,则BC的长为( )
A.4cm B.10cm C.12cm D.13cm
2.(2025 淮安区校级一模)下列生肖图案中,是轴对称图形的为( )
A. B.
C. D.
3.(2025 罗湖区校级模拟)如图,在△ABC中,∠A=90°,AB=2,BC=5,BD是∠ABC的平分线,设△ABD和△BDC的面积分别是S1,S2,则S1:S2的值为( )
A.5:2 B.2:5 C.1:2 D.1:5
4.(2024秋 太康县期末)如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为( )
A.AD<DE B.AD=DE C.AD>DE D.不确定
5.(2025春 丹阳市期中)如图,△ABC与△A′B′C′关于直线l对称,则∠C的度数为( )
A.30° B.50° C.80° D.100°
6.(2025 台湾)如图方格纸网格线上的八条等长线段形成一个线对称图形.图中有四条线段标示上号码,判断擦去下列哪个选项中的两条线段后,剩下的图形不是线对称图形?( )
A.①和② B.①和③ C.②和③ D.②和④
7.(2024秋 颍州区期末)如图,AB=AC,点B关于AD的对称点E恰好落在CD上,∠BAC=124°,AF为△ACE中CE边上的中线,则∠ADB的度数为( )
A.24° B.28° C.30° D.38°
8.(2024秋 临洮县期末)如图,在△ABC中,∠C=90°,AD平分∠BAC,过点D作DE⊥AB于点E,若BC=9,DE=4,则BD的长为( )
A.4 B.5 C.6 D.7
二.填空题(共4小题)
9.(2025春 福州期中)一张台球桌的桌面如图所示,一个球从图示方向击出,经过多次反弹最终落入2号袋.在反弹过程中,球滚动的路线和击出方向平行的次数是 次.
10.(2025春 盐城期中)如图,直线l是四边形ABCD的对称轴,AD∥BC.若∠D=120°,则∠B= °.
11.(2025春 宿迁期中)如图,在△ABC中,DE是线段BC的垂直平分线,点F是线段AC的中点,其中CF=5,DF=4,则△ABE的周长为 .
12.(2024秋 平泉市期末)如图,在2×2的正方形网格中,有一个格点△(阴影部分),则网格中所有与成轴对称的格点三角形有 个.
三.解答题(共3小题)
13.(2024秋 萧县期末)如图,已知直线l和直线外A,B,C三点,按下列要求画图:
(1)画射线AB;
(2)连接BC,延长BC至点D使得CD=BC;
(3)在直线l上确定点E,使得点E到点A,点C的距离之和最短.
14.(2025春 白云区期中)如图,请按要求画图.
(1)过点C画出点C到AB的最短路径CM;
(2)过点D画出DN⊥FC,垂足为N;
(3)过点E画出EP∥FC,交直线DF于点P.
15.(2025 武汉模拟)如图是由小正方形组成的7×7网格,△ABC的顶点A,B,C都是格点,仅用无刻度的直尺在给定网格中完成下列画图.
(1)在图1中,先画△ABC的高CP,再在AC上画一点Q,使得∠AQB=∠ABC;
(2)在图2中,D是AB与网格线的交点,先画线段AD关于AC对称的线段AE,再在AC上画点F,使得EF=AE.
期末核心考点 轴对称
参考答案与试题解析
一.选择题(共8小题)
1.(2024秋 醴陵市期末)如图,直线DE是△BAC的边AB的垂直平分线,已知AC=5cm,△ADC的周长为18cm,则BC的长为( )
A.4cm B.10cm C.12cm D.13cm
【考点】线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】D
【分析】根据线段垂直平分线的性质得到DA=DB,再根据三角形周长公式计算,得到答案.
【解答】解:∵直线DE是AB的垂直平分线,
∴DA=DB,
由条件可知AC+CD+DA=18cm,
∴AC+CD+DB=18cm,
∵AC=5cm,
∴BC=13cm,
故选:D.
【点评】本题考查的是线段的垂直平分线的性质,熟记线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
2.(2025 淮安区校级一模)下列生肖图案中,是轴对称图形的为( )
A. B.
C. D.
【考点】轴对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】A
【分析】如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,据此进行判断即可.
【解答】解:根据轴对称图形的概念逐项分析判断如下:
A.它是轴对称图形,符合题意;
B.它不是轴对称图形,不符合题意;
C.它不是轴对称图形,不符合题意;
D.它不是轴对称图形,不符合题意;
故选:A.
【点评】本题考查轴对称图形的概念,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线成轴对称,熟练掌握此知识点是解题的关键.
3.(2025 罗湖区校级模拟)如图,在△ABC中,∠A=90°,AB=2,BC=5,BD是∠ABC的平分线,设△ABD和△BDC的面积分别是S1,S2,则S1:S2的值为( )
A.5:2 B.2:5 C.1:2 D.1:5
【考点】角平分线的性质.
【专题】线段、角、相交线与平行线;运算能力.
【答案】B
【分析】过D点作DE⊥BC于E,根据角平分线的性质得到DE=DA,然后利用三角形的面积公式求S1:S2的值.
【解答】解:过D点作DE⊥BC于E,如图,
∵BD是∠ABC的平分线,DE⊥BC,DA⊥AB,
∴DE=DA,
∴.
故选:B.
【点评】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.
4.(2024秋 太康县期末)如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为( )
A.AD<DE B.AD=DE C.AD>DE D.不确定
【考点】角平分线的性质.
【答案】D
【分析】根据角平分线上的点到角的两边距离相等可得点D到AB、BC的距离相等,AD、BE都不是点D到AB、BC的距离,大小不确定.
【解答】解:∵BD平分∠ABC,
∴点D到AB、BC的距离相等,
∵AD不是点D到AB的距离,点E是BC上一点,
∴AD、DE的大小不确定.
故选:D.
【点评】本题考查了角平分线上的点到角的两边距离相等的性质,熟记性质并准确识图判断出AD、BE都不是点D到AB、BC的距离是解题的关键.
5.(2025春 丹阳市期中)如图,△ABC与△A′B′C′关于直线l对称,则∠C的度数为( )
A.30° B.50° C.80° D.100°
【考点】轴对称的性质.
【专题】平移、旋转与对称;推理能力.
【答案】A
【分析】根据成轴对称的两条图形的对应角相等,进行求解即可.
【解答】解:由题意,得:∠C=∠C′=30.
故选:A.
【点评】本题考查成轴对称的性质,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.
6.(2025 台湾)如图方格纸网格线上的八条等长线段形成一个线对称图形.图中有四条线段标示上号码,判断擦去下列哪个选项中的两条线段后,剩下的图形不是线对称图形?( )
A.①和② B.①和③ C.②和③ D.②和④
【考点】轴对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】C
【分析】根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,进行分析即可.
【解答】解:擦去①和②,①和③,②和④,剩下的图形是线对称图形;
擦去②和③,剩下的图形不是线对称图形;
故选:C.
【点评】此题主要考查了轴对称图形,轴对称图形是针对一个图形而言的,是一种具有特殊性质图形,被一条直线分割成的两部分沿着对称轴折叠时,互相重合;轴对称图形的对称轴可以是一条,也可以是多条甚至无数条.
7.(2024秋 颍州区期末)如图,AB=AC,点B关于AD的对称点E恰好落在CD上,∠BAC=124°,AF为△ACE中CE边上的中线,则∠ADB的度数为( )
A.24° B.28° C.30° D.38°
【考点】轴对称的性质.
【专题】平移、旋转与对称;推理能力.
【答案】B
【分析】证明AC=AE,利用等腰三角形的三线合一的性质证明∠AFD=90°,求出∠DAF,即可解决问题.
【解答】解:如图,∵△AED与△ABD关于AD对称,
∴AB=AE,∠ADB=∠ADE,∠BAD=∠DAE,
∵AC=AB,
∴AC=AE,
∵AF是△ACE的中线,
∴∠CAF=∠EAF,AF⊥CE,
∴∠DAF∠BAC=62°,
∵∠AFD=90°,
∴∠ADF=90°﹣62°=28°,
∴∠ADB=∠ADF=28°,
故选:B.
【点评】本题考查轴对称的性质,等腰三角形的性质,三角形内角和定理等知识,解题的关键是证明AC=AE,利用等腰三角形的三线合一的性质解决问题.
8.(2024秋 临洮县期末)如图,在△ABC中,∠C=90°,AD平分∠BAC,过点D作DE⊥AB于点E,若BC=9,DE=4,则BD的长为( )
A.4 B.5 C.6 D.7
【考点】角平分线的性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】B
【分析】由角平分线的性质推出CD=ED=4,即可求出BD的长.
【解答】解:∵∠C=90°,
∴DC⊥AC,
∵AD平分∠BAC,DE⊥AB,
∴CD=ED=4,
∴BD=BC﹣CD=9﹣4=5.
故选:B.
【点评】本题考查角平分线的性质,关键是由角平分线的性质推出CD=DE.
二.填空题(共4小题)
9.(2025春 福州期中)一张台球桌的桌面如图所示,一个球从图示方向击出,经过多次反弹最终落入2号袋.在反弹过程中,球滚动的路线和击出方向平行的次数是 3 次.
【考点】生活中的轴对称现象;平行线的判定.
【专题】平移、旋转与对称;推理能力.
【答案】3.
【分析】利用轴对称画出图形即可求解.
【解答】解:利用轴对称画出图形可知球的运动路线如图:
∴经过多次反弹最终落入2号袋.在反弹过程中,球滚动的路线和击出方向平行的次数是3次;
故答案为:3.
【点评】本题主要考查了生活中的轴对称现象,关键是正确画出图形.
10.(2025春 盐城期中)如图,直线l是四边形ABCD的对称轴,AD∥BC.若∠D=120°,则∠B= 60 °.
【考点】轴对称的性质;平行线的性质.
【专题】平移、旋转与对称;推理能力.
【答案】60.
【分析】先由平行线的性质求出∠C的度数,再由轴对称图形的性质即可得到答案.
【解答】解:∵AD∥BC,
∴∠D+∠C=180°,
∵∠D=120°,
∴∠C=180°﹣∠D=180°﹣120°=60°,
∵直线l是四边形ABCD的对称轴,
∴∠B=∠C=60°,
故答案为:60.
【点评】本题主要考查了轴对称的性质,平行线的性质,熟知如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线是解题的关键.
11.(2025春 宿迁期中)如图,在△ABC中,DE是线段BC的垂直平分线,点F是线段AC的中点,其中CF=5,DF=4,则△ABE的周长为 18 .
【考点】线段垂直平分线的性质.
【专题】线段、角、相交线与平行线;运算能力.
【答案】18.
【分析】根据垂直平分线的性质得到CE=BE,BD=CD,根据中位线的性质可得AB=2DF=8,AC=2CF=10,进而求解即可.
【解答】解:有条件可知CE=BE,BD=CD,AB=2DF=8,AC=2CF=10,
∴△ABE的周长=AB+AE+BE=AB+AE+CE=AB+AC=18.
故答案为:18.
【点评】本题主要考查了线段垂直平分线的性质及三角形中位线的性质,熟练掌握线段垂直平分线的性质及三角形中位线的性质是解题的关键.
12.(2024秋 平泉市期末)如图,在2×2的正方形网格中,有一个格点△(阴影部分),则网格中所有与成轴对称的格点三角形有 5 个.
【考点】轴对称图形.
【专题】平移、旋转与对称.
【答案】5.
【分析】因为对称图形是全等的,所以面积相等,据此连接矩形的对角线,观察得到的三角形即可解答.
【解答】解:如图,与△ABC成轴对称的格点三角形有△ACF、△ACD、△DBC,△HEG,△HBG共5个,
故答案为:5.
【点评】此题考查轴对称图形,掌握轴对称图形的定义是解答本题的关键.
三.解答题(共3小题)
13.(2024秋 萧县期末)如图,已知直线l和直线外A,B,C三点,按下列要求画图:
(1)画射线AB;
(2)连接BC,延长BC至点D使得CD=BC;
(3)在直线l上确定点E,使得点E到点A,点C的距离之和最短.
【考点】作图—复杂作图;直线、射线、线段;线段的性质:两点之间线段最短;两点间的距离.
【专题】作图题;几何直观.
【答案】(1)(2)(3)作图见解析部分.
【分析】(1)根据射线的定义画出图形.
(2)根据线段的定义画出图形即可.
(3)连接AC交直线l于点E,点E即为所求.
【解答】解:(1)如图,射线AB即为所求.
(2)如图,线段BC,线段CD即为所求.
(3)如图,点E即为所求.
【点评】本题考查作图﹣复杂作图,直线,射线,线段的定义,两点之间线段最短等知识,解题的关键是掌握直线,射线,线段的定义,属于中考常考题型.
14.(2025春 白云区期中)如图,请按要求画图.
(1)过点C画出点C到AB的最短路径CM;
(2)过点D画出DN⊥FC,垂足为N;
(3)过点E画出EP∥FC,交直线DF于点P.
【考点】作图—复杂作图.
【专题】作图题;几何直观.
【答案】见解析.
【分析】(1)根据垂线段的定义画出图形;
(2)根据垂线的定义画出图形;
(3)根据平行线的定义画出图形.
【解答】解:(1)如图,线段CM即为所求;
(2)如图,直线DN即为所求;
(3)如图,直线PE即为所求.
【点评】本题考查作图﹣复杂作图,解题的关键是理解题意,正确画出图形.
15.(2025 武汉模拟)如图是由小正方形组成的7×7网格,△ABC的顶点A,B,C都是格点,仅用无刻度的直尺在给定网格中完成下列画图.
(1)在图1中,先画△ABC的高CP,再在AC上画一点Q,使得∠AQB=∠ABC;
(2)在图2中,D是AB与网格线的交点,先画线段AD关于AC对称的线段AE,再在AC上画点F,使得EF=AE.
【考点】作图﹣轴对称变换.
【专题】几何直观;推理能力.
【答案】(1)图见解析;
(2)图见解析.
【分析】(1)取格点D、E,延长AB交CE于P,连接BD交AC于Q,则点P和点Q即为所求;
(2)如图所示,取格点L、M,连接AM,BL分别交格线于E,R,连接ER交AC于F,则线段AE和点F即为所求.
【解答】解:(1)如图,取格点D、E,延长AB交CE于P,连接BD交AC于Q,则点P和点Q即为所求;
可证明CE⊥AB,即CP⊥AB,则CP即为△ABC的高;
可证明△ABD是等腰直角三角形,则∠ABD=45°,
根据网格的特点可证明∠ACB=45°,
由∠QAB=∠BAC,∠QBA=∠BCA,可得∠AQB=∠ABC;
(2)如图,取格点L、M,连接AM,BL分别交格线于E,R,连接ER交AC于F,则线段AE和点F即为所求;
【点评】本题考查作图—轴对称变换,掌握轴对称变换的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
