【期末核心考点】图形的全等(含解析)2024-2025学年七年级下册数学华东师大版(2024)
文档属性
| 名称 | 【期末核心考点】图形的全等(含解析)2024-2025学年七年级下册数学华东师大版(2024) |

|
|
| 格式 | docx | ||
| 文件大小 | 917.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-14 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末核心考点 图形的全等
一.选择题(共7小题)
1.(2025 平阴县二模)如图,△ABC≌△CDE,若∠D=35°,∠ACB=45°,则∠DCE的度数( )
A.35° B.45° C.80° D.100°
2.(2024秋 安阳期末)如图,△ABC≌△AEF,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
3.(2025 厦门校级模拟)如图,△ABC≌△ADE,∠D=25°,∠C=105°,∠CAE=70°,则∠BAE的度数是( )
A.20° B.25° C.30° D.35°
4.(2024秋 阳新县期末)如图所示的网格是由9个相同的小正方形拼成的,图形的各个顶点均为格点,则∠1﹣∠2﹣∠3的度数为( )
A.30° B.45° C.55° D.60°
5.(2024秋 河池期末)如图,Rt△ABC≌Rt△DBE,若∠A=30°,则∠D的度数为( )
A.60° B.45° C.35° D.30°
6.(2024秋 滦州市期末)已知图中的两个三角形全等,则∠α的度数是( )
A.40° B.50° C.60° D.70°
7.(2025春 市中区校级期中)如图,AC⊥BE,DE⊥BE,若△ABC≌△BDE,AC=8,DE=3,则CE等于( )
A.4 B.4.5 C.5 D.5.5
二.填空题(共5小题)
8.(2024秋 广信区期末)如图所示,△ACB≌△DEF,其中A与D,C与E是对应顶点,则∠ABC= .
9.(2025 椒江区二模)如图,△ABC≌△CDE,点D在边AC上,若AB=3,CE=8,则AD= .
10.(2024秋 青浦区校级期末)我们规定:在四边形ABCD中,O是边BC上的一点,如果△OAB与△OCD全等,那么点O叫做该四边形的“等形点”.在四边形EFGH中,∠EFG=90°,EF∥GH,EF=5,FG=17,如果该四边形的“等形点”在边FG上,那么四边形EFGH的面积是 .
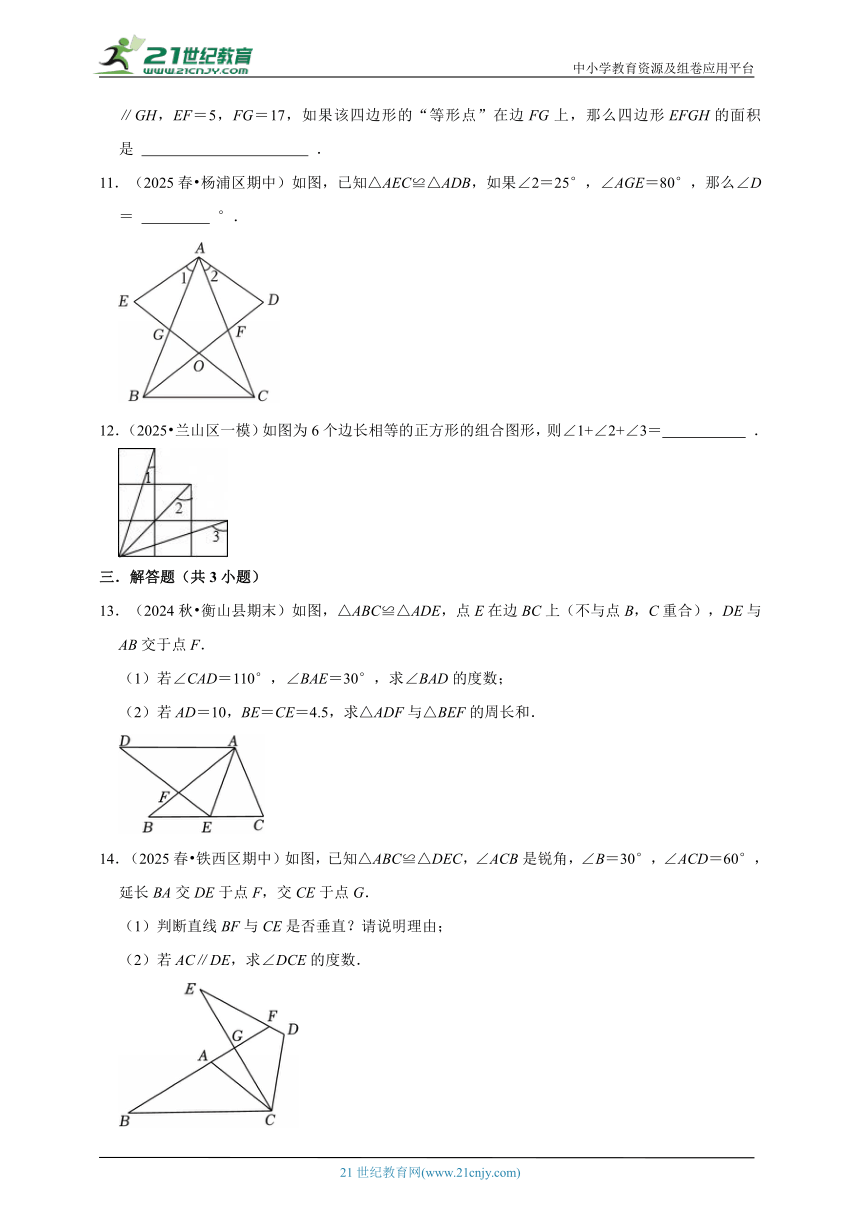
11.(2025春 杨浦区期中)如图,已知△AEC≌△ADB,如果∠2=25°,∠AGE=80°,那么∠D= °.
12.(2025 兰山区一模)如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3= .
三.解答题(共3小题)
13.(2024秋 衡山县期末)如图,△ABC≌△ADE,点E在边BC上(不与点B,C重合),DE与AB交于点F.
(1)若∠CAD=110°,∠BAE=30°,求∠BAD的度数;
(2)若AD=10,BE=CE=4.5,求△ADF与△BEF的周长和.
14.(2025春 铁西区期中)如图,已知△ABC≌△DEC,∠ACB是锐角,∠B=30°,∠ACD=60°,延长BA交DE于点F,交CE于点G.
(1)判断直线BF与CE是否垂直?请说明理由;
(2)若AC∥DE,求∠DCE的度数.
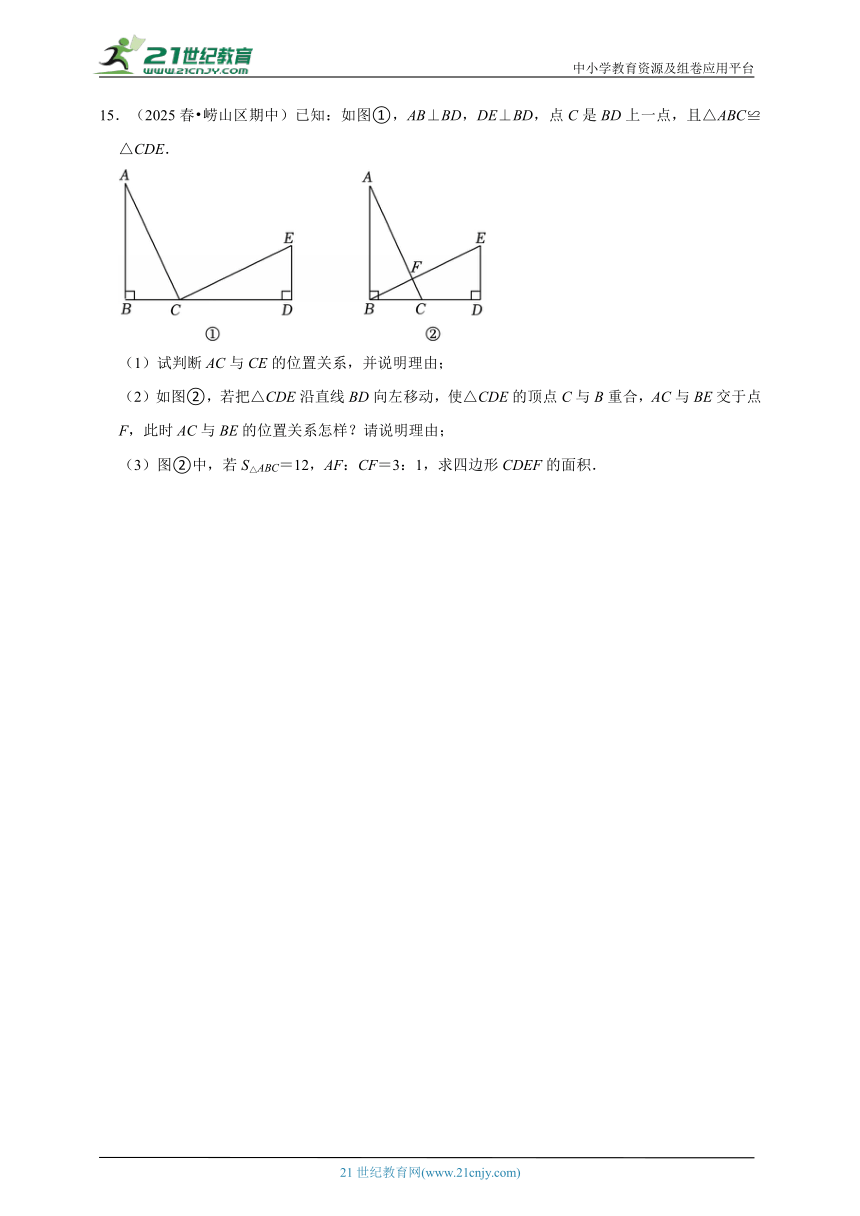
15.(2025春 崂山区期中)已知:如图①,AB⊥BD,DE⊥BD,点C是BD上一点,且△ABC≌△CDE.
(1)试判断AC与CE的位置关系,并说明理由;
(2)如图②,若把△CDE沿直线BD向左移动,使△CDE的顶点C与B重合,AC与BE交于点F,此时AC与BE的位置关系怎样?请说明理由;
(3)图②中,若S△ABC=12,AF:CF=3:1,求四边形CDEF的面积.
期末核心考点 图形的全等
参考答案与试题解析
一.选择题(共7小题)
1.(2025 平阴县二模)如图,△ABC≌△CDE,若∠D=35°,∠ACB=45°,则∠DCE的度数( )
A.35° B.45° C.80° D.100°
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】D
【分析】由全等三角形的对应角相等得到∠E=∠ACB=45°,由三角形内角和定理即可求出∠DCE的度数.
【解答】解:∵△ABC≌△CDE,
∴∠E=∠ACB=45°,
∵∠D=35°,
∴∠DCE=180°﹣45°﹣35°=100°.
故选:D.
【点评】本题考查全等三角形的性质,关键是掌握全等三角形的对应角相等.
2.(2024秋 安阳期末)如图,△ABC≌△AEF,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
【考点】全等三角形的性质.
【专题】图形的全等;运算能力.
【答案】C
【分析】根据全等三角形的性质可得到AF=AC,EF=BC,∠EAF=∠BAC,从而得到∠EAB=∠FAC,最后证明∠EAB=∠FAB不成立即可.
【解答】解:∵△ABC≌△AEF,
∴AF=AC,EF=BC,∠EAF=∠BAC,故①、③符合题意,
∵∠EAB+BAF=∠EAF,∠FAC+∠BAF=∠BAC,
∴∠EAB+BAF=∠FAC+∠BAF,
∴∠EAB=∠FAC,故④符合题意,
∵∠EAF=∠BAC,
∴∠EAB=∠CAF,
∴∠EAB=∠FAB不一定成立,故②不符合题意,
故选:C.
【点评】本题考查全等三角形的性质,掌握全等三角形的性质是关键.
3.(2025 厦门校级模拟)如图,△ABC≌△ADE,∠D=25°,∠C=105°,∠CAE=70°,则∠BAE的度数是( )
A.20° B.25° C.30° D.35°
【考点】全等三角形的性质;三角形内角和定理.
【专题】三角形;图形的全等;推理能力.
【答案】A
【分析】由全等三角形性质推出∠B=∠D=25°,由三角形内角和定理求出∠BAC=50°,即可求出∠BAE的度数.
【解答】解:∵△ABC≌△ADE,
∴∠B=∠D=25°,
∵∠C=105°,
∴∠BAC=180°﹣∠B﹣∠C=50°,
∵∠CAE=70°,
∴∠BAE=∠CAE﹣∠BAC=20°.
故选:A.
【点评】本题考查全等三角形的性质,三角形内角和定理,关键是掌握掌握全等三角形的对应角相等.
4.(2024秋 阳新县期末)如图所示的网格是由9个相同的小正方形拼成的,图形的各个顶点均为格点,则∠1﹣∠2﹣∠3的度数为( )
A.30° B.45° C.55° D.60°
【考点】全等图形.
【专题】图形的全等;推理能力.
【答案】B
【分析】根据网格特点,可得出∠1=90°,∠2=∠4,∠3+∠4=45°,进而可求解.
【解答】解:如图,则∠1=90°,∠2=∠4,∠3+∠4=45°,
∴∠1﹣∠2﹣∠3=90°﹣45°=45°,
故选:B.
【点评】本题考查网格中的全等图形、三角形的外角性质,会利用全等图形求正方形网格中角度之和是解答的关键.
5.(2024秋 河池期末)如图,Rt△ABC≌Rt△DBE,若∠A=30°,则∠D的度数为( )
A.60° B.45° C.35° D.30°
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】D
【分析】由全等三角形的对应角相等即可得到答案.
【解答】解:∵Rt△ABC≌Rt△DBE,
∴∠D=∠A=30°.
故选:D.
【点评】本题考查全等三角形的性质,关键是掌握全等三角形的对应角相等.
6.(2024秋 滦州市期末)已知图中的两个三角形全等,则∠α的度数是( )
A.40° B.50° C.60° D.70°
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】D
【分析】根据全等三角形的对应角相等解答.
【解答】解:∵图中的两个三角形全等,
∴∠α=70°,
故选:D.
【点评】本题考查的是全等三角形的性质,熟记全等三角形的对应角相等是解题的关键.
7.(2025春 市中区校级期中)如图,AC⊥BE,DE⊥BE,若△ABC≌△BDE,AC=8,DE=3,则CE等于( )
A.4 B.4.5 C.5 D.5.5
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】C
【分析】根据全等三角形的性质得到BE=AC=8,BC=DE=3,结合图形根据线段的和差计算即可.
【解答】解:∵△ABC≌△BDE,AC=8,DE=3,
∴BE=AC=8,BC=DE=3,
∴CE=BE﹣BC=8﹣3=5,
故选:C.
【点评】本题考查的是全等三角形的性质,掌握全等三角形的对应边相等是解题的关键.
二.填空题(共5小题)
8.(2024秋 广信区期末)如图所示,△ACB≌△DEF,其中A与D,C与E是对应顶点,则∠ABC= ∠DFE .
【考点】全等三角形的性质.
【专题】图形的全等;运算能力.
【答案】∠DFE.
【分析】注意:全等三角形书写时各对应顶点应在相应位置,可由此准确地找到对应关系.
【解答】解:由题意可得:△ACB≌△DEF,
∴∠ABC=∠DFE.
故答案为:∠DFE.
【点评】本题考查全等三角形的性质,解题的关键是掌握:全等三角形的对应边相等,对应角相等.
9.(2025 椒江区二模)如图,△ABC≌△CDE,点D在边AC上,若AB=3,CE=8,则AD= 5 .
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】5.
【分析】由全等三角形的性质推出CD=AB=3,AC=CE=8,即可求出AD的长.
【解答】解:∵△ABC≌△CDE,
∴CD=AB=3,AC=CE=8,
∴AD=AC﹣CD=5.
故答案为:5.
【点评】本题考查全等三角形的性质,关键是掌握全等三角形的对应边相等.
10.(2024秋 青浦区校级期末)我们规定:在四边形ABCD中,O是边BC上的一点,如果△OAB与△OCD全等,那么点O叫做该四边形的“等形点”.在四边形EFGH中,∠EFG=90°,EF∥GH,EF=5,FG=17,如果该四边形的“等形点”在边FG上,那么四边形EFGH的面积是 或85 .
【考点】全等三角形的性质.
【专题】图形的全等;几何直观;运算能力;推理能力.
【答案】或85.
【分析】依题意得∠EFG=∠HGF=90°,设OF=a,则OG=17﹣a,分两种情况讨论如下:①当EF=FG,OF=HG时,△OEF≌△HOG,由EF=FG得5=17﹣a,解得a=12,则OF=HG=12,此时四边形EFGH是直角梯形,然后根据梯形的面积公式即可求出四边形EFGH的面积;②当EF=HF=5,OF=OG时,△OEF≌△OHG,根据EF∥GH,EF=HF=5,∠EFG=∠HGF=90°得此时四边形EFGH是矩形,然后根据长方形的面积公式即可得出四边形EF的面积,综上所述即可得出答案.
【解答】解:设四边形EFGH的“等形点”为O,
∵∠EFG=90°,EF∥GH,
∴∠EFG=∠HGF=90°,
设OF=a,
∵EF=5,FG=17,点O在FG上,
∴OG=FG﹣OF=17﹣a,
∴有以下两种情况:
①当EF=FG,OF=HG时,△OEF≌△HOG,如图1所示:
由EF=FG,得:5=17﹣a,
解得:a=12,
∴OF=a=12,OG=17﹣12=5,
∴OF=HG=12,
∴EF∥GH,则此时四边形EFGH是直角梯形,
∴S四边形EFGH(EF+HG) FG(5+12)×17;
②当EF=HF=5,OF=OG时,△OEF≌△OHG,如图2所示:
∵EF∥GH,EF=HF=5,∠EFG=∠HGF=90°,
∴四边形EFGH是长方形,
∴S四边形EFGH=EF FG=5×17=85,
综上所述:四边形EFGH的面积是或85.
故答案为:或85.
【点评】此题主要考查了全等三角形的性质,理解四边形的“等形点”的定义,熟练掌握全等三角形的性质是解决问题的关键,分类讨论是解决问题的易错点.
11.(2025春 杨浦区期中)如图,已知△AEC≌△ADB,如果∠2=25°,∠AGE=80°,那么∠D= 75 °.
【考点】全等三角形的性质.
【专题】三角形;图形的全等;几何直观;推理能力.
【答案】75.
【分析】根据全等三角形的性质得∠E=∠D,∠EAC=∠DAB,进而得∠1=∠2=25°,再由三角形内角和定理求出∠E=75°,由此即可得∠D的度数.
【解答】解:∵△AEC≌△ADB,∠2=25°,
∴∠E=∠D,∠EAC=∠DAB,
∴∠1+∠GAC=∠GAC+∠2,
∴∠1=∠2=25°,
在△AEG中,∠AGE=80°,
∴∠E=180°﹣(∠1+∠AGE)=180°﹣(25°+80°)=75°,
∴∠D=75°,
故答案为:75.
【点评】此题主要考查了全等三角形的性质,理解全等三角形的对应角相等,对应边相等是解决问题的关键.
12.(2025 兰山区一模)如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3= 135° .
【考点】全等图形.
【答案】见试题解答内容
【分析】首先利用SAS定理判定△ABC≌△DBE,根据全等三角形的性质可得∠3=∠ACB,再由∠ACB+∠1=∠1+∠3=90°,可得∠1+∠2+∠3=90°.
【解答】解:∵在△ABC和△DBE中,
∴△ABC≌△DBE(SAS),
∴∠3=∠ACB,
∵∠ACB+∠1=90°,
∴∠1+∠3=90°,
∴∠1+∠2+∠3=90°+45°=135°,
故答案为:135°.
【点评】此题主要考查了全等图形,关键是掌握全等三角形的判定,以及全等三角形对应角相等.
三.解答题(共3小题)
13.(2024秋 衡山县期末)如图,△ABC≌△ADE,点E在边BC上(不与点B,C重合),DE与AB交于点F.
(1)若∠CAD=110°,∠BAE=30°,求∠BAD的度数;
(2)若AD=10,BE=CE=4.5,求△ADF与△BEF的周长和.
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】(1)40°;
(2)33.5.
【分析】(1)利用全等三角形的性质、等式的性质可得出∠CAE=∠BAD,然后利用角的和差关系求解即可;
(2)利用全等三角形的性质可求出AB=AD=10,BC=DE=9,然后利用三角形的周长公式求解即可.
【解答】解:(1)∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠CAE=∠BAD,
由条件可知∠CAE+∠BAD=∠CAD﹣∠BAE=80°,
∴∠CAE=∠BAD=40°;
(2)∵AD=10,BE=CE=4.5,△ABC≌△ADE,
∴AB=AD=10,BC=DE=BE+CE=9,
AD+DF+AF+BF+EF+BE
=AD+(DF+EF)+(AF+BF)+BE
=AD+DE+AB+BE
=10+9+10+4.5
=33.5.
【点评】本题考查了全等三角形的性质等知识,熟练掌握该知识点是关键.
14.(2025春 铁西区期中)如图,已知△ABC≌△DEC,∠ACB是锐角,∠B=30°,∠ACD=60°,延长BA交DE于点F,交CE于点G.
(1)判断直线BF与CE是否垂直?请说明理由;
(2)若AC∥DE,求∠DCE的度数.
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】(1)BF⊥CE,理由见解析;
(2)30°.
【分析】(1)先根据全等三角形的性质得出∠B=∠E=30°,∠ACB=∠DCE,故可得出∠ACB+∠ACG=∠DCE+∠ACG=∠ACD=60°,故可得出∠BGC=90°,据此得出结论;
(2)由AC∥DE可知∠E=∠ACG=30°,再根据∠ACD=60°即可得出结论.
【解答】解:(1)BF⊥CE,理由:
∵△ABC≌△DEC,∠B=30°,∠ACD=60°,
∴∠B=∠E=30°,∠ACB=∠DCE,
∴∠BCG=∠ACB+∠ACG=∠DCE+∠ACG=∠ACD=60°,
∴∠BGC=180°﹣∠B﹣∠BCG=180°﹣30°﹣60°=90°,
∴BF⊥CE;
(2)由(1)知∠E=30°,
∵AC∥DE,
∴∠ACG=∠E=30°,
∵∠ACD=60°,
∴∠DCE=∠ACD﹣∠ACG=60°﹣30°=30°.
【点评】本题考查的是全等三角形的性质,熟知全等三角形的对应角相等是解题的关键.
15.(2025春 崂山区期中)已知:如图①,AB⊥BD,DE⊥BD,点C是BD上一点,且△ABC≌△CDE.
(1)试判断AC与CE的位置关系,并说明理由;
(2)如图②,若把△CDE沿直线BD向左移动,使△CDE的顶点C与B重合,AC与BE交于点F,此时AC与BE的位置关系怎样?请说明理由;
(3)图②中,若S△ABC=12,AF:CF=3:1,求四边形CDEF的面积.
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】(1)AC⊥CE,理由见解答过程;
(2)AC⊥BE,理由见解答过程;
(3)9.
【分析】(1)根据全等三角形的性质及直角三角形的性质求出∠ACE=90°,就可以得出AC⊥CE;
(2)如图2,根据△ABC≌△CDE可以得出∠BFC=90°,从而得出结论;
(3)根据S△ABC=12,AF:CF=3:1,可得S△BFCS△ABC=3,由△ABC≌△BDE,得S△BDE=S△ABC=12,进而可以解决问题.
【解答】解:(1)AC⊥CE,理由如下:
∵AB⊥BD,
∴∠B=90°,
∴∠A+∠ACB=90°,
∵△ABC≌△CDE,
∴∠A=∠DCE,∠ACB=∠E,
∴∠DCE+∠ACB=90°,
∵∠DCE+∠ACB+∠ACE=180°,
∴∠ACE=90°,
∴AC⊥CE;
(2)AC⊥BE,理由如下:
∵△ABC≌△BDE,
∴∠A=∠EBD,∠ACB=∠E,
∵∠B=90°,
∴∠A+∠ACB=90°,
∴∠EBD+∠ACB=90°,
∴∠BFC=90°,
∴AC⊥BE;
(3)∵S△ABC=12,AF:CF=3:1,
∴S△BFCS△ABC=3,
∵△ABC≌△BDE,
∴S△BDE=S△ABC=12,
∴四边形CDEF的面积=12﹣3=9.
【点评】本题考查了全等三角形的性质,平移的性质的运用,垂直的判定及性质的运用,熟记全等三角形的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末核心考点 图形的全等
一.选择题(共7小题)
1.(2025 平阴县二模)如图,△ABC≌△CDE,若∠D=35°,∠ACB=45°,则∠DCE的度数( )
A.35° B.45° C.80° D.100°
2.(2024秋 安阳期末)如图,△ABC≌△AEF,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
3.(2025 厦门校级模拟)如图,△ABC≌△ADE,∠D=25°,∠C=105°,∠CAE=70°,则∠BAE的度数是( )
A.20° B.25° C.30° D.35°
4.(2024秋 阳新县期末)如图所示的网格是由9个相同的小正方形拼成的,图形的各个顶点均为格点,则∠1﹣∠2﹣∠3的度数为( )
A.30° B.45° C.55° D.60°
5.(2024秋 河池期末)如图,Rt△ABC≌Rt△DBE,若∠A=30°,则∠D的度数为( )
A.60° B.45° C.35° D.30°
6.(2024秋 滦州市期末)已知图中的两个三角形全等,则∠α的度数是( )
A.40° B.50° C.60° D.70°
7.(2025春 市中区校级期中)如图,AC⊥BE,DE⊥BE,若△ABC≌△BDE,AC=8,DE=3,则CE等于( )
A.4 B.4.5 C.5 D.5.5
二.填空题(共5小题)
8.(2024秋 广信区期末)如图所示,△ACB≌△DEF,其中A与D,C与E是对应顶点,则∠ABC= .
9.(2025 椒江区二模)如图,△ABC≌△CDE,点D在边AC上,若AB=3,CE=8,则AD= .
10.(2024秋 青浦区校级期末)我们规定:在四边形ABCD中,O是边BC上的一点,如果△OAB与△OCD全等,那么点O叫做该四边形的“等形点”.在四边形EFGH中,∠EFG=90°,EF∥GH,EF=5,FG=17,如果该四边形的“等形点”在边FG上,那么四边形EFGH的面积是 .
11.(2025春 杨浦区期中)如图,已知△AEC≌△ADB,如果∠2=25°,∠AGE=80°,那么∠D= °.
12.(2025 兰山区一模)如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3= .
三.解答题(共3小题)
13.(2024秋 衡山县期末)如图,△ABC≌△ADE,点E在边BC上(不与点B,C重合),DE与AB交于点F.
(1)若∠CAD=110°,∠BAE=30°,求∠BAD的度数;
(2)若AD=10,BE=CE=4.5,求△ADF与△BEF的周长和.
14.(2025春 铁西区期中)如图,已知△ABC≌△DEC,∠ACB是锐角,∠B=30°,∠ACD=60°,延长BA交DE于点F,交CE于点G.
(1)判断直线BF与CE是否垂直?请说明理由;
(2)若AC∥DE,求∠DCE的度数.
15.(2025春 崂山区期中)已知:如图①,AB⊥BD,DE⊥BD,点C是BD上一点,且△ABC≌△CDE.
(1)试判断AC与CE的位置关系,并说明理由;
(2)如图②,若把△CDE沿直线BD向左移动,使△CDE的顶点C与B重合,AC与BE交于点F,此时AC与BE的位置关系怎样?请说明理由;
(3)图②中,若S△ABC=12,AF:CF=3:1,求四边形CDEF的面积.
期末核心考点 图形的全等
参考答案与试题解析
一.选择题(共7小题)
1.(2025 平阴县二模)如图,△ABC≌△CDE,若∠D=35°,∠ACB=45°,则∠DCE的度数( )
A.35° B.45° C.80° D.100°
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】D
【分析】由全等三角形的对应角相等得到∠E=∠ACB=45°,由三角形内角和定理即可求出∠DCE的度数.
【解答】解:∵△ABC≌△CDE,
∴∠E=∠ACB=45°,
∵∠D=35°,
∴∠DCE=180°﹣45°﹣35°=100°.
故选:D.
【点评】本题考查全等三角形的性质,关键是掌握全等三角形的对应角相等.
2.(2024秋 安阳期末)如图,△ABC≌△AEF,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
【考点】全等三角形的性质.
【专题】图形的全等;运算能力.
【答案】C
【分析】根据全等三角形的性质可得到AF=AC,EF=BC,∠EAF=∠BAC,从而得到∠EAB=∠FAC,最后证明∠EAB=∠FAB不成立即可.
【解答】解:∵△ABC≌△AEF,
∴AF=AC,EF=BC,∠EAF=∠BAC,故①、③符合题意,
∵∠EAB+BAF=∠EAF,∠FAC+∠BAF=∠BAC,
∴∠EAB+BAF=∠FAC+∠BAF,
∴∠EAB=∠FAC,故④符合题意,
∵∠EAF=∠BAC,
∴∠EAB=∠CAF,
∴∠EAB=∠FAB不一定成立,故②不符合题意,
故选:C.
【点评】本题考查全等三角形的性质,掌握全等三角形的性质是关键.
3.(2025 厦门校级模拟)如图,△ABC≌△ADE,∠D=25°,∠C=105°,∠CAE=70°,则∠BAE的度数是( )
A.20° B.25° C.30° D.35°
【考点】全等三角形的性质;三角形内角和定理.
【专题】三角形;图形的全等;推理能力.
【答案】A
【分析】由全等三角形性质推出∠B=∠D=25°,由三角形内角和定理求出∠BAC=50°,即可求出∠BAE的度数.
【解答】解:∵△ABC≌△ADE,
∴∠B=∠D=25°,
∵∠C=105°,
∴∠BAC=180°﹣∠B﹣∠C=50°,
∵∠CAE=70°,
∴∠BAE=∠CAE﹣∠BAC=20°.
故选:A.
【点评】本题考查全等三角形的性质,三角形内角和定理,关键是掌握掌握全等三角形的对应角相等.
4.(2024秋 阳新县期末)如图所示的网格是由9个相同的小正方形拼成的,图形的各个顶点均为格点,则∠1﹣∠2﹣∠3的度数为( )
A.30° B.45° C.55° D.60°
【考点】全等图形.
【专题】图形的全等;推理能力.
【答案】B
【分析】根据网格特点,可得出∠1=90°,∠2=∠4,∠3+∠4=45°,进而可求解.
【解答】解:如图,则∠1=90°,∠2=∠4,∠3+∠4=45°,
∴∠1﹣∠2﹣∠3=90°﹣45°=45°,
故选:B.
【点评】本题考查网格中的全等图形、三角形的外角性质,会利用全等图形求正方形网格中角度之和是解答的关键.
5.(2024秋 河池期末)如图,Rt△ABC≌Rt△DBE,若∠A=30°,则∠D的度数为( )
A.60° B.45° C.35° D.30°
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】D
【分析】由全等三角形的对应角相等即可得到答案.
【解答】解:∵Rt△ABC≌Rt△DBE,
∴∠D=∠A=30°.
故选:D.
【点评】本题考查全等三角形的性质,关键是掌握全等三角形的对应角相等.
6.(2024秋 滦州市期末)已知图中的两个三角形全等,则∠α的度数是( )
A.40° B.50° C.60° D.70°
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】D
【分析】根据全等三角形的对应角相等解答.
【解答】解:∵图中的两个三角形全等,
∴∠α=70°,
故选:D.
【点评】本题考查的是全等三角形的性质,熟记全等三角形的对应角相等是解题的关键.
7.(2025春 市中区校级期中)如图,AC⊥BE,DE⊥BE,若△ABC≌△BDE,AC=8,DE=3,则CE等于( )
A.4 B.4.5 C.5 D.5.5
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】C
【分析】根据全等三角形的性质得到BE=AC=8,BC=DE=3,结合图形根据线段的和差计算即可.
【解答】解:∵△ABC≌△BDE,AC=8,DE=3,
∴BE=AC=8,BC=DE=3,
∴CE=BE﹣BC=8﹣3=5,
故选:C.
【点评】本题考查的是全等三角形的性质,掌握全等三角形的对应边相等是解题的关键.
二.填空题(共5小题)
8.(2024秋 广信区期末)如图所示,△ACB≌△DEF,其中A与D,C与E是对应顶点,则∠ABC= ∠DFE .
【考点】全等三角形的性质.
【专题】图形的全等;运算能力.
【答案】∠DFE.
【分析】注意:全等三角形书写时各对应顶点应在相应位置,可由此准确地找到对应关系.
【解答】解:由题意可得:△ACB≌△DEF,
∴∠ABC=∠DFE.
故答案为:∠DFE.
【点评】本题考查全等三角形的性质,解题的关键是掌握:全等三角形的对应边相等,对应角相等.
9.(2025 椒江区二模)如图,△ABC≌△CDE,点D在边AC上,若AB=3,CE=8,则AD= 5 .
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】5.
【分析】由全等三角形的性质推出CD=AB=3,AC=CE=8,即可求出AD的长.
【解答】解:∵△ABC≌△CDE,
∴CD=AB=3,AC=CE=8,
∴AD=AC﹣CD=5.
故答案为:5.
【点评】本题考查全等三角形的性质,关键是掌握全等三角形的对应边相等.
10.(2024秋 青浦区校级期末)我们规定:在四边形ABCD中,O是边BC上的一点,如果△OAB与△OCD全等,那么点O叫做该四边形的“等形点”.在四边形EFGH中,∠EFG=90°,EF∥GH,EF=5,FG=17,如果该四边形的“等形点”在边FG上,那么四边形EFGH的面积是 或85 .
【考点】全等三角形的性质.
【专题】图形的全等;几何直观;运算能力;推理能力.
【答案】或85.
【分析】依题意得∠EFG=∠HGF=90°,设OF=a,则OG=17﹣a,分两种情况讨论如下:①当EF=FG,OF=HG时,△OEF≌△HOG,由EF=FG得5=17﹣a,解得a=12,则OF=HG=12,此时四边形EFGH是直角梯形,然后根据梯形的面积公式即可求出四边形EFGH的面积;②当EF=HF=5,OF=OG时,△OEF≌△OHG,根据EF∥GH,EF=HF=5,∠EFG=∠HGF=90°得此时四边形EFGH是矩形,然后根据长方形的面积公式即可得出四边形EF的面积,综上所述即可得出答案.
【解答】解:设四边形EFGH的“等形点”为O,
∵∠EFG=90°,EF∥GH,
∴∠EFG=∠HGF=90°,
设OF=a,
∵EF=5,FG=17,点O在FG上,
∴OG=FG﹣OF=17﹣a,
∴有以下两种情况:
①当EF=FG,OF=HG时,△OEF≌△HOG,如图1所示:
由EF=FG,得:5=17﹣a,
解得:a=12,
∴OF=a=12,OG=17﹣12=5,
∴OF=HG=12,
∴EF∥GH,则此时四边形EFGH是直角梯形,
∴S四边形EFGH(EF+HG) FG(5+12)×17;
②当EF=HF=5,OF=OG时,△OEF≌△OHG,如图2所示:
∵EF∥GH,EF=HF=5,∠EFG=∠HGF=90°,
∴四边形EFGH是长方形,
∴S四边形EFGH=EF FG=5×17=85,
综上所述:四边形EFGH的面积是或85.
故答案为:或85.
【点评】此题主要考查了全等三角形的性质,理解四边形的“等形点”的定义,熟练掌握全等三角形的性质是解决问题的关键,分类讨论是解决问题的易错点.
11.(2025春 杨浦区期中)如图,已知△AEC≌△ADB,如果∠2=25°,∠AGE=80°,那么∠D= 75 °.
【考点】全等三角形的性质.
【专题】三角形;图形的全等;几何直观;推理能力.
【答案】75.
【分析】根据全等三角形的性质得∠E=∠D,∠EAC=∠DAB,进而得∠1=∠2=25°,再由三角形内角和定理求出∠E=75°,由此即可得∠D的度数.
【解答】解:∵△AEC≌△ADB,∠2=25°,
∴∠E=∠D,∠EAC=∠DAB,
∴∠1+∠GAC=∠GAC+∠2,
∴∠1=∠2=25°,
在△AEG中,∠AGE=80°,
∴∠E=180°﹣(∠1+∠AGE)=180°﹣(25°+80°)=75°,
∴∠D=75°,
故答案为:75.
【点评】此题主要考查了全等三角形的性质,理解全等三角形的对应角相等,对应边相等是解决问题的关键.
12.(2025 兰山区一模)如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3= 135° .
【考点】全等图形.
【答案】见试题解答内容
【分析】首先利用SAS定理判定△ABC≌△DBE,根据全等三角形的性质可得∠3=∠ACB,再由∠ACB+∠1=∠1+∠3=90°,可得∠1+∠2+∠3=90°.
【解答】解:∵在△ABC和△DBE中,
∴△ABC≌△DBE(SAS),
∴∠3=∠ACB,
∵∠ACB+∠1=90°,
∴∠1+∠3=90°,
∴∠1+∠2+∠3=90°+45°=135°,
故答案为:135°.
【点评】此题主要考查了全等图形,关键是掌握全等三角形的判定,以及全等三角形对应角相等.
三.解答题(共3小题)
13.(2024秋 衡山县期末)如图,△ABC≌△ADE,点E在边BC上(不与点B,C重合),DE与AB交于点F.
(1)若∠CAD=110°,∠BAE=30°,求∠BAD的度数;
(2)若AD=10,BE=CE=4.5,求△ADF与△BEF的周长和.
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】(1)40°;
(2)33.5.
【分析】(1)利用全等三角形的性质、等式的性质可得出∠CAE=∠BAD,然后利用角的和差关系求解即可;
(2)利用全等三角形的性质可求出AB=AD=10,BC=DE=9,然后利用三角形的周长公式求解即可.
【解答】解:(1)∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠CAE=∠BAD,
由条件可知∠CAE+∠BAD=∠CAD﹣∠BAE=80°,
∴∠CAE=∠BAD=40°;
(2)∵AD=10,BE=CE=4.5,△ABC≌△ADE,
∴AB=AD=10,BC=DE=BE+CE=9,
AD+DF+AF+BF+EF+BE
=AD+(DF+EF)+(AF+BF)+BE
=AD+DE+AB+BE
=10+9+10+4.5
=33.5.
【点评】本题考查了全等三角形的性质等知识,熟练掌握该知识点是关键.
14.(2025春 铁西区期中)如图,已知△ABC≌△DEC,∠ACB是锐角,∠B=30°,∠ACD=60°,延长BA交DE于点F,交CE于点G.
(1)判断直线BF与CE是否垂直?请说明理由;
(2)若AC∥DE,求∠DCE的度数.
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】(1)BF⊥CE,理由见解析;
(2)30°.
【分析】(1)先根据全等三角形的性质得出∠B=∠E=30°,∠ACB=∠DCE,故可得出∠ACB+∠ACG=∠DCE+∠ACG=∠ACD=60°,故可得出∠BGC=90°,据此得出结论;
(2)由AC∥DE可知∠E=∠ACG=30°,再根据∠ACD=60°即可得出结论.
【解答】解:(1)BF⊥CE,理由:
∵△ABC≌△DEC,∠B=30°,∠ACD=60°,
∴∠B=∠E=30°,∠ACB=∠DCE,
∴∠BCG=∠ACB+∠ACG=∠DCE+∠ACG=∠ACD=60°,
∴∠BGC=180°﹣∠B﹣∠BCG=180°﹣30°﹣60°=90°,
∴BF⊥CE;
(2)由(1)知∠E=30°,
∵AC∥DE,
∴∠ACG=∠E=30°,
∵∠ACD=60°,
∴∠DCE=∠ACD﹣∠ACG=60°﹣30°=30°.
【点评】本题考查的是全等三角形的性质,熟知全等三角形的对应角相等是解题的关键.
15.(2025春 崂山区期中)已知:如图①,AB⊥BD,DE⊥BD,点C是BD上一点,且△ABC≌△CDE.
(1)试判断AC与CE的位置关系,并说明理由;
(2)如图②,若把△CDE沿直线BD向左移动,使△CDE的顶点C与B重合,AC与BE交于点F,此时AC与BE的位置关系怎样?请说明理由;
(3)图②中,若S△ABC=12,AF:CF=3:1,求四边形CDEF的面积.
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】(1)AC⊥CE,理由见解答过程;
(2)AC⊥BE,理由见解答过程;
(3)9.
【分析】(1)根据全等三角形的性质及直角三角形的性质求出∠ACE=90°,就可以得出AC⊥CE;
(2)如图2,根据△ABC≌△CDE可以得出∠BFC=90°,从而得出结论;
(3)根据S△ABC=12,AF:CF=3:1,可得S△BFCS△ABC=3,由△ABC≌△BDE,得S△BDE=S△ABC=12,进而可以解决问题.
【解答】解:(1)AC⊥CE,理由如下:
∵AB⊥BD,
∴∠B=90°,
∴∠A+∠ACB=90°,
∵△ABC≌△CDE,
∴∠A=∠DCE,∠ACB=∠E,
∴∠DCE+∠ACB=90°,
∵∠DCE+∠ACB+∠ACE=180°,
∴∠ACE=90°,
∴AC⊥CE;
(2)AC⊥BE,理由如下:
∵△ABC≌△BDE,
∴∠A=∠EBD,∠ACB=∠E,
∵∠B=90°,
∴∠A+∠ACB=90°,
∴∠EBD+∠ACB=90°,
∴∠BFC=90°,
∴AC⊥BE;
(3)∵S△ABC=12,AF:CF=3:1,
∴S△BFCS△ABC=3,
∵△ABC≌△BDE,
∴S△BDE=S△ABC=12,
∴四边形CDEF的面积=12﹣3=9.
【点评】本题考查了全等三角形的性质,平移的性质的运用,垂直的判定及性质的运用,熟记全等三角形的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
