【期末核心考点】旋转(含解析)2024-2025学年七年级下册数学华东师大版(2024)
文档属性
| 名称 | 【期末核心考点】旋转(含解析)2024-2025学年七年级下册数学华东师大版(2024) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-14 19:21:21 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末核心考点 旋转
一.选择题(共7小题)
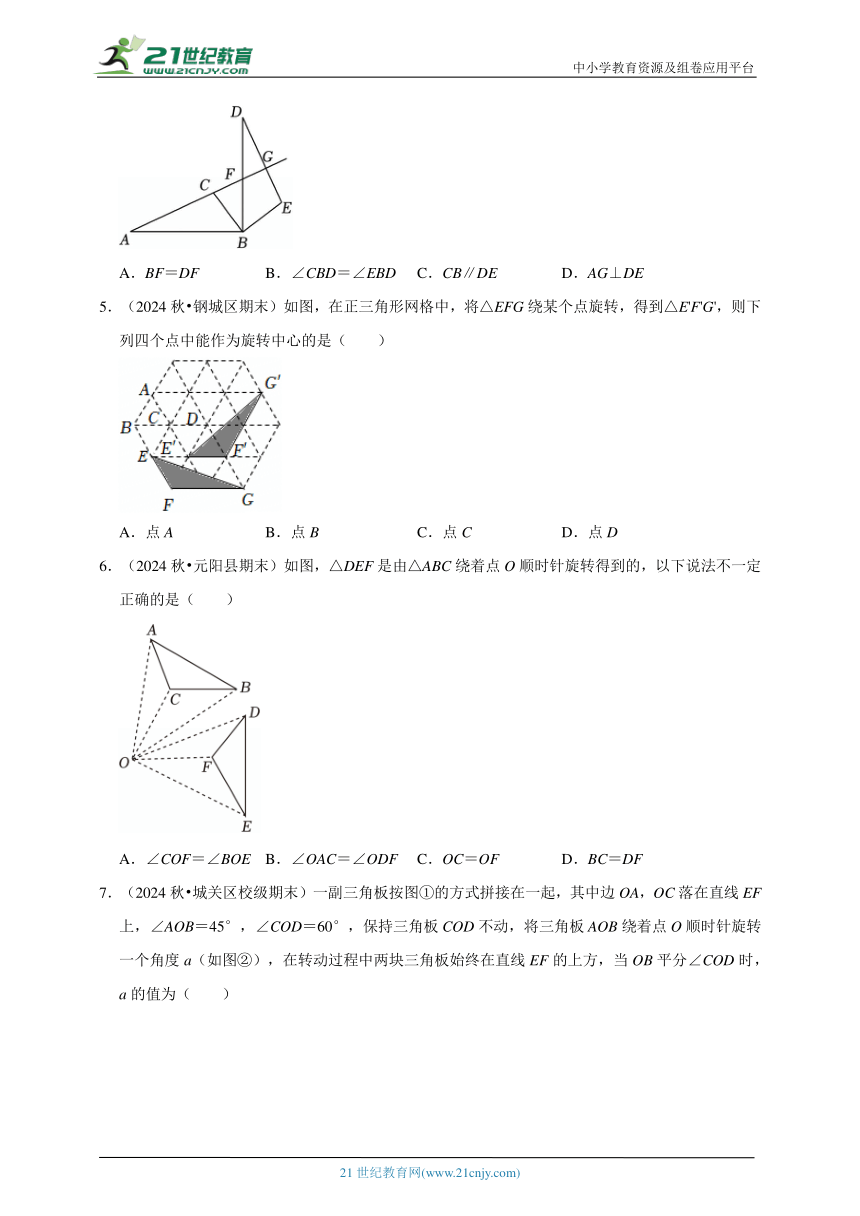
1.(2025 河北区二模)如图,把△ABC以点A为中心顺时针旋转得到△ADE,点B,C的对应点分别是点D,E,若∠ADE的平分线经过点B,连接EC,则下列结论一定正确的是( )
A.AB=DE B.DB∥EC C.BD⊥AE D.∠BDE=∠ACE
2.(2025 红桥区二模)如图,把△ABC以点B为中心顺时针旋转60°得到△DBE,点A,C的对应点分别为D,E,且点D恰好在AC的延长线上,连接CE,则下列结论一定正确的是( )
A.AB=EB B.DE∥AB C.∠DEC=∠ABC D.CE⊥BD
3.(2025春 青岛期中)如图,在△ABC中,∠B=75°,∠C=40°,点E是边AC上一点.如果△ABC经过旋转后能与△AED重合,那么这一旋转的旋转角的度数可能是( )
A.65° B.75° C.105° D.130°
4.(2025 吴兴区二模)如图,将△ABC绕点B顺时针旋转90°得到△DBE,点A,C的对应点分别为点D,E,AC的延长线分别交BD,DE于点F,G,下列结论一定正确的是( )
A.BF=DF B.∠CBD=∠EBD C.CB∥DE D.AG⊥DE
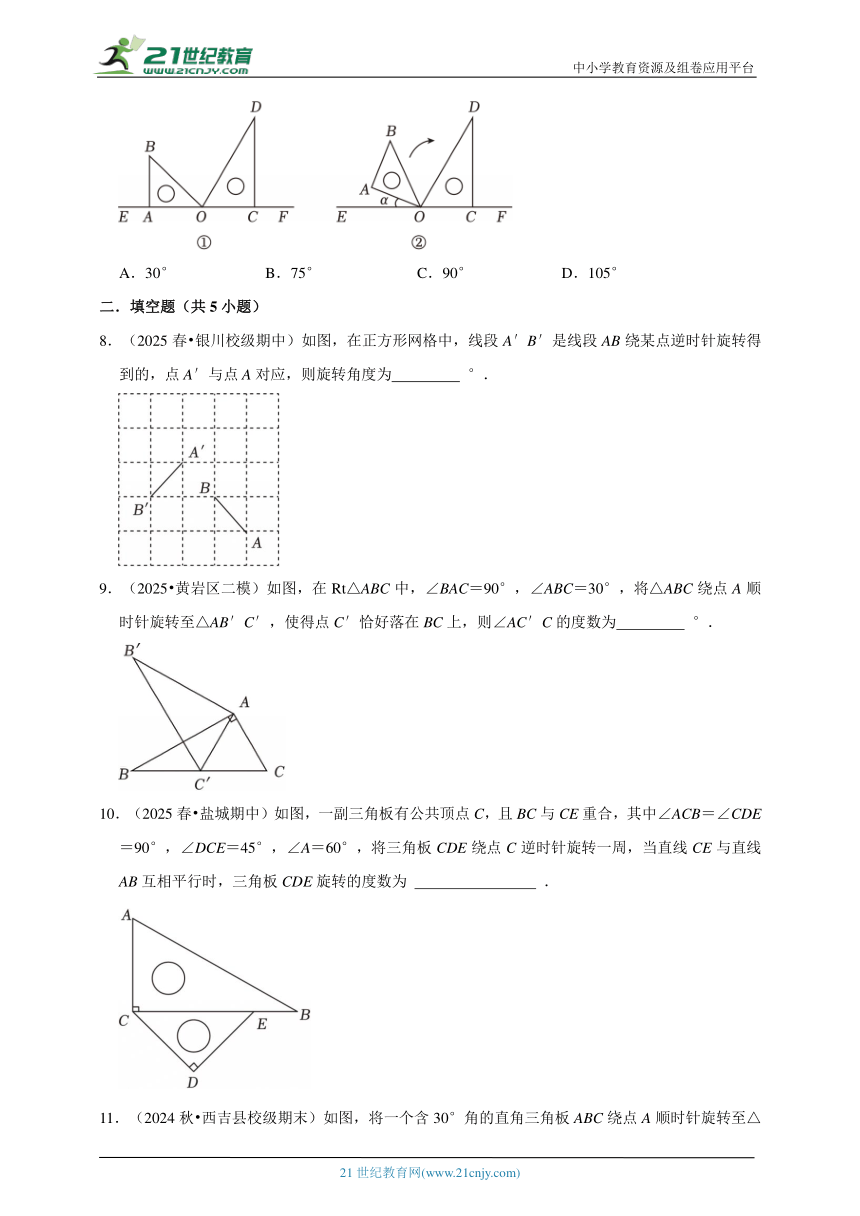
5.(2024秋 钢城区期末)如图,在正三角形网格中,将△EFG绕某个点旋转,得到△E'F'G',则下列四个点中能作为旋转中心的是( )
A.点A B.点B C.点C D.点D
6.(2024秋 元阳县期末)如图,△DEF是由△ABC绕着点O顺时针旋转得到的,以下说法不一定正确的是( )
A.∠COF=∠BOE B.∠OAC=∠ODF C.OC=OF D.BC=DF
7.(2024秋 城关区校级期末)一副三角板按图①的方式拼接在一起,其中边OA,OC落在直线EF上,∠AOB=45°,∠COD=60°,保持三角板COD不动,将三角板AOB绕着点O顺时针旋转一个角度a(如图②),在转动过程中两块三角板始终在直线EF的上方,当OB平分∠COD时,a的值为( )
A.30° B.75° C.90° D.105°
二.填空题(共5小题)
8.(2025春 银川校级期中)如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转得到的,点A′与点A对应,则旋转角度为 °.
9.(2025 黄岩区二模)如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,将△ABC绕点A顺时针旋转至△AB′C′,使得点C′恰好落在BC上,则∠AC′C的度数为 °.
10.(2025春 盐城期中)如图,一副三角板有公共顶点C,且BC与CE重合,其中∠ACB=∠CDE=90°,∠DCE=45°,∠A=60°,将三角板CDE绕点C逆时针旋转一周,当直线CE与直线AB互相平行时,三角板CDE旋转的度数为 .
11.(2024秋 西吉县校级期末)如图,将一个含30°角的直角三角板ABC绕点A顺时针旋转至△AB′C′,使得B,A,C′三点在同一条直线上,则旋转角∠BAB′的度数是 .
12.(2025春 成华区校级期中)如图,在△ABC中,∠ABC=48°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B′恰好落在BC边上,且AB'=CB',则∠C′的度数为 .
三.解答题(共3小题)
13.(2025 太湖县模拟)如图,在每个小正方形的边长为1个单位的网格中,△ABC的顶点均在格点(网格线的交点)上.
(1)将△ABC向右平移3个单位,再向下平移2个单位得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕点C1逆时针旋转90°得到△A2B2C2,画出△A2B2C2.
14.(2025春 丹阳市期中)如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D落在边BC上.
(1)若∠A=60°,求∠BDE的度数;
(2)若AC=5,CE=7,求BD的长度.
15.(2025春 宜兴市期中)如图,在5×5的方格网中,所有标出的点均为格点,请按要求画图.
(1)如图1,画出△ABC关于点O成中心对称的图形,并标上对应的字母;
(2)如图2,△ABC绕旋转中心顺时针旋转得到△DEF,直接标出旋转中心点P,写出旋转角的度数为 .
期末核心考点 旋转
参考答案与试题解析
一.选择题(共7小题)
1.(2025 河北区二模)如图,把△ABC以点A为中心顺时针旋转得到△ADE,点B,C的对应点分别是点D,E,若∠ADE的平分线经过点B,连接EC,则下列结论一定正确的是( )
A.AB=DE B.DB∥EC C.BD⊥AE D.∠BDE=∠ACE
【考点】旋转的性质;平行线的判定.
【专题】平移、旋转与对称;几何直观.
【答案】D
【分析】由旋转得AB=AD,AC=AE,∠DAE=∠BAC,可得∠BAD=∠CAE,,,则可得∠ACE=∠ADB.由角平分线的定义可得∠BDE=∠ADB,进而可得∠BDE=∠ACE,即可得出答案.
【解答】解:∵把△ABC以点A为中心顺时针旋转得到△ADE,
∴AB=AD,AC=AE,∠DAE=∠BAC,
∴∠BAD=∠CAE,,,
∴∠ACE=∠ADB.
∵DB为∠ADE的平分线,
∴∠BDE=∠ADB,
∴∠BDE=∠ACE.
故D选项正确,符合题意.
根据已知条件不能得出A,B,C选项,
故A,B,C选项不正确,不符合题意.
故选:D.
【点评】本题考查旋转的性质、平行线的判定,解题的关键是理解题意,灵活运用所学知识解决问题.
2.(2025 红桥区二模)如图,把△ABC以点B为中心顺时针旋转60°得到△DBE,点A,C的对应点分别为D,E,且点D恰好在AC的延长线上,连接CE,则下列结论一定正确的是( )
A.AB=EB B.DE∥AB C.∠DEC=∠ABC D.CE⊥BD
【考点】旋转的性质;平行线的判定.
【专题】平移、旋转与对称;运算能力.
【答案】B
【分析】根据旋转的性质、等边三角形的判定以及全等三角形的判定与性质逐项判定即可.
【解答】解:根据旋转的性质、等边三角形的判定以及全等三角形的判定与性质逐项判定如下:
A.∵AB=BD,BC=BE,而AB=EB不一定成立,故错误,不符合题意;
B.∵把△ABC以点B为中心顺时针旋转60°得到△DBE,
∴∠ABD=∠CBE=60°,AB=BD,BC=BE
∴△ABD是等边三角形,∠ABD﹣∠CBD=∠CBE﹣∠CBD,即∠ABC=∠DBE,
∴∠ADB=60°,
∵AB=BD,∠ABC=∠DBE,BC=BE,
∴△ABC≌△DBE(SAS),
∴∠A=∠BDE=60°,
由外角的性质可得:∠ADE=∠ADB+∠BDE=120°,
∴∠ADE+∠A=180°,
∴DE∥AB,即B正确,符合题意;
C.∵△ABC≌△DBE(SAS),
∴∠ABC=∠DBE≠∠DEC,故错误,不符合题意;
D.由不能证明BD平分∠CBE,即不能证明CE⊥BD,故错误,不符合题意.
故选:B.
【点评】本题主要考查了旋转的性质、等边三角形的判定与性质、全等三角形的判定与性质等知识点,灵活运用相关知识成为解题的关键.
3.(2025春 青岛期中)如图,在△ABC中,∠B=75°,∠C=40°,点E是边AC上一点.如果△ABC经过旋转后能与△AED重合,那么这一旋转的旋转角的度数可能是( )
A.65° B.75° C.105° D.130°
【考点】旋转的性质.
【专题】平移、旋转与对称;推理能力.
【答案】A
【分析】根据三角形内角和定理和旋转的性质即可得到结论.
【解答】解:∵∠B=75°,∠C=40°,
∴∠BAC=180°﹣∠B﹣∠C=65°,
∵△ABC经过旋转后能与△AED重合,
∴∠EAB=∠CAB=65°,
∴这一旋转的旋转角的度数可能是65°.
故选:A.
【点评】本题考查了旋转的性质,轴对称的性质,含30°角的直角三角形的性质,等边三角形的判定和性质,三角形全等的判定和性质,作出辅助线构建直角三角形和等边三角形是解题的关键.
4.(2025 吴兴区二模)如图,将△ABC绕点B顺时针旋转90°得到△DBE,点A,C的对应点分别为点D,E,AC的延长线分别交BD,DE于点F,G,下列结论一定正确的是( )
A.BF=DF B.∠CBD=∠EBD C.CB∥DE D.AG⊥DE
【考点】旋转的性质;平行线的判定.
【专题】平移、旋转与对称;几何直观.
【答案】D
【分析】由旋转得∠A=∠D,∠ABD=90°,可得∠A+∠AFB=90°,进而可得∠D+∠DFG=90°,则∠DGF=90°,即AG⊥DE,从而可得答案.
【解答】解:∵△ABC绕点B顺时针旋转90°得到△DBE,
∴∠A=∠D,∠ABD=90°,
∴∠A+∠AFB=90°.
∵∠AFB=∠DFG,
∴∠D+∠DFG=90°,
∴∠DGF=90°,
即AG⊥DE,
故D选项正确,符合题意;
根据已知条件不能得出A,B,C选项,
故A,B,C选项不正确,不符合题意.
故选:D.
【点评】本题考查旋转的性质、平行线的判定,熟练掌握旋转的性质是解答本题的关键.
5.(2024秋 钢城区期末)如图,在正三角形网格中,将△EFG绕某个点旋转,得到△E'F'G',则下列四个点中能作为旋转中心的是( )
A.点A B.点B C.点C D.点D
【考点】旋转的性质.
【专题】平移、旋转与对称;推理能力.
【答案】C
【分析】分别作EE',FF'的中垂线,交点为点C,即点C是旋转中心.
【解答】解:如图,连接FF',分别作EE',FF'的中垂线,交点为点C,即点C是旋转中心,
故选:C.
【点评】本题考查了旋转的性质,掌握旋转的中心在对应点所连线段的垂直平分线上是解题的关键.
6.(2024秋 元阳县期末)如图,△DEF是由△ABC绕着点O顺时针旋转得到的,以下说法不一定正确的是( )
A.∠COF=∠BOE B.∠OAC=∠ODF C.OC=OF D.BC=DF
【考点】旋转的性质.
【专题】平移、旋转与对称;推理能力.
【答案】D
【分析】根据旋转的性质逐一判断即可.
【解答】解:∵△DEF是由△ABC绕着点O顺时针旋转得到的,
∴∠COF=∠BOE,∠OAC=∠ODF,OC=OF,BC=EF,
由已知条件无法得知BC=DF,
故选:D.
【点评】本题考查了旋转的性质,熟记旋转前后对应边、对应角相等是解题的关键.
7.(2024秋 城关区校级期末)一副三角板按图①的方式拼接在一起,其中边OA,OC落在直线EF上,∠AOB=45°,∠COD=60°,保持三角板COD不动,将三角板AOB绕着点O顺时针旋转一个角度a(如图②),在转动过程中两块三角板始终在直线EF的上方,当OB平分∠COD时,a的值为( )
A.30° B.75° C.90° D.105°
【考点】旋转的性质.
【专题】平移、旋转与对称;几何直观;推理能力.
【答案】D
【分析】根据角平分线的定义求出∠BOC=30°,得出∠AOC=75°,根据平角求出α=∠AOE=105°.
【解答】解:∠AOB=45°,∠COD=60°,保持三角板COD不动,将三角板AOB绕着点O顺时针旋转一个角度a,OB平分∠COD时,如图,
∴∠DOB=60°÷2=30°,
∴∠AOD=45°﹣30°=15°,
∴α=180°﹣60°﹣15°=105°;
故选:D.
【点评】本题考查旋转的性质,解题的关键是熟练掌握旋转的性质.
二.填空题(共5小题)
8.(2025春 银川校级期中)如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转得到的,点A′与点A对应,则旋转角度为 90 °.
【考点】旋转的性质.
【专题】平移、旋转与对称;几何直观.
【答案】90.
【分析】分别作线段AA',BB'的垂直平分线,相交于点O,则线段A′B′是线段AB绕点O逆时针旋转90°得到的,即可得出答案.
【解答】解:如图,分别作线段AA',BB'的垂直平分线,相交于点O,
则线段A′B′是线段AB绕点O逆时针旋转90°得到的,
∴旋转角度为90°.
故答案为:90.
【点评】本题考查旋转的性质,熟练掌握旋转的性质是解答本题的关键.
9.(2025 黄岩区二模)如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,将△ABC绕点A顺时针旋转至△AB′C′,使得点C′恰好落在BC上,则∠AC′C的度数为 60 °.
【考点】旋转的性质.
【答案】60°.
【分析】本题主要考查了旋转变换的性质及其应用问题;如图,证明C′A=CA,∠C=∠AC′C,求出∠C=60°,得到∠C'AC=60°,即可解决问题.
【解答】解:由题意得:C′A=CA,
∴∠C=∠AC′C,
∵∠BAC=90°,∠ABC=30°,
∴∠C=90°﹣30°=60°,
∴∠C'AC=180°﹣2×60°,
故答案为:60°.
【点评】本题考查了旋转的性质,直角三角形两锐角互余,等边三角形的判定与性质,熟记各性质并准确识图是解题的关键.
10.(2025春 盐城期中)如图,一副三角板有公共顶点C,且BC与CE重合,其中∠ACB=∠CDE=90°,∠DCE=45°,∠A=60°,将三角板CDE绕点C逆时针旋转一周,当直线CE与直线AB互相平行时,三角板CDE旋转的度数为 150°或330° .
【考点】旋转的性质;平行线的性质.
【专题】平移、旋转与对称;运算能力.
【答案】150°或330°.
【分析】分CE在直线BC的上方和下方两种情况讨论,画出图形,根据平行线的性质求解即可.
【解答】解:∵∠ACB=∠CDE=90°,∠DCE=45°,∠A=60°,
∴∠B=30°,
当CE在直线BC的上方时,如图,
∵CE∥AB,
∴∠ECB+∠B=180°,
∴∠ECB=150°,
即三角板CDE旋转的度数为150°,
当CE在直线BC的下方时,如图,
∵CE∥AB,
∴∠ECB=∠B=30°,
即三角板CDE旋转的度数为360°﹣30°=330°.
故答案为:150°或330°.
【点评】本题考查了旋转的性质,平行线的性质,正确进行计算是解题关键.
11.(2024秋 西吉县校级期末)如图,将一个含30°角的直角三角板ABC绕点A顺时针旋转至△AB′C′,使得B,A,C′三点在同一条直线上,则旋转角∠BAB′的度数是 150° .
【考点】旋转的性质.
【专题】平移、旋转与对称;几何直观.
【答案】150°.
【分析】由旋转得,∠B'AC'=∠BAC=30°,由题意得∠BAC'=180°,再根据∠BAB′=∠BAC'﹣∠B'AC'可得答案.
【解答】解:由旋转得,∠B'AC'=∠BAC=30°,
∵B,A,C′三点在同一条直线上,
∴∠BAC'=180°,
∴∠BAB′=∠BAC'﹣∠B'AC'=150°.
故答案为:150°.
【点评】本题考查旋转的性质,熟练掌握旋转的性质是解答本题的关键.
12.(2025春 成华区校级期中)如图,在△ABC中,∠ABC=48°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B′恰好落在BC边上,且AB'=CB',则∠C′的度数为 24° .
【考点】旋转的性质.
【专题】平移、旋转与对称;几何直观.
【答案】24°.
【分析】由旋转得∠C=∠C',AB=AB',可得∠AB'B=∠ABC=48°.由已知条件可得∠C=∠CAB',根据∠AB'B=∠C+∠CAB'=2∠C=48°,可得∠C=24°,即可得∠C'=24°.
【解答】解:∵将△ABC绕点A按逆时针方向旋转得到△AB'C',
∴∠C=∠C',AB=AB',
∴∠AB'B=∠ABC=48°.
∵AB'=CB',
∴∠C=∠CAB',
∵∠AB'B=∠C+∠CAB'=2∠C=48°,
∴∠C=24°,
∴∠C'=24°.
故答案为:24°.
【点评】本题考查旋转的性质,熟练掌握旋转的性质是解答本题的关键.
三.解答题(共3小题)
13.(2025 太湖县模拟)如图,在每个小正方形的边长为1个单位的网格中,△ABC的顶点均在格点(网格线的交点)上.
(1)将△ABC向右平移3个单位,再向下平移2个单位得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕点C1逆时针旋转90°得到△A2B2C2,画出△A2B2C2.
【考点】作图﹣旋转变换;作图﹣平移变换.
【专题】平移、旋转与对称;推理能力.
【答案】(1)△A1B1C1见解答过程;
(2)△A2B2C2见解答过程.
【分析】(1)利用点平移的规律找出A1、B1、C1,然后依次描点即可;
(2)利用网格特点和旋转的性质画出点A2、B2、C2即可.
【解答】解:(1)如图,△A1B1C1即为所求作;
(2)如图,△A2B2C1即为所求作.
【点评】本题考查了作图﹣平移变换、旋转变换,熟练掌握平移和旋转的性质是解题的关键.
14.(2025春 丹阳市期中)如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D落在边BC上.
(1)若∠A=60°,求∠BDE的度数;
(2)若AC=5,CE=7,求BD的长度.
【考点】旋转的性质.
【专题】平移、旋转与对称;推理能力.
【答案】(1)∠BDE=120°;
(2)2.
【分析】(1)由旋转的性质可得∠A=∠CDE=60°,即可求解;
(2)由旋转的性质可得AC=CD=5,CE=BC=7,即可求解.
【解答】解:(1)∵将△ABC绕点C顺时针旋转得到△DEC,
∴∠A=∠CDE=60°,
∴∠BDE=120°;
(2)∵将△ABC绕点C顺时针旋转得到△DEC,
∴AC=CD=5,CE=BC=7,
∴BD=BC﹣CD=2.
【点评】本题考查了旋转的性质,掌握旋转的性质是解题的关键.
15.(2025春 宜兴市期中)如图,在5×5的方格网中,所有标出的点均为格点,请按要求画图.
(1)如图1,画出△ABC关于点O成中心对称的图形,并标上对应的字母;
(2)如图2,△ABC绕旋转中心顺时针旋转得到△DEF,直接标出旋转中心点P,写出旋转角的度数为 90° .
【考点】作图﹣旋转变换.
【专题】作图题;平移、旋转与对称;几何直观;推理能力.
【答案】(1)作图见解析;
(2)作图见解析;90°.
【分析】(1)作出点A的对应点D,连接CD,BD即可;
(2)线段AD,CF的垂直平分线的交点P即为所求,直接根据旋转角∠CPF=90°即可得出答案.
【解答】(1)△ABC关于点O成中心对称的图形,如图1,△DCB即为所求;
(2)如图2,点P即为所求.
根据图可知旋转角∠CPF=90°,
故答案为:90°.
【点评】本题考查作图﹣旋转变换,解题的关键是掌握旋转变换的性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末核心考点 旋转
一.选择题(共7小题)
1.(2025 河北区二模)如图,把△ABC以点A为中心顺时针旋转得到△ADE,点B,C的对应点分别是点D,E,若∠ADE的平分线经过点B,连接EC,则下列结论一定正确的是( )
A.AB=DE B.DB∥EC C.BD⊥AE D.∠BDE=∠ACE
2.(2025 红桥区二模)如图,把△ABC以点B为中心顺时针旋转60°得到△DBE,点A,C的对应点分别为D,E,且点D恰好在AC的延长线上,连接CE,则下列结论一定正确的是( )
A.AB=EB B.DE∥AB C.∠DEC=∠ABC D.CE⊥BD
3.(2025春 青岛期中)如图,在△ABC中,∠B=75°,∠C=40°,点E是边AC上一点.如果△ABC经过旋转后能与△AED重合,那么这一旋转的旋转角的度数可能是( )
A.65° B.75° C.105° D.130°
4.(2025 吴兴区二模)如图,将△ABC绕点B顺时针旋转90°得到△DBE,点A,C的对应点分别为点D,E,AC的延长线分别交BD,DE于点F,G,下列结论一定正确的是( )
A.BF=DF B.∠CBD=∠EBD C.CB∥DE D.AG⊥DE
5.(2024秋 钢城区期末)如图,在正三角形网格中,将△EFG绕某个点旋转,得到△E'F'G',则下列四个点中能作为旋转中心的是( )
A.点A B.点B C.点C D.点D
6.(2024秋 元阳县期末)如图,△DEF是由△ABC绕着点O顺时针旋转得到的,以下说法不一定正确的是( )
A.∠COF=∠BOE B.∠OAC=∠ODF C.OC=OF D.BC=DF
7.(2024秋 城关区校级期末)一副三角板按图①的方式拼接在一起,其中边OA,OC落在直线EF上,∠AOB=45°,∠COD=60°,保持三角板COD不动,将三角板AOB绕着点O顺时针旋转一个角度a(如图②),在转动过程中两块三角板始终在直线EF的上方,当OB平分∠COD时,a的值为( )
A.30° B.75° C.90° D.105°
二.填空题(共5小题)
8.(2025春 银川校级期中)如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转得到的,点A′与点A对应,则旋转角度为 °.
9.(2025 黄岩区二模)如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,将△ABC绕点A顺时针旋转至△AB′C′,使得点C′恰好落在BC上,则∠AC′C的度数为 °.
10.(2025春 盐城期中)如图,一副三角板有公共顶点C,且BC与CE重合,其中∠ACB=∠CDE=90°,∠DCE=45°,∠A=60°,将三角板CDE绕点C逆时针旋转一周,当直线CE与直线AB互相平行时,三角板CDE旋转的度数为 .
11.(2024秋 西吉县校级期末)如图,将一个含30°角的直角三角板ABC绕点A顺时针旋转至△AB′C′,使得B,A,C′三点在同一条直线上,则旋转角∠BAB′的度数是 .
12.(2025春 成华区校级期中)如图,在△ABC中,∠ABC=48°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B′恰好落在BC边上,且AB'=CB',则∠C′的度数为 .
三.解答题(共3小题)
13.(2025 太湖县模拟)如图,在每个小正方形的边长为1个单位的网格中,△ABC的顶点均在格点(网格线的交点)上.
(1)将△ABC向右平移3个单位,再向下平移2个单位得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕点C1逆时针旋转90°得到△A2B2C2,画出△A2B2C2.
14.(2025春 丹阳市期中)如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D落在边BC上.
(1)若∠A=60°,求∠BDE的度数;
(2)若AC=5,CE=7,求BD的长度.
15.(2025春 宜兴市期中)如图,在5×5的方格网中,所有标出的点均为格点,请按要求画图.
(1)如图1,画出△ABC关于点O成中心对称的图形,并标上对应的字母;
(2)如图2,△ABC绕旋转中心顺时针旋转得到△DEF,直接标出旋转中心点P,写出旋转角的度数为 .
期末核心考点 旋转
参考答案与试题解析
一.选择题(共7小题)
1.(2025 河北区二模)如图,把△ABC以点A为中心顺时针旋转得到△ADE,点B,C的对应点分别是点D,E,若∠ADE的平分线经过点B,连接EC,则下列结论一定正确的是( )
A.AB=DE B.DB∥EC C.BD⊥AE D.∠BDE=∠ACE
【考点】旋转的性质;平行线的判定.
【专题】平移、旋转与对称;几何直观.
【答案】D
【分析】由旋转得AB=AD,AC=AE,∠DAE=∠BAC,可得∠BAD=∠CAE,,,则可得∠ACE=∠ADB.由角平分线的定义可得∠BDE=∠ADB,进而可得∠BDE=∠ACE,即可得出答案.
【解答】解:∵把△ABC以点A为中心顺时针旋转得到△ADE,
∴AB=AD,AC=AE,∠DAE=∠BAC,
∴∠BAD=∠CAE,,,
∴∠ACE=∠ADB.
∵DB为∠ADE的平分线,
∴∠BDE=∠ADB,
∴∠BDE=∠ACE.
故D选项正确,符合题意.
根据已知条件不能得出A,B,C选项,
故A,B,C选项不正确,不符合题意.
故选:D.
【点评】本题考查旋转的性质、平行线的判定,解题的关键是理解题意,灵活运用所学知识解决问题.
2.(2025 红桥区二模)如图,把△ABC以点B为中心顺时针旋转60°得到△DBE,点A,C的对应点分别为D,E,且点D恰好在AC的延长线上,连接CE,则下列结论一定正确的是( )
A.AB=EB B.DE∥AB C.∠DEC=∠ABC D.CE⊥BD
【考点】旋转的性质;平行线的判定.
【专题】平移、旋转与对称;运算能力.
【答案】B
【分析】根据旋转的性质、等边三角形的判定以及全等三角形的判定与性质逐项判定即可.
【解答】解:根据旋转的性质、等边三角形的判定以及全等三角形的判定与性质逐项判定如下:
A.∵AB=BD,BC=BE,而AB=EB不一定成立,故错误,不符合题意;
B.∵把△ABC以点B为中心顺时针旋转60°得到△DBE,
∴∠ABD=∠CBE=60°,AB=BD,BC=BE
∴△ABD是等边三角形,∠ABD﹣∠CBD=∠CBE﹣∠CBD,即∠ABC=∠DBE,
∴∠ADB=60°,
∵AB=BD,∠ABC=∠DBE,BC=BE,
∴△ABC≌△DBE(SAS),
∴∠A=∠BDE=60°,
由外角的性质可得:∠ADE=∠ADB+∠BDE=120°,
∴∠ADE+∠A=180°,
∴DE∥AB,即B正确,符合题意;
C.∵△ABC≌△DBE(SAS),
∴∠ABC=∠DBE≠∠DEC,故错误,不符合题意;
D.由不能证明BD平分∠CBE,即不能证明CE⊥BD,故错误,不符合题意.
故选:B.
【点评】本题主要考查了旋转的性质、等边三角形的判定与性质、全等三角形的判定与性质等知识点,灵活运用相关知识成为解题的关键.
3.(2025春 青岛期中)如图,在△ABC中,∠B=75°,∠C=40°,点E是边AC上一点.如果△ABC经过旋转后能与△AED重合,那么这一旋转的旋转角的度数可能是( )
A.65° B.75° C.105° D.130°
【考点】旋转的性质.
【专题】平移、旋转与对称;推理能力.
【答案】A
【分析】根据三角形内角和定理和旋转的性质即可得到结论.
【解答】解:∵∠B=75°,∠C=40°,
∴∠BAC=180°﹣∠B﹣∠C=65°,
∵△ABC经过旋转后能与△AED重合,
∴∠EAB=∠CAB=65°,
∴这一旋转的旋转角的度数可能是65°.
故选:A.
【点评】本题考查了旋转的性质,轴对称的性质,含30°角的直角三角形的性质,等边三角形的判定和性质,三角形全等的判定和性质,作出辅助线构建直角三角形和等边三角形是解题的关键.
4.(2025 吴兴区二模)如图,将△ABC绕点B顺时针旋转90°得到△DBE,点A,C的对应点分别为点D,E,AC的延长线分别交BD,DE于点F,G,下列结论一定正确的是( )
A.BF=DF B.∠CBD=∠EBD C.CB∥DE D.AG⊥DE
【考点】旋转的性质;平行线的判定.
【专题】平移、旋转与对称;几何直观.
【答案】D
【分析】由旋转得∠A=∠D,∠ABD=90°,可得∠A+∠AFB=90°,进而可得∠D+∠DFG=90°,则∠DGF=90°,即AG⊥DE,从而可得答案.
【解答】解:∵△ABC绕点B顺时针旋转90°得到△DBE,
∴∠A=∠D,∠ABD=90°,
∴∠A+∠AFB=90°.
∵∠AFB=∠DFG,
∴∠D+∠DFG=90°,
∴∠DGF=90°,
即AG⊥DE,
故D选项正确,符合题意;
根据已知条件不能得出A,B,C选项,
故A,B,C选项不正确,不符合题意.
故选:D.
【点评】本题考查旋转的性质、平行线的判定,熟练掌握旋转的性质是解答本题的关键.
5.(2024秋 钢城区期末)如图,在正三角形网格中,将△EFG绕某个点旋转,得到△E'F'G',则下列四个点中能作为旋转中心的是( )
A.点A B.点B C.点C D.点D
【考点】旋转的性质.
【专题】平移、旋转与对称;推理能力.
【答案】C
【分析】分别作EE',FF'的中垂线,交点为点C,即点C是旋转中心.
【解答】解:如图,连接FF',分别作EE',FF'的中垂线,交点为点C,即点C是旋转中心,
故选:C.
【点评】本题考查了旋转的性质,掌握旋转的中心在对应点所连线段的垂直平分线上是解题的关键.
6.(2024秋 元阳县期末)如图,△DEF是由△ABC绕着点O顺时针旋转得到的,以下说法不一定正确的是( )
A.∠COF=∠BOE B.∠OAC=∠ODF C.OC=OF D.BC=DF
【考点】旋转的性质.
【专题】平移、旋转与对称;推理能力.
【答案】D
【分析】根据旋转的性质逐一判断即可.
【解答】解:∵△DEF是由△ABC绕着点O顺时针旋转得到的,
∴∠COF=∠BOE,∠OAC=∠ODF,OC=OF,BC=EF,
由已知条件无法得知BC=DF,
故选:D.
【点评】本题考查了旋转的性质,熟记旋转前后对应边、对应角相等是解题的关键.
7.(2024秋 城关区校级期末)一副三角板按图①的方式拼接在一起,其中边OA,OC落在直线EF上,∠AOB=45°,∠COD=60°,保持三角板COD不动,将三角板AOB绕着点O顺时针旋转一个角度a(如图②),在转动过程中两块三角板始终在直线EF的上方,当OB平分∠COD时,a的值为( )
A.30° B.75° C.90° D.105°
【考点】旋转的性质.
【专题】平移、旋转与对称;几何直观;推理能力.
【答案】D
【分析】根据角平分线的定义求出∠BOC=30°,得出∠AOC=75°,根据平角求出α=∠AOE=105°.
【解答】解:∠AOB=45°,∠COD=60°,保持三角板COD不动,将三角板AOB绕着点O顺时针旋转一个角度a,OB平分∠COD时,如图,
∴∠DOB=60°÷2=30°,
∴∠AOD=45°﹣30°=15°,
∴α=180°﹣60°﹣15°=105°;
故选:D.
【点评】本题考查旋转的性质,解题的关键是熟练掌握旋转的性质.
二.填空题(共5小题)
8.(2025春 银川校级期中)如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转得到的,点A′与点A对应,则旋转角度为 90 °.
【考点】旋转的性质.
【专题】平移、旋转与对称;几何直观.
【答案】90.
【分析】分别作线段AA',BB'的垂直平分线,相交于点O,则线段A′B′是线段AB绕点O逆时针旋转90°得到的,即可得出答案.
【解答】解:如图,分别作线段AA',BB'的垂直平分线,相交于点O,
则线段A′B′是线段AB绕点O逆时针旋转90°得到的,
∴旋转角度为90°.
故答案为:90.
【点评】本题考查旋转的性质,熟练掌握旋转的性质是解答本题的关键.
9.(2025 黄岩区二模)如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,将△ABC绕点A顺时针旋转至△AB′C′,使得点C′恰好落在BC上,则∠AC′C的度数为 60 °.
【考点】旋转的性质.
【答案】60°.
【分析】本题主要考查了旋转变换的性质及其应用问题;如图,证明C′A=CA,∠C=∠AC′C,求出∠C=60°,得到∠C'AC=60°,即可解决问题.
【解答】解:由题意得:C′A=CA,
∴∠C=∠AC′C,
∵∠BAC=90°,∠ABC=30°,
∴∠C=90°﹣30°=60°,
∴∠C'AC=180°﹣2×60°,
故答案为:60°.
【点评】本题考查了旋转的性质,直角三角形两锐角互余,等边三角形的判定与性质,熟记各性质并准确识图是解题的关键.
10.(2025春 盐城期中)如图,一副三角板有公共顶点C,且BC与CE重合,其中∠ACB=∠CDE=90°,∠DCE=45°,∠A=60°,将三角板CDE绕点C逆时针旋转一周,当直线CE与直线AB互相平行时,三角板CDE旋转的度数为 150°或330° .
【考点】旋转的性质;平行线的性质.
【专题】平移、旋转与对称;运算能力.
【答案】150°或330°.
【分析】分CE在直线BC的上方和下方两种情况讨论,画出图形,根据平行线的性质求解即可.
【解答】解:∵∠ACB=∠CDE=90°,∠DCE=45°,∠A=60°,
∴∠B=30°,
当CE在直线BC的上方时,如图,
∵CE∥AB,
∴∠ECB+∠B=180°,
∴∠ECB=150°,
即三角板CDE旋转的度数为150°,
当CE在直线BC的下方时,如图,
∵CE∥AB,
∴∠ECB=∠B=30°,
即三角板CDE旋转的度数为360°﹣30°=330°.
故答案为:150°或330°.
【点评】本题考查了旋转的性质,平行线的性质,正确进行计算是解题关键.
11.(2024秋 西吉县校级期末)如图,将一个含30°角的直角三角板ABC绕点A顺时针旋转至△AB′C′,使得B,A,C′三点在同一条直线上,则旋转角∠BAB′的度数是 150° .
【考点】旋转的性质.
【专题】平移、旋转与对称;几何直观.
【答案】150°.
【分析】由旋转得,∠B'AC'=∠BAC=30°,由题意得∠BAC'=180°,再根据∠BAB′=∠BAC'﹣∠B'AC'可得答案.
【解答】解:由旋转得,∠B'AC'=∠BAC=30°,
∵B,A,C′三点在同一条直线上,
∴∠BAC'=180°,
∴∠BAB′=∠BAC'﹣∠B'AC'=150°.
故答案为:150°.
【点评】本题考查旋转的性质,熟练掌握旋转的性质是解答本题的关键.
12.(2025春 成华区校级期中)如图,在△ABC中,∠ABC=48°,将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B′恰好落在BC边上,且AB'=CB',则∠C′的度数为 24° .
【考点】旋转的性质.
【专题】平移、旋转与对称;几何直观.
【答案】24°.
【分析】由旋转得∠C=∠C',AB=AB',可得∠AB'B=∠ABC=48°.由已知条件可得∠C=∠CAB',根据∠AB'B=∠C+∠CAB'=2∠C=48°,可得∠C=24°,即可得∠C'=24°.
【解答】解:∵将△ABC绕点A按逆时针方向旋转得到△AB'C',
∴∠C=∠C',AB=AB',
∴∠AB'B=∠ABC=48°.
∵AB'=CB',
∴∠C=∠CAB',
∵∠AB'B=∠C+∠CAB'=2∠C=48°,
∴∠C=24°,
∴∠C'=24°.
故答案为:24°.
【点评】本题考查旋转的性质,熟练掌握旋转的性质是解答本题的关键.
三.解答题(共3小题)
13.(2025 太湖县模拟)如图,在每个小正方形的边长为1个单位的网格中,△ABC的顶点均在格点(网格线的交点)上.
(1)将△ABC向右平移3个单位,再向下平移2个单位得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕点C1逆时针旋转90°得到△A2B2C2,画出△A2B2C2.
【考点】作图﹣旋转变换;作图﹣平移变换.
【专题】平移、旋转与对称;推理能力.
【答案】(1)△A1B1C1见解答过程;
(2)△A2B2C2见解答过程.
【分析】(1)利用点平移的规律找出A1、B1、C1,然后依次描点即可;
(2)利用网格特点和旋转的性质画出点A2、B2、C2即可.
【解答】解:(1)如图,△A1B1C1即为所求作;
(2)如图,△A2B2C1即为所求作.
【点评】本题考查了作图﹣平移变换、旋转变换,熟练掌握平移和旋转的性质是解题的关键.
14.(2025春 丹阳市期中)如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D落在边BC上.
(1)若∠A=60°,求∠BDE的度数;
(2)若AC=5,CE=7,求BD的长度.
【考点】旋转的性质.
【专题】平移、旋转与对称;推理能力.
【答案】(1)∠BDE=120°;
(2)2.
【分析】(1)由旋转的性质可得∠A=∠CDE=60°,即可求解;
(2)由旋转的性质可得AC=CD=5,CE=BC=7,即可求解.
【解答】解:(1)∵将△ABC绕点C顺时针旋转得到△DEC,
∴∠A=∠CDE=60°,
∴∠BDE=120°;
(2)∵将△ABC绕点C顺时针旋转得到△DEC,
∴AC=CD=5,CE=BC=7,
∴BD=BC﹣CD=2.
【点评】本题考查了旋转的性质,掌握旋转的性质是解题的关键.
15.(2025春 宜兴市期中)如图,在5×5的方格网中,所有标出的点均为格点,请按要求画图.
(1)如图1,画出△ABC关于点O成中心对称的图形,并标上对应的字母;
(2)如图2,△ABC绕旋转中心顺时针旋转得到△DEF,直接标出旋转中心点P,写出旋转角的度数为 90° .
【考点】作图﹣旋转变换.
【专题】作图题;平移、旋转与对称;几何直观;推理能力.
【答案】(1)作图见解析;
(2)作图见解析;90°.
【分析】(1)作出点A的对应点D,连接CD,BD即可;
(2)线段AD,CF的垂直平分线的交点P即为所求,直接根据旋转角∠CPF=90°即可得出答案.
【解答】(1)△ABC关于点O成中心对称的图形,如图1,△DCB即为所求;
(2)如图2,点P即为所求.
根据图可知旋转角∠CPF=90°,
故答案为:90°.
【点评】本题考查作图﹣旋转变换,解题的关键是掌握旋转变换的性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
