【期末核心考点】图形的平移与旋转(含解析)2024-2025学年八年级下册数学北师大版
文档属性
| 名称 | 【期末核心考点】图形的平移与旋转(含解析)2024-2025学年八年级下册数学北师大版 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-14 19:27:15 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末核心考点 图形的平移与旋转
一.选择题(共7小题)
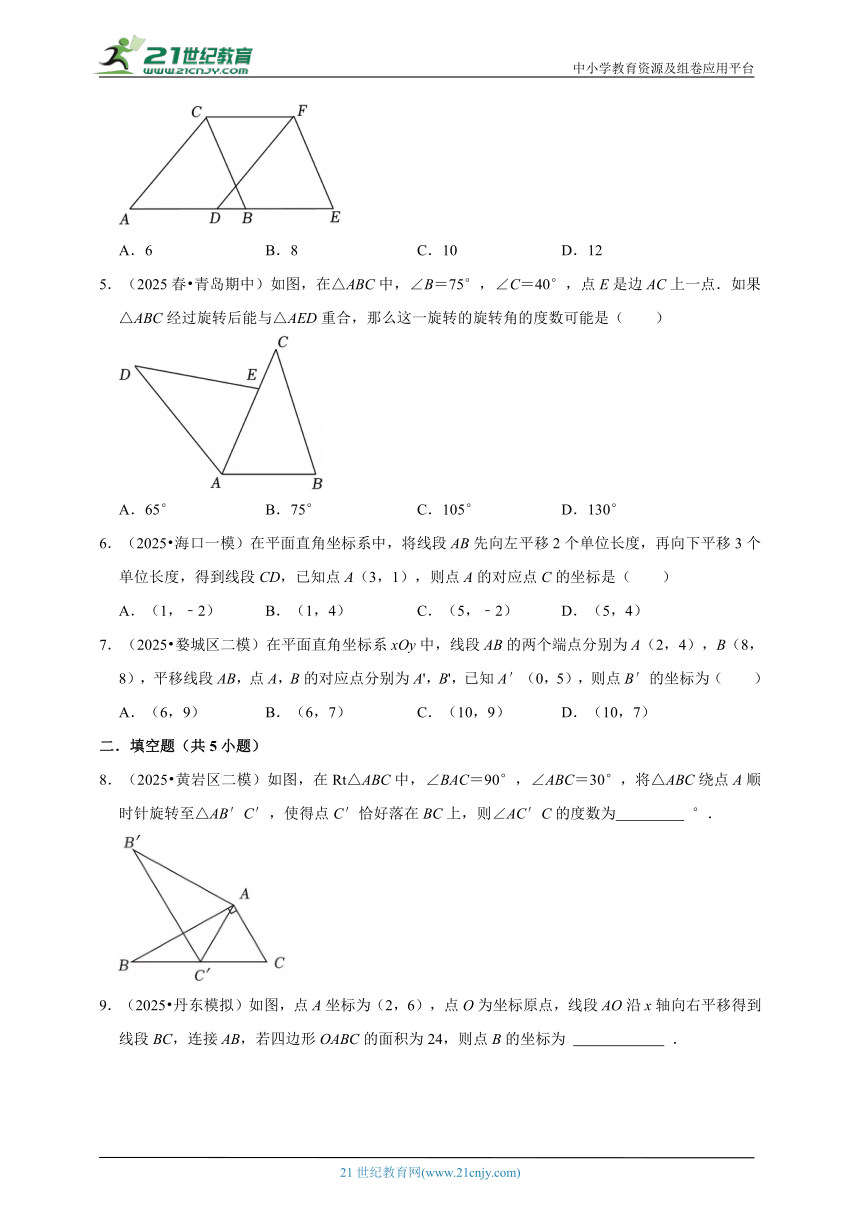
1.(2025 河北区二模)如图,把△ABC以点A为中心顺时针旋转得到△ADE,点B,C的对应点分别是点D,E,若∠ADE的平分线经过点B,连接EC,则下列结论一定正确的是( )
A.AB=DE B.DB∥EC C.BD⊥AE D.∠BDE=∠ACE
2.(2025 西宁校级二模)下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
3.(2025 辽阳模拟)如图,边长为4cm的正方形ABCD先向上平移2cm,再向右平移1cm,得到正方形A′B′C′D′,此时阴影部分的面积为( )
A.7cm2 B.6cm2 C.5cm2 D.4cm2
4.(2025春 青岛期中)如图,将△ABC沿AB方向平移得到△DEF.若CF=8,BD=2,则AB的长为( )
A.6 B.8 C.10 D.12
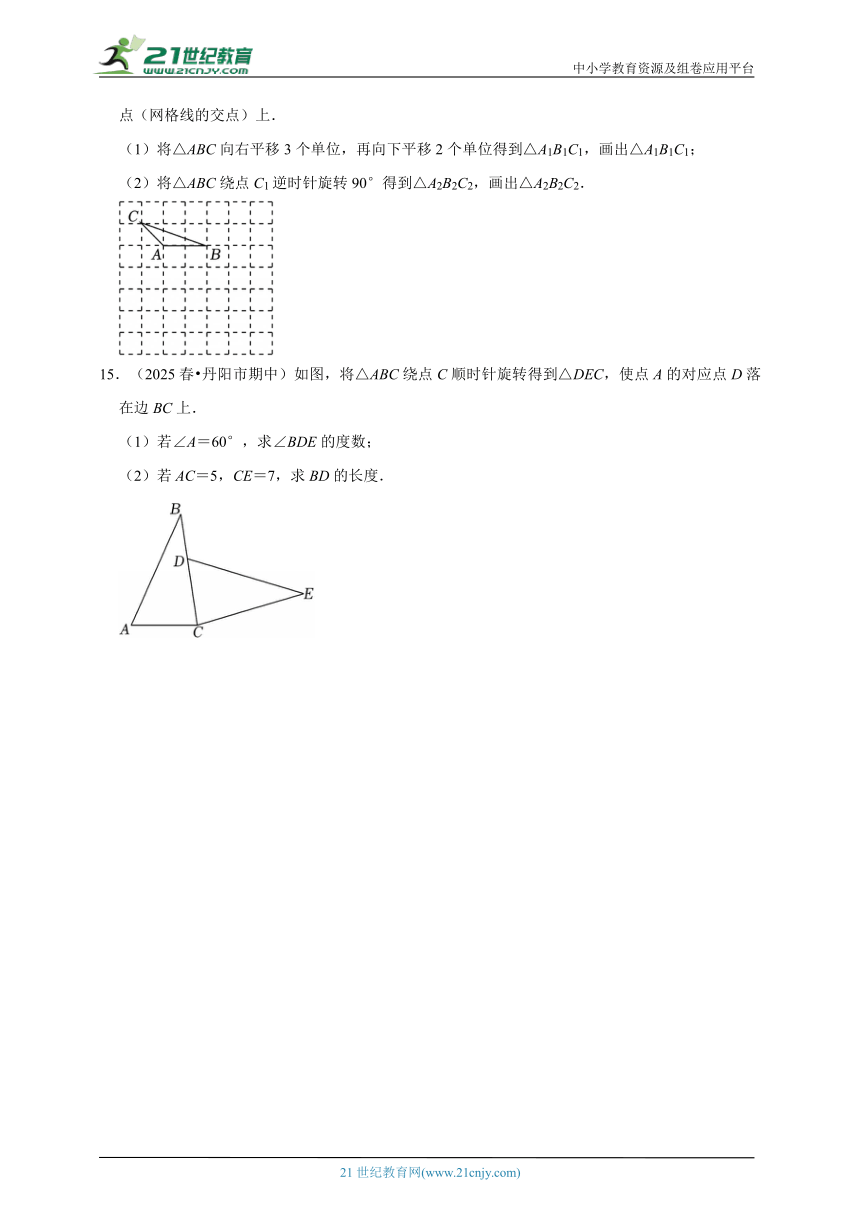
5.(2025春 青岛期中)如图,在△ABC中,∠B=75°,∠C=40°,点E是边AC上一点.如果△ABC经过旋转后能与△AED重合,那么这一旋转的旋转角的度数可能是( )
A.65° B.75° C.105° D.130°
6.(2025 海口一模)在平面直角坐标系中,将线段AB先向左平移2个单位长度,再向下平移3个单位长度,得到线段CD,已知点A(3,1),则点A的对应点C的坐标是( )
A.(1,﹣2) B.(1,4) C.(5,﹣2) D.(5,4)
7.(2025 婺城区二模)在平面直角坐标系xOy中,线段AB的两个端点分别为A(2,4),B(8,8),平移线段AB,点A,B的对应点分别为A',B',已知A′(0,5),则点B′的坐标为( )
A.(6,9) B.(6,7) C.(10,9) D.(10,7)
二.填空题(共5小题)
8.(2025 黄岩区二模)如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,将△ABC绕点A顺时针旋转至△AB′C′,使得点C′恰好落在BC上,则∠AC′C的度数为 °.
9.(2025 丹东模拟)如图,点A坐标为(2,6),点O为坐标原点,线段AO沿x轴向右平移得到线段BC,连接AB,若四边形OABC的面积为24,则点B的坐标为 .
10.(2025春 青岛期中)如图,将△ABC绕点B顺时针方向旋转90°得到△DBE,若点C,D,E在同一条直线上,∠ABC=26°,则∠BDE的度数为 °.
11.(2025 五华区校级模拟)点A(a,2)与点B(﹣1,b)关于原点对称,则(a+b)2023的值为 .
12.(2024秋 东营期末)如图,是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移得到△DEF,如果AB=8,BE=4,DH=2,则图中阴影部分的面积为 .
三.解答题(共3小题)
13.(2025 南岗区模拟)如图,方格纸中每个小正方形的边长均为1个单位长度,△ABC的三个顶点均在小正方形顶点上.
(1)在图1中画出△ACD,使四边形ABCD是中心对称图形,点D在小正方形格点上.连接BD,并直接写出线段BD的长;
(2)在图2中画出△ACE,使四边形ABCE是轴对称图形,点E在小正方形格点上.
14.(2025 太湖县模拟)如图,在每个小正方形的边长为1个单位的网格中,△ABC的顶点均在格点(网格线的交点)上.
(1)将△ABC向右平移3个单位,再向下平移2个单位得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕点C1逆时针旋转90°得到△A2B2C2,画出△A2B2C2.
15.(2025春 丹阳市期中)如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D落在边BC上.
(1)若∠A=60°,求∠BDE的度数;
(2)若AC=5,CE=7,求BD的长度.
期末核心考点 图形的平移与旋转
参考答案与试题解析
一.选择题(共7小题)
1.(2025 河北区二模)如图,把△ABC以点A为中心顺时针旋转得到△ADE,点B,C的对应点分别是点D,E,若∠ADE的平分线经过点B,连接EC,则下列结论一定正确的是( )
A.AB=DE B.DB∥EC C.BD⊥AE D.∠BDE=∠ACE
【考点】旋转的性质;平行线的判定.
【专题】平移、旋转与对称;几何直观.
【答案】D
【分析】由旋转得AB=AD,AC=AE,∠DAE=∠BAC,可得∠BAD=∠CAE,,,则可得∠ACE=∠ADB.由角平分线的定义可得∠BDE=∠ADB,进而可得∠BDE=∠ACE,即可得出答案.
【解答】解:∵把△ABC以点A为中心顺时针旋转得到△ADE,
∴AB=AD,AC=AE,∠DAE=∠BAC,
∴∠BAD=∠CAE,,,
∴∠ACE=∠ADB.
∵DB为∠ADE的平分线,
∴∠BDE=∠ADB,
∴∠BDE=∠ACE.
故D选项正确,符合题意.
根据已知条件不能得出A,B,C选项,
故A,B,C选项不正确,不符合题意.
故选:D.
【点评】本题考查旋转的性质、平行线的判定,解题的关键是理解题意,灵活运用所学知识解决问题.
2.(2025 西宁校级二模)下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
【考点】中心对称图形;轴对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】B
【分析】根据中心对称图形和轴对称图形的定义一一判断即可.
【解答】解:根据中心对称图形和轴对称图形的定义一一判断如下:
A、是轴对称图形,不是中心对称图形,故不符合题意;
B、是轴对称图形,也是中心对称图形,故符合题意;
C、不是轴对称图形,是中心对称图形,故不符合题意;
D、是轴对称图形,不是中心对称图形,故不符合题意.
故选:B.
【点评】本题考查了中心对称图形和轴对称图形,熟练掌握以上知识点是解题的关键.
3.(2025 辽阳模拟)如图,边长为4cm的正方形ABCD先向上平移2cm,再向右平移1cm,得到正方形A′B′C′D′,此时阴影部分的面积为( )
A.7cm2 B.6cm2 C.5cm2 D.4cm2
【考点】平移的性质.
【专题】矩形 菱形 正方形;平移、旋转与对称;推理能力.
【答案】B
【分析】由平移的性质可得A'E=2cm,AE=1cm,可求B'E=2cm,DE=3cm,即可求解.
【解答】解:如图,设AD与A'B'交于点E,
∵将边长为4cm的正方形ABCD先向上平移2cm,再向右平移1cm,
∴A'E=2cm,AE=1cm,
∴B'E=2cm,DE=3cm,
∴阴影部分的面积=2×3=6cm2,
故选:B.
【点评】本题考查了正方形的性质,平移的性质,掌握平移的性质是解题的关键.
4.(2025春 青岛期中)如图,将△ABC沿AB方向平移得到△DEF.若CF=8,BD=2,则AB的长为( )
A.6 B.8 C.10 D.12
【考点】平移的性质.
【专题】平移、旋转与对称;推理能力.
【答案】C
【分析】根据图形平移的性质解答即可.
【解答】解:∵△ABC沿AB方向平移得到△DEF,CF=8,BD=2,
∴AD=CF=8,
∴AB=AD+BD=8+2=10.
故选:C.
【点评】本题考查的是平移的性质,熟知把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等是解题的关键.
5.(2025春 青岛期中)如图,在△ABC中,∠B=75°,∠C=40°,点E是边AC上一点.如果△ABC经过旋转后能与△AED重合,那么这一旋转的旋转角的度数可能是( )
A.65° B.75° C.105° D.130°
【考点】旋转的性质.
【专题】平移、旋转与对称;推理能力.
【答案】A
【分析】根据三角形内角和定理和旋转的性质即可得到结论.
【解答】解:∵∠B=75°,∠C=40°,
∴∠BAC=180°﹣∠B﹣∠C=65°,
∵△ABC经过旋转后能与△AED重合,
∴∠EAB=∠CAB=65°,
∴这一旋转的旋转角的度数可能是65°.
故选:A.
【点评】本题考查了旋转的性质,轴对称的性质,含30°角的直角三角形的性质,等边三角形的判定和性质,三角形全等的判定和性质,作出辅助线构建直角三角形和等边三角形是解题的关键.
6.(2025 海口一模)在平面直角坐标系中,将线段AB先向左平移2个单位长度,再向下平移3个单位长度,得到线段CD,已知点A(3,1),则点A的对应点C的坐标是( )
A.(1,﹣2) B.(1,4) C.(5,﹣2) D.(5,4)
【考点】坐标与图形变化﹣平移.
【专题】平面直角坐标系;平移、旋转与对称;运算能力.
【答案】A
【分析】平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减,据此进行解答,即可.
【解答】解:根据横坐标右移加,左移减;纵坐标上移加,下移减可得:
平移以后点A对应的点C(1,﹣2).
故选:A.
【点评】本题考查了坐标与图形变化﹣平移,熟练掌握该知识点是关键.
7.(2025 婺城区二模)在平面直角坐标系xOy中,线段AB的两个端点分别为A(2,4),B(8,8),平移线段AB,点A,B的对应点分别为A',B',已知A′(0,5),则点B′的坐标为( )
A.(6,9) B.(6,7) C.(10,9) D.(10,7)
【考点】坐标与图形变化﹣平移.
【专题】平面直角坐标系.
【答案】A
【分析】根据A点的坐标及其对应点A′的坐标可得线段AB向左平移了2个单位,向上平移了1个单位,即可得到点B′的坐标.
【解答】解:∵A(2,4)平移后得到A′的坐标为(0,5),
∴向左平移了2个单位,向上平移了1个单位,
∴B(8,8)平移后的点的坐标为(8﹣2,8+1),即点B′的坐标为(6,9),
故选:A.
【点评】本题考查了坐标与图形的变化﹣﹣平移,掌握横坐标右加左减,纵坐标上加下减的规律是解题的关键.
二.填空题(共5小题)
8.(2025 黄岩区二模)如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,将△ABC绕点A顺时针旋转至△AB′C′,使得点C′恰好落在BC上,则∠AC′C的度数为 60 °.
【考点】旋转的性质.
【答案】60°.
【分析】本题主要考查了旋转变换的性质及其应用问题;如图,证明C′A=CA,∠C=∠AC′C,求出∠C=60°,得到∠C'AC=60°,即可解决问题.
【解答】解:由题意得:C′A=CA,
∴∠C=∠AC′C,
∵∠BAC=90°,∠ABC=30°,
∴∠C=90°﹣30°=60°,
∴∠C'AC=180°﹣2×60°,
故答案为:60°.
【点评】本题考查了旋转的性质,直角三角形两锐角互余,等边三角形的判定与性质,熟记各性质并准确识图是解题的关键.
9.(2025 丹东模拟)如图,点A坐标为(2,6),点O为坐标原点,线段AO沿x轴向右平移得到线段BC,连接AB,若四边形OABC的面积为24,则点B的坐标为 (6,6) .
【考点】坐标与图形变化﹣平移;三角形的面积.
【专题】平移、旋转与对称;几何直观.
【答案】(6,6).
【分析】过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,由题意可得OD=2,AD=6,四边形ABED为矩形,可得DE=AB=OC=4,BE=AD=6,则OE=OD+DE=6,即可得点B的坐标为(6,6).
【解答】解:过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,
∴∠ADE=∠BED=90°.
∵点A坐标为(2,6),
∴OD=2,AD=6.
∵线段AO沿x轴向右平移得到线段BC,
∴OA∥BC,OA=BC,
∴四边形OABC为平行四边形,
∴AB∥OC,AB=OC,
∴∠ADE=∠BED=∠DAB=90°,
∴四边形ABED为矩形,
∴DE=AB,BE=AD=6.
∵四边形OABC的面积为24,
∴OC AD=6OC=24,
∴OC=4,
∴AB=DE=4,
∴OE=OD+DE=6,
∴点B的坐标为(6,6).
故答案为:(6,6).
【点评】本题考查坐标与图形变化﹣平移、三角形的面积,解题的关键是理解题意,灵活运用所学知识解决问题.
10.(2025春 青岛期中)如图,将△ABC绕点B顺时针方向旋转90°得到△DBE,若点C,D,E在同一条直线上,∠ABC=26°,则∠BDE的度数为 109 °.
【考点】旋转的性质.
【专题】平移、旋转与对称;几何直观.
【答案】109.
【分析】由旋转得,BC=BE,∠ABD=∠CBE=90°,则可得∠BCE=∠E=45°,∠CBD=∠ABD﹣∠ABC=64°,再根据∠BDE=∠CBD+∠BCD可得答案.
【解答】解:由旋转得,BC=BE,∠ABD=∠CBE=90°,
∴∠BCE=∠E=45°,∠CBD=∠ABD﹣∠ABC=90°﹣26°=64°,
∴∠BDE=∠CBD+∠BCD=64°+45°=109°.
故答案为:109.
【点评】本题考查旋转的性质,熟练掌握旋转的性质是解答本题的关键.
11.(2025 五华区校级模拟)点A(a,2)与点B(﹣1,b)关于原点对称,则(a+b)2023的值为 ﹣1 .
【考点】关于原点对称的点的坐标.
【专题】平移、旋转与对称;运算能力.
【答案】﹣1.
【分析】先根据关于原点对称的点的坐标特点求出a、b的值,代入代数式进行计算即可.
【解答】解:∵点A(a,2),点B(﹣1,b)关于原点对称,
∴a=1,b=﹣2,
∴(a+b)2023=(1﹣2)2023=﹣1.
故答案为:﹣1.
【点评】本题考查的是关于x、y轴对称的点的坐标特点,熟知关于x轴的对称点的坐标横坐标不变,纵坐标互为相反数;关于y轴的对称点的坐标横坐标互为相反数,纵坐标不变是解题的关键.
12.(2024秋 东营期末)如图,是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移得到△DEF,如果AB=8,BE=4,DH=2,则图中阴影部分的面积为 28 .
【考点】平移的性质.
【专题】平移、旋转与对称;几何直观.
【答案】见试题解答内容
【分析】根据平移的性质得到AB=DE,S△ABC=S△DEF,进而得出阴影部分的面积=S梯形ABEH,根据梯形的面积公式计算即可.
【解答】解:由平移的性质可知,AB=DE,S△ABC=S△DEF,
∴S△ABC﹣S△HEC=S△DEF﹣S△HEC,即阴影部分的面积=S梯形ABEH,
∵AB=8,
∴DE=AB=8,
∴EH=DE﹣DH=6,
∴阴影部分的面积=S梯形ABEH(6+8)×4=28,
故答案为:28.
【点评】本题考查的是平移的性质、梯形的面积计算,掌握把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同是解题的关键.
三.解答题(共3小题)
13.(2025 南岗区模拟)如图,方格纸中每个小正方形的边长均为1个单位长度,△ABC的三个顶点均在小正方形顶点上.
(1)在图1中画出△ACD,使四边形ABCD是中心对称图形,点D在小正方形格点上.连接BD,并直接写出线段BD的长;
(2)在图2中画出△ACE,使四边形ABCE是轴对称图形,点E在小正方形格点上.
【考点】作图﹣旋转变换;勾股定理;作图﹣轴对称变换.
【专题】网格型;几何直观.
【答案】(1)图形见解析,;
(2)见解析.
【分析】(1)根据中心对称图形的定义作出图形,再根据勾股定理求出BD的长即可;
(2)根据轴对称图形的定义作出图形即可.
【解答】解:(1)如图1所示,△ACD即为所求;
BD;
(2)如图2所示,△ACE即为所求.
【点评】本题考查了作图﹣轴对称变换,旋转变换,熟记轴对称变换,旋转变换的性质是解题的关键.
14.(2025 太湖县模拟)如图,在每个小正方形的边长为1个单位的网格中,△ABC的顶点均在格点(网格线的交点)上.
(1)将△ABC向右平移3个单位,再向下平移2个单位得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕点C1逆时针旋转90°得到△A2B2C2,画出△A2B2C2.
【考点】作图﹣旋转变换;作图﹣平移变换.
【专题】平移、旋转与对称;推理能力.
【答案】(1)△A1B1C1见解答过程;
(2)△A2B2C2见解答过程.
【分析】(1)利用点平移的规律找出A1、B1、C1,然后依次描点即可;
(2)利用网格特点和旋转的性质画出点A2、B2、C2即可.
【解答】解:(1)如图,△A1B1C1即为所求作;
(2)如图,△A2B2C1即为所求作.
【点评】本题考查了作图﹣平移变换、旋转变换,熟练掌握平移和旋转的性质是解题的关键.
15.(2025春 丹阳市期中)如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D落在边BC上.
(1)若∠A=60°,求∠BDE的度数;
(2)若AC=5,CE=7,求BD的长度.
【考点】旋转的性质.
【专题】平移、旋转与对称;推理能力.
【答案】(1)∠BDE=120°;
(2)2.
【分析】(1)由旋转的性质可得∠A=∠CDE=60°,即可求解;
(2)由旋转的性质可得AC=CD=5,CE=BC=7,即可求解.
【解答】解:(1)∵将△ABC绕点C顺时针旋转得到△DEC,
∴∠A=∠CDE=60°,
∴∠BDE=120°;
(2)∵将△ABC绕点C顺时针旋转得到△DEC,
∴AC=CD=5,CE=BC=7,
∴BD=BC﹣CD=2.
【点评】本题考查了旋转的性质,掌握旋转的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末核心考点 图形的平移与旋转
一.选择题(共7小题)
1.(2025 河北区二模)如图,把△ABC以点A为中心顺时针旋转得到△ADE,点B,C的对应点分别是点D,E,若∠ADE的平分线经过点B,连接EC,则下列结论一定正确的是( )
A.AB=DE B.DB∥EC C.BD⊥AE D.∠BDE=∠ACE
2.(2025 西宁校级二模)下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
3.(2025 辽阳模拟)如图,边长为4cm的正方形ABCD先向上平移2cm,再向右平移1cm,得到正方形A′B′C′D′,此时阴影部分的面积为( )
A.7cm2 B.6cm2 C.5cm2 D.4cm2
4.(2025春 青岛期中)如图,将△ABC沿AB方向平移得到△DEF.若CF=8,BD=2,则AB的长为( )
A.6 B.8 C.10 D.12
5.(2025春 青岛期中)如图,在△ABC中,∠B=75°,∠C=40°,点E是边AC上一点.如果△ABC经过旋转后能与△AED重合,那么这一旋转的旋转角的度数可能是( )
A.65° B.75° C.105° D.130°
6.(2025 海口一模)在平面直角坐标系中,将线段AB先向左平移2个单位长度,再向下平移3个单位长度,得到线段CD,已知点A(3,1),则点A的对应点C的坐标是( )
A.(1,﹣2) B.(1,4) C.(5,﹣2) D.(5,4)
7.(2025 婺城区二模)在平面直角坐标系xOy中,线段AB的两个端点分别为A(2,4),B(8,8),平移线段AB,点A,B的对应点分别为A',B',已知A′(0,5),则点B′的坐标为( )
A.(6,9) B.(6,7) C.(10,9) D.(10,7)
二.填空题(共5小题)
8.(2025 黄岩区二模)如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,将△ABC绕点A顺时针旋转至△AB′C′,使得点C′恰好落在BC上,则∠AC′C的度数为 °.
9.(2025 丹东模拟)如图,点A坐标为(2,6),点O为坐标原点,线段AO沿x轴向右平移得到线段BC,连接AB,若四边形OABC的面积为24,则点B的坐标为 .
10.(2025春 青岛期中)如图,将△ABC绕点B顺时针方向旋转90°得到△DBE,若点C,D,E在同一条直线上,∠ABC=26°,则∠BDE的度数为 °.
11.(2025 五华区校级模拟)点A(a,2)与点B(﹣1,b)关于原点对称,则(a+b)2023的值为 .
12.(2024秋 东营期末)如图,是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移得到△DEF,如果AB=8,BE=4,DH=2,则图中阴影部分的面积为 .
三.解答题(共3小题)
13.(2025 南岗区模拟)如图,方格纸中每个小正方形的边长均为1个单位长度,△ABC的三个顶点均在小正方形顶点上.
(1)在图1中画出△ACD,使四边形ABCD是中心对称图形,点D在小正方形格点上.连接BD,并直接写出线段BD的长;
(2)在图2中画出△ACE,使四边形ABCE是轴对称图形,点E在小正方形格点上.
14.(2025 太湖县模拟)如图,在每个小正方形的边长为1个单位的网格中,△ABC的顶点均在格点(网格线的交点)上.
(1)将△ABC向右平移3个单位,再向下平移2个单位得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕点C1逆时针旋转90°得到△A2B2C2,画出△A2B2C2.
15.(2025春 丹阳市期中)如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D落在边BC上.
(1)若∠A=60°,求∠BDE的度数;
(2)若AC=5,CE=7,求BD的长度.
期末核心考点 图形的平移与旋转
参考答案与试题解析
一.选择题(共7小题)
1.(2025 河北区二模)如图,把△ABC以点A为中心顺时针旋转得到△ADE,点B,C的对应点分别是点D,E,若∠ADE的平分线经过点B,连接EC,则下列结论一定正确的是( )
A.AB=DE B.DB∥EC C.BD⊥AE D.∠BDE=∠ACE
【考点】旋转的性质;平行线的判定.
【专题】平移、旋转与对称;几何直观.
【答案】D
【分析】由旋转得AB=AD,AC=AE,∠DAE=∠BAC,可得∠BAD=∠CAE,,,则可得∠ACE=∠ADB.由角平分线的定义可得∠BDE=∠ADB,进而可得∠BDE=∠ACE,即可得出答案.
【解答】解:∵把△ABC以点A为中心顺时针旋转得到△ADE,
∴AB=AD,AC=AE,∠DAE=∠BAC,
∴∠BAD=∠CAE,,,
∴∠ACE=∠ADB.
∵DB为∠ADE的平分线,
∴∠BDE=∠ADB,
∴∠BDE=∠ACE.
故D选项正确,符合题意.
根据已知条件不能得出A,B,C选项,
故A,B,C选项不正确,不符合题意.
故选:D.
【点评】本题考查旋转的性质、平行线的判定,解题的关键是理解题意,灵活运用所学知识解决问题.
2.(2025 西宁校级二模)下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
【考点】中心对称图形;轴对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】B
【分析】根据中心对称图形和轴对称图形的定义一一判断即可.
【解答】解:根据中心对称图形和轴对称图形的定义一一判断如下:
A、是轴对称图形,不是中心对称图形,故不符合题意;
B、是轴对称图形,也是中心对称图形,故符合题意;
C、不是轴对称图形,是中心对称图形,故不符合题意;
D、是轴对称图形,不是中心对称图形,故不符合题意.
故选:B.
【点评】本题考查了中心对称图形和轴对称图形,熟练掌握以上知识点是解题的关键.
3.(2025 辽阳模拟)如图,边长为4cm的正方形ABCD先向上平移2cm,再向右平移1cm,得到正方形A′B′C′D′,此时阴影部分的面积为( )
A.7cm2 B.6cm2 C.5cm2 D.4cm2
【考点】平移的性质.
【专题】矩形 菱形 正方形;平移、旋转与对称;推理能力.
【答案】B
【分析】由平移的性质可得A'E=2cm,AE=1cm,可求B'E=2cm,DE=3cm,即可求解.
【解答】解:如图,设AD与A'B'交于点E,
∵将边长为4cm的正方形ABCD先向上平移2cm,再向右平移1cm,
∴A'E=2cm,AE=1cm,
∴B'E=2cm,DE=3cm,
∴阴影部分的面积=2×3=6cm2,
故选:B.
【点评】本题考查了正方形的性质,平移的性质,掌握平移的性质是解题的关键.
4.(2025春 青岛期中)如图,将△ABC沿AB方向平移得到△DEF.若CF=8,BD=2,则AB的长为( )
A.6 B.8 C.10 D.12
【考点】平移的性质.
【专题】平移、旋转与对称;推理能力.
【答案】C
【分析】根据图形平移的性质解答即可.
【解答】解:∵△ABC沿AB方向平移得到△DEF,CF=8,BD=2,
∴AD=CF=8,
∴AB=AD+BD=8+2=10.
故选:C.
【点评】本题考查的是平移的性质,熟知把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等是解题的关键.
5.(2025春 青岛期中)如图,在△ABC中,∠B=75°,∠C=40°,点E是边AC上一点.如果△ABC经过旋转后能与△AED重合,那么这一旋转的旋转角的度数可能是( )
A.65° B.75° C.105° D.130°
【考点】旋转的性质.
【专题】平移、旋转与对称;推理能力.
【答案】A
【分析】根据三角形内角和定理和旋转的性质即可得到结论.
【解答】解:∵∠B=75°,∠C=40°,
∴∠BAC=180°﹣∠B﹣∠C=65°,
∵△ABC经过旋转后能与△AED重合,
∴∠EAB=∠CAB=65°,
∴这一旋转的旋转角的度数可能是65°.
故选:A.
【点评】本题考查了旋转的性质,轴对称的性质,含30°角的直角三角形的性质,等边三角形的判定和性质,三角形全等的判定和性质,作出辅助线构建直角三角形和等边三角形是解题的关键.
6.(2025 海口一模)在平面直角坐标系中,将线段AB先向左平移2个单位长度,再向下平移3个单位长度,得到线段CD,已知点A(3,1),则点A的对应点C的坐标是( )
A.(1,﹣2) B.(1,4) C.(5,﹣2) D.(5,4)
【考点】坐标与图形变化﹣平移.
【专题】平面直角坐标系;平移、旋转与对称;运算能力.
【答案】A
【分析】平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减,据此进行解答,即可.
【解答】解:根据横坐标右移加,左移减;纵坐标上移加,下移减可得:
平移以后点A对应的点C(1,﹣2).
故选:A.
【点评】本题考查了坐标与图形变化﹣平移,熟练掌握该知识点是关键.
7.(2025 婺城区二模)在平面直角坐标系xOy中,线段AB的两个端点分别为A(2,4),B(8,8),平移线段AB,点A,B的对应点分别为A',B',已知A′(0,5),则点B′的坐标为( )
A.(6,9) B.(6,7) C.(10,9) D.(10,7)
【考点】坐标与图形变化﹣平移.
【专题】平面直角坐标系.
【答案】A
【分析】根据A点的坐标及其对应点A′的坐标可得线段AB向左平移了2个单位,向上平移了1个单位,即可得到点B′的坐标.
【解答】解:∵A(2,4)平移后得到A′的坐标为(0,5),
∴向左平移了2个单位,向上平移了1个单位,
∴B(8,8)平移后的点的坐标为(8﹣2,8+1),即点B′的坐标为(6,9),
故选:A.
【点评】本题考查了坐标与图形的变化﹣﹣平移,掌握横坐标右加左减,纵坐标上加下减的规律是解题的关键.
二.填空题(共5小题)
8.(2025 黄岩区二模)如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,将△ABC绕点A顺时针旋转至△AB′C′,使得点C′恰好落在BC上,则∠AC′C的度数为 60 °.
【考点】旋转的性质.
【答案】60°.
【分析】本题主要考查了旋转变换的性质及其应用问题;如图,证明C′A=CA,∠C=∠AC′C,求出∠C=60°,得到∠C'AC=60°,即可解决问题.
【解答】解:由题意得:C′A=CA,
∴∠C=∠AC′C,
∵∠BAC=90°,∠ABC=30°,
∴∠C=90°﹣30°=60°,
∴∠C'AC=180°﹣2×60°,
故答案为:60°.
【点评】本题考查了旋转的性质,直角三角形两锐角互余,等边三角形的判定与性质,熟记各性质并准确识图是解题的关键.
9.(2025 丹东模拟)如图,点A坐标为(2,6),点O为坐标原点,线段AO沿x轴向右平移得到线段BC,连接AB,若四边形OABC的面积为24,则点B的坐标为 (6,6) .
【考点】坐标与图形变化﹣平移;三角形的面积.
【专题】平移、旋转与对称;几何直观.
【答案】(6,6).
【分析】过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,由题意可得OD=2,AD=6,四边形ABED为矩形,可得DE=AB=OC=4,BE=AD=6,则OE=OD+DE=6,即可得点B的坐标为(6,6).
【解答】解:过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,
∴∠ADE=∠BED=90°.
∵点A坐标为(2,6),
∴OD=2,AD=6.
∵线段AO沿x轴向右平移得到线段BC,
∴OA∥BC,OA=BC,
∴四边形OABC为平行四边形,
∴AB∥OC,AB=OC,
∴∠ADE=∠BED=∠DAB=90°,
∴四边形ABED为矩形,
∴DE=AB,BE=AD=6.
∵四边形OABC的面积为24,
∴OC AD=6OC=24,
∴OC=4,
∴AB=DE=4,
∴OE=OD+DE=6,
∴点B的坐标为(6,6).
故答案为:(6,6).
【点评】本题考查坐标与图形变化﹣平移、三角形的面积,解题的关键是理解题意,灵活运用所学知识解决问题.
10.(2025春 青岛期中)如图,将△ABC绕点B顺时针方向旋转90°得到△DBE,若点C,D,E在同一条直线上,∠ABC=26°,则∠BDE的度数为 109 °.
【考点】旋转的性质.
【专题】平移、旋转与对称;几何直观.
【答案】109.
【分析】由旋转得,BC=BE,∠ABD=∠CBE=90°,则可得∠BCE=∠E=45°,∠CBD=∠ABD﹣∠ABC=64°,再根据∠BDE=∠CBD+∠BCD可得答案.
【解答】解:由旋转得,BC=BE,∠ABD=∠CBE=90°,
∴∠BCE=∠E=45°,∠CBD=∠ABD﹣∠ABC=90°﹣26°=64°,
∴∠BDE=∠CBD+∠BCD=64°+45°=109°.
故答案为:109.
【点评】本题考查旋转的性质,熟练掌握旋转的性质是解答本题的关键.
11.(2025 五华区校级模拟)点A(a,2)与点B(﹣1,b)关于原点对称,则(a+b)2023的值为 ﹣1 .
【考点】关于原点对称的点的坐标.
【专题】平移、旋转与对称;运算能力.
【答案】﹣1.
【分析】先根据关于原点对称的点的坐标特点求出a、b的值,代入代数式进行计算即可.
【解答】解:∵点A(a,2),点B(﹣1,b)关于原点对称,
∴a=1,b=﹣2,
∴(a+b)2023=(1﹣2)2023=﹣1.
故答案为:﹣1.
【点评】本题考查的是关于x、y轴对称的点的坐标特点,熟知关于x轴的对称点的坐标横坐标不变,纵坐标互为相反数;关于y轴的对称点的坐标横坐标互为相反数,纵坐标不变是解题的关键.
12.(2024秋 东营期末)如图,是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移得到△DEF,如果AB=8,BE=4,DH=2,则图中阴影部分的面积为 28 .
【考点】平移的性质.
【专题】平移、旋转与对称;几何直观.
【答案】见试题解答内容
【分析】根据平移的性质得到AB=DE,S△ABC=S△DEF,进而得出阴影部分的面积=S梯形ABEH,根据梯形的面积公式计算即可.
【解答】解:由平移的性质可知,AB=DE,S△ABC=S△DEF,
∴S△ABC﹣S△HEC=S△DEF﹣S△HEC,即阴影部分的面积=S梯形ABEH,
∵AB=8,
∴DE=AB=8,
∴EH=DE﹣DH=6,
∴阴影部分的面积=S梯形ABEH(6+8)×4=28,
故答案为:28.
【点评】本题考查的是平移的性质、梯形的面积计算,掌握把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同是解题的关键.
三.解答题(共3小题)
13.(2025 南岗区模拟)如图,方格纸中每个小正方形的边长均为1个单位长度,△ABC的三个顶点均在小正方形顶点上.
(1)在图1中画出△ACD,使四边形ABCD是中心对称图形,点D在小正方形格点上.连接BD,并直接写出线段BD的长;
(2)在图2中画出△ACE,使四边形ABCE是轴对称图形,点E在小正方形格点上.
【考点】作图﹣旋转变换;勾股定理;作图﹣轴对称变换.
【专题】网格型;几何直观.
【答案】(1)图形见解析,;
(2)见解析.
【分析】(1)根据中心对称图形的定义作出图形,再根据勾股定理求出BD的长即可;
(2)根据轴对称图形的定义作出图形即可.
【解答】解:(1)如图1所示,△ACD即为所求;
BD;
(2)如图2所示,△ACE即为所求.
【点评】本题考查了作图﹣轴对称变换,旋转变换,熟记轴对称变换,旋转变换的性质是解题的关键.
14.(2025 太湖县模拟)如图,在每个小正方形的边长为1个单位的网格中,△ABC的顶点均在格点(网格线的交点)上.
(1)将△ABC向右平移3个单位,再向下平移2个单位得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕点C1逆时针旋转90°得到△A2B2C2,画出△A2B2C2.
【考点】作图﹣旋转变换;作图﹣平移变换.
【专题】平移、旋转与对称;推理能力.
【答案】(1)△A1B1C1见解答过程;
(2)△A2B2C2见解答过程.
【分析】(1)利用点平移的规律找出A1、B1、C1,然后依次描点即可;
(2)利用网格特点和旋转的性质画出点A2、B2、C2即可.
【解答】解:(1)如图,△A1B1C1即为所求作;
(2)如图,△A2B2C1即为所求作.
【点评】本题考查了作图﹣平移变换、旋转变换,熟练掌握平移和旋转的性质是解题的关键.
15.(2025春 丹阳市期中)如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D落在边BC上.
(1)若∠A=60°,求∠BDE的度数;
(2)若AC=5,CE=7,求BD的长度.
【考点】旋转的性质.
【专题】平移、旋转与对称;推理能力.
【答案】(1)∠BDE=120°;
(2)2.
【分析】(1)由旋转的性质可得∠A=∠CDE=60°,即可求解;
(2)由旋转的性质可得AC=CD=5,CE=BC=7,即可求解.
【解答】解:(1)∵将△ABC绕点C顺时针旋转得到△DEC,
∴∠A=∠CDE=60°,
∴∠BDE=120°;
(2)∵将△ABC绕点C顺时针旋转得到△DEC,
∴AC=CD=5,CE=BC=7,
∴BD=BC﹣CD=2.
【点评】本题考查了旋转的性质,掌握旋转的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
