【期末核心考点】多边形的内角和与外角和(含解析)2024-2025学年八年级下册数学北师大版
文档属性
| 名称 | 【期末核心考点】多边形的内角和与外角和(含解析)2024-2025学年八年级下册数学北师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 744.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-14 19:31:11 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末核心考点 多边形的内角和与外角和
一.选择题(共7小题)
1.(2025春 淮阴区校级期中)如图,将△ABC纸片沿DE折叠,当点C落在四边形ABDE的外部时,此时测得∠1=120°,∠C=40°,则∠2的度数是( )
A.30° B.40° C.50° D.60°
2.(2025 顺德区二模)若一个多边形的内角和为1800°,则这个多边形的边数为( )
A.5 B.7 C.10 D.12
3.(2024秋 安顺期末)每一个外角都是60°的正多边形是( )
A.正三边形 B.正四边形 C.正五边形 D.正六边形
4.(2025 济阳区模拟)一个多边形的内角和为720°,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
5.(2025春 鲤城区校级期中)如图,从△ABC纸片中剪去△CDE,得到四边形ABDE.如果∠1+∠2=240°,那么∠C度数为( )
A.40° B.60° C.50° D.55°
6.(2024秋 玉林期末)已知正多边形的每一个内角为135°,则这个正多边形的边数为( )
A.12 B.10 C.8 D.6
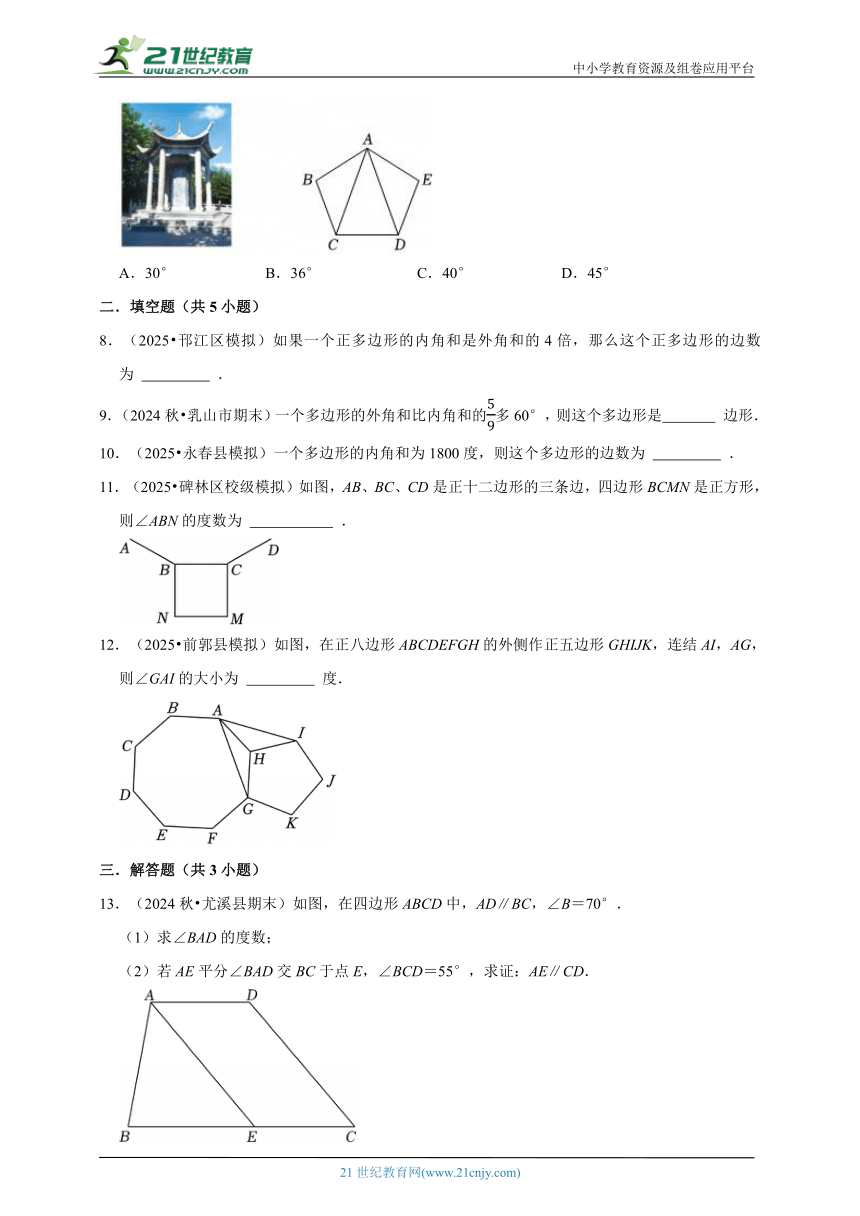
7.(2024秋 召陵区期末)受降亭是中国历史上一个重要的纪念性建筑,它是为了纪念抗日战争胜利后日军在中国的投降仪式而建立的.如图,某亭子的地基平面图是一个正五边形,记为正五边形ABCDE,连接AC和AD,已知∠BAC=∠BCA=∠EAD=∠EDA,则∠CAD的度数为( )
A.30° B.36° C.40° D.45°
二.填空题(共5小题)
8.(2025 邗江区模拟)如果一个正多边形的内角和是外角和的4倍,那么这个正多边形的边数为 .
9.(2024秋 乳山市期末)一个多边形的外角和比内角和的多60°,则这个多边形是 边形.
10.(2025 永春县模拟)一个多边形的内角和为1800度,则这个多边形的边数为 .
11.(2025 碑林区校级模拟)如图,AB、BC、CD是正十二边形的三条边,四边形BCMN是正方形,则∠ABN的度数为 .
12.(2025 前郭县模拟)如图,在正八边形ABCDEFGH的外侧作正五边形GHIJK,连结AI,AG,则∠GAI的大小为 度.
三.解答题(共3小题)
13.(2024秋 尤溪县期末)如图,在四边形ABCD中,AD∥BC,∠B=70°.
(1)求∠BAD的度数;
(2)若AE平分∠BAD交BC于点E,∠BCD=55°,求证:AE∥CD.
14.(2024秋 玉林期末)如图,在四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.
(1)若∠1=33°,求∠2的度数:
(2)判断BE与DF的位置关系,并说明理由.
15.(2024秋 大余县期末)阅读小明和小红的对话,解决下列问题.
(1)这个“多加的锐角”是 度.
(2)小明求的是几边形内角和?
(3)若这是个正多边形,则这个正多边形的一个内角是多少度?
期末核心考点 多边形的内角和与外角和
参考答案与试题解析
一.选择题(共7小题)
1.(2025春 淮阴区校级期中)如图,将△ABC纸片沿DE折叠,当点C落在四边形ABDE的外部时,此时测得∠1=120°,∠C=40°,则∠2的度数是( )
A.30° B.40° C.50° D.60°
【考点】多边形内角与外角;三角形内角和定理.
【专题】三角形;运算能力.
【答案】B
【分析】根据折叠性质得出∠C'=∠C=40°,根据三角形外角性质得出∠DOC=∠1﹣∠C=120°﹣40°=80°,∠2=∠DOC﹣∠C'=80°﹣40°=40°.
【解答】解:如图,设C'D与AC交于点O,
∵∠C=40°,
∴∠C'=∠C=40°,
∵∠1=∠DOC+∠C,∠1=120°,
∴∠DOC=∠1﹣∠C=120°﹣40°=80°,
∵∠DOC=∠2+∠C',
∴∠2=∠DOC﹣∠C'=80°﹣40°=40°.
故选:B.
【点评】本题考查了三角形外角的性质,折叠的性质,熟记三角形外角和折叠的性质是解题的关键.
2.(2025 顺德区二模)若一个多边形的内角和为1800°,则这个多边形的边数为( )
A.5 B.7 C.10 D.12
【考点】多边形内角与外角.
【专题】多边形与平行四边形;推理能力.
【答案】D
【分析】根据多边形内角和定理计算即可.
【解答】解:设这个多边形的边数为n,
根据题意得(n﹣2)×180°=1800°,
解得n=12,
故选:D.
【点评】本题考查了多边形的内角与外角,熟练掌握多边形的内角和定理是解题的关键.
3.(2024秋 安顺期末)每一个外角都是60°的正多边形是( )
A.正三边形 B.正四边形 C.正五边形 D.正六边形
【考点】多边形内角与外角.
【专题】多边形与平行四边形;运算能力.
【答案】D
【分析】根据正多边形的每个外角相等,且外角和为360°,即可求解.
【解答】解:根据正多边形的每个外角相等及外角和为360°可得:
360°÷60°=6(边),
∴这个正多边形是正六边形.
故选:D.
【点评】本题考查正多边形的外角及外角和.熟练掌握该知识点是关键.
4.(2025 济阳区模拟)一个多边形的内角和为720°,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
【考点】多边形内角与外角.
【专题】多边形与平行四边形;运算能力.
【答案】B
【分析】根据多边形的内角和公式解答即可.
【解答】解:设边数为n,根据题意,得
(n﹣2) 180°=720°,
解得n=6.
∴这个多边形为六边形,
故选:B.
【点评】本题考查了多边形的内角和公式,关键是记住多边形的内角和公式.
5.(2025春 鲤城区校级期中)如图,从△ABC纸片中剪去△CDE,得到四边形ABDE.如果∠1+∠2=240°,那么∠C度数为( )
A.40° B.60° C.50° D.55°
【考点】多边形内角与外角.
【专题】多边形与平行四边形;应用意识.
【答案】B
【分析】根据三角形外角的性质,进而得出答案.
【解答】解:∵∠1=∠CDE+∠C,∠2=∠CED+∠C,
∴∠1+∠2=∠CDE+∠C+∠CED+∠C=180°+∠C,
∵∠1+∠2=240°,
∴∠C=240°﹣180°=60°.
故选:B.
【点评】本题主要考查多边形内角与外角,熟练掌握三角形外角的性质是解题的关键.
6.(2024秋 玉林期末)已知正多边形的每一个内角为135°,则这个正多边形的边数为( )
A.12 B.10 C.8 D.6
【考点】多边形内角与外角.
【专题】多边形与平行四边形;几何直观.
【答案】C
【分析】由多边形的外角和是360°即可求解.
【解答】解:∵正多边形的每一个内角为135°,
∴正多边形的每一个外角为45°,
∴正多边形的边数是360÷45=8,
故选:C.
【点评】本题考查多边形的有关知识,关键是掌握:多边形的外角和是360°.
7.(2024秋 召陵区期末)受降亭是中国历史上一个重要的纪念性建筑,它是为了纪念抗日战争胜利后日军在中国的投降仪式而建立的.如图,某亭子的地基平面图是一个正五边形,记为正五边形ABCDE,连接AC和AD,已知∠BAC=∠BCA=∠EAD=∠EDA,则∠CAD的度数为( )
A.30° B.36° C.40° D.45°
【考点】多边形内角与外角.
【专题】多边形与平行四边形;运算能力.
【答案】B
【分析】先求出正五边形的一个内角的度数,等边对等角,求出∠BAC,∠DAE的度数,再根据角的和差关系进行求解即可.
【解答】解:由条件可得,
∵∠BAC=∠BCA=∠EAD=∠EDA,
∴,
∴∠CAD=∠BAE﹣∠BAC﹣∠EAD=36°;
故选:B.
【点评】本题考查正多边形的内角问题,等边对等角,熟练掌握以上知识点是关键.
二.填空题(共5小题)
8.(2025 邗江区模拟)如果一个正多边形的内角和是外角和的4倍,那么这个正多边形的边数为 10 .
【考点】多边形内角与外角.
【专题】多边形与平行四边形;运算能力.
【答案】10.
【分析】设这个正多边形的边数为n,根据这个正多边形的内角和是外角和的4倍,列出方程,解方程求出答案即可.
【解答】解:设这个正多边形的边数为n,由题意得:
180(n﹣2)=4×360,
n﹣2=8,
n=10,
∴这个正多边形的边数是10,
故答案为:10.
【点评】本题主要考查了多边形的外角和内角,解题关键是熟练掌握多边形的内角和公式和外角和.
9.(2024秋 乳山市期末)一个多边形的外角和比内角和的多60°,则这个多边形是 5 边形.
【考点】多边形内角与外角.
【专题】多边形与平行四边形;运算能力.
【答案】5.
【分析】设这个多边形的边数为n,根据题意得出,求解即可.
【解答】解:设这个多边形的边数为n,则:
,
解得:n=5,
故答案为:5.
【点评】本题考查了多边形的内角和与外角和问题,熟练掌握该知识点是关键.
10.(2025 永春县模拟)一个多边形的内角和为1800度,则这个多边形的边数为 12 .
【考点】多边形内角与外角.
【专题】多边形与平行四边形;运算能力.
【答案】见试题解答内容
【分析】根据多边形的内角和=(n﹣2) 180°列出方程求解即可.
【解答】解:设这个多边形的边数为n,
(n﹣2) 180°=1800°,
解得:n=12.
故答案为:12.
【点评】本题考查多边形的内角与外角,掌握多边形的内角和=(n﹣2) 180°是解题的关键.
11.(2025 碑林区校级模拟)如图,AB、BC、CD是正十二边形的三条边,四边形BCMN是正方形,则∠ABN的度数为 120° .
【考点】多边形内角与外角.
【专题】多边形与平行四边形;几何直观.
【答案】120°.
【分析】先求出∠ABC的度数,进而得出答案.
【解答】解:∵360°÷12=30°,
∴∠ABC=180°﹣30°=150°,
∵∠CBN=90°,
∴∠ABN=360°﹣∠ABC﹣∠CBN=360°﹣150°﹣90°=120°.
故答案为:120°.
【点评】本题主要考查多边形内角与外角,求出∠ABC的度数是解题的关键.
12.(2025 前郭县模拟)如图,在正八边形ABCDEFGH的外侧作正五边形GHIJK,连结AI,AG,则∠GAI的大小为 54 度.
【考点】多边形内角与外角;等腰三角形的性质.
【专题】等腰三角形与直角三角形;正多边形与圆;运算能力;推理能力.
【答案】54.
【分析】先根据正多边形的性质和多边形的内角和公式,证明∠HAG=∠HGA,∠HAI=∠AIH,求出∠AHG和∠GHI,再根据周角定义求出∠AHI,然后根据等腰三角形的性质和三角形内角和定理,求出∠HAG和∠HAI,从而求出答案即可.
【解答】解:∵八边形ABCDEFGH是正八边形,五边形GHIJK是正五边形,
∴AH=HG=HI,
∴∠HAG=∠HGA,∠HAI=∠AIH,
∠AHG,,
∵∠AHG+∠GHI+∠AHI=360°,
∴∠AHI=360°﹣∠AHG﹣∠GHI=117°,
∵∠HAG+∠HGA+∠AGH=180°,∠HAI+∠AIH+∠AHI=180°,
∴∠HAG=∠HGA,∠HAI=∠AIH,
∴∠GAI=∠HAG+∠HAI=22.5°+31.5°=54°,
故答案为:54.
【点评】本题主要考查了正多边形的性质和等腰三角形的性质与判定,解题关键是正确识别图形,熟练掌握正多边形的性质和等腰三角形的性质与判定.
三.解答题(共3小题)
13.(2024秋 尤溪县期末)如图,在四边形ABCD中,AD∥BC,∠B=70°.
(1)求∠BAD的度数;
(2)若AE平分∠BAD交BC于点E,∠BCD=55°,求证:AE∥CD.
【考点】多边形内角与外角;平行线的判定与性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】(1)110°;
(2)证明见解答过程.
【分析】(1)根据两直线平行,同旁内角互补求出∠BAD;
(2)根据角平分线的定义求出∠DAE,根据平行线的性质求出∠AEB,得到∠AEB=∠BCD,根据平行线的判定定理证明结论.
【解答】(1)解:∵AD∥BC,
∴∠BAD+∠B=180°,
∵∠B=70°,
∴∠BAD=180°﹣∠B=180°﹣70°=110°,
∴∠BAD的度数是 110°;
(2)证明:∵AE平分∠BAD交BC于点E,∠BAD=110°,
∴,
∵AD∥BC,
∴∠AEB=∠DAE=55°,
∠BCD=55°,
∴∠AEB=∠BCD,
∴AE∥CD.
【点评】本题考查的是平行线的判定和性质、角平分线的定义,掌握平行线的性质是解题的关键.
14.(2024秋 玉林期末)如图,在四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.
(1)若∠1=33°,求∠2的度数:
(2)判断BE与DF的位置关系,并说明理由.
【考点】多边形内角与外角;三角形内角和定理.
【专题】多边形与平行四边形;推理能力.
【答案】(1)57°;
(2)BE∥DF,理由见解析.
【分析】(1)由角平分线的定义得∠1=∠ABE,∠2=∠ADF,根据四边形的内角和可得∠ABC+∠ADC=180°,从而推出∠1+∠2=90°,进而可求出答案;
(2)由互余的性质可得∠1=∠DFC,根据平行线的判定即可得出.
【解答】解:(1)∵BE,DF分别是∠ABC,∠ADC的平分线,
∴∠1=∠ABE,∠2=∠ADF,
∵∠A=∠C=90°,
∴∠ABC+∠ADC=360°﹣90°﹣90°=180°,
∴2(∠1+∠2)=180°,
∴∠1+∠2=90°,
∵∠1=33°,
∴∠2=90°﹣∠1=57°;
(2)BE∥DF,理由如下:
在△FCD中,∵∠C=90°,
∴∠DFC+∠2=90°,
∵∠1+∠2=90°,
∴∠1=∠DFC,
∴BE∥DF.
【点评】本题考查了平行线的判定,多边形的内角和,直角三角形两锐角互余,关键是掌握四边形内角和为360°、同位角相等,两直线平行.
15.(2024秋 大余县期末)阅读小明和小红的对话,解决下列问题.
(1)这个“多加的锐角”是 30 度.
(2)小明求的是几边形内角和?
(3)若这是个正多边形,则这个正多边形的一个内角是多少度?
【考点】多边形内角与外角.
【专题】多边形与平行四边形;运算能力.
【答案】见试题解答内容
【分析】(1)根据多边形内角和的计算方法进行估算即可;
(2)根据对话和多边形内角和的计算方法列方程求解即可;
(3)根据正多边形内角的计算方法进行计算即可.
【解答】解:(1)12边形的内角和为(12﹣2)×180°=1800°,而13边形的内角和为(13﹣2)×180°=1980°,
由于小红说“多边形的内角和不可能是1830°,你一定是多加了一个锐角”,
所以这个“多加的锐角”是1830°﹣1800°=30°,
故答案为:30;
(2)设这个多边形为n边形,由题意得,
(n﹣2)×180°=1800°,
解得n=12,
答:小明求的是12边形内角和;
(3)正十二边形的每一个内角为150°,
答:这个正多边形的一个内角是150°.
【点评】本题考查多边形的内角和和外角和,掌握多边形内角和的计算方法以及正多边形的性质是正确解答的前提.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末核心考点 多边形的内角和与外角和
一.选择题(共7小题)
1.(2025春 淮阴区校级期中)如图,将△ABC纸片沿DE折叠,当点C落在四边形ABDE的外部时,此时测得∠1=120°,∠C=40°,则∠2的度数是( )
A.30° B.40° C.50° D.60°
2.(2025 顺德区二模)若一个多边形的内角和为1800°,则这个多边形的边数为( )
A.5 B.7 C.10 D.12
3.(2024秋 安顺期末)每一个外角都是60°的正多边形是( )
A.正三边形 B.正四边形 C.正五边形 D.正六边形
4.(2025 济阳区模拟)一个多边形的内角和为720°,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
5.(2025春 鲤城区校级期中)如图,从△ABC纸片中剪去△CDE,得到四边形ABDE.如果∠1+∠2=240°,那么∠C度数为( )
A.40° B.60° C.50° D.55°
6.(2024秋 玉林期末)已知正多边形的每一个内角为135°,则这个正多边形的边数为( )
A.12 B.10 C.8 D.6
7.(2024秋 召陵区期末)受降亭是中国历史上一个重要的纪念性建筑,它是为了纪念抗日战争胜利后日军在中国的投降仪式而建立的.如图,某亭子的地基平面图是一个正五边形,记为正五边形ABCDE,连接AC和AD,已知∠BAC=∠BCA=∠EAD=∠EDA,则∠CAD的度数为( )
A.30° B.36° C.40° D.45°
二.填空题(共5小题)
8.(2025 邗江区模拟)如果一个正多边形的内角和是外角和的4倍,那么这个正多边形的边数为 .
9.(2024秋 乳山市期末)一个多边形的外角和比内角和的多60°,则这个多边形是 边形.
10.(2025 永春县模拟)一个多边形的内角和为1800度,则这个多边形的边数为 .
11.(2025 碑林区校级模拟)如图,AB、BC、CD是正十二边形的三条边,四边形BCMN是正方形,则∠ABN的度数为 .
12.(2025 前郭县模拟)如图,在正八边形ABCDEFGH的外侧作正五边形GHIJK,连结AI,AG,则∠GAI的大小为 度.
三.解答题(共3小题)
13.(2024秋 尤溪县期末)如图,在四边形ABCD中,AD∥BC,∠B=70°.
(1)求∠BAD的度数;
(2)若AE平分∠BAD交BC于点E,∠BCD=55°,求证:AE∥CD.
14.(2024秋 玉林期末)如图,在四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.
(1)若∠1=33°,求∠2的度数:
(2)判断BE与DF的位置关系,并说明理由.
15.(2024秋 大余县期末)阅读小明和小红的对话,解决下列问题.
(1)这个“多加的锐角”是 度.
(2)小明求的是几边形内角和?
(3)若这是个正多边形,则这个正多边形的一个内角是多少度?
期末核心考点 多边形的内角和与外角和
参考答案与试题解析
一.选择题(共7小题)
1.(2025春 淮阴区校级期中)如图,将△ABC纸片沿DE折叠,当点C落在四边形ABDE的外部时,此时测得∠1=120°,∠C=40°,则∠2的度数是( )
A.30° B.40° C.50° D.60°
【考点】多边形内角与外角;三角形内角和定理.
【专题】三角形;运算能力.
【答案】B
【分析】根据折叠性质得出∠C'=∠C=40°,根据三角形外角性质得出∠DOC=∠1﹣∠C=120°﹣40°=80°,∠2=∠DOC﹣∠C'=80°﹣40°=40°.
【解答】解:如图,设C'D与AC交于点O,
∵∠C=40°,
∴∠C'=∠C=40°,
∵∠1=∠DOC+∠C,∠1=120°,
∴∠DOC=∠1﹣∠C=120°﹣40°=80°,
∵∠DOC=∠2+∠C',
∴∠2=∠DOC﹣∠C'=80°﹣40°=40°.
故选:B.
【点评】本题考查了三角形外角的性质,折叠的性质,熟记三角形外角和折叠的性质是解题的关键.
2.(2025 顺德区二模)若一个多边形的内角和为1800°,则这个多边形的边数为( )
A.5 B.7 C.10 D.12
【考点】多边形内角与外角.
【专题】多边形与平行四边形;推理能力.
【答案】D
【分析】根据多边形内角和定理计算即可.
【解答】解:设这个多边形的边数为n,
根据题意得(n﹣2)×180°=1800°,
解得n=12,
故选:D.
【点评】本题考查了多边形的内角与外角,熟练掌握多边形的内角和定理是解题的关键.
3.(2024秋 安顺期末)每一个外角都是60°的正多边形是( )
A.正三边形 B.正四边形 C.正五边形 D.正六边形
【考点】多边形内角与外角.
【专题】多边形与平行四边形;运算能力.
【答案】D
【分析】根据正多边形的每个外角相等,且外角和为360°,即可求解.
【解答】解:根据正多边形的每个外角相等及外角和为360°可得:
360°÷60°=6(边),
∴这个正多边形是正六边形.
故选:D.
【点评】本题考查正多边形的外角及外角和.熟练掌握该知识点是关键.
4.(2025 济阳区模拟)一个多边形的内角和为720°,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
【考点】多边形内角与外角.
【专题】多边形与平行四边形;运算能力.
【答案】B
【分析】根据多边形的内角和公式解答即可.
【解答】解:设边数为n,根据题意,得
(n﹣2) 180°=720°,
解得n=6.
∴这个多边形为六边形,
故选:B.
【点评】本题考查了多边形的内角和公式,关键是记住多边形的内角和公式.
5.(2025春 鲤城区校级期中)如图,从△ABC纸片中剪去△CDE,得到四边形ABDE.如果∠1+∠2=240°,那么∠C度数为( )
A.40° B.60° C.50° D.55°
【考点】多边形内角与外角.
【专题】多边形与平行四边形;应用意识.
【答案】B
【分析】根据三角形外角的性质,进而得出答案.
【解答】解:∵∠1=∠CDE+∠C,∠2=∠CED+∠C,
∴∠1+∠2=∠CDE+∠C+∠CED+∠C=180°+∠C,
∵∠1+∠2=240°,
∴∠C=240°﹣180°=60°.
故选:B.
【点评】本题主要考查多边形内角与外角,熟练掌握三角形外角的性质是解题的关键.
6.(2024秋 玉林期末)已知正多边形的每一个内角为135°,则这个正多边形的边数为( )
A.12 B.10 C.8 D.6
【考点】多边形内角与外角.
【专题】多边形与平行四边形;几何直观.
【答案】C
【分析】由多边形的外角和是360°即可求解.
【解答】解:∵正多边形的每一个内角为135°,
∴正多边形的每一个外角为45°,
∴正多边形的边数是360÷45=8,
故选:C.
【点评】本题考查多边形的有关知识,关键是掌握:多边形的外角和是360°.
7.(2024秋 召陵区期末)受降亭是中国历史上一个重要的纪念性建筑,它是为了纪念抗日战争胜利后日军在中国的投降仪式而建立的.如图,某亭子的地基平面图是一个正五边形,记为正五边形ABCDE,连接AC和AD,已知∠BAC=∠BCA=∠EAD=∠EDA,则∠CAD的度数为( )
A.30° B.36° C.40° D.45°
【考点】多边形内角与外角.
【专题】多边形与平行四边形;运算能力.
【答案】B
【分析】先求出正五边形的一个内角的度数,等边对等角,求出∠BAC,∠DAE的度数,再根据角的和差关系进行求解即可.
【解答】解:由条件可得,
∵∠BAC=∠BCA=∠EAD=∠EDA,
∴,
∴∠CAD=∠BAE﹣∠BAC﹣∠EAD=36°;
故选:B.
【点评】本题考查正多边形的内角问题,等边对等角,熟练掌握以上知识点是关键.
二.填空题(共5小题)
8.(2025 邗江区模拟)如果一个正多边形的内角和是外角和的4倍,那么这个正多边形的边数为 10 .
【考点】多边形内角与外角.
【专题】多边形与平行四边形;运算能力.
【答案】10.
【分析】设这个正多边形的边数为n,根据这个正多边形的内角和是外角和的4倍,列出方程,解方程求出答案即可.
【解答】解:设这个正多边形的边数为n,由题意得:
180(n﹣2)=4×360,
n﹣2=8,
n=10,
∴这个正多边形的边数是10,
故答案为:10.
【点评】本题主要考查了多边形的外角和内角,解题关键是熟练掌握多边形的内角和公式和外角和.
9.(2024秋 乳山市期末)一个多边形的外角和比内角和的多60°,则这个多边形是 5 边形.
【考点】多边形内角与外角.
【专题】多边形与平行四边形;运算能力.
【答案】5.
【分析】设这个多边形的边数为n,根据题意得出,求解即可.
【解答】解:设这个多边形的边数为n,则:
,
解得:n=5,
故答案为:5.
【点评】本题考查了多边形的内角和与外角和问题,熟练掌握该知识点是关键.
10.(2025 永春县模拟)一个多边形的内角和为1800度,则这个多边形的边数为 12 .
【考点】多边形内角与外角.
【专题】多边形与平行四边形;运算能力.
【答案】见试题解答内容
【分析】根据多边形的内角和=(n﹣2) 180°列出方程求解即可.
【解答】解:设这个多边形的边数为n,
(n﹣2) 180°=1800°,
解得:n=12.
故答案为:12.
【点评】本题考查多边形的内角与外角,掌握多边形的内角和=(n﹣2) 180°是解题的关键.
11.(2025 碑林区校级模拟)如图,AB、BC、CD是正十二边形的三条边,四边形BCMN是正方形,则∠ABN的度数为 120° .
【考点】多边形内角与外角.
【专题】多边形与平行四边形;几何直观.
【答案】120°.
【分析】先求出∠ABC的度数,进而得出答案.
【解答】解:∵360°÷12=30°,
∴∠ABC=180°﹣30°=150°,
∵∠CBN=90°,
∴∠ABN=360°﹣∠ABC﹣∠CBN=360°﹣150°﹣90°=120°.
故答案为:120°.
【点评】本题主要考查多边形内角与外角,求出∠ABC的度数是解题的关键.
12.(2025 前郭县模拟)如图,在正八边形ABCDEFGH的外侧作正五边形GHIJK,连结AI,AG,则∠GAI的大小为 54 度.
【考点】多边形内角与外角;等腰三角形的性质.
【专题】等腰三角形与直角三角形;正多边形与圆;运算能力;推理能力.
【答案】54.
【分析】先根据正多边形的性质和多边形的内角和公式,证明∠HAG=∠HGA,∠HAI=∠AIH,求出∠AHG和∠GHI,再根据周角定义求出∠AHI,然后根据等腰三角形的性质和三角形内角和定理,求出∠HAG和∠HAI,从而求出答案即可.
【解答】解:∵八边形ABCDEFGH是正八边形,五边形GHIJK是正五边形,
∴AH=HG=HI,
∴∠HAG=∠HGA,∠HAI=∠AIH,
∠AHG,,
∵∠AHG+∠GHI+∠AHI=360°,
∴∠AHI=360°﹣∠AHG﹣∠GHI=117°,
∵∠HAG+∠HGA+∠AGH=180°,∠HAI+∠AIH+∠AHI=180°,
∴∠HAG=∠HGA,∠HAI=∠AIH,
∴∠GAI=∠HAG+∠HAI=22.5°+31.5°=54°,
故答案为:54.
【点评】本题主要考查了正多边形的性质和等腰三角形的性质与判定,解题关键是正确识别图形,熟练掌握正多边形的性质和等腰三角形的性质与判定.
三.解答题(共3小题)
13.(2024秋 尤溪县期末)如图,在四边形ABCD中,AD∥BC,∠B=70°.
(1)求∠BAD的度数;
(2)若AE平分∠BAD交BC于点E,∠BCD=55°,求证:AE∥CD.
【考点】多边形内角与外角;平行线的判定与性质.
【专题】线段、角、相交线与平行线;推理能力.
【答案】(1)110°;
(2)证明见解答过程.
【分析】(1)根据两直线平行,同旁内角互补求出∠BAD;
(2)根据角平分线的定义求出∠DAE,根据平行线的性质求出∠AEB,得到∠AEB=∠BCD,根据平行线的判定定理证明结论.
【解答】(1)解:∵AD∥BC,
∴∠BAD+∠B=180°,
∵∠B=70°,
∴∠BAD=180°﹣∠B=180°﹣70°=110°,
∴∠BAD的度数是 110°;
(2)证明:∵AE平分∠BAD交BC于点E,∠BAD=110°,
∴,
∵AD∥BC,
∴∠AEB=∠DAE=55°,
∠BCD=55°,
∴∠AEB=∠BCD,
∴AE∥CD.
【点评】本题考查的是平行线的判定和性质、角平分线的定义,掌握平行线的性质是解题的关键.
14.(2024秋 玉林期末)如图,在四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.
(1)若∠1=33°,求∠2的度数:
(2)判断BE与DF的位置关系,并说明理由.
【考点】多边形内角与外角;三角形内角和定理.
【专题】多边形与平行四边形;推理能力.
【答案】(1)57°;
(2)BE∥DF,理由见解析.
【分析】(1)由角平分线的定义得∠1=∠ABE,∠2=∠ADF,根据四边形的内角和可得∠ABC+∠ADC=180°,从而推出∠1+∠2=90°,进而可求出答案;
(2)由互余的性质可得∠1=∠DFC,根据平行线的判定即可得出.
【解答】解:(1)∵BE,DF分别是∠ABC,∠ADC的平分线,
∴∠1=∠ABE,∠2=∠ADF,
∵∠A=∠C=90°,
∴∠ABC+∠ADC=360°﹣90°﹣90°=180°,
∴2(∠1+∠2)=180°,
∴∠1+∠2=90°,
∵∠1=33°,
∴∠2=90°﹣∠1=57°;
(2)BE∥DF,理由如下:
在△FCD中,∵∠C=90°,
∴∠DFC+∠2=90°,
∵∠1+∠2=90°,
∴∠1=∠DFC,
∴BE∥DF.
【点评】本题考查了平行线的判定,多边形的内角和,直角三角形两锐角互余,关键是掌握四边形内角和为360°、同位角相等,两直线平行.
15.(2024秋 大余县期末)阅读小明和小红的对话,解决下列问题.
(1)这个“多加的锐角”是 30 度.
(2)小明求的是几边形内角和?
(3)若这是个正多边形,则这个正多边形的一个内角是多少度?
【考点】多边形内角与外角.
【专题】多边形与平行四边形;运算能力.
【答案】见试题解答内容
【分析】(1)根据多边形内角和的计算方法进行估算即可;
(2)根据对话和多边形内角和的计算方法列方程求解即可;
(3)根据正多边形内角的计算方法进行计算即可.
【解答】解:(1)12边形的内角和为(12﹣2)×180°=1800°,而13边形的内角和为(13﹣2)×180°=1980°,
由于小红说“多边形的内角和不可能是1830°,你一定是多加了一个锐角”,
所以这个“多加的锐角”是1830°﹣1800°=30°,
故答案为:30;
(2)设这个多边形为n边形,由题意得,
(n﹣2)×180°=1800°,
解得n=12,
答:小明求的是12边形内角和;
(3)正十二边形的每一个内角为150°,
答:这个正多边形的一个内角是150°.
【点评】本题考查多边形的内角和和外角和,掌握多边形内角和的计算方法以及正多边形的性质是正确解答的前提.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
