苏科版数学(2024)七年级上册 第6章 平面图形的初步认识 学情评估卷(含答案)
文档属性
| 名称 | 苏科版数学(2024)七年级上册 第6章 平面图形的初步认识 学情评估卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 499.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 00:09:47 | ||
图片预览



文档简介
第6章 学情评估卷
一、选择题(每小题3分,共24分)
1.如图,与是一对( )
(第1题)
A. 同位角 B. 内错角 C. 同旁内角 D. 对顶角
2.如图,推动水桶,以点为支点,使其向右倾斜.若在点处分别施加推力,,则的力臂大于的力臂.这一判断过程体现的数学依据是( )
(第2题)
A. 垂线段最短
B. 过一点有且只有一条直线与已知直线垂直
C. 两点确定一条直线
D. 过直线外一点有且只有一条直线与已知直线平行
3.泰勒斯被誉为古希腊及西方第一个自然科学家和哲学家,据说“两条直线相交,对顶角相等”就是泰勒斯首次发现并论证的.论证“对顶角相等”使用的依据是( )
A. 等角的补角相等 B. 同角的余角相等
C. 等角的余角相等 D. 同角的补角相等
4.用一副三角板(其中一个内角分别为 与)不能画出的角度是( )
A. B. C. D.
5.如图,,交于点,,则与一定满足的关系是( )
(第5题)
A. 互为对顶角 B. 相等 C. 互补 D. 互余
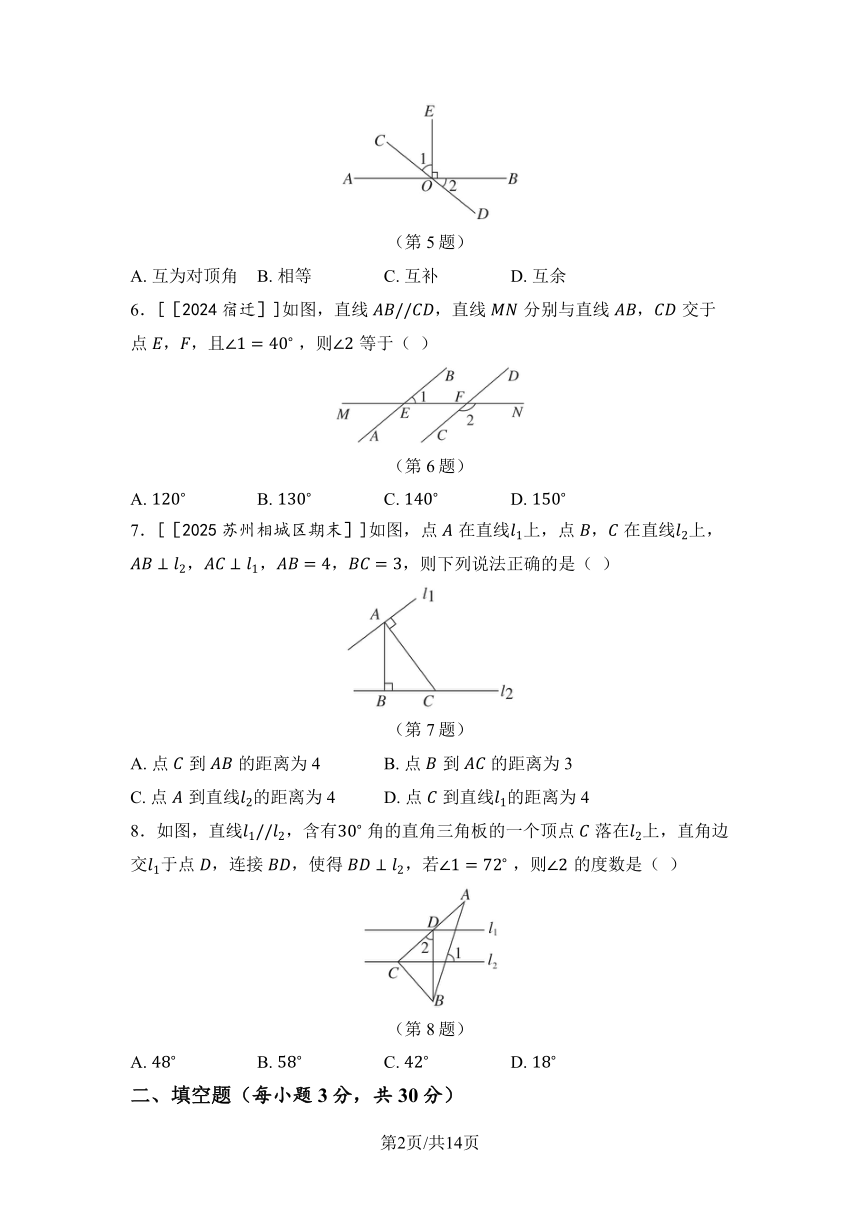
6.[[2024宿迁]]如图,直线,直线分别与直线,交于点,,且 ,则等于( )
(第6题)
A. B. C. D.
7.[[2025苏州相城区期末]]如图,点在直线上,点,在直线上,,,,,则下列说法正确的是( )
(第7题)
A. 点到的距离为4 B. 点到的距离为3
C. 点到直线的距离为4 D. 点到直线的距离为4
8.如图,直线,含有 角的直角三角板的一个顶点落在上,直角边交于点,连接,使得,若 ,则的度数是( )
(第8题)
A. B. C. D.
二、填空题(每小题3分,共30分)
9.已知,则 的余角的度数是_ _ .
10.如图所示,可以用字母表示出来的不同射线有_ _ _ _ 条.
(第10题)
11.如图,运动会上,三名同学测得黎明的跳远成绩分别为米,米,米,则黎明的跳远成绩应该为_ _ 米.
(第11题)
12.[[2025南通期末]]从一个多边形的一个顶点出发最多可画6条对角线,则这个多边形是边形.
13.如图所示,在中, , ,外角_ _ _ _ _ _ .
(第13题)
14.[[2025南京玄武区月考]]如图,点,在线段上,,线段,的中点,之间的距离是,则.
(第14题)
15.如图,,, ,则_ _ .
(第15题)
16.已知 ,平分,,垂足为,则_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ .
17.如图,中, ,点为边上一点,将沿直线折叠后,点落到点处,若,则的度数为_ _ .
(第17题)
18.图①是某自行车的实物图,图②是图①的示意图.测得,且都与地面平行, .有如下四个结论: ;②若 ,则;③若 ,则;④若 ,则.在这四个结论中正确的为_ _ .(填序号)
三、解答题(共66分)
19.(8分)如图,已知四点,,,.读下列语句,并分别画出图形.(要求尺规作图,不写作法,保留作图痕迹)
(1) 画直线,射线,线段;
(2) 延长至点,使;
(3) 连接,在线段上取点,使的值最小.
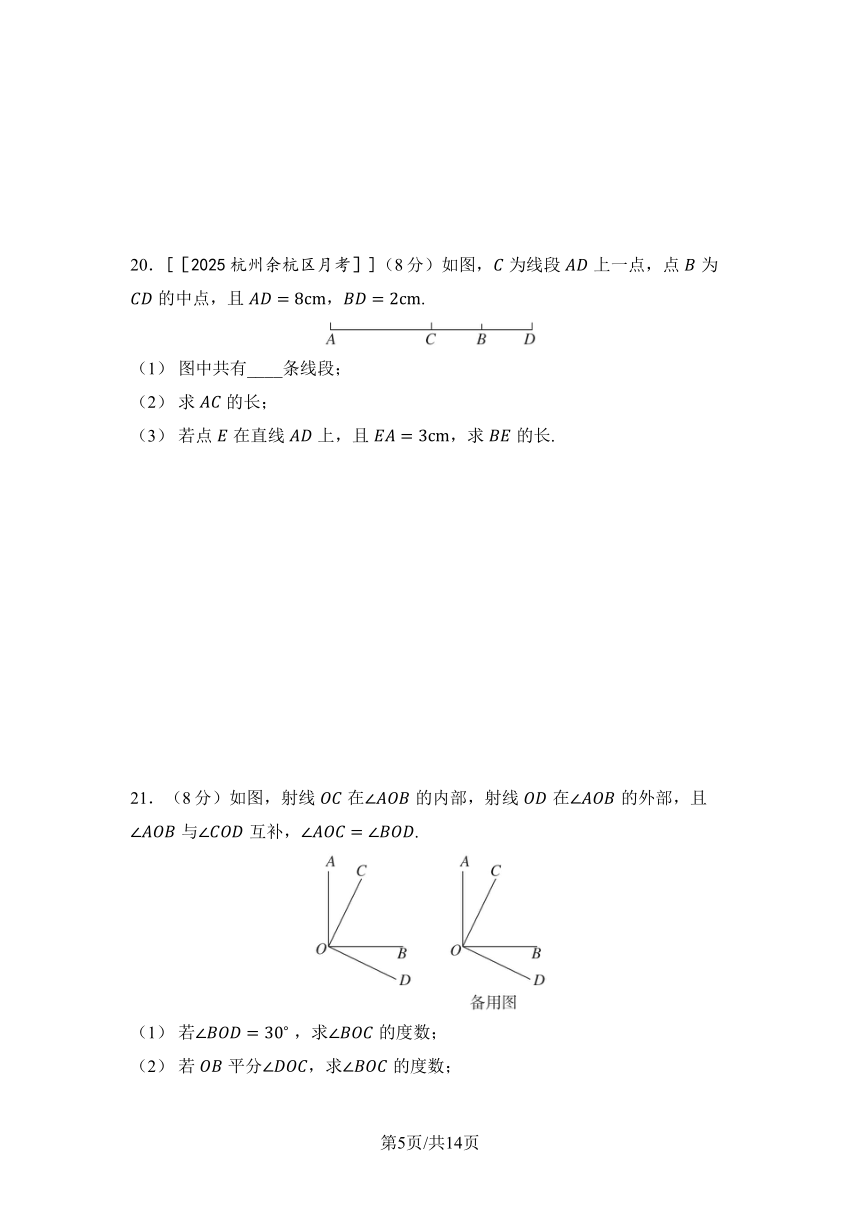
20.[[2025杭州余杭区月考]](8分)如图,为线段上一点,点为的中点,且,.
(1) 图中共有_ _ _ _ 条线段;
(2) 求的长;
(3) 若点在直线上,且,求的长.
21.(8分)如图,射线在的内部,射线在的外部,且与互补,.
(1) 若 ,求的度数;
(2) 若平分,求的度数;
(3) 射线满足,写出与的数量关系,并说明理由.
22.(10分)在下列解题过程的空白处填上适当的内容(推理的依据或数学表达式).
如图, ,.说明:.
解:因为 (已知),(对顶角相等),
所以_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ,
所以(_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ),
所以_ _ _ _ _ _ _ _ _ _ _ _ (_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ).
因为(已知),
所以_ _ _ _ _ _ _ _ (等式的基本性质),
所以_ _ _ _ _ _ _ _ _ _ _ _ ,
所以.
23.(10分)【教材回顾】如下是苏科版七年级上册教材第185页,关于同旁内角的定义.
如图①,两条直线,被第三条直线所截形成八个角,具有和这种位置关系的一对角叫作同旁内角.
【类比探究】
(1) 如图②,具有与这种位置关系的两个角叫作同旁外角,请在图中再找出一对同旁外角,分别用,在图中标记出来;
(2) 如图③,直线,当 时,的度数是_ _ _ _ _ _ _ _ .
(3) 如图④,已知 时,试说明直线,并用文字叙述由此你能得出什么结论.
24.(10分)将两块直角三角板的直角顶点按如图的方式叠放在一起(其中, , ;).
(1)
① 若 ,则的度数为_ _ _ _ _ _ _ _ ;
② 若 ,求的度数.
(2) 由(1)猜想与的数量关系,并说明理由.
(3) 当 且点在直线的上方时,这两块三角板是否存在一组边互相平行?若存在,请直接写出此时的度数的所有可能的值(不必说明理由);若不存在,请说明理由.
25.(12分)如图①,已知两条直线,被直线所截,分别交于点,,平分交于点,且.
(1) 判断直线与直线是否平行,并说明理由.
(2) 点是射线上一动点(不与点,重合),平分交于点,过点作于点,设 , .
① 如图②,若 ,求 的度数;
② 在点的运动过程中, 和 之间有怎样的数量关系?请写出你的猜想,并说明理由.
参考答案
1.A
2.A
3.D
4.D
5.D
6.C
7.C
8.A
【解析】点拨:如图,设与相交于点,
因为, ,所以 .
易知 ,又因为 ,
所以 .
因为 ,,
所以易得 .
9.42.5
10.3
11.1.96
12九
13.
14.12
【解析】点拨:设,则,,,
因为点,点分别为,的中点,所以,.
所以.
因为,所以,解得,所以.
15.108
16. 或
17.110
【解析】点拨:因为, ,
所以 .
由折叠的性质得,
所以 ,
因为 ,
所以 ,
所以 ,
所以 .
18.①②④
19.(1) 解:如图所示,直线,射线,线段即为所求.
(2) 如图所示,即为所求.
(3) 如图所示,点即为所求.
20.(1) 6
(2) 解:因为点为的中点,所以.
因为,所以.
因为,且,,
所以.
(3) 由题知,.当在点的左边时,
,
所以;
当在点的右边时,
,
所以.
综上,的长为 或.
21.(1) 解:因为,
所以,
即,
因为与互补,
所以 ,
所以 ,
因为 ,
所以 .
(2) 由(1)可知 ,
因为平分,
所以 .
(3) ,理由如下:因为,
所以.
因为 ,
所以 .
22.; 同旁内角互补,两直线平行; ; 两直线平行,内错角相等; ;
23.(1) 解:如图①.
①
(2)
(3) 如图②.
因为 , ,
所以,所以.
结论:同旁外角互补,两直线平行.
②
24.①
② 解:易知 ,
所以 .
(2) .
理由:因为,所以 .
(3) 存在.
当 时,,
当 时,,
当 时,,
当 时,,
当 时,.
25.(1) 解:.理由:因为平分,
所以.
又因为,所以,
所以.
(2) ① 因为, ,
所以 .
又因为平分,平分,
所以,,
所以 .
因为,所以 ,
所以 ,
即 .
② 点是射线上一动点,故分两种情况讨论:
如图①,当点在点的右侧时, .
理由:因为, ,所以 .因为平分,平分,
所以,,
所以.
因为,所以 ,
所以 ,即 .
如图②,当点在点的左侧时, .
理由:因为,
所以 .
因为平分,平分,
所以,,
所以
.
因为,所以 ,
所以,
即 .
第页/共页
一、选择题(每小题3分,共24分)
1.如图,与是一对( )
(第1题)
A. 同位角 B. 内错角 C. 同旁内角 D. 对顶角
2.如图,推动水桶,以点为支点,使其向右倾斜.若在点处分别施加推力,,则的力臂大于的力臂.这一判断过程体现的数学依据是( )
(第2题)
A. 垂线段最短
B. 过一点有且只有一条直线与已知直线垂直
C. 两点确定一条直线
D. 过直线外一点有且只有一条直线与已知直线平行
3.泰勒斯被誉为古希腊及西方第一个自然科学家和哲学家,据说“两条直线相交,对顶角相等”就是泰勒斯首次发现并论证的.论证“对顶角相等”使用的依据是( )
A. 等角的补角相等 B. 同角的余角相等
C. 等角的余角相等 D. 同角的补角相等
4.用一副三角板(其中一个内角分别为 与)不能画出的角度是( )
A. B. C. D.
5.如图,,交于点,,则与一定满足的关系是( )
(第5题)
A. 互为对顶角 B. 相等 C. 互补 D. 互余
6.[[2024宿迁]]如图,直线,直线分别与直线,交于点,,且 ,则等于( )
(第6题)
A. B. C. D.
7.[[2025苏州相城区期末]]如图,点在直线上,点,在直线上,,,,,则下列说法正确的是( )
(第7题)
A. 点到的距离为4 B. 点到的距离为3
C. 点到直线的距离为4 D. 点到直线的距离为4
8.如图,直线,含有 角的直角三角板的一个顶点落在上,直角边交于点,连接,使得,若 ,则的度数是( )
(第8题)
A. B. C. D.
二、填空题(每小题3分,共30分)
9.已知,则 的余角的度数是_ _ .
10.如图所示,可以用字母表示出来的不同射线有_ _ _ _ 条.
(第10题)
11.如图,运动会上,三名同学测得黎明的跳远成绩分别为米,米,米,则黎明的跳远成绩应该为_ _ 米.
(第11题)
12.[[2025南通期末]]从一个多边形的一个顶点出发最多可画6条对角线,则这个多边形是边形.
13.如图所示,在中, , ,外角_ _ _ _ _ _ .
(第13题)
14.[[2025南京玄武区月考]]如图,点,在线段上,,线段,的中点,之间的距离是,则.
(第14题)
15.如图,,, ,则_ _ .
(第15题)
16.已知 ,平分,,垂足为,则_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ .
17.如图,中, ,点为边上一点,将沿直线折叠后,点落到点处,若,则的度数为_ _ .
(第17题)
18.图①是某自行车的实物图,图②是图①的示意图.测得,且都与地面平行, .有如下四个结论: ;②若 ,则;③若 ,则;④若 ,则.在这四个结论中正确的为_ _ .(填序号)
三、解答题(共66分)
19.(8分)如图,已知四点,,,.读下列语句,并分别画出图形.(要求尺规作图,不写作法,保留作图痕迹)
(1) 画直线,射线,线段;
(2) 延长至点,使;
(3) 连接,在线段上取点,使的值最小.
20.[[2025杭州余杭区月考]](8分)如图,为线段上一点,点为的中点,且,.
(1) 图中共有_ _ _ _ 条线段;
(2) 求的长;
(3) 若点在直线上,且,求的长.
21.(8分)如图,射线在的内部,射线在的外部,且与互补,.
(1) 若 ,求的度数;
(2) 若平分,求的度数;
(3) 射线满足,写出与的数量关系,并说明理由.
22.(10分)在下列解题过程的空白处填上适当的内容(推理的依据或数学表达式).
如图, ,.说明:.
解:因为 (已知),(对顶角相等),
所以_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ,
所以(_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ),
所以_ _ _ _ _ _ _ _ _ _ _ _ (_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ).
因为(已知),
所以_ _ _ _ _ _ _ _ (等式的基本性质),
所以_ _ _ _ _ _ _ _ _ _ _ _ ,
所以.
23.(10分)【教材回顾】如下是苏科版七年级上册教材第185页,关于同旁内角的定义.
如图①,两条直线,被第三条直线所截形成八个角,具有和这种位置关系的一对角叫作同旁内角.
【类比探究】
(1) 如图②,具有与这种位置关系的两个角叫作同旁外角,请在图中再找出一对同旁外角,分别用,在图中标记出来;
(2) 如图③,直线,当 时,的度数是_ _ _ _ _ _ _ _ .
(3) 如图④,已知 时,试说明直线,并用文字叙述由此你能得出什么结论.
24.(10分)将两块直角三角板的直角顶点按如图的方式叠放在一起(其中, , ;).
(1)
① 若 ,则的度数为_ _ _ _ _ _ _ _ ;
② 若 ,求的度数.
(2) 由(1)猜想与的数量关系,并说明理由.
(3) 当 且点在直线的上方时,这两块三角板是否存在一组边互相平行?若存在,请直接写出此时的度数的所有可能的值(不必说明理由);若不存在,请说明理由.
25.(12分)如图①,已知两条直线,被直线所截,分别交于点,,平分交于点,且.
(1) 判断直线与直线是否平行,并说明理由.
(2) 点是射线上一动点(不与点,重合),平分交于点,过点作于点,设 , .
① 如图②,若 ,求 的度数;
② 在点的运动过程中, 和 之间有怎样的数量关系?请写出你的猜想,并说明理由.
参考答案
1.A
2.A
3.D
4.D
5.D
6.C
7.C
8.A
【解析】点拨:如图,设与相交于点,
因为, ,所以 .
易知 ,又因为 ,
所以 .
因为 ,,
所以易得 .
9.42.5
10.3
11.1.96
12九
13.
14.12
【解析】点拨:设,则,,,
因为点,点分别为,的中点,所以,.
所以.
因为,所以,解得,所以.
15.108
16. 或
17.110
【解析】点拨:因为, ,
所以 .
由折叠的性质得,
所以 ,
因为 ,
所以 ,
所以 ,
所以 .
18.①②④
19.(1) 解:如图所示,直线,射线,线段即为所求.
(2) 如图所示,即为所求.
(3) 如图所示,点即为所求.
20.(1) 6
(2) 解:因为点为的中点,所以.
因为,所以.
因为,且,,
所以.
(3) 由题知,.当在点的左边时,
,
所以;
当在点的右边时,
,
所以.
综上,的长为 或.
21.(1) 解:因为,
所以,
即,
因为与互补,
所以 ,
所以 ,
因为 ,
所以 .
(2) 由(1)可知 ,
因为平分,
所以 .
(3) ,理由如下:因为,
所以.
因为 ,
所以 .
22.; 同旁内角互补,两直线平行; ; 两直线平行,内错角相等; ;
23.(1) 解:如图①.
①
(2)
(3) 如图②.
因为 , ,
所以,所以.
结论:同旁外角互补,两直线平行.
②
24.①
② 解:易知 ,
所以 .
(2) .
理由:因为,所以 .
(3) 存在.
当 时,,
当 时,,
当 时,,
当 时,,
当 时,.
25.(1) 解:.理由:因为平分,
所以.
又因为,所以,
所以.
(2) ① 因为, ,
所以 .
又因为平分,平分,
所以,,
所以 .
因为,所以 ,
所以 ,
即 .
② 点是射线上一动点,故分两种情况讨论:
如图①,当点在点的右侧时, .
理由:因为, ,所以 .因为平分,平分,
所以,,
所以.
因为,所以 ,
所以 ,即 .
如图②,当点在点的左侧时, .
理由:因为,
所以 .
因为平分,平分,
所以,,
所以
.
因为,所以 ,
所以,
即 .
第页/共页
同课章节目录
