【中考核心考点】2025年北师大版中考数学考前冲刺 二次函数(含解析)
文档属性
| 名称 | 【中考核心考点】2025年北师大版中考数学考前冲刺 二次函数(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 512.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 17:20:09 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中考核心考点 二次函数
一.选择题(共7小题)
1.(2024.广陵区二模)我们常用“y随x的增大而增大(或减小)”来表示两个变量之间的变化关系.有这样一个情境:如图,小王从点A经过路灯C的正下方沿直线走到点B,他与路灯C的距离y随他与点A之间的距离x的变化而变化.下列函数中y与x之间的变化关系,最有可能与上述情境类似的是( )
A. B.y=﹣x+3
C.y=(x﹣3)2+3 D.y=﹣(x﹣3)2+3
2.(2024秋 海港区)在平面直角坐标系中,二次函数y=x2+mx﹣m2+m(m为常数)的图象经过点(0,﹣6),其对称轴在y轴右侧,则该二次函数有( )
A.最大值﹣7 B.最大值
C.最小值﹣7 D.最小值
3.(2024.铜山区二模)将抛物线y=﹣x2先向左平移3个单位长度,再向上平移2个单位长度,所得抛物线的表达式是( )
A.y=(x﹣3)2+2 B.y=﹣(x﹣3)2﹣2
C.y=(x+3)2﹣2 D.y=﹣(x+3)2+2
4.(2024秋 鹿邑县)老师设计了接力游戏,用合作的方式完成“求抛物线y=2x2+4x﹣4的顶点坐标”,规则如下:每个人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成解答.接力顺序及每个人的计算结果如图所示:
接力比赛中,自己负责的一步出错的是( )
A.只有丁 B.甲和丁 C.乙和丙 D.乙和丁
5.(2024秋 银川)对于二次函数y=2x2+8x﹣3,下列说法错误的是( )
A.图象开口向上
B.对称轴是直线x=﹣2
C.当0<x≤2时,y的最大值为21
D.将图象向右平移3个单位长度,再向上平移1个单位长度后的顶点坐标为(1,﹣12)
6.(2024秋 谯城区)已知3x﹣6是二次函数,则a=( )
A.0 B.1 C.﹣1 D.1或﹣1
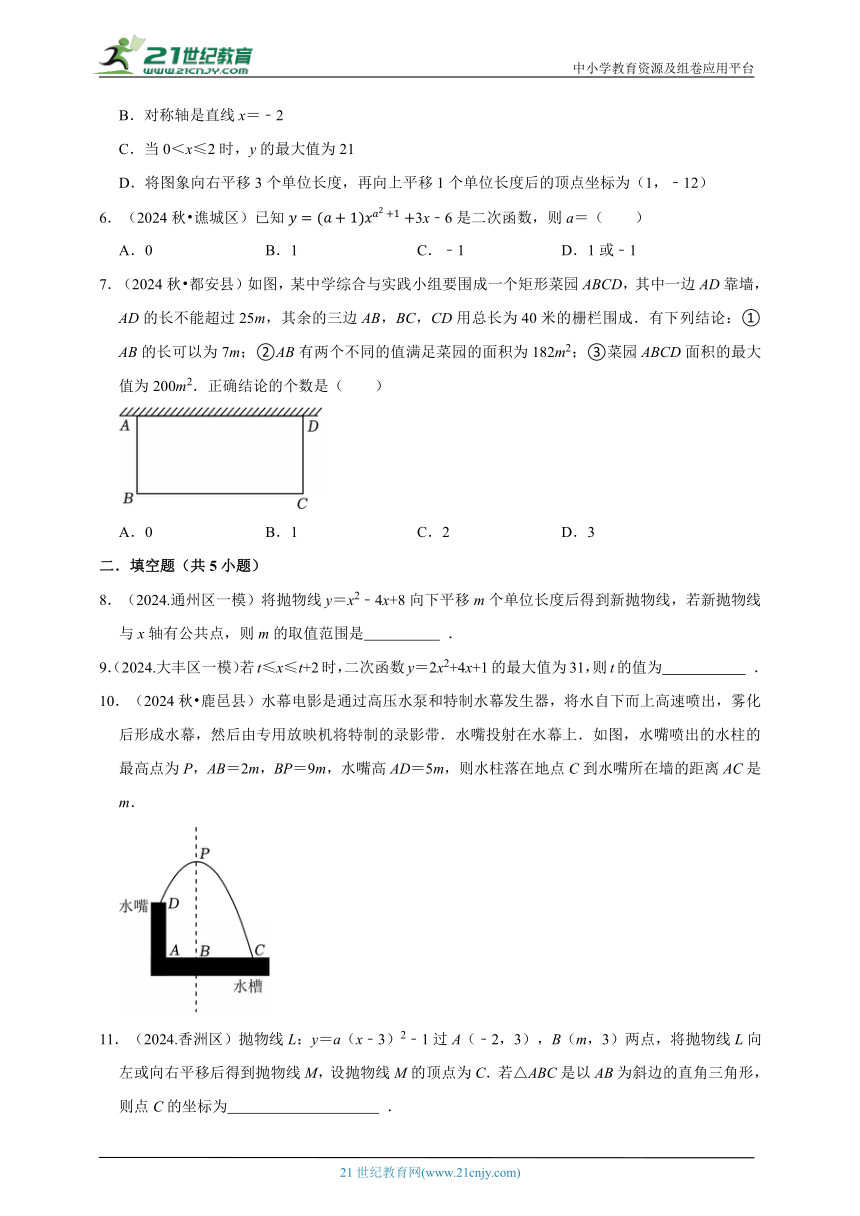
7.(2024秋 都安县)如图,某中学综合与实践小组要围成一个矩形菜园ABCD,其中一边AD靠墙,AD的长不能超过25m,其余的三边AB,BC,CD用总长为40米的栅栏围成.有下列结论:①AB的长可以为7m;②AB有两个不同的值满足菜园的面积为182m2;③菜园ABCD面积的最大值为200m2.正确结论的个数是( )
A.0 B.1 C.2 D.3
二.填空题(共5小题)
8.(2024.通州区一模)将抛物线y=x2﹣4x+8向下平移m个单位长度后得到新抛物线,若新抛物线与x轴有公共点,则m的取值范围是 .
9.(2024.大丰区一模)若t≤x≤t+2时,二次函数y=2x2+4x+1的最大值为31,则t的值为 .
10.(2024秋 鹿邑县)水幕电影是通过高压水泵和特制水幕发生器,将水自下而上高速喷出,雾化后形成水幕,然后由专用放映机将特制的录影带.水嘴投射在水幕上.如图,水嘴喷出的水柱的最高点为P,AB=2m,BP=9m,水嘴高AD=5m,则水柱落在地点C到水嘴所在墙的距离AC是 m.
11.(2024.香洲区)抛物线L:y=a(x﹣3)2﹣1过A(﹣2,3),B(m,3)两点,将抛物线L向左或向右平移后得到抛物线M,设抛物线M的顶点为C.若△ABC是以AB为斜边的直角三角形,则点C的坐标为 .
12.(2024秋 沭阳县)如图,直线y=mx+n与抛物线y=ax2+bx+c交于A(﹣1,p),B(5,q)两点,则关于x的不等式mx+n<ax2+bx+c解集是 .
三.解答题(共3小题)
13.(2024.西宁二模)某宾馆有若干间标准房,经市场调查表明,该宾馆每间标准房的价格在150~240元之间(含150元,240元)浮动时,每天入住的房间数y(间)与每间标准房的价格x(元)满足一次函数关系,部分数据如表:
x(元) … 190 200 210 220 …
y(间) … 65 60 55 50 …
(1)根据所给数据在坐标中描出相应的点,并画出图象;
(2)求y关于x(150≤x≤240)的函数解析式;
(3)若不考虑其他因素,宾馆标准房的价格定为多少元时,客房的日营业额最大?最大为多少元?
14.(2024.通州区一模)已知关于x的二次函数y=ax2﹣6ax+5a.
(1)若x=2时,y=﹣3,求该函数的解析式;
(2)当a>0,2≤x≤6时,该函数的最大值与最小值的差为18,求a的值;
(3)若A(x1,y1),B(x2,y2)是该函数图象上的两点,且对于x1=a+3,4≤x2≤6,都有y1≥y2,求a的取值范围.
15.(2024.浙江)为了响应环保号召,某工厂开展节能减排行动.已知工厂每月的利润y(万元)与每月减少的碳排放量x(吨)之间存在一定的函数关系.当每月减少的碳排放量为0吨时,工厂利润为50万元;之后每减少1吨碳排放量,工厂的生产成本会降低一部分,利润随之增加,且增加的幅度逐渐变小.经过数据分析,发现利润y与减少碳排放量x之间满足二次函数关系:y=﹣x2+20x+50.
(1)求该二次函数图象的对称轴和顶点坐标,并说明它们在本题中的实际意义.
(2)若该工厂计划下个月利润达到125万元,则下个月需要减少多少吨碳排放量?
(3)根据环保政策要求,该工厂下个月要减少12吨碳排放量,在满足政策要求的前提下,求该工厂下个月利润的最大值.
中考核心考点 二次函数
参考答案与试题解析
一.选择题(共7小题)
1.(2024.广陵区二模)我们常用“y随x的增大而增大(或减小)”来表示两个变量之间的变化关系.有这样一个情境:如图,小王从点A经过路灯C的正下方沿直线走到点B,他与路灯C的距离y随他与点A之间的距离x的变化而变化.下列函数中y与x之间的变化关系,最有可能与上述情境类似的是( )
A. B.y=﹣x+3
C.y=(x﹣3)2+3 D.y=﹣(x﹣3)2+3
【考点】根据实际问题列二次函数关系式.
【专题】一次函数及其应用;反比例函数及其应用;二次函数图象及其性质;应用意识.
【答案】C
【分析】根据从A到路灯的正下方前他与路灯的距离逐渐减少,经过路灯后他与路灯的距离逐渐增加,可得答案.
【解答】解:由题意,得
从A到路灯的正下方前他与路灯的距离逐渐减少,经过路灯后他与路灯的距离逐渐增加.
A、y随x的增加而减少,与题意不符,故A错误;
B、y随x的增加而减少,与题意不符,故B错误;
C、当x<3时,y随x的增加而减少;当x>3时,y随x的增加而增加,故C正确;
D、当x<3时,y随x的增加而增大;当x>3时,y随x的增加而减少,故D错误;
故选:C.
【点评】本题考查了函数的性质,熟记一次函数的性质、反比例函数的性质、二次函数的性质是解题关键.
2.(2024秋 海港区)在平面直角坐标系中,二次函数y=x2+mx﹣m2+m(m为常数)的图象经过点(0,﹣6),其对称轴在y轴右侧,则该二次函数有( )
A.最大值﹣7 B.最大值
C.最小值﹣7 D.最小值
【考点】二次函数的性质;二次函数图象上点的坐标特征;二次函数的最值.
【专题】二次函数图象及其性质;运算能力.
【答案】C
【分析】依据题意,由二次函数y=x2+mx﹣m2+m(m为常数)的图象经过点(0,﹣6),可以得到m的值,然后根据对称轴在y轴的右侧,可以得到m的值,从而可以得到二次函数的解析式,再将函数解析式化为顶点式,即可得到该函数的最值.
【解答】解:∵二次函数y=x2+mx﹣m2+m(m为常数)的图象经过点(0,﹣6),
∴﹣6=﹣m2+m.
∴m=3或m=﹣2.
∵对称轴在y轴的右侧,a=1>0,
∴对称轴是直线x0.
∴m<0.
∴m=﹣2,
∴二次函数y=x2﹣2x﹣6=(x﹣1)2﹣7.
∴该函数的最小值为﹣7.
故选:C.
【点评】本题考查二次函数的性质、二次函数的最值,解答本题的关键是明确题意,求出m的值,利用二次函数的性质求最值.
3.(2024.铜山区二模)将抛物线y=﹣x2先向左平移3个单位长度,再向上平移2个单位长度,所得抛物线的表达式是( )
A.y=(x﹣3)2+2 B.y=﹣(x﹣3)2﹣2
C.y=(x+3)2﹣2 D.y=﹣(x+3)2+2
【考点】二次函数图象与几何变换.
【专题】二次函数图象及其性质;应用意识.
【答案】D
【分析】根据“上加下减,左加右减”的平移规律,即得答案.
【解答】解:将抛物线y=﹣x2先向左平移3个单位长度,再向上平移2个单位长度,所得抛物线的表达式为y=﹣(x+3)2+2.
故选:D.
【点评】本题考查了二次函数的平移,正确理解二次函数的平移规律是解答本题的关键.
4.(2024秋 鹿邑县)老师设计了接力游戏,用合作的方式完成“求抛物线y=2x2+4x﹣4的顶点坐标”,规则如下:每个人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成解答.接力顺序及每个人的计算结果如图所示:
接力比赛中,自己负责的一步出错的是( )
A.只有丁 B.甲和丁 C.乙和丙 D.乙和丁
【考点】二次函数的性质.
【专题】二次函数图象及其性质;运算能力.
【答案】B
【分析】观察每一项的变化,发现甲将老师给的式子等式右边缩小两倍,到了丁处根据丙的式子得出了错误的顶点坐标.
【解答】解:老师:y=2x2+4x﹣4,
=2(x2+2x)﹣4
=2(x2+2x+1)﹣6
=2(x+1)2﹣6
可得顶点坐标为(﹣1,﹣6).
根据题中过程可知从甲开始出错,按照此步骤下去到了丁处可得顶点应为(1,﹣3),所以错误的只有甲和丁.
故选:B.
【点评】本题主要考查了把二次函数一般解析式化成顶点式,以及二次函数顶点式的图象和性质,掌握配方法是解题的关键.
5.(2024秋 银川)对于二次函数y=2x2+8x﹣3,下列说法错误的是( )
A.图象开口向上
B.对称轴是直线x=﹣2
C.当0<x≤2时,y的最大值为21
D.将图象向右平移3个单位长度,再向上平移1个单位长度后的顶点坐标为(1,﹣12)
【考点】二次函数图象与几何变换;二次函数的最值;二次函数的性质.
【专题】二次函数图象及其性质;推理能力.
【答案】D
【分析】根据题目中的函数解析式和二次函数的性质,可以判断各个选项中的说法是否正确,从而可以解答本题.
【解答】解:∵二次函数y=2x2+8x﹣3=2(x+2)2﹣11,
∴函数的图象开口向上,对称轴为直线x=﹣2,顶点为(﹣2,﹣11),
∴当x>﹣2时,y随x的增大而增大,
∴在0<x≤2中,x=2时,有最大值为y=2(2+2)2﹣11=21,
故A、B、C选项正确,不合题意;
∵顶点为(﹣2,﹣11),
∴将图象向右平移3个单位长度,再向上平移1个单位长度后的顶点坐标为(1,﹣10),
故D选项不正确,符合题意;
故选:D.
【点评】本题考查二次函数的图象与几何变换,二次函数的性质,二次函数的最值,掌握二次函数的性质是解答本题的关键.
6.(2024秋 谯城区)已知3x﹣6是二次函数,则a=( )
A.0 B.1 C.﹣1 D.1或﹣1
【考点】二次函数的定义.
【专题】二次函数图象及其性质;运算能力.
【答案】B
【分析】根据二次函数的定义可得a2+1=2且a+1≠0,从而可得答案.
【解答】解:由条件可知a2+1=2,
解得a1=﹣1或a2=1,
∵a+1≠0,
∴a≠﹣1,
∴a=1.
故选:B.
【点评】本题考查了二次函数的定义.熟练掌握定义是关键.
7.(2024秋 都安县)如图,某中学综合与实践小组要围成一个矩形菜园ABCD,其中一边AD靠墙,AD的长不能超过25m,其余的三边AB,BC,CD用总长为40米的栅栏围成.有下列结论:①AB的长可以为7m;②AB有两个不同的值满足菜园的面积为182m2;③菜园ABCD面积的最大值为200m2.正确结论的个数是( )
A.0 B.1 C.2 D.3
【考点】二次函数的应用;一元二次方程的应用.
【专题】一元二次方程及应用;二次函数的应用;应用意识.
【答案】B
【分析】设AD边长为x m,则AB边长为,根据AB=7列出方程,解方程求出x的值,根据x取值范围判断①;根据矩形的面积=182,解方程求出x的值可以判断②;设矩形菜园的面积为y m2,根据矩形的面积公式列出函数解析式,再根据函数的性质求函数的最值可以判断③.
【解答】解:设AD边长为x m,则AB边长为,
当AB=7时,,
解得x=26,
∵AD的长不能超过25m,
∴x≤25,
故①不正确;
∵菜园ABCD面积为182m2,
∴,
整理得:x2﹣40x+364=0,
解得x=26或x=14,
∵x<25,
∴x=14,
∴AB的长只有一个值满足菜园ABCD面积为182m2,
故②错误;
设矩形菜园的面积为ym2,
根据题意得:,
∵,
∴当x=20时,y有最大值,最大值为200.
故③正确;
∴正确的有1个,
故选:B.
【点评】本题主要考查一元二次方程的应用和二次函数的应用,解答本题的关键是找准等量关系,列出二次函数解析式或一元二次方程.
二.填空题(共5小题)
8.(2024.通州区一模)将抛物线y=x2﹣4x+8向下平移m个单位长度后得到新抛物线,若新抛物线与x轴有公共点,则m的取值范围是 m≥4 .
【考点】抛物线与x轴的交点;二次函数的性质;二次函数图象与几何变换.
【专题】二次函数图象及其性质;运算能力.
【答案】m≥4.
【分析】先根据平移的规律写出抛物线y=x2﹣4x+8向下平移m个单位长度后的抛物线的表达式,再根据平移后得到的抛物线与x轴有公共点可得Δ≥0,由此列不等式即可求出m的取值范围.
【解答】解:平移m个单位长度得y=x2﹣4x+8﹣m,
由题意可得:
∴Δ≥0,
即(﹣4)2﹣4(8﹣m)≥0,
∴m≥4,
故答案为:m≥4.
【点评】此题考查了二次函数图象的平移与几何变换,以及抛物线与x轴的交点问题,利用抛物线解析式的变化规律:左加右减,上加下减是解题关键.
9.(2024.大丰区一模)若t≤x≤t+2时,二次函数y=2x2+4x+1的最大值为31,则t的值为 ﹣5或1 .
【考点】二次函数的最值.
【答案】见试题解答内容
【分析】将标准式化为顶点式为y=2x2+4x+1=2(x+1)2﹣1,由t≤x≤t+2时,y最大值=2(x+1)2﹣1,结合二次函数图象的性质解答.
【解答】解:y=2x2+4x+1=2(x+1)2﹣1,
∵二次函数y=2x2+4x+1的最大值为31,
∴①当﹣1﹣t>t+3,即t<﹣2时,2t2+4t+1=31
解得 t1=﹣5,t2=3(舍去).
②当﹣1﹣t<t+3,即t>﹣2时,2(t+2)2+4(t+2)+1=31,
解得 t1=﹣7(舍去),t2=1;
③当t>﹣1时,2(t+2)2+4(t+2)+1=31,
解得 t1=﹣7(舍去),t2=1;
综上所述,t的值是﹣5或1.
故答案为:﹣5或1.
【点评】本题考查了二次函数的最值,难度较大,关键是判断出当x≥﹣1时,y随x的增大而增大,由此此解决这类题.
10.(2024秋 鹿邑县)水幕电影是通过高压水泵和特制水幕发生器,将水自下而上高速喷出,雾化后形成水幕,然后由专用放映机将特制的录影带.水嘴投射在水幕上.如图,水嘴喷出的水柱的最高点为P,AB=2m,BP=9m,水嘴高AD=5m,则水柱落在地点C到水嘴所在墙的距离AC是 5 m.
【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【答案】5.
【分析】以A为坐标原点,AB所在的直线为x轴,AD所在的直线为y轴建立平面直角坐标系,易得点D和点P的坐标,设抛物线的解析式为:y=a(x﹣2)2+9,代入点D的坐标求得函数的解析式,再求出点C的坐标即可得到AC的长度.
【解答】解:以A为坐标原点,AB所在的直线为x轴,AD所在的直线为y轴建立平面直角坐标系,如图所示,
则A(0,0),D(0,5),P(2,9),
∵点P是最高点,
∴设抛物线的解析式为:y=a(x﹣2)2+9,
将点D坐标代入,可得:5=4a+9,
解得:a=﹣1,
∴y=﹣(x﹣2)2+9,
令y=0,则﹣(x﹣2)2+9=0,
解得:x1=5,x2=﹣1,
∴点C(5,0),
∴AC=5m,
故答案为:5.
【点评】本题考查了二次函数的实际应用,建立适当的坐标系,设出顶点式是解题的关键.
11.(2024.香洲区)抛物线L:y=a(x﹣3)2﹣1过A(﹣2,3),B(m,3)两点,将抛物线L向左或向右平移后得到抛物线M,设抛物线M的顶点为C.若△ABC是以AB为斜边的直角三角形,则点C的坐标为 (0,﹣1)或(6,﹣1) .
【考点】二次函数图象与几何变换;勾股定理的逆定理;二次函数的性质;二次函数图象上点的坐标特征.
【专题】二次函数图象及其性质;运算能力.
【答案】(0,﹣1)或(6,﹣1).
【分析】由抛物线的对称性求出点B的坐标,由抛物线的平移表示出点C的坐标,再根据勾股定理列方程即可求解.
【解答】解:由抛物线L的解析式可知抛物线L的对称轴为直线x=3,顶点坐标为(3,﹣1),
由条件可得﹣2+m=2×3,
∴m=8,
∴A(﹣2,3),B(8,3),AB=8﹣(﹣2)=10,
∵抛物线L向左或向右平移后得到抛物线M,
∴设抛物线M的顶点C(n,﹣1),
∴AC2=(n+2)2+(﹣1﹣3)2=n2+4n+20,BC2=(n﹣8)2+(﹣1﹣3)2=n2﹣16n+80,
∵△ABC是以AB为斜边的直角三角形,
∴n2+4n+20+n2﹣16n+80=102=100,
整理得n2﹣6n=0,
解得n1=0,n2=6,
∴点C的坐标为(0,﹣1)或(6,﹣1)
故答案为:(0,﹣1)或(6,﹣1).
【点评】本题考查二次函数的图象和性质,二次函数图象的平移,勾股定理等.熟练掌握以上知识点是关键.
12.(2024秋 沭阳县)如图,直线y=mx+n与抛物线y=ax2+bx+c交于A(﹣1,p),B(5,q)两点,则关于x的不等式mx+n<ax2+bx+c解集是 ﹣1<x<5 .
【考点】二次函数与不等式(组).
【专题】数形结合;二次函数图象及其性质.
【答案】见试题解答内容
【分析】直接利用函数的交点坐标进而结合函数图象得出不等式mx+n<ax2+bx+c的解集.
【解答】解:∵直线y=mx+n与抛物线y=ax2+bx+c交于A(﹣1,p),B(5,q)两点,
∴关于x的不等式mx+n<ax2+bx+c解集是﹣1<x<5
故答案为:﹣1<x<5
【点评】此题主要考查了二次函数与不等式,正确数形结合分析是解题关键.
三.解答题(共3小题)
13.(2024.西宁二模)某宾馆有若干间标准房,经市场调查表明,该宾馆每间标准房的价格在150~240元之间(含150元,240元)浮动时,每天入住的房间数y(间)与每间标准房的价格x(元)满足一次函数关系,部分数据如表:
x(元) … 190 200 210 220 …
y(间) … 65 60 55 50 …
(1)根据所给数据在坐标中描出相应的点,并画出图象;
(2)求y关于x(150≤x≤240)的函数解析式;
(3)若不考虑其他因素,宾馆标准房的价格定为多少元时,客房的日营业额最大?最大为多少元?
【考点】二次函数的应用.
【专题】二次函数的应用;运算能力;应用意识.
【答案】(1)作图见解析;(2)yx+160(150≤x≤240);(3)宾馆标准房的价格定为160元时,客房的日营业额最大,最大为12800元.
【分析】(1)依据题意,描点、连线即可得;
(2)依据题意,待定系数法求解可得;
(3)依据题意,由营业额=入住房间数量×房价得出函数解析式,再利用二次函数的性质求解可得.
【解答】解:(1)如图所示:
(2)由题意,设 y=kx+b,将(200,60)、(220,50)代入,
∴,
∴
∴yx+160(150≤x≤240).
(3)由题意得,,
∴对称轴为直线,
∵,
∴当x=160时,w有最大值,最大值为12800元.
答:宾馆标准房的价格定为160元时,客房的日营业额最大,最大为12800元.
【点评】本题主要考查了二次函数的应用以及待定系数法求一次函数解析式以及二次函数最值问题,由营业额=入住房间数量×房价得出函数解析式及二次函数的性质是解题关键.
14.(2024.通州区一模)已知关于x的二次函数y=ax2﹣6ax+5a.
(1)若x=2时,y=﹣3,求该函数的解析式;
(2)当a>0,2≤x≤6时,该函数的最大值与最小值的差为18,求a的值;
(3)若A(x1,y1),B(x2,y2)是该函数图象上的两点,且对于x1=a+3,4≤x2≤6,都有y1≥y2,求a的取值范围.
【考点】二次函数图象与系数的关系;二次函数图象上点的坐标特征;二次函数的最值;待定系数法求二次函数解析式.
【专题】二次函数图象及其性质;运算能力.
【答案】(1)y=x2﹣6x+5;
(2)a=2;
(3)a≥3或﹣1≤a<0.
【分析】(1)把x=2,y=﹣3,分别代入y=ax2﹣6ax+5a,得出a=1,即可作答.
(2)先整理y=a(x﹣3)2﹣4a,故图象的对称轴为直线x=3,结合a>0,2≤x≤6.故当x=3时,y最小=﹣4a,当x=6时,y最大=5a,列式5a﹣(﹣4a)=18,即可作答.
(3)进行分类讨论,即①若a>0,则函数图象开口向上.②若a<0,则函数图象开口向下,再结合二次函数的图象性质,进行分析列式,即可作答.
【解答】解:(1)∵y=ax2﹣6ax+5a,
当x=2时,y=﹣3,
∴4a﹣12a+5a=﹣3,
∴a=1.
∴该函数的解析式为y=x2﹣6x+5.
(2)配方得y=ax2﹣6ax+5a=a(x﹣3)2﹣4a,
∴图象的对称轴为直线x=3.
由条件可知当x=3时,y最小=﹣4a,
∵|6﹣3|=3>|2﹣3|,
∴当x=6时,y=a(6﹣3)2﹣4a=9a﹣4a=5a,
∴y最大=5a.
∴5a﹣(﹣4a)=18.
∴a=2;
(3)①若a>0,则函数图象开口向上.
又∵对称轴为直线x=3,
∴当x>3时,y随x的增大而增大.
∵x1=a+3>3,
∴点A在对称轴的右侧.
又∵对于x1=a+3,4≤x2≤6,都有y1≥y2,
∴a+3≥6,
∴a≥3.
②若a<0,则函数图象开口向下,
∵x1=a+3<3,
∴点A在对称轴的左侧.
∵对称轴为直线x=3,
∴当x=2或x=4时函数值相等.
由条件可知2≤a+3<3,
∴﹣1≤a<0.
综上:a≥3或﹣1≤a<0.
【点评】本题考查了二次函数的图象性质,求二次函数的解析式,正确掌握相关性质内容是解题的关键.
15.(2024.浙江)为了响应环保号召,某工厂开展节能减排行动.已知工厂每月的利润y(万元)与每月减少的碳排放量x(吨)之间存在一定的函数关系.当每月减少的碳排放量为0吨时,工厂利润为50万元;之后每减少1吨碳排放量,工厂的生产成本会降低一部分,利润随之增加,且增加的幅度逐渐变小.经过数据分析,发现利润y与减少碳排放量x之间满足二次函数关系:y=﹣x2+20x+50.
(1)求该二次函数图象的对称轴和顶点坐标,并说明它们在本题中的实际意义.
(2)若该工厂计划下个月利润达到125万元,则下个月需要减少多少吨碳排放量?
(3)根据环保政策要求,该工厂下个月要减少12吨碳排放量,在满足政策要求的前提下,求该工厂下个月利润的最大值.
【考点】二次函数的应用;一元二次方程的应用.
【专题】二次函数的应用;运算能力.
【答案】(1)x=10,(10,150),当减少碳排放量等于10吨时,最大利润为150万元;
(2)当利润达到125万元时,需要减少5吨或15吨;
(3)满足政策要求的前提下,该工厂下个月利润的最大值146万元.
【分析】(1)由二次函数解析式,根据对称轴直线的计算公式,顶点坐标的计算方法,顶点坐标表示的含义计算即可求解;
(2)当y=125时,代入计算即可求解;
(3)根据题意图象开口向下,当x≤10时,y随x的增大而增大,当x≥10时,y随x的增大而减小,当x=12时,确定最大值,代入计算即可求解.
【解答】解:(1)∵y=﹣x2+20x+50,
∴对称轴直线为,
当x=10时,y=﹣102+20×10+50=150,
∴顶点坐标为(10,150),
∵﹣1<0,即图象的开口象限,
∴当减少碳排放量等于10吨时,最大利润为150万元;
(2)当y=125时,﹣x2+20x+50=125,
∴x2﹣20x+75=0,
∴(x﹣5)(x﹣15)=0,
∴x1=5,x2=15,
∴当利润达到125万元时,需要减少5吨或15吨;
(3)∵y=﹣x2+20x+50=﹣(x﹣10)2+150,
∵﹣1<0,顶点坐标为(10,150),
∴图象开口向下,当x≤10时,y随x的增大而增大,当x≥10时,y随x的增大而减小,
由题意可得:当x=12时,确定最大值,
∴y=﹣(12﹣10)2+150=146,
∴满足政策要求的前提下,该工厂下个月利润的最大值146万元.
【点评】本题主要考查二次函数的运用,掌握顶点式,二次函数函数值、自变量值的计算是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考核心考点 二次函数
一.选择题(共7小题)
1.(2024.广陵区二模)我们常用“y随x的增大而增大(或减小)”来表示两个变量之间的变化关系.有这样一个情境:如图,小王从点A经过路灯C的正下方沿直线走到点B,他与路灯C的距离y随他与点A之间的距离x的变化而变化.下列函数中y与x之间的变化关系,最有可能与上述情境类似的是( )
A. B.y=﹣x+3
C.y=(x﹣3)2+3 D.y=﹣(x﹣3)2+3
2.(2024秋 海港区)在平面直角坐标系中,二次函数y=x2+mx﹣m2+m(m为常数)的图象经过点(0,﹣6),其对称轴在y轴右侧,则该二次函数有( )
A.最大值﹣7 B.最大值
C.最小值﹣7 D.最小值
3.(2024.铜山区二模)将抛物线y=﹣x2先向左平移3个单位长度,再向上平移2个单位长度,所得抛物线的表达式是( )
A.y=(x﹣3)2+2 B.y=﹣(x﹣3)2﹣2
C.y=(x+3)2﹣2 D.y=﹣(x+3)2+2
4.(2024秋 鹿邑县)老师设计了接力游戏,用合作的方式完成“求抛物线y=2x2+4x﹣4的顶点坐标”,规则如下:每个人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成解答.接力顺序及每个人的计算结果如图所示:
接力比赛中,自己负责的一步出错的是( )
A.只有丁 B.甲和丁 C.乙和丙 D.乙和丁
5.(2024秋 银川)对于二次函数y=2x2+8x﹣3,下列说法错误的是( )
A.图象开口向上
B.对称轴是直线x=﹣2
C.当0<x≤2时,y的最大值为21
D.将图象向右平移3个单位长度,再向上平移1个单位长度后的顶点坐标为(1,﹣12)
6.(2024秋 谯城区)已知3x﹣6是二次函数,则a=( )
A.0 B.1 C.﹣1 D.1或﹣1
7.(2024秋 都安县)如图,某中学综合与实践小组要围成一个矩形菜园ABCD,其中一边AD靠墙,AD的长不能超过25m,其余的三边AB,BC,CD用总长为40米的栅栏围成.有下列结论:①AB的长可以为7m;②AB有两个不同的值满足菜园的面积为182m2;③菜园ABCD面积的最大值为200m2.正确结论的个数是( )
A.0 B.1 C.2 D.3
二.填空题(共5小题)
8.(2024.通州区一模)将抛物线y=x2﹣4x+8向下平移m个单位长度后得到新抛物线,若新抛物线与x轴有公共点,则m的取值范围是 .
9.(2024.大丰区一模)若t≤x≤t+2时,二次函数y=2x2+4x+1的最大值为31,则t的值为 .
10.(2024秋 鹿邑县)水幕电影是通过高压水泵和特制水幕发生器,将水自下而上高速喷出,雾化后形成水幕,然后由专用放映机将特制的录影带.水嘴投射在水幕上.如图,水嘴喷出的水柱的最高点为P,AB=2m,BP=9m,水嘴高AD=5m,则水柱落在地点C到水嘴所在墙的距离AC是 m.
11.(2024.香洲区)抛物线L:y=a(x﹣3)2﹣1过A(﹣2,3),B(m,3)两点,将抛物线L向左或向右平移后得到抛物线M,设抛物线M的顶点为C.若△ABC是以AB为斜边的直角三角形,则点C的坐标为 .
12.(2024秋 沭阳县)如图,直线y=mx+n与抛物线y=ax2+bx+c交于A(﹣1,p),B(5,q)两点,则关于x的不等式mx+n<ax2+bx+c解集是 .
三.解答题(共3小题)
13.(2024.西宁二模)某宾馆有若干间标准房,经市场调查表明,该宾馆每间标准房的价格在150~240元之间(含150元,240元)浮动时,每天入住的房间数y(间)与每间标准房的价格x(元)满足一次函数关系,部分数据如表:
x(元) … 190 200 210 220 …
y(间) … 65 60 55 50 …
(1)根据所给数据在坐标中描出相应的点,并画出图象;
(2)求y关于x(150≤x≤240)的函数解析式;
(3)若不考虑其他因素,宾馆标准房的价格定为多少元时,客房的日营业额最大?最大为多少元?
14.(2024.通州区一模)已知关于x的二次函数y=ax2﹣6ax+5a.
(1)若x=2时,y=﹣3,求该函数的解析式;
(2)当a>0,2≤x≤6时,该函数的最大值与最小值的差为18,求a的值;
(3)若A(x1,y1),B(x2,y2)是该函数图象上的两点,且对于x1=a+3,4≤x2≤6,都有y1≥y2,求a的取值范围.
15.(2024.浙江)为了响应环保号召,某工厂开展节能减排行动.已知工厂每月的利润y(万元)与每月减少的碳排放量x(吨)之间存在一定的函数关系.当每月减少的碳排放量为0吨时,工厂利润为50万元;之后每减少1吨碳排放量,工厂的生产成本会降低一部分,利润随之增加,且增加的幅度逐渐变小.经过数据分析,发现利润y与减少碳排放量x之间满足二次函数关系:y=﹣x2+20x+50.
(1)求该二次函数图象的对称轴和顶点坐标,并说明它们在本题中的实际意义.
(2)若该工厂计划下个月利润达到125万元,则下个月需要减少多少吨碳排放量?
(3)根据环保政策要求,该工厂下个月要减少12吨碳排放量,在满足政策要求的前提下,求该工厂下个月利润的最大值.
中考核心考点 二次函数
参考答案与试题解析
一.选择题(共7小题)
1.(2024.广陵区二模)我们常用“y随x的增大而增大(或减小)”来表示两个变量之间的变化关系.有这样一个情境:如图,小王从点A经过路灯C的正下方沿直线走到点B,他与路灯C的距离y随他与点A之间的距离x的变化而变化.下列函数中y与x之间的变化关系,最有可能与上述情境类似的是( )
A. B.y=﹣x+3
C.y=(x﹣3)2+3 D.y=﹣(x﹣3)2+3
【考点】根据实际问题列二次函数关系式.
【专题】一次函数及其应用;反比例函数及其应用;二次函数图象及其性质;应用意识.
【答案】C
【分析】根据从A到路灯的正下方前他与路灯的距离逐渐减少,经过路灯后他与路灯的距离逐渐增加,可得答案.
【解答】解:由题意,得
从A到路灯的正下方前他与路灯的距离逐渐减少,经过路灯后他与路灯的距离逐渐增加.
A、y随x的增加而减少,与题意不符,故A错误;
B、y随x的增加而减少,与题意不符,故B错误;
C、当x<3时,y随x的增加而减少;当x>3时,y随x的增加而增加,故C正确;
D、当x<3时,y随x的增加而增大;当x>3时,y随x的增加而减少,故D错误;
故选:C.
【点评】本题考查了函数的性质,熟记一次函数的性质、反比例函数的性质、二次函数的性质是解题关键.
2.(2024秋 海港区)在平面直角坐标系中,二次函数y=x2+mx﹣m2+m(m为常数)的图象经过点(0,﹣6),其对称轴在y轴右侧,则该二次函数有( )
A.最大值﹣7 B.最大值
C.最小值﹣7 D.最小值
【考点】二次函数的性质;二次函数图象上点的坐标特征;二次函数的最值.
【专题】二次函数图象及其性质;运算能力.
【答案】C
【分析】依据题意,由二次函数y=x2+mx﹣m2+m(m为常数)的图象经过点(0,﹣6),可以得到m的值,然后根据对称轴在y轴的右侧,可以得到m的值,从而可以得到二次函数的解析式,再将函数解析式化为顶点式,即可得到该函数的最值.
【解答】解:∵二次函数y=x2+mx﹣m2+m(m为常数)的图象经过点(0,﹣6),
∴﹣6=﹣m2+m.
∴m=3或m=﹣2.
∵对称轴在y轴的右侧,a=1>0,
∴对称轴是直线x0.
∴m<0.
∴m=﹣2,
∴二次函数y=x2﹣2x﹣6=(x﹣1)2﹣7.
∴该函数的最小值为﹣7.
故选:C.
【点评】本题考查二次函数的性质、二次函数的最值,解答本题的关键是明确题意,求出m的值,利用二次函数的性质求最值.
3.(2024.铜山区二模)将抛物线y=﹣x2先向左平移3个单位长度,再向上平移2个单位长度,所得抛物线的表达式是( )
A.y=(x﹣3)2+2 B.y=﹣(x﹣3)2﹣2
C.y=(x+3)2﹣2 D.y=﹣(x+3)2+2
【考点】二次函数图象与几何变换.
【专题】二次函数图象及其性质;应用意识.
【答案】D
【分析】根据“上加下减,左加右减”的平移规律,即得答案.
【解答】解:将抛物线y=﹣x2先向左平移3个单位长度,再向上平移2个单位长度,所得抛物线的表达式为y=﹣(x+3)2+2.
故选:D.
【点评】本题考查了二次函数的平移,正确理解二次函数的平移规律是解答本题的关键.
4.(2024秋 鹿邑县)老师设计了接力游戏,用合作的方式完成“求抛物线y=2x2+4x﹣4的顶点坐标”,规则如下:每个人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成解答.接力顺序及每个人的计算结果如图所示:
接力比赛中,自己负责的一步出错的是( )
A.只有丁 B.甲和丁 C.乙和丙 D.乙和丁
【考点】二次函数的性质.
【专题】二次函数图象及其性质;运算能力.
【答案】B
【分析】观察每一项的变化,发现甲将老师给的式子等式右边缩小两倍,到了丁处根据丙的式子得出了错误的顶点坐标.
【解答】解:老师:y=2x2+4x﹣4,
=2(x2+2x)﹣4
=2(x2+2x+1)﹣6
=2(x+1)2﹣6
可得顶点坐标为(﹣1,﹣6).
根据题中过程可知从甲开始出错,按照此步骤下去到了丁处可得顶点应为(1,﹣3),所以错误的只有甲和丁.
故选:B.
【点评】本题主要考查了把二次函数一般解析式化成顶点式,以及二次函数顶点式的图象和性质,掌握配方法是解题的关键.
5.(2024秋 银川)对于二次函数y=2x2+8x﹣3,下列说法错误的是( )
A.图象开口向上
B.对称轴是直线x=﹣2
C.当0<x≤2时,y的最大值为21
D.将图象向右平移3个单位长度,再向上平移1个单位长度后的顶点坐标为(1,﹣12)
【考点】二次函数图象与几何变换;二次函数的最值;二次函数的性质.
【专题】二次函数图象及其性质;推理能力.
【答案】D
【分析】根据题目中的函数解析式和二次函数的性质,可以判断各个选项中的说法是否正确,从而可以解答本题.
【解答】解:∵二次函数y=2x2+8x﹣3=2(x+2)2﹣11,
∴函数的图象开口向上,对称轴为直线x=﹣2,顶点为(﹣2,﹣11),
∴当x>﹣2时,y随x的增大而增大,
∴在0<x≤2中,x=2时,有最大值为y=2(2+2)2﹣11=21,
故A、B、C选项正确,不合题意;
∵顶点为(﹣2,﹣11),
∴将图象向右平移3个单位长度,再向上平移1个单位长度后的顶点坐标为(1,﹣10),
故D选项不正确,符合题意;
故选:D.
【点评】本题考查二次函数的图象与几何变换,二次函数的性质,二次函数的最值,掌握二次函数的性质是解答本题的关键.
6.(2024秋 谯城区)已知3x﹣6是二次函数,则a=( )
A.0 B.1 C.﹣1 D.1或﹣1
【考点】二次函数的定义.
【专题】二次函数图象及其性质;运算能力.
【答案】B
【分析】根据二次函数的定义可得a2+1=2且a+1≠0,从而可得答案.
【解答】解:由条件可知a2+1=2,
解得a1=﹣1或a2=1,
∵a+1≠0,
∴a≠﹣1,
∴a=1.
故选:B.
【点评】本题考查了二次函数的定义.熟练掌握定义是关键.
7.(2024秋 都安县)如图,某中学综合与实践小组要围成一个矩形菜园ABCD,其中一边AD靠墙,AD的长不能超过25m,其余的三边AB,BC,CD用总长为40米的栅栏围成.有下列结论:①AB的长可以为7m;②AB有两个不同的值满足菜园的面积为182m2;③菜园ABCD面积的最大值为200m2.正确结论的个数是( )
A.0 B.1 C.2 D.3
【考点】二次函数的应用;一元二次方程的应用.
【专题】一元二次方程及应用;二次函数的应用;应用意识.
【答案】B
【分析】设AD边长为x m,则AB边长为,根据AB=7列出方程,解方程求出x的值,根据x取值范围判断①;根据矩形的面积=182,解方程求出x的值可以判断②;设矩形菜园的面积为y m2,根据矩形的面积公式列出函数解析式,再根据函数的性质求函数的最值可以判断③.
【解答】解:设AD边长为x m,则AB边长为,
当AB=7时,,
解得x=26,
∵AD的长不能超过25m,
∴x≤25,
故①不正确;
∵菜园ABCD面积为182m2,
∴,
整理得:x2﹣40x+364=0,
解得x=26或x=14,
∵x<25,
∴x=14,
∴AB的长只有一个值满足菜园ABCD面积为182m2,
故②错误;
设矩形菜园的面积为ym2,
根据题意得:,
∵,
∴当x=20时,y有最大值,最大值为200.
故③正确;
∴正确的有1个,
故选:B.
【点评】本题主要考查一元二次方程的应用和二次函数的应用,解答本题的关键是找准等量关系,列出二次函数解析式或一元二次方程.
二.填空题(共5小题)
8.(2024.通州区一模)将抛物线y=x2﹣4x+8向下平移m个单位长度后得到新抛物线,若新抛物线与x轴有公共点,则m的取值范围是 m≥4 .
【考点】抛物线与x轴的交点;二次函数的性质;二次函数图象与几何变换.
【专题】二次函数图象及其性质;运算能力.
【答案】m≥4.
【分析】先根据平移的规律写出抛物线y=x2﹣4x+8向下平移m个单位长度后的抛物线的表达式,再根据平移后得到的抛物线与x轴有公共点可得Δ≥0,由此列不等式即可求出m的取值范围.
【解答】解:平移m个单位长度得y=x2﹣4x+8﹣m,
由题意可得:
∴Δ≥0,
即(﹣4)2﹣4(8﹣m)≥0,
∴m≥4,
故答案为:m≥4.
【点评】此题考查了二次函数图象的平移与几何变换,以及抛物线与x轴的交点问题,利用抛物线解析式的变化规律:左加右减,上加下减是解题关键.
9.(2024.大丰区一模)若t≤x≤t+2时,二次函数y=2x2+4x+1的最大值为31,则t的值为 ﹣5或1 .
【考点】二次函数的最值.
【答案】见试题解答内容
【分析】将标准式化为顶点式为y=2x2+4x+1=2(x+1)2﹣1,由t≤x≤t+2时,y最大值=2(x+1)2﹣1,结合二次函数图象的性质解答.
【解答】解:y=2x2+4x+1=2(x+1)2﹣1,
∵二次函数y=2x2+4x+1的最大值为31,
∴①当﹣1﹣t>t+3,即t<﹣2时,2t2+4t+1=31
解得 t1=﹣5,t2=3(舍去).
②当﹣1﹣t<t+3,即t>﹣2时,2(t+2)2+4(t+2)+1=31,
解得 t1=﹣7(舍去),t2=1;
③当t>﹣1时,2(t+2)2+4(t+2)+1=31,
解得 t1=﹣7(舍去),t2=1;
综上所述,t的值是﹣5或1.
故答案为:﹣5或1.
【点评】本题考查了二次函数的最值,难度较大,关键是判断出当x≥﹣1时,y随x的增大而增大,由此此解决这类题.
10.(2024秋 鹿邑县)水幕电影是通过高压水泵和特制水幕发生器,将水自下而上高速喷出,雾化后形成水幕,然后由专用放映机将特制的录影带.水嘴投射在水幕上.如图,水嘴喷出的水柱的最高点为P,AB=2m,BP=9m,水嘴高AD=5m,则水柱落在地点C到水嘴所在墙的距离AC是 5 m.
【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【答案】5.
【分析】以A为坐标原点,AB所在的直线为x轴,AD所在的直线为y轴建立平面直角坐标系,易得点D和点P的坐标,设抛物线的解析式为:y=a(x﹣2)2+9,代入点D的坐标求得函数的解析式,再求出点C的坐标即可得到AC的长度.
【解答】解:以A为坐标原点,AB所在的直线为x轴,AD所在的直线为y轴建立平面直角坐标系,如图所示,
则A(0,0),D(0,5),P(2,9),
∵点P是最高点,
∴设抛物线的解析式为:y=a(x﹣2)2+9,
将点D坐标代入,可得:5=4a+9,
解得:a=﹣1,
∴y=﹣(x﹣2)2+9,
令y=0,则﹣(x﹣2)2+9=0,
解得:x1=5,x2=﹣1,
∴点C(5,0),
∴AC=5m,
故答案为:5.
【点评】本题考查了二次函数的实际应用,建立适当的坐标系,设出顶点式是解题的关键.
11.(2024.香洲区)抛物线L:y=a(x﹣3)2﹣1过A(﹣2,3),B(m,3)两点,将抛物线L向左或向右平移后得到抛物线M,设抛物线M的顶点为C.若△ABC是以AB为斜边的直角三角形,则点C的坐标为 (0,﹣1)或(6,﹣1) .
【考点】二次函数图象与几何变换;勾股定理的逆定理;二次函数的性质;二次函数图象上点的坐标特征.
【专题】二次函数图象及其性质;运算能力.
【答案】(0,﹣1)或(6,﹣1).
【分析】由抛物线的对称性求出点B的坐标,由抛物线的平移表示出点C的坐标,再根据勾股定理列方程即可求解.
【解答】解:由抛物线L的解析式可知抛物线L的对称轴为直线x=3,顶点坐标为(3,﹣1),
由条件可得﹣2+m=2×3,
∴m=8,
∴A(﹣2,3),B(8,3),AB=8﹣(﹣2)=10,
∵抛物线L向左或向右平移后得到抛物线M,
∴设抛物线M的顶点C(n,﹣1),
∴AC2=(n+2)2+(﹣1﹣3)2=n2+4n+20,BC2=(n﹣8)2+(﹣1﹣3)2=n2﹣16n+80,
∵△ABC是以AB为斜边的直角三角形,
∴n2+4n+20+n2﹣16n+80=102=100,
整理得n2﹣6n=0,
解得n1=0,n2=6,
∴点C的坐标为(0,﹣1)或(6,﹣1)
故答案为:(0,﹣1)或(6,﹣1).
【点评】本题考查二次函数的图象和性质,二次函数图象的平移,勾股定理等.熟练掌握以上知识点是关键.
12.(2024秋 沭阳县)如图,直线y=mx+n与抛物线y=ax2+bx+c交于A(﹣1,p),B(5,q)两点,则关于x的不等式mx+n<ax2+bx+c解集是 ﹣1<x<5 .
【考点】二次函数与不等式(组).
【专题】数形结合;二次函数图象及其性质.
【答案】见试题解答内容
【分析】直接利用函数的交点坐标进而结合函数图象得出不等式mx+n<ax2+bx+c的解集.
【解答】解:∵直线y=mx+n与抛物线y=ax2+bx+c交于A(﹣1,p),B(5,q)两点,
∴关于x的不等式mx+n<ax2+bx+c解集是﹣1<x<5
故答案为:﹣1<x<5
【点评】此题主要考查了二次函数与不等式,正确数形结合分析是解题关键.
三.解答题(共3小题)
13.(2024.西宁二模)某宾馆有若干间标准房,经市场调查表明,该宾馆每间标准房的价格在150~240元之间(含150元,240元)浮动时,每天入住的房间数y(间)与每间标准房的价格x(元)满足一次函数关系,部分数据如表:
x(元) … 190 200 210 220 …
y(间) … 65 60 55 50 …
(1)根据所给数据在坐标中描出相应的点,并画出图象;
(2)求y关于x(150≤x≤240)的函数解析式;
(3)若不考虑其他因素,宾馆标准房的价格定为多少元时,客房的日营业额最大?最大为多少元?
【考点】二次函数的应用.
【专题】二次函数的应用;运算能力;应用意识.
【答案】(1)作图见解析;(2)yx+160(150≤x≤240);(3)宾馆标准房的价格定为160元时,客房的日营业额最大,最大为12800元.
【分析】(1)依据题意,描点、连线即可得;
(2)依据题意,待定系数法求解可得;
(3)依据题意,由营业额=入住房间数量×房价得出函数解析式,再利用二次函数的性质求解可得.
【解答】解:(1)如图所示:
(2)由题意,设 y=kx+b,将(200,60)、(220,50)代入,
∴,
∴
∴yx+160(150≤x≤240).
(3)由题意得,,
∴对称轴为直线,
∵,
∴当x=160时,w有最大值,最大值为12800元.
答:宾馆标准房的价格定为160元时,客房的日营业额最大,最大为12800元.
【点评】本题主要考查了二次函数的应用以及待定系数法求一次函数解析式以及二次函数最值问题,由营业额=入住房间数量×房价得出函数解析式及二次函数的性质是解题关键.
14.(2024.通州区一模)已知关于x的二次函数y=ax2﹣6ax+5a.
(1)若x=2时,y=﹣3,求该函数的解析式;
(2)当a>0,2≤x≤6时,该函数的最大值与最小值的差为18,求a的值;
(3)若A(x1,y1),B(x2,y2)是该函数图象上的两点,且对于x1=a+3,4≤x2≤6,都有y1≥y2,求a的取值范围.
【考点】二次函数图象与系数的关系;二次函数图象上点的坐标特征;二次函数的最值;待定系数法求二次函数解析式.
【专题】二次函数图象及其性质;运算能力.
【答案】(1)y=x2﹣6x+5;
(2)a=2;
(3)a≥3或﹣1≤a<0.
【分析】(1)把x=2,y=﹣3,分别代入y=ax2﹣6ax+5a,得出a=1,即可作答.
(2)先整理y=a(x﹣3)2﹣4a,故图象的对称轴为直线x=3,结合a>0,2≤x≤6.故当x=3时,y最小=﹣4a,当x=6时,y最大=5a,列式5a﹣(﹣4a)=18,即可作答.
(3)进行分类讨论,即①若a>0,则函数图象开口向上.②若a<0,则函数图象开口向下,再结合二次函数的图象性质,进行分析列式,即可作答.
【解答】解:(1)∵y=ax2﹣6ax+5a,
当x=2时,y=﹣3,
∴4a﹣12a+5a=﹣3,
∴a=1.
∴该函数的解析式为y=x2﹣6x+5.
(2)配方得y=ax2﹣6ax+5a=a(x﹣3)2﹣4a,
∴图象的对称轴为直线x=3.
由条件可知当x=3时,y最小=﹣4a,
∵|6﹣3|=3>|2﹣3|,
∴当x=6时,y=a(6﹣3)2﹣4a=9a﹣4a=5a,
∴y最大=5a.
∴5a﹣(﹣4a)=18.
∴a=2;
(3)①若a>0,则函数图象开口向上.
又∵对称轴为直线x=3,
∴当x>3时,y随x的增大而增大.
∵x1=a+3>3,
∴点A在对称轴的右侧.
又∵对于x1=a+3,4≤x2≤6,都有y1≥y2,
∴a+3≥6,
∴a≥3.
②若a<0,则函数图象开口向下,
∵x1=a+3<3,
∴点A在对称轴的左侧.
∵对称轴为直线x=3,
∴当x=2或x=4时函数值相等.
由条件可知2≤a+3<3,
∴﹣1≤a<0.
综上:a≥3或﹣1≤a<0.
【点评】本题考查了二次函数的图象性质,求二次函数的解析式,正确掌握相关性质内容是解题的关键.
15.(2024.浙江)为了响应环保号召,某工厂开展节能减排行动.已知工厂每月的利润y(万元)与每月减少的碳排放量x(吨)之间存在一定的函数关系.当每月减少的碳排放量为0吨时,工厂利润为50万元;之后每减少1吨碳排放量,工厂的生产成本会降低一部分,利润随之增加,且增加的幅度逐渐变小.经过数据分析,发现利润y与减少碳排放量x之间满足二次函数关系:y=﹣x2+20x+50.
(1)求该二次函数图象的对称轴和顶点坐标,并说明它们在本题中的实际意义.
(2)若该工厂计划下个月利润达到125万元,则下个月需要减少多少吨碳排放量?
(3)根据环保政策要求,该工厂下个月要减少12吨碳排放量,在满足政策要求的前提下,求该工厂下个月利润的最大值.
【考点】二次函数的应用;一元二次方程的应用.
【专题】二次函数的应用;运算能力.
【答案】(1)x=10,(10,150),当减少碳排放量等于10吨时,最大利润为150万元;
(2)当利润达到125万元时,需要减少5吨或15吨;
(3)满足政策要求的前提下,该工厂下个月利润的最大值146万元.
【分析】(1)由二次函数解析式,根据对称轴直线的计算公式,顶点坐标的计算方法,顶点坐标表示的含义计算即可求解;
(2)当y=125时,代入计算即可求解;
(3)根据题意图象开口向下,当x≤10时,y随x的增大而增大,当x≥10时,y随x的增大而减小,当x=12时,确定最大值,代入计算即可求解.
【解答】解:(1)∵y=﹣x2+20x+50,
∴对称轴直线为,
当x=10时,y=﹣102+20×10+50=150,
∴顶点坐标为(10,150),
∵﹣1<0,即图象的开口象限,
∴当减少碳排放量等于10吨时,最大利润为150万元;
(2)当y=125时,﹣x2+20x+50=125,
∴x2﹣20x+75=0,
∴(x﹣5)(x﹣15)=0,
∴x1=5,x2=15,
∴当利润达到125万元时,需要减少5吨或15吨;
(3)∵y=﹣x2+20x+50=﹣(x﹣10)2+150,
∵﹣1<0,顶点坐标为(10,150),
∴图象开口向下,当x≤10时,y随x的增大而增大,当x≥10时,y随x的增大而减小,
由题意可得:当x=12时,确定最大值,
∴y=﹣(12﹣10)2+150=146,
∴满足政策要求的前提下,该工厂下个月利润的最大值146万元.
【点评】本题主要考查二次函数的运用,掌握顶点式,二次函数函数值、自变量值的计算是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
