【中考核心考点】2025年北师大版中考数学考前冲刺 弧长及扇形的面积(含解析)
文档属性
| 名称 | 【中考核心考点】2025年北师大版中考数学考前冲刺 弧长及扇形的面积(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 17:26:41 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
中考核心考点 弧长及扇形的面积
一.选择题(共7小题)
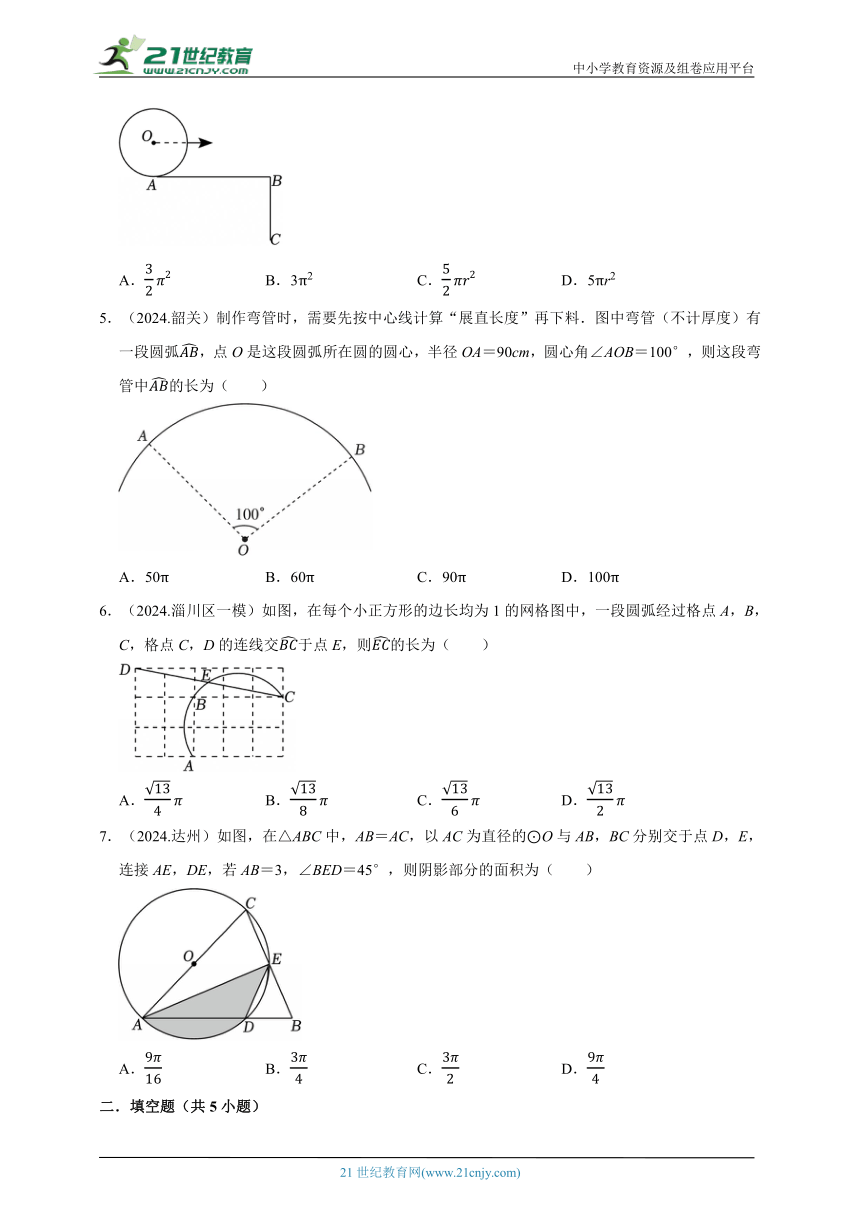
1.(2024.海勃湾区)如图,在矩形ABCD中,AB=2,BC=4,以点D为圆心,DA的长为半径画弧,交BC于点E,交DC的延长线于点F,则图中阴影部分的面积为( )
A.4 B.2 C. D.2
2.(2024.彭水县)如图,在正方形ABCD中,AB=1,以B为圆心,BA为半径作圆弧,交CB的延长线于点E,连结DE.则图中阴影部分的面积为( )
A. B. C. D.
3.(2025春 徐闻县)折扇最早出现于我国南北朝时期,《南齐书》中说:“司徒褚渊入朝,以腰扇障日.”这里的“腰扇”在《通鉴注》中的解释为折叠扇.如图,一折扇的骨柄长为21cm,折扇张开后为扇形,圆心角∠AOB为120°,则弧AB的长为( )
A.7πcm B.14πcm C.21πcm D.42πcm
4.(2025春 宝山区)如图,已知∠ABC=90°,AB=πr,AB=2BC,半径为r的⊙O从点A出发,沿A→B→C方向滚动到点C时停止.则在此运动过程中,⊙O扫过的面积是( )
A. B.3π2 C. D.5πr2
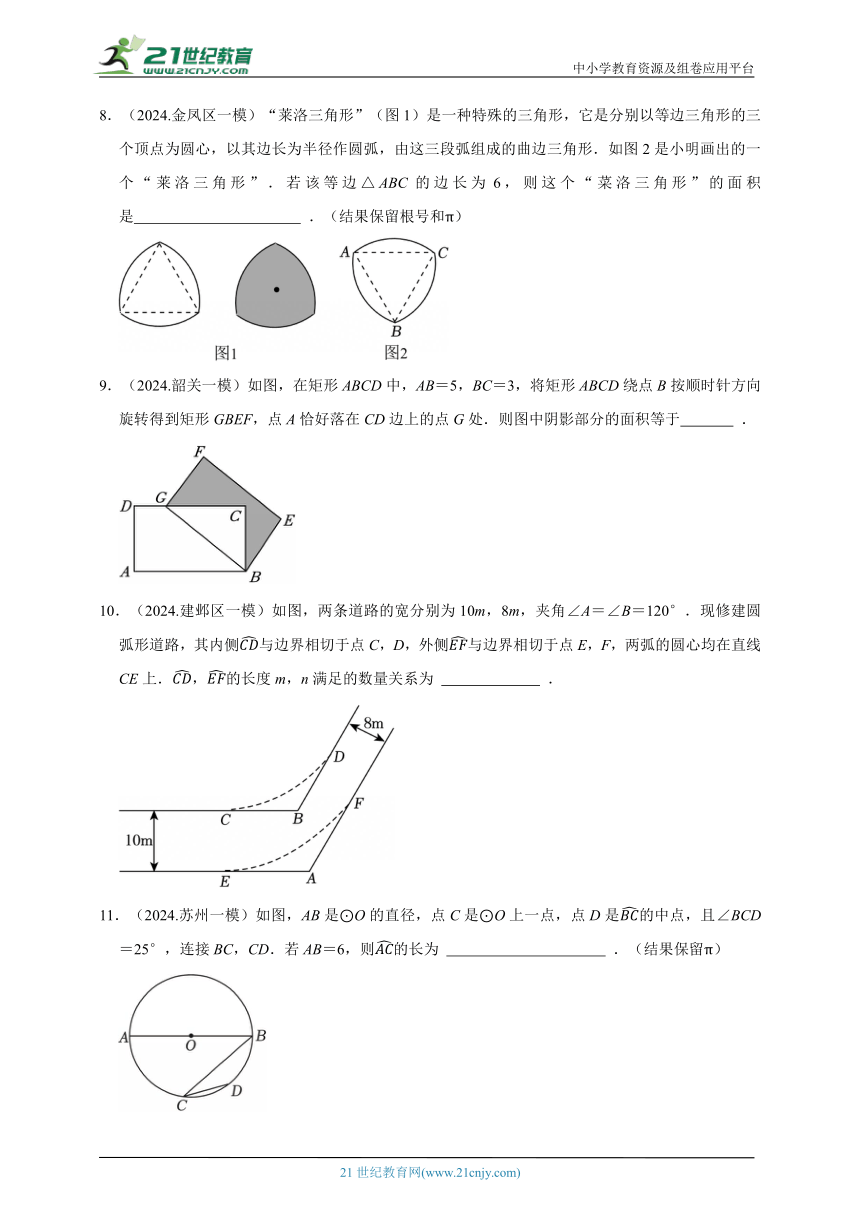
5.(2024.韶关)制作弯管时,需要先按中心线计算“展直长度”再下料.图中弯管(不计厚度)有一段圆弧,点O是这段圆弧所在圆的圆心,半径OA=90cm,圆心角∠AOB=100°,则这段弯管中的长为( )
A.50π B.60π C.90π D.100π
6.(2024.淄川区一模)如图,在每个小正方形的边长均为1的网格图中,一段圆弧经过格点A,B,C,格点C,D的连线交于点E,则的长为( )
A. B. C. D.
7.(2024.达州)如图,在△ABC中,AB=AC,以AC为直径的⊙O与AB,BC分别交于点D,E,连接AE,DE,若AB=3,∠BED=45°,则阴影部分的面积为( )
A. B. C. D.
二.填空题(共5小题)
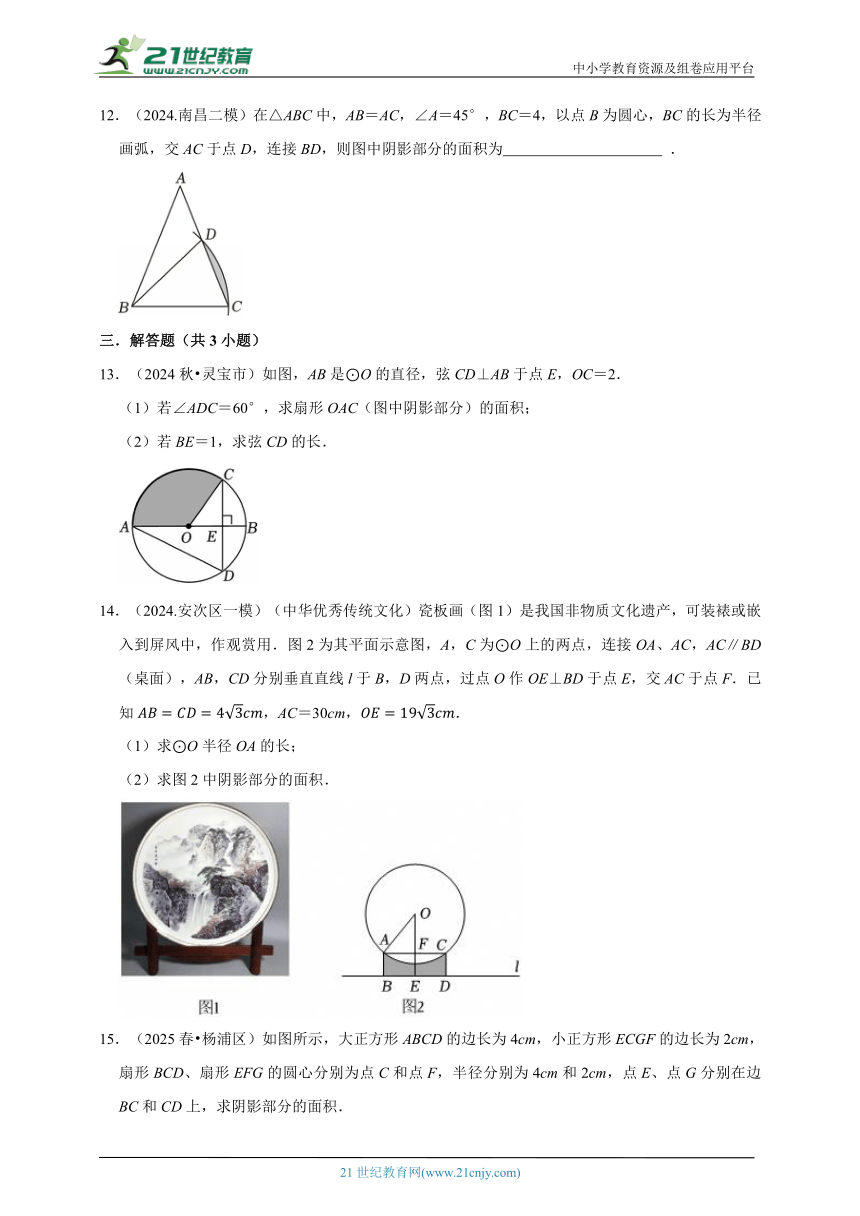
8.(2024.金凤区一模)“莱洛三角形”(图1)是一种特殊的三角形,它是分别以等边三角形的三个顶点为圆心,以其边长为半径作圆弧,由这三段弧组成的曲边三角形.如图2是小明画出的一个“莱洛三角形”.若该等边△ABC的边长为6,则这个“菜洛三角形”的面积是 .(结果保留根号和π)
9.(2024.韶关一模)如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A恰好落在CD边上的点G处.则图中阴影部分的面积等于 .
10.(2024.建邺区一模)如图,两条道路的宽分别为10m,8m,夹角∠A=∠B=120°.现修建圆弧形道路,其内侧与边界相切于点C,D,外侧与边界相切于点E,F,两弧的圆心均在直线CE上.,的长度m,n满足的数量关系为 .
11.(2024.苏州一模)如图,AB是⊙O的直径,点C是⊙O上一点,点D是的中点,且∠BCD=25°,连接BC,CD.若AB=6,则的长为 .(结果保留π)
12.(2024.南昌二模)在△ABC中,AB=AC,∠A=45°,BC=4,以点B为圆心,BC的长为半径画弧,交AC于点D,连接BD,则图中阴影部分的面积为 .
三.解答题(共3小题)
13.(2024秋 灵宝市)如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=2.
(1)若∠ADC=60°,求扇形OAC(图中阴影部分)的面积;
(2)若BE=1,求弦CD的长.
14.(2024.安次区一模)(中华优秀传统文化)瓷板画(图1)是我国非物质文化遗产,可装裱或嵌入到屏风中,作观赏用.图2为其平面示意图,A,C为⊙O上的两点,连接OA、AC,AC∥BD(桌面),AB,CD分别垂直直线l于B,D两点,过点O作OE⊥BD于点E,交AC于点F.已知,AC=30cm,.
(1)求⊙O半径OA的长;
(2)求图2中阴影部分的面积.
15.(2025春 杨浦区)如图所示,大正方形ABCD的边长为4cm,小正方形ECGF的边长为2cm,扇形BCD、扇形EFG的圆心分别为点C和点F,半径分别为4cm和2cm,点E、点G分别在边BC和CD上,求阴影部分的面积.
中考核心考点 弧长及扇形的面积
参考答案与试题解析
一.选择题(共7小题)
1.(2024.海勃湾区)如图,在矩形ABCD中,AB=2,BC=4,以点D为圆心,DA的长为半径画弧,交BC于点E,交DC的延长线于点F,则图中阴影部分的面积为( )
A.4 B.2 C. D.2
【考点】扇形面积的计算;矩形的性质.
【专题】与圆有关的计算;运算能力;推理能力.
【答案】B
【分析】连接DE,利用矩形的性质以及勾股定理求出CE的长以及∠CDE的度数,进而利用图中阴影部分的面积=S扇形DEF﹣S△DEC,求出答案.
【解答】解:连接DE,
在矩形ABCD中,AB=2,BC=4,
∴CD=AB=2,AD=BC=4,∠BCD=90°,
∴DE=AD=4,
∴CE2,
∴CEDE,
∴∠EDC=30°,
∴图中阴影部分的面积=S扇形DEF﹣S△DEC
2×2
2.
故选:B.
【点评】此题主要考查了扇形面积求法以及矩形的性质等知识,正确得出CE的长以及∠CDE的度数是解题关键.
2.(2024.彭水县)如图,在正方形ABCD中,AB=1,以B为圆心,BA为半径作圆弧,交CB的延长线于点E,连结DE.则图中阴影部分的面积为( )
A. B. C. D.
【考点】扇形面积的计算;正方形的性质.
【专题】与圆有关的计算;运算能力.
【答案】D
【分析】根据S阴影=S扇形ABE+S正方形ABCD﹣S△DCE,进行计算即可得出答案,不规则图形的面积通常转化为规则图形的面积的和差.
【解答】解:在正方形ABCD中,∠ABC=90°,AB=1,
∴BE=1,∠ABE=90°,BC=CD=1,
∴BE+BC=CE=2,
∴S阴影=S扇形ABE+S正方形ABCD﹣S△DCE
,
故选:D.
【点评】本题主要考查了扇形的面积计算方法,掌握其公式是解决此题的关键.
3.(2025春 徐闻县)折扇最早出现于我国南北朝时期,《南齐书》中说:“司徒褚渊入朝,以腰扇障日.”这里的“腰扇”在《通鉴注》中的解释为折叠扇.如图,一折扇的骨柄长为21cm,折扇张开后为扇形,圆心角∠AOB为120°,则弧AB的长为( )
A.7πcm B.14πcm C.21πcm D.42πcm
【考点】弧长的计算.
【专题】与圆有关的计算;运算能力.
【答案】B
【分析】直接根据扇形弧长的求解公式,求解即可.
【解答】解:∵折扇的骨柄长为21cm,折扇张开的角度为120°,
∴弧AB的长,
故选:B.
【点评】此题考查了扇形弧长的计算,解题的关键是掌握弧长公式.
4.(2025春 宝山区)如图,已知∠ABC=90°,AB=πr,AB=2BC,半径为r的⊙O从点A出发,沿A→B→C方向滚动到点C时停止.则在此运动过程中,⊙O扫过的面积是( )
A. B.3π2 C. D.5πr2
【考点】扇形面积的计算.
【专题】平移、旋转与对称;与圆有关的计算;运算能力.
【答案】D
【分析】根据圆面积、扇形面积以及矩形面积的计算方法进行计算即可.
【解答】解:如图,⊙O扫过的面积S=S圆O+S矩形ABED+S扇形BEF+S矩形BCGF
=πr2+πr×2rπr×2r
=πr2+2πr2+πr2+πr2
=5πr2;
故选:D.
【点评】本题考查扇形面积的计算,掌握圆面积、扇形面积以及矩形面积的计算方法是正确解答的关键.
5.(2024.韶关)制作弯管时,需要先按中心线计算“展直长度”再下料.图中弯管(不计厚度)有一段圆弧,点O是这段圆弧所在圆的圆心,半径OA=90cm,圆心角∠AOB=100°,则这段弯管中的长为( )
A.50π B.60π C.90π D.100π
【考点】弧长的计算.
【专题】与圆有关的计算;运算能力.
【答案】A
【分析】直接利用弧长公式求解即可.
【解答】解:有弧长公式可得:这段弯管中的长为,
故选:A.
【点评】本题考查了弧长公式的应用,解答本题的关键是明确弧长计算公式.
6.(2024.淄川区一模)如图,在每个小正方形的边长均为1的网格图中,一段圆弧经过格点A,B,C,格点C,D的连线交于点E,则的长为( )
A. B. C. D.
【考点】弧长的计算;勾股定理的逆定理;圆周角定理.
【专题】圆的有关概念及性质;与圆有关的计算;运算能力.
【答案】A
【分析】连接AE、AC、AD,由∠ABC=90°,可知AC是直径且值为,可知∠AEC=90°,根据勾股定理逆定理可判断出△ACD是等腰直角三角形,求出∠ACE=∠CAE=45°,利用弧长公式求解即可.
【解答】解:如图所示:连接AE、AC、AD,
∵∠ABC=90°,
∴AC是直径,
∴∠ABC=∠AEC=90°,
根据网格图形可知:AC=AD,CD,
∴AC2+AD2=CD2=26,
∴△ACD是等腰直角三角形,
∴∠CAD=90°,∠ACE=45°,
∴∠EAC=45°,
∴所对的圆心角是90°,
∴的长为.
故选:A.
【点评】本题考查了勾股定理逆定理、圆周角定理及其推论、弧长的计算公式、利用网格求线段长等知识,准确地作出辅助线构造出直角三角形和正确的计算是解决本题的关键.
7.(2024.达州)如图,在△ABC中,AB=AC,以AC为直径的⊙O与AB,BC分别交于点D,E,连接AE,DE,若AB=3,∠BED=45°,则阴影部分的面积为( )
A. B. C. D.
【考点】扇形面积的计算;等腰三角形的性质;圆周角定理.
【专题】与圆有关的计算;运算能力.
【答案】A
【分析】连接OE,OD,证明S△AOD=S△AED,可得S阴影=S扇形OAD,求解∠AOD=90°,再利用扇形的面积公式计算即可.
【解答】解:连接OE,OD,
由条件可知∠AEC=90°,BE=CE,
即点E是BC的中点,
∵点O是AC的中点,
∴OE是△ABC的中位线,
∴OE∥AB,
∴S△AOD=S△AED,
∴S阴影=S扇形OAD,
∵∠AEC=90°,
∴∠AEB=90°,
∵∠BED=45°,
∴∠AED=45°,
∴∠AOD=90°,
又∵AC=AB=3,
∴,
∴,
∴,
故选:A.
【点评】本题考查的是等腰三角形的性质,圆周角定理的应用,扇形面积的计算.熟练掌握以上知识点是关键.
二.填空题(共5小题)
8.(2024.金凤区一模)“莱洛三角形”(图1)是一种特殊的三角形,它是分别以等边三角形的三个顶点为圆心,以其边长为半径作圆弧,由这三段弧组成的曲边三角形.如图2是小明画出的一个“莱洛三角形”.若该等边△ABC的边长为6,则这个“菜洛三角形”的面积是 .(结果保留根号和π)
【考点】扇形面积的计算;等边三角形的性质.
【专题】与圆有关的计算;运算能力.
【答案】.
【分析】先根据等边三角形的性质得∠A=∠B=∠C=60°,AB=BC=AC=6,再运用勾股定理算得,,观察图形得这个“菜洛三角形”的面积是3S扇形BAC﹣2S△BAC,代入数值进行计算,即可作答.
【解答】解:由条件可知∠A=∠B=∠C=60°,AB=BC=AC=6,
过点B作BH⊥AC,如图所示:
∴,
由勾股定理得BH3,
∴,
∴这个“菜洛三角形”的面积是:
;
故答案为:.
【点评】本题考查了等边三角形的性质,勾股定理,扇形面积,发现这个“菜洛三角形”的面积是3S扇形BAC﹣2S△BAC是关键.
9.(2024.韶关一模)如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A恰好落在CD边上的点G处.则图中阴影部分的面积等于 9 .
【考点】扇形面积的计算;旋转的性质;矩形的性质.
【专题】与圆有关的计算;运算能力.
【答案】9.
【分析】旋转得到BG=AB=5,勾股定理求出CG的长,利用矩形的面积减去直角三角形的面积求出阴影部分的面积即可.
【解答】解:由条件可知BG=AB=5,BE=BC=3,∠BCG=90°,
在Rt△BCG中,,
∴S阴影;
故答案为:9.
【点评】本题考查旋转的性质,矩形的性质,勾股定理,熟练掌握以上知识点是关键.
10.(2024.建邺区一模)如图,两条道路的宽分别为10m,8m,夹角∠A=∠B=120°.现修建圆弧形道路,其内侧与边界相切于点C,D,外侧与边界相切于点E,F,两弧的圆心均在直线CE上.,的长度m,n满足的数量关系为 n=m+6π .
【考点】弧长的计算.
【专题】与圆有关的计算;运算能力.
【答案】n=m+6π.
【分析】根据题意表示两条弧所对应的半径,圆心角,然后利用弧长公式计算即可.
【解答】解:设内侧弧所在圆的半径为r m,
∵两条道路的宽分别为10m,8m,
∴外侧弧所在圆的半径为r+10+8=(r+18)m,
∵∠A=∠B=120°,
∴两弧所对的圆心角n=180°﹣120°=60°,
∴内侧弧的长度m(m),
外侧弧的长度n()m,
∴n=m+6π.
故答案为:n=m+6π.
【点评】本题考查了弧长的计算,熟练掌握计算公式是解题的关键.
11.(2024.苏州一模)如图,AB是⊙O的直径,点C是⊙O上一点,点D是的中点,且∠BCD=25°,连接BC,CD.若AB=6,则的长为 π .(结果保留π)
【考点】弧长的计算;圆周角定理.
【专题】圆的有关概念及性质;与圆有关的计算;运算能力.
【答案】π.
【分析】连接OC,OD,根据圆周角定理得∠BOD=2∠BCD=50°,所以∠BOC=2∠BOD=100°,即可得∠AOC=80°,再根据弧长公式计算即可.
【解答】解:连接OC,OD,
∵∠BCD=25°,
∴∠BOD=2∠BCD=50°,
∵点D是的中点,
∴∠BOC=2∠BOD=100°,
∴∠AOC=80°,
∴的长为π.
故答案为:π.
【点评】本题考查了弧长的计算和圆周角定理,熟练掌握圆周角定理和弧长公式是解题的关键.
12.(2024.南昌二模)在△ABC中,AB=AC,∠A=45°,BC=4,以点B为圆心,BC的长为半径画弧,交AC于点D,连接BD,则图中阴影部分的面积为 .
【考点】扇形面积的计算;等腰三角形的性质.
【专题】运算能力.
【答案】.
【分析】过点D作DM⊥BC于点M,先根据等腰三角形的性质求出∠DBC的度数,再用扇形BDC的面积减去三角形BDC的面积即可解决问题.
【解答】解:过点D作DM⊥BC于点M,
∵AB=AC,∠A=45°,
∴∠ABC=∠BCD=67.5°.
又∵BC=BD,
∴∠BDC=∠BCD=67.5°,
∴∠CBD=45°.
∵DM⊥BC,BD=BC=4,
∴DM,
∴.
又∵,
∴阴影部分的面积为.
故答案为:.
【点评】本题主要考查了扇形面积的计算及等腰三角形的性质,熟知扇形的面积公式及等腰三角形的性质是解题的关键.
三.解答题(共3小题)
13.(2024秋 灵宝市)如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=2.
(1)若∠ADC=60°,求扇形OAC(图中阴影部分)的面积;
(2)若BE=1,求弦CD的长.
【考点】扇形面积的计算;勾股定理;垂径定理;圆周角定理.
【专题】与圆有关的计算;运算能力.
【答案】(1);
(2).
【分析】(1)先根据圆周角定理求出∠AOC的度数,再根据扇形面积公式求解即可;
(2)根据勾股定理和垂径定理求解即可.
【解答】解:(1)∵∠ADC=60°,
∴∠AOC=2∠ADC=2×60°=120°,
∴;
(2)OB=OC=2,BE=1,
∴OE=OB﹣BE=2﹣1=1,
又∵AB⊥CD,
在Rt△OCE中,利用勾股定理,可得,
∴.
【点评】本题考查了圆的综合,熟练运用圆周角定理,勾股定理和垂径定理是解题的关键.
14.(2024.安次区一模)(中华优秀传统文化)瓷板画(图1)是我国非物质文化遗产,可装裱或嵌入到屏风中,作观赏用.图2为其平面示意图,A,C为⊙O上的两点,连接OA、AC,AC∥BD(桌面),AB,CD分别垂直直线l于B,D两点,过点O作OE⊥BD于点E,交AC于点F.已知,AC=30cm,.
(1)求⊙O半径OA的长;
(2)求图2中阴影部分的面积.
【考点】扇形面积的计算;勾股定理;垂径定理.
【专题】与圆有关的计算;推理能力.
【答案】(1)30;
(2).
【分析】(1)先根据AC∥l,OE⊥l,可得OF⊥AC,,再根据垂径定理得,然后根据勾股定理得,即可得出答案.
(2)根据S阴=S四边形ABDC+S△AOC﹣S扇形AOC,即可求解.
【解答】解:(1)由条件可知OF⊥AC,
∵AC=30cm,
∴,
∵,由题意得,
∴,
在Rt△OAF中,由勾股定理可得:,
即⊙O的半径OA的长为30cm.
(2)连接OC,
,
,
由条件可知△OAC为等边三角形,∠AOC=60°,
(cm2),
.
【点评】本题主要考查了垂径定理,勾股定理,平行线间的距离,熟练掌握以上知识点是关键.
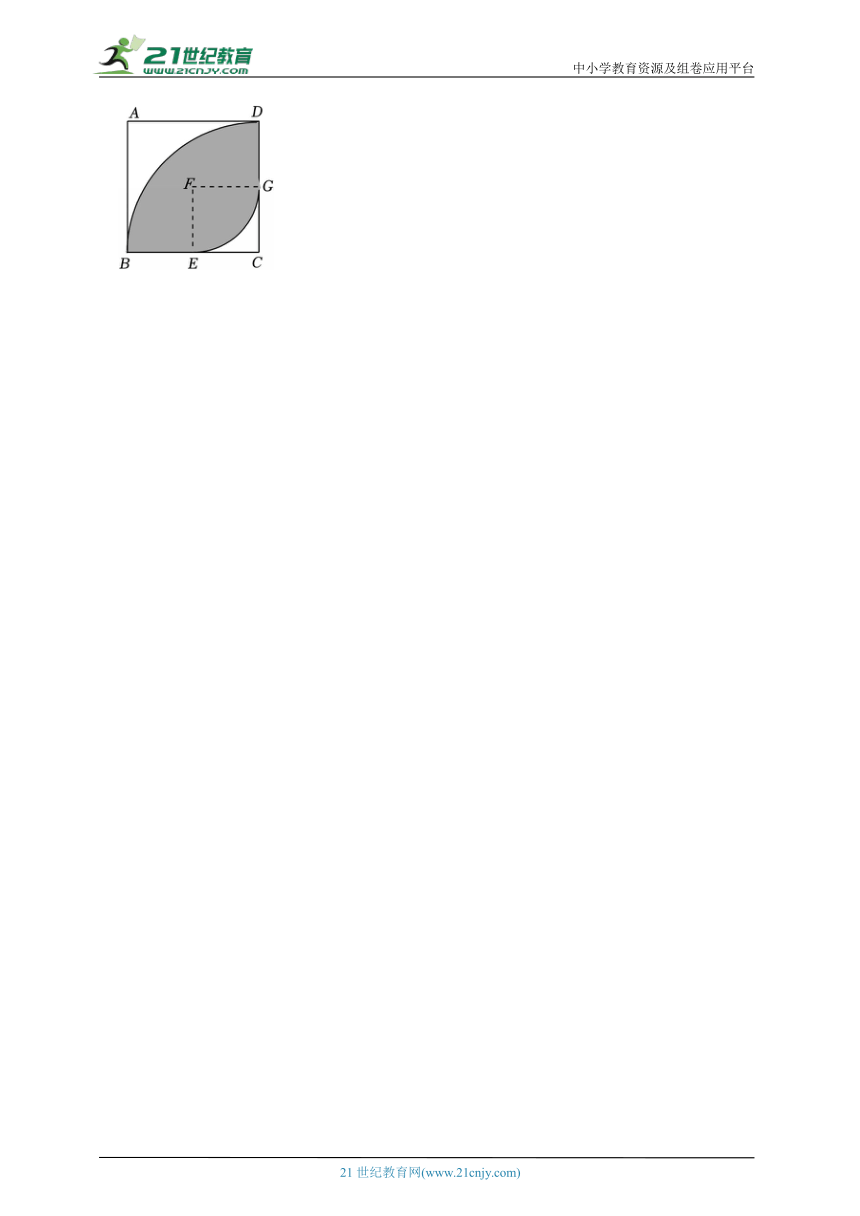
15.(2025春 杨浦区)如图所示,大正方形ABCD的边长为4cm,小正方形ECGF的边长为2cm,扇形BCD、扇形EFG的圆心分别为点C和点F,半径分别为4cm和2cm,点E、点G分别在边BC和CD上,求阴影部分的面积.
【考点】扇形面积的计算;正方形的性质.
【专题】运算能力.
【答案】(5π﹣4)cm2.
【分析】先求出小正方形的面积,进一步得出右下角空白部分的面积,最后用大扇形的面积减去空白部分的面积即可解决问题.
【解答】解:由题知,
小正方形EFGC的面积为:22=4(cm2).
又因为(cm2),
所以右下角空白部分的面积为(4﹣π)cm2.
又因为(cm2),
所以阴影部分的面积为:4π﹣(4﹣π)=5π﹣4(cm2).
【点评】本题主要考查了扇形面积的计算及正方形的性质,熟知扇形的面积公式及正方形的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考核心考点 弧长及扇形的面积
一.选择题(共7小题)
1.(2024.海勃湾区)如图,在矩形ABCD中,AB=2,BC=4,以点D为圆心,DA的长为半径画弧,交BC于点E,交DC的延长线于点F,则图中阴影部分的面积为( )
A.4 B.2 C. D.2
2.(2024.彭水县)如图,在正方形ABCD中,AB=1,以B为圆心,BA为半径作圆弧,交CB的延长线于点E,连结DE.则图中阴影部分的面积为( )
A. B. C. D.
3.(2025春 徐闻县)折扇最早出现于我国南北朝时期,《南齐书》中说:“司徒褚渊入朝,以腰扇障日.”这里的“腰扇”在《通鉴注》中的解释为折叠扇.如图,一折扇的骨柄长为21cm,折扇张开后为扇形,圆心角∠AOB为120°,则弧AB的长为( )
A.7πcm B.14πcm C.21πcm D.42πcm
4.(2025春 宝山区)如图,已知∠ABC=90°,AB=πr,AB=2BC,半径为r的⊙O从点A出发,沿A→B→C方向滚动到点C时停止.则在此运动过程中,⊙O扫过的面积是( )
A. B.3π2 C. D.5πr2
5.(2024.韶关)制作弯管时,需要先按中心线计算“展直长度”再下料.图中弯管(不计厚度)有一段圆弧,点O是这段圆弧所在圆的圆心,半径OA=90cm,圆心角∠AOB=100°,则这段弯管中的长为( )
A.50π B.60π C.90π D.100π
6.(2024.淄川区一模)如图,在每个小正方形的边长均为1的网格图中,一段圆弧经过格点A,B,C,格点C,D的连线交于点E,则的长为( )
A. B. C. D.
7.(2024.达州)如图,在△ABC中,AB=AC,以AC为直径的⊙O与AB,BC分别交于点D,E,连接AE,DE,若AB=3,∠BED=45°,则阴影部分的面积为( )
A. B. C. D.
二.填空题(共5小题)
8.(2024.金凤区一模)“莱洛三角形”(图1)是一种特殊的三角形,它是分别以等边三角形的三个顶点为圆心,以其边长为半径作圆弧,由这三段弧组成的曲边三角形.如图2是小明画出的一个“莱洛三角形”.若该等边△ABC的边长为6,则这个“菜洛三角形”的面积是 .(结果保留根号和π)
9.(2024.韶关一模)如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A恰好落在CD边上的点G处.则图中阴影部分的面积等于 .
10.(2024.建邺区一模)如图,两条道路的宽分别为10m,8m,夹角∠A=∠B=120°.现修建圆弧形道路,其内侧与边界相切于点C,D,外侧与边界相切于点E,F,两弧的圆心均在直线CE上.,的长度m,n满足的数量关系为 .
11.(2024.苏州一模)如图,AB是⊙O的直径,点C是⊙O上一点,点D是的中点,且∠BCD=25°,连接BC,CD.若AB=6,则的长为 .(结果保留π)
12.(2024.南昌二模)在△ABC中,AB=AC,∠A=45°,BC=4,以点B为圆心,BC的长为半径画弧,交AC于点D,连接BD,则图中阴影部分的面积为 .
三.解答题(共3小题)
13.(2024秋 灵宝市)如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=2.
(1)若∠ADC=60°,求扇形OAC(图中阴影部分)的面积;
(2)若BE=1,求弦CD的长.
14.(2024.安次区一模)(中华优秀传统文化)瓷板画(图1)是我国非物质文化遗产,可装裱或嵌入到屏风中,作观赏用.图2为其平面示意图,A,C为⊙O上的两点,连接OA、AC,AC∥BD(桌面),AB,CD分别垂直直线l于B,D两点,过点O作OE⊥BD于点E,交AC于点F.已知,AC=30cm,.
(1)求⊙O半径OA的长;
(2)求图2中阴影部分的面积.
15.(2025春 杨浦区)如图所示,大正方形ABCD的边长为4cm,小正方形ECGF的边长为2cm,扇形BCD、扇形EFG的圆心分别为点C和点F,半径分别为4cm和2cm,点E、点G分别在边BC和CD上,求阴影部分的面积.
中考核心考点 弧长及扇形的面积
参考答案与试题解析
一.选择题(共7小题)
1.(2024.海勃湾区)如图,在矩形ABCD中,AB=2,BC=4,以点D为圆心,DA的长为半径画弧,交BC于点E,交DC的延长线于点F,则图中阴影部分的面积为( )
A.4 B.2 C. D.2
【考点】扇形面积的计算;矩形的性质.
【专题】与圆有关的计算;运算能力;推理能力.
【答案】B
【分析】连接DE,利用矩形的性质以及勾股定理求出CE的长以及∠CDE的度数,进而利用图中阴影部分的面积=S扇形DEF﹣S△DEC,求出答案.
【解答】解:连接DE,
在矩形ABCD中,AB=2,BC=4,
∴CD=AB=2,AD=BC=4,∠BCD=90°,
∴DE=AD=4,
∴CE2,
∴CEDE,
∴∠EDC=30°,
∴图中阴影部分的面积=S扇形DEF﹣S△DEC
2×2
2.
故选:B.
【点评】此题主要考查了扇形面积求法以及矩形的性质等知识,正确得出CE的长以及∠CDE的度数是解题关键.
2.(2024.彭水县)如图,在正方形ABCD中,AB=1,以B为圆心,BA为半径作圆弧,交CB的延长线于点E,连结DE.则图中阴影部分的面积为( )
A. B. C. D.
【考点】扇形面积的计算;正方形的性质.
【专题】与圆有关的计算;运算能力.
【答案】D
【分析】根据S阴影=S扇形ABE+S正方形ABCD﹣S△DCE,进行计算即可得出答案,不规则图形的面积通常转化为规则图形的面积的和差.
【解答】解:在正方形ABCD中,∠ABC=90°,AB=1,
∴BE=1,∠ABE=90°,BC=CD=1,
∴BE+BC=CE=2,
∴S阴影=S扇形ABE+S正方形ABCD﹣S△DCE
,
故选:D.
【点评】本题主要考查了扇形的面积计算方法,掌握其公式是解决此题的关键.
3.(2025春 徐闻县)折扇最早出现于我国南北朝时期,《南齐书》中说:“司徒褚渊入朝,以腰扇障日.”这里的“腰扇”在《通鉴注》中的解释为折叠扇.如图,一折扇的骨柄长为21cm,折扇张开后为扇形,圆心角∠AOB为120°,则弧AB的长为( )
A.7πcm B.14πcm C.21πcm D.42πcm
【考点】弧长的计算.
【专题】与圆有关的计算;运算能力.
【答案】B
【分析】直接根据扇形弧长的求解公式,求解即可.
【解答】解:∵折扇的骨柄长为21cm,折扇张开的角度为120°,
∴弧AB的长,
故选:B.
【点评】此题考查了扇形弧长的计算,解题的关键是掌握弧长公式.
4.(2025春 宝山区)如图,已知∠ABC=90°,AB=πr,AB=2BC,半径为r的⊙O从点A出发,沿A→B→C方向滚动到点C时停止.则在此运动过程中,⊙O扫过的面积是( )
A. B.3π2 C. D.5πr2
【考点】扇形面积的计算.
【专题】平移、旋转与对称;与圆有关的计算;运算能力.
【答案】D
【分析】根据圆面积、扇形面积以及矩形面积的计算方法进行计算即可.
【解答】解:如图,⊙O扫过的面积S=S圆O+S矩形ABED+S扇形BEF+S矩形BCGF
=πr2+πr×2rπr×2r
=πr2+2πr2+πr2+πr2
=5πr2;
故选:D.
【点评】本题考查扇形面积的计算,掌握圆面积、扇形面积以及矩形面积的计算方法是正确解答的关键.
5.(2024.韶关)制作弯管时,需要先按中心线计算“展直长度”再下料.图中弯管(不计厚度)有一段圆弧,点O是这段圆弧所在圆的圆心,半径OA=90cm,圆心角∠AOB=100°,则这段弯管中的长为( )
A.50π B.60π C.90π D.100π
【考点】弧长的计算.
【专题】与圆有关的计算;运算能力.
【答案】A
【分析】直接利用弧长公式求解即可.
【解答】解:有弧长公式可得:这段弯管中的长为,
故选:A.
【点评】本题考查了弧长公式的应用,解答本题的关键是明确弧长计算公式.
6.(2024.淄川区一模)如图,在每个小正方形的边长均为1的网格图中,一段圆弧经过格点A,B,C,格点C,D的连线交于点E,则的长为( )
A. B. C. D.
【考点】弧长的计算;勾股定理的逆定理;圆周角定理.
【专题】圆的有关概念及性质;与圆有关的计算;运算能力.
【答案】A
【分析】连接AE、AC、AD,由∠ABC=90°,可知AC是直径且值为,可知∠AEC=90°,根据勾股定理逆定理可判断出△ACD是等腰直角三角形,求出∠ACE=∠CAE=45°,利用弧长公式求解即可.
【解答】解:如图所示:连接AE、AC、AD,
∵∠ABC=90°,
∴AC是直径,
∴∠ABC=∠AEC=90°,
根据网格图形可知:AC=AD,CD,
∴AC2+AD2=CD2=26,
∴△ACD是等腰直角三角形,
∴∠CAD=90°,∠ACE=45°,
∴∠EAC=45°,
∴所对的圆心角是90°,
∴的长为.
故选:A.
【点评】本题考查了勾股定理逆定理、圆周角定理及其推论、弧长的计算公式、利用网格求线段长等知识,准确地作出辅助线构造出直角三角形和正确的计算是解决本题的关键.
7.(2024.达州)如图,在△ABC中,AB=AC,以AC为直径的⊙O与AB,BC分别交于点D,E,连接AE,DE,若AB=3,∠BED=45°,则阴影部分的面积为( )
A. B. C. D.
【考点】扇形面积的计算;等腰三角形的性质;圆周角定理.
【专题】与圆有关的计算;运算能力.
【答案】A
【分析】连接OE,OD,证明S△AOD=S△AED,可得S阴影=S扇形OAD,求解∠AOD=90°,再利用扇形的面积公式计算即可.
【解答】解:连接OE,OD,
由条件可知∠AEC=90°,BE=CE,
即点E是BC的中点,
∵点O是AC的中点,
∴OE是△ABC的中位线,
∴OE∥AB,
∴S△AOD=S△AED,
∴S阴影=S扇形OAD,
∵∠AEC=90°,
∴∠AEB=90°,
∵∠BED=45°,
∴∠AED=45°,
∴∠AOD=90°,
又∵AC=AB=3,
∴,
∴,
∴,
故选:A.
【点评】本题考查的是等腰三角形的性质,圆周角定理的应用,扇形面积的计算.熟练掌握以上知识点是关键.
二.填空题(共5小题)
8.(2024.金凤区一模)“莱洛三角形”(图1)是一种特殊的三角形,它是分别以等边三角形的三个顶点为圆心,以其边长为半径作圆弧,由这三段弧组成的曲边三角形.如图2是小明画出的一个“莱洛三角形”.若该等边△ABC的边长为6,则这个“菜洛三角形”的面积是 .(结果保留根号和π)
【考点】扇形面积的计算;等边三角形的性质.
【专题】与圆有关的计算;运算能力.
【答案】.
【分析】先根据等边三角形的性质得∠A=∠B=∠C=60°,AB=BC=AC=6,再运用勾股定理算得,,观察图形得这个“菜洛三角形”的面积是3S扇形BAC﹣2S△BAC,代入数值进行计算,即可作答.
【解答】解:由条件可知∠A=∠B=∠C=60°,AB=BC=AC=6,
过点B作BH⊥AC,如图所示:
∴,
由勾股定理得BH3,
∴,
∴这个“菜洛三角形”的面积是:
;
故答案为:.
【点评】本题考查了等边三角形的性质,勾股定理,扇形面积,发现这个“菜洛三角形”的面积是3S扇形BAC﹣2S△BAC是关键.
9.(2024.韶关一模)如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A恰好落在CD边上的点G处.则图中阴影部分的面积等于 9 .
【考点】扇形面积的计算;旋转的性质;矩形的性质.
【专题】与圆有关的计算;运算能力.
【答案】9.
【分析】旋转得到BG=AB=5,勾股定理求出CG的长,利用矩形的面积减去直角三角形的面积求出阴影部分的面积即可.
【解答】解:由条件可知BG=AB=5,BE=BC=3,∠BCG=90°,
在Rt△BCG中,,
∴S阴影;
故答案为:9.
【点评】本题考查旋转的性质,矩形的性质,勾股定理,熟练掌握以上知识点是关键.
10.(2024.建邺区一模)如图,两条道路的宽分别为10m,8m,夹角∠A=∠B=120°.现修建圆弧形道路,其内侧与边界相切于点C,D,外侧与边界相切于点E,F,两弧的圆心均在直线CE上.,的长度m,n满足的数量关系为 n=m+6π .
【考点】弧长的计算.
【专题】与圆有关的计算;运算能力.
【答案】n=m+6π.
【分析】根据题意表示两条弧所对应的半径,圆心角,然后利用弧长公式计算即可.
【解答】解:设内侧弧所在圆的半径为r m,
∵两条道路的宽分别为10m,8m,
∴外侧弧所在圆的半径为r+10+8=(r+18)m,
∵∠A=∠B=120°,
∴两弧所对的圆心角n=180°﹣120°=60°,
∴内侧弧的长度m(m),
外侧弧的长度n()m,
∴n=m+6π.
故答案为:n=m+6π.
【点评】本题考查了弧长的计算,熟练掌握计算公式是解题的关键.
11.(2024.苏州一模)如图,AB是⊙O的直径,点C是⊙O上一点,点D是的中点,且∠BCD=25°,连接BC,CD.若AB=6,则的长为 π .(结果保留π)
【考点】弧长的计算;圆周角定理.
【专题】圆的有关概念及性质;与圆有关的计算;运算能力.
【答案】π.
【分析】连接OC,OD,根据圆周角定理得∠BOD=2∠BCD=50°,所以∠BOC=2∠BOD=100°,即可得∠AOC=80°,再根据弧长公式计算即可.
【解答】解:连接OC,OD,
∵∠BCD=25°,
∴∠BOD=2∠BCD=50°,
∵点D是的中点,
∴∠BOC=2∠BOD=100°,
∴∠AOC=80°,
∴的长为π.
故答案为:π.
【点评】本题考查了弧长的计算和圆周角定理,熟练掌握圆周角定理和弧长公式是解题的关键.
12.(2024.南昌二模)在△ABC中,AB=AC,∠A=45°,BC=4,以点B为圆心,BC的长为半径画弧,交AC于点D,连接BD,则图中阴影部分的面积为 .
【考点】扇形面积的计算;等腰三角形的性质.
【专题】运算能力.
【答案】.
【分析】过点D作DM⊥BC于点M,先根据等腰三角形的性质求出∠DBC的度数,再用扇形BDC的面积减去三角形BDC的面积即可解决问题.
【解答】解:过点D作DM⊥BC于点M,
∵AB=AC,∠A=45°,
∴∠ABC=∠BCD=67.5°.
又∵BC=BD,
∴∠BDC=∠BCD=67.5°,
∴∠CBD=45°.
∵DM⊥BC,BD=BC=4,
∴DM,
∴.
又∵,
∴阴影部分的面积为.
故答案为:.
【点评】本题主要考查了扇形面积的计算及等腰三角形的性质,熟知扇形的面积公式及等腰三角形的性质是解题的关键.
三.解答题(共3小题)
13.(2024秋 灵宝市)如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=2.
(1)若∠ADC=60°,求扇形OAC(图中阴影部分)的面积;
(2)若BE=1,求弦CD的长.
【考点】扇形面积的计算;勾股定理;垂径定理;圆周角定理.
【专题】与圆有关的计算;运算能力.
【答案】(1);
(2).
【分析】(1)先根据圆周角定理求出∠AOC的度数,再根据扇形面积公式求解即可;
(2)根据勾股定理和垂径定理求解即可.
【解答】解:(1)∵∠ADC=60°,
∴∠AOC=2∠ADC=2×60°=120°,
∴;
(2)OB=OC=2,BE=1,
∴OE=OB﹣BE=2﹣1=1,
又∵AB⊥CD,
在Rt△OCE中,利用勾股定理,可得,
∴.
【点评】本题考查了圆的综合,熟练运用圆周角定理,勾股定理和垂径定理是解题的关键.
14.(2024.安次区一模)(中华优秀传统文化)瓷板画(图1)是我国非物质文化遗产,可装裱或嵌入到屏风中,作观赏用.图2为其平面示意图,A,C为⊙O上的两点,连接OA、AC,AC∥BD(桌面),AB,CD分别垂直直线l于B,D两点,过点O作OE⊥BD于点E,交AC于点F.已知,AC=30cm,.
(1)求⊙O半径OA的长;
(2)求图2中阴影部分的面积.
【考点】扇形面积的计算;勾股定理;垂径定理.
【专题】与圆有关的计算;推理能力.
【答案】(1)30;
(2).
【分析】(1)先根据AC∥l,OE⊥l,可得OF⊥AC,,再根据垂径定理得,然后根据勾股定理得,即可得出答案.
(2)根据S阴=S四边形ABDC+S△AOC﹣S扇形AOC,即可求解.
【解答】解:(1)由条件可知OF⊥AC,
∵AC=30cm,
∴,
∵,由题意得,
∴,
在Rt△OAF中,由勾股定理可得:,
即⊙O的半径OA的长为30cm.
(2)连接OC,
,
,
由条件可知△OAC为等边三角形,∠AOC=60°,
(cm2),
.
【点评】本题主要考查了垂径定理,勾股定理,平行线间的距离,熟练掌握以上知识点是关键.
15.(2025春 杨浦区)如图所示,大正方形ABCD的边长为4cm,小正方形ECGF的边长为2cm,扇形BCD、扇形EFG的圆心分别为点C和点F,半径分别为4cm和2cm,点E、点G分别在边BC和CD上,求阴影部分的面积.
【考点】扇形面积的计算;正方形的性质.
【专题】运算能力.
【答案】(5π﹣4)cm2.
【分析】先求出小正方形的面积,进一步得出右下角空白部分的面积,最后用大扇形的面积减去空白部分的面积即可解决问题.
【解答】解:由题知,
小正方形EFGC的面积为:22=4(cm2).
又因为(cm2),
所以右下角空白部分的面积为(4﹣π)cm2.
又因为(cm2),
所以阴影部分的面积为:4π﹣(4﹣π)=5π﹣4(cm2).
【点评】本题主要考查了扇形面积的计算及正方形的性质,熟知扇形的面积公式及正方形的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
