【中考核心考点】2025年北师大版中考数学考前冲刺 切线长定理(含解析)
文档属性
| 名称 | 【中考核心考点】2025年北师大版中考数学考前冲刺 切线长定理(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 694.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 17:31:49 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中考核心考点 切线长定理
一.选择题(共7小题)
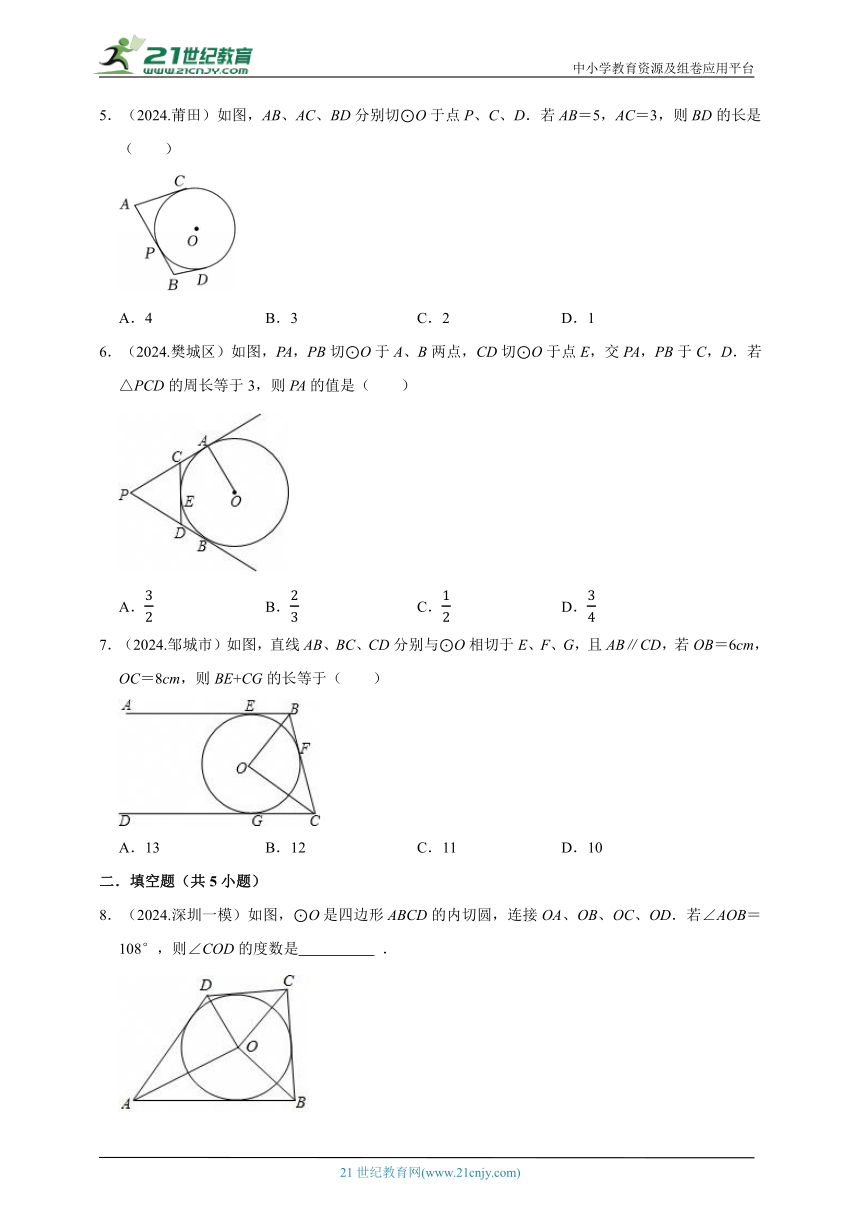
1.(2024.金东区)如图,⊙O是△ABC的内切圆,点D、E分别为边AB、AC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是( )
A.7 B.8 C.9 D.16
2.(2024.城关区)如图,PA,PB分别切⊙O于点A,B,CD切⊙O于点E,且分别交PA,PB于点C,D,若PA=6,则△PCD的周长为( )
A.5 B.7 C.12 D.10
3.(2024.江门)如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA的长为( )
A.12 B.6 C.8 D.4
4.(2024.沧州)如图,⊙O为△ABC的内切圆,AC=10,AB=8,BC=9,点D,E分别为BC,AC上的点,且DE为⊙O的切线,则△CDE的周长为( )
A.9 B.7 C.11 D.8
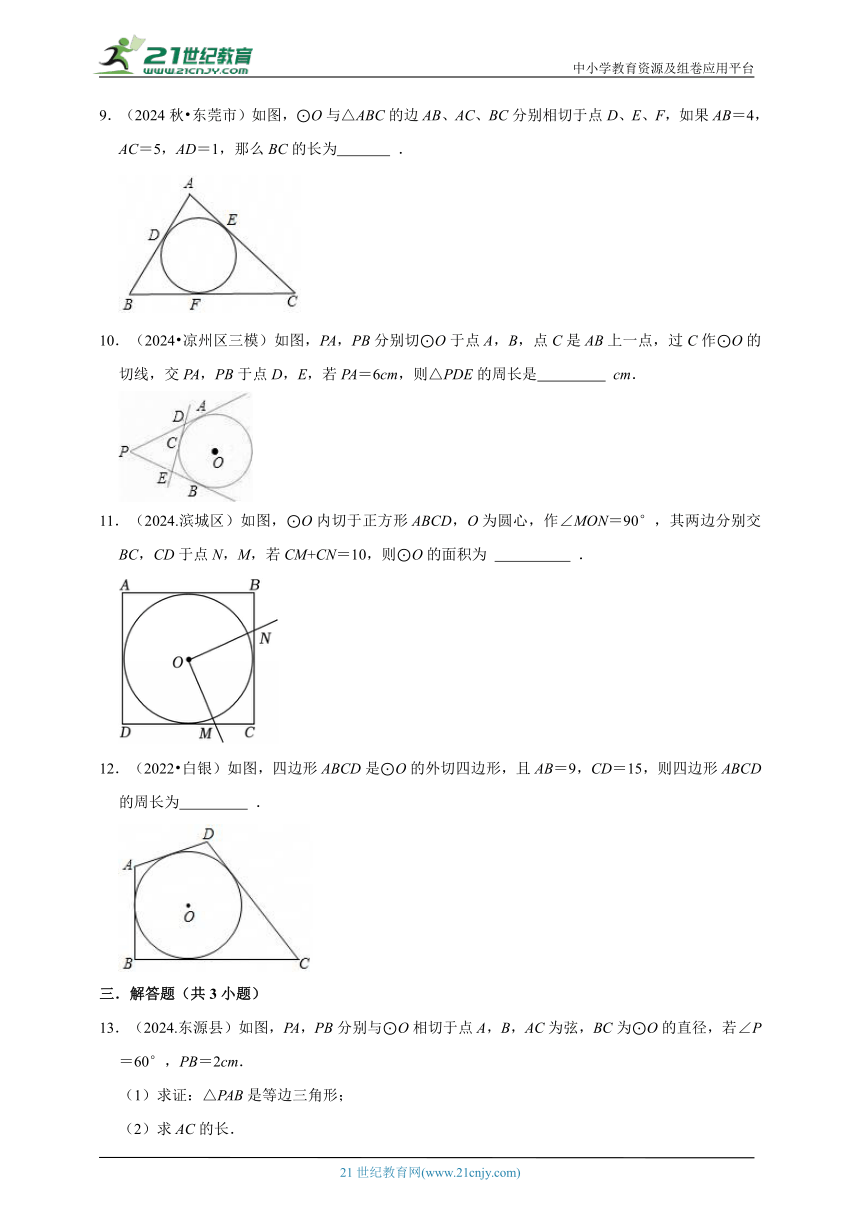
5.(2024.莆田)如图,AB、AC、BD分别切⊙O于点P、C、D.若AB=5,AC=3,则BD的长是( )
A.4 B.3 C.2 D.1
6.(2024.樊城区)如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若△PCD的周长等于3,则PA的值是( )
A. B. C. D.
7.(2024.邹城市)如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,若OB=6cm,OC=8cm,则BE+CG的长等于( )
A.13 B.12 C.11 D.10
二.填空题(共5小题)
8.(2024.深圳一模)如图,⊙O是四边形ABCD的内切圆,连接OA、OB、OC、OD.若∠AOB=108°,则∠COD的度数是 .
9.(2024秋 东莞市)如图,⊙O与△ABC的边AB、AC、BC分别相切于点D、E、F,如果AB=4,AC=5,AD=1,那么BC的长为 .
10.(2024 凉州区三模)如图,PA,PB分别切⊙O于点A,B,点C是AB上一点,过C作⊙O的切线,交PA,PB于点D,E,若PA=6cm,则△PDE的周长是 cm.
11.(2024.滨城区)如图,⊙O内切于正方形ABCD,O为圆心,作∠MON=90°,其两边分别交BC,CD于点N,M,若CM+CN=10,则⊙O的面积为 .
12.(2022 白银)如图,四边形ABCD是⊙O的外切四边形,且AB=9,CD=15,则四边形ABCD的周长为 .
三.解答题(共3小题)
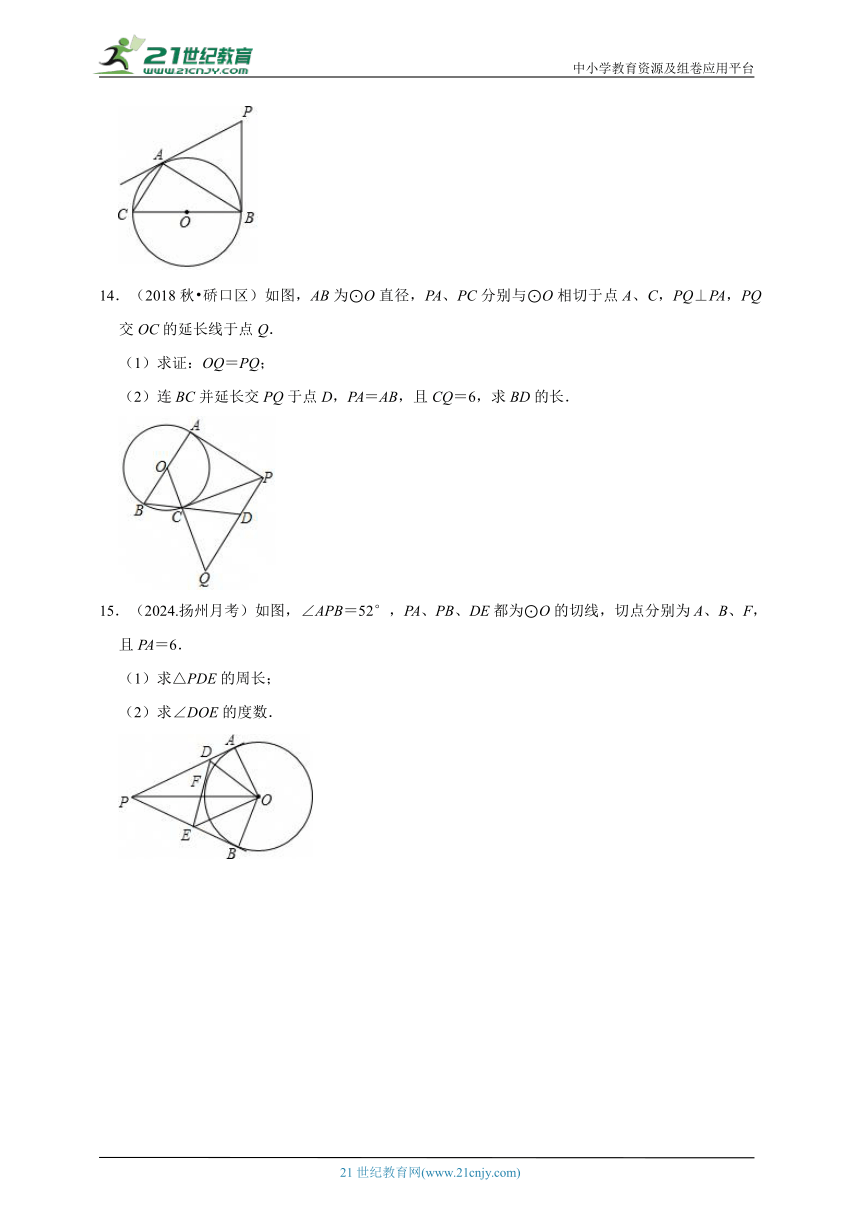
13.(2024.东源县)如图,PA,PB分别与⊙O相切于点A,B,AC为弦,BC为⊙O的直径,若∠P=60°,PB=2cm.
(1)求证:△PAB是等边三角形;
(2)求AC的长.
14.(2018秋 硚口区)如图,AB为⊙O直径,PA、PC分别与⊙O相切于点A、C,PQ⊥PA,PQ交OC的延长线于点Q.
(1)求证:OQ=PQ;
(2)连BC并延长交PQ于点D,PA=AB,且CQ=6,求BD的长.
15.(2024.扬州月考)如图,∠APB=52°,PA、PB、DE都为⊙O的切线,切点分别为A、B、F,且PA=6.
(1)求△PDE的周长;
(2)求∠DOE的度数.
中考核心考点 切线长定理
参考答案与试题解析
一.选择题(共7小题)
1.(2024.金东区)如图,⊙O是△ABC的内切圆,点D、E分别为边AB、AC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是( )
A.7 B.8 C.9 D.16
【考点】切线长定理.
【答案】A
【分析】根据切线长定理,可得BI=BG,CI=CH,DG=DF,EF=EH,则C△ADE=AD+AE+DE=AD+AE+DF+EF=AD+DG+EH+AE=AG+AH=C△ABC﹣(BG+CH+BC),据此即可求解.
【解答】解:∵AB、AC、BC、DE都和⊙O相切,
∴BI=BG,CI=CH,DG=DF,EF=EH.
∴BG+CH=BI+CI=BC=9,
∴C△ADE=AD+AE+DE=AD+AE+DF+EF=AD+DG+EH+AE=AG+AH=C△ABC﹣(BG+EH+BC)=25﹣2×9=7.
故选:A.
【点评】本题考查了切线长定理,理解定理,找出图形中存在的相等的线段是关键.
2.(2024.城关区)如图,PA,PB分别切⊙O于点A,B,CD切⊙O于点E,且分别交PA,PB于点C,D,若PA=6,则△PCD的周长为( )
A.5 B.7 C.12 D.10
【考点】切线长定理.
【专题】与圆有关的位置关系;推理能力.
【答案】C
【分析】根据切线长定理得到PB=PA=6,CA=CE,DB=DE,再根据三角形的周长公式计算,得到答案.
【解答】解:∵PA,PB分别切⊙O于点A,B,CD切⊙O于点E,PA=6,
∴PB=PA=6,CA=CE,DB=DE,
∴△PCD的周长=PC+CE+PD+DE=PC+CA+PD+DB=PA+PB=12,
故选:C.
【点评】本题考查的是切线长定理,从圆外一点引圆的两条切线,它们的切线长相等.
3.(2024.江门)如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA的长为( )
A.12 B.6 C.8 D.4
【考点】切线长定理.
【答案】B
【分析】由PA,PB分别和⊙O切于A,B两点与DE是⊙O的切线,根据切线长定理,即可得PA=PB,DA=DC,EB=EC,又由△PDE的周长为12,易求得PA+PB=12,则可求得答案.
【解答】解:∵PA,PB分别和⊙O切于A,B两点,
∴PA=PB,
∵DE是⊙O的切线,
∴DA=DC,EB=EC,
∵△PDE的周长为12,
即PD+DE+PE=PD+DC+EC+PE=PD+AD+EB+PE=PA+PB=2PA=12,
∴PA=6.
故选:B.
【点评】此题考查了切线长定理.此题难度不大,解题的关键是熟练应用切线长定理,注意数形结合思想与整体思想的应用.
4.(2024.沧州)如图,⊙O为△ABC的内切圆,AC=10,AB=8,BC=9,点D,E分别为BC,AC上的点,且DE为⊙O的切线,则△CDE的周长为( )
A.9 B.7 C.11 D.8
【考点】切线长定理.
【专题】与圆有关的位置关系.
【答案】C
【分析】设AB,AC,BC,DE和圆的切点分别是P,N,M,Q.根据切线长定理得到NC=MC,QE=DQ.所以三角形CDE的周长即是CM+CN的值,再进一步根据切线长定理由三角形ABC的三边进行求解即可.
【解答】解:设AB,AC,BC,DE和圆的切点分别是P,N,M,Q,CM=x,根据切线长定理,得
CN=CM=x,BM=BP=9﹣x,AN=AP=10﹣x.
则有9﹣x+10﹣x=8,
解得:x=5.5.
所以△CDE的周长=CD+CE+QE+DQ=2x=11.
故选:C.
【点评】此题主要是考查了切线长定理.要掌握圆中的有关定理,才能灵活解题.
5.(2024.莆田)如图,AB、AC、BD分别切⊙O于点P、C、D.若AB=5,AC=3,则BD的长是( )
A.4 B.3 C.2 D.1
【考点】切线长定理.
【专题】与圆有关的位置关系;推理能力.
【答案】C
【分析】由于AB、AC、BD是⊙O的切线,则AC=AP,BP=BD,求出BP的长即可求出BD的长.
【解答】解:∵AC、AP为⊙O的切线,
∴AC=AP=3,
∵BP、BD为⊙O的切线,
∴BP=BD,
∴BD=PB=AB﹣AP=5﹣3=2.
故选:C.
【点评】本题考查了切线长定理,两次运用切线长定理并利用等式的性质是解题的关键.
6.(2024.樊城区)如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若△PCD的周长等于3,则PA的值是( )
A. B. C. D.
【考点】切线长定理.
【答案】A
【分析】直接利用切线长定理得出AC=EC,DE=DB,PA=PB,进而求出PA的长.
【解答】解:∵PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D,
∴AC=EC,DE=DB,PA=PB
∵△PCD的周长等于3,
∴PA+PB=3,
∴PA.
故选:A.
【点评】此题主要考查了切线长定理,熟练应用切线长定理是解题关键.
7.(2024.邹城市)如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,若OB=6cm,OC=8cm,则BE+CG的长等于( )
A.13 B.12 C.11 D.10
【考点】切线长定理;勾股定理.
【专题】空间观念;运算能力;推理能力.
【答案】D
【分析】根据平行线的性质以及切线长定理,即可证明∠BOC=90°,再根据勾股定理即可求得BC的长,再结合切线长定理即可求解.
【解答】解:∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵CD、BC,AB分别与⊙O相切于G、F、E,
∴∠OBC∠ABC,∠OCB∠BCD,BE=BF,CG=CF,
∴∠OBC+∠OCB=90°,
∴∠BOC=90°,
∴BC10,
∴BE+CG=10(cm).
故选:D.
【点评】此题主要是考查了切线长定理.从圆外一点引圆的两条切线,它们的切线长相等,且圆心和这点的连线平分两条切线的夹角.
二.填空题(共5小题)
8.(2024.深圳一模)如图,⊙O是四边形ABCD的内切圆,连接OA、OB、OC、OD.若∠AOB=108°,则∠COD的度数是 72° .
【考点】切线长定理;多边形内角与外角;圆心角、弧、弦的关系.
【专题】图形的全等;与圆有关的位置关系;推理能力.
【答案】见试题解答内容
【分析】直接利用切线的性质定理结合全等三角形的判定和性质得出∠2+∠3=∠DOC=72°.
【解答】解:如图所示:连接圆心与各切点,
在Rt△DEO和Rt△DFO中,
∴Rt△DEO≌Rt△DFO(HL),
∴∠1=∠2,
同理可得:Rt△AFO≌Rt△AMO,Rt△BMO≌Rt△BNO,Rt△CEO≌Rt△CNO,
∴∠3=∠4,∠5=∠7,∠6=∠8,
∴∠5+∠6=∠7+∠8=108°,
∴2∠2+2∠3=360°﹣2×108°,
∴∠2+∠3=∠DOC=72°.
故答案为:72°.
【点评】此题主要考查了切线的性质定理、全等三角形的判定和性质,正确应用切线的性质定理是解题关键.
9.(2024秋 东莞市)如图,⊙O与△ABC的边AB、AC、BC分别相切于点D、E、F,如果AB=4,AC=5,AD=1,那么BC的长为 7 .
【考点】切线长定理.
【专题】计算题.
【答案】见试题解答内容
【分析】由切线长定理得AD=AE,BD=BF,CE=CF,根据已知条件,先求出BD,即BF的长,再求出CE=4,即CF的长,求和即可.
【解答】解:∵AB、AC、BC都是⊙O的切线,
∴AD=AE,BD=BF,CE=CF,
∵AB=4,AC=5,AD=1,
∴AE=1,BD=3,CE=CF=4,
∴BC=BF+CF=3+4=7.
【点评】本题考查的是切线长定理,分析图形时关键是要仔细探索,找出图形的各对相等切线长.
10.(2024 凉州区三模)如图,PA,PB分别切⊙O于点A,B,点C是AB上一点,过C作⊙O的切线,交PA,PB于点D,E,若PA=6cm,则△PDE的周长是 12 cm.
【考点】切线长定理.
【答案】见试题解答内容
【分析】根据切线长定理将△PDE的周长转化为切线长即可.
【解答】解:根据切线长定理得:AD=CD,BE=CE,PA=PB,则△PDE的周长=2PA=12cm.
【点评】此题主要考查切线长定理的运用能力.
11.(2024.滨城区)如图,⊙O内切于正方形ABCD,O为圆心,作∠MON=90°,其两边分别交BC,CD于点N,M,若CM+CN=10,则⊙O的面积为 25π .
【考点】切线长定理;正方形的性质;圆心角、弧、弦的关系.
【专题】计算题;运算能力;推理能力.
【答案】25π
【分析】设⊙O与正方形ABCD的边CD切于E,与BC切于F,连接OE,OF,得到四边形OECF是正方形,求得CF=CE=OE=OF,∠OEM=∠OFN=∠EOF=90°,根据全等三角形的性质得到EM=NF,得到OE=5,进而求出⊙O的面积.
【解答】解:设⊙O与正方形ABCD的边CD切于E,与BC切于F,
连接OE,OF,
则四边形OECF是正方形,
∴CF=CE=OE=OF,∠OEM=∠OFN=∠EOF=90°,
∵∠MON=90°,
∴∠EOM=∠FON,
∴△OEM≌△OFN(ASA),
∴EM=NF,
∴CM+CN=CE+CF=10,
∴OE=5,
∴⊙O的面积为25π,
故答案为:25π.
【点评】本题考查了切线的性质,正方形的判定和性质,全等三角形的判定和性质,正确的作出辅助线是解题的关键.
12.(2022 白银)如图,四边形ABCD是⊙O的外切四边形,且AB=9,CD=15,则四边形ABCD的周长为 48 .
【考点】切线长定理.
【专题】与圆有关的位置关系;推理能力.
【答案】48.
【分析】根据切线长定理得到AE=AH,BE=BF,CF=CG,DH=DG,得到AD+BC=AB+CD=24,根据四边形的周长公式计算,得到答案.
【解答】解:∵四边形ABCD是⊙O的外切四边形,
∴AE=AH,BE=BF,CF=CG,DH=DG,
∴AD+BC=AB+CD=24,
∴四边形ABCD的周长=AD+BC+AB+CD=24+24=48,
故答案为:48.
【点评】本题考查的是切线长定理,掌握从圆外一点引圆的两条切线,它们的切线长相等是解题的关键.
三.解答题(共3小题)
13.(2024.东源县)如图,PA,PB分别与⊙O相切于点A,B,AC为弦,BC为⊙O的直径,若∠P=60°,PB=2cm.
(1)求证:△PAB是等边三角形;
(2)求AC的长.
【考点】切线长定理;解直角三角形的应用.
【专题】等腰三角形与直角三角形;圆的有关概念及性质;与圆有关的位置关系;解直角三角形及其应用;推理能力.
【答案】见试题解答内容
【分析】(1)由切线长定理可得PA=PB,且∠P=60°,可得△PAB是等边三角形;
(2)由等边三角形的性质可得PB=AB=2cm,∠PBA=60°,由圆周角定理和切线的性质可得∠CAB=90°,∠PBC=90°,由锐角三角函数可求AC的长,
【解答】解:(1)∵PA,PB分别与⊙O相切于点A,B,
∴PA=PB,且∠P=60°,
∴△PAB是等边三角形;
(2)∵△PAB是等边三角形;
∴PB=AB=2cm,∠PBA=60°,
∵BC是直径,PB是⊙O切线,
∴∠CAB=90°,∠PBC=90°,
∴∠ABC=30°,
∴tan∠ABC,
∴AC=2cm.
【点评】本题考查了切线长定理,切线的性质,圆周角定理,锐角三角函数,等边三角形的判定和性质,灵活运用这些性质是本题的关键.
14.(2018秋 硚口区)如图,AB为⊙O直径,PA、PC分别与⊙O相切于点A、C,PQ⊥PA,PQ交OC的延长线于点Q.
(1)求证:OQ=PQ;
(2)连BC并延长交PQ于点D,PA=AB,且CQ=6,求BD的长.
【考点】切线长定理;勾股定理;圆周角定理;切线的性质.
【专题】圆的有关概念及性质.
【答案】见试题解答内容
【分析】(1)欲证明OQ=PQ,只要证明∠QOP=∠QPO即可;
(2)设OA=r.在Rt△PCQ中,利用勾股定理构建方程求出r,再证明四边形OPDB是平行四边形,求出OP即可解决问题;
【解答】(1)证明:连接OP.
∵PA、PC分别与⊙O相切于点A,C,
∴PA=PC,OA⊥PA,
∵OA=OC,OP=OP,
∴△OPA≌△OPC(SSS),
∴∠AOP=∠POC,
∵QP⊥PA,
∴QP∥BA,
∴∠QPO=∠AOP,
∴∠QOP=∠QPO,
∴OQ=PQ.
(2)设OA=r.
∵OB=OC,
∴∠OBC=∠OCB,
∵OB∥QD,
∴∠QDC=∠B,
∵∠OCB=∠QCD,
∴∠QCD=∠QDC,
∴QC=QD=6,∵QO=QP,
∴OC=DP=r,
∵PC是⊙O的切线,
∴OC⊥PC,
∴∠OCP=∠PCQ=90°,
在Rt△PCQ中,∵PQ2=PC2+QC2,
∴(6+r)2=62+(2r)2,
r=4或0(舍弃),
∴OP4,
∵OB=PD,OB∥PD,
∴四边形OBDP是平行四边形,
∴BD=OP=4.
【点评】本题考查切线长定理,全等三角形的判定和性质,勾股定理,平行四边形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数构建方程解决问题,属于中考常考题型.
15.(2024.扬州月考)如图,∠APB=52°,PA、PB、DE都为⊙O的切线,切点分别为A、B、F,且PA=6.
(1)求△PDE的周长;
(2)求∠DOE的度数.
【考点】切线长定理.
【答案】见试题解答内容
【分析】(1)根据切线长定理得到DA=DF,EB=EF,PA=PB=6,于是得到DE=DA+EB,即可得到结论;
(2)根据切线的性质得到OB⊥PB,OA⊥PA,∠BOE=∠FOE∠BOF,∠FOD=∠AOD∠AOF,根据四边形的内角和得到∠AOB=360°﹣90°﹣90°﹣52°=128°,即可得到结论.
【解答】解:(1)∵PA、PB、DE都为⊙O的切线,
∴DA=DF,EB=EF,PA=PB=6,
∴DE=DA+EB,
∴PE+PD+DE=PA+PB=12,
即△PDE的周长为12;
(2)连接OF,
∵PA、PB、DE分别切⊙O于A、B、F三点,
∴OB⊥PB,OA⊥PA,∠BOE=∠FOE∠BOF,∠FOD=∠AOD∠AOF,
∵∠APB=52°,
∴∠AOB=360°﹣90°﹣90°﹣52°=128°,
∴∠DOE=∠FOE+∠FOD(∠BOF+∠AOF)∠BOA=64°.
【点评】主要考查了切线的性质、切线长定理、勾股定理等几何知识点的应用问题;解题的关键是作辅助线,灵活运用有关定理来分析、判断.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考核心考点 切线长定理
一.选择题(共7小题)
1.(2024.金东区)如图,⊙O是△ABC的内切圆,点D、E分别为边AB、AC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是( )
A.7 B.8 C.9 D.16
2.(2024.城关区)如图,PA,PB分别切⊙O于点A,B,CD切⊙O于点E,且分别交PA,PB于点C,D,若PA=6,则△PCD的周长为( )
A.5 B.7 C.12 D.10
3.(2024.江门)如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA的长为( )
A.12 B.6 C.8 D.4
4.(2024.沧州)如图,⊙O为△ABC的内切圆,AC=10,AB=8,BC=9,点D,E分别为BC,AC上的点,且DE为⊙O的切线,则△CDE的周长为( )
A.9 B.7 C.11 D.8
5.(2024.莆田)如图,AB、AC、BD分别切⊙O于点P、C、D.若AB=5,AC=3,则BD的长是( )
A.4 B.3 C.2 D.1
6.(2024.樊城区)如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若△PCD的周长等于3,则PA的值是( )
A. B. C. D.
7.(2024.邹城市)如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,若OB=6cm,OC=8cm,则BE+CG的长等于( )
A.13 B.12 C.11 D.10
二.填空题(共5小题)
8.(2024.深圳一模)如图,⊙O是四边形ABCD的内切圆,连接OA、OB、OC、OD.若∠AOB=108°,则∠COD的度数是 .
9.(2024秋 东莞市)如图,⊙O与△ABC的边AB、AC、BC分别相切于点D、E、F,如果AB=4,AC=5,AD=1,那么BC的长为 .
10.(2024 凉州区三模)如图,PA,PB分别切⊙O于点A,B,点C是AB上一点,过C作⊙O的切线,交PA,PB于点D,E,若PA=6cm,则△PDE的周长是 cm.
11.(2024.滨城区)如图,⊙O内切于正方形ABCD,O为圆心,作∠MON=90°,其两边分别交BC,CD于点N,M,若CM+CN=10,则⊙O的面积为 .
12.(2022 白银)如图,四边形ABCD是⊙O的外切四边形,且AB=9,CD=15,则四边形ABCD的周长为 .
三.解答题(共3小题)
13.(2024.东源县)如图,PA,PB分别与⊙O相切于点A,B,AC为弦,BC为⊙O的直径,若∠P=60°,PB=2cm.
(1)求证:△PAB是等边三角形;
(2)求AC的长.
14.(2018秋 硚口区)如图,AB为⊙O直径,PA、PC分别与⊙O相切于点A、C,PQ⊥PA,PQ交OC的延长线于点Q.
(1)求证:OQ=PQ;
(2)连BC并延长交PQ于点D,PA=AB,且CQ=6,求BD的长.
15.(2024.扬州月考)如图,∠APB=52°,PA、PB、DE都为⊙O的切线,切点分别为A、B、F,且PA=6.
(1)求△PDE的周长;
(2)求∠DOE的度数.
中考核心考点 切线长定理
参考答案与试题解析
一.选择题(共7小题)
1.(2024.金东区)如图,⊙O是△ABC的内切圆,点D、E分别为边AB、AC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是( )
A.7 B.8 C.9 D.16
【考点】切线长定理.
【答案】A
【分析】根据切线长定理,可得BI=BG,CI=CH,DG=DF,EF=EH,则C△ADE=AD+AE+DE=AD+AE+DF+EF=AD+DG+EH+AE=AG+AH=C△ABC﹣(BG+CH+BC),据此即可求解.
【解答】解:∵AB、AC、BC、DE都和⊙O相切,
∴BI=BG,CI=CH,DG=DF,EF=EH.
∴BG+CH=BI+CI=BC=9,
∴C△ADE=AD+AE+DE=AD+AE+DF+EF=AD+DG+EH+AE=AG+AH=C△ABC﹣(BG+EH+BC)=25﹣2×9=7.
故选:A.
【点评】本题考查了切线长定理,理解定理,找出图形中存在的相等的线段是关键.
2.(2024.城关区)如图,PA,PB分别切⊙O于点A,B,CD切⊙O于点E,且分别交PA,PB于点C,D,若PA=6,则△PCD的周长为( )
A.5 B.7 C.12 D.10
【考点】切线长定理.
【专题】与圆有关的位置关系;推理能力.
【答案】C
【分析】根据切线长定理得到PB=PA=6,CA=CE,DB=DE,再根据三角形的周长公式计算,得到答案.
【解答】解:∵PA,PB分别切⊙O于点A,B,CD切⊙O于点E,PA=6,
∴PB=PA=6,CA=CE,DB=DE,
∴△PCD的周长=PC+CE+PD+DE=PC+CA+PD+DB=PA+PB=12,
故选:C.
【点评】本题考查的是切线长定理,从圆外一点引圆的两条切线,它们的切线长相等.
3.(2024.江门)如图所示,P是⊙O外一点,PA,PB分别和⊙O切于A,B两点,C是上任意一点,过C作⊙O的切线分别交PA,PB于D,E.若△PDE的周长为12,则PA的长为( )
A.12 B.6 C.8 D.4
【考点】切线长定理.
【答案】B
【分析】由PA,PB分别和⊙O切于A,B两点与DE是⊙O的切线,根据切线长定理,即可得PA=PB,DA=DC,EB=EC,又由△PDE的周长为12,易求得PA+PB=12,则可求得答案.
【解答】解:∵PA,PB分别和⊙O切于A,B两点,
∴PA=PB,
∵DE是⊙O的切线,
∴DA=DC,EB=EC,
∵△PDE的周长为12,
即PD+DE+PE=PD+DC+EC+PE=PD+AD+EB+PE=PA+PB=2PA=12,
∴PA=6.
故选:B.
【点评】此题考查了切线长定理.此题难度不大,解题的关键是熟练应用切线长定理,注意数形结合思想与整体思想的应用.
4.(2024.沧州)如图,⊙O为△ABC的内切圆,AC=10,AB=8,BC=9,点D,E分别为BC,AC上的点,且DE为⊙O的切线,则△CDE的周长为( )
A.9 B.7 C.11 D.8
【考点】切线长定理.
【专题】与圆有关的位置关系.
【答案】C
【分析】设AB,AC,BC,DE和圆的切点分别是P,N,M,Q.根据切线长定理得到NC=MC,QE=DQ.所以三角形CDE的周长即是CM+CN的值,再进一步根据切线长定理由三角形ABC的三边进行求解即可.
【解答】解:设AB,AC,BC,DE和圆的切点分别是P,N,M,Q,CM=x,根据切线长定理,得
CN=CM=x,BM=BP=9﹣x,AN=AP=10﹣x.
则有9﹣x+10﹣x=8,
解得:x=5.5.
所以△CDE的周长=CD+CE+QE+DQ=2x=11.
故选:C.
【点评】此题主要是考查了切线长定理.要掌握圆中的有关定理,才能灵活解题.
5.(2024.莆田)如图,AB、AC、BD分别切⊙O于点P、C、D.若AB=5,AC=3,则BD的长是( )
A.4 B.3 C.2 D.1
【考点】切线长定理.
【专题】与圆有关的位置关系;推理能力.
【答案】C
【分析】由于AB、AC、BD是⊙O的切线,则AC=AP,BP=BD,求出BP的长即可求出BD的长.
【解答】解:∵AC、AP为⊙O的切线,
∴AC=AP=3,
∵BP、BD为⊙O的切线,
∴BP=BD,
∴BD=PB=AB﹣AP=5﹣3=2.
故选:C.
【点评】本题考查了切线长定理,两次运用切线长定理并利用等式的性质是解题的关键.
6.(2024.樊城区)如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若△PCD的周长等于3,则PA的值是( )
A. B. C. D.
【考点】切线长定理.
【答案】A
【分析】直接利用切线长定理得出AC=EC,DE=DB,PA=PB,进而求出PA的长.
【解答】解:∵PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D,
∴AC=EC,DE=DB,PA=PB
∵△PCD的周长等于3,
∴PA+PB=3,
∴PA.
故选:A.
【点评】此题主要考查了切线长定理,熟练应用切线长定理是解题关键.
7.(2024.邹城市)如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,若OB=6cm,OC=8cm,则BE+CG的长等于( )
A.13 B.12 C.11 D.10
【考点】切线长定理;勾股定理.
【专题】空间观念;运算能力;推理能力.
【答案】D
【分析】根据平行线的性质以及切线长定理,即可证明∠BOC=90°,再根据勾股定理即可求得BC的长,再结合切线长定理即可求解.
【解答】解:∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵CD、BC,AB分别与⊙O相切于G、F、E,
∴∠OBC∠ABC,∠OCB∠BCD,BE=BF,CG=CF,
∴∠OBC+∠OCB=90°,
∴∠BOC=90°,
∴BC10,
∴BE+CG=10(cm).
故选:D.
【点评】此题主要是考查了切线长定理.从圆外一点引圆的两条切线,它们的切线长相等,且圆心和这点的连线平分两条切线的夹角.
二.填空题(共5小题)
8.(2024.深圳一模)如图,⊙O是四边形ABCD的内切圆,连接OA、OB、OC、OD.若∠AOB=108°,则∠COD的度数是 72° .
【考点】切线长定理;多边形内角与外角;圆心角、弧、弦的关系.
【专题】图形的全等;与圆有关的位置关系;推理能力.
【答案】见试题解答内容
【分析】直接利用切线的性质定理结合全等三角形的判定和性质得出∠2+∠3=∠DOC=72°.
【解答】解:如图所示:连接圆心与各切点,
在Rt△DEO和Rt△DFO中,
∴Rt△DEO≌Rt△DFO(HL),
∴∠1=∠2,
同理可得:Rt△AFO≌Rt△AMO,Rt△BMO≌Rt△BNO,Rt△CEO≌Rt△CNO,
∴∠3=∠4,∠5=∠7,∠6=∠8,
∴∠5+∠6=∠7+∠8=108°,
∴2∠2+2∠3=360°﹣2×108°,
∴∠2+∠3=∠DOC=72°.
故答案为:72°.
【点评】此题主要考查了切线的性质定理、全等三角形的判定和性质,正确应用切线的性质定理是解题关键.
9.(2024秋 东莞市)如图,⊙O与△ABC的边AB、AC、BC分别相切于点D、E、F,如果AB=4,AC=5,AD=1,那么BC的长为 7 .
【考点】切线长定理.
【专题】计算题.
【答案】见试题解答内容
【分析】由切线长定理得AD=AE,BD=BF,CE=CF,根据已知条件,先求出BD,即BF的长,再求出CE=4,即CF的长,求和即可.
【解答】解:∵AB、AC、BC都是⊙O的切线,
∴AD=AE,BD=BF,CE=CF,
∵AB=4,AC=5,AD=1,
∴AE=1,BD=3,CE=CF=4,
∴BC=BF+CF=3+4=7.
【点评】本题考查的是切线长定理,分析图形时关键是要仔细探索,找出图形的各对相等切线长.
10.(2024 凉州区三模)如图,PA,PB分别切⊙O于点A,B,点C是AB上一点,过C作⊙O的切线,交PA,PB于点D,E,若PA=6cm,则△PDE的周长是 12 cm.
【考点】切线长定理.
【答案】见试题解答内容
【分析】根据切线长定理将△PDE的周长转化为切线长即可.
【解答】解:根据切线长定理得:AD=CD,BE=CE,PA=PB,则△PDE的周长=2PA=12cm.
【点评】此题主要考查切线长定理的运用能力.
11.(2024.滨城区)如图,⊙O内切于正方形ABCD,O为圆心,作∠MON=90°,其两边分别交BC,CD于点N,M,若CM+CN=10,则⊙O的面积为 25π .
【考点】切线长定理;正方形的性质;圆心角、弧、弦的关系.
【专题】计算题;运算能力;推理能力.
【答案】25π
【分析】设⊙O与正方形ABCD的边CD切于E,与BC切于F,连接OE,OF,得到四边形OECF是正方形,求得CF=CE=OE=OF,∠OEM=∠OFN=∠EOF=90°,根据全等三角形的性质得到EM=NF,得到OE=5,进而求出⊙O的面积.
【解答】解:设⊙O与正方形ABCD的边CD切于E,与BC切于F,
连接OE,OF,
则四边形OECF是正方形,
∴CF=CE=OE=OF,∠OEM=∠OFN=∠EOF=90°,
∵∠MON=90°,
∴∠EOM=∠FON,
∴△OEM≌△OFN(ASA),
∴EM=NF,
∴CM+CN=CE+CF=10,
∴OE=5,
∴⊙O的面积为25π,
故答案为:25π.
【点评】本题考查了切线的性质,正方形的判定和性质,全等三角形的判定和性质,正确的作出辅助线是解题的关键.
12.(2022 白银)如图,四边形ABCD是⊙O的外切四边形,且AB=9,CD=15,则四边形ABCD的周长为 48 .
【考点】切线长定理.
【专题】与圆有关的位置关系;推理能力.
【答案】48.
【分析】根据切线长定理得到AE=AH,BE=BF,CF=CG,DH=DG,得到AD+BC=AB+CD=24,根据四边形的周长公式计算,得到答案.
【解答】解:∵四边形ABCD是⊙O的外切四边形,
∴AE=AH,BE=BF,CF=CG,DH=DG,
∴AD+BC=AB+CD=24,
∴四边形ABCD的周长=AD+BC+AB+CD=24+24=48,
故答案为:48.
【点评】本题考查的是切线长定理,掌握从圆外一点引圆的两条切线,它们的切线长相等是解题的关键.
三.解答题(共3小题)
13.(2024.东源县)如图,PA,PB分别与⊙O相切于点A,B,AC为弦,BC为⊙O的直径,若∠P=60°,PB=2cm.
(1)求证:△PAB是等边三角形;
(2)求AC的长.
【考点】切线长定理;解直角三角形的应用.
【专题】等腰三角形与直角三角形;圆的有关概念及性质;与圆有关的位置关系;解直角三角形及其应用;推理能力.
【答案】见试题解答内容
【分析】(1)由切线长定理可得PA=PB,且∠P=60°,可得△PAB是等边三角形;
(2)由等边三角形的性质可得PB=AB=2cm,∠PBA=60°,由圆周角定理和切线的性质可得∠CAB=90°,∠PBC=90°,由锐角三角函数可求AC的长,
【解答】解:(1)∵PA,PB分别与⊙O相切于点A,B,
∴PA=PB,且∠P=60°,
∴△PAB是等边三角形;
(2)∵△PAB是等边三角形;
∴PB=AB=2cm,∠PBA=60°,
∵BC是直径,PB是⊙O切线,
∴∠CAB=90°,∠PBC=90°,
∴∠ABC=30°,
∴tan∠ABC,
∴AC=2cm.
【点评】本题考查了切线长定理,切线的性质,圆周角定理,锐角三角函数,等边三角形的判定和性质,灵活运用这些性质是本题的关键.
14.(2018秋 硚口区)如图,AB为⊙O直径,PA、PC分别与⊙O相切于点A、C,PQ⊥PA,PQ交OC的延长线于点Q.
(1)求证:OQ=PQ;
(2)连BC并延长交PQ于点D,PA=AB,且CQ=6,求BD的长.
【考点】切线长定理;勾股定理;圆周角定理;切线的性质.
【专题】圆的有关概念及性质.
【答案】见试题解答内容
【分析】(1)欲证明OQ=PQ,只要证明∠QOP=∠QPO即可;
(2)设OA=r.在Rt△PCQ中,利用勾股定理构建方程求出r,再证明四边形OPDB是平行四边形,求出OP即可解决问题;
【解答】(1)证明:连接OP.
∵PA、PC分别与⊙O相切于点A,C,
∴PA=PC,OA⊥PA,
∵OA=OC,OP=OP,
∴△OPA≌△OPC(SSS),
∴∠AOP=∠POC,
∵QP⊥PA,
∴QP∥BA,
∴∠QPO=∠AOP,
∴∠QOP=∠QPO,
∴OQ=PQ.
(2)设OA=r.
∵OB=OC,
∴∠OBC=∠OCB,
∵OB∥QD,
∴∠QDC=∠B,
∵∠OCB=∠QCD,
∴∠QCD=∠QDC,
∴QC=QD=6,∵QO=QP,
∴OC=DP=r,
∵PC是⊙O的切线,
∴OC⊥PC,
∴∠OCP=∠PCQ=90°,
在Rt△PCQ中,∵PQ2=PC2+QC2,
∴(6+r)2=62+(2r)2,
r=4或0(舍弃),
∴OP4,
∵OB=PD,OB∥PD,
∴四边形OBDP是平行四边形,
∴BD=OP=4.
【点评】本题考查切线长定理,全等三角形的判定和性质,勾股定理,平行四边形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数构建方程解决问题,属于中考常考题型.
15.(2024.扬州月考)如图,∠APB=52°,PA、PB、DE都为⊙O的切线,切点分别为A、B、F,且PA=6.
(1)求△PDE的周长;
(2)求∠DOE的度数.
【考点】切线长定理.
【答案】见试题解答内容
【分析】(1)根据切线长定理得到DA=DF,EB=EF,PA=PB=6,于是得到DE=DA+EB,即可得到结论;
(2)根据切线的性质得到OB⊥PB,OA⊥PA,∠BOE=∠FOE∠BOF,∠FOD=∠AOD∠AOF,根据四边形的内角和得到∠AOB=360°﹣90°﹣90°﹣52°=128°,即可得到结论.
【解答】解:(1)∵PA、PB、DE都为⊙O的切线,
∴DA=DF,EB=EF,PA=PB=6,
∴DE=DA+EB,
∴PE+PD+DE=PA+PB=12,
即△PDE的周长为12;
(2)连接OF,
∵PA、PB、DE分别切⊙O于A、B、F三点,
∴OB⊥PB,OA⊥PA,∠BOE=∠FOE∠BOF,∠FOD=∠AOD∠AOF,
∵∠APB=52°,
∴∠AOB=360°﹣90°﹣90°﹣52°=128°,
∴∠DOE=∠FOE+∠FOD(∠BOF+∠AOF)∠BOA=64°.
【点评】主要考查了切线的性质、切线长定理、勾股定理等几何知识点的应用问题;解题的关键是作辅助线,灵活运用有关定理来分析、判断.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
