【中考核心考点】2025年北师大版中考数学考前冲刺 确定圆的条件(含解析)
文档属性
| 名称 | 【中考核心考点】2025年北师大版中考数学考前冲刺 确定圆的条件(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 17:39:29 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中考核心考点 确定圆的条件
一.选择题(共7小题)
1.(2024秋 海港区)如图,⊙O中,弦AB的长为,点C在⊙O上,OC⊥AB,∠ABC=30°,⊙O所在的平面内有一点P,若OP=2,则点P与⊙O的位置关系是( )
A.点P在⊙O上 B.点P在⊙O内 C.点P在⊙O外 D.无法确定
2.(2024秋 定兴县)已知⊙O的半径为9,点A在⊙O内,则OA的长可能为( )
A.13 B.11 C.9 D.7
3.(2024.汕头一模)如图,⊙O是△CDB的外接圆,AB为直径,若∠ABC=10°,则∠BDC的度数是( )
A.90° B.80° C.70° D.60°
4.(2024秋 裕安区)如图,在平面直角坐标系中,直线y=﹣x﹣4与x轴,y轴分别交于A,B两点,C,D是半径为2的⊙O上两动点,且,P为弦CD的中点,Q为线段AB的中点,当C,D两点在圆上运动时,PQ的最小值是( )
A. B.2 C.2 D.1
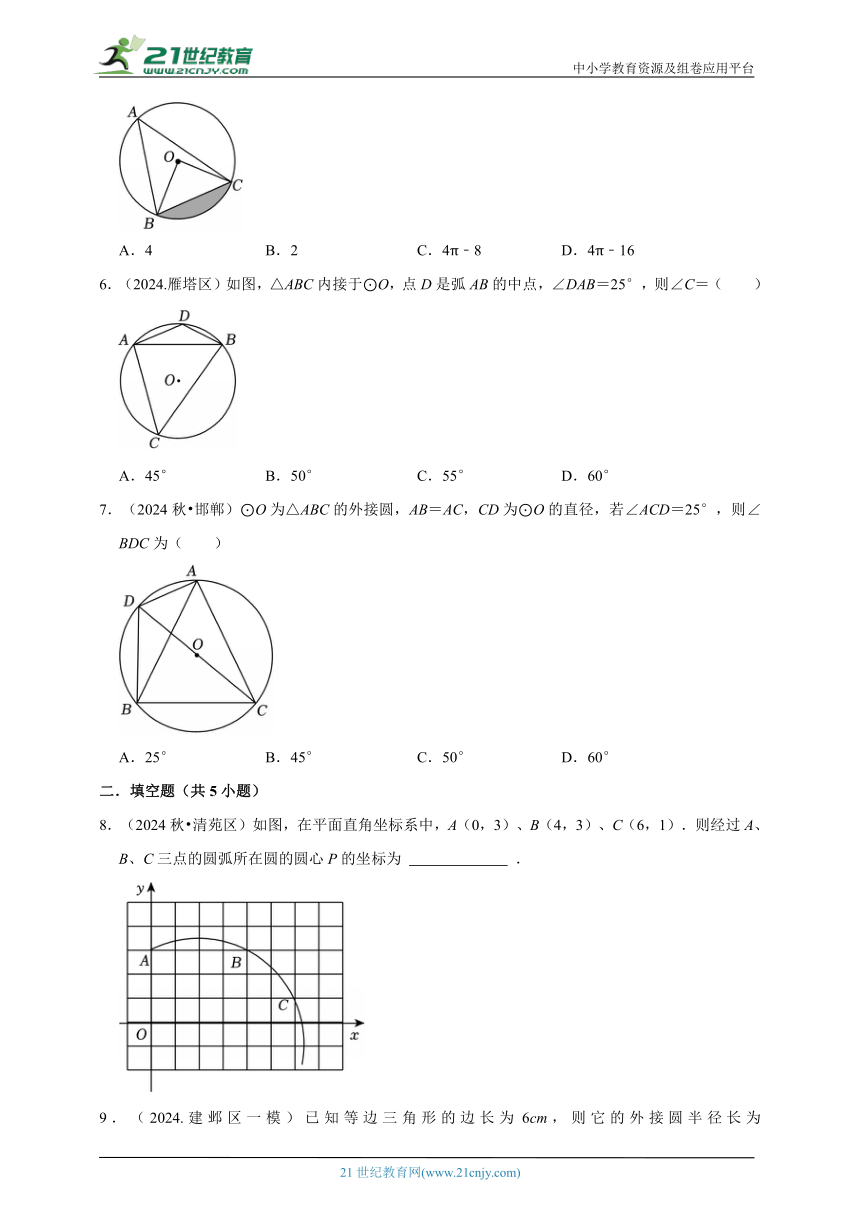
5.(2024秋 新市区)如图,△ABC内接于⊙O,若∠A=45°,⊙O的半径r=4,则阴影部分的面积为( )
A.4 B.2 C.4π﹣8 D.4π﹣16
6.(2024.雁塔区)如图,△ABC内接于⊙O,点D是弧AB的中点,∠DAB=25°,则∠C=( )
A.45° B.50° C.55° D.60°
7.(2024秋 邯郸)⊙O为△ABC的外接圆,AB=AC,CD为⊙O的直径,若∠ACD=25°,则∠BDC为( )
A.25° B.45° C.50° D.60°
二.填空题(共5小题)
8.(2024秋 清苑区)如图,在平面直角坐标系中,A(0,3)、B(4,3)、C(6,1).则经过A、B、C三点的圆弧所在圆的圆心P的坐标为 .
9.(2024.建邺区一模)已知等边三角形的边长为6cm,则它的外接圆半径长为 cm.
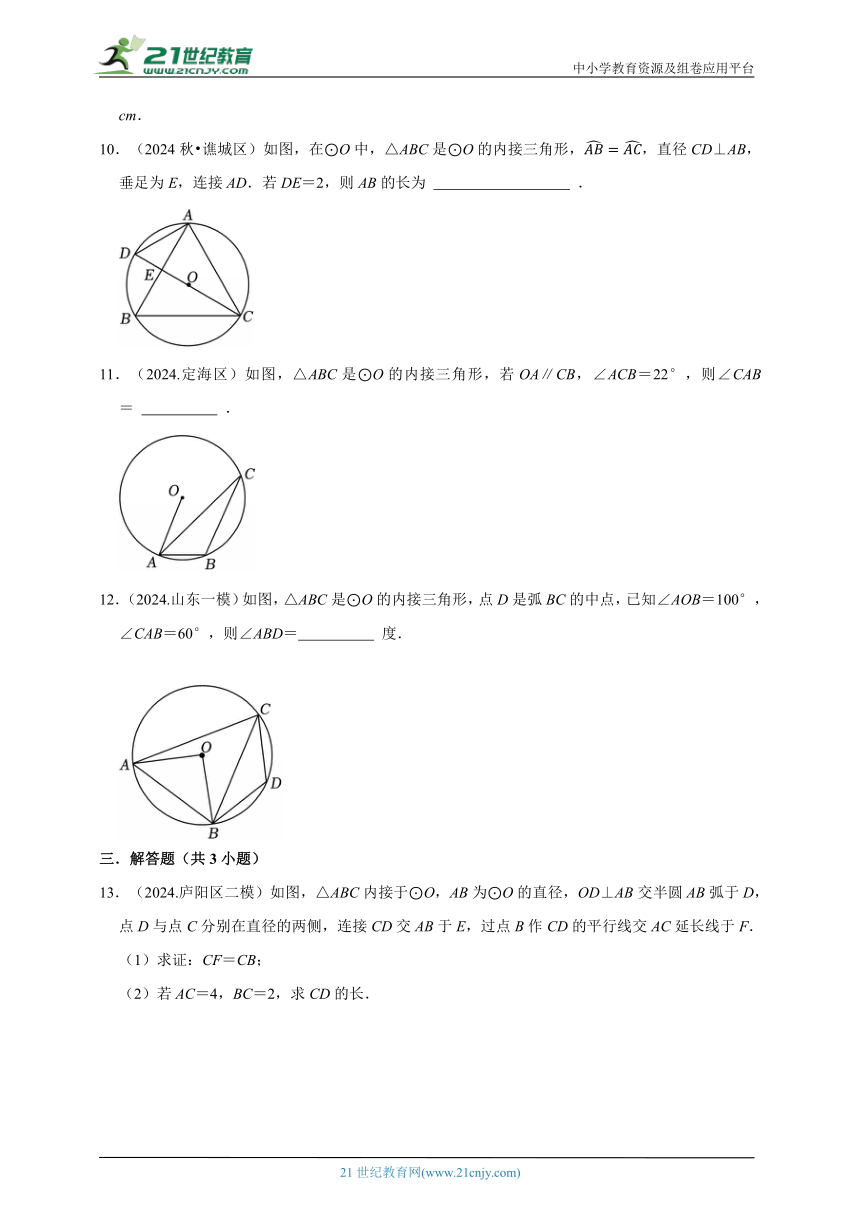
10.(2024秋 谯城区)如图,在⊙O中,△ABC是⊙O的内接三角形,,直径CD⊥AB,垂足为E,连接AD.若DE=2,则AB的长为 .
11.(2024.定海区)如图,△ABC是⊙O的内接三角形,若OA∥CB,∠ACB=22°,则∠CAB= .
12.(2024.山东一模)如图,△ABC是⊙O的内接三角形,点D是弧BC的中点,已知∠AOB=100°,∠CAB=60°,则∠ABD= 度.
三.解答题(共3小题)
13.(2024.庐阳区二模)如图,△ABC内接于⊙O,AB为⊙O的直径,OD⊥AB交半圆AB弧于D,点D与点C分别在直径的两侧,连接CD交AB于E,过点B作CD的平行线交AC延长线于F.
(1)求证:CF=CB;
(2)若AC=4,BC=2,求CD的长.
14.(2024.庆元县一模)如图,三角形ABC内接于⊙O,AB=AC,连结BO并延长交AC于点E,交⊙O于点D,连结AO,AD,CD.
(1)求证:∠ABC=∠ADB;
(2)猜想OA与CD的位置关系,并说明理由;
(3)若,求AE的长.
15.(2024.张家口一模)如图,AB是半圆O的直径,点C是半圆O上一点(不含端点),连接AC,OC,BC,在OC右侧作∠OCD=∠OCA,DC=AC.
(1)判断点D与半圆O所在圆的位置关系,并说明理由.
(2)连接DB并延长,与过点C的切线交于点E.
①求∠E的度数;
②若AB=10,∠CDB=30°,求与线段BD的长度,并比较大小.
中考核心考点 确定圆的条件
参考答案与试题解析
一.选择题(共7小题)
1.(2024秋 海港区)如图,⊙O中,弦AB的长为,点C在⊙O上,OC⊥AB,∠ABC=30°,⊙O所在的平面内有一点P,若OP=2,则点P与⊙O的位置关系是( )
A.点P在⊙O上 B.点P在⊙O内 C.点P在⊙O外 D.无法确定
【考点】点与圆的位置关系;勾股定理;垂径定理;圆周角定理.
【专题】与圆有关的位置关系;推理能力.
【答案】A
【分析】由垂径定理可得AD,由圆周角定理可得∠AOC=60°,再结合特殊角的正弦值,求出⊙O的半径,即可得到答案.
【解答】解:如图,设OC与AB的交点为D,
∵OC为⊙O的半径,弦AB的长为,且OC⊥AB,
∴,
∵,∠ABC=30°,
∴∠AOC=2∠ABC=60°,
在△ADO中,∠ADO=90°,∠AOD=60°,
∵sin∠AOD,
∴2,即⊙O的半径为2,
∵OP=2,
∴点P在⊙O上,
故选:A.
【点评】本题考查了垂径定理,圆周角定理,点与圆的位置关系,锐角三角函数,掌握圆的相关性质是解题关键.
2.(2024秋 定兴县)已知⊙O的半径为9,点A在⊙O内,则OA的长可能为( )
A.13 B.11 C.9 D.7
【考点】点与圆的位置关系.
【专题】与圆有关的位置关系;运算能力.
【答案】D
【分析】由点A在⊙O内,可知点A到该圆圆心的距离小于其半径,即可得解.
【解答】解:∵⊙O的半径为9,且点A在⊙O内,
∴OA的长小于半径,即OA<9,
故选:D.
【点评】本题考查点与圆的位置关系.掌握点到圆心的距离小于圆的半径,则点在圆内;点到圆心的距离等于圆的半径,则点在圆上;点到圆心的距离大于圆的半径,则点在圆外是解题关键.
3.(2024.汕头一模)如图,⊙O是△CDB的外接圆,AB为直径,若∠ABC=10°,则∠BDC的度数是( )
A.90° B.80° C.70° D.60°
【考点】三角形的外接圆与外心;圆周角定理.
【专题】圆的有关概念及性质;运算能力;推理能力.
【答案】B
【分析】连接AD,由AB是⊙O的直径,得∠ADB=90°,而∠ADC=∠ABC=10°,所以∠BDC=∠ADB﹣∠ADC=80°,于是得到问题的答案.
【解答】解:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ADC=∠ABC=10°,
∴∠BDC=∠ADB﹣∠ADC=90°﹣10°=80°,
故选:B.
【点评】此题重点考查同弧所对的圆周角相等、直径所对的圆周角等于90°等知识,正确地作出所需要的辅助线是解题的关键.
4.(2024秋 裕安区)如图,在平面直角坐标系中,直线y=﹣x﹣4与x轴,y轴分别交于A,B两点,C,D是半径为2的⊙O上两动点,且,P为弦CD的中点,Q为线段AB的中点,当C,D两点在圆上运动时,PQ的最小值是( )
A. B.2 C.2 D.1
【考点】点与圆的位置关系;一次函数的性质;一次函数图象上点的坐标特征;三角形三边关系;勾股定理;三角形中位线定理;垂径定理.
【专题】一次函数及其应用;等腰三角形与直角三角形;圆的有关概念及性质;与圆有关的计算;运算能力;推理能力.
【答案】A
【分析】连接OP,利用垂径定理和勾股定理求得OP,则点P在以点O为圆心,为半径的圆上运动,连接OQ,交小⊙O于点F,则QF为PQ的最小值,OF=OP;利用一次函数的图象与性质求得AB,利用直角三角形的斜边上的中线的性质求得OQ,结论可求.
【解答】解:连接OP,如图,
∵P为弦CD的中点,
∴OP⊥CD,DP=CP,
∴OP,
∵C,D是半径为2的⊙O上两动点,
∴点P在以点O为圆心,为半径的圆上运动,
连接OQ,交小⊙O于点F,则QF为PQ的最小值,OF=OP.
∵直线y=﹣x﹣4与x轴,y轴分别交于A,B两点,
∴A(﹣4,0),B(0,﹣4),
∴OA=4,OB=4,
∵∠AOB=90°,
∴AB=4,
∵Q为线段AB的中点,
∴OQ,
∴QF=OQ﹣OF.
∴PQ的最小值是.
故选:A.
【点评】本题主要考查了圆的有关性质,垂径定理,点的轨迹,直角三角形的性质,勾股定理,等腰直角三角形的性质,斜边上的中线的性质,一次函数的图象与性质,点的坐标的特征,熟练掌握上述性质是解题的关键.
5.(2024秋 新市区)如图,△ABC内接于⊙O,若∠A=45°,⊙O的半径r=4,则阴影部分的面积为( )
A.4 B.2 C.4π﹣8 D.4π﹣16
【考点】三角形的外接圆与外心;扇形面积的计算.
【专题】圆的有关概念及性质;运算能力.
【答案】C
【分析】根据圆周角定理可得∠BOC=90°,然后根据阴影部分的面积=扇形BOC的面积﹣△BOC的面积,进行计算即可解答.
【解答】解:∵∠A=45°,
∴∠BOC=2∠A=90°,
∵⊙O的半径r=4,
∴阴影部分的面积=扇形BOC的面积﹣△BOC的面积
OB OC
=4π4×4
=4π﹣8,
故选:C.
【点评】本题考查了三角形的外接圆与外心,扇形面积的计算,根据题目的已知条件并结合图形进行分析是解题的关键.
6.(2024.雁塔区)如图,△ABC内接于⊙O,点D是弧AB的中点,∠DAB=25°,则∠C=( )
A.45° B.50° C.55° D.60°
【考点】三角形的外接圆与外心;圆心角、弧、弦的关系;圆周角定理.
【专题】圆的有关概念及性质;运算能力.
【答案】B
【分析】根据已知易得:,从而可得∠DAB=∠DBA=25°,然后利用三角形内角和定理可得∠D=130°,再利用圆内接四边形对角互补进行计算,即可解答.
【解答】解:∵点D是弧AB的中点,
∴,
∴∠DAB=∠DBA=25°,
∴∠D=180°﹣∠DAB﹣∠DBA=130°,
∵四边形ACBD是⊙O的内接四边形,
∴∠C=180°﹣∠D=50°,
故选:B.
【点评】本题考查了三角形的外接圆与外心,圆周角定理,圆心角、弧、弦的关系,根据题目的已知条件并结合图形进行分析是解题的关键.
7.(2024秋 邯郸)⊙O为△ABC的外接圆,AB=AC,CD为⊙O的直径,若∠ACD=25°,则∠BDC为( )
A.25° B.45° C.50° D.60°
【考点】三角形的外接圆与外心;等腰三角形的性质;圆周角定理.
【专题】三角形;圆的有关概念及性质.
【答案】C
【分析】根据直径所对的圆周角为直角,得到∠CAD=∠CBD=90°,三角形的内角和求出∠ADC,等弦对等弧,得到,进而得到∠ACB=∠ADC=65°,进而求出∠BCD=40°,再根据三角形的内角和定理求出∠BDC的度数即可.
【解答】解:∵CD为⊙O的直径,
∴∠CAD=∠CBD=90°,
∵∠ACD=25°,
∴∠ADC=90°﹣∠ACD=65°,
∵AB=AC,
∴,
∴∠ACB=∠ADC=65°,
∴∠BCD=∠ACB﹣∠ACD=40°,
∴∠BDC=90°﹣∠BCD=50°;
故选:C.
【点评】本题考查圆周角定理,等弦对等弧,掌握以上知识点是解题的关键.
二.填空题(共5小题)
8.(2024秋 清苑区)如图,在平面直角坐标系中,A(0,3)、B(4,3)、C(6,1).则经过A、B、C三点的圆弧所在圆的圆心P的坐标为 (2,﹣1) .
【考点】三角形的外接圆与外心;坐标与图形性质;垂径定理;点与圆的位置关系.
【专题】推理能力.
【答案】(2,﹣1).
【分析】AB的垂直平分线所在的直线为x=2,可知圆心P在直线x=2上,设P(2,m),根据PA=PC,可求点P坐标.
【解答】解:∵A(0,3)、B(4,3),
∴AB的垂直平分线是直线x=2,
∵经过A、B、C三点的圆弧所在圆的圆心为点P,
∴圆心P在直线x=2上,
设P(2,m),
∵PA=PC,
∴4+(m﹣3)2=16+(m﹣1)2,
解得m=﹣1,
∴P(2,﹣1),
故答案为:(2,﹣1).
【点评】本题主要考查了三角形的外心,掌握三角形的外心是三边垂直平分线的交点是正确解答此题的关键.
9.(2024.建邺区一模)已知等边三角形的边长为6cm,则它的外接圆半径长为 2 cm.
【考点】三角形的外接圆与外心;等边三角形的性质.
【专题】圆的有关概念及性质;推理能力.
【答案】2.
【分析】连接OB、OC,过点O作OH⊥BC于H,根据圆周角定理得到∠BOC=120°,根据等腰三角形的性质求出∠BOH、BH,再根据正弦的定义计算即可.
【解答】解:如图,连接OB、OC,过点O作OH⊥BC于H,
∵△ABC为等边三角形,
∴∠A=60°,
由圆周角定理得:∠BOC=2∠A=120°,
∵OB=OC,OH⊥BC,
∴∠BOH=60°,BH=HCBC=3cm,
∴OB2(cm),
故答案为:2.
【点评】本题考查的是三角形的外接圆与外心,掌握等边三角形的性质、圆周角定理是解题的关键.
10.(2024秋 谯城区)如图,在⊙O中,△ABC是⊙O的内接三角形,,直径CD⊥AB,垂足为E,连接AD.若DE=2,则AB的长为 .
【考点】三角形的外接圆与外心;特殊角的三角函数值;含30度角的直角三角形;勾股定理;垂径定理;圆周角定理.
【专题】等腰三角形与直角三角形;与圆有关的计算;几何直观;推理能力.
【答案】.
【分析】如图:连接OA,由垂径定理可得,再结合圆周角定理可得,然后运用特殊角三角函数值可得,进而得到∠EAO=30°,即,然后求得OE=DE=2、OA=2OE=4,再运用勾股定理求得AE,最后结合垂径定理即可解答.
【解答】解:如图:连接OA,
∵直径CD⊥AB,垂足为E,
∴,
∵,
∴,
∴,即∠ACE=30°,
∵AO=OC,
∴∠OAC=∠ACE=30°,
∴∠AOD=60°,
∵∠AEC=90°,
∴∠EAO=30°,
∴,
∴点E是OD的中点,即OE=DE=2,
∴OA=2OE=4,
在直角三角形AOE中,由勾股定理得:,
∴.
故答案为:.
【点评】本题考查了三角形的外接圆与外心,含30度角的直角三角形,勾股定理,垂径定理,圆周角定理,特殊角的三角函数值,掌握圆周角定理和垂径定理是解题的关键.
11.(2024.定海区)如图,△ABC是⊙O的内接三角形,若OA∥CB,∠ACB=22°,则∠CAB= 46° .
【考点】三角形的外接圆与外心;圆周角定理.
【专题】圆的有关概念及性质;运算能力.
【答案】46°.
【分析】连接OB,根据圆周角定理得∠AOB=2∠ACB=44°,然后根据等腰三角形”等边对等角“性质,结合三角形内角和定理得∠OAB=∠OBA=68°,接下来根据平行线的性质得∠OAC=∠ACB=22°,最后求出∠CAB=∠OAB﹣∠OAC的值即可.
【解答】解:连接OB,
∵∠ACB=22°,
∴∠AOB=2∠ACB=2×22°=44°,
∵OA=OB,
∴,
∵OA∥CB,
∴∠OAC=∠ACB=22°,
∴∠CAB=∠OAB﹣∠OAC=68°﹣22°=46°,
故答案为:46°.
【点评】本题考查了圆周角定理,三角形的外接圆与外心,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
12.(2024.山东一模)如图,△ABC是⊙O的内接三角形,点D是弧BC的中点,已知∠AOB=100°,∠CAB=60°,则∠ABD= 100 度.
【考点】三角形的外接圆与外心;圆心角、弧、弦的关系;圆周角定理.
【专题】圆的有关概念及性质;推理能力.
【答案】100.
【分析】接OD,易得∠OAB=∠OBA,根据三角形内角和定理得∠OBA(180°﹣∠AOB)=40°,由点D是弧BC的中点得∠BOD=60°,所以∠OBD=60°,然后利用∠ABD=∠OBA+∠OBD进行计算.
【解答】解:连接OD,如图,
∵OA=OB,
∴∠OAB=∠OBA,
∴∠OBA(180°﹣∠AOB)(180°﹣100°)=40°,
∵点D是弧BC的中点,
∴∠BOD=∠CAB=60°,
∴∠OBD=60°,
∴∠ABD=∠OBA+∠OBD=40°+60°=100°.
故答案为:100.
【点评】本题考查了三角形的外接圆与外心,圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
三.解答题(共3小题)
13.(2024.庐阳区二模)如图,△ABC内接于⊙O,AB为⊙O的直径,OD⊥AB交半圆AB弧于D,点D与点C分别在直径的两侧,连接CD交AB于E,过点B作CD的平行线交AC延长线于F.
(1)求证:CF=CB;
(2)若AC=4,BC=2,求CD的长.
【考点】三角形的外接圆与外心;平行线的性质;圆周角定理.
【专题】圆的有关概念及性质.
【答案】(1)证明见解析;(2)3.
【分析】(1)由圆周角定理得到,则由平行线的性质得到∠CBF=∠BCD=45°,再证明∠FCB=90°,则可证明△BCF是等腰直角三角形,则CF=CB;
(2)过点C作CH⊥AB于H,由勾股定理得,解直角三角形得到,则可求出,,OH,证明△DEO∽△CEH,得到,则,,最后利用勾股定理求出CE,DE的长即可得到答案.
【解答】(1)证明:∵OD⊥AB,
∴∠BOD=90°,
∴,
∵BF∥CD,
∴∠CBF=∠BCD=45°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠FCB=180°﹣∠ACB=90°,
∴△BCF是等腰直角三角形,
∴CF=CB;
(2)解:如图所示,过点C作CH⊥AB于H,
在 Rt△ABC中,由勾股定理得,
∴sin,,
∵在Rt△HBC中,,,
∴,
∴∠DOE=∠CHE=90°,∠DEO=∠CEH,
∴△DEO∽△CEH,
∴,
∴,OE,
∴CE,DE,
∴CD=CE+DE=3.
【点评】本题主要考查了解直角三角形,相似三角形的性质与判定,勾股定理,等腰直角三角形的性质与判定,圆的相关性质,正确作出辅助线是解题的关键.
14.(2024.庆元县一模)如图,三角形ABC内接于⊙O,AB=AC,连结BO并延长交AC于点E,交⊙O于点D,连结AO,AD,CD.
(1)求证:∠ABC=∠ADB;
(2)猜想OA与CD的位置关系,并说明理由;
(3)若,求AE的长.
【考点】三角形的外接圆与外心;解直角三角形;圆周角定理.
【专题】圆的有关概念及性质.
【答案】(1)见解析;(2)AO∥CD,证明见解析;(3)AE.
【分析】(1)由题意易得∠ABC=∠ACB,然后根据圆周角的性质可进行求解;
(2)延长AO交BC于点F,由题意易得AF⊥BC,则有∠AFB=90°,然后问题可求证;
(3)由(2)易得,由可设BF=x,则 AF=2x,然后根据勾股定理可得 x=4,进而可得△AOE∽△CDE,最后根据相似三角形的性质可进行求解.
【解答】(1)证明:∵AB=BC,
∴∠ABC=∠ACB,
∵∠ADB=∠ACB,
∴∠ABC=∠ADB;
(2)解:平行,如图,延长AO交BC于点F,
∵AB=BC,
∴∠ABC=∠ACB,
∴,即点A为的中点,
∵AO是半径,
∴AF⊥BC,
∴∠AFB=90°,
∵BD是直径,
∴∠BCD=90°,
∴AO∥CD;
(3)解:由(2)易得,
∵,
∴设BF=x,则AF=2x,
∴OA=OB=2x﹣3,
∵BF2+OF2=OB2,
∴x2+32=(2x﹣3)2,
解得:x=4,
∴OA=5,
∴ABAC,
∵AO∥CD,
∴△AOE∽△CDE,
∴,
∴.
【点评】本题主要考查圆周角的性质、勾股定理、相似三角形的性质与判定及三角函数,熟练掌握圆周角的性质、勾股定理、相似三角形的性质与判定及三角函数是解题的关键.
15.(2024.张家口一模)如图,AB是半圆O的直径,点C是半圆O上一点(不含端点),连接AC,OC,BC,在OC右侧作∠OCD=∠OCA,DC=AC.
(1)判断点D与半圆O所在圆的位置关系,并说明理由.
(2)连接DB并延长,与过点C的切线交于点E.
①求∠E的度数;
②若AB=10,∠CDB=30°,求与线段BD的长度,并比较大小.
【考点】点与圆的位置关系;全等三角形的判定与性质;角平分线的性质;勾股定理;三角形中位线定理;垂径定理;圆周角定理.
【专题】与圆有关的计算;运算能力.
【答案】(1)点D在半圆O所在的圆上,见解析;
(2)①∠E=90°;②,见解析.
【分析】(1)连接OD,证明△OCD≌△OCA,即可得到结论;
(2)①证明OC∥DE,根据∠OCE=90°即可得到答案;
②根据弧长公式计算出BC的长度为,证明∠BCD=∠CDB,得到BC=BD=5即可得到结论.
【解答】解:(1)点D在半圆O所在的圆上.
理由如下:如图,连接OD.
∵DC=AC,∠OCD=∠OCA,OC=OC,
∴△OCD≌△OCA(SAS),
∴OD=OA,
∴点D在半圆O所在的圆上;
(2)①∵点D在半圆O所在的圆上,
∴∠CDE=∠CAB.
由条件可知∠CDE=∠OCD,
∴OC∥DE,
由条件可知∠OCE=90°,
∴∠E=90°;
②由题意,得∠CAB=∠CDB=∠OCA=∠OCD=30°,
∴∠BOC=60°,
∴BC的长度为,
由条件可知∠ACB=90°,
∴,∠BCD=∠ACB﹣∠OCA﹣∠OCD=30°,
∴∠BCD=∠CDB,
∴BC=BD=5.
∵,
∴.
【点评】本题主要考查了切线的性质、点与圆的位置关系、弧长、全等三角形的判定和锐角三角函数,熟练掌握切线的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考核心考点 确定圆的条件
一.选择题(共7小题)
1.(2024秋 海港区)如图,⊙O中,弦AB的长为,点C在⊙O上,OC⊥AB,∠ABC=30°,⊙O所在的平面内有一点P,若OP=2,则点P与⊙O的位置关系是( )
A.点P在⊙O上 B.点P在⊙O内 C.点P在⊙O外 D.无法确定
2.(2024秋 定兴县)已知⊙O的半径为9,点A在⊙O内,则OA的长可能为( )
A.13 B.11 C.9 D.7
3.(2024.汕头一模)如图,⊙O是△CDB的外接圆,AB为直径,若∠ABC=10°,则∠BDC的度数是( )
A.90° B.80° C.70° D.60°
4.(2024秋 裕安区)如图,在平面直角坐标系中,直线y=﹣x﹣4与x轴,y轴分别交于A,B两点,C,D是半径为2的⊙O上两动点,且,P为弦CD的中点,Q为线段AB的中点,当C,D两点在圆上运动时,PQ的最小值是( )
A. B.2 C.2 D.1
5.(2024秋 新市区)如图,△ABC内接于⊙O,若∠A=45°,⊙O的半径r=4,则阴影部分的面积为( )
A.4 B.2 C.4π﹣8 D.4π﹣16
6.(2024.雁塔区)如图,△ABC内接于⊙O,点D是弧AB的中点,∠DAB=25°,则∠C=( )
A.45° B.50° C.55° D.60°
7.(2024秋 邯郸)⊙O为△ABC的外接圆,AB=AC,CD为⊙O的直径,若∠ACD=25°,则∠BDC为( )
A.25° B.45° C.50° D.60°
二.填空题(共5小题)
8.(2024秋 清苑区)如图,在平面直角坐标系中,A(0,3)、B(4,3)、C(6,1).则经过A、B、C三点的圆弧所在圆的圆心P的坐标为 .
9.(2024.建邺区一模)已知等边三角形的边长为6cm,则它的外接圆半径长为 cm.
10.(2024秋 谯城区)如图,在⊙O中,△ABC是⊙O的内接三角形,,直径CD⊥AB,垂足为E,连接AD.若DE=2,则AB的长为 .
11.(2024.定海区)如图,△ABC是⊙O的内接三角形,若OA∥CB,∠ACB=22°,则∠CAB= .
12.(2024.山东一模)如图,△ABC是⊙O的内接三角形,点D是弧BC的中点,已知∠AOB=100°,∠CAB=60°,则∠ABD= 度.
三.解答题(共3小题)
13.(2024.庐阳区二模)如图,△ABC内接于⊙O,AB为⊙O的直径,OD⊥AB交半圆AB弧于D,点D与点C分别在直径的两侧,连接CD交AB于E,过点B作CD的平行线交AC延长线于F.
(1)求证:CF=CB;
(2)若AC=4,BC=2,求CD的长.
14.(2024.庆元县一模)如图,三角形ABC内接于⊙O,AB=AC,连结BO并延长交AC于点E,交⊙O于点D,连结AO,AD,CD.
(1)求证:∠ABC=∠ADB;
(2)猜想OA与CD的位置关系,并说明理由;
(3)若,求AE的长.
15.(2024.张家口一模)如图,AB是半圆O的直径,点C是半圆O上一点(不含端点),连接AC,OC,BC,在OC右侧作∠OCD=∠OCA,DC=AC.
(1)判断点D与半圆O所在圆的位置关系,并说明理由.
(2)连接DB并延长,与过点C的切线交于点E.
①求∠E的度数;
②若AB=10,∠CDB=30°,求与线段BD的长度,并比较大小.
中考核心考点 确定圆的条件
参考答案与试题解析
一.选择题(共7小题)
1.(2024秋 海港区)如图,⊙O中,弦AB的长为,点C在⊙O上,OC⊥AB,∠ABC=30°,⊙O所在的平面内有一点P,若OP=2,则点P与⊙O的位置关系是( )
A.点P在⊙O上 B.点P在⊙O内 C.点P在⊙O外 D.无法确定
【考点】点与圆的位置关系;勾股定理;垂径定理;圆周角定理.
【专题】与圆有关的位置关系;推理能力.
【答案】A
【分析】由垂径定理可得AD,由圆周角定理可得∠AOC=60°,再结合特殊角的正弦值,求出⊙O的半径,即可得到答案.
【解答】解:如图,设OC与AB的交点为D,
∵OC为⊙O的半径,弦AB的长为,且OC⊥AB,
∴,
∵,∠ABC=30°,
∴∠AOC=2∠ABC=60°,
在△ADO中,∠ADO=90°,∠AOD=60°,
∵sin∠AOD,
∴2,即⊙O的半径为2,
∵OP=2,
∴点P在⊙O上,
故选:A.
【点评】本题考查了垂径定理,圆周角定理,点与圆的位置关系,锐角三角函数,掌握圆的相关性质是解题关键.
2.(2024秋 定兴县)已知⊙O的半径为9,点A在⊙O内,则OA的长可能为( )
A.13 B.11 C.9 D.7
【考点】点与圆的位置关系.
【专题】与圆有关的位置关系;运算能力.
【答案】D
【分析】由点A在⊙O内,可知点A到该圆圆心的距离小于其半径,即可得解.
【解答】解:∵⊙O的半径为9,且点A在⊙O内,
∴OA的长小于半径,即OA<9,
故选:D.
【点评】本题考查点与圆的位置关系.掌握点到圆心的距离小于圆的半径,则点在圆内;点到圆心的距离等于圆的半径,则点在圆上;点到圆心的距离大于圆的半径,则点在圆外是解题关键.
3.(2024.汕头一模)如图,⊙O是△CDB的外接圆,AB为直径,若∠ABC=10°,则∠BDC的度数是( )
A.90° B.80° C.70° D.60°
【考点】三角形的外接圆与外心;圆周角定理.
【专题】圆的有关概念及性质;运算能力;推理能力.
【答案】B
【分析】连接AD,由AB是⊙O的直径,得∠ADB=90°,而∠ADC=∠ABC=10°,所以∠BDC=∠ADB﹣∠ADC=80°,于是得到问题的答案.
【解答】解:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ADC=∠ABC=10°,
∴∠BDC=∠ADB﹣∠ADC=90°﹣10°=80°,
故选:B.
【点评】此题重点考查同弧所对的圆周角相等、直径所对的圆周角等于90°等知识,正确地作出所需要的辅助线是解题的关键.
4.(2024秋 裕安区)如图,在平面直角坐标系中,直线y=﹣x﹣4与x轴,y轴分别交于A,B两点,C,D是半径为2的⊙O上两动点,且,P为弦CD的中点,Q为线段AB的中点,当C,D两点在圆上运动时,PQ的最小值是( )
A. B.2 C.2 D.1
【考点】点与圆的位置关系;一次函数的性质;一次函数图象上点的坐标特征;三角形三边关系;勾股定理;三角形中位线定理;垂径定理.
【专题】一次函数及其应用;等腰三角形与直角三角形;圆的有关概念及性质;与圆有关的计算;运算能力;推理能力.
【答案】A
【分析】连接OP,利用垂径定理和勾股定理求得OP,则点P在以点O为圆心,为半径的圆上运动,连接OQ,交小⊙O于点F,则QF为PQ的最小值,OF=OP;利用一次函数的图象与性质求得AB,利用直角三角形的斜边上的中线的性质求得OQ,结论可求.
【解答】解:连接OP,如图,
∵P为弦CD的中点,
∴OP⊥CD,DP=CP,
∴OP,
∵C,D是半径为2的⊙O上两动点,
∴点P在以点O为圆心,为半径的圆上运动,
连接OQ,交小⊙O于点F,则QF为PQ的最小值,OF=OP.
∵直线y=﹣x﹣4与x轴,y轴分别交于A,B两点,
∴A(﹣4,0),B(0,﹣4),
∴OA=4,OB=4,
∵∠AOB=90°,
∴AB=4,
∵Q为线段AB的中点,
∴OQ,
∴QF=OQ﹣OF.
∴PQ的最小值是.
故选:A.
【点评】本题主要考查了圆的有关性质,垂径定理,点的轨迹,直角三角形的性质,勾股定理,等腰直角三角形的性质,斜边上的中线的性质,一次函数的图象与性质,点的坐标的特征,熟练掌握上述性质是解题的关键.
5.(2024秋 新市区)如图,△ABC内接于⊙O,若∠A=45°,⊙O的半径r=4,则阴影部分的面积为( )
A.4 B.2 C.4π﹣8 D.4π﹣16
【考点】三角形的外接圆与外心;扇形面积的计算.
【专题】圆的有关概念及性质;运算能力.
【答案】C
【分析】根据圆周角定理可得∠BOC=90°,然后根据阴影部分的面积=扇形BOC的面积﹣△BOC的面积,进行计算即可解答.
【解答】解:∵∠A=45°,
∴∠BOC=2∠A=90°,
∵⊙O的半径r=4,
∴阴影部分的面积=扇形BOC的面积﹣△BOC的面积
OB OC
=4π4×4
=4π﹣8,
故选:C.
【点评】本题考查了三角形的外接圆与外心,扇形面积的计算,根据题目的已知条件并结合图形进行分析是解题的关键.
6.(2024.雁塔区)如图,△ABC内接于⊙O,点D是弧AB的中点,∠DAB=25°,则∠C=( )
A.45° B.50° C.55° D.60°
【考点】三角形的外接圆与外心;圆心角、弧、弦的关系;圆周角定理.
【专题】圆的有关概念及性质;运算能力.
【答案】B
【分析】根据已知易得:,从而可得∠DAB=∠DBA=25°,然后利用三角形内角和定理可得∠D=130°,再利用圆内接四边形对角互补进行计算,即可解答.
【解答】解:∵点D是弧AB的中点,
∴,
∴∠DAB=∠DBA=25°,
∴∠D=180°﹣∠DAB﹣∠DBA=130°,
∵四边形ACBD是⊙O的内接四边形,
∴∠C=180°﹣∠D=50°,
故选:B.
【点评】本题考查了三角形的外接圆与外心,圆周角定理,圆心角、弧、弦的关系,根据题目的已知条件并结合图形进行分析是解题的关键.
7.(2024秋 邯郸)⊙O为△ABC的外接圆,AB=AC,CD为⊙O的直径,若∠ACD=25°,则∠BDC为( )
A.25° B.45° C.50° D.60°
【考点】三角形的外接圆与外心;等腰三角形的性质;圆周角定理.
【专题】三角形;圆的有关概念及性质.
【答案】C
【分析】根据直径所对的圆周角为直角,得到∠CAD=∠CBD=90°,三角形的内角和求出∠ADC,等弦对等弧,得到,进而得到∠ACB=∠ADC=65°,进而求出∠BCD=40°,再根据三角形的内角和定理求出∠BDC的度数即可.
【解答】解:∵CD为⊙O的直径,
∴∠CAD=∠CBD=90°,
∵∠ACD=25°,
∴∠ADC=90°﹣∠ACD=65°,
∵AB=AC,
∴,
∴∠ACB=∠ADC=65°,
∴∠BCD=∠ACB﹣∠ACD=40°,
∴∠BDC=90°﹣∠BCD=50°;
故选:C.
【点评】本题考查圆周角定理,等弦对等弧,掌握以上知识点是解题的关键.
二.填空题(共5小题)
8.(2024秋 清苑区)如图,在平面直角坐标系中,A(0,3)、B(4,3)、C(6,1).则经过A、B、C三点的圆弧所在圆的圆心P的坐标为 (2,﹣1) .
【考点】三角形的外接圆与外心;坐标与图形性质;垂径定理;点与圆的位置关系.
【专题】推理能力.
【答案】(2,﹣1).
【分析】AB的垂直平分线所在的直线为x=2,可知圆心P在直线x=2上,设P(2,m),根据PA=PC,可求点P坐标.
【解答】解:∵A(0,3)、B(4,3),
∴AB的垂直平分线是直线x=2,
∵经过A、B、C三点的圆弧所在圆的圆心为点P,
∴圆心P在直线x=2上,
设P(2,m),
∵PA=PC,
∴4+(m﹣3)2=16+(m﹣1)2,
解得m=﹣1,
∴P(2,﹣1),
故答案为:(2,﹣1).
【点评】本题主要考查了三角形的外心,掌握三角形的外心是三边垂直平分线的交点是正确解答此题的关键.
9.(2024.建邺区一模)已知等边三角形的边长为6cm,则它的外接圆半径长为 2 cm.
【考点】三角形的外接圆与外心;等边三角形的性质.
【专题】圆的有关概念及性质;推理能力.
【答案】2.
【分析】连接OB、OC,过点O作OH⊥BC于H,根据圆周角定理得到∠BOC=120°,根据等腰三角形的性质求出∠BOH、BH,再根据正弦的定义计算即可.
【解答】解:如图,连接OB、OC,过点O作OH⊥BC于H,
∵△ABC为等边三角形,
∴∠A=60°,
由圆周角定理得:∠BOC=2∠A=120°,
∵OB=OC,OH⊥BC,
∴∠BOH=60°,BH=HCBC=3cm,
∴OB2(cm),
故答案为:2.
【点评】本题考查的是三角形的外接圆与外心,掌握等边三角形的性质、圆周角定理是解题的关键.
10.(2024秋 谯城区)如图,在⊙O中,△ABC是⊙O的内接三角形,,直径CD⊥AB,垂足为E,连接AD.若DE=2,则AB的长为 .
【考点】三角形的外接圆与外心;特殊角的三角函数值;含30度角的直角三角形;勾股定理;垂径定理;圆周角定理.
【专题】等腰三角形与直角三角形;与圆有关的计算;几何直观;推理能力.
【答案】.
【分析】如图:连接OA,由垂径定理可得,再结合圆周角定理可得,然后运用特殊角三角函数值可得,进而得到∠EAO=30°,即,然后求得OE=DE=2、OA=2OE=4,再运用勾股定理求得AE,最后结合垂径定理即可解答.
【解答】解:如图:连接OA,
∵直径CD⊥AB,垂足为E,
∴,
∵,
∴,
∴,即∠ACE=30°,
∵AO=OC,
∴∠OAC=∠ACE=30°,
∴∠AOD=60°,
∵∠AEC=90°,
∴∠EAO=30°,
∴,
∴点E是OD的中点,即OE=DE=2,
∴OA=2OE=4,
在直角三角形AOE中,由勾股定理得:,
∴.
故答案为:.
【点评】本题考查了三角形的外接圆与外心,含30度角的直角三角形,勾股定理,垂径定理,圆周角定理,特殊角的三角函数值,掌握圆周角定理和垂径定理是解题的关键.
11.(2024.定海区)如图,△ABC是⊙O的内接三角形,若OA∥CB,∠ACB=22°,则∠CAB= 46° .
【考点】三角形的外接圆与外心;圆周角定理.
【专题】圆的有关概念及性质;运算能力.
【答案】46°.
【分析】连接OB,根据圆周角定理得∠AOB=2∠ACB=44°,然后根据等腰三角形”等边对等角“性质,结合三角形内角和定理得∠OAB=∠OBA=68°,接下来根据平行线的性质得∠OAC=∠ACB=22°,最后求出∠CAB=∠OAB﹣∠OAC的值即可.
【解答】解:连接OB,
∵∠ACB=22°,
∴∠AOB=2∠ACB=2×22°=44°,
∵OA=OB,
∴,
∵OA∥CB,
∴∠OAC=∠ACB=22°,
∴∠CAB=∠OAB﹣∠OAC=68°﹣22°=46°,
故答案为:46°.
【点评】本题考查了圆周角定理,三角形的外接圆与外心,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
12.(2024.山东一模)如图,△ABC是⊙O的内接三角形,点D是弧BC的中点,已知∠AOB=100°,∠CAB=60°,则∠ABD= 100 度.
【考点】三角形的外接圆与外心;圆心角、弧、弦的关系;圆周角定理.
【专题】圆的有关概念及性质;推理能力.
【答案】100.
【分析】接OD,易得∠OAB=∠OBA,根据三角形内角和定理得∠OBA(180°﹣∠AOB)=40°,由点D是弧BC的中点得∠BOD=60°,所以∠OBD=60°,然后利用∠ABD=∠OBA+∠OBD进行计算.
【解答】解:连接OD,如图,
∵OA=OB,
∴∠OAB=∠OBA,
∴∠OBA(180°﹣∠AOB)(180°﹣100°)=40°,
∵点D是弧BC的中点,
∴∠BOD=∠CAB=60°,
∴∠OBD=60°,
∴∠ABD=∠OBA+∠OBD=40°+60°=100°.
故答案为:100.
【点评】本题考查了三角形的外接圆与外心,圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
三.解答题(共3小题)
13.(2024.庐阳区二模)如图,△ABC内接于⊙O,AB为⊙O的直径,OD⊥AB交半圆AB弧于D,点D与点C分别在直径的两侧,连接CD交AB于E,过点B作CD的平行线交AC延长线于F.
(1)求证:CF=CB;
(2)若AC=4,BC=2,求CD的长.
【考点】三角形的外接圆与外心;平行线的性质;圆周角定理.
【专题】圆的有关概念及性质.
【答案】(1)证明见解析;(2)3.
【分析】(1)由圆周角定理得到,则由平行线的性质得到∠CBF=∠BCD=45°,再证明∠FCB=90°,则可证明△BCF是等腰直角三角形,则CF=CB;
(2)过点C作CH⊥AB于H,由勾股定理得,解直角三角形得到,则可求出,,OH,证明△DEO∽△CEH,得到,则,,最后利用勾股定理求出CE,DE的长即可得到答案.
【解答】(1)证明:∵OD⊥AB,
∴∠BOD=90°,
∴,
∵BF∥CD,
∴∠CBF=∠BCD=45°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠FCB=180°﹣∠ACB=90°,
∴△BCF是等腰直角三角形,
∴CF=CB;
(2)解:如图所示,过点C作CH⊥AB于H,
在 Rt△ABC中,由勾股定理得,
∴sin,,
∵在Rt△HBC中,,,
∴,
∴∠DOE=∠CHE=90°,∠DEO=∠CEH,
∴△DEO∽△CEH,
∴,
∴,OE,
∴CE,DE,
∴CD=CE+DE=3.
【点评】本题主要考查了解直角三角形,相似三角形的性质与判定,勾股定理,等腰直角三角形的性质与判定,圆的相关性质,正确作出辅助线是解题的关键.
14.(2024.庆元县一模)如图,三角形ABC内接于⊙O,AB=AC,连结BO并延长交AC于点E,交⊙O于点D,连结AO,AD,CD.
(1)求证:∠ABC=∠ADB;
(2)猜想OA与CD的位置关系,并说明理由;
(3)若,求AE的长.
【考点】三角形的外接圆与外心;解直角三角形;圆周角定理.
【专题】圆的有关概念及性质.
【答案】(1)见解析;(2)AO∥CD,证明见解析;(3)AE.
【分析】(1)由题意易得∠ABC=∠ACB,然后根据圆周角的性质可进行求解;
(2)延长AO交BC于点F,由题意易得AF⊥BC,则有∠AFB=90°,然后问题可求证;
(3)由(2)易得,由可设BF=x,则 AF=2x,然后根据勾股定理可得 x=4,进而可得△AOE∽△CDE,最后根据相似三角形的性质可进行求解.
【解答】(1)证明:∵AB=BC,
∴∠ABC=∠ACB,
∵∠ADB=∠ACB,
∴∠ABC=∠ADB;
(2)解:平行,如图,延长AO交BC于点F,
∵AB=BC,
∴∠ABC=∠ACB,
∴,即点A为的中点,
∵AO是半径,
∴AF⊥BC,
∴∠AFB=90°,
∵BD是直径,
∴∠BCD=90°,
∴AO∥CD;
(3)解:由(2)易得,
∵,
∴设BF=x,则AF=2x,
∴OA=OB=2x﹣3,
∵BF2+OF2=OB2,
∴x2+32=(2x﹣3)2,
解得:x=4,
∴OA=5,
∴ABAC,
∵AO∥CD,
∴△AOE∽△CDE,
∴,
∴.
【点评】本题主要考查圆周角的性质、勾股定理、相似三角形的性质与判定及三角函数,熟练掌握圆周角的性质、勾股定理、相似三角形的性质与判定及三角函数是解题的关键.
15.(2024.张家口一模)如图,AB是半圆O的直径,点C是半圆O上一点(不含端点),连接AC,OC,BC,在OC右侧作∠OCD=∠OCA,DC=AC.
(1)判断点D与半圆O所在圆的位置关系,并说明理由.
(2)连接DB并延长,与过点C的切线交于点E.
①求∠E的度数;
②若AB=10,∠CDB=30°,求与线段BD的长度,并比较大小.
【考点】点与圆的位置关系;全等三角形的判定与性质;角平分线的性质;勾股定理;三角形中位线定理;垂径定理;圆周角定理.
【专题】与圆有关的计算;运算能力.
【答案】(1)点D在半圆O所在的圆上,见解析;
(2)①∠E=90°;②,见解析.
【分析】(1)连接OD,证明△OCD≌△OCA,即可得到结论;
(2)①证明OC∥DE,根据∠OCE=90°即可得到答案;
②根据弧长公式计算出BC的长度为,证明∠BCD=∠CDB,得到BC=BD=5即可得到结论.
【解答】解:(1)点D在半圆O所在的圆上.
理由如下:如图,连接OD.
∵DC=AC,∠OCD=∠OCA,OC=OC,
∴△OCD≌△OCA(SAS),
∴OD=OA,
∴点D在半圆O所在的圆上;
(2)①∵点D在半圆O所在的圆上,
∴∠CDE=∠CAB.
由条件可知∠CDE=∠OCD,
∴OC∥DE,
由条件可知∠OCE=90°,
∴∠E=90°;
②由题意,得∠CAB=∠CDB=∠OCA=∠OCD=30°,
∴∠BOC=60°,
∴BC的长度为,
由条件可知∠ACB=90°,
∴,∠BCD=∠ACB﹣∠OCA﹣∠OCD=30°,
∴∠BCD=∠CDB,
∴BC=BD=5.
∵,
∴.
【点评】本题主要考查了切线的性质、点与圆的位置关系、弧长、全等三角形的判定和锐角三角函数,熟练掌握切线的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
