【中考核心考点】2025年北师大版中考数学考前冲刺 直角三角形的边角关系(含解析)
文档属性
| 名称 | 【中考核心考点】2025年北师大版中考数学考前冲刺 直角三角形的边角关系(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 18:59:13 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中考核心考点 直角三角形的边角关系
一.选择题(共7小题)
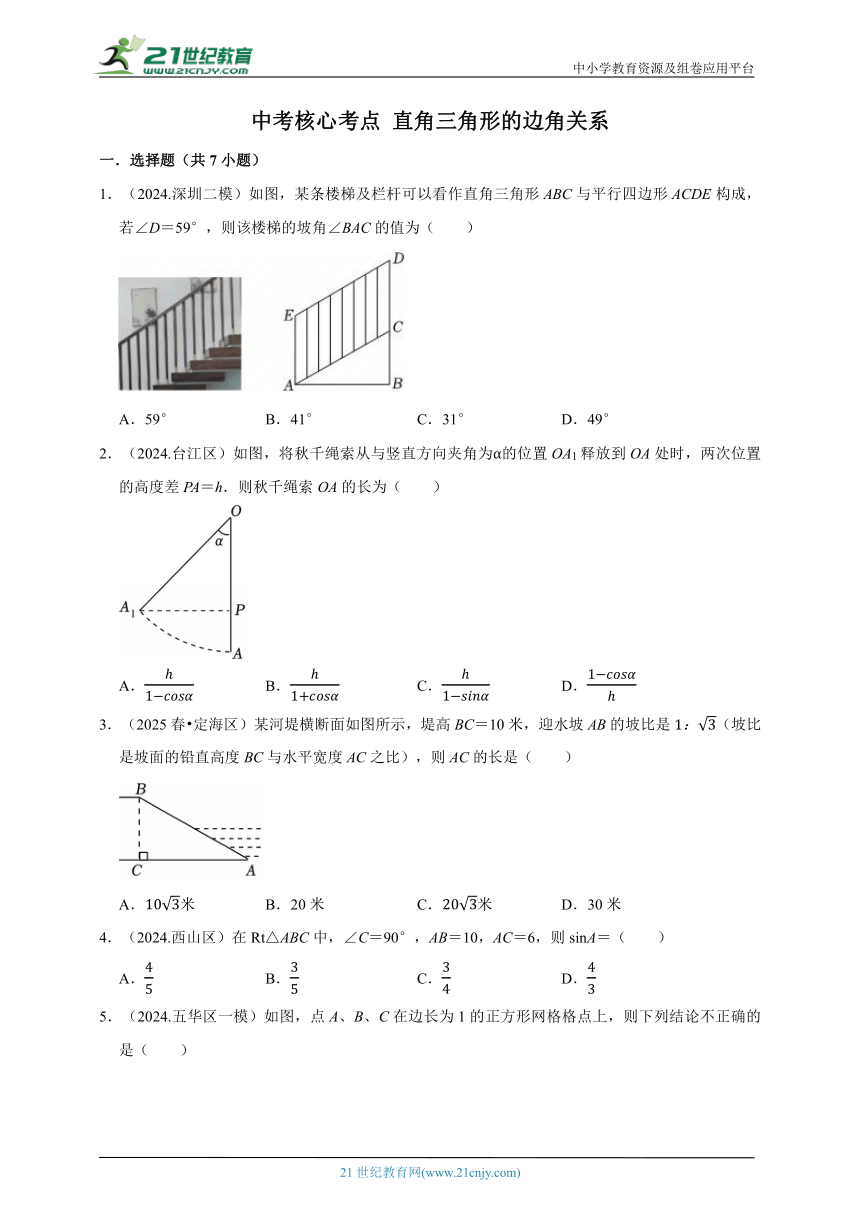
1.(2024.深圳二模)如图,某条楼梯及栏杆可以看作直角三角形ABC与平行四边形ACDE构成,若∠D=59°,则该楼梯的坡角∠BAC的值为( )
A.59° B.41° C.31° D.49°
2.(2024.台江区)如图,将秋千绳索从与竖直方向夹角为α的位置OA1释放到OA处时,两次位置的高度差PA=h.则秋千绳索OA的长为( )
A. B. C. D.
3.(2025春 定海区)某河堤横断面如图所示,堤高BC=10米,迎水坡AB的坡比是(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是( )
A.米 B.20米 C.米 D.30米
4.(2024.西山区)在Rt△ABC中,∠C=90°,AB=10,AC=6,则sinA=( )
A. B. C. D.
5.(2024.五华区一模)如图,点A、B、C在边长为1的正方形网格格点上,则下列结论不正确的是( )
A.△ABC是直角三角形 B.
C. D.tanC=2
6.(2024.郑州)一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力F1的方向与斜面垂直,摩擦力F2的方向与斜面平行.若斜面的坡角α=25°,则摩擦力F2与重力G方向的夹角β的度数为( )
A.155° B.125° C.115° D.65°
7.(2024.宝安区)港珠澳大桥是世界上最长的跨海大桥,被誉为“现代世界七大奇迹”的超级工程,它是我国从桥梁大国走向桥梁强国的里程碑之作.港珠澳大桥主桥为三座大跨度钢结构斜拉桥,其中九洲航道桥主塔造型取自“风帆”,寓意“扬帆起航”,某校九年级学生为了测量该主塔的高度,站在B处看塔顶A,仰角为60°,然后向后走190米,到达C处,此时看塔顶A,仰角为30°,则该主塔的高度是( )
A.95米 B.米 C.190米 D.米
二.填空题(共5小题)
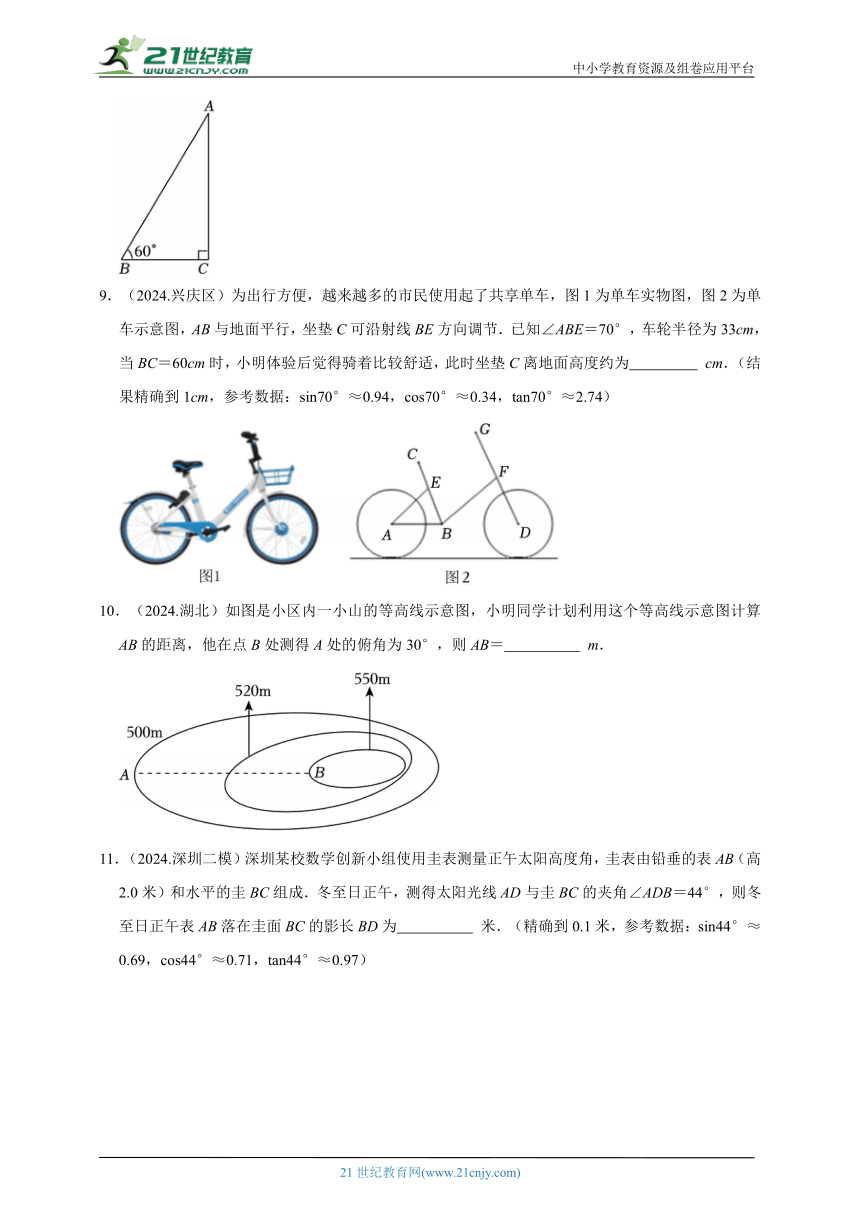
8.(2024秋 海港区)社团活动课上,九年级学习小组测量学校旗杆的高度.如图,他们在B处测得旗杆顶部A的仰角为60°,BC=8m,则旗杆AC的高度为 m.
9.(2024.兴庆区)为出行方便,越来越多的市民使用起了共享单车,图1为单车实物图,图2为单车示意图,AB与地面平行,坐垫C可沿射线BE方向调节.已知∠ABE=70°,车轮半径为33cm,当BC=60cm时,小明体验后觉得骑着比较舒适,此时坐垫C离地面高度约为 cm.(结果精确到1cm,参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.74)
10.(2024.湖北)如图是小区内一小山的等高线示意图,小明同学计划利用这个等高线示意图计算AB的距离,他在点B处测得A处的俯角为30°,则AB= m.
11.(2024.深圳二模)深圳某校数学创新小组使用圭表测量正午太阳高度角,圭表由铅垂的表AB(高2.0米)和水平的圭BC组成.冬至日正午,测得太阳光线AD与圭BC的夹角∠ADB=44°,则冬至日正午表AB落在圭面BC的影长BD为 米.(精确到0.1米,参考数据:sin44°≈0.69,cos44°≈0.71,tan44°≈0.97)
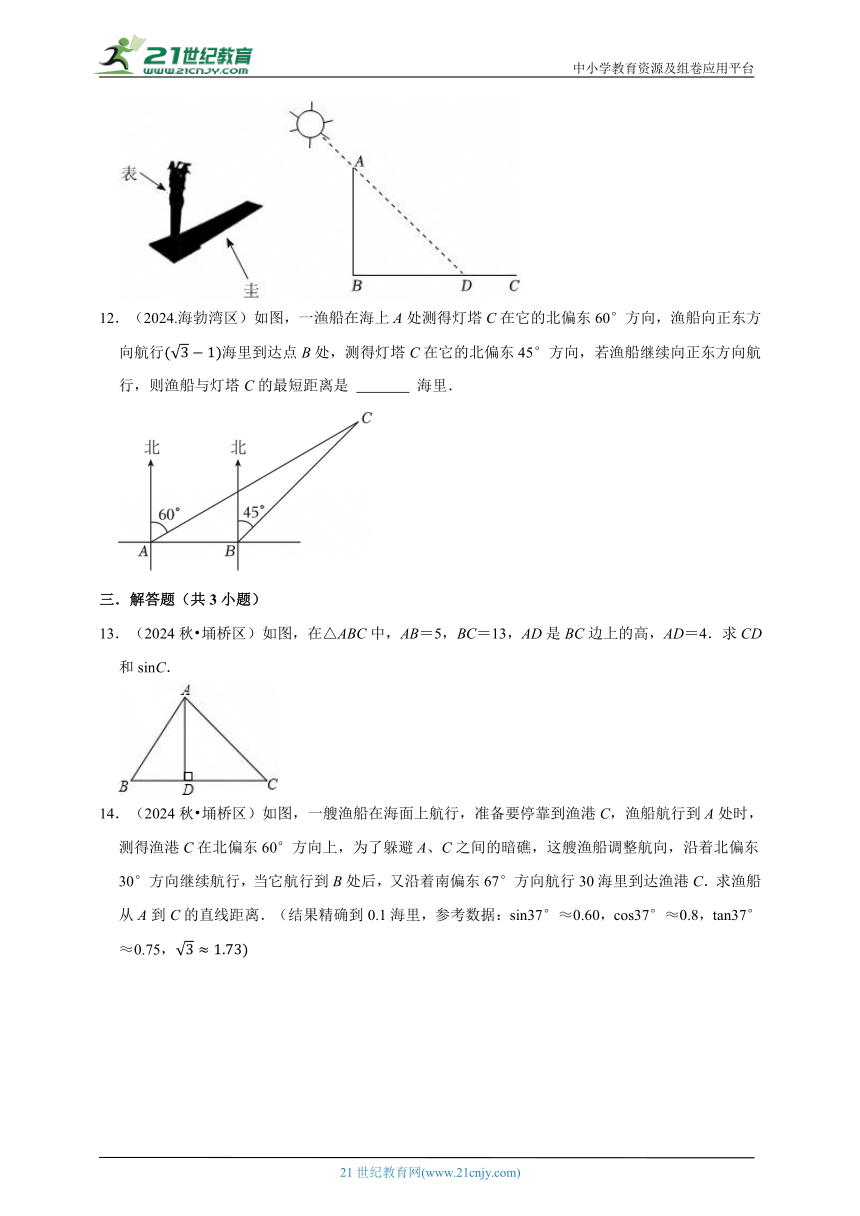
12.(2024.海勃湾区)如图,一渔船在海上A处测得灯塔C在它的北偏东60°方向,渔船向正东方向航行海里到达点B处,测得灯塔C在它的北偏东45°方向,若渔船继续向正东方向航行,则渔船与灯塔C的最短距离是 海里.
三.解答题(共3小题)
13.(2024秋 埇桥区)如图,在△ABC中,AB=5,BC=13,AD是BC边上的高,AD=4.求CD和sinC.
14.(2024秋 埇桥区)如图,一艘渔船在海面上航行,准备要停靠到渔港C,渔船航行到A处时,测得渔港C在北偏东60°方向上,为了躲避A、C之间的暗礁,这艘渔船调整航向,沿着北偏东30°方向继续航行,当它航行到B处后,又沿着南偏东67°方向航行30海里到达渔港C.求渔船从A到C的直线距离.(结果精确到0.1海里,参考数据:sin37°≈0.60,cos37°≈0.8,tan37°≈0.75,
15.(2024.河北)图﹣1是一款可旋转的太阳能路灯,太阳能光伏板面向太阳,且随太阳的升起到落下方向旋转,图﹣2是其侧面示意图,线段AB表示路灯的灯支架,PM为路灯灯杆.线段CD为太阳能光伏板,可绕点P旋转,CD=1m,AB=2m,∠BAM=120°.(图中所有点均在同一平面)(参考数据:sin80°≈0.98,cos80°≈0.17,.结果精确到0.1m)
(1)当C,D,B三点共线时,∠DPM=80°,求PA的长度;
(2)若某一时刻太阳光线与地面l的夹角为60°时,恰好太阳能光伏板CD与PM所成夹角∠DPM=60°,求太阳能光伏板CD落在地面l上的影子EF的长.
中考核心考点 直角三角形的边角关系
参考答案与试题解析
一.选择题(共7小题)
1.(2024.深圳二模)如图,某条楼梯及栏杆可以看作直角三角形ABC与平行四边形ACDE构成,若∠D=59°,则该楼梯的坡角∠BAC的值为( )
A.59° B.41° C.31° D.49°
【考点】解直角三角形的应用﹣坡度坡角问题;平行四边形的性质.
【专题】解直角三角形及其应用;应用意识.
【答案】C
【分析】先根据平行线的性质求出∠ACB,再根据直角三角形的两锐角互余求出∠BAC.
【解答】解:∵四边形ACDE是平行四边形,
∴AC∥DE,
∴∠ACB=∠D=59°,
∵∠ABC=90°,
∴∠BAC=90°﹣∠ABC=90°﹣59°=31°,
故选:C.
【点评】本题考查的是解直角三角形的应用﹣坡度坡角问题,掌握平行四边形的性质、直角三角形的性质是解题的关键.
2.(2024.台江区)如图,将秋千绳索从与竖直方向夹角为α的位置OA1释放到OA处时,两次位置的高度差PA=h.则秋千绳索OA的长为( )
A. B. C. D.
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;推理能力.
【答案】A
【分析】由题意可知,OA=OA1,再根据余弦的定义求解即可.
【解答】解:由题意可知,OA=OA1,
∵cosα,
∴OA1,
又∵OP=OA﹣PA=OA1﹣PA=OA1﹣h,
∴OA,
∴OA=OA1,
故选:A.
【点评】本题考查了解直角三角形的应用,熟记三角形函数的定义是解题的关键.
3.(2025春 定海区)某河堤横断面如图所示,堤高BC=10米,迎水坡AB的坡比是(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是( )
A.米 B.20米 C.米 D.30米
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】运算能力.
【答案】A
【分析】由堤高BC=10米,迎水坡AB的坡比,根据坡度的定义,即可求得AC的长.
【解答】解:∵迎水坡AB的坡比,
∴,
∵堤高BC=10米,
∴(米).
故选:A.
【点评】本题考查了解直角三角形的应用﹣坡度坡角问题,掌握坡比的概念是解题的关键.
4.(2024.西山区)在Rt△ABC中,∠C=90°,AB=10,AC=6,则sinA=( )
A. B. C. D.
【考点】锐角三角函数的定义.
【专题】解直角三角形及其应用;运算能力.
【答案】A
【分析】由勾股定理求出BC=8,由锐角的正弦定义即可求出sinA的值.
【解答】解:∵∠C=90°,AB=10,AC=6,
∴BC8,
sinA.
故选:A.
【点评】本题考查锐角三角函数定义,关键是掌握锐角的正弦定义.
5.(2024.五华区一模)如图,点A、B、C在边长为1的正方形网格格点上,则下列结论不正确的是( )
A.△ABC是直角三角形 B.
C. D.tanC=2
【考点】解直角三角形;勾股定理;勾股定理的逆定理.
【专题】等腰三角形与直角三角形;推理能力.
【答案】C
【分析】根据勾股定理得出AB,AC,BC的长,进而利用勾股定理的逆定理得出△ABC是直角三角形,然后结合解直角三角函数的性质进而解答即可.
【解答】解:由勾股定理得:,,,
∴BC2=AB2+AC2,
∴△ABC是直角三角形,∠BAC=90°,
∴,,,
故选:C.
【点评】此题考查的是解直角三角形,勾股定理,勾股定理的逆定理,熟记锐角三角函数的定义是解题的关键.
6.(2024.郑州)一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力F1的方向与斜面垂直,摩擦力F2的方向与斜面平行.若斜面的坡角α=25°,则摩擦力F2与重力G方向的夹角β的度数为( )
A.155° B.125° C.115° D.65°
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】C
【分析】根据题意结合图形可知β是重力G与斜面形成的三角形的外角,从而可求得β的度数.
【解答】解:∵重力G的方向竖直向下,
∴重力G与水平方向夹角为90°,
由题意可得:
∴β=∠1=α+90°=115°,
故选:C.
【点评】本题考查了平行线的性质和三角形外角性质,正确进行计算是解题关键.
7.(2024.宝安区)港珠澳大桥是世界上最长的跨海大桥,被誉为“现代世界七大奇迹”的超级工程,它是我国从桥梁大国走向桥梁强国的里程碑之作.港珠澳大桥主桥为三座大跨度钢结构斜拉桥,其中九洲航道桥主塔造型取自“风帆”,寓意“扬帆起航”,某校九年级学生为了测量该主塔的高度,站在B处看塔顶A,仰角为60°,然后向后走190米,到达C处,此时看塔顶A,仰角为30°,则该主塔的高度是( )
A.95米 B.米 C.190米 D.米
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】B
【分析】该主塔为AD=x,在Rt△ABD中,利用正切函数的定义求得,同理,在Rt△ACD中,求得,根据CD﹣BD=190,列出方程求解即可.
【解答】解:如图,该主塔为AD=x,
由题意,得:∠ADC=90°,BC=190,∠ACD=30°,∠ABD=60°,
∵,
∴,
∵,
∴,
∵BC=CD﹣BD=190,
∴,
∴.
故选:B.
【点评】本题考查解直角三角形的实际应用,正确进行计算是解题关键.
二.填空题(共5小题)
8.(2024秋 海港区)社团活动课上,九年级学习小组测量学校旗杆的高度.如图,他们在B处测得旗杆顶部A的仰角为60°,BC=8m,则旗杆AC的高度为 m.
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;几何直观.
【答案】.
【分析】在Rt△ABC中,tan∠ABC=tan60°,可得AC=BC tan60°m.
【解答】解:在Rt△ABC中,tan∠ABC=tan60°,
∴AC=BC tan60°(m).
故答案为:.
【点评】本题考查解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解答本题的关键.
9.(2024.兴庆区)为出行方便,越来越多的市民使用起了共享单车,图1为单车实物图,图2为单车示意图,AB与地面平行,坐垫C可沿射线BE方向调节.已知∠ABE=70°,车轮半径为33cm,当BC=60cm时,小明体验后觉得骑着比较舒适,此时坐垫C离地面高度约为 89 cm.(结果精确到1cm,参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.74)
【考点】解直角三角形的应用.
【专题】等腰三角形与直角三角形;应用意识.
【答案】89.
【分析】本题主要考查解直角三角形的应用,作CH⊥AB于H,作AP⊥地面于P,利用三角函数求出CH+AP即可.
【解答】解:如图2,作CH⊥AB于H,作AP⊥地面于P,
∵∠ABE=70°,车轮半径为33cm,BC=60cm,
∴AP=33cm,
∴CH=BC sin70°≈60×0.94=56.4(cm),
∴坐垫C离地面高度约为56.4+33≈89(cm),
故答案为:89.
【点评】本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形是解题的关键.
10.(2024.湖北)如图是小区内一小山的等高线示意图,小明同学计划利用这个等高线示意图计算AB的距离,他在点B处测得A处的俯角为30°,则AB= 100 m.
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;应用意识.
【答案】100.
【分析】根据由等高线可知A、B两地的高度差为50米,然后点B处测得A处的俯角为30°求值即可.
【解答】解:作示意图如下:
由题意知:A、B两地的实际高度差为AH:550﹣500=50(m),∠B=30°,∠AHB=90°,
∴sinB,即sin30°,
解得:AB=100,
故答案为:100.
【点评】本题主要考查了解直角三角形的应用﹣仰角俯角问题,解答本题的关键是根据题意,作出直角三角形解决问题.
11.(2024.深圳二模)深圳某校数学创新小组使用圭表测量正午太阳高度角,圭表由铅垂的表AB(高2.0米)和水平的圭BC组成.冬至日正午,测得太阳光线AD与圭BC的夹角∠ADB=44°,则冬至日正午表AB落在圭面BC的影长BD为 2.1 米.(精确到0.1米,参考数据:sin44°≈0.69,cos44°≈0.71,tan44°≈0.97)
【考点】解直角三角形的应用;平行投影.
【专题】解直角三角形及其应用;运算能力;应用意识.
【答案】2.1.
【分析】依据题意,圭表由铅垂的表AB(高2.0米)和水平的圭BC组成,结合冬至日正午,太阳光线AD与圭BC的夹角为∠ADB=44°,从而在直角三角形ABD中,AB为垂直高度(2.0米),BD为水平影长,太阳高度角∠ADB=44°,可得,进而2.1(米),故可得解.
【解答】解:由题意,圭表由铅垂的表AB(高2.0米)和水平的圭BC组成,
又∵冬至日正午,太阳光线AD与圭BC的夹角为∠ADB=44°,
∴在直角三角形ABD中,AB为垂直高度(2.0米),BD为水平影长,太阳高度角∠ADB=44°.
∴.
∴2.1(米).
故答案为:2.1.
【点评】本题主要考查了解直角三角形的应用、平行投影,解题时要熟练掌握并能利用锐角三角形函数求解是关键.
12.(2024.海勃湾区)如图,一渔船在海上A处测得灯塔C在它的北偏东60°方向,渔船向正东方向航行海里到达点B处,测得灯塔C在它的北偏东45°方向,若渔船继续向正东方向航行,则渔船与灯塔C的最短距离是 1 海里.
【考点】解直角三角形的应用﹣方向角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】1.
【分析】过点C作CD⊥AB,垂足为D,根据题意可得:AB=(1)海里,然后设CD=x海里,分别在Rt△ACD和Rt△BCD中,利用锐角三角函数的定义求出AD和BD的长,从而列出关于x的方程,进行计算即可解答.
【解答】解:过点C作CD⊥AB,垂足为D,
由题意得:AB=(1)海里,
设CD=x海里,
在Rt△ACD中,∠CAD=90°﹣60°=30°,
∴ADx(海里),
在Rt△BCD中,∠CBD=90°﹣45°=45°,
∴BDx(海里),
∵AD﹣BD=AB,
∴x﹣x1,
解得:x=1,
∴CD=1海里,
∴渔船与灯塔C的最短距离是1海里,
故答案为:1.
【点评】本题考查了解直角三角形的应用﹣方向角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
三.解答题(共3小题)
13.(2024秋 埇桥区)如图,在△ABC中,AB=5,BC=13,AD是BC边上的高,AD=4.求CD和sinC.
【考点】解直角三角形.
【答案】见试题解答内容
【分析】先解直角三角形ABD,得出BD的值,求出CD的值.再解直角三角形ADC求sinC的值.
【解答】解:在Rt△ABD中,由勾股定理,得:
BD
∴CD=BC﹣BD=10;
在Rt△ADC中,
AC
∴sinC.
【点评】本题考查了解直角三角形中三角函数的应用,要熟练掌握好边角之间的关系.
14.(2024秋 埇桥区)如图,一艘渔船在海面上航行,准备要停靠到渔港C,渔船航行到A处时,测得渔港C在北偏东60°方向上,为了躲避A、C之间的暗礁,这艘渔船调整航向,沿着北偏东30°方向继续航行,当它航行到B处后,又沿着南偏东67°方向航行30海里到达渔港C.求渔船从A到C的直线距离.(结果精确到0.1海里,参考数据:sin37°≈0.60,cos37°≈0.8,tan37°≈0.75,
【考点】解直角三角形的应用﹣方向角问题.
【专题】解直角三角形及其应用;应用意识.
【答案】AC的距离约为59.5海里.
【分析】过B作BD⊥AC于D,在Rt△DBC中,利用正弦函数求得BD≈24.0海里,CD≈18.0海里,再在Rt△ABD中,利用正切函数求出AD≈41.5海里即可得到答案.
【解答】解:如图,过B作BD⊥AC于D,
由题意可知∠BAF=30°,∠FAC=60°,∠CBE=67°,BC=30海里,
∴∠BAC=30°,∠ABE=∠BAF=30°
∴∠C=180°﹣∠BAC﹣∠ABE﹣∠CBE=53°,
在Rt△DBC中,∠BDC=90°,∠C=53°,BC=30海里,
∴∠CBD=37°,
∴CD=BC sin∠CBD≈30×0.60=18.0海里,BD=BC cos∠CBD≈30×0.8=24.0(海里),
在Rt△ABD中,∠BDA=90°,∠BAD=30°,
∴(海里),
∴AC=AD+CD=41.5+18.0=59.5(海里),
∴AC的距离约为59.5海里.
【点评】本题考查了解直角三角形的应用﹣方向角问题,正确作出辅助线构造直角三角形是解题的关键.
15.(2024.河北)图﹣1是一款可旋转的太阳能路灯,太阳能光伏板面向太阳,且随太阳的升起到落下方向旋转,图﹣2是其侧面示意图,线段AB表示路灯的灯支架,PM为路灯灯杆.线段CD为太阳能光伏板,可绕点P旋转,CD=1m,AB=2m,∠BAM=120°.(图中所有点均在同一平面)(参考数据:sin80°≈0.98,cos80°≈0.17,.结果精确到0.1m)
(1)当C,D,B三点共线时,∠DPM=80°,求PA的长度;
(2)若某一时刻太阳光线与地面l的夹角为60°时,恰好太阳能光伏板CD与PM所成夹角∠DPM=60°,求太阳能光伏板CD落在地面l上的影子EF的长.
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】(1)2.0m;
(2)1.2m.
【分析】(1)连接BD,过点B作BE⊥PM于点E,先解Rt△ABE,求得AE,BE,进而解Rt△PBE,求得PE,进而根据PA=PE+AE,即可求解;
(2)连接DF,CE,过点F作FH⊥CE于点H,设PM,DF交于点G,证明四边形CDFH是平行四边形,则FH=CD=1,解Rt△EFH,即可求解.
【解答】解:(1)连接BD,过点B作BE⊥PM于点E,
在Rt△ABE中,∠BAE=180°﹣∠BAM=60°,
∴,,
当C,D,B三点共线时,在Rt△PBE中,∠BPE=∠DPM=80°,
∴,
∴PA=PE+AE≈0.3+1.73≈2.0m;
(2)如图,
连接DF,CE,过点F作FH⊥CE于点H,设PM,DF交于点G,
∵∠GFM=60°,∠GMF=90°,
∴∠DPG=∠MGF=30°,
又∠DPM=60°,
∴∠PDG=90°,
由题意可得:FH⊥DF
∴CD∥FH,
∴四边形CDFH是平行四边形,
∴FH=CD=1,
∵∠HEF=∠DFM=60°,
,
答:EF的长为1.2m.
【点评】本题主要考查了解直角三角形的应用,解题的关键是熟练掌握三角函数的定义,作出辅助线构造直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考核心考点 直角三角形的边角关系
一.选择题(共7小题)
1.(2024.深圳二模)如图,某条楼梯及栏杆可以看作直角三角形ABC与平行四边形ACDE构成,若∠D=59°,则该楼梯的坡角∠BAC的值为( )
A.59° B.41° C.31° D.49°
2.(2024.台江区)如图,将秋千绳索从与竖直方向夹角为α的位置OA1释放到OA处时,两次位置的高度差PA=h.则秋千绳索OA的长为( )
A. B. C. D.
3.(2025春 定海区)某河堤横断面如图所示,堤高BC=10米,迎水坡AB的坡比是(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是( )
A.米 B.20米 C.米 D.30米
4.(2024.西山区)在Rt△ABC中,∠C=90°,AB=10,AC=6,则sinA=( )
A. B. C. D.
5.(2024.五华区一模)如图,点A、B、C在边长为1的正方形网格格点上,则下列结论不正确的是( )
A.△ABC是直角三角形 B.
C. D.tanC=2
6.(2024.郑州)一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力F1的方向与斜面垂直,摩擦力F2的方向与斜面平行.若斜面的坡角α=25°,则摩擦力F2与重力G方向的夹角β的度数为( )
A.155° B.125° C.115° D.65°
7.(2024.宝安区)港珠澳大桥是世界上最长的跨海大桥,被誉为“现代世界七大奇迹”的超级工程,它是我国从桥梁大国走向桥梁强国的里程碑之作.港珠澳大桥主桥为三座大跨度钢结构斜拉桥,其中九洲航道桥主塔造型取自“风帆”,寓意“扬帆起航”,某校九年级学生为了测量该主塔的高度,站在B处看塔顶A,仰角为60°,然后向后走190米,到达C处,此时看塔顶A,仰角为30°,则该主塔的高度是( )
A.95米 B.米 C.190米 D.米
二.填空题(共5小题)
8.(2024秋 海港区)社团活动课上,九年级学习小组测量学校旗杆的高度.如图,他们在B处测得旗杆顶部A的仰角为60°,BC=8m,则旗杆AC的高度为 m.
9.(2024.兴庆区)为出行方便,越来越多的市民使用起了共享单车,图1为单车实物图,图2为单车示意图,AB与地面平行,坐垫C可沿射线BE方向调节.已知∠ABE=70°,车轮半径为33cm,当BC=60cm时,小明体验后觉得骑着比较舒适,此时坐垫C离地面高度约为 cm.(结果精确到1cm,参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.74)
10.(2024.湖北)如图是小区内一小山的等高线示意图,小明同学计划利用这个等高线示意图计算AB的距离,他在点B处测得A处的俯角为30°,则AB= m.
11.(2024.深圳二模)深圳某校数学创新小组使用圭表测量正午太阳高度角,圭表由铅垂的表AB(高2.0米)和水平的圭BC组成.冬至日正午,测得太阳光线AD与圭BC的夹角∠ADB=44°,则冬至日正午表AB落在圭面BC的影长BD为 米.(精确到0.1米,参考数据:sin44°≈0.69,cos44°≈0.71,tan44°≈0.97)
12.(2024.海勃湾区)如图,一渔船在海上A处测得灯塔C在它的北偏东60°方向,渔船向正东方向航行海里到达点B处,测得灯塔C在它的北偏东45°方向,若渔船继续向正东方向航行,则渔船与灯塔C的最短距离是 海里.
三.解答题(共3小题)
13.(2024秋 埇桥区)如图,在△ABC中,AB=5,BC=13,AD是BC边上的高,AD=4.求CD和sinC.
14.(2024秋 埇桥区)如图,一艘渔船在海面上航行,准备要停靠到渔港C,渔船航行到A处时,测得渔港C在北偏东60°方向上,为了躲避A、C之间的暗礁,这艘渔船调整航向,沿着北偏东30°方向继续航行,当它航行到B处后,又沿着南偏东67°方向航行30海里到达渔港C.求渔船从A到C的直线距离.(结果精确到0.1海里,参考数据:sin37°≈0.60,cos37°≈0.8,tan37°≈0.75,
15.(2024.河北)图﹣1是一款可旋转的太阳能路灯,太阳能光伏板面向太阳,且随太阳的升起到落下方向旋转,图﹣2是其侧面示意图,线段AB表示路灯的灯支架,PM为路灯灯杆.线段CD为太阳能光伏板,可绕点P旋转,CD=1m,AB=2m,∠BAM=120°.(图中所有点均在同一平面)(参考数据:sin80°≈0.98,cos80°≈0.17,.结果精确到0.1m)
(1)当C,D,B三点共线时,∠DPM=80°,求PA的长度;
(2)若某一时刻太阳光线与地面l的夹角为60°时,恰好太阳能光伏板CD与PM所成夹角∠DPM=60°,求太阳能光伏板CD落在地面l上的影子EF的长.
中考核心考点 直角三角形的边角关系
参考答案与试题解析
一.选择题(共7小题)
1.(2024.深圳二模)如图,某条楼梯及栏杆可以看作直角三角形ABC与平行四边形ACDE构成,若∠D=59°,则该楼梯的坡角∠BAC的值为( )
A.59° B.41° C.31° D.49°
【考点】解直角三角形的应用﹣坡度坡角问题;平行四边形的性质.
【专题】解直角三角形及其应用;应用意识.
【答案】C
【分析】先根据平行线的性质求出∠ACB,再根据直角三角形的两锐角互余求出∠BAC.
【解答】解:∵四边形ACDE是平行四边形,
∴AC∥DE,
∴∠ACB=∠D=59°,
∵∠ABC=90°,
∴∠BAC=90°﹣∠ABC=90°﹣59°=31°,
故选:C.
【点评】本题考查的是解直角三角形的应用﹣坡度坡角问题,掌握平行四边形的性质、直角三角形的性质是解题的关键.
2.(2024.台江区)如图,将秋千绳索从与竖直方向夹角为α的位置OA1释放到OA处时,两次位置的高度差PA=h.则秋千绳索OA的长为( )
A. B. C. D.
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;推理能力.
【答案】A
【分析】由题意可知,OA=OA1,再根据余弦的定义求解即可.
【解答】解:由题意可知,OA=OA1,
∵cosα,
∴OA1,
又∵OP=OA﹣PA=OA1﹣PA=OA1﹣h,
∴OA,
∴OA=OA1,
故选:A.
【点评】本题考查了解直角三角形的应用,熟记三角形函数的定义是解题的关键.
3.(2025春 定海区)某河堤横断面如图所示,堤高BC=10米,迎水坡AB的坡比是(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是( )
A.米 B.20米 C.米 D.30米
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】运算能力.
【答案】A
【分析】由堤高BC=10米,迎水坡AB的坡比,根据坡度的定义,即可求得AC的长.
【解答】解:∵迎水坡AB的坡比,
∴,
∵堤高BC=10米,
∴(米).
故选:A.
【点评】本题考查了解直角三角形的应用﹣坡度坡角问题,掌握坡比的概念是解题的关键.
4.(2024.西山区)在Rt△ABC中,∠C=90°,AB=10,AC=6,则sinA=( )
A. B. C. D.
【考点】锐角三角函数的定义.
【专题】解直角三角形及其应用;运算能力.
【答案】A
【分析】由勾股定理求出BC=8,由锐角的正弦定义即可求出sinA的值.
【解答】解:∵∠C=90°,AB=10,AC=6,
∴BC8,
sinA.
故选:A.
【点评】本题考查锐角三角函数定义,关键是掌握锐角的正弦定义.
5.(2024.五华区一模)如图,点A、B、C在边长为1的正方形网格格点上,则下列结论不正确的是( )
A.△ABC是直角三角形 B.
C. D.tanC=2
【考点】解直角三角形;勾股定理;勾股定理的逆定理.
【专题】等腰三角形与直角三角形;推理能力.
【答案】C
【分析】根据勾股定理得出AB,AC,BC的长,进而利用勾股定理的逆定理得出△ABC是直角三角形,然后结合解直角三角函数的性质进而解答即可.
【解答】解:由勾股定理得:,,,
∴BC2=AB2+AC2,
∴△ABC是直角三角形,∠BAC=90°,
∴,,,
故选:C.
【点评】此题考查的是解直角三角形,勾股定理,勾股定理的逆定理,熟记锐角三角函数的定义是解题的关键.
6.(2024.郑州)一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力F1的方向与斜面垂直,摩擦力F2的方向与斜面平行.若斜面的坡角α=25°,则摩擦力F2与重力G方向的夹角β的度数为( )
A.155° B.125° C.115° D.65°
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】C
【分析】根据题意结合图形可知β是重力G与斜面形成的三角形的外角,从而可求得β的度数.
【解答】解:∵重力G的方向竖直向下,
∴重力G与水平方向夹角为90°,
由题意可得:
∴β=∠1=α+90°=115°,
故选:C.
【点评】本题考查了平行线的性质和三角形外角性质,正确进行计算是解题关键.
7.(2024.宝安区)港珠澳大桥是世界上最长的跨海大桥,被誉为“现代世界七大奇迹”的超级工程,它是我国从桥梁大国走向桥梁强国的里程碑之作.港珠澳大桥主桥为三座大跨度钢结构斜拉桥,其中九洲航道桥主塔造型取自“风帆”,寓意“扬帆起航”,某校九年级学生为了测量该主塔的高度,站在B处看塔顶A,仰角为60°,然后向后走190米,到达C处,此时看塔顶A,仰角为30°,则该主塔的高度是( )
A.95米 B.米 C.190米 D.米
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】B
【分析】该主塔为AD=x,在Rt△ABD中,利用正切函数的定义求得,同理,在Rt△ACD中,求得,根据CD﹣BD=190,列出方程求解即可.
【解答】解:如图,该主塔为AD=x,
由题意,得:∠ADC=90°,BC=190,∠ACD=30°,∠ABD=60°,
∵,
∴,
∵,
∴,
∵BC=CD﹣BD=190,
∴,
∴.
故选:B.
【点评】本题考查解直角三角形的实际应用,正确进行计算是解题关键.
二.填空题(共5小题)
8.(2024秋 海港区)社团活动课上,九年级学习小组测量学校旗杆的高度.如图,他们在B处测得旗杆顶部A的仰角为60°,BC=8m,则旗杆AC的高度为 m.
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;几何直观.
【答案】.
【分析】在Rt△ABC中,tan∠ABC=tan60°,可得AC=BC tan60°m.
【解答】解:在Rt△ABC中,tan∠ABC=tan60°,
∴AC=BC tan60°(m).
故答案为:.
【点评】本题考查解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解答本题的关键.
9.(2024.兴庆区)为出行方便,越来越多的市民使用起了共享单车,图1为单车实物图,图2为单车示意图,AB与地面平行,坐垫C可沿射线BE方向调节.已知∠ABE=70°,车轮半径为33cm,当BC=60cm时,小明体验后觉得骑着比较舒适,此时坐垫C离地面高度约为 89 cm.(结果精确到1cm,参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.74)
【考点】解直角三角形的应用.
【专题】等腰三角形与直角三角形;应用意识.
【答案】89.
【分析】本题主要考查解直角三角形的应用,作CH⊥AB于H,作AP⊥地面于P,利用三角函数求出CH+AP即可.
【解答】解:如图2,作CH⊥AB于H,作AP⊥地面于P,
∵∠ABE=70°,车轮半径为33cm,BC=60cm,
∴AP=33cm,
∴CH=BC sin70°≈60×0.94=56.4(cm),
∴坐垫C离地面高度约为56.4+33≈89(cm),
故答案为:89.
【点评】本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形是解题的关键.
10.(2024.湖北)如图是小区内一小山的等高线示意图,小明同学计划利用这个等高线示意图计算AB的距离,他在点B处测得A处的俯角为30°,则AB= 100 m.
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;应用意识.
【答案】100.
【分析】根据由等高线可知A、B两地的高度差为50米,然后点B处测得A处的俯角为30°求值即可.
【解答】解:作示意图如下:
由题意知:A、B两地的实际高度差为AH:550﹣500=50(m),∠B=30°,∠AHB=90°,
∴sinB,即sin30°,
解得:AB=100,
故答案为:100.
【点评】本题主要考查了解直角三角形的应用﹣仰角俯角问题,解答本题的关键是根据题意,作出直角三角形解决问题.
11.(2024.深圳二模)深圳某校数学创新小组使用圭表测量正午太阳高度角,圭表由铅垂的表AB(高2.0米)和水平的圭BC组成.冬至日正午,测得太阳光线AD与圭BC的夹角∠ADB=44°,则冬至日正午表AB落在圭面BC的影长BD为 2.1 米.(精确到0.1米,参考数据:sin44°≈0.69,cos44°≈0.71,tan44°≈0.97)
【考点】解直角三角形的应用;平行投影.
【专题】解直角三角形及其应用;运算能力;应用意识.
【答案】2.1.
【分析】依据题意,圭表由铅垂的表AB(高2.0米)和水平的圭BC组成,结合冬至日正午,太阳光线AD与圭BC的夹角为∠ADB=44°,从而在直角三角形ABD中,AB为垂直高度(2.0米),BD为水平影长,太阳高度角∠ADB=44°,可得,进而2.1(米),故可得解.
【解答】解:由题意,圭表由铅垂的表AB(高2.0米)和水平的圭BC组成,
又∵冬至日正午,太阳光线AD与圭BC的夹角为∠ADB=44°,
∴在直角三角形ABD中,AB为垂直高度(2.0米),BD为水平影长,太阳高度角∠ADB=44°.
∴.
∴2.1(米).
故答案为:2.1.
【点评】本题主要考查了解直角三角形的应用、平行投影,解题时要熟练掌握并能利用锐角三角形函数求解是关键.
12.(2024.海勃湾区)如图,一渔船在海上A处测得灯塔C在它的北偏东60°方向,渔船向正东方向航行海里到达点B处,测得灯塔C在它的北偏东45°方向,若渔船继续向正东方向航行,则渔船与灯塔C的最短距离是 1 海里.
【考点】解直角三角形的应用﹣方向角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】1.
【分析】过点C作CD⊥AB,垂足为D,根据题意可得:AB=(1)海里,然后设CD=x海里,分别在Rt△ACD和Rt△BCD中,利用锐角三角函数的定义求出AD和BD的长,从而列出关于x的方程,进行计算即可解答.
【解答】解:过点C作CD⊥AB,垂足为D,
由题意得:AB=(1)海里,
设CD=x海里,
在Rt△ACD中,∠CAD=90°﹣60°=30°,
∴ADx(海里),
在Rt△BCD中,∠CBD=90°﹣45°=45°,
∴BDx(海里),
∵AD﹣BD=AB,
∴x﹣x1,
解得:x=1,
∴CD=1海里,
∴渔船与灯塔C的最短距离是1海里,
故答案为:1.
【点评】本题考查了解直角三角形的应用﹣方向角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
三.解答题(共3小题)
13.(2024秋 埇桥区)如图,在△ABC中,AB=5,BC=13,AD是BC边上的高,AD=4.求CD和sinC.
【考点】解直角三角形.
【答案】见试题解答内容
【分析】先解直角三角形ABD,得出BD的值,求出CD的值.再解直角三角形ADC求sinC的值.
【解答】解:在Rt△ABD中,由勾股定理,得:
BD
∴CD=BC﹣BD=10;
在Rt△ADC中,
AC
∴sinC.
【点评】本题考查了解直角三角形中三角函数的应用,要熟练掌握好边角之间的关系.
14.(2024秋 埇桥区)如图,一艘渔船在海面上航行,准备要停靠到渔港C,渔船航行到A处时,测得渔港C在北偏东60°方向上,为了躲避A、C之间的暗礁,这艘渔船调整航向,沿着北偏东30°方向继续航行,当它航行到B处后,又沿着南偏东67°方向航行30海里到达渔港C.求渔船从A到C的直线距离.(结果精确到0.1海里,参考数据:sin37°≈0.60,cos37°≈0.8,tan37°≈0.75,
【考点】解直角三角形的应用﹣方向角问题.
【专题】解直角三角形及其应用;应用意识.
【答案】AC的距离约为59.5海里.
【分析】过B作BD⊥AC于D,在Rt△DBC中,利用正弦函数求得BD≈24.0海里,CD≈18.0海里,再在Rt△ABD中,利用正切函数求出AD≈41.5海里即可得到答案.
【解答】解:如图,过B作BD⊥AC于D,
由题意可知∠BAF=30°,∠FAC=60°,∠CBE=67°,BC=30海里,
∴∠BAC=30°,∠ABE=∠BAF=30°
∴∠C=180°﹣∠BAC﹣∠ABE﹣∠CBE=53°,
在Rt△DBC中,∠BDC=90°,∠C=53°,BC=30海里,
∴∠CBD=37°,
∴CD=BC sin∠CBD≈30×0.60=18.0海里,BD=BC cos∠CBD≈30×0.8=24.0(海里),
在Rt△ABD中,∠BDA=90°,∠BAD=30°,
∴(海里),
∴AC=AD+CD=41.5+18.0=59.5(海里),
∴AC的距离约为59.5海里.
【点评】本题考查了解直角三角形的应用﹣方向角问题,正确作出辅助线构造直角三角形是解题的关键.
15.(2024.河北)图﹣1是一款可旋转的太阳能路灯,太阳能光伏板面向太阳,且随太阳的升起到落下方向旋转,图﹣2是其侧面示意图,线段AB表示路灯的灯支架,PM为路灯灯杆.线段CD为太阳能光伏板,可绕点P旋转,CD=1m,AB=2m,∠BAM=120°.(图中所有点均在同一平面)(参考数据:sin80°≈0.98,cos80°≈0.17,.结果精确到0.1m)
(1)当C,D,B三点共线时,∠DPM=80°,求PA的长度;
(2)若某一时刻太阳光线与地面l的夹角为60°时,恰好太阳能光伏板CD与PM所成夹角∠DPM=60°,求太阳能光伏板CD落在地面l上的影子EF的长.
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】(1)2.0m;
(2)1.2m.
【分析】(1)连接BD,过点B作BE⊥PM于点E,先解Rt△ABE,求得AE,BE,进而解Rt△PBE,求得PE,进而根据PA=PE+AE,即可求解;
(2)连接DF,CE,过点F作FH⊥CE于点H,设PM,DF交于点G,证明四边形CDFH是平行四边形,则FH=CD=1,解Rt△EFH,即可求解.
【解答】解:(1)连接BD,过点B作BE⊥PM于点E,
在Rt△ABE中,∠BAE=180°﹣∠BAM=60°,
∴,,
当C,D,B三点共线时,在Rt△PBE中,∠BPE=∠DPM=80°,
∴,
∴PA=PE+AE≈0.3+1.73≈2.0m;
(2)如图,
连接DF,CE,过点F作FH⊥CE于点H,设PM,DF交于点G,
∵∠GFM=60°,∠GMF=90°,
∴∠DPG=∠MGF=30°,
又∠DPM=60°,
∴∠PDG=90°,
由题意可得:FH⊥DF
∴CD∥FH,
∴四边形CDFH是平行四边形,
∴FH=CD=1,
∵∠HEF=∠DFM=60°,
,
答:EF的长为1.2m.
【点评】本题主要考查了解直角三角形的应用,解题的关键是熟练掌握三角函数的定义,作出辅助线构造直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
