【中考核心考点】2025年北师大版中考数学考前冲刺 直线和圆的位置关系(含解析)
文档属性
| 名称 | 【中考核心考点】2025年北师大版中考数学考前冲刺 直线和圆的位置关系(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中考核心考点 直线和圆的位置关系
一.选择题(共7小题)
1.(2024.平房区二模)如图,在△ABC中,AC=BC,以AB上一点O为圆心,OA为半径的圆与BC相切于点C,若,则⊙O的半径为( )
A.4 B.3 C. D.
2.(2024.洛阳二模)如图,AB为⊙O的直径,PB,PC分别与⊙O相切于点B,C,过点C作AB的垂线,垂足为E,交⊙O于点D.若,则⊙O的半径长为( )
A.1 B.2 C.3 D.4
3.(2024.海口一模)如图,△ABC是⊙O的内接三角形,∠A=116°,过点C作⊙O的切线CD交BO的延长线于点D,则∠D的度数为( )
A.36° B.38° C.40° D.42°
4.(2024.郑州)如图,一个边长为4的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点D,则图中阴影部分的面积为( )
A.π B.2π C.π D.π
5.(2024秋 孝昌县)如图,OA交⊙O于点B,AC切⊙O于点C,D点在⊙O上.若∠D=25°,则∠A为( )
A.25° B.40° C.50° D.65°
6.(2024.滨江区开学)如图,直线m与半径为3的⊙O相切于点A,C是⊙O上的一个动点(不与点A重合),过点C作CB⊥m,垂足为点B,连结AC,设AC=x,CB=y,则x﹣y的最大值为( )
A. B.1 C. D.2
7.(2024.九龙坡区二模)如图,已知四边形ABCD是⊙O的内接四边形,且AD=BC,过点D作⊙O的切线交BA的延长线于点E,连接OB、OC,若∠BOC=64°,则∠ADE的度数为( )
A.32° B.36° C.26° D.32.5°
二.填空题(共5小题)
8.(2024.南岗区)如图,AB与⊙O相切于点A,连接OA,点C在⊙O上,连接BC并延长BC交⊙O于点D,连接DO,若∠AOC=80°,∠DOC=40°,则∠B= 度.
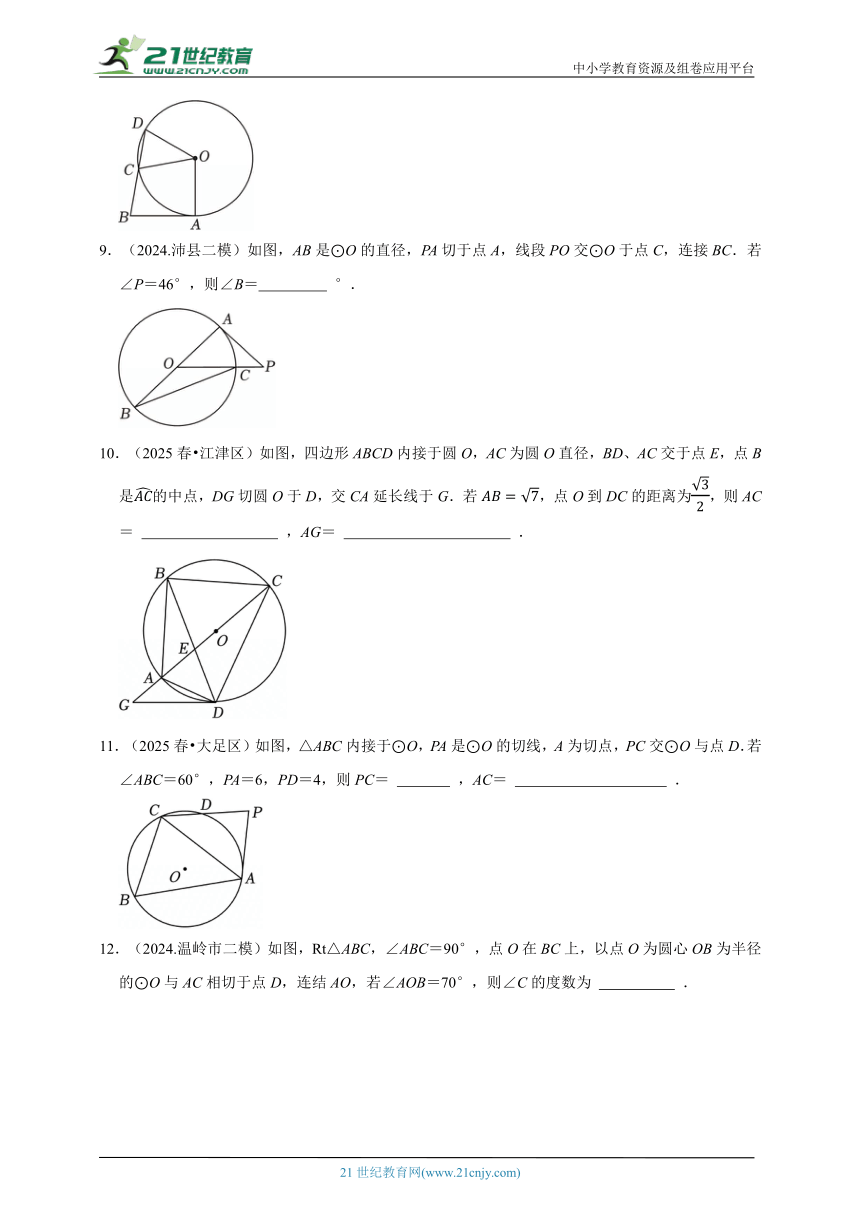
9.(2024.沛县二模)如图,AB是⊙O的直径,PA切于点A,线段PO交⊙O于点C,连接BC.若∠P=46°,则∠B= °.
10.(2025春 江津区)如图,四边形ABCD内接于圆O,AC为圆O直径,BD、AC交于点E,点B是的中点,DG切圆O于D,交CA延长线于G.若,点O到DC的距离为,则AC= ,AG= .
11.(2025春 大足区)如图,△ABC内接于⊙O,PA是⊙O的切线,A为切点,PC交⊙O与点D.若∠ABC=60°,PA=6,PD=4,则PC= ,AC= .
12.(2024.温岭市二模)如图,Rt△ABC,∠ABC=90°,点O在BC上,以点O为圆心OB为半径的⊙O与AC相切于点D,连结AO,若∠AOB=70°,则∠C的度数为 .
三.解答题(共3小题)
13.(2024.庐江县二模)如图,AB为⊙O的直径,BC为⊙O的切线,连接AC交⊙O于点D,DH⊥AB于点H,E是的中点,连接AE并延长交BC于点F,交DH,DB于点M,N.
(1)求证:DM=DN;
(2)AD=4,BD=3,求EF的长.
14.(2024.兴庆区)已知,如图,AB为⊙O的直径,△ABC内接于⊙O,BC>AC,点P是△ABC的内心,延长CP交⊙O于点D,连接BP.
(1)求证:BD=PD;
(2)已知⊙O的半径是,CD=8,求BC的长.
15.(2024秋 海港区)如图,AB为半圆O的直径,点F在半圆上,连接OF,点P在AB的延长线上,PC与半圆相切于点C,与OF的延长线相交于点D.连接AC与OF相交于点E,OD⊥AB.
(1)求证:DC=DE;
(2)若OA=2OE,DF=2,求PD的长.
中考核心考点 直线和圆的位置关系
参考答案与试题解析
一.选择题(共7小题)
1.(2024.平房区二模)如图,在△ABC中,AC=BC,以AB上一点O为圆心,OA为半径的圆与BC相切于点C,若,则⊙O的半径为( )
A.4 B.3 C. D.
【考点】切线的性质;等腰三角形的性质.
【专题】与圆有关的位置关系;推理能力.
【答案】A
【分析】连接OC,根据切线的性质得到OC⊥BC,根据圆周角定理得到∠BOC=2∠A,求出∠B=30°,再根据正切的定义计算即可.
【解答】解:如图,连接OC,
∵BC是⊙O的切线,
∴OC⊥BC,
∴∠BOC+∠A=90°,
∵AC=BC,
∴∠A=∠B,
由圆周角定理得:∠BOC=2∠A,
∴∠B=30°,
∴OC=BC tanB=44,
故选:A.
【点评】本题考查的是切线的性质、圆周角定理,熟记圆的切线垂直于经过切点的半径是解题的关键.
2.(2024.洛阳二模)如图,AB为⊙O的直径,PB,PC分别与⊙O相切于点B,C,过点C作AB的垂线,垂足为E,交⊙O于点D.若,则⊙O的半径长为( )
A.1 B.2 C.3 D.4
【考点】切线的性质.
【专题】与圆有关的位置关系;推理能力.
【答案】B
【分析】连接OD、BD,根据切线的性质得到PC=PB=2,AB⊥PB,根据平行四边形的性质求出BD,根据勾股定理求出BE,再根据勾股定理计算即可.
【解答】解:如图,连接OD、BD,
∵PB,PC分别与⊙O相切于点B,C,
∴PC=PB=2,AB⊥PB,
∵AB⊥CD,
∴CD∥PB,
∵CD=PB,
∴四边形CPBD为平行四边形,
∴BD=PC=2,
∵AB⊥CD,
∴DECD,
由勾股定理得:BE3,
在Rt△DOE中,OD2=OE2+DE2,即OD2=(3﹣OD)2+()2,
解得:OD=2,
故选:B.
【点评】本题考查的是切线的性质、圆周角定理,熟记圆的切线垂直于经过切点的半径是解题的关键.
3.(2024.海口一模)如图,△ABC是⊙O的内接三角形,∠A=116°,过点C作⊙O的切线CD交BO的延长线于点D,则∠D的度数为( )
A.36° B.38° C.40° D.42°
【考点】切线的性质;圆周角定理;三角形的外接圆与外心.
【专题】与圆有关的位置关系;运算能力.
【答案】B
【分析】连接OC,设DB交⊙O于点M,连接CM,切线的性质,得到∠OCD=90°,圆内接四边形的性质结合等边对等角,求出∠OMC,∠OCM的度数,再根据角的和差关系和三角形的外角的性质,进行求解即可.
【解答】解:连接OC,设DB交⊙O于点M,连接CM,则:OC=OM,
由题意可得:∠OCD=90°,
∵∠A=116°,
∴∠OMC=180°﹣116°=64°,
∵OC=OM,
∴∠OCM=∠OMC=64°,
∴∠MCD=∠OCD﹣∠OCM=90°﹣64°=26°,
∵∠BMC=∠MCD+∠D,
∴∠D=64°﹣26°=38°.
故选:B.
【点评】本题考查切线的性质,圆内接四边形的性质,正确进行计算是解题关键.
4.(2024.郑州)如图,一个边长为4的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点D,则图中阴影部分的面积为( )
A.π B.2π C.π D.π
【考点】切线的性质;扇形面积的计算;等边三角形的性质.
【专题】与圆有关的位置关系;与圆有关的计算;推理能力.
【答案】D
【分析】过点A作AE⊥BC于E,过点O作OF⊥CD于F,连接OC、OD,根据等边三角形的性质求出AE,根据切线的性质得到OC⊥BC,求出∠COD=120°,根据扇形面积公式、三角形面积公式计算即可.
【解答】解:如图,过点A作AE⊥BC于E,过点O作OF⊥CD于F,连接OC、OD,
∵△ABC为等边三角形,AE⊥BC,
∴CEBC=2,∠ACB=60°,
由勾股定理得:AE2,
∵⊙O与BC相切于点C,
∴OC⊥BC,
∴∠OCF=90°﹣60°=30°,
∴OFOC,CF,
∵OF⊥CD,
∴∠COF=60°,CD=2CF=3,
∴∠COD=120°,
∴S阴影部分=S扇形COD﹣S△COD3π,
故选:D.
【点评】本题考查的是切线的性质、扇形面积计算,熟记圆的切线垂直于经过切点的半径是解题的关键.
5.(2024秋 孝昌县)如图,OA交⊙O于点B,AC切⊙O于点C,D点在⊙O上.若∠D=25°,则∠A为( )
A.25° B.40° C.50° D.65°
【考点】切线的性质;圆周角定理.
【专题】与圆有关的计算;推理能力.
【答案】B
【分析】根据切线的性质得到∠OCA=90°,根据直角三角形的性质求出∠A.
【解答】解:∵∠D=25°,
∴∠AOC=2∠D=2×25°=50°,
∵AC切⊙O于点C,
∴OC⊥AC
∴∠OCA=90°
∴∠A=90°﹣∠AOC=90°﹣50°=40°,故B正确.
故选:B.
【点评】本题主要考查了切线的性质,圆周角定理,直角三角形性质,解题的关键是熟练掌握圆心与切点的连线垂直切线.
6.(2024.滨江区开学)如图,直线m与半径为3的⊙O相切于点A,C是⊙O上的一个动点(不与点A重合),过点C作CB⊥m,垂足为点B,连结AC,设AC=x,CB=y,则x﹣y的最大值为( )
A. B.1 C. D.2
【考点】切线的性质;相似三角形的判定与性质;二次函数的最值.
【专题】二次函数图象及其性质;与圆有关的位置关系;运算能力.
【答案】C
【分析】作直径AP,连接CP,得出△APC∽△CAB,得比例式,得出yx2,代入所求式配方后即可解答.
【解答】解:如图,作直径AP,连接CP,
∴∠ACP=90°,
∵AB是切线,
∴PA⊥AB,
∵CB⊥m,
∴AP∥CB,
∴∠CAP=∠ACB,
∴△APC∽△CAB,
∴,
∵CA=x,CB=y,半径为3,
∴,
∴yx2,
∴x﹣y=xx2x2+x(x﹣3)2,
当x=3时,x﹣y有最大值是;
故选:C.
【点评】此题考查了切线的性质,平行线的性质和判定,相似三角形的判定与性质,以及二次函数的性质,熟练掌握二次函数的性质是解本题的关键.
7.(2024.九龙坡区二模)如图,已知四边形ABCD是⊙O的内接四边形,且AD=BC,过点D作⊙O的切线交BA的延长线于点E,连接OB、OC,若∠BOC=64°,则∠ADE的度数为( )
A.32° B.36° C.26° D.32.5°
【考点】切线的性质;圆周角定理;圆内接四边形的性质.
【专题】与圆有关的位置关系;推理能力.
【答案】A
【分析】连接OA,OD,由AD=BC,得到,求得∠AOD=∠BOC=64°,根据等腰三角形的性质得到∠ODA=∠OAD(180°﹣∠AOD)(180°﹣64°)=58°,根据切线的性质得到∠ODE=90°,于是得到∠ADE=∠ODE﹣∠ODA=90°﹣58°=32°.
【解答】解:连接OA,OD,
∵AD=BC,
∴,
∴∠AOD=∠BOC=64°,
∵OA=OD,
∴∠ODA=∠OAD(180°﹣∠AOD)(180°﹣64°)=58°,
∵DE是⊙O的切线,
∴∠ODE=90°,
∴∠ADE=∠ODE﹣∠ODA=90°﹣58°=32°,
故选:A.
【点评】本题考查了切线的性质,圆周角定理,等腰三角形的性质,正确地找出辅助线是解题的关键.
二.填空题(共5小题)
8.(2024.南岗区)如图,AB与⊙O相切于点A,连接OA,点C在⊙O上,连接BC并延长BC交⊙O于点D,连接DO,若∠AOC=80°,∠DOC=40°,则∠B= 80 度.
【考点】切线的性质;圆周角定理.
【专题】多边形与平行四边形;圆的有关概念及性质;与圆有关的位置关系;运算能力;推理能力.
【答案】80.
【分析】由切线的性质得∠A=90°,由OC=OD,得∠OCD=∠D,而∠AOC=80°,∠DOC=40°,则∠AOD=120°,2∠D+40°=180°,求得∠D=70°,则∠B=360°﹣∠A﹣∠AOD﹣∠D=80°,于是得到问题的答案.
【解答】解:∵AB与⊙O相切于点A,
∴AB⊥OA,
∴∠A=90°,
∵OC=OD,
∴∠OCD=∠D,
∵∠AOC=80°,∠DOC=40°,且∠OCD+∠D+∠DOC=180°,
∴∠AOD=∠AOC+∠DOC=120°,2∠D+40°=180°,
∴∠D=70°,
∴∠B=360°﹣∠A﹣∠AOD﹣∠D=80°,
故答案为:80.
【点评】此题重点考查切线的性质、等腰三角形的性质、三角形内角和定理、四边形的内角和等于360°等知识,推导出AB⊥OA,并且求得∠D=70°是解题的关键.
9.(2024.沛县二模)如图,AB是⊙O的直径,PA切于点A,线段PO交⊙O于点C,连接BC.若∠P=46°,则∠B= 22 °.
【考点】切线的性质;圆周角定理.
【专题】与圆有关的位置关系;运算能力.
【答案】22.
【分析】根据切线的性质可得∠PAB=90°,进而可得∠POA的度数,然后根据圆周角定理即得答案.
【解答】解:由切线的性质可得:∠PAB=90°,
∵∠P=46°,
∴∠POA=90°﹣46°=44°,
∵,
∴.
故答案为:22.
【点评】本题考查了圆的切线的性质、直角三角形的性质、圆周角定理,正确进行计算是解题关键.
10.(2025春 江津区)如图,四边形ABCD内接于圆O,AC为圆O直径,BD、AC交于点E,点B是的中点,DG切圆O于D,交CA延长线于G.若,点O到DC的距离为,则AC= ,AG= .
【考点】切线的性质;垂径定理;圆周角定理.
【专题】与圆有关的位置关系;推理能力.
【答案】,.
【分析】过O点作OH⊥CD于H点,连结OD,如图,则OH,先根据圆周角定理得到∠ABC=∠ADC=90°,再判断△ABC为等腰直角三角形得到ACAB,接着证明OH为△ACD的中位线得到AD=2OH,则利用勾股定理可计算出CD,然后根据切线的性质得到∠ODG=90°,接着证明△GAD∽△GDC得到,,所以DGAG,从而得到(AG)2=AG (AG),于是可求出AG的长.
【解答】解:过O点作OH⊥CD于H点,连结OD,如图,则OH,
∵AC为⊙O直径,
∴∠ABC=∠ADC=90°,
∵点B是的中点,
∴AB=BC,
∴△ABC为等腰直角三角形,
∴ACAB,
∵OH⊥CD,
∴CH=DH,
而OA=OC,
∴AD=2OH,
在Rt△ADC中,CD,
∵DG为切线,
∴OD⊥DG,
∴∠ODG=90°,
∵∠ADG+∠ODA=90°,∠ODC+∠ODA=90°,
∴∠ADG=∠ODC,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ADG=∠OCD,
∵∠AGD=∠DGC,
∴△GAD∽△GDC,
∴,,
即DGAG,
∴(AG)2=AG (AG),
解得AG= .
故答案为:,.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理和相似三角形的判定与性质.
11.(2025春 大足区)如图,△ABC内接于⊙O,PA是⊙O的切线,A为切点,PC交⊙O与点D.若∠ABC=60°,PA=6,PD=4,则PC= 6 ,AC= 3+3 .
【考点】切线的性质;三角形的外接圆与外心.
【专题】与圆有关的位置关系;推理能力.
【答案】6,3+3.
【分析】连接OA、OC,过P点作PH⊥AC于H点,如图,根据圆周角定理得到∠AOC=120°,再利用等腰三角形的性质和三角形内角和定理求出∠OAC=30°,接着根据切线的性质得到∠OAP=90°,则∠PAC=60°,然后根据切割线定理得到PC9,接着利用含30度的直角三角形三边的关系得到AH=3,PH=3,最后利用勾股定理计算出CH,从而得到AC的长.
【解答】解:连接OA、OC,过P点作PH⊥AC于H点,如图,
∵∠AOC=2∠ABC=120°,
而OA=OC,
∴∠OAC(1280°﹣120°)=30°,
∵PA是⊙O的切线,A为切点,
∴OA⊥PA,
∴∠OAP=90°,
∴∠PAC=90°﹣30°=60°,
∵PA为⊙O的切线,PC为割线,
∴PA2=PD PC,
∴PC9,
在Rt△APH中,∵∠PAH=60°,
∴AHPA=3,
∴PHAH=3,
在Rt△PCH中,CH3,
∴AC=AH+CH=3+6.
故答案为:6,3+3.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了切割线定理.
12.(2024.温岭市二模)如图,Rt△ABC,∠ABC=90°,点O在BC上,以点O为圆心OB为半径的⊙O与AC相切于点D,连结AO,若∠AOB=70°,则∠C的度数为 50° .
【考点】切线的性质;全等三角形的判定与性质;圆周角定理.
【专题】图形的全等;与圆有关的位置关系;推理能力.
【答案】50°.
【分析】连接OD,根据切线性质得到∠ADO=90,根据全等三角形的性质得到∠AOD=∠AOB=70°,求得∠COD=180°﹣70°﹣70°=40°,得到∠C=90°﹣40°=50°.
【解答】解:连接OD,
∵AC是⊙O的切线,
∴∠ADO=90,
∴∠ABC=∠ADO=90°,
∵OB=OD,AO=AO,
∴Rt△ABO≌Rt△ADO(HL),
∴∠AOD=∠AOB=70°,
∴∠COD=180°﹣70°﹣70°=40°,
∴∠C=90°﹣40°=50°,
故答案为:50°.
【点评】本题考查了切线的性质,全等三角形的判定和性质,正确地作出辅助线是解题的关键.
三.解答题(共3小题)
13.(2024.庐江县二模)如图,AB为⊙O的直径,BC为⊙O的切线,连接AC交⊙O于点D,DH⊥AB于点H,E是的中点,连接AE并延长交BC于点F,交DH,DB于点M,N.
(1)求证:DM=DN;
(2)AD=4,BD=3,求EF的长.
【考点】切线的性质;勾股定理;垂径定理;圆周角定理.
【专题】等腰三角形与直角三角形;圆的有关概念及性质;与圆有关的位置关系;推理能力.
【答案】(1)证明见解答过程;
(2).
【分析】(1)根据切线的性质求出∠ABC=90°,结合垂直的定义、平行线的判定与性质、圆周角定理求出∠AND=∠DMF=∠AFB=∠FNB,再根据等腰三角形的判定即可得证;
(2)连接BE,过点N作NG⊥AB于点G,根据圆周角定理、角平分线的性质定理求出DN=GN,根据勾股定理求出AB=5,根据三角形面积公式求出,,根据勾股定理求出AN,AF,则NF=AF﹣AN,再根据等腰三角形的性质求解即可.
【解答】(1)证明:∵BC为⊙O的切线,
∴∠ABC=90°,
∴∠FAB+∠AFB=90°,
∵DH⊥AB,
∴∠AHD=90°=∠ABC,
∴DH∥BC,
∴∠DMF=∠AFB,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠FAD+∠AND=90°,
∵E是的中点,
∴,
∴∠FAD=∠FAB,
∴∠AND=∠AFB,
∴∠AND=∠DMF=∠AFB=∠FNB,
∴DM=DN;
(2)解:连接BE,过点N作NG⊥AB于点G,
∵,
∴∠FAD=∠FAB,
∵NG⊥AB,∠ADB=90°,
∴DN=GN,
∵AD=4,BD=3,
∴AB5,
∴,
∴,
∴,
∴,
由(1)知∠AFB=∠FNB,
∴,
∴,
∴NF=AF﹣AN,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴.
【点评】此题考查了切线的性质、勾股定理、圆周角定理等知识,熟练运用切线的性质、勾股定理、圆周角定理是解题的关键.
14.(2024.兴庆区)已知,如图,AB为⊙O的直径,△ABC内接于⊙O,BC>AC,点P是△ABC的内心,延长CP交⊙O于点D,连接BP.
(1)求证:BD=PD;
(2)已知⊙O的半径是,CD=8,求BC的长.
【考点】三角形的内切圆与内心;三角形的外接圆与外心.
【专题】推理能力.
【答案】(1)见解析;
(2).
【分析】(1)由圆周角定理得出∠ACB=90°,由内心得出∠ACD=∠BCP=45°,∠CBP=∠EBP,∠ABD=∠ACD=45°,由三角形的外角性质得出∠DPB=∠DBP,即可得出结论;
(2)连接AD,过点B作BH⊥CD于H,由圆周角定理得出∠ABD=45°,证出△ABD是等腰直角三角形,得出,由∠BCD=45°,BH⊥CD,推出BH=CH,得到,根据勾股定理可求BH的长,即可得出结果.
【解答】(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∵点P是△ABC的内心,
∴∠ACD=∠BCP=45°,∠CBP=∠EBP,
∴∠ABD=∠ACD=45°,
∵∠DPB=∠BCP+∠CBP=45°+∠CBP,∠DBP=∠ABD+∠EBP=45°+∠EBP,
∴∠DPB=∠DBP,
∴BD=DP;
(2)解:连接AD,过点B作BH⊥CD于H,
∵AB为⊙O的直径,⊙O的半径是,∠ABD=45°,
∴,
∵∠ABD=45°,
∴△ABD是等腰直角三角形,
∴,
∵BH⊥CD,
∴∠BHE=90°,
∵∠BCD=45°,
∴∠BCH=∠CBH=45°,
∴BH=CH,
∴,
∵BD2=DH2+BH2,
∴36=(8﹣BH)2+BH2,
∴,
∴,
∵BC>AC,AC2+BC2=AB2=72,
∴BC>6,
∴.
【点评】本题考查了三角形的内切圆与内心、圆周角定理、三角形的外角性质、等腰三角形的判定、等腰直角三角形的判定与性质等知识,掌握相关知识是解题的关键.
15.(2024秋 海港区)如图,AB为半圆O的直径,点F在半圆上,连接OF,点P在AB的延长线上,PC与半圆相切于点C,与OF的延长线相交于点D.连接AC与OF相交于点E,OD⊥AB.
(1)求证:DC=DE;
(2)若OA=2OE,DF=2,求PD的长.
【考点】切线的性质.
【专题】等腰三角形与直角三角形;与圆有关的位置关系;图形的相似;运算能力;推理能力.
【答案】(1)证明见解析;
(2).
【分析】(1)连接OC,由切线的性质推出∠OCD=90°,由余角的性质推出∠DCE=∠AEO,由对顶角的性质得到∠DEC=∠AEO,因此∠DCE=∠DEC,推出DC=DE;
(2)设OE=x,由勾股定理得到(2x+2)2=(2+x)2+(2x)2,求出x=4,得到DC=6,OC=8,判定△PCO∽△OCD,推出CO:CD=PC:OC,求出PC,即可得到PD的长.
【解答】(1)证明:连接OC,
∵PC与半圆相切于点C,
∴半径OC⊥PC,
∴∠OCD=90°,
∴∠DCE+∠OCE=90°,
∵OD⊥AB,
∴∠AOE=90°,
∴∠AEO+∠OAE=90°,
∵OA=OC,
∴∠OCE=∠OAE,
∴∠DCE=∠AEO,
∵∠DEC=∠AEO,
∴∠DCE=∠DEC,
∴DC=DE;
(2)解:设OE=x,
∵OF=OA=2OE=2x,
∴EF=OE=x,OD=OF+DF=2x+2,
∴DE=DF+FE=2+x,
由(1)知:DC=DE=2+x,
∵∠OCD=90°,
∴OD2=CD2+OC2,
∴(2x+2)2=(2+x)2+(2x)2,
∴x=4,
∴DC=2+x=6,OC=2x=8,
∵∠P+∠POC=∠COD+∠POC=90°,
∴∠P=∠COD,
∵∠PCO=∠DCO,
∴△PCO∽△OCD,
∴CO:CD=PC:OC,
∴8:6=PC:8,
∴PC,
∴PD=PC+DC6.
【点评】本题考查切线的性质,相似三角形的判定和性质,勾股定理,关键是由切线的性质推出∠OCD=90°,由余角的性质和对顶角的性质推出∠DCE=∠DEC,由勾股定理列出关于x的方程,判定△PCO∽△OCD,推出CO:CD=PC:OC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考核心考点 直线和圆的位置关系
一.选择题(共7小题)
1.(2024.平房区二模)如图,在△ABC中,AC=BC,以AB上一点O为圆心,OA为半径的圆与BC相切于点C,若,则⊙O的半径为( )
A.4 B.3 C. D.
2.(2024.洛阳二模)如图,AB为⊙O的直径,PB,PC分别与⊙O相切于点B,C,过点C作AB的垂线,垂足为E,交⊙O于点D.若,则⊙O的半径长为( )
A.1 B.2 C.3 D.4
3.(2024.海口一模)如图,△ABC是⊙O的内接三角形,∠A=116°,过点C作⊙O的切线CD交BO的延长线于点D,则∠D的度数为( )
A.36° B.38° C.40° D.42°
4.(2024.郑州)如图,一个边长为4的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点D,则图中阴影部分的面积为( )
A.π B.2π C.π D.π
5.(2024秋 孝昌县)如图,OA交⊙O于点B,AC切⊙O于点C,D点在⊙O上.若∠D=25°,则∠A为( )
A.25° B.40° C.50° D.65°
6.(2024.滨江区开学)如图,直线m与半径为3的⊙O相切于点A,C是⊙O上的一个动点(不与点A重合),过点C作CB⊥m,垂足为点B,连结AC,设AC=x,CB=y,则x﹣y的最大值为( )
A. B.1 C. D.2
7.(2024.九龙坡区二模)如图,已知四边形ABCD是⊙O的内接四边形,且AD=BC,过点D作⊙O的切线交BA的延长线于点E,连接OB、OC,若∠BOC=64°,则∠ADE的度数为( )
A.32° B.36° C.26° D.32.5°
二.填空题(共5小题)
8.(2024.南岗区)如图,AB与⊙O相切于点A,连接OA,点C在⊙O上,连接BC并延长BC交⊙O于点D,连接DO,若∠AOC=80°,∠DOC=40°,则∠B= 度.
9.(2024.沛县二模)如图,AB是⊙O的直径,PA切于点A,线段PO交⊙O于点C,连接BC.若∠P=46°,则∠B= °.
10.(2025春 江津区)如图,四边形ABCD内接于圆O,AC为圆O直径,BD、AC交于点E,点B是的中点,DG切圆O于D,交CA延长线于G.若,点O到DC的距离为,则AC= ,AG= .
11.(2025春 大足区)如图,△ABC内接于⊙O,PA是⊙O的切线,A为切点,PC交⊙O与点D.若∠ABC=60°,PA=6,PD=4,则PC= ,AC= .
12.(2024.温岭市二模)如图,Rt△ABC,∠ABC=90°,点O在BC上,以点O为圆心OB为半径的⊙O与AC相切于点D,连结AO,若∠AOB=70°,则∠C的度数为 .
三.解答题(共3小题)
13.(2024.庐江县二模)如图,AB为⊙O的直径,BC为⊙O的切线,连接AC交⊙O于点D,DH⊥AB于点H,E是的中点,连接AE并延长交BC于点F,交DH,DB于点M,N.
(1)求证:DM=DN;
(2)AD=4,BD=3,求EF的长.
14.(2024.兴庆区)已知,如图,AB为⊙O的直径,△ABC内接于⊙O,BC>AC,点P是△ABC的内心,延长CP交⊙O于点D,连接BP.
(1)求证:BD=PD;
(2)已知⊙O的半径是,CD=8,求BC的长.
15.(2024秋 海港区)如图,AB为半圆O的直径,点F在半圆上,连接OF,点P在AB的延长线上,PC与半圆相切于点C,与OF的延长线相交于点D.连接AC与OF相交于点E,OD⊥AB.
(1)求证:DC=DE;
(2)若OA=2OE,DF=2,求PD的长.
中考核心考点 直线和圆的位置关系
参考答案与试题解析
一.选择题(共7小题)
1.(2024.平房区二模)如图,在△ABC中,AC=BC,以AB上一点O为圆心,OA为半径的圆与BC相切于点C,若,则⊙O的半径为( )
A.4 B.3 C. D.
【考点】切线的性质;等腰三角形的性质.
【专题】与圆有关的位置关系;推理能力.
【答案】A
【分析】连接OC,根据切线的性质得到OC⊥BC,根据圆周角定理得到∠BOC=2∠A,求出∠B=30°,再根据正切的定义计算即可.
【解答】解:如图,连接OC,
∵BC是⊙O的切线,
∴OC⊥BC,
∴∠BOC+∠A=90°,
∵AC=BC,
∴∠A=∠B,
由圆周角定理得:∠BOC=2∠A,
∴∠B=30°,
∴OC=BC tanB=44,
故选:A.
【点评】本题考查的是切线的性质、圆周角定理,熟记圆的切线垂直于经过切点的半径是解题的关键.
2.(2024.洛阳二模)如图,AB为⊙O的直径,PB,PC分别与⊙O相切于点B,C,过点C作AB的垂线,垂足为E,交⊙O于点D.若,则⊙O的半径长为( )
A.1 B.2 C.3 D.4
【考点】切线的性质.
【专题】与圆有关的位置关系;推理能力.
【答案】B
【分析】连接OD、BD,根据切线的性质得到PC=PB=2,AB⊥PB,根据平行四边形的性质求出BD,根据勾股定理求出BE,再根据勾股定理计算即可.
【解答】解:如图,连接OD、BD,
∵PB,PC分别与⊙O相切于点B,C,
∴PC=PB=2,AB⊥PB,
∵AB⊥CD,
∴CD∥PB,
∵CD=PB,
∴四边形CPBD为平行四边形,
∴BD=PC=2,
∵AB⊥CD,
∴DECD,
由勾股定理得:BE3,
在Rt△DOE中,OD2=OE2+DE2,即OD2=(3﹣OD)2+()2,
解得:OD=2,
故选:B.
【点评】本题考查的是切线的性质、圆周角定理,熟记圆的切线垂直于经过切点的半径是解题的关键.
3.(2024.海口一模)如图,△ABC是⊙O的内接三角形,∠A=116°,过点C作⊙O的切线CD交BO的延长线于点D,则∠D的度数为( )
A.36° B.38° C.40° D.42°
【考点】切线的性质;圆周角定理;三角形的外接圆与外心.
【专题】与圆有关的位置关系;运算能力.
【答案】B
【分析】连接OC,设DB交⊙O于点M,连接CM,切线的性质,得到∠OCD=90°,圆内接四边形的性质结合等边对等角,求出∠OMC,∠OCM的度数,再根据角的和差关系和三角形的外角的性质,进行求解即可.
【解答】解:连接OC,设DB交⊙O于点M,连接CM,则:OC=OM,
由题意可得:∠OCD=90°,
∵∠A=116°,
∴∠OMC=180°﹣116°=64°,
∵OC=OM,
∴∠OCM=∠OMC=64°,
∴∠MCD=∠OCD﹣∠OCM=90°﹣64°=26°,
∵∠BMC=∠MCD+∠D,
∴∠D=64°﹣26°=38°.
故选:B.
【点评】本题考查切线的性质,圆内接四边形的性质,正确进行计算是解题关键.
4.(2024.郑州)如图,一个边长为4的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点D,则图中阴影部分的面积为( )
A.π B.2π C.π D.π
【考点】切线的性质;扇形面积的计算;等边三角形的性质.
【专题】与圆有关的位置关系;与圆有关的计算;推理能力.
【答案】D
【分析】过点A作AE⊥BC于E,过点O作OF⊥CD于F,连接OC、OD,根据等边三角形的性质求出AE,根据切线的性质得到OC⊥BC,求出∠COD=120°,根据扇形面积公式、三角形面积公式计算即可.
【解答】解:如图,过点A作AE⊥BC于E,过点O作OF⊥CD于F,连接OC、OD,
∵△ABC为等边三角形,AE⊥BC,
∴CEBC=2,∠ACB=60°,
由勾股定理得:AE2,
∵⊙O与BC相切于点C,
∴OC⊥BC,
∴∠OCF=90°﹣60°=30°,
∴OFOC,CF,
∵OF⊥CD,
∴∠COF=60°,CD=2CF=3,
∴∠COD=120°,
∴S阴影部分=S扇形COD﹣S△COD3π,
故选:D.
【点评】本题考查的是切线的性质、扇形面积计算,熟记圆的切线垂直于经过切点的半径是解题的关键.
5.(2024秋 孝昌县)如图,OA交⊙O于点B,AC切⊙O于点C,D点在⊙O上.若∠D=25°,则∠A为( )
A.25° B.40° C.50° D.65°
【考点】切线的性质;圆周角定理.
【专题】与圆有关的计算;推理能力.
【答案】B
【分析】根据切线的性质得到∠OCA=90°,根据直角三角形的性质求出∠A.
【解答】解:∵∠D=25°,
∴∠AOC=2∠D=2×25°=50°,
∵AC切⊙O于点C,
∴OC⊥AC
∴∠OCA=90°
∴∠A=90°﹣∠AOC=90°﹣50°=40°,故B正确.
故选:B.
【点评】本题主要考查了切线的性质,圆周角定理,直角三角形性质,解题的关键是熟练掌握圆心与切点的连线垂直切线.
6.(2024.滨江区开学)如图,直线m与半径为3的⊙O相切于点A,C是⊙O上的一个动点(不与点A重合),过点C作CB⊥m,垂足为点B,连结AC,设AC=x,CB=y,则x﹣y的最大值为( )
A. B.1 C. D.2
【考点】切线的性质;相似三角形的判定与性质;二次函数的最值.
【专题】二次函数图象及其性质;与圆有关的位置关系;运算能力.
【答案】C
【分析】作直径AP,连接CP,得出△APC∽△CAB,得比例式,得出yx2,代入所求式配方后即可解答.
【解答】解:如图,作直径AP,连接CP,
∴∠ACP=90°,
∵AB是切线,
∴PA⊥AB,
∵CB⊥m,
∴AP∥CB,
∴∠CAP=∠ACB,
∴△APC∽△CAB,
∴,
∵CA=x,CB=y,半径为3,
∴,
∴yx2,
∴x﹣y=xx2x2+x(x﹣3)2,
当x=3时,x﹣y有最大值是;
故选:C.
【点评】此题考查了切线的性质,平行线的性质和判定,相似三角形的判定与性质,以及二次函数的性质,熟练掌握二次函数的性质是解本题的关键.
7.(2024.九龙坡区二模)如图,已知四边形ABCD是⊙O的内接四边形,且AD=BC,过点D作⊙O的切线交BA的延长线于点E,连接OB、OC,若∠BOC=64°,则∠ADE的度数为( )
A.32° B.36° C.26° D.32.5°
【考点】切线的性质;圆周角定理;圆内接四边形的性质.
【专题】与圆有关的位置关系;推理能力.
【答案】A
【分析】连接OA,OD,由AD=BC,得到,求得∠AOD=∠BOC=64°,根据等腰三角形的性质得到∠ODA=∠OAD(180°﹣∠AOD)(180°﹣64°)=58°,根据切线的性质得到∠ODE=90°,于是得到∠ADE=∠ODE﹣∠ODA=90°﹣58°=32°.
【解答】解:连接OA,OD,
∵AD=BC,
∴,
∴∠AOD=∠BOC=64°,
∵OA=OD,
∴∠ODA=∠OAD(180°﹣∠AOD)(180°﹣64°)=58°,
∵DE是⊙O的切线,
∴∠ODE=90°,
∴∠ADE=∠ODE﹣∠ODA=90°﹣58°=32°,
故选:A.
【点评】本题考查了切线的性质,圆周角定理,等腰三角形的性质,正确地找出辅助线是解题的关键.
二.填空题(共5小题)
8.(2024.南岗区)如图,AB与⊙O相切于点A,连接OA,点C在⊙O上,连接BC并延长BC交⊙O于点D,连接DO,若∠AOC=80°,∠DOC=40°,则∠B= 80 度.
【考点】切线的性质;圆周角定理.
【专题】多边形与平行四边形;圆的有关概念及性质;与圆有关的位置关系;运算能力;推理能力.
【答案】80.
【分析】由切线的性质得∠A=90°,由OC=OD,得∠OCD=∠D,而∠AOC=80°,∠DOC=40°,则∠AOD=120°,2∠D+40°=180°,求得∠D=70°,则∠B=360°﹣∠A﹣∠AOD﹣∠D=80°,于是得到问题的答案.
【解答】解:∵AB与⊙O相切于点A,
∴AB⊥OA,
∴∠A=90°,
∵OC=OD,
∴∠OCD=∠D,
∵∠AOC=80°,∠DOC=40°,且∠OCD+∠D+∠DOC=180°,
∴∠AOD=∠AOC+∠DOC=120°,2∠D+40°=180°,
∴∠D=70°,
∴∠B=360°﹣∠A﹣∠AOD﹣∠D=80°,
故答案为:80.
【点评】此题重点考查切线的性质、等腰三角形的性质、三角形内角和定理、四边形的内角和等于360°等知识,推导出AB⊥OA,并且求得∠D=70°是解题的关键.
9.(2024.沛县二模)如图,AB是⊙O的直径,PA切于点A,线段PO交⊙O于点C,连接BC.若∠P=46°,则∠B= 22 °.
【考点】切线的性质;圆周角定理.
【专题】与圆有关的位置关系;运算能力.
【答案】22.
【分析】根据切线的性质可得∠PAB=90°,进而可得∠POA的度数,然后根据圆周角定理即得答案.
【解答】解:由切线的性质可得:∠PAB=90°,
∵∠P=46°,
∴∠POA=90°﹣46°=44°,
∵,
∴.
故答案为:22.
【点评】本题考查了圆的切线的性质、直角三角形的性质、圆周角定理,正确进行计算是解题关键.
10.(2025春 江津区)如图,四边形ABCD内接于圆O,AC为圆O直径,BD、AC交于点E,点B是的中点,DG切圆O于D,交CA延长线于G.若,点O到DC的距离为,则AC= ,AG= .
【考点】切线的性质;垂径定理;圆周角定理.
【专题】与圆有关的位置关系;推理能力.
【答案】,.
【分析】过O点作OH⊥CD于H点,连结OD,如图,则OH,先根据圆周角定理得到∠ABC=∠ADC=90°,再判断△ABC为等腰直角三角形得到ACAB,接着证明OH为△ACD的中位线得到AD=2OH,则利用勾股定理可计算出CD,然后根据切线的性质得到∠ODG=90°,接着证明△GAD∽△GDC得到,,所以DGAG,从而得到(AG)2=AG (AG),于是可求出AG的长.
【解答】解:过O点作OH⊥CD于H点,连结OD,如图,则OH,
∵AC为⊙O直径,
∴∠ABC=∠ADC=90°,
∵点B是的中点,
∴AB=BC,
∴△ABC为等腰直角三角形,
∴ACAB,
∵OH⊥CD,
∴CH=DH,
而OA=OC,
∴AD=2OH,
在Rt△ADC中,CD,
∵DG为切线,
∴OD⊥DG,
∴∠ODG=90°,
∵∠ADG+∠ODA=90°,∠ODC+∠ODA=90°,
∴∠ADG=∠ODC,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ADG=∠OCD,
∵∠AGD=∠DGC,
∴△GAD∽△GDC,
∴,,
即DGAG,
∴(AG)2=AG (AG),
解得AG= .
故答案为:,.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理和相似三角形的判定与性质.
11.(2025春 大足区)如图,△ABC内接于⊙O,PA是⊙O的切线,A为切点,PC交⊙O与点D.若∠ABC=60°,PA=6,PD=4,则PC= 6 ,AC= 3+3 .
【考点】切线的性质;三角形的外接圆与外心.
【专题】与圆有关的位置关系;推理能力.
【答案】6,3+3.
【分析】连接OA、OC,过P点作PH⊥AC于H点,如图,根据圆周角定理得到∠AOC=120°,再利用等腰三角形的性质和三角形内角和定理求出∠OAC=30°,接着根据切线的性质得到∠OAP=90°,则∠PAC=60°,然后根据切割线定理得到PC9,接着利用含30度的直角三角形三边的关系得到AH=3,PH=3,最后利用勾股定理计算出CH,从而得到AC的长.
【解答】解:连接OA、OC,过P点作PH⊥AC于H点,如图,
∵∠AOC=2∠ABC=120°,
而OA=OC,
∴∠OAC(1280°﹣120°)=30°,
∵PA是⊙O的切线,A为切点,
∴OA⊥PA,
∴∠OAP=90°,
∴∠PAC=90°﹣30°=60°,
∵PA为⊙O的切线,PC为割线,
∴PA2=PD PC,
∴PC9,
在Rt△APH中,∵∠PAH=60°,
∴AHPA=3,
∴PHAH=3,
在Rt△PCH中,CH3,
∴AC=AH+CH=3+6.
故答案为:6,3+3.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了切割线定理.
12.(2024.温岭市二模)如图,Rt△ABC,∠ABC=90°,点O在BC上,以点O为圆心OB为半径的⊙O与AC相切于点D,连结AO,若∠AOB=70°,则∠C的度数为 50° .
【考点】切线的性质;全等三角形的判定与性质;圆周角定理.
【专题】图形的全等;与圆有关的位置关系;推理能力.
【答案】50°.
【分析】连接OD,根据切线性质得到∠ADO=90,根据全等三角形的性质得到∠AOD=∠AOB=70°,求得∠COD=180°﹣70°﹣70°=40°,得到∠C=90°﹣40°=50°.
【解答】解:连接OD,
∵AC是⊙O的切线,
∴∠ADO=90,
∴∠ABC=∠ADO=90°,
∵OB=OD,AO=AO,
∴Rt△ABO≌Rt△ADO(HL),
∴∠AOD=∠AOB=70°,
∴∠COD=180°﹣70°﹣70°=40°,
∴∠C=90°﹣40°=50°,
故答案为:50°.
【点评】本题考查了切线的性质,全等三角形的判定和性质,正确地作出辅助线是解题的关键.
三.解答题(共3小题)
13.(2024.庐江县二模)如图,AB为⊙O的直径,BC为⊙O的切线,连接AC交⊙O于点D,DH⊥AB于点H,E是的中点,连接AE并延长交BC于点F,交DH,DB于点M,N.
(1)求证:DM=DN;
(2)AD=4,BD=3,求EF的长.
【考点】切线的性质;勾股定理;垂径定理;圆周角定理.
【专题】等腰三角形与直角三角形;圆的有关概念及性质;与圆有关的位置关系;推理能力.
【答案】(1)证明见解答过程;
(2).
【分析】(1)根据切线的性质求出∠ABC=90°,结合垂直的定义、平行线的判定与性质、圆周角定理求出∠AND=∠DMF=∠AFB=∠FNB,再根据等腰三角形的判定即可得证;
(2)连接BE,过点N作NG⊥AB于点G,根据圆周角定理、角平分线的性质定理求出DN=GN,根据勾股定理求出AB=5,根据三角形面积公式求出,,根据勾股定理求出AN,AF,则NF=AF﹣AN,再根据等腰三角形的性质求解即可.
【解答】(1)证明:∵BC为⊙O的切线,
∴∠ABC=90°,
∴∠FAB+∠AFB=90°,
∵DH⊥AB,
∴∠AHD=90°=∠ABC,
∴DH∥BC,
∴∠DMF=∠AFB,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠FAD+∠AND=90°,
∵E是的中点,
∴,
∴∠FAD=∠FAB,
∴∠AND=∠AFB,
∴∠AND=∠DMF=∠AFB=∠FNB,
∴DM=DN;
(2)解:连接BE,过点N作NG⊥AB于点G,
∵,
∴∠FAD=∠FAB,
∵NG⊥AB,∠ADB=90°,
∴DN=GN,
∵AD=4,BD=3,
∴AB5,
∴,
∴,
∴,
∴,
由(1)知∠AFB=∠FNB,
∴,
∴,
∴NF=AF﹣AN,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴.
【点评】此题考查了切线的性质、勾股定理、圆周角定理等知识,熟练运用切线的性质、勾股定理、圆周角定理是解题的关键.
14.(2024.兴庆区)已知,如图,AB为⊙O的直径,△ABC内接于⊙O,BC>AC,点P是△ABC的内心,延长CP交⊙O于点D,连接BP.
(1)求证:BD=PD;
(2)已知⊙O的半径是,CD=8,求BC的长.
【考点】三角形的内切圆与内心;三角形的外接圆与外心.
【专题】推理能力.
【答案】(1)见解析;
(2).
【分析】(1)由圆周角定理得出∠ACB=90°,由内心得出∠ACD=∠BCP=45°,∠CBP=∠EBP,∠ABD=∠ACD=45°,由三角形的外角性质得出∠DPB=∠DBP,即可得出结论;
(2)连接AD,过点B作BH⊥CD于H,由圆周角定理得出∠ABD=45°,证出△ABD是等腰直角三角形,得出,由∠BCD=45°,BH⊥CD,推出BH=CH,得到,根据勾股定理可求BH的长,即可得出结果.
【解答】(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∵点P是△ABC的内心,
∴∠ACD=∠BCP=45°,∠CBP=∠EBP,
∴∠ABD=∠ACD=45°,
∵∠DPB=∠BCP+∠CBP=45°+∠CBP,∠DBP=∠ABD+∠EBP=45°+∠EBP,
∴∠DPB=∠DBP,
∴BD=DP;
(2)解:连接AD,过点B作BH⊥CD于H,
∵AB为⊙O的直径,⊙O的半径是,∠ABD=45°,
∴,
∵∠ABD=45°,
∴△ABD是等腰直角三角形,
∴,
∵BH⊥CD,
∴∠BHE=90°,
∵∠BCD=45°,
∴∠BCH=∠CBH=45°,
∴BH=CH,
∴,
∵BD2=DH2+BH2,
∴36=(8﹣BH)2+BH2,
∴,
∴,
∵BC>AC,AC2+BC2=AB2=72,
∴BC>6,
∴.
【点评】本题考查了三角形的内切圆与内心、圆周角定理、三角形的外角性质、等腰三角形的判定、等腰直角三角形的判定与性质等知识,掌握相关知识是解题的关键.
15.(2024秋 海港区)如图,AB为半圆O的直径,点F在半圆上,连接OF,点P在AB的延长线上,PC与半圆相切于点C,与OF的延长线相交于点D.连接AC与OF相交于点E,OD⊥AB.
(1)求证:DC=DE;
(2)若OA=2OE,DF=2,求PD的长.
【考点】切线的性质.
【专题】等腰三角形与直角三角形;与圆有关的位置关系;图形的相似;运算能力;推理能力.
【答案】(1)证明见解析;
(2).
【分析】(1)连接OC,由切线的性质推出∠OCD=90°,由余角的性质推出∠DCE=∠AEO,由对顶角的性质得到∠DEC=∠AEO,因此∠DCE=∠DEC,推出DC=DE;
(2)设OE=x,由勾股定理得到(2x+2)2=(2+x)2+(2x)2,求出x=4,得到DC=6,OC=8,判定△PCO∽△OCD,推出CO:CD=PC:OC,求出PC,即可得到PD的长.
【解答】(1)证明:连接OC,
∵PC与半圆相切于点C,
∴半径OC⊥PC,
∴∠OCD=90°,
∴∠DCE+∠OCE=90°,
∵OD⊥AB,
∴∠AOE=90°,
∴∠AEO+∠OAE=90°,
∵OA=OC,
∴∠OCE=∠OAE,
∴∠DCE=∠AEO,
∵∠DEC=∠AEO,
∴∠DCE=∠DEC,
∴DC=DE;
(2)解:设OE=x,
∵OF=OA=2OE=2x,
∴EF=OE=x,OD=OF+DF=2x+2,
∴DE=DF+FE=2+x,
由(1)知:DC=DE=2+x,
∵∠OCD=90°,
∴OD2=CD2+OC2,
∴(2x+2)2=(2+x)2+(2x)2,
∴x=4,
∴DC=2+x=6,OC=2x=8,
∵∠P+∠POC=∠COD+∠POC=90°,
∴∠P=∠COD,
∵∠PCO=∠DCO,
∴△PCO∽△OCD,
∴CO:CD=PC:OC,
∴8:6=PC:8,
∴PC,
∴PD=PC+DC6.
【点评】本题考查切线的性质,相似三角形的判定和性质,勾股定理,关键是由切线的性质推出∠OCD=90°,由余角的性质和对顶角的性质推出∠DCE=∠DEC,由勾股定理列出关于x的方程,判定△PCO∽△OCD,推出CO:CD=PC:OC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
