【中考核心考点】2025年华东师大版中考数学考前冲刺 二次函数(含解析)
文档属性
| 名称 | 【中考核心考点】2025年华东师大版中考数学考前冲刺 二次函数(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 550.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-16 07:48:22 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中考核心考点 二次函数
一.选择题(共7小题)
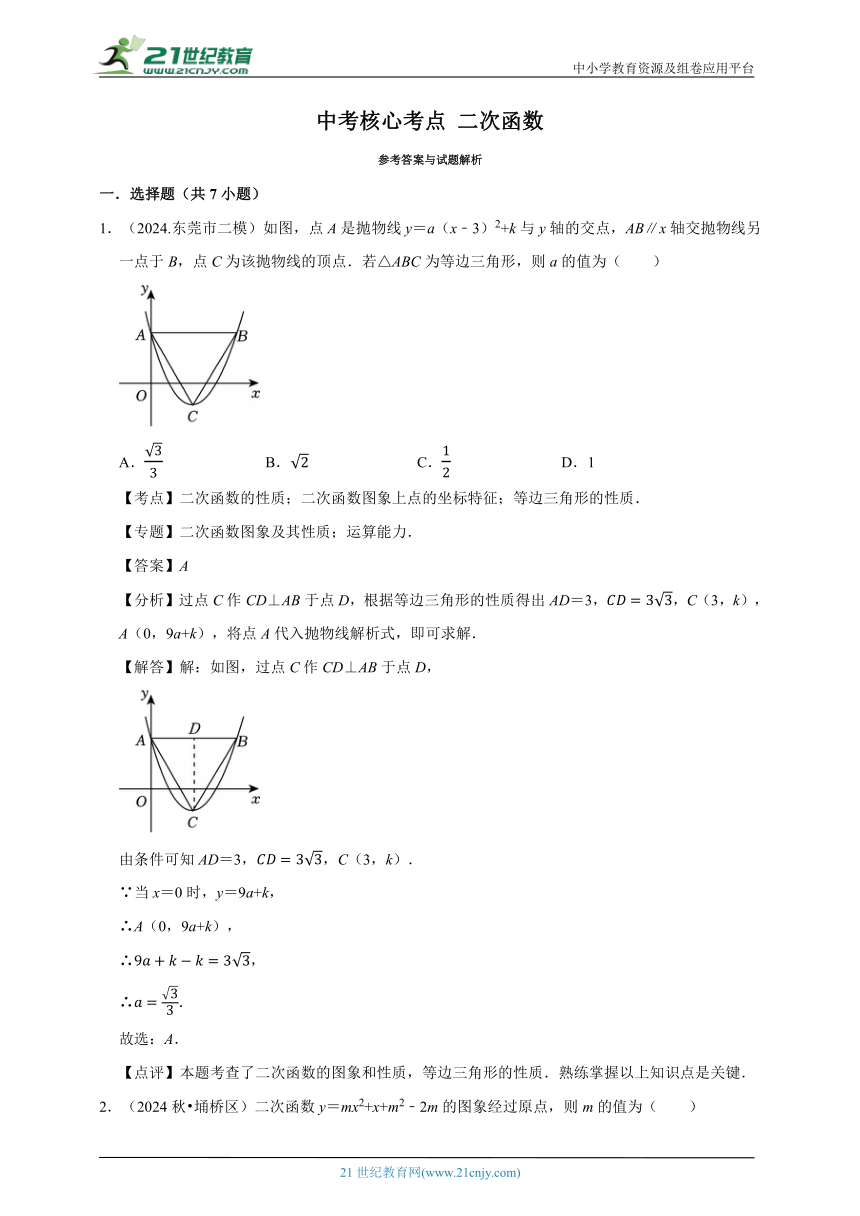
1.(2024.东莞市二模)如图,点A是抛物线y=a(x﹣3)2+k与y轴的交点,AB∥x轴交抛物线另一点于B,点C为该抛物线的顶点.若△ABC为等边三角形,则a的值为( )
A. B. C. D.1
2.(2024秋 埇桥区)二次函数y=mx2+x+m2﹣2m的图象经过原点,则m的值为( )
A.0 B.2 C.2或0 D.无法确定
3.(2024.新都区)关于二次函数y=ax2﹣2ax﹣3a(a是常数且a>0),下列说法正确的是( )
A.函数图象开口向下
B.对称轴为直线x=﹣1
C.函数图象与x轴没有交点
D.在y轴左侧,y的值随x值的增大而减小
4.(2024.淮南二模)对于抛物线y=﹣5(x﹣1)2+3,下列判断正确的是( )
A.抛物线的开口向上
B.抛物线的顶点坐标是(﹣1,3)
C.对称轴为直线x=1
D.当x=3时,y>0
5.(2024.金东区二模)将二次函数y=﹣x2的图象先向下平移2个单位,再向右平移2个单位所得新函数表达式为( )
A.y=﹣(x﹣2)2+2 B.y=﹣(x+2)2﹣2
C.y=﹣(x+2)2+2 D.y=﹣(x﹣2)2﹣2
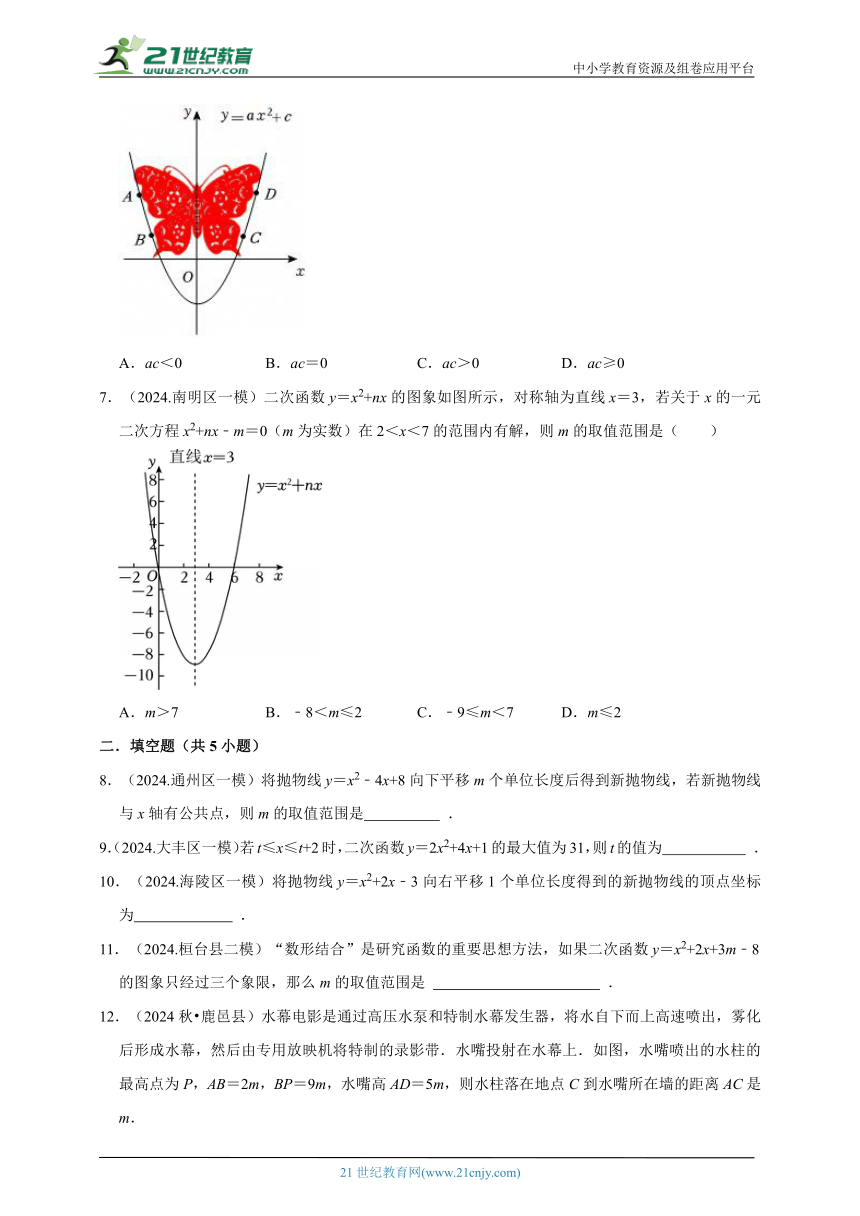
6.(2024.崇左二模)剪纸是我国的民间传统艺术,能为节日增加许多喜庆的氛围.剪纸中有一种“抛物线剪纸”艺术,即作品的外轮廓在抛物线上,体现了一种曲线美,如图,这是利用“抛物线剪纸”艺术剪出的蝴蝶,建立适当的平面直角坐标系,使外轮廓上的A,B,C,D四点落在抛物线y=ax2+c上,则下列结论正确的是( )
A.ac<0 B.ac=0 C.ac>0 D.ac≥0
7.(2024.南明区一模)二次函数y=x2+nx的图象如图所示,对称轴为直线x=3,若关于x的一元二次方程x2+nx﹣m=0(m为实数)在2<x<7的范围内有解,则m的取值范围是( )
A.m>7 B.﹣8<m≤2 C.﹣9≤m<7 D.m≤2
二.填空题(共5小题)
8.(2024.通州区一模)将抛物线y=x2﹣4x+8向下平移m个单位长度后得到新抛物线,若新抛物线与x轴有公共点,则m的取值范围是 .
9.(2024.大丰区一模)若t≤x≤t+2时,二次函数y=2x2+4x+1的最大值为31,则t的值为 .
10.(2024.海陵区一模)将抛物线y=x2+2x﹣3向右平移1个单位长度得到的新抛物线的顶点坐标为 .
11.(2024.桓台县二模)“数形结合”是研究函数的重要思想方法,如果二次函数y=x2+2x+3m﹣8的图象只经过三个象限,那么m的取值范围是 .
12.(2024秋 鹿邑县)水幕电影是通过高压水泵和特制水幕发生器,将水自下而上高速喷出,雾化后形成水幕,然后由专用放映机将特制的录影带.水嘴投射在水幕上.如图,水嘴喷出的水柱的最高点为P,AB=2m,BP=9m,水嘴高AD=5m,则水柱落在地点C到水嘴所在墙的距离AC是 m.
三.解答题(共3小题)
13.(2024秋 埇桥区)如图在平面直角坐标系xOy中,O为坐标原点,二次函数y=x2+bx+c的图象经过点A(3,0)、点B(0,3),顶点为M.
(1)求该二次函数的解析式;
(2)求∠OBM的正切值.
14.(2024.通州区一模)已知关于x的二次函数y=ax2﹣6ax+5a.
(1)若x=2时,y=﹣3,求该函数的解析式;
(2)当a>0,2≤x≤6时,该函数的最大值与最小值的差为18,求a的值;
(3)若A(x1,y1),B(x2,y2)是该函数图象上的两点,且对于x1=a+3,4≤x2≤6,都有y1≥y2,求a的取值范围.
15.(2024.濮阳一模)在节假日期间,濮阳龙湖论语广场的音乐喷泉上演了绚丽的灯光秀.随着音乐的节拍,喷泉的水线起伏跳跃,勾勒出迷人的抛物线图案.假设喷泉的出水口为坐标原点,出水口离岸边18米.随着音乐的变化,抛物线的顶点在直线y=kx(k≠0)上变动,从而产生一组不同的抛物线,设这组抛物线的统一形式为y=ax2+bx(a<0).
(1)若,
①若喷出的水恰好达到岸边,则此时喷出的抛物线形水线最大高度是多少米?
②若喷出的抛物线形水线最大高度为4m,求a、b的值;
(2)当音乐节奏加快,抛物线的顶点在直线y=x上,喷出的水不能触及岸边.请直接写出此时a的取值范围.
中考核心考点 二次函数
参考答案与试题解析
一.选择题(共7小题)
1.(2024.东莞市二模)如图,点A是抛物线y=a(x﹣3)2+k与y轴的交点,AB∥x轴交抛物线另一点于B,点C为该抛物线的顶点.若△ABC为等边三角形,则a的值为( )
A. B. C. D.1
【考点】二次函数的性质;二次函数图象上点的坐标特征;等边三角形的性质.
【专题】二次函数图象及其性质;运算能力.
【答案】A
【分析】过点C作CD⊥AB于点D,根据等边三角形的性质得出AD=3,,C(3,k),A(0,9a+k),将点A代入抛物线解析式,即可求解.
【解答】解:如图,过点C作CD⊥AB于点D,
由条件可知AD=3,,C(3,k).
∵当x=0时,y=9a+k,
∴A(0,9a+k),
∴,
∴.
故选:A.
【点评】本题考查了二次函数的图象和性质,等边三角形的性质.熟练掌握以上知识点是关键.
2.(2024秋 埇桥区)二次函数y=mx2+x+m2﹣2m的图象经过原点,则m的值为( )
A.0 B.2 C.2或0 D.无法确定
【考点】二次函数的性质;二次函数图象上点的坐标特征.
【专题】二次函数图象及其性质;运算能力.
【答案】B
【分析】把(0,0)代入y=mx2+x+m2﹣2m求解,注意m的取值范围.
【解答】解:由条件可得m2﹣2m=0,
解得m=0或m=2,
∵m≠0,
∴m=2,
故选:B.
【点评】本题考查二次函数的性质,解题关键是掌握二次函数与方程的关系,注意二次函数二次项系数不为0.
3.(2024.新都区)关于二次函数y=ax2﹣2ax﹣3a(a是常数且a>0),下列说法正确的是( )
A.函数图象开口向下
B.对称轴为直线x=﹣1
C.函数图象与x轴没有交点
D.在y轴左侧,y的值随x值的增大而减小
【考点】抛物线与x轴的交点;二次函数的性质.
【专题】二次函数图象及其性质;应用意识.
【答案】D
【分析】由a>0,可得函数图象开口向上;二次函数y=ax2﹣2ax﹣3a图象的对称轴为直线x1;根据Δ=(﹣2a)2﹣4a×(﹣3a)=4a2+12a2=16a2>0,可知函数图象与x轴有两个交点;结合图象可知,在y轴左侧,y的值随x值的增大而减小,即可得出答案.
【解答】解:∵a>0,
∴函数图象开口向上,
故A选项不正确,不符合题意;
二次函数y=ax2﹣2ax﹣3a图象的对称轴为直线x1,
故B选项不正确,不符合题意;
∵Δ=(﹣2a)2﹣4a×(﹣3a)=4a2+12a2=16a2>0,
∴函数图象与x轴有两个交点,
故C选项不正确,不符合题意;
∵函数图象开口向上,对称轴为直线x=1,
∴在y轴左侧,y的值随x值的增大而减小,
故D选项正确,符合题意.
故选:D.
【点评】本题考查抛物线与x轴的交点、二次函数的性质,解题的关键是理解题意,灵活运用所学知识解决问题.
4.(2024.淮南二模)对于抛物线y=﹣5(x﹣1)2+3,下列判断正确的是( )
A.抛物线的开口向上
B.抛物线的顶点坐标是(﹣1,3)
C.对称轴为直线x=1
D.当x=3时,y>0
【考点】二次函数的性质.
【专题】二次函数图象及其性质;运算能力;推理能力.
【答案】C
【分析】根据二次函数解析式结合二次函数的性质,即可得出结论.
【解答】解:A、∵﹣5<0,
∴抛物线的开口向下,本选项错误,
B、抛物线的顶点为(1,3),本选项错误,
C、抛物线的对称轴为直线x=1,本选项正确,
D、把x=3代入y=﹣5(x﹣1)2+3,解得:y=﹣17<0,本选项错误,
故选:C.
【点评】本题考查了二次函数的性质,根据二次函数的性质逐一对照四个选项即可得出结论.
5.(2024.金东区二模)将二次函数y=﹣x2的图象先向下平移2个单位,再向右平移2个单位所得新函数表达式为( )
A.y=﹣(x﹣2)2+2 B.y=﹣(x+2)2﹣2
C.y=﹣(x+2)2+2 D.y=﹣(x﹣2)2﹣2
【考点】二次函数图象与几何变换.
【专题】二次函数图象及其性质;应用意识.
【答案】D
【分析】根据“上加下减,左加右减”的平移规律,即得答案.
【解答】解:将二次函数y=﹣x2的图象先向下平移2个单位,再向右平移2个单位所得新函数表达式为y=﹣(x﹣2)2﹣2.
故选:D.
【点评】本题考查了二次函数的平移,正确理解二次函数的平移规律是解答本题的关键.
6.(2024.崇左二模)剪纸是我国的民间传统艺术,能为节日增加许多喜庆的氛围.剪纸中有一种“抛物线剪纸”艺术,即作品的外轮廓在抛物线上,体现了一种曲线美,如图,这是利用“抛物线剪纸”艺术剪出的蝴蝶,建立适当的平面直角坐标系,使外轮廓上的A,B,C,D四点落在抛物线y=ax2+c上,则下列结论正确的是( )
A.ac<0 B.ac=0 C.ac>0 D.ac≥0
【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【答案】A
【分析】根据抛物线开口向上,与y轴交于负半轴,即可判断a,c的符号,即可求解.
【解答】解:建立适当的平面直角坐标系,使外轮廓上的A,B,C,D四点落在抛物线y=ax2+c上,
∵根据抛物线开口向上,与y轴交于负半轴,
∴a>0,c<0,则ac<0,
故选:A.
【点评】本题考查了二次函数的应用,解答本题的关键是熟练掌握二次函数图象与系数的关系.
7.(2024.南明区一模)二次函数y=x2+nx的图象如图所示,对称轴为直线x=3,若关于x的一元二次方程x2+nx﹣m=0(m为实数)在2<x<7的范围内有解,则m的取值范围是( )
A.m>7 B.﹣8<m≤2 C.﹣9≤m<7 D.m≤2
【考点】抛物线与x轴的交点;二次函数的性质.
【专题】二次函数图象及其性质;应用意识.
【答案】C
【分析】若关于x的一元二次方程x2+nx﹣m=0(m为实数)在2<x<7的范围内有解,则二次函数y=x2+nx的图象与直线y=m在2<x<7的范围内有交点.由题意可得,解得n=﹣6,则二次函数解析式为y=x2﹣6x,进而可得二次函数y=x2﹣6x的图象的顶点坐标为(3,﹣9),当x=7时,y=7,再结合图象可得m的取值范围是﹣9≤m<7.
【解答】解:∵关于x的一元二次方程x2+nx﹣m=0(m为实数)在2<x<7的范围内有解,
∴二次函数y=x2+nx的图象与直线y=m在2<x<7的范围内有交点.
∵二次函数y=x2+nx的图象的对称轴为直线x=3,
∴,
解得n=﹣6,
∴二次函数解析式为y=x2﹣6x,
∴二次函数y=x2﹣6x的图象的顶点坐标为(3,﹣9),当x=7时,y=7,
∴m的取值范围是﹣9≤m<7.
故选:C.
【点评】本题考查抛物线与x轴的交点、二次函数的性质,解题的关键是理解题意,灵活运用所学知识解决问题.
二.填空题(共5小题)
8.(2024.通州区一模)将抛物线y=x2﹣4x+8向下平移m个单位长度后得到新抛物线,若新抛物线与x轴有公共点,则m的取值范围是 m≥4 .
【考点】抛物线与x轴的交点;二次函数的性质;二次函数图象与几何变换.
【专题】二次函数图象及其性质;运算能力.
【答案】m≥4.
【分析】先根据平移的规律写出抛物线y=x2﹣4x+8向下平移m个单位长度后的抛物线的表达式,再根据平移后得到的抛物线与x轴有公共点可得Δ≥0,由此列不等式即可求出m的取值范围.
【解答】解:平移m个单位长度得y=x2﹣4x+8﹣m,
由题意可得:
∴Δ≥0,
即(﹣4)2﹣4(8﹣m)≥0,
∴m≥4,
故答案为:m≥4.
【点评】此题考查了二次函数图象的平移与几何变换,以及抛物线与x轴的交点问题,利用抛物线解析式的变化规律:左加右减,上加下减是解题关键.
9.(2024.大丰区一模)若t≤x≤t+2时,二次函数y=2x2+4x+1的最大值为31,则t的值为 ﹣5或1 .
【考点】二次函数的最值.
【答案】见试题解答内容
【分析】将标准式化为顶点式为y=2x2+4x+1=2(x+1)2﹣1,由t≤x≤t+2时,y最大值=2(x+1)2﹣1,结合二次函数图象的性质解答.
【解答】解:y=2x2+4x+1=2(x+1)2﹣1,
∵二次函数y=2x2+4x+1的最大值为31,
∴①当﹣1﹣t>t+3,即t<﹣2时,2t2+4t+1=31
解得 t1=﹣5,t2=3(舍去).
②当﹣1﹣t<t+3,即t>﹣2时,2(t+2)2+4(t+2)+1=31,
解得 t1=﹣7(舍去),t2=1;
③当t>﹣1时,2(t+2)2+4(t+2)+1=31,
解得 t1=﹣7(舍去),t2=1;
综上所述,t的值是﹣5或1.
故答案为:﹣5或1.
【点评】本题考查了二次函数的最值,难度较大,关键是判断出当x≥﹣1时,y随x的增大而增大,由此此解决这类题.
10.(2024.海陵区一模)将抛物线y=x2+2x﹣3向右平移1个单位长度得到的新抛物线的顶点坐标为 (0,﹣4) .
【考点】二次函数图象与几何变换;二次函数的性质.
【专题】二次函数图象及其性质;运算能力.
【答案】(0,﹣4).
【分析】依据题意,根据“左加右减,上加下减”的平移规律,结合y=x2+2x﹣3=(x+1)2﹣4,又向右平移1个单位长度,进而可以判断得解.
【解答】解:由题意得,抛物线为y=x2+2x﹣3=(x+1)2﹣4.
根据“左加右减,上加下减”的平移规律,∵抛物线向右平移1个单位长度,
∴新抛物线为y=(x+1﹣1)2﹣4即y=x2﹣4.
∴顶点坐标为(0,﹣4).
故答案为:(0,﹣4).
【点评】本题主要考查了二次函数图象与几何变换、二次函数的性质,解题时要熟练并灵活运用二次函数的性质是关键.
11.(2024.桓台县二模)“数形结合”是研究函数的重要思想方法,如果二次函数y=x2+2x+3m﹣8的图象只经过三个象限,那么m的取值范围是 .
【考点】二次函数图象与系数的关系.
【专题】二次函数图象及其性质;运算能力.
【答案】.
【分析】首先配方得到y=x2+2x+3m﹣8=(x+1)2+3m﹣9,然后得出抛物线开口向上,对称轴为直线x=﹣1,顶点坐标为(﹣1,3m﹣9),然后根据二次函数y=x2+2x+3m﹣8的图象只经过三个象限,得到3m﹣8≥0,3m﹣9<0求解即可.
【解答】解:y=x2+2x+3m﹣8=(x+1)2+3m﹣9,
∴抛物线开口向上,对称轴为直线x=﹣1,顶点坐标为(﹣1,3m﹣9),
由条件可知二次函数y=x2+2x+3m﹣8的图象经过第一,二,三象限,
∴3m﹣8≥0,3m﹣9<0,
∴.
故答案为:.
【点评】本题考查二次函数图象与系数的关系,二次函数的图象与性质,解答本题的关键是利用数形结合的思想解答.
12.(2024秋 鹿邑县)水幕电影是通过高压水泵和特制水幕发生器,将水自下而上高速喷出,雾化后形成水幕,然后由专用放映机将特制的录影带.水嘴投射在水幕上.如图,水嘴喷出的水柱的最高点为P,AB=2m,BP=9m,水嘴高AD=5m,则水柱落在地点C到水嘴所在墙的距离AC是 5 m.
【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【答案】5.
【分析】以A为坐标原点,AB所在的直线为x轴,AD所在的直线为y轴建立平面直角坐标系,易得点D和点P的坐标,设抛物线的解析式为:y=a(x﹣2)2+9,代入点D的坐标求得函数的解析式,再求出点C的坐标即可得到AC的长度.
【解答】解:以A为坐标原点,AB所在的直线为x轴,AD所在的直线为y轴建立平面直角坐标系,如图所示,
则A(0,0),D(0,5),P(2,9),
∵点P是最高点,
∴设抛物线的解析式为:y=a(x﹣2)2+9,
将点D坐标代入,可得:5=4a+9,
解得:a=﹣1,
∴y=﹣(x﹣2)2+9,
令y=0,则﹣(x﹣2)2+9=0,
解得:x1=5,x2=﹣1,
∴点C(5,0),
∴AC=5m,
故答案为:5.
【点评】本题考查了二次函数的实际应用,建立适当的坐标系,设出顶点式是解题的关键.
三.解答题(共3小题)
13.(2024秋 埇桥区)如图在平面直角坐标系xOy中,O为坐标原点,二次函数y=x2+bx+c的图象经过点A(3,0)、点B(0,3),顶点为M.
(1)求该二次函数的解析式;
(2)求∠OBM的正切值.
【考点】待定系数法求二次函数解析式;解直角三角形;二次函数的图象;二次函数的性质;二次函数图象上点的坐标特征.
【专题】计算题.
【答案】见试题解答内容
【分析】(1)先把A、B两点的坐标代入y=x2+bx+c得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;
(2)作MH⊥y轴于H,如图,先把抛物线解析式配成顶点式得到M点坐标,然后根据正切的定义求∠HBM的正切值即可.
【解答】解:(1)把A(3,0)、B(0,3)代入y=x2+bx+c得,解得,
所以y=x2﹣4x+3;
(2)作MH⊥y轴于H,如图,
∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴M(2,﹣1),
∵MH⊥y轴,
∴H(0,﹣1),
在Rt△BMH中,tan∠HBM,
即∠OBM的正切值为.
【点评】本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.也考查了二次函数的性质和解直角三角形.
14.(2024.通州区一模)已知关于x的二次函数y=ax2﹣6ax+5a.
(1)若x=2时,y=﹣3,求该函数的解析式;
(2)当a>0,2≤x≤6时,该函数的最大值与最小值的差为18,求a的值;
(3)若A(x1,y1),B(x2,y2)是该函数图象上的两点,且对于x1=a+3,4≤x2≤6,都有y1≥y2,求a的取值范围.
【考点】二次函数图象与系数的关系;二次函数图象上点的坐标特征;二次函数的最值;待定系数法求二次函数解析式.
【专题】二次函数图象及其性质;运算能力.
【答案】(1)y=x2﹣6x+5;
(2)a=2;
(3)a≥3或﹣1≤a<0.
【分析】(1)把x=2,y=﹣3,分别代入y=ax2﹣6ax+5a,得出a=1,即可作答.
(2)先整理y=a(x﹣3)2﹣4a,故图象的对称轴为直线x=3,结合a>0,2≤x≤6.故当x=3时,y最小=﹣4a,当x=6时,y最大=5a,列式5a﹣(﹣4a)=18,即可作答.
(3)进行分类讨论,即①若a>0,则函数图象开口向上.②若a<0,则函数图象开口向下,再结合二次函数的图象性质,进行分析列式,即可作答.
【解答】解:(1)∵y=ax2﹣6ax+5a,
当x=2时,y=﹣3,
∴4a﹣12a+5a=﹣3,
∴a=1.
∴该函数的解析式为y=x2﹣6x+5.
(2)配方得y=ax2﹣6ax+5a=a(x﹣3)2﹣4a,
∴图象的对称轴为直线x=3.
由条件可知当x=3时,y最小=﹣4a,
∵|6﹣3|=3>|2﹣3|,
∴当x=6时,y=a(6﹣3)2﹣4a=9a﹣4a=5a,
∴y最大=5a.
∴5a﹣(﹣4a)=18.
∴a=2;
(3)①若a>0,则函数图象开口向上.
又∵对称轴为直线x=3,
∴当x>3时,y随x的增大而增大.
∵x1=a+3>3,
∴点A在对称轴的右侧.
又∵对于x1=a+3,4≤x2≤6,都有y1≥y2,
∴a+3≥6,
∴a≥3.
②若a<0,则函数图象开口向下,
∵x1=a+3<3,
∴点A在对称轴的左侧.
∵对称轴为直线x=3,
∴当x=2或x=4时函数值相等.
由条件可知2≤a+3<3,
∴﹣1≤a<0.
综上:a≥3或﹣1≤a<0.
【点评】本题考查了二次函数的图象性质,求二次函数的解析式,正确掌握相关性质内容是解题的关键.
15.(2024.濮阳一模)在节假日期间,濮阳龙湖论语广场的音乐喷泉上演了绚丽的灯光秀.随着音乐的节拍,喷泉的水线起伏跳跃,勾勒出迷人的抛物线图案.假设喷泉的出水口为坐标原点,出水口离岸边18米.随着音乐的变化,抛物线的顶点在直线y=kx(k≠0)上变动,从而产生一组不同的抛物线,设这组抛物线的统一形式为y=ax2+bx(a<0).
(1)若,
①若喷出的水恰好达到岸边,则此时喷出的抛物线形水线最大高度是多少米?
②若喷出的抛物线形水线最大高度为4m,求a、b的值;
(2)当音乐节奏加快,抛物线的顶点在直线y=x上,喷出的水不能触及岸边.请直接写出此时a的取值范围.
【考点】二次函数的应用.
【专题】二次函数图象及其性质;运算能力.
【答案】(1)①抛物线水线最大高度是米;②,b=1;
(2).
【分析】(1)①根据喷出的水恰好达到岸边,由抛物线的对称性可求得抛物线的对称轴是直线x=9,再把x=9代入,求出y值即可求解;
②根据抛物线水线最大高度达4米,则抛物线顶点的纵坐标为4m,把y=4代入求得x=8,即可求解;
(2)根据,得出抛物线的顶点坐标为,再根据抛物线的顶点在直线y=x上,得到,求得b=2,然后根据喷出的抛物线水线不能到岸边,出水口离岸边18m,得,求解即可.
【解答】解:(1)由条件可知,
①∵喷出的水恰好达到岸边,
∴抛物线过(18,0),
∵抛物线过原点(0,0),
∴抛物线的对称轴是直线,
∵抛物线的顶点在直线上,
∴当x=9时,,
∴抛物线水线最大高度是米;
②由条件可知抛物线顶点的纵坐标为4m,
当 y=4时,,
解得:x=8,
∴抛物线的顶点是(8,4),
∴y=ax2+bx=a(x﹣8)2+4,
∵抛物线过原点(0,0),
∴64a+4=0,
解得,
∴,
∴,b=1.
(2)∵,
∴抛物线的顶点坐标为,
∵抛物线的顶点在直线y=x上,
∴,
解得:b=2,
由条件可知,即,
解得.
【点评】本题考查二次函数的应用,正确求出二次函数的解析式,掌握二次函数的图象性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考核心考点 二次函数
一.选择题(共7小题)
1.(2024.东莞市二模)如图,点A是抛物线y=a(x﹣3)2+k与y轴的交点,AB∥x轴交抛物线另一点于B,点C为该抛物线的顶点.若△ABC为等边三角形,则a的值为( )
A. B. C. D.1
2.(2024秋 埇桥区)二次函数y=mx2+x+m2﹣2m的图象经过原点,则m的值为( )
A.0 B.2 C.2或0 D.无法确定
3.(2024.新都区)关于二次函数y=ax2﹣2ax﹣3a(a是常数且a>0),下列说法正确的是( )
A.函数图象开口向下
B.对称轴为直线x=﹣1
C.函数图象与x轴没有交点
D.在y轴左侧,y的值随x值的增大而减小
4.(2024.淮南二模)对于抛物线y=﹣5(x﹣1)2+3,下列判断正确的是( )
A.抛物线的开口向上
B.抛物线的顶点坐标是(﹣1,3)
C.对称轴为直线x=1
D.当x=3时,y>0
5.(2024.金东区二模)将二次函数y=﹣x2的图象先向下平移2个单位,再向右平移2个单位所得新函数表达式为( )
A.y=﹣(x﹣2)2+2 B.y=﹣(x+2)2﹣2
C.y=﹣(x+2)2+2 D.y=﹣(x﹣2)2﹣2
6.(2024.崇左二模)剪纸是我国的民间传统艺术,能为节日增加许多喜庆的氛围.剪纸中有一种“抛物线剪纸”艺术,即作品的外轮廓在抛物线上,体现了一种曲线美,如图,这是利用“抛物线剪纸”艺术剪出的蝴蝶,建立适当的平面直角坐标系,使外轮廓上的A,B,C,D四点落在抛物线y=ax2+c上,则下列结论正确的是( )
A.ac<0 B.ac=0 C.ac>0 D.ac≥0
7.(2024.南明区一模)二次函数y=x2+nx的图象如图所示,对称轴为直线x=3,若关于x的一元二次方程x2+nx﹣m=0(m为实数)在2<x<7的范围内有解,则m的取值范围是( )
A.m>7 B.﹣8<m≤2 C.﹣9≤m<7 D.m≤2
二.填空题(共5小题)
8.(2024.通州区一模)将抛物线y=x2﹣4x+8向下平移m个单位长度后得到新抛物线,若新抛物线与x轴有公共点,则m的取值范围是 .
9.(2024.大丰区一模)若t≤x≤t+2时,二次函数y=2x2+4x+1的最大值为31,则t的值为 .
10.(2024.海陵区一模)将抛物线y=x2+2x﹣3向右平移1个单位长度得到的新抛物线的顶点坐标为 .
11.(2024.桓台县二模)“数形结合”是研究函数的重要思想方法,如果二次函数y=x2+2x+3m﹣8的图象只经过三个象限,那么m的取值范围是 .
12.(2024秋 鹿邑县)水幕电影是通过高压水泵和特制水幕发生器,将水自下而上高速喷出,雾化后形成水幕,然后由专用放映机将特制的录影带.水嘴投射在水幕上.如图,水嘴喷出的水柱的最高点为P,AB=2m,BP=9m,水嘴高AD=5m,则水柱落在地点C到水嘴所在墙的距离AC是 m.
三.解答题(共3小题)
13.(2024秋 埇桥区)如图在平面直角坐标系xOy中,O为坐标原点,二次函数y=x2+bx+c的图象经过点A(3,0)、点B(0,3),顶点为M.
(1)求该二次函数的解析式;
(2)求∠OBM的正切值.
14.(2024.通州区一模)已知关于x的二次函数y=ax2﹣6ax+5a.
(1)若x=2时,y=﹣3,求该函数的解析式;
(2)当a>0,2≤x≤6时,该函数的最大值与最小值的差为18,求a的值;
(3)若A(x1,y1),B(x2,y2)是该函数图象上的两点,且对于x1=a+3,4≤x2≤6,都有y1≥y2,求a的取值范围.
15.(2024.濮阳一模)在节假日期间,濮阳龙湖论语广场的音乐喷泉上演了绚丽的灯光秀.随着音乐的节拍,喷泉的水线起伏跳跃,勾勒出迷人的抛物线图案.假设喷泉的出水口为坐标原点,出水口离岸边18米.随着音乐的变化,抛物线的顶点在直线y=kx(k≠0)上变动,从而产生一组不同的抛物线,设这组抛物线的统一形式为y=ax2+bx(a<0).
(1)若,
①若喷出的水恰好达到岸边,则此时喷出的抛物线形水线最大高度是多少米?
②若喷出的抛物线形水线最大高度为4m,求a、b的值;
(2)当音乐节奏加快,抛物线的顶点在直线y=x上,喷出的水不能触及岸边.请直接写出此时a的取值范围.
中考核心考点 二次函数
参考答案与试题解析
一.选择题(共7小题)
1.(2024.东莞市二模)如图,点A是抛物线y=a(x﹣3)2+k与y轴的交点,AB∥x轴交抛物线另一点于B,点C为该抛物线的顶点.若△ABC为等边三角形,则a的值为( )
A. B. C. D.1
【考点】二次函数的性质;二次函数图象上点的坐标特征;等边三角形的性质.
【专题】二次函数图象及其性质;运算能力.
【答案】A
【分析】过点C作CD⊥AB于点D,根据等边三角形的性质得出AD=3,,C(3,k),A(0,9a+k),将点A代入抛物线解析式,即可求解.
【解答】解:如图,过点C作CD⊥AB于点D,
由条件可知AD=3,,C(3,k).
∵当x=0时,y=9a+k,
∴A(0,9a+k),
∴,
∴.
故选:A.
【点评】本题考查了二次函数的图象和性质,等边三角形的性质.熟练掌握以上知识点是关键.
2.(2024秋 埇桥区)二次函数y=mx2+x+m2﹣2m的图象经过原点,则m的值为( )
A.0 B.2 C.2或0 D.无法确定
【考点】二次函数的性质;二次函数图象上点的坐标特征.
【专题】二次函数图象及其性质;运算能力.
【答案】B
【分析】把(0,0)代入y=mx2+x+m2﹣2m求解,注意m的取值范围.
【解答】解:由条件可得m2﹣2m=0,
解得m=0或m=2,
∵m≠0,
∴m=2,
故选:B.
【点评】本题考查二次函数的性质,解题关键是掌握二次函数与方程的关系,注意二次函数二次项系数不为0.
3.(2024.新都区)关于二次函数y=ax2﹣2ax﹣3a(a是常数且a>0),下列说法正确的是( )
A.函数图象开口向下
B.对称轴为直线x=﹣1
C.函数图象与x轴没有交点
D.在y轴左侧,y的值随x值的增大而减小
【考点】抛物线与x轴的交点;二次函数的性质.
【专题】二次函数图象及其性质;应用意识.
【答案】D
【分析】由a>0,可得函数图象开口向上;二次函数y=ax2﹣2ax﹣3a图象的对称轴为直线x1;根据Δ=(﹣2a)2﹣4a×(﹣3a)=4a2+12a2=16a2>0,可知函数图象与x轴有两个交点;结合图象可知,在y轴左侧,y的值随x值的增大而减小,即可得出答案.
【解答】解:∵a>0,
∴函数图象开口向上,
故A选项不正确,不符合题意;
二次函数y=ax2﹣2ax﹣3a图象的对称轴为直线x1,
故B选项不正确,不符合题意;
∵Δ=(﹣2a)2﹣4a×(﹣3a)=4a2+12a2=16a2>0,
∴函数图象与x轴有两个交点,
故C选项不正确,不符合题意;
∵函数图象开口向上,对称轴为直线x=1,
∴在y轴左侧,y的值随x值的增大而减小,
故D选项正确,符合题意.
故选:D.
【点评】本题考查抛物线与x轴的交点、二次函数的性质,解题的关键是理解题意,灵活运用所学知识解决问题.
4.(2024.淮南二模)对于抛物线y=﹣5(x﹣1)2+3,下列判断正确的是( )
A.抛物线的开口向上
B.抛物线的顶点坐标是(﹣1,3)
C.对称轴为直线x=1
D.当x=3时,y>0
【考点】二次函数的性质.
【专题】二次函数图象及其性质;运算能力;推理能力.
【答案】C
【分析】根据二次函数解析式结合二次函数的性质,即可得出结论.
【解答】解:A、∵﹣5<0,
∴抛物线的开口向下,本选项错误,
B、抛物线的顶点为(1,3),本选项错误,
C、抛物线的对称轴为直线x=1,本选项正确,
D、把x=3代入y=﹣5(x﹣1)2+3,解得:y=﹣17<0,本选项错误,
故选:C.
【点评】本题考查了二次函数的性质,根据二次函数的性质逐一对照四个选项即可得出结论.
5.(2024.金东区二模)将二次函数y=﹣x2的图象先向下平移2个单位,再向右平移2个单位所得新函数表达式为( )
A.y=﹣(x﹣2)2+2 B.y=﹣(x+2)2﹣2
C.y=﹣(x+2)2+2 D.y=﹣(x﹣2)2﹣2
【考点】二次函数图象与几何变换.
【专题】二次函数图象及其性质;应用意识.
【答案】D
【分析】根据“上加下减,左加右减”的平移规律,即得答案.
【解答】解:将二次函数y=﹣x2的图象先向下平移2个单位,再向右平移2个单位所得新函数表达式为y=﹣(x﹣2)2﹣2.
故选:D.
【点评】本题考查了二次函数的平移,正确理解二次函数的平移规律是解答本题的关键.
6.(2024.崇左二模)剪纸是我国的民间传统艺术,能为节日增加许多喜庆的氛围.剪纸中有一种“抛物线剪纸”艺术,即作品的外轮廓在抛物线上,体现了一种曲线美,如图,这是利用“抛物线剪纸”艺术剪出的蝴蝶,建立适当的平面直角坐标系,使外轮廓上的A,B,C,D四点落在抛物线y=ax2+c上,则下列结论正确的是( )
A.ac<0 B.ac=0 C.ac>0 D.ac≥0
【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【答案】A
【分析】根据抛物线开口向上,与y轴交于负半轴,即可判断a,c的符号,即可求解.
【解答】解:建立适当的平面直角坐标系,使外轮廓上的A,B,C,D四点落在抛物线y=ax2+c上,
∵根据抛物线开口向上,与y轴交于负半轴,
∴a>0,c<0,则ac<0,
故选:A.
【点评】本题考查了二次函数的应用,解答本题的关键是熟练掌握二次函数图象与系数的关系.
7.(2024.南明区一模)二次函数y=x2+nx的图象如图所示,对称轴为直线x=3,若关于x的一元二次方程x2+nx﹣m=0(m为实数)在2<x<7的范围内有解,则m的取值范围是( )
A.m>7 B.﹣8<m≤2 C.﹣9≤m<7 D.m≤2
【考点】抛物线与x轴的交点;二次函数的性质.
【专题】二次函数图象及其性质;应用意识.
【答案】C
【分析】若关于x的一元二次方程x2+nx﹣m=0(m为实数)在2<x<7的范围内有解,则二次函数y=x2+nx的图象与直线y=m在2<x<7的范围内有交点.由题意可得,解得n=﹣6,则二次函数解析式为y=x2﹣6x,进而可得二次函数y=x2﹣6x的图象的顶点坐标为(3,﹣9),当x=7时,y=7,再结合图象可得m的取值范围是﹣9≤m<7.
【解答】解:∵关于x的一元二次方程x2+nx﹣m=0(m为实数)在2<x<7的范围内有解,
∴二次函数y=x2+nx的图象与直线y=m在2<x<7的范围内有交点.
∵二次函数y=x2+nx的图象的对称轴为直线x=3,
∴,
解得n=﹣6,
∴二次函数解析式为y=x2﹣6x,
∴二次函数y=x2﹣6x的图象的顶点坐标为(3,﹣9),当x=7时,y=7,
∴m的取值范围是﹣9≤m<7.
故选:C.
【点评】本题考查抛物线与x轴的交点、二次函数的性质,解题的关键是理解题意,灵活运用所学知识解决问题.
二.填空题(共5小题)
8.(2024.通州区一模)将抛物线y=x2﹣4x+8向下平移m个单位长度后得到新抛物线,若新抛物线与x轴有公共点,则m的取值范围是 m≥4 .
【考点】抛物线与x轴的交点;二次函数的性质;二次函数图象与几何变换.
【专题】二次函数图象及其性质;运算能力.
【答案】m≥4.
【分析】先根据平移的规律写出抛物线y=x2﹣4x+8向下平移m个单位长度后的抛物线的表达式,再根据平移后得到的抛物线与x轴有公共点可得Δ≥0,由此列不等式即可求出m的取值范围.
【解答】解:平移m个单位长度得y=x2﹣4x+8﹣m,
由题意可得:
∴Δ≥0,
即(﹣4)2﹣4(8﹣m)≥0,
∴m≥4,
故答案为:m≥4.
【点评】此题考查了二次函数图象的平移与几何变换,以及抛物线与x轴的交点问题,利用抛物线解析式的变化规律:左加右减,上加下减是解题关键.
9.(2024.大丰区一模)若t≤x≤t+2时,二次函数y=2x2+4x+1的最大值为31,则t的值为 ﹣5或1 .
【考点】二次函数的最值.
【答案】见试题解答内容
【分析】将标准式化为顶点式为y=2x2+4x+1=2(x+1)2﹣1,由t≤x≤t+2时,y最大值=2(x+1)2﹣1,结合二次函数图象的性质解答.
【解答】解:y=2x2+4x+1=2(x+1)2﹣1,
∵二次函数y=2x2+4x+1的最大值为31,
∴①当﹣1﹣t>t+3,即t<﹣2时,2t2+4t+1=31
解得 t1=﹣5,t2=3(舍去).
②当﹣1﹣t<t+3,即t>﹣2时,2(t+2)2+4(t+2)+1=31,
解得 t1=﹣7(舍去),t2=1;
③当t>﹣1时,2(t+2)2+4(t+2)+1=31,
解得 t1=﹣7(舍去),t2=1;
综上所述,t的值是﹣5或1.
故答案为:﹣5或1.
【点评】本题考查了二次函数的最值,难度较大,关键是判断出当x≥﹣1时,y随x的增大而增大,由此此解决这类题.
10.(2024.海陵区一模)将抛物线y=x2+2x﹣3向右平移1个单位长度得到的新抛物线的顶点坐标为 (0,﹣4) .
【考点】二次函数图象与几何变换;二次函数的性质.
【专题】二次函数图象及其性质;运算能力.
【答案】(0,﹣4).
【分析】依据题意,根据“左加右减,上加下减”的平移规律,结合y=x2+2x﹣3=(x+1)2﹣4,又向右平移1个单位长度,进而可以判断得解.
【解答】解:由题意得,抛物线为y=x2+2x﹣3=(x+1)2﹣4.
根据“左加右减,上加下减”的平移规律,∵抛物线向右平移1个单位长度,
∴新抛物线为y=(x+1﹣1)2﹣4即y=x2﹣4.
∴顶点坐标为(0,﹣4).
故答案为:(0,﹣4).
【点评】本题主要考查了二次函数图象与几何变换、二次函数的性质,解题时要熟练并灵活运用二次函数的性质是关键.
11.(2024.桓台县二模)“数形结合”是研究函数的重要思想方法,如果二次函数y=x2+2x+3m﹣8的图象只经过三个象限,那么m的取值范围是 .
【考点】二次函数图象与系数的关系.
【专题】二次函数图象及其性质;运算能力.
【答案】.
【分析】首先配方得到y=x2+2x+3m﹣8=(x+1)2+3m﹣9,然后得出抛物线开口向上,对称轴为直线x=﹣1,顶点坐标为(﹣1,3m﹣9),然后根据二次函数y=x2+2x+3m﹣8的图象只经过三个象限,得到3m﹣8≥0,3m﹣9<0求解即可.
【解答】解:y=x2+2x+3m﹣8=(x+1)2+3m﹣9,
∴抛物线开口向上,对称轴为直线x=﹣1,顶点坐标为(﹣1,3m﹣9),
由条件可知二次函数y=x2+2x+3m﹣8的图象经过第一,二,三象限,
∴3m﹣8≥0,3m﹣9<0,
∴.
故答案为:.
【点评】本题考查二次函数图象与系数的关系,二次函数的图象与性质,解答本题的关键是利用数形结合的思想解答.
12.(2024秋 鹿邑县)水幕电影是通过高压水泵和特制水幕发生器,将水自下而上高速喷出,雾化后形成水幕,然后由专用放映机将特制的录影带.水嘴投射在水幕上.如图,水嘴喷出的水柱的最高点为P,AB=2m,BP=9m,水嘴高AD=5m,则水柱落在地点C到水嘴所在墙的距离AC是 5 m.
【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【答案】5.
【分析】以A为坐标原点,AB所在的直线为x轴,AD所在的直线为y轴建立平面直角坐标系,易得点D和点P的坐标,设抛物线的解析式为:y=a(x﹣2)2+9,代入点D的坐标求得函数的解析式,再求出点C的坐标即可得到AC的长度.
【解答】解:以A为坐标原点,AB所在的直线为x轴,AD所在的直线为y轴建立平面直角坐标系,如图所示,
则A(0,0),D(0,5),P(2,9),
∵点P是最高点,
∴设抛物线的解析式为:y=a(x﹣2)2+9,
将点D坐标代入,可得:5=4a+9,
解得:a=﹣1,
∴y=﹣(x﹣2)2+9,
令y=0,则﹣(x﹣2)2+9=0,
解得:x1=5,x2=﹣1,
∴点C(5,0),
∴AC=5m,
故答案为:5.
【点评】本题考查了二次函数的实际应用,建立适当的坐标系,设出顶点式是解题的关键.
三.解答题(共3小题)
13.(2024秋 埇桥区)如图在平面直角坐标系xOy中,O为坐标原点,二次函数y=x2+bx+c的图象经过点A(3,0)、点B(0,3),顶点为M.
(1)求该二次函数的解析式;
(2)求∠OBM的正切值.
【考点】待定系数法求二次函数解析式;解直角三角形;二次函数的图象;二次函数的性质;二次函数图象上点的坐标特征.
【专题】计算题.
【答案】见试题解答内容
【分析】(1)先把A、B两点的坐标代入y=x2+bx+c得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;
(2)作MH⊥y轴于H,如图,先把抛物线解析式配成顶点式得到M点坐标,然后根据正切的定义求∠HBM的正切值即可.
【解答】解:(1)把A(3,0)、B(0,3)代入y=x2+bx+c得,解得,
所以y=x2﹣4x+3;
(2)作MH⊥y轴于H,如图,
∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴M(2,﹣1),
∵MH⊥y轴,
∴H(0,﹣1),
在Rt△BMH中,tan∠HBM,
即∠OBM的正切值为.
【点评】本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.也考查了二次函数的性质和解直角三角形.
14.(2024.通州区一模)已知关于x的二次函数y=ax2﹣6ax+5a.
(1)若x=2时,y=﹣3,求该函数的解析式;
(2)当a>0,2≤x≤6时,该函数的最大值与最小值的差为18,求a的值;
(3)若A(x1,y1),B(x2,y2)是该函数图象上的两点,且对于x1=a+3,4≤x2≤6,都有y1≥y2,求a的取值范围.
【考点】二次函数图象与系数的关系;二次函数图象上点的坐标特征;二次函数的最值;待定系数法求二次函数解析式.
【专题】二次函数图象及其性质;运算能力.
【答案】(1)y=x2﹣6x+5;
(2)a=2;
(3)a≥3或﹣1≤a<0.
【分析】(1)把x=2,y=﹣3,分别代入y=ax2﹣6ax+5a,得出a=1,即可作答.
(2)先整理y=a(x﹣3)2﹣4a,故图象的对称轴为直线x=3,结合a>0,2≤x≤6.故当x=3时,y最小=﹣4a,当x=6时,y最大=5a,列式5a﹣(﹣4a)=18,即可作答.
(3)进行分类讨论,即①若a>0,则函数图象开口向上.②若a<0,则函数图象开口向下,再结合二次函数的图象性质,进行分析列式,即可作答.
【解答】解:(1)∵y=ax2﹣6ax+5a,
当x=2时,y=﹣3,
∴4a﹣12a+5a=﹣3,
∴a=1.
∴该函数的解析式为y=x2﹣6x+5.
(2)配方得y=ax2﹣6ax+5a=a(x﹣3)2﹣4a,
∴图象的对称轴为直线x=3.
由条件可知当x=3时,y最小=﹣4a,
∵|6﹣3|=3>|2﹣3|,
∴当x=6时,y=a(6﹣3)2﹣4a=9a﹣4a=5a,
∴y最大=5a.
∴5a﹣(﹣4a)=18.
∴a=2;
(3)①若a>0,则函数图象开口向上.
又∵对称轴为直线x=3,
∴当x>3时,y随x的增大而增大.
∵x1=a+3>3,
∴点A在对称轴的右侧.
又∵对于x1=a+3,4≤x2≤6,都有y1≥y2,
∴a+3≥6,
∴a≥3.
②若a<0,则函数图象开口向下,
∵x1=a+3<3,
∴点A在对称轴的左侧.
∵对称轴为直线x=3,
∴当x=2或x=4时函数值相等.
由条件可知2≤a+3<3,
∴﹣1≤a<0.
综上:a≥3或﹣1≤a<0.
【点评】本题考查了二次函数的图象性质,求二次函数的解析式,正确掌握相关性质内容是解题的关键.
15.(2024.濮阳一模)在节假日期间,濮阳龙湖论语广场的音乐喷泉上演了绚丽的灯光秀.随着音乐的节拍,喷泉的水线起伏跳跃,勾勒出迷人的抛物线图案.假设喷泉的出水口为坐标原点,出水口离岸边18米.随着音乐的变化,抛物线的顶点在直线y=kx(k≠0)上变动,从而产生一组不同的抛物线,设这组抛物线的统一形式为y=ax2+bx(a<0).
(1)若,
①若喷出的水恰好达到岸边,则此时喷出的抛物线形水线最大高度是多少米?
②若喷出的抛物线形水线最大高度为4m,求a、b的值;
(2)当音乐节奏加快,抛物线的顶点在直线y=x上,喷出的水不能触及岸边.请直接写出此时a的取值范围.
【考点】二次函数的应用.
【专题】二次函数图象及其性质;运算能力.
【答案】(1)①抛物线水线最大高度是米;②,b=1;
(2).
【分析】(1)①根据喷出的水恰好达到岸边,由抛物线的对称性可求得抛物线的对称轴是直线x=9,再把x=9代入,求出y值即可求解;
②根据抛物线水线最大高度达4米,则抛物线顶点的纵坐标为4m,把y=4代入求得x=8,即可求解;
(2)根据,得出抛物线的顶点坐标为,再根据抛物线的顶点在直线y=x上,得到,求得b=2,然后根据喷出的抛物线水线不能到岸边,出水口离岸边18m,得,求解即可.
【解答】解:(1)由条件可知,
①∵喷出的水恰好达到岸边,
∴抛物线过(18,0),
∵抛物线过原点(0,0),
∴抛物线的对称轴是直线,
∵抛物线的顶点在直线上,
∴当x=9时,,
∴抛物线水线最大高度是米;
②由条件可知抛物线顶点的纵坐标为4m,
当 y=4时,,
解得:x=8,
∴抛物线的顶点是(8,4),
∴y=ax2+bx=a(x﹣8)2+4,
∵抛物线过原点(0,0),
∴64a+4=0,
解得,
∴,
∴,b=1.
(2)∵,
∴抛物线的顶点坐标为,
∵抛物线的顶点在直线y=x上,
∴,
解得:b=2,
由条件可知,即,
解得.
【点评】本题考查二次函数的应用,正确求出二次函数的解析式,掌握二次函数的图象性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
