【中考核心考点】2025年华东师大版中考数学考前冲刺 圆中的计算问题(含解析)
文档属性
| 名称 | 【中考核心考点】2025年华东师大版中考数学考前冲刺 圆中的计算问题(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-16 07:49:20 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中考核心考点 圆中的计算问题
一.选择题(共8小题)
1.(2024.姑苏区一模)已知一个圆锥侧面展开图是一个半圆,其母线长为4,则其底面圆半径为( )
A.1 B.2 C.3 D.4
2.(2024.东莞市二模)如图,在正方形ABCD中,先以点B为圆心,AB长为半径画弧,再以CD为直径作半圆O,交前弧于点E,连接CE,DE.若AB=10,则图中阴影部分的面积为( )
A. B.25π﹣20 C. D.25π﹣18
3.(2024.包河区二模)如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠C=50°,则的长为( )
A. B. C.2π D.
4.(2024.海勃湾区)如图,在矩形ABCD中,AB=2,BC=4,以点D为圆心,DA的长为半径画弧,交BC于点E,交DC的延长线于点F,则图中阴影部分的面积为( )
A.4 B.2 C. D.2
5.(2024.彭水县)如图,在正方形ABCD中,AB=1,以B为圆心,BA为半径作圆弧,交CB的延长线于点E,连结DE.则图中阴影部分的面积为( )
A. B. C. D.
6.(2024.上城区一模)如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,把△ABC绕直线AB旋转一周,所得几何体的侧面积为( )
A.π B. C. D.4π
7.(2024.平遥县一模)如图,将扇形纸片AOB沿OB方向平移一定距离得到扇形纸片A′O′B′,点O的对应点O'恰好在OB的中点处,O'A'与AB交于点C.若∠AOB=90°,OA=4,则图中阴影部分的面积为( )
A. B. C. D.
8.(2024.济南)如图⊙A、⊙B、⊙C、⊙D、⊙E的半径都是1,顺次连接这些圆心得到五边形ABCDE,则图中的阴影部分面积之和为( )
A.π B. C.2π D.
二.填空题(共4小题)
9.(2024.濮阳一模)如图,菱形ABCD中,E是边BC上一点,把这个菱形放置在边长为1的正方形网格中,若点A、B、E在网格的格点上,以B为圆心,BC长为半径画弧,图中阴影部分的面积为 .
10.(2024.梅州二模)已知扇形的半径为9cm,弧长为6πcm,则此扇形的面积是 .
11.(2024.韶关一模)如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A恰好落在CD边上的点G处.则图中阴影部分的面积等于 .
12.(2024.吉林二模)如图,在菱形ABCD中,∠A=60°,AB=2,分别以点A,C为圆心,AB,CD为半径画弧,图中阴影部分面积为 (结果保留π).
三.解答题(共3小题)
13.(2024秋 海港区)如图1,冰激凌的外壳(不计厚度)可近似的看作圆锥,其母线长为12cm,底面圆直径长为10cm.
(1)这个冰激凌外壳的侧面展开图的形状是 ;
(2)当冰激凌被吃掉一部分后,其外壳仍可近似的看作圆锥,如图2,其母线长为9cm,求此时冰激凌外壳的侧面积.(结果保留π)
14.(2024秋 栾城区)团扇是中国传统工艺品,代表着团圆友善、吉祥如意,某社团组织学生制作团扇,扇面有圆形和正方形两种,每种扇面面积均为300平方厘米.为了提升团扇的耐用性和美观度、需对扇面边缘用缎带进行包边处理,如图所示.
(1)圆形团扇的半径为 厘米,正方形团扇的边长为 厘米;
(2)请你通过计算说明哪种形状的扇面所用的包边长度更短.
15.(2025春 南岗区)用底面半径和高分别为3cm、9cm的空心圆锥和空心圆柱各一个,组成竖放的容器(如图).在这个容器内注入一些细沙,能填满圆锥,还填了部分圆柱,圆柱部分的细沙高1cm.若将这个容器上面封住倒立,细沙的高度是多少厘米?
中考核心考点 圆中的计算问题
参考答案与试题解析
一.选择题(共8小题)
1.(2024.姑苏区一模)已知一个圆锥侧面展开图是一个半圆,其母线长为4,则其底面圆半径为( )
A.1 B.2 C.3 D.4
【考点】圆锥的计算.
【专题】与圆有关的计算;运算能力.
【答案】B
【分析】设圆锥底面圆半径为r,得到,求出r=2,即可得到答案.
【解答】解:设圆锥底面圆半径为r,圆锥侧面展开图是一个半圆根据可得,
∴r=2,
故选:B.
【点评】本题考查了弧长公式,圆锥的侧面展开图,熟练掌握相关知识点是解题的关键.
2.(2024.东莞市二模)如图,在正方形ABCD中,先以点B为圆心,AB长为半径画弧,再以CD为直径作半圆O,交前弧于点E,连接CE,DE.若AB=10,则图中阴影部分的面积为( )
A. B.25π﹣20 C. D.25π﹣18
【考点】扇形面积的计算;正方形的性质.
【专题】与圆有关的计算;运算能力.
【答案】A
【分析】作BH⊥CE于H,利用垂径定理可得,利用圆周角定理得到∠CED=90°,然后通过证得△BCH≌△CDE(AAS),得出,设DE=x,CE=2x,根据勾股定理得出x2=20,然后根据S阴影=S半圆CED﹣S△CED即可求解.
【解答】解:如图,作BH⊥CE于H,则,
∵CD是直径,
∴∠CED=90°,
∴∠ECD+∠EDC=90°,
由条件可知∠BCH+∠ECD=90°,
∴∠EDC=∠BCH,
∵BC=CD,∠BHC=∠CED=90°,
∴△BCH≌△CDE(AAS),
∴DE=CH,
∴,
设DE=x,CE=2x,
由勾股定理得x2+(2x)2=102,
∴x2=20,
∴,
∴,
故选:A.
【点评】本题考查扇形面积的计算,正方形的性质,垂径定理,圆周角定理,熟练掌握以上知识点是关键.
3.(2024.包河区二模)如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠C=50°,则的长为( )
A. B. C.2π D.
【考点】弧长的计算;圆周角定理.
【专题】圆的有关概念及性质;与圆有关的计算;运算能力.
【答案】B
【分析】根据圆内接四边形的性质可得∠D=60°,再根据圆周角定理得∠AOC=120°,根据弧长公式计算即可.
【解答】解:∵OA=OC,
∴∠A=∠C=50°,
∴∠BOC=2∠A=100°,
∴的长为π.
故选:B.
【点评】本题主要考查弧长的计算以及圆周角定理,熟练掌握弧长公式和圆周角定理是解题的关键.
4.(2024.海勃湾区)如图,在矩形ABCD中,AB=2,BC=4,以点D为圆心,DA的长为半径画弧,交BC于点E,交DC的延长线于点F,则图中阴影部分的面积为( )
A.4 B.2 C. D.2
【考点】扇形面积的计算;矩形的性质.
【专题】与圆有关的计算;运算能力;推理能力.
【答案】B
【分析】连接DE,利用矩形的性质以及勾股定理求出CE的长以及∠CDE的度数,进而利用图中阴影部分的面积=S扇形DEF﹣S△DEC,求出答案.
【解答】解:连接DE,
在矩形ABCD中,AB=2,BC=4,
∴CD=AB=2,AD=BC=4,∠BCD=90°,
∴DE=AD=4,
∴CE2,
∴CEDE,
∴∠EDC=30°,
∴图中阴影部分的面积=S扇形DEF﹣S△DEC
2×2
2.
故选:B.
【点评】此题主要考查了扇形面积求法以及矩形的性质等知识,正确得出CE的长以及∠CDE的度数是解题关键.
5.(2024.彭水县)如图,在正方形ABCD中,AB=1,以B为圆心,BA为半径作圆弧,交CB的延长线于点E,连结DE.则图中阴影部分的面积为( )
A. B. C. D.
【考点】扇形面积的计算;正方形的性质.
【专题】与圆有关的计算;运算能力.
【答案】D
【分析】根据S阴影=S扇形ABE+S正方形ABCD﹣S△DCE,进行计算即可得出答案,不规则图形的面积通常转化为规则图形的面积的和差.
【解答】解:在正方形ABCD中,∠ABC=90°,AB=1,
∴BE=1,∠ABE=90°,BC=CD=1,
∴BE+BC=CE=2,
∴S阴影=S扇形ABE+S正方形ABCD﹣S△DCE
,
故选:D.
【点评】本题主要考查了扇形的面积计算方法,掌握其公式是解决此题的关键.
6.(2024.上城区一模)如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,把△ABC绕直线AB旋转一周,所得几何体的侧面积为( )
A.π B. C. D.4π
【考点】圆锥的计算;点、线、面、体;勾股定理.
【专题】几何图形;与圆有关的计算;运算能力.
【答案】B
【分析】将△ABC绕AB所在直线旋转一周,得到的几何体为圆锥,圆锥的底面圆的半径为1,利用勾股定理计算母线长,然后利用圆锥的侧面展开图为一扇形和扇形的面积公式计算即可.
【解答】解:将△ABC绕AB所在直线旋转一周,得到的几何体为圆锥,
圆锥的底面圆的半径为1,母线长,
所以圆锥的侧面积 2π×1π.
故选:B.
【点评】本题考查了圆锥的计算,点、线、面、体以及勾股定理,圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
7.(2024.平遥县一模)如图,将扇形纸片AOB沿OB方向平移一定距离得到扇形纸片A′O′B′,点O的对应点O'恰好在OB的中点处,O'A'与AB交于点C.若∠AOB=90°,OA=4,则图中阴影部分的面积为( )
A. B. C. D.
【考点】扇形面积的计算;平移的性质.
【专题】运算能力.
【答案】D
【分析】连接OC,根据点O'为OB的中点及OC=OB,得出∠OCO'的度数,进一步得出∠COB的度数,最后用扇形OBC的面积减去△COO'的面积即可解决问题.
【解答】解:连接OC,
∵点O'为OB的中点,OB=OC,
∴OO'.
在Rt△COO'中,
sin∠OCO',
∴∠OCO'=30°,
∴∠COB=60°.
∵OA=4,
∴OO',
∴CO',
∴.
又∵,
∴阴影部分的面积为:.
故选:D.
【点评】本题主要考查了扇形面积的计算及平移的性质,熟知图形平移的性质及扇形的面积公式是解题的关键.
8.(2024.济南)如图⊙A、⊙B、⊙C、⊙D、⊙E的半径都是1,顺次连接这些圆心得到五边形ABCDE,则图中的阴影部分面积之和为( )
A.π B. C.2π D.
【考点】扇形面积的计算;多边形内角与外角.
【答案】B
【分析】首先求得五边形的内角和,然后利用扇形的面积公式即可求解.
【解答】解:五边形的内角和是:(5﹣2)×180°=540°,
则阴影部分面积之和是:,
故选:B.
【点评】本题主要考查多边形的内角和以及扇形的面积公式.解决本题的关键是把阴影部分当成一个扇形的面积来求,圆心角为五边形的内角和.
二.填空题(共4小题)
9.(2024.濮阳一模)如图,菱形ABCD中,E是边BC上一点,把这个菱形放置在边长为1的正方形网格中,若点A、B、E在网格的格点上,以B为圆心,BC长为半径画弧,图中阴影部分的面积为 .
【考点】扇形面积的计算;勾股定理;菱形的性质.
【专题】与圆有关的计算;运算能力.
【答案】.
【分析】连接AE,先根据勾股定理和勾股定理的逆定理求出∠AEB=90°,∠B=45°,根据菱形的性质和扇形的面积公式分别求出=菱形ABCD的面积与扇形ABC的面积,根据阴影部分的面积=菱形ABCD的面积﹣扇形ABC的面积即可求解.
【解答】解:连接AE,如图:
∵点A、B、E在网格的格点上,
∴,,,
∵BE2+AE2=20=AB2,
∴△ABE是等腰直角三角形,
即∠AEB=90°,∠B=45°,
由条件可知,
∴S菱形ABCD,
S扇形ABC,
∴S阴影=S菱形ABCD﹣S扇形ABC.
故答案为:.
【点评】本题考查了勾股定理,勾股定理的逆定理,菱形的性质,扇形的面积,割补法求不规则图形的面积.熟练掌握勾股定理的逆定理是解题的关键.
10.(2024.梅州二模)已知扇形的半径为9cm,弧长为6πcm,则此扇形的面积是 27πcm2 .
【考点】扇形面积的计算;弧长的计算.
【专题】与圆有关的计算;运算能力.
【答案】27πcm2.
【分析】根据扇形的面积计算即可得到答案.
【解答】解:根据扇形的面积计算公式可得:
S扇形LR27π(cm2),
故答案为:27πcm2.
【点评】此题考查了扇形的面积的计算公式,解题的关键是扇形的面积计算.
11.(2024.韶关一模)如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A恰好落在CD边上的点G处.则图中阴影部分的面积等于 9 .
【考点】扇形面积的计算;旋转的性质;矩形的性质.
【专题】与圆有关的计算;运算能力.
【答案】9.
【分析】旋转得到BG=AB=5,勾股定理求出CG的长,利用矩形的面积减去直角三角形的面积求出阴影部分的面积即可.
【解答】解:由条件可知BG=AB=5,BE=BC=3,∠BCG=90°,
在Rt△BCG中,,
∴S阴影;
故答案为:9.
【点评】本题考查旋转的性质,矩形的性质,勾股定理,熟练掌握以上知识点是关键.
12.(2024.吉林二模)如图,在菱形ABCD中,∠A=60°,AB=2,分别以点A,C为圆心,AB,CD为半径画弧,图中阴影部分面积为 2 (结果保留π).
【考点】扇形面积的计算;等边三角形的判定与性质;菱形的性质.
【专题】矩形 菱形 正方形;与圆有关的计算;运算能力.
【答案】见试题解答内容
【分析】根据“割补法”求面积.
【解答】解:阴影部分的面积为:2×2sinA,
故答案为:.
【点评】本题考查了扇形面积的计算,知道阴影面积的表示方法是解题的关键.
三.解答题(共3小题)
13.(2024秋 海港区)如图1,冰激凌的外壳(不计厚度)可近似的看作圆锥,其母线长为12cm,底面圆直径长为10cm.
(1)这个冰激凌外壳的侧面展开图的形状是 扇形 ;
(2)当冰激凌被吃掉一部分后,其外壳仍可近似的看作圆锥,如图2,其母线长为9cm,求此时冰激凌外壳的侧面积.(结果保留π)
【考点】圆锥的计算.
【专题】几何图形问题;运算能力.
【答案】(1)扇形;
(2)27πcm2.
【分析】(1)圆锥的侧面展开图是一个扇形,据此作答即可;
(2)根据弧长公式求出这个冰激凌外壳的侧面展开后所得扇形的圆心角的度数,再计算冰激凌被吃掉一部分后外壳的侧面积即可.
【解答】解:(1)这个冰激凌外壳的侧面展开图的形状是扇形.
故答案为:扇形.
(2)设这个冰激凌外壳的侧面展开后所得扇形的圆心角是n°.
根据题意,得2π×12=8π,
解得n=120,
∴这个冰激凌外壳的侧面展开后所得扇形的圆心角是120°,
π×92=27π(cm2).
答:此时冰激凌外壳的侧面积是27πcm2.
【点评】本题考查圆锥的计算,掌握弧长计算公式、扇形面积计算公式是解题的关键.
14.(2024秋 栾城区)团扇是中国传统工艺品,代表着团圆友善、吉祥如意,某社团组织学生制作团扇,扇面有圆形和正方形两种,每种扇面面积均为300平方厘米.为了提升团扇的耐用性和美观度、需对扇面边缘用缎带进行包边处理,如图所示.
(1)圆形团扇的半径为 厘米,正方形团扇的边长为 厘米;
(2)请你通过计算说明哪种形状的扇面所用的包边长度更短.
【考点】扇形面积的计算.
【专题】与圆有关的计算;运算能力.
【答案】(1),;
(2)圆形团扇所用的包边长度更短.
【分析】(1)分别根据圆和正方形的面积公式解答即可;
(2)根据圆和正方形的周长公式解答即可.
【解答】解:(1)由题意得:
圆形团扇的半径为:(厘米),正方形团扇的边长为:(厘米),
故答案为:,;
(2)∵圆形团扇的半径为厘米,
∴圆形团扇的周长为:(厘米),
∵正方形团扇的边长为厘米,
∴正方形团扇的周长为:(厘米),
∵,3<π<4,
∴,
∴圆形团扇所用的包边长度更短.
【点评】本题考查了扇形的面积,掌握圆和正方形的面积和周长公式是解答本题的关键.
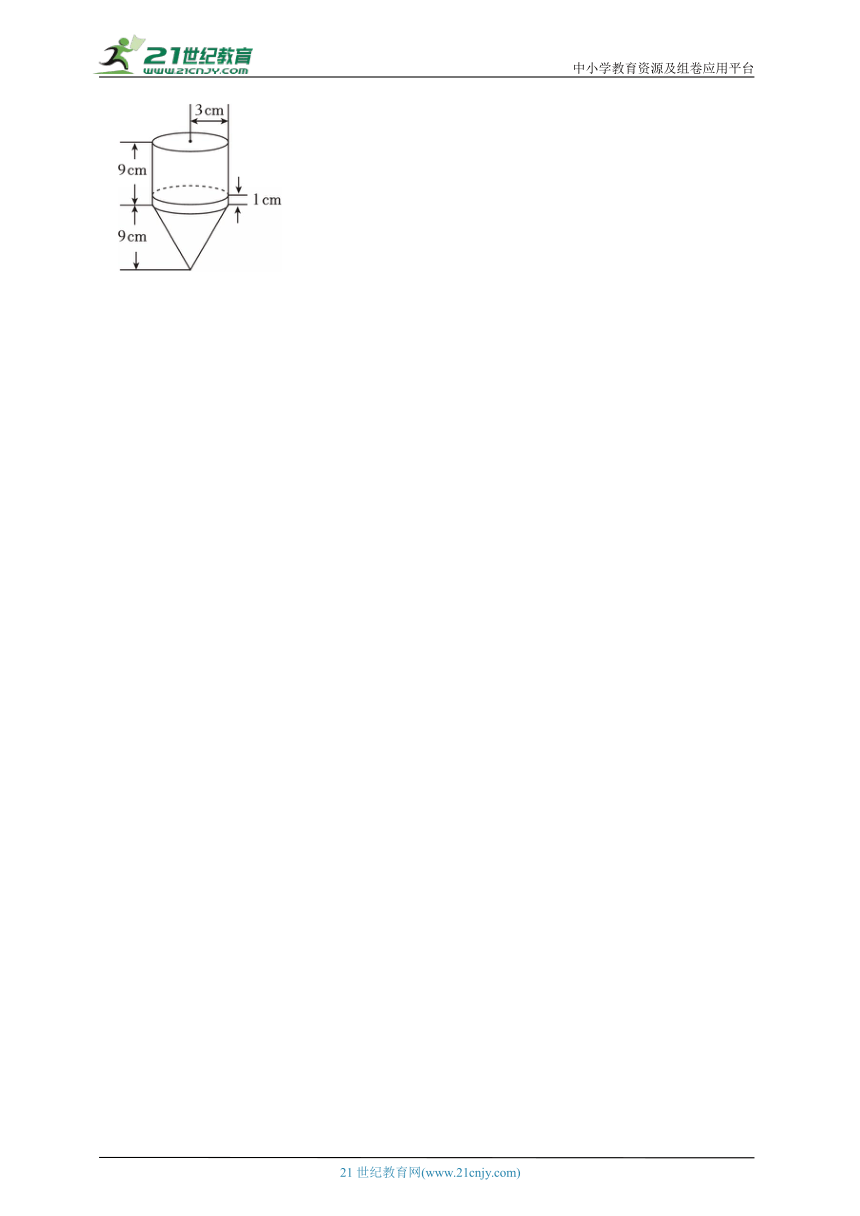
15.(2025春 南岗区)用底面半径和高分别为3cm、9cm的空心圆锥和空心圆柱各一个,组成竖放的容器(如图).在这个容器内注入一些细沙,能填满圆锥,还填了部分圆柱,圆柱部分的细沙高1cm.若将这个容器上面封住倒立,细沙的高度是多少厘米?
【考点】圆锥的计算.
【专题】与圆有关的计算;运算能力.
【答案】细沙的高度是4厘米.
【分析】根据等体积等底面积的圆柱和圆锥,圆锥的高是圆柱高的3倍,圆锥部分的高÷3=倒入圆柱部分的高,再加上圆柱部分原来的高即可.
【解答】解:9÷3+1
=3+1
=4(厘米)
答:细沙的高度是4厘米.
【点评】本题考查的是等底等高的圆柱体积与圆锥体积的关系,掌握等底等高的圆柱体积是圆锥体积的3倍是解答关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考核心考点 圆中的计算问题
一.选择题(共8小题)
1.(2024.姑苏区一模)已知一个圆锥侧面展开图是一个半圆,其母线长为4,则其底面圆半径为( )
A.1 B.2 C.3 D.4
2.(2024.东莞市二模)如图,在正方形ABCD中,先以点B为圆心,AB长为半径画弧,再以CD为直径作半圆O,交前弧于点E,连接CE,DE.若AB=10,则图中阴影部分的面积为( )
A. B.25π﹣20 C. D.25π﹣18
3.(2024.包河区二模)如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠C=50°,则的长为( )
A. B. C.2π D.
4.(2024.海勃湾区)如图,在矩形ABCD中,AB=2,BC=4,以点D为圆心,DA的长为半径画弧,交BC于点E,交DC的延长线于点F,则图中阴影部分的面积为( )
A.4 B.2 C. D.2
5.(2024.彭水县)如图,在正方形ABCD中,AB=1,以B为圆心,BA为半径作圆弧,交CB的延长线于点E,连结DE.则图中阴影部分的面积为( )
A. B. C. D.
6.(2024.上城区一模)如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,把△ABC绕直线AB旋转一周,所得几何体的侧面积为( )
A.π B. C. D.4π
7.(2024.平遥县一模)如图,将扇形纸片AOB沿OB方向平移一定距离得到扇形纸片A′O′B′,点O的对应点O'恰好在OB的中点处,O'A'与AB交于点C.若∠AOB=90°,OA=4,则图中阴影部分的面积为( )
A. B. C. D.
8.(2024.济南)如图⊙A、⊙B、⊙C、⊙D、⊙E的半径都是1,顺次连接这些圆心得到五边形ABCDE,则图中的阴影部分面积之和为( )
A.π B. C.2π D.
二.填空题(共4小题)
9.(2024.濮阳一模)如图,菱形ABCD中,E是边BC上一点,把这个菱形放置在边长为1的正方形网格中,若点A、B、E在网格的格点上,以B为圆心,BC长为半径画弧,图中阴影部分的面积为 .
10.(2024.梅州二模)已知扇形的半径为9cm,弧长为6πcm,则此扇形的面积是 .
11.(2024.韶关一模)如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A恰好落在CD边上的点G处.则图中阴影部分的面积等于 .
12.(2024.吉林二模)如图,在菱形ABCD中,∠A=60°,AB=2,分别以点A,C为圆心,AB,CD为半径画弧,图中阴影部分面积为 (结果保留π).
三.解答题(共3小题)
13.(2024秋 海港区)如图1,冰激凌的外壳(不计厚度)可近似的看作圆锥,其母线长为12cm,底面圆直径长为10cm.
(1)这个冰激凌外壳的侧面展开图的形状是 ;
(2)当冰激凌被吃掉一部分后,其外壳仍可近似的看作圆锥,如图2,其母线长为9cm,求此时冰激凌外壳的侧面积.(结果保留π)
14.(2024秋 栾城区)团扇是中国传统工艺品,代表着团圆友善、吉祥如意,某社团组织学生制作团扇,扇面有圆形和正方形两种,每种扇面面积均为300平方厘米.为了提升团扇的耐用性和美观度、需对扇面边缘用缎带进行包边处理,如图所示.
(1)圆形团扇的半径为 厘米,正方形团扇的边长为 厘米;
(2)请你通过计算说明哪种形状的扇面所用的包边长度更短.
15.(2025春 南岗区)用底面半径和高分别为3cm、9cm的空心圆锥和空心圆柱各一个,组成竖放的容器(如图).在这个容器内注入一些细沙,能填满圆锥,还填了部分圆柱,圆柱部分的细沙高1cm.若将这个容器上面封住倒立,细沙的高度是多少厘米?
中考核心考点 圆中的计算问题
参考答案与试题解析
一.选择题(共8小题)
1.(2024.姑苏区一模)已知一个圆锥侧面展开图是一个半圆,其母线长为4,则其底面圆半径为( )
A.1 B.2 C.3 D.4
【考点】圆锥的计算.
【专题】与圆有关的计算;运算能力.
【答案】B
【分析】设圆锥底面圆半径为r,得到,求出r=2,即可得到答案.
【解答】解:设圆锥底面圆半径为r,圆锥侧面展开图是一个半圆根据可得,
∴r=2,
故选:B.
【点评】本题考查了弧长公式,圆锥的侧面展开图,熟练掌握相关知识点是解题的关键.
2.(2024.东莞市二模)如图,在正方形ABCD中,先以点B为圆心,AB长为半径画弧,再以CD为直径作半圆O,交前弧于点E,连接CE,DE.若AB=10,则图中阴影部分的面积为( )
A. B.25π﹣20 C. D.25π﹣18
【考点】扇形面积的计算;正方形的性质.
【专题】与圆有关的计算;运算能力.
【答案】A
【分析】作BH⊥CE于H,利用垂径定理可得,利用圆周角定理得到∠CED=90°,然后通过证得△BCH≌△CDE(AAS),得出,设DE=x,CE=2x,根据勾股定理得出x2=20,然后根据S阴影=S半圆CED﹣S△CED即可求解.
【解答】解:如图,作BH⊥CE于H,则,
∵CD是直径,
∴∠CED=90°,
∴∠ECD+∠EDC=90°,
由条件可知∠BCH+∠ECD=90°,
∴∠EDC=∠BCH,
∵BC=CD,∠BHC=∠CED=90°,
∴△BCH≌△CDE(AAS),
∴DE=CH,
∴,
设DE=x,CE=2x,
由勾股定理得x2+(2x)2=102,
∴x2=20,
∴,
∴,
故选:A.
【点评】本题考查扇形面积的计算,正方形的性质,垂径定理,圆周角定理,熟练掌握以上知识点是关键.
3.(2024.包河区二模)如图,AB是⊙O的直径,C是⊙O上一点,连接AC,OC,若AB=6,∠C=50°,则的长为( )
A. B. C.2π D.
【考点】弧长的计算;圆周角定理.
【专题】圆的有关概念及性质;与圆有关的计算;运算能力.
【答案】B
【分析】根据圆内接四边形的性质可得∠D=60°,再根据圆周角定理得∠AOC=120°,根据弧长公式计算即可.
【解答】解:∵OA=OC,
∴∠A=∠C=50°,
∴∠BOC=2∠A=100°,
∴的长为π.
故选:B.
【点评】本题主要考查弧长的计算以及圆周角定理,熟练掌握弧长公式和圆周角定理是解题的关键.
4.(2024.海勃湾区)如图,在矩形ABCD中,AB=2,BC=4,以点D为圆心,DA的长为半径画弧,交BC于点E,交DC的延长线于点F,则图中阴影部分的面积为( )
A.4 B.2 C. D.2
【考点】扇形面积的计算;矩形的性质.
【专题】与圆有关的计算;运算能力;推理能力.
【答案】B
【分析】连接DE,利用矩形的性质以及勾股定理求出CE的长以及∠CDE的度数,进而利用图中阴影部分的面积=S扇形DEF﹣S△DEC,求出答案.
【解答】解:连接DE,
在矩形ABCD中,AB=2,BC=4,
∴CD=AB=2,AD=BC=4,∠BCD=90°,
∴DE=AD=4,
∴CE2,
∴CEDE,
∴∠EDC=30°,
∴图中阴影部分的面积=S扇形DEF﹣S△DEC
2×2
2.
故选:B.
【点评】此题主要考查了扇形面积求法以及矩形的性质等知识,正确得出CE的长以及∠CDE的度数是解题关键.
5.(2024.彭水县)如图,在正方形ABCD中,AB=1,以B为圆心,BA为半径作圆弧,交CB的延长线于点E,连结DE.则图中阴影部分的面积为( )
A. B. C. D.
【考点】扇形面积的计算;正方形的性质.
【专题】与圆有关的计算;运算能力.
【答案】D
【分析】根据S阴影=S扇形ABE+S正方形ABCD﹣S△DCE,进行计算即可得出答案,不规则图形的面积通常转化为规则图形的面积的和差.
【解答】解:在正方形ABCD中,∠ABC=90°,AB=1,
∴BE=1,∠ABE=90°,BC=CD=1,
∴BE+BC=CE=2,
∴S阴影=S扇形ABE+S正方形ABCD﹣S△DCE
,
故选:D.
【点评】本题主要考查了扇形的面积计算方法,掌握其公式是解决此题的关键.
6.(2024.上城区一模)如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,把△ABC绕直线AB旋转一周,所得几何体的侧面积为( )
A.π B. C. D.4π
【考点】圆锥的计算;点、线、面、体;勾股定理.
【专题】几何图形;与圆有关的计算;运算能力.
【答案】B
【分析】将△ABC绕AB所在直线旋转一周,得到的几何体为圆锥,圆锥的底面圆的半径为1,利用勾股定理计算母线长,然后利用圆锥的侧面展开图为一扇形和扇形的面积公式计算即可.
【解答】解:将△ABC绕AB所在直线旋转一周,得到的几何体为圆锥,
圆锥的底面圆的半径为1,母线长,
所以圆锥的侧面积 2π×1π.
故选:B.
【点评】本题考查了圆锥的计算,点、线、面、体以及勾股定理,圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
7.(2024.平遥县一模)如图,将扇形纸片AOB沿OB方向平移一定距离得到扇形纸片A′O′B′,点O的对应点O'恰好在OB的中点处,O'A'与AB交于点C.若∠AOB=90°,OA=4,则图中阴影部分的面积为( )
A. B. C. D.
【考点】扇形面积的计算;平移的性质.
【专题】运算能力.
【答案】D
【分析】连接OC,根据点O'为OB的中点及OC=OB,得出∠OCO'的度数,进一步得出∠COB的度数,最后用扇形OBC的面积减去△COO'的面积即可解决问题.
【解答】解:连接OC,
∵点O'为OB的中点,OB=OC,
∴OO'.
在Rt△COO'中,
sin∠OCO',
∴∠OCO'=30°,
∴∠COB=60°.
∵OA=4,
∴OO',
∴CO',
∴.
又∵,
∴阴影部分的面积为:.
故选:D.
【点评】本题主要考查了扇形面积的计算及平移的性质,熟知图形平移的性质及扇形的面积公式是解题的关键.
8.(2024.济南)如图⊙A、⊙B、⊙C、⊙D、⊙E的半径都是1,顺次连接这些圆心得到五边形ABCDE,则图中的阴影部分面积之和为( )
A.π B. C.2π D.
【考点】扇形面积的计算;多边形内角与外角.
【答案】B
【分析】首先求得五边形的内角和,然后利用扇形的面积公式即可求解.
【解答】解:五边形的内角和是:(5﹣2)×180°=540°,
则阴影部分面积之和是:,
故选:B.
【点评】本题主要考查多边形的内角和以及扇形的面积公式.解决本题的关键是把阴影部分当成一个扇形的面积来求,圆心角为五边形的内角和.
二.填空题(共4小题)
9.(2024.濮阳一模)如图,菱形ABCD中,E是边BC上一点,把这个菱形放置在边长为1的正方形网格中,若点A、B、E在网格的格点上,以B为圆心,BC长为半径画弧,图中阴影部分的面积为 .
【考点】扇形面积的计算;勾股定理;菱形的性质.
【专题】与圆有关的计算;运算能力.
【答案】.
【分析】连接AE,先根据勾股定理和勾股定理的逆定理求出∠AEB=90°,∠B=45°,根据菱形的性质和扇形的面积公式分别求出=菱形ABCD的面积与扇形ABC的面积,根据阴影部分的面积=菱形ABCD的面积﹣扇形ABC的面积即可求解.
【解答】解:连接AE,如图:
∵点A、B、E在网格的格点上,
∴,,,
∵BE2+AE2=20=AB2,
∴△ABE是等腰直角三角形,
即∠AEB=90°,∠B=45°,
由条件可知,
∴S菱形ABCD,
S扇形ABC,
∴S阴影=S菱形ABCD﹣S扇形ABC.
故答案为:.
【点评】本题考查了勾股定理,勾股定理的逆定理,菱形的性质,扇形的面积,割补法求不规则图形的面积.熟练掌握勾股定理的逆定理是解题的关键.
10.(2024.梅州二模)已知扇形的半径为9cm,弧长为6πcm,则此扇形的面积是 27πcm2 .
【考点】扇形面积的计算;弧长的计算.
【专题】与圆有关的计算;运算能力.
【答案】27πcm2.
【分析】根据扇形的面积计算即可得到答案.
【解答】解:根据扇形的面积计算公式可得:
S扇形LR27π(cm2),
故答案为:27πcm2.
【点评】此题考查了扇形的面积的计算公式,解题的关键是扇形的面积计算.
11.(2024.韶关一模)如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A恰好落在CD边上的点G处.则图中阴影部分的面积等于 9 .
【考点】扇形面积的计算;旋转的性质;矩形的性质.
【专题】与圆有关的计算;运算能力.
【答案】9.
【分析】旋转得到BG=AB=5,勾股定理求出CG的长,利用矩形的面积减去直角三角形的面积求出阴影部分的面积即可.
【解答】解:由条件可知BG=AB=5,BE=BC=3,∠BCG=90°,
在Rt△BCG中,,
∴S阴影;
故答案为:9.
【点评】本题考查旋转的性质,矩形的性质,勾股定理,熟练掌握以上知识点是关键.
12.(2024.吉林二模)如图,在菱形ABCD中,∠A=60°,AB=2,分别以点A,C为圆心,AB,CD为半径画弧,图中阴影部分面积为 2 (结果保留π).
【考点】扇形面积的计算;等边三角形的判定与性质;菱形的性质.
【专题】矩形 菱形 正方形;与圆有关的计算;运算能力.
【答案】见试题解答内容
【分析】根据“割补法”求面积.
【解答】解:阴影部分的面积为:2×2sinA,
故答案为:.
【点评】本题考查了扇形面积的计算,知道阴影面积的表示方法是解题的关键.
三.解答题(共3小题)
13.(2024秋 海港区)如图1,冰激凌的外壳(不计厚度)可近似的看作圆锥,其母线长为12cm,底面圆直径长为10cm.
(1)这个冰激凌外壳的侧面展开图的形状是 扇形 ;
(2)当冰激凌被吃掉一部分后,其外壳仍可近似的看作圆锥,如图2,其母线长为9cm,求此时冰激凌外壳的侧面积.(结果保留π)
【考点】圆锥的计算.
【专题】几何图形问题;运算能力.
【答案】(1)扇形;
(2)27πcm2.
【分析】(1)圆锥的侧面展开图是一个扇形,据此作答即可;
(2)根据弧长公式求出这个冰激凌外壳的侧面展开后所得扇形的圆心角的度数,再计算冰激凌被吃掉一部分后外壳的侧面积即可.
【解答】解:(1)这个冰激凌外壳的侧面展开图的形状是扇形.
故答案为:扇形.
(2)设这个冰激凌外壳的侧面展开后所得扇形的圆心角是n°.
根据题意,得2π×12=8π,
解得n=120,
∴这个冰激凌外壳的侧面展开后所得扇形的圆心角是120°,
π×92=27π(cm2).
答:此时冰激凌外壳的侧面积是27πcm2.
【点评】本题考查圆锥的计算,掌握弧长计算公式、扇形面积计算公式是解题的关键.
14.(2024秋 栾城区)团扇是中国传统工艺品,代表着团圆友善、吉祥如意,某社团组织学生制作团扇,扇面有圆形和正方形两种,每种扇面面积均为300平方厘米.为了提升团扇的耐用性和美观度、需对扇面边缘用缎带进行包边处理,如图所示.
(1)圆形团扇的半径为 厘米,正方形团扇的边长为 厘米;
(2)请你通过计算说明哪种形状的扇面所用的包边长度更短.
【考点】扇形面积的计算.
【专题】与圆有关的计算;运算能力.
【答案】(1),;
(2)圆形团扇所用的包边长度更短.
【分析】(1)分别根据圆和正方形的面积公式解答即可;
(2)根据圆和正方形的周长公式解答即可.
【解答】解:(1)由题意得:
圆形团扇的半径为:(厘米),正方形团扇的边长为:(厘米),
故答案为:,;
(2)∵圆形团扇的半径为厘米,
∴圆形团扇的周长为:(厘米),
∵正方形团扇的边长为厘米,
∴正方形团扇的周长为:(厘米),
∵,3<π<4,
∴,
∴圆形团扇所用的包边长度更短.
【点评】本题考查了扇形的面积,掌握圆和正方形的面积和周长公式是解答本题的关键.
15.(2025春 南岗区)用底面半径和高分别为3cm、9cm的空心圆锥和空心圆柱各一个,组成竖放的容器(如图).在这个容器内注入一些细沙,能填满圆锥,还填了部分圆柱,圆柱部分的细沙高1cm.若将这个容器上面封住倒立,细沙的高度是多少厘米?
【考点】圆锥的计算.
【专题】与圆有关的计算;运算能力.
【答案】细沙的高度是4厘米.
【分析】根据等体积等底面积的圆柱和圆锥,圆锥的高是圆柱高的3倍,圆锥部分的高÷3=倒入圆柱部分的高,再加上圆柱部分原来的高即可.
【解答】解:9÷3+1
=3+1
=4(厘米)
答:细沙的高度是4厘米.
【点评】本题考查的是等底等高的圆柱体积与圆锥体积的关系,掌握等底等高的圆柱体积是圆锥体积的3倍是解答关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
