【中考核心考点】2025年人教版中考数学考前冲刺 反比例函数(含解析)
文档属性
| 名称 | 【中考核心考点】2025年人教版中考数学考前冲刺 反比例函数(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 897.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-16 09:20:27 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中考冲刺核心考点 反比例函数
一.选择题(共7小题)
1.(2025春 九龙坡区)反比例函数的图象位于( )
A.第一,第三象限 B.第一,第四象限
C.第二,第三象限 D.第二,第四象限
2.(2024.东莞市二模)在如图1所示的电源电压恒定的电路中,小明闭合开关S后,移动滑动变阻器的滑片,电流I与电阻R成反比例函数关系,函数图象如图2所示,点P的坐标为(5,2),则电源电压U为(提示:)( )
A.5V B.10V C.15V D.20V
3.(2024.昆明)对于反比例函数y,下列说法不正确的是( )
A.当x>0时,y随x的增大而增大
B.当x<0时,y随x的增大而减小
C.点(﹣2,﹣1)在它的图象上
D.它的图象在第一、三象限
4.(2024.通许县)根据物理学知识,作用于物体上的压力F(N)所产生的压强p(Pa)与物体受力面积S(m2)三者之间满足.若压力为100N时,压强要大于1000Pa,则此时关于S的说法正确的是( )
A.S小于0.1m2 B.S大于0.1m2
C.S小于10m2 D.S大于10m2
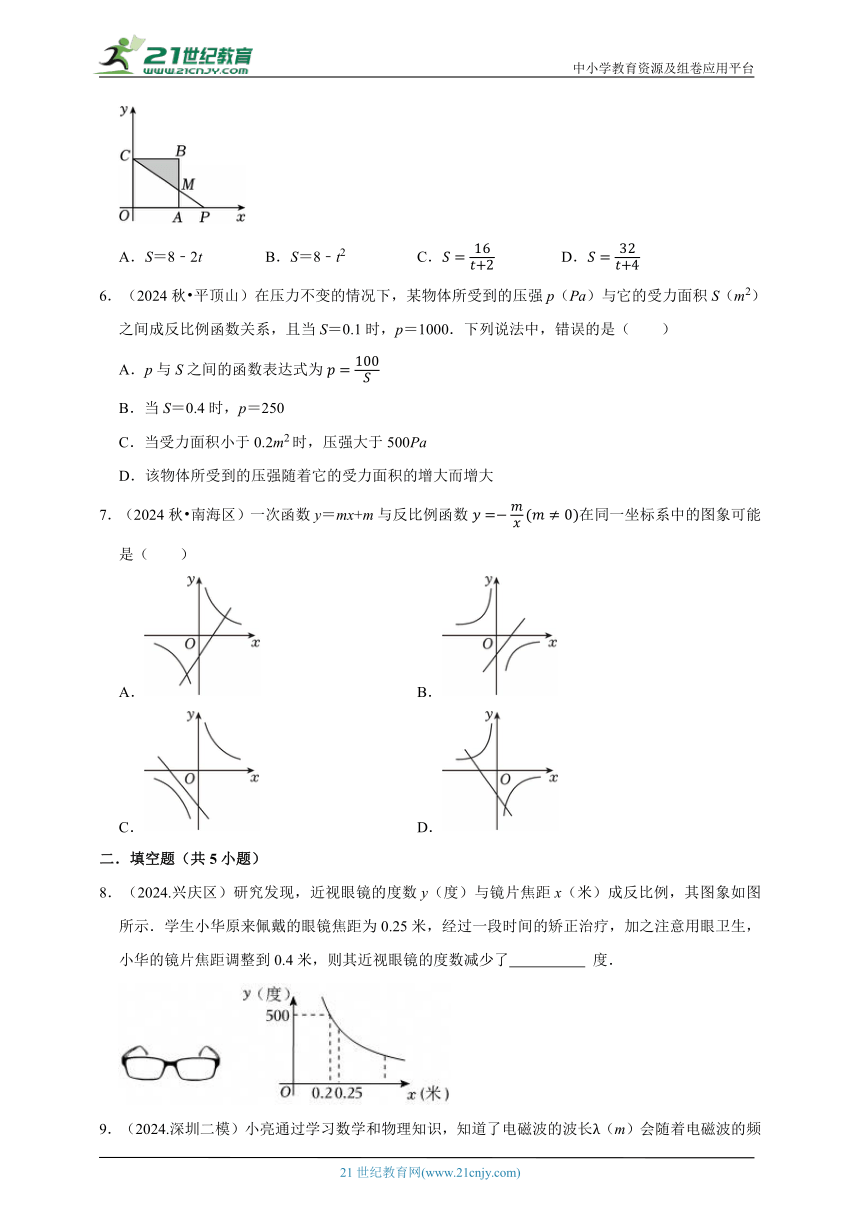
5.(2024.梅州一模)如图,在平面直角坐标系中,已知点A的坐标为(4,0),以OA为边,在x轴上方作正方形OABC,动点P从点A出发,沿x轴正方向以每秒2个单位长度的速度运动.线段CP交AB于点M.设点P运动时间为t秒,△BCM的面积为S,则S关于t的函数表达式为( )
A.S=8﹣2t B.S=8﹣t2 C. D.
6.(2024秋 平顶山)在压力不变的情况下,某物体所受到的压强p(Pa)与它的受力面积S(m2)之间成反比例函数关系,且当S=0.1时,p=1000.下列说法中,错误的是( )
A.p与S之间的函数表达式为
B.当S=0.4时,p=250
C.当受力面积小于0.2m2时,压强大于500Pa
D.该物体所受到的压强随着它的受力面积的增大而增大
7.(2024秋 南海区)一次函数y=mx+m与反比例函数在同一坐标系中的图象可能是( )
A. B.
C. D.
二.填空题(共5小题)
8.(2024.兴庆区)研究发现,近视眼镜的度数y(度)与镜片焦距x(米)成反比例,其图象如图所示.学生小华原来佩戴的眼镜焦距为0.25米,经过一段时间的矫正治疗,加之注意用眼卫生,小华的镜片焦距调整到0.4米,则其近视眼镜的度数减少了 度.
9.(2024.深圳二模)小亮通过学习数学和物理知识,知道了电磁波的波长λ(m)会随着电磁波的频率f(MHz)的变化而变化.已知波长λ与频率f是反比例函数关系,如表是它们的部分对应值.若f=60MHz,则电磁波的波长λ= m.
频率f/MHz 10 15 50
波长λ/m 30 20 6
10.(2024.平房区二模)快递运载机器人是一种应用于配送领域的智能机器人,它的最快移动速度v(m/s)是载重后总质量m(kg)的反比例函数.已知一款快递运载机器人载重后总质量m=60kg时,它的最快移动速度v=6m/s;当其载重后总质量m=100kg时,它的最快移动速度v= m/s.
11.(2024秋 兰州)已知反比例函数,当x<0时,y随x的增大而减小,则a的值可以是 .
12.(2024.运城二模)春晚机器人扭秧歌转手帕,实力出圈,其实是在用电机控制手帕转速,已知直流电动机在空载状态下的转速计算公式为(其中n为转速(转/分钟),U为电源电压(V),k为常数,φ为电枢磁通(Wb).当直流电动机的k值与φ值一定时,转数n是电压U的正比例函数.若一台12V直流电动机的空载转数为300转/分钟,则在36V的电压下该电动机的空载转速为 转/分钟.
三.解答题(共3小题)
13.(2024.普陀区三模)在现代智能仓储系统中,一款名为“SwiftBot”的智能机器狗,为了研究其载重能力W(千克)与其运动速度v(米/秒)的关系,工程师通过实验测得以下数据:
载重W(kg) … 10 12 15 20 30 …
速度v(m/s) … 6 5 4 3 2 …
(1)把表中W,v的各组对应值作为点的坐标,如(10,6),(12,5)…,已在图中坐标系描出了相应的点,请用平滑的曲线顺次连接这些点;
(2)观察所画的图象,猜测v与W之间的函数关系,并求出函数关系式;
(3)某次任务要求机器狗在8分钟内将货物运送至2400米外的分区货架,求此时机器狗能承载的最大货物重量.
14.(2024秋 埇桥区)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求该反比例函数的表达式;
(2)当气球内的气压大于140kPa时,气球将爆炸.为了安全起见,气体的体积应不小于多少?
15.(2024秋 宣城)如图,已知一次函数y1=kx+b与反比例函数的图象在第一、三象限分别交于A(6,1),B(a,﹣3)两点,连接OA,OB.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出y1≥y2时x的取值范围.
中考核心考点 反比例函数
参考答案与试题解析
一.选择题(共7小题)
1.(2025春 九龙坡区)反比例函数的图象位于( )
A.第一,第三象限 B.第一,第四象限
C.第二,第三象限 D.第二,第四象限
【考点】反比例函数的性质;反比例函数的图象.
【专题】反比例函数及其应用;符号意识.
【答案】D
【分析】根据反比例函数的性质即可得到结论,
【解答】解:∵﹣2<0,
∴反比例函数的图象位于第二,第四象限,
故选:D.
【点评】本题考查了反比例函数的性质,熟练掌握反比例函数的性质是解题的关键.
2.(2024.东莞市二模)在如图1所示的电源电压恒定的电路中,小明闭合开关S后,移动滑动变阻器的滑片,电流I与电阻R成反比例函数关系,函数图象如图2所示,点P的坐标为(5,2),则电源电压U为(提示:)( )
A.5V B.10V C.15V D.20V
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力.
【答案】B
【分析】将点P(5,2)代入即可得到答案.
【解答】解:将P(5,2)代入得,
,
∴U=2×5=10.
故选:B.
【点评】本题主要考查反比例函数的解析式,将点的坐标代入到解析式中是解题的关键.
3.(2024.昆明)对于反比例函数y,下列说法不正确的是( )
A.当x>0时,y随x的增大而增大
B.当x<0时,y随x的增大而减小
C.点(﹣2,﹣1)在它的图象上
D.它的图象在第一、三象限
【考点】反比例函数的性质.
【答案】A
【分析】首先判断反比例函数的比例系数的符号,然后根据反比例函数的性质进行判断.
【解答】解:A、当x>0时,y随x的增大而减小,故此选项错误;
B、当x<0时,y随x的增大而减小,故D选项正确.
C、把点(﹣2,﹣1)代入反比例函数y得﹣1=﹣1,故此选项正确;
D、∵k=2>0,∴图象在第一、三象限,故B选项正确;
故选:A.
【点评】本题主要考查了反比例函数y(k≠0)的性质:
①k>0时,函数图象在第一,三象限.在每个象限内y随x的增大而减小;
②k<0时,函数图象在第二,四象限.在每个象限内y随x的增大而增大.
4.(2024.通许县)根据物理学知识,作用于物体上的压力F(N)所产生的压强p(Pa)与物体受力面积S(m2)三者之间满足.若压力为100N时,压强要大于1000Pa,则此时关于S的说法正确的是( )
A.S小于0.1m2 B.S大于0.1m2
C.S小于10m2 D.S大于10m2
【考点】反比例函数的应用.
【专题】反比例函数及其应用;应用意识.
【答案】A
【分析】根据已知条件利用压强公式推导即可得到答案.
【解答】解:∵,F=100,
∴p,
∵产生的压强P要大于1000Pa,
∴1000,
∴S<0.1,
故选:A.
【点评】本题考查了反比例的应用等知识点,熟练掌握其性质是解决此题的关键.
5.(2024.梅州一模)如图,在平面直角坐标系中,已知点A的坐标为(4,0),以OA为边,在x轴上方作正方形OABC,动点P从点A出发,沿x轴正方向以每秒2个单位长度的速度运动.线段CP交AB于点M.设点P运动时间为t秒,△BCM的面积为S,则S关于t的函数表达式为( )
A.S=8﹣2t B.S=8﹣t2 C. D.
【考点】根据实际问题列反比例函数关系式.
【专题】反比例函数及其应用;运算能力.
【答案】C
【分析】根据相似三角形的性质求解.
【解答】解:由题意得:BC=AB=OC=OA=4,BC∥OA,
∴△APM∽△BCM,
∴,即,
解得:BM,
∴S4 ,
故选:C.
【点评】本题考查了由实际问题列反比例函数关系式,掌握相似三角形的性质是解题的关键.
6.(2024秋 平顶山)在压力不变的情况下,某物体所受到的压强p(Pa)与它的受力面积S(m2)之间成反比例函数关系,且当S=0.1时,p=1000.下列说法中,错误的是( )
A.p与S之间的函数表达式为
B.当S=0.4时,p=250
C.当受力面积小于0.2m2时,压强大于500Pa
D.该物体所受到的压强随着它的受力面积的增大而增大
【考点】反比例函数的应用.
【专题】反比例函数及其应用;应用意识.
【答案】D
【分析】压力一定时,压强和受力面积成反比,根据当S=0.1时,p=1000写出解析式,根据解析式即可判定各个选项.
【解答】解:压力一定时,压强和受力面积成反比;
∵当S=0.1时,p=1000,
∴p(S>0),
当S=0.4时,p250,
故选项A,B不符合题意;
当S=0.2时,p500,
∴当受力面积小于0.2m2时,压强大于500Pa,
故选项C不符合题意;
该物体所受到的压强随着它的受力面积的增大而减小,
故选项D符合题意;
故选:D.
【点评】本题考查反比例函数的应用,根据题意写出反比例函数的解析式是解题的关键.
7.(2024秋 南海区)一次函数y=mx+m与反比例函数在同一坐标系中的图象可能是( )
A. B.
C. D.
【考点】反比例函数的图象;一次函数的图象.
【专题】反比例函数及其应用;应用意识.
【答案】C
【分析】先根据一次函数的性质判断出m取值,再根据反比例函数的性质判断出m的取值,二者一致的即为正确答案.
【解答】解:A、由函数y=mx+m的增减性可知m>0,但从函数图象与y轴的交点来看m<0,相矛盾,故A错误;
B、由函数y=mx+m的增减性可知m<0,但从函数图象与y轴的交点来看m>0,相矛盾,故B错误;
C、由函数y=mx+m的图象可知m<0,由函数y的图象可知m<0,故C正确;
D、由函数y=mx+m的图象可知m<0,由函数y的图象可知m>0,相矛盾,故D错误;
故选:C.
【点评】本题主要考查了反比例函数的图象性质和一次函数的图象性质,要掌握它们的性质才能灵活解题.
二.填空题(共5小题)
8.(2024.兴庆区)研究发现,近视眼镜的度数y(度)与镜片焦距x(米)成反比例,其图象如图所示.学生小华原来佩戴的眼镜焦距为0.25米,经过一段时间的矫正治疗,加之注意用眼卫生,小华的镜片焦距调整到0.4米,则其近视眼镜的度数减少了 150 度.
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力.
【答案】150.
【分析】设函数的解析式为,由x=500时,y=0.2可求k,进而可求函数关系式,然后把x=0.4及x=0.25代入解析式,即可求得答案.
【解答】解:设函数的解析式为,有条件可得,
解得k=100,
∴函数的解析式为,
∴当x=0.4时,,
∴当x=0.25时,,
则400﹣250=150,
∴小雪的近视眼镜的度数减少了150度.
故答案为:150.
【点评】本题考查了反比例函数的应用,正确地求出反比例函数的解析式是解题的关键.
9.(2024.深圳二模)小亮通过学习数学和物理知识,知道了电磁波的波长λ(m)会随着电磁波的频率f(MHz)的变化而变化.已知波长λ与频率f是反比例函数关系,如表是它们的部分对应值.若f=60MHz,则电磁波的波长λ= 5 m.
频率f/MHz 10 15 50
波长λ/m 30 20 6
【考点】反比例函数的应用.
【专题】反比例函数及其应用;应用意识.
【答案】5.
【分析】设解析式为λ( k≠0),用待定系数法求解得到把f=60MHz值代入所求得的解析式中,即可求得此电磁波的波长λ.
【解答】解:设波长λ关于频率f的函数解析式为λ( k≠0),
把点(10,30)代入上式中得:30,
解得:k=300,
∴λ;
当f=60MHz时,λ5,
答:当f=60MHz时,此电磁波的波长λ为5m.
故答案为:5.
【点评】本题是反比例函数的应用问题,考查了求反比例函数的解析式及求反比例函数的函数值等知识,利用待定系数法求得反比例函数解析式是解题的关键.
10.(2024.平房区二模)快递运载机器人是一种应用于配送领域的智能机器人,它的最快移动速度v(m/s)是载重后总质量m(kg)的反比例函数.已知一款快递运载机器人载重后总质量m=60kg时,它的最快移动速度v=6m/s;当其载重后总质量m=100kg时,它的最快移动速度v= 3.6 m/s.
【考点】反比例函数的应用.
【专题】反比例函数及其应用;应用意识.
【答案】3.6.
【分析】利用待定系数法求出反比例函数解析式,后再将m=100代入计算即可.
【解答】解:∵智能机器人的最快移动速度v(m/s)是载重后总质量m(kg)的反比例函数,机器狗载重后总质量m=60kg时,它的最快移动速度v=6m/s,
设反比例函数解析式为,代入得:
k=60×6=360,
∴反比例函数解析式为,
当m=100时,,
故答案为:3.6.
【点评】本题考查了反比例函数的应用,解答本题的关键是利用待定系数法求反比例函数解析式.
11.(2024秋 兰州)已知反比例函数,当x<0时,y随x的增大而减小,则a的值可以是 1(答案不唯一) .
【考点】反比例函数的性质.
【专题】反比例函数及其应用;运算能力.
【答案】见试题解答内容
【分析】反比例函数(k是常数,k≠0)的图象是双曲线,当k>0,反比例函数图象的两个分支在第一、三象限,在每一象限内,y随x的增大而减小;当k<0,反比例函数图象的两个分支在第二、四象限,在每一象限内,y随x的增大而增大.根据当x<0时,y随x的增大而减小列式求解即可.
【解答】解:由当x<0时,y随x的增大而减小可知2﹣a>0,
则a<2,
∴不妨令a=1.
故答案为:1(答案不唯一).
【点评】本题考查了反比例函数的图象与性质,熟练掌握该知识点是关键.
12.(2024.运城二模)春晚机器人扭秧歌转手帕,实力出圈,其实是在用电机控制手帕转速,已知直流电动机在空载状态下的转速计算公式为(其中n为转速(转/分钟),U为电源电压(V),k为常数,φ为电枢磁通(Wb).当直流电动机的k值与φ值一定时,转数n是电压U的正比例函数.若一台12V直流电动机的空载转数为300转/分钟,则在36V的电压下该电动机的空载转速为 900 转/分钟.
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力.
【答案】900.
【分析】根据一台12V直流电动机的空载转数为300转/分钟,可得,可得n=25U,再进一步可得答案.
【解答】解:由条件可知,
∴n=25U,
当U=36V时,
∴n=25U=25×36=900,
故答案为:900.
【点评】本题考查的是正比例函数的应用,理解题意是关键.
三.解答题(共3小题)
13.(2024.普陀区三模)在现代智能仓储系统中,一款名为“SwiftBot”的智能机器狗,为了研究其载重能力W(千克)与其运动速度v(米/秒)的关系,工程师通过实验测得以下数据:
载重W(kg) … 10 12 15 20 30 …
速度v(m/s) … 6 5 4 3 2 …
(1)把表中W,v的各组对应值作为点的坐标,如(10,6),(12,5)…,已在图中坐标系描出了相应的点,请用平滑的曲线顺次连接这些点;
(2)观察所画的图象,猜测v与W之间的函数关系,并求出函数关系式;
(3)某次任务要求机器狗在8分钟内将货物运送至2400米外的分区货架,求此时机器狗能承载的最大货物重量.
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力.
【答案】(1)作图见解析;(2)v;(3)12千克.
【分析】(1)依据题意,连线即可作图得解;
(2)依据题意可得,函数是反比例函数图象,从而可设v,又图象过(10,6),求出k=10×6=60,进而可以判断得解;
(3)依据题意,又8分钟内将货物运送至2400米,从而v=2400÷(8×60)=5(米/秒),故可得此时机器狗能承载的最大货物重量W12(千克),即可得解.
【解答】解:(1)由题意,连线作图如下.
(2)由题意可得,函数是反比例函数图象,
∴可设v,
又∵图象过(10,6),
∴k=10×6=60.
∴函数关系式为v.
(3)由题意,∵8分钟内将货物运送至2400米,
∴v=2400÷(8×60)=5(米/秒).
∴此时机器狗能承载的最大货物重量W12(千克).
【点评】本题主要考查了反比例函数的应用,解题时要熟练掌握并能灵活运用反比例函数的性质是关键.
14.(2024秋 埇桥区)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求该反比例函数的表达式;
(2)当气球内的气压大于140kPa时,气球将爆炸.为了安全起见,气体的体积应不小于多少?
【考点】反比例函数的应用.
【专题】数形结合;待定系数法;反比例函数及其应用;应用意识.
【答案】(1)反比例函数的表达式为p;
(2)气体的体积应不小于m3.
【分析】(1)设出反比例函数解析式,把点A的坐标代入即可求得比例系数;
(2)易得气球内的气压应不超过140kPa,列出不等式,求得相应的解集即可.
【解答】解:(1)设p,
∵点A(0.8,120)在反比例函数解析式上,
∴k=0.8×120=96,
∴反比例函数的表达式为p;
(2)由题意得:140,
140V≥96,
解得:V.
答:气体的体积应不小于m3.
【点评】本题考查二次函数的应用.用待定系数法求得二次函数的解析式是解决本题的关键.
15.(2024秋 宣城)如图,已知一次函数y1=kx+b与反比例函数的图象在第一、三象限分别交于A(6,1),B(a,﹣3)两点,连接OA,OB.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出y1≥y2时x的取值范围.
【考点】反比例函数与一次函数的交点问题.
【专题】反比例函数及其应用;应用意识.
【答案】(1)y2,y1x﹣2;
(2)8;
(3)﹣2≤x<0或x≥6.
【分析】(1)首先把A(6,1)代入反比例函数解析式中确定m,然后把B(a,﹣3)代入反比例函数的解析式确定a,然后根据A,B两点坐标利用待定系数法确定一次函数的解析式;
(2)求得一次函数与x轴的交点,根据S△AOB=S△AOC+S△BOC即可求解;
(3)根据图象,求出自变量的取值范围即可.
【解答】解:(1)把A(6,1)代入y2中,
解得:m=6,
故反比例函数的解析式为y2;
把B(a,﹣3)代入y2,解得a=﹣2,
故B(﹣2,﹣3),
把A(6,1),B(﹣2,﹣3)代入y1=kx+b,
得,解得:,
故一次函数解析式为y1x﹣2;
(2)如图,设一次函数y1x﹣2与x轴交于点C,
令y=0,得x=4.
∴点C的坐标是(4,0),
∴S△AOB=S△AOC+S△BOC4×14×3=8.
故答案为:8;
(3)由图象可知,当﹣2≤x<0或x≥6时,y1≥y2,
所以y1≥y2时x的取值范围是﹣2≤x<0或x≥6.
【点评】此题考查了一次函数与反比例函数的交点问题,待定系数法求一次函数与反比例函数的解析式,三角形的面积,待定系数法求函数解析式是中学阶段求函数解析式常用的方法,一定要熟练掌握并灵活运用.利用了数形结合思想.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考冲刺核心考点 反比例函数
一.选择题(共7小题)
1.(2025春 九龙坡区)反比例函数的图象位于( )
A.第一,第三象限 B.第一,第四象限
C.第二,第三象限 D.第二,第四象限
2.(2024.东莞市二模)在如图1所示的电源电压恒定的电路中,小明闭合开关S后,移动滑动变阻器的滑片,电流I与电阻R成反比例函数关系,函数图象如图2所示,点P的坐标为(5,2),则电源电压U为(提示:)( )
A.5V B.10V C.15V D.20V
3.(2024.昆明)对于反比例函数y,下列说法不正确的是( )
A.当x>0时,y随x的增大而增大
B.当x<0时,y随x的增大而减小
C.点(﹣2,﹣1)在它的图象上
D.它的图象在第一、三象限
4.(2024.通许县)根据物理学知识,作用于物体上的压力F(N)所产生的压强p(Pa)与物体受力面积S(m2)三者之间满足.若压力为100N时,压强要大于1000Pa,则此时关于S的说法正确的是( )
A.S小于0.1m2 B.S大于0.1m2
C.S小于10m2 D.S大于10m2
5.(2024.梅州一模)如图,在平面直角坐标系中,已知点A的坐标为(4,0),以OA为边,在x轴上方作正方形OABC,动点P从点A出发,沿x轴正方向以每秒2个单位长度的速度运动.线段CP交AB于点M.设点P运动时间为t秒,△BCM的面积为S,则S关于t的函数表达式为( )
A.S=8﹣2t B.S=8﹣t2 C. D.
6.(2024秋 平顶山)在压力不变的情况下,某物体所受到的压强p(Pa)与它的受力面积S(m2)之间成反比例函数关系,且当S=0.1时,p=1000.下列说法中,错误的是( )
A.p与S之间的函数表达式为
B.当S=0.4时,p=250
C.当受力面积小于0.2m2时,压强大于500Pa
D.该物体所受到的压强随着它的受力面积的增大而增大
7.(2024秋 南海区)一次函数y=mx+m与反比例函数在同一坐标系中的图象可能是( )
A. B.
C. D.
二.填空题(共5小题)
8.(2024.兴庆区)研究发现,近视眼镜的度数y(度)与镜片焦距x(米)成反比例,其图象如图所示.学生小华原来佩戴的眼镜焦距为0.25米,经过一段时间的矫正治疗,加之注意用眼卫生,小华的镜片焦距调整到0.4米,则其近视眼镜的度数减少了 度.
9.(2024.深圳二模)小亮通过学习数学和物理知识,知道了电磁波的波长λ(m)会随着电磁波的频率f(MHz)的变化而变化.已知波长λ与频率f是反比例函数关系,如表是它们的部分对应值.若f=60MHz,则电磁波的波长λ= m.
频率f/MHz 10 15 50
波长λ/m 30 20 6
10.(2024.平房区二模)快递运载机器人是一种应用于配送领域的智能机器人,它的最快移动速度v(m/s)是载重后总质量m(kg)的反比例函数.已知一款快递运载机器人载重后总质量m=60kg时,它的最快移动速度v=6m/s;当其载重后总质量m=100kg时,它的最快移动速度v= m/s.
11.(2024秋 兰州)已知反比例函数,当x<0时,y随x的增大而减小,则a的值可以是 .
12.(2024.运城二模)春晚机器人扭秧歌转手帕,实力出圈,其实是在用电机控制手帕转速,已知直流电动机在空载状态下的转速计算公式为(其中n为转速(转/分钟),U为电源电压(V),k为常数,φ为电枢磁通(Wb).当直流电动机的k值与φ值一定时,转数n是电压U的正比例函数.若一台12V直流电动机的空载转数为300转/分钟,则在36V的电压下该电动机的空载转速为 转/分钟.
三.解答题(共3小题)
13.(2024.普陀区三模)在现代智能仓储系统中,一款名为“SwiftBot”的智能机器狗,为了研究其载重能力W(千克)与其运动速度v(米/秒)的关系,工程师通过实验测得以下数据:
载重W(kg) … 10 12 15 20 30 …
速度v(m/s) … 6 5 4 3 2 …
(1)把表中W,v的各组对应值作为点的坐标,如(10,6),(12,5)…,已在图中坐标系描出了相应的点,请用平滑的曲线顺次连接这些点;
(2)观察所画的图象,猜测v与W之间的函数关系,并求出函数关系式;
(3)某次任务要求机器狗在8分钟内将货物运送至2400米外的分区货架,求此时机器狗能承载的最大货物重量.
14.(2024秋 埇桥区)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求该反比例函数的表达式;
(2)当气球内的气压大于140kPa时,气球将爆炸.为了安全起见,气体的体积应不小于多少?
15.(2024秋 宣城)如图,已知一次函数y1=kx+b与反比例函数的图象在第一、三象限分别交于A(6,1),B(a,﹣3)两点,连接OA,OB.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出y1≥y2时x的取值范围.
中考核心考点 反比例函数
参考答案与试题解析
一.选择题(共7小题)
1.(2025春 九龙坡区)反比例函数的图象位于( )
A.第一,第三象限 B.第一,第四象限
C.第二,第三象限 D.第二,第四象限
【考点】反比例函数的性质;反比例函数的图象.
【专题】反比例函数及其应用;符号意识.
【答案】D
【分析】根据反比例函数的性质即可得到结论,
【解答】解:∵﹣2<0,
∴反比例函数的图象位于第二,第四象限,
故选:D.
【点评】本题考查了反比例函数的性质,熟练掌握反比例函数的性质是解题的关键.
2.(2024.东莞市二模)在如图1所示的电源电压恒定的电路中,小明闭合开关S后,移动滑动变阻器的滑片,电流I与电阻R成反比例函数关系,函数图象如图2所示,点P的坐标为(5,2),则电源电压U为(提示:)( )
A.5V B.10V C.15V D.20V
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力.
【答案】B
【分析】将点P(5,2)代入即可得到答案.
【解答】解:将P(5,2)代入得,
,
∴U=2×5=10.
故选:B.
【点评】本题主要考查反比例函数的解析式,将点的坐标代入到解析式中是解题的关键.
3.(2024.昆明)对于反比例函数y,下列说法不正确的是( )
A.当x>0时,y随x的增大而增大
B.当x<0时,y随x的增大而减小
C.点(﹣2,﹣1)在它的图象上
D.它的图象在第一、三象限
【考点】反比例函数的性质.
【答案】A
【分析】首先判断反比例函数的比例系数的符号,然后根据反比例函数的性质进行判断.
【解答】解:A、当x>0时,y随x的增大而减小,故此选项错误;
B、当x<0时,y随x的增大而减小,故D选项正确.
C、把点(﹣2,﹣1)代入反比例函数y得﹣1=﹣1,故此选项正确;
D、∵k=2>0,∴图象在第一、三象限,故B选项正确;
故选:A.
【点评】本题主要考查了反比例函数y(k≠0)的性质:
①k>0时,函数图象在第一,三象限.在每个象限内y随x的增大而减小;
②k<0时,函数图象在第二,四象限.在每个象限内y随x的增大而增大.
4.(2024.通许县)根据物理学知识,作用于物体上的压力F(N)所产生的压强p(Pa)与物体受力面积S(m2)三者之间满足.若压力为100N时,压强要大于1000Pa,则此时关于S的说法正确的是( )
A.S小于0.1m2 B.S大于0.1m2
C.S小于10m2 D.S大于10m2
【考点】反比例函数的应用.
【专题】反比例函数及其应用;应用意识.
【答案】A
【分析】根据已知条件利用压强公式推导即可得到答案.
【解答】解:∵,F=100,
∴p,
∵产生的压强P要大于1000Pa,
∴1000,
∴S<0.1,
故选:A.
【点评】本题考查了反比例的应用等知识点,熟练掌握其性质是解决此题的关键.
5.(2024.梅州一模)如图,在平面直角坐标系中,已知点A的坐标为(4,0),以OA为边,在x轴上方作正方形OABC,动点P从点A出发,沿x轴正方向以每秒2个单位长度的速度运动.线段CP交AB于点M.设点P运动时间为t秒,△BCM的面积为S,则S关于t的函数表达式为( )
A.S=8﹣2t B.S=8﹣t2 C. D.
【考点】根据实际问题列反比例函数关系式.
【专题】反比例函数及其应用;运算能力.
【答案】C
【分析】根据相似三角形的性质求解.
【解答】解:由题意得:BC=AB=OC=OA=4,BC∥OA,
∴△APM∽△BCM,
∴,即,
解得:BM,
∴S4 ,
故选:C.
【点评】本题考查了由实际问题列反比例函数关系式,掌握相似三角形的性质是解题的关键.
6.(2024秋 平顶山)在压力不变的情况下,某物体所受到的压强p(Pa)与它的受力面积S(m2)之间成反比例函数关系,且当S=0.1时,p=1000.下列说法中,错误的是( )
A.p与S之间的函数表达式为
B.当S=0.4时,p=250
C.当受力面积小于0.2m2时,压强大于500Pa
D.该物体所受到的压强随着它的受力面积的增大而增大
【考点】反比例函数的应用.
【专题】反比例函数及其应用;应用意识.
【答案】D
【分析】压力一定时,压强和受力面积成反比,根据当S=0.1时,p=1000写出解析式,根据解析式即可判定各个选项.
【解答】解:压力一定时,压强和受力面积成反比;
∵当S=0.1时,p=1000,
∴p(S>0),
当S=0.4时,p250,
故选项A,B不符合题意;
当S=0.2时,p500,
∴当受力面积小于0.2m2时,压强大于500Pa,
故选项C不符合题意;
该物体所受到的压强随着它的受力面积的增大而减小,
故选项D符合题意;
故选:D.
【点评】本题考查反比例函数的应用,根据题意写出反比例函数的解析式是解题的关键.
7.(2024秋 南海区)一次函数y=mx+m与反比例函数在同一坐标系中的图象可能是( )
A. B.
C. D.
【考点】反比例函数的图象;一次函数的图象.
【专题】反比例函数及其应用;应用意识.
【答案】C
【分析】先根据一次函数的性质判断出m取值,再根据反比例函数的性质判断出m的取值,二者一致的即为正确答案.
【解答】解:A、由函数y=mx+m的增减性可知m>0,但从函数图象与y轴的交点来看m<0,相矛盾,故A错误;
B、由函数y=mx+m的增减性可知m<0,但从函数图象与y轴的交点来看m>0,相矛盾,故B错误;
C、由函数y=mx+m的图象可知m<0,由函数y的图象可知m<0,故C正确;
D、由函数y=mx+m的图象可知m<0,由函数y的图象可知m>0,相矛盾,故D错误;
故选:C.
【点评】本题主要考查了反比例函数的图象性质和一次函数的图象性质,要掌握它们的性质才能灵活解题.
二.填空题(共5小题)
8.(2024.兴庆区)研究发现,近视眼镜的度数y(度)与镜片焦距x(米)成反比例,其图象如图所示.学生小华原来佩戴的眼镜焦距为0.25米,经过一段时间的矫正治疗,加之注意用眼卫生,小华的镜片焦距调整到0.4米,则其近视眼镜的度数减少了 150 度.
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力.
【答案】150.
【分析】设函数的解析式为,由x=500时,y=0.2可求k,进而可求函数关系式,然后把x=0.4及x=0.25代入解析式,即可求得答案.
【解答】解:设函数的解析式为,有条件可得,
解得k=100,
∴函数的解析式为,
∴当x=0.4时,,
∴当x=0.25时,,
则400﹣250=150,
∴小雪的近视眼镜的度数减少了150度.
故答案为:150.
【点评】本题考查了反比例函数的应用,正确地求出反比例函数的解析式是解题的关键.
9.(2024.深圳二模)小亮通过学习数学和物理知识,知道了电磁波的波长λ(m)会随着电磁波的频率f(MHz)的变化而变化.已知波长λ与频率f是反比例函数关系,如表是它们的部分对应值.若f=60MHz,则电磁波的波长λ= 5 m.
频率f/MHz 10 15 50
波长λ/m 30 20 6
【考点】反比例函数的应用.
【专题】反比例函数及其应用;应用意识.
【答案】5.
【分析】设解析式为λ( k≠0),用待定系数法求解得到把f=60MHz值代入所求得的解析式中,即可求得此电磁波的波长λ.
【解答】解:设波长λ关于频率f的函数解析式为λ( k≠0),
把点(10,30)代入上式中得:30,
解得:k=300,
∴λ;
当f=60MHz时,λ5,
答:当f=60MHz时,此电磁波的波长λ为5m.
故答案为:5.
【点评】本题是反比例函数的应用问题,考查了求反比例函数的解析式及求反比例函数的函数值等知识,利用待定系数法求得反比例函数解析式是解题的关键.
10.(2024.平房区二模)快递运载机器人是一种应用于配送领域的智能机器人,它的最快移动速度v(m/s)是载重后总质量m(kg)的反比例函数.已知一款快递运载机器人载重后总质量m=60kg时,它的最快移动速度v=6m/s;当其载重后总质量m=100kg时,它的最快移动速度v= 3.6 m/s.
【考点】反比例函数的应用.
【专题】反比例函数及其应用;应用意识.
【答案】3.6.
【分析】利用待定系数法求出反比例函数解析式,后再将m=100代入计算即可.
【解答】解:∵智能机器人的最快移动速度v(m/s)是载重后总质量m(kg)的反比例函数,机器狗载重后总质量m=60kg时,它的最快移动速度v=6m/s,
设反比例函数解析式为,代入得:
k=60×6=360,
∴反比例函数解析式为,
当m=100时,,
故答案为:3.6.
【点评】本题考查了反比例函数的应用,解答本题的关键是利用待定系数法求反比例函数解析式.
11.(2024秋 兰州)已知反比例函数,当x<0时,y随x的增大而减小,则a的值可以是 1(答案不唯一) .
【考点】反比例函数的性质.
【专题】反比例函数及其应用;运算能力.
【答案】见试题解答内容
【分析】反比例函数(k是常数,k≠0)的图象是双曲线,当k>0,反比例函数图象的两个分支在第一、三象限,在每一象限内,y随x的增大而减小;当k<0,反比例函数图象的两个分支在第二、四象限,在每一象限内,y随x的增大而增大.根据当x<0时,y随x的增大而减小列式求解即可.
【解答】解:由当x<0时,y随x的增大而减小可知2﹣a>0,
则a<2,
∴不妨令a=1.
故答案为:1(答案不唯一).
【点评】本题考查了反比例函数的图象与性质,熟练掌握该知识点是关键.
12.(2024.运城二模)春晚机器人扭秧歌转手帕,实力出圈,其实是在用电机控制手帕转速,已知直流电动机在空载状态下的转速计算公式为(其中n为转速(转/分钟),U为电源电压(V),k为常数,φ为电枢磁通(Wb).当直流电动机的k值与φ值一定时,转数n是电压U的正比例函数.若一台12V直流电动机的空载转数为300转/分钟,则在36V的电压下该电动机的空载转速为 900 转/分钟.
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力.
【答案】900.
【分析】根据一台12V直流电动机的空载转数为300转/分钟,可得,可得n=25U,再进一步可得答案.
【解答】解:由条件可知,
∴n=25U,
当U=36V时,
∴n=25U=25×36=900,
故答案为:900.
【点评】本题考查的是正比例函数的应用,理解题意是关键.
三.解答题(共3小题)
13.(2024.普陀区三模)在现代智能仓储系统中,一款名为“SwiftBot”的智能机器狗,为了研究其载重能力W(千克)与其运动速度v(米/秒)的关系,工程师通过实验测得以下数据:
载重W(kg) … 10 12 15 20 30 …
速度v(m/s) … 6 5 4 3 2 …
(1)把表中W,v的各组对应值作为点的坐标,如(10,6),(12,5)…,已在图中坐标系描出了相应的点,请用平滑的曲线顺次连接这些点;
(2)观察所画的图象,猜测v与W之间的函数关系,并求出函数关系式;
(3)某次任务要求机器狗在8分钟内将货物运送至2400米外的分区货架,求此时机器狗能承载的最大货物重量.
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力.
【答案】(1)作图见解析;(2)v;(3)12千克.
【分析】(1)依据题意,连线即可作图得解;
(2)依据题意可得,函数是反比例函数图象,从而可设v,又图象过(10,6),求出k=10×6=60,进而可以判断得解;
(3)依据题意,又8分钟内将货物运送至2400米,从而v=2400÷(8×60)=5(米/秒),故可得此时机器狗能承载的最大货物重量W12(千克),即可得解.
【解答】解:(1)由题意,连线作图如下.
(2)由题意可得,函数是反比例函数图象,
∴可设v,
又∵图象过(10,6),
∴k=10×6=60.
∴函数关系式为v.
(3)由题意,∵8分钟内将货物运送至2400米,
∴v=2400÷(8×60)=5(米/秒).
∴此时机器狗能承载的最大货物重量W12(千克).
【点评】本题主要考查了反比例函数的应用,解题时要熟练掌握并能灵活运用反比例函数的性质是关键.
14.(2024秋 埇桥区)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求该反比例函数的表达式;
(2)当气球内的气压大于140kPa时,气球将爆炸.为了安全起见,气体的体积应不小于多少?
【考点】反比例函数的应用.
【专题】数形结合;待定系数法;反比例函数及其应用;应用意识.
【答案】(1)反比例函数的表达式为p;
(2)气体的体积应不小于m3.
【分析】(1)设出反比例函数解析式,把点A的坐标代入即可求得比例系数;
(2)易得气球内的气压应不超过140kPa,列出不等式,求得相应的解集即可.
【解答】解:(1)设p,
∵点A(0.8,120)在反比例函数解析式上,
∴k=0.8×120=96,
∴反比例函数的表达式为p;
(2)由题意得:140,
140V≥96,
解得:V.
答:气体的体积应不小于m3.
【点评】本题考查二次函数的应用.用待定系数法求得二次函数的解析式是解决本题的关键.
15.(2024秋 宣城)如图,已知一次函数y1=kx+b与反比例函数的图象在第一、三象限分别交于A(6,1),B(a,﹣3)两点,连接OA,OB.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出y1≥y2时x的取值范围.
【考点】反比例函数与一次函数的交点问题.
【专题】反比例函数及其应用;应用意识.
【答案】(1)y2,y1x﹣2;
(2)8;
(3)﹣2≤x<0或x≥6.
【分析】(1)首先把A(6,1)代入反比例函数解析式中确定m,然后把B(a,﹣3)代入反比例函数的解析式确定a,然后根据A,B两点坐标利用待定系数法确定一次函数的解析式;
(2)求得一次函数与x轴的交点,根据S△AOB=S△AOC+S△BOC即可求解;
(3)根据图象,求出自变量的取值范围即可.
【解答】解:(1)把A(6,1)代入y2中,
解得:m=6,
故反比例函数的解析式为y2;
把B(a,﹣3)代入y2,解得a=﹣2,
故B(﹣2,﹣3),
把A(6,1),B(﹣2,﹣3)代入y1=kx+b,
得,解得:,
故一次函数解析式为y1x﹣2;
(2)如图,设一次函数y1x﹣2与x轴交于点C,
令y=0,得x=4.
∴点C的坐标是(4,0),
∴S△AOB=S△AOC+S△BOC4×14×3=8.
故答案为:8;
(3)由图象可知,当﹣2≤x<0或x≥6时,y1≥y2,
所以y1≥y2时x的取值范围是﹣2≤x<0或x≥6.
【点评】此题考查了一次函数与反比例函数的交点问题,待定系数法求一次函数与反比例函数的解析式,三角形的面积,待定系数法求函数解析式是中学阶段求函数解析式常用的方法,一定要熟练掌握并灵活运用.利用了数形结合思想.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
