【中考核心考点】2025年人教版中考数学考前冲刺 解直角三角形及其应用(含解析)
文档属性
| 名称 | 【中考核心考点】2025年人教版中考数学考前冲刺 解直角三角形及其应用(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-16 13:54:51 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中考冲刺核心考点 解直角三角形及其应用
一.选择题(共7小题)
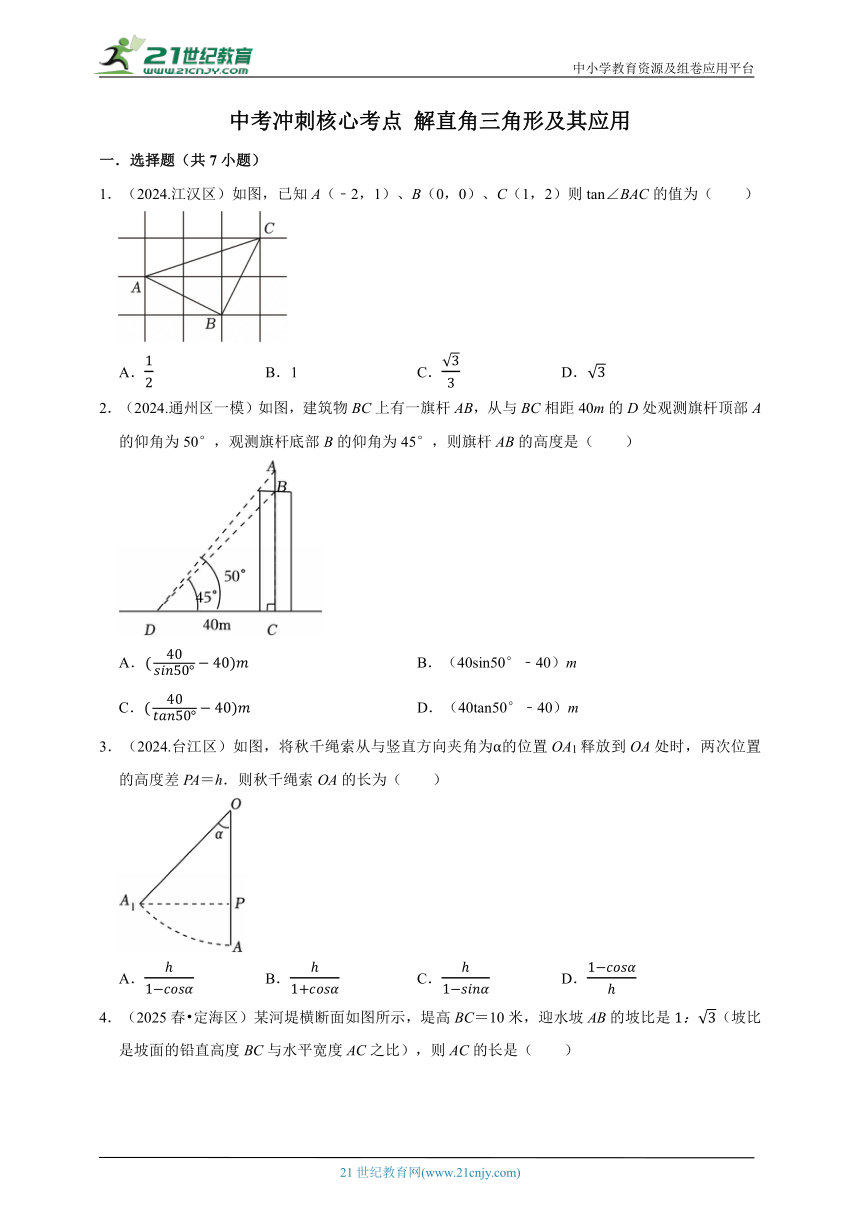
1.(2024.江汉区)如图,已知A(﹣2,1)、B(0,0)、C(1,2)则tan∠BAC的值为( )
A. B.1 C. D.
2.(2024.通州区一模)如图,建筑物BC上有一旗杆AB,从与BC相距40m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,则旗杆AB的高度是( )
A. B.(40sin50°﹣40)m
C. D.(40tan50°﹣40)m
3.(2024.台江区)如图,将秋千绳索从与竖直方向夹角为α的位置OA1释放到OA处时,两次位置的高度差PA=h.则秋千绳索OA的长为( )
A. B. C. D.
4.(2025春 定海区)某河堤横断面如图所示,堤高BC=10米,迎水坡AB的坡比是(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是( )
A.米 B.20米 C.米 D.30米
5.(2024.郑州)一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力F1的方向与斜面垂直,摩擦力F2的方向与斜面平行.若斜面的坡角α=25°,则摩擦力F2与重力G方向的夹角β的度数为( )
A.155° B.125° C.115° D.65°
6.(2024.宝安区)港珠澳大桥是世界上最长的跨海大桥,被誉为“现代世界七大奇迹”的超级工程,它是我国从桥梁大国走向桥梁强国的里程碑之作.港珠澳大桥主桥为三座大跨度钢结构斜拉桥,其中九洲航道桥主塔造型取自“风帆”,寓意“扬帆起航”,某校九年级学生为了测量该主塔的高度,站在B处看塔顶A,仰角为60°,然后向后走190米,到达C处,此时看塔顶A,仰角为30°,则该主塔的高度是( )
A.95米 B.米 C.190米 D.米
7.(2024.南山区一模)图1是某市一地铁站入口的双翼闸机,双翼展开时示意图如图2所示,它是一个轴对称图形,AC=40cm,α=37°,则双翼边缘端点C与D之间的距离为( )cm
A.60﹣40sin37° B.60﹣2×40cos37°
C.60﹣2×40tan37° D.60﹣2×40sin37°
二.填空题(共5小题)
8.(2024.湖北)如图是小区内一小山的等高线示意图,小明同学计划利用这个等高线示意图计算AB的距离,他在点B处测得A处的俯角为30°,则AB= m.
9.(2024.平房区二模)已知,在△ABC中,∠ABC=60°,AC,AB=4,则BC= .
10.(2024.呼和浩特二模)如图,兴康社区附近有A、B、C三个快递中转站:B站在A站南偏西53°方向上,C站在B站的东北方向上,A站在C站的北偏东60°方向上且距离C站4km处,则B站到C站的距离为 km(精确到0.1km).(A、B、C、D在同一平面内,参考数据:1.41,,,,,
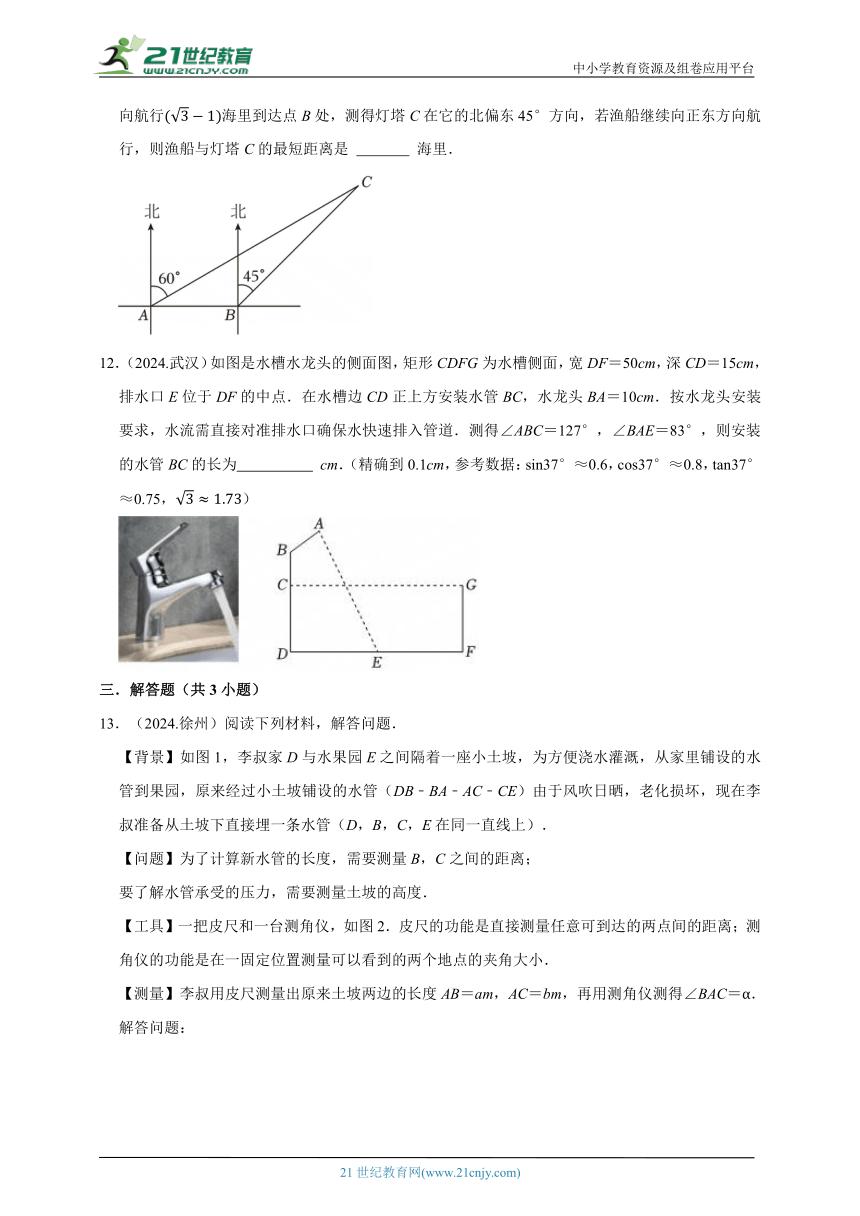
11.(2024.海勃湾区)如图,一渔船在海上A处测得灯塔C在它的北偏东60°方向,渔船向正东方向航行海里到达点B处,测得灯塔C在它的北偏东45°方向,若渔船继续向正东方向航行,则渔船与灯塔C的最短距离是 海里.
12.(2024.武汉)如图是水槽水龙头的侧面图,矩形CDFG为水槽侧面,宽DF=50cm,深CD=15cm,排水口E位于DF的中点.在水槽边CD正上方安装水管BC,水龙头BA=10cm.按水龙头安装要求,水流需直接对准排水口确保水快速排入管道.测得∠ABC=127°,∠BAE=83°,则安装的水管BC的长为 cm.(精确到0.1cm,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,)
三.解答题(共3小题)
13.(2024.徐州)阅读下列材料,解答问题.
【背景】如图1,李叔家D与水果园E之间隔着一座小土坡,为方便浇水灌溉,从家里铺设的水管到果园,原来经过小土坡铺设的水管(DB﹣BA﹣AC﹣CE)由于风吹日晒,老化损坏,现在李叔准备从土坡下直接埋一条水管(D,B,C,E在同一直线上).
【问题】为了计算新水管的长度,需要测量B,C之间的距离;
要了解水管承受的压力,需要测量土坡的高度.
【工具】一把皮尺和一台测角仪,如图2.皮尺的功能是直接测量任意可到达的两点间的距离;测角仪的功能是在一固定位置测量可以看到的两个地点的夹角大小.
【测量】李叔用皮尺测量出原来土坡两边的长度AB=am,AC=bm,再用测角仪测得∠BAC=α.
解答问题:
(1)求BC的长度;(结果用含a,b,α的代数式表示)
(2)若测得a=20m,b=25m,α=120°,求出小土坡的高度.
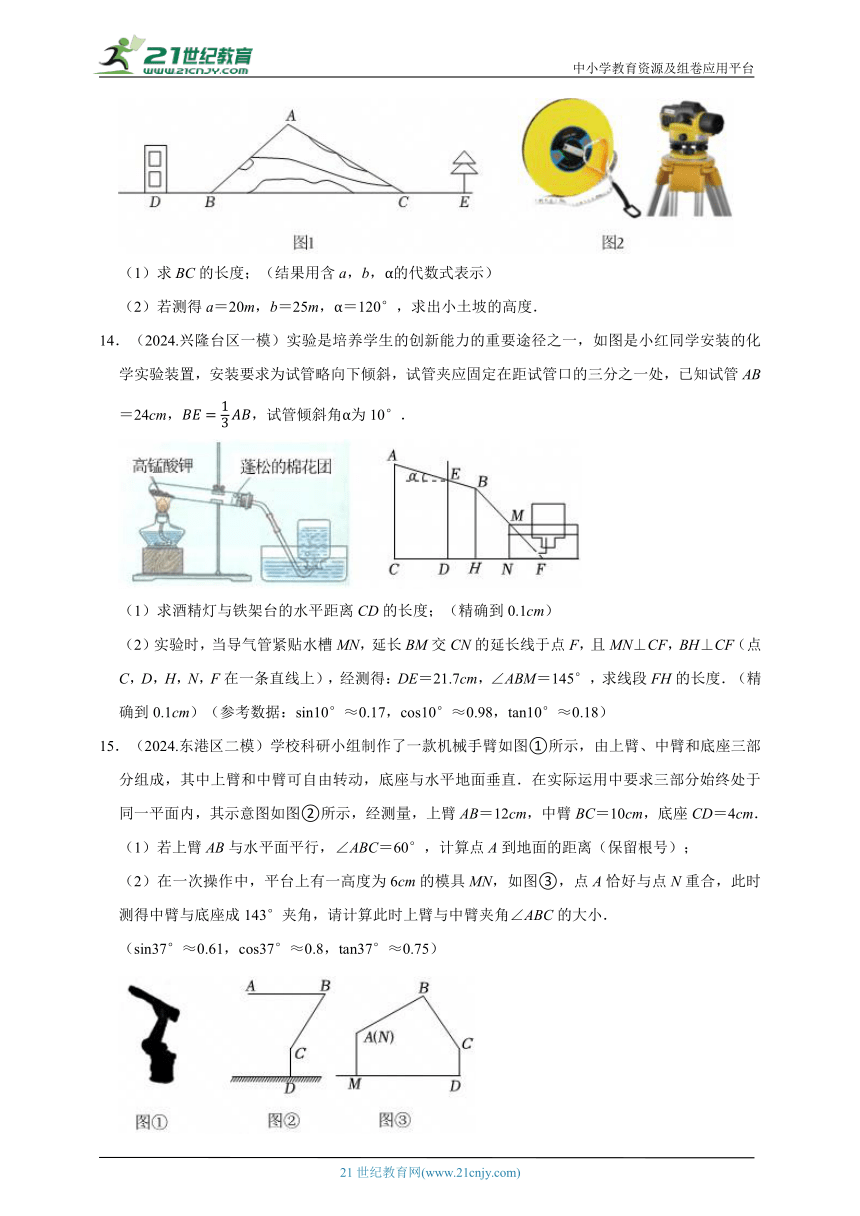
14.(2024.兴隆台区一模)实验是培养学生的创新能力的重要途径之一,如图是小红同学安装的化学实验装置,安装要求为试管略向下倾斜,试管夹应固定在距试管口的三分之一处,已知试管AB=24cm,,试管倾斜角α为10°.
(1)求酒精灯与铁架台的水平距离CD的长度;(精确到0.1cm)
(2)实验时,当导气管紧贴水槽MN,延长BM交CN的延长线于点F,且MN⊥CF,BH⊥CF(点C,D,H,N,F在一条直线上),经测得:DE=21.7cm,∠ABM=145°,求线段FH的长度.(精确到0.1cm)(参考数据:sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)
15.(2024.东港区二模)学校科研小组制作了一款机械手臂如图①所示,由上臂、中臂和底座三部分组成,其中上臂和中臂可自由转动,底座与水平地面垂直.在实际运用中要求三部分始终处于同一平面内,其示意图如图②所示,经测量,上臂AB=12cm,中臂BC=10cm,底座CD=4cm.
(1)若上臂AB与水平面平行,∠ABC=60°,计算点A到地面的距离(保留根号);
(2)在一次操作中,平台上有一高度为6cm的模具MN,如图③,点A恰好与点N重合,此时测得中臂与底座成143°夹角,请计算此时上臂与中臂夹角∠ABC的大小.
(sin37°≈0.61,cos37°≈0.8,tan37°≈0.75)
中考冲刺核心考点 解直角三角形及其应用
参考答案与试题解析
一.选择题(共7小题)
1.(2024.江汉区)如图,已知A(﹣2,1)、B(0,0)、C(1,2)则tan∠BAC的值为( )
A. B.1 C. D.
【考点】解直角三角形;坐标与图形性质.
【专题】平面直角坐标系;解直角三角形及其应用;运算能力.
【答案】B
【分析】根据题意,分别求出AB,BC,AC的长,再结合正切的定义即可解决问题.
【解答】解:由题知,
因为A(﹣2,1)、B(0,0)、C(1,2),
所以AB,
BC,
AC,
则AB2+BC2=AC2,
所以∠ABC=90°.
在Rt△ABC中,
tan∠BAC.
故选:B.
【点评】本题主要考查了坐标与图形性质及解直角三角形,熟知正切的定义是解题的关键.
2.(2024.通州区一模)如图,建筑物BC上有一旗杆AB,从与BC相距40m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,则旗杆AB的高度是( )
A. B.(40sin50°﹣40)m
C. D.(40tan50°﹣40)m
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】D
【分析】分别解直角三角形求出AC,BC的长,再用AC﹣BC进行求解即可.
【解答】解:∵AC=CD tan50°=40tan50°,
BC=CD tan45°=40,
∴AB=AC﹣BC=(40tan50°﹣40)m;
故选:D.
【点评】本题考查解直角三角形的应用,正确进行计算是解题关键.
3.(2024.台江区)如图,将秋千绳索从与竖直方向夹角为α的位置OA1释放到OA处时,两次位置的高度差PA=h.则秋千绳索OA的长为( )
A. B. C. D.
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;推理能力.
【答案】A
【分析】由题意可知,OA=OA1,再根据余弦的定义求解即可.
【解答】解:由题意可知,OA=OA1,
∵cosα,
∴OA1,
又∵OP=OA﹣PA=OA1﹣PA=OA1﹣h,
∴OA,
∴OA=OA1,
故选:A.
【点评】本题考查了解直角三角形的应用,熟记三角形函数的定义是解题的关键.
4.(2025春 定海区)某河堤横断面如图所示,堤高BC=10米,迎水坡AB的坡比是(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是( )
A.米 B.20米 C.米 D.30米
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】运算能力.
【答案】A
【分析】由堤高BC=10米,迎水坡AB的坡比,根据坡度的定义,即可求得AC的长.
【解答】解:∵迎水坡AB的坡比,
∴,
∵堤高BC=10米,
∴(米).
故选:A.
【点评】本题考查了解直角三角形的应用﹣坡度坡角问题,掌握坡比的概念是解题的关键.
5.(2024.郑州)一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力F1的方向与斜面垂直,摩擦力F2的方向与斜面平行.若斜面的坡角α=25°,则摩擦力F2与重力G方向的夹角β的度数为( )
A.155° B.125° C.115° D.65°
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】C
【分析】根据题意结合图形可知β是重力G与斜面形成的三角形的外角,从而可求得β的度数.
【解答】解:∵重力G的方向竖直向下,
∴重力G与水平方向夹角为90°,
由题意可得:
∴β=∠1=α+90°=115°,
故选:C.
【点评】本题考查了平行线的性质和三角形外角性质,正确进行计算是解题关键.
6.(2024.宝安区)港珠澳大桥是世界上最长的跨海大桥,被誉为“现代世界七大奇迹”的超级工程,它是我国从桥梁大国走向桥梁强国的里程碑之作.港珠澳大桥主桥为三座大跨度钢结构斜拉桥,其中九洲航道桥主塔造型取自“风帆”,寓意“扬帆起航”,某校九年级学生为了测量该主塔的高度,站在B处看塔顶A,仰角为60°,然后向后走190米,到达C处,此时看塔顶A,仰角为30°,则该主塔的高度是( )
A.95米 B.米 C.190米 D.米
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】B
【分析】该主塔为AD=x,在Rt△ABD中,利用正切函数的定义求得,同理,在Rt△ACD中,求得,根据CD﹣BD=190,列出方程求解即可.
【解答】解:如图,该主塔为AD=x,
由题意,得:∠ADC=90°,BC=190,∠ACD=30°,∠ABD=60°,
∵,
∴,
∵,
∴,
∵BC=CD﹣BD=190,
∴,
∴.
故选:B.
【点评】本题考查解直角三角形的实际应用,正确进行计算是解题关键.
7.(2024.南山区一模)图1是某市一地铁站入口的双翼闸机,双翼展开时示意图如图2所示,它是一个轴对称图形,AC=40cm,α=37°,则双翼边缘端点C与D之间的距离为( )cm
A.60﹣40sin37° B.60﹣2×40cos37°
C.60﹣2×40tan37° D.60﹣2×40sin37°
【考点】解直角三角形的应用;轴对称图形.
【专题】解直角三角形及其应用;应用意识.
【答案】D
【分析】作辅助线如图,由题意可得CE=DF,EF=60cm,解直角三角形ACE求出CE=40sin37° cm,然后根据CD=EF﹣2CE即可得出答案.
【解答】解:如图,作直线CD,交双翼闸机于点E、F,则CE⊥AE,DF⊥BF,
由题意可得CE=DF,EF=60cm,
在直角三角形ACE中,
CE=AC sin37°=40sin37°cm,
∴CD=EF﹣2CE=60﹣2×40sin37° (cm).
故选:D.
【点评】本题考查了解直角三角形的应用,正确理解题意、熟练掌握锐角三角函数的知识是解题的关键.
二.填空题(共5小题)
8.(2024.湖北)如图是小区内一小山的等高线示意图,小明同学计划利用这个等高线示意图计算AB的距离,他在点B处测得A处的俯角为30°,则AB= 100 m.
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;应用意识.
【答案】100.
【分析】根据由等高线可知A、B两地的高度差为50米,然后点B处测得A处的俯角为30°求值即可.
【解答】解:作示意图如下:
由题意知:A、B两地的实际高度差为AH:550﹣500=50(m),∠B=30°,∠AHB=90°,
∴sinB,即sin30°,
解得:AB=100,
故答案为:100.
【点评】本题主要考查了解直角三角形的应用﹣仰角俯角问题,解答本题的关键是根据题意,作出直角三角形解决问题.
9.(2024.平房区二模)已知,在△ABC中,∠ABC=60°,AC,AB=4,则BC= 或 .
【考点】解直角三角形;勾股定理.
【专题】作图题;几何直观.
【答案】或.
【分析】如图,过点A作AH⊥BC于点H.解直角三角形求出CH,分两种情形求出BC即可.
【解答】解:如图,过点A作AH⊥BC于点H.
在Rt△ABH中,∠AHB=90°.AB=4,∠B=60°,
∴BH=AB cos60°=2,AHBH=2,
∴CH,
∴BC=BH+CH,
当点C在点H的左侧时,BC′=BH﹣HC′,
综上所述,BC的长为或.
故答案为:或.
【点评】本题考查解直角三角形,勾股定理,解题的关键是学会用分类讨论的思想思考问题.
10.(2024.呼和浩特二模)如图,兴康社区附近有A、B、C三个快递中转站:B站在A站南偏西53°方向上,C站在B站的东北方向上,A站在C站的北偏东60°方向上且距离C站4km处,则B站到C站的距离为 3.4 km(精确到0.1km).(A、B、C、D在同一平面内,参考数据:1.41,,,,,
【考点】解直角三角形的应用﹣方向角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】3.4.
【分析】过点C作CF⊥AD于点F,作CE⊥BD于点E,证明四边形CFDE是矩形,则CF=DE,DF=CE,求出AF=2,米,设BC=x,根据,列式计算即可求解即可.
【解答】解:过点C作CF⊥AD于点F,作CE⊥BD于点E,则∠CFD=∠CED=∠D=90°,
∴CF=DE,DF=CE,
在Rt△ACF中,∠ACF=30°,
∴,
,
∴,
设BC=x km,
在Rt△BCE中,
∴ km,
∴ km,
∵∠ABD=90°﹣53°=37°,
∴,
∴,
解得,
即B站到C站的距离为3.4km.
【点评】此题考查了解直角三角形的应用,正确进行计算是解题关键.
11.(2024.海勃湾区)如图,一渔船在海上A处测得灯塔C在它的北偏东60°方向,渔船向正东方向航行海里到达点B处,测得灯塔C在它的北偏东45°方向,若渔船继续向正东方向航行,则渔船与灯塔C的最短距离是 1 海里.
【考点】解直角三角形的应用﹣方向角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】1.
【分析】过点C作CD⊥AB,垂足为D,根据题意可得:AB=(1)海里,然后设CD=x海里,分别在Rt△ACD和Rt△BCD中,利用锐角三角函数的定义求出AD和BD的长,从而列出关于x的方程,进行计算即可解答.
【解答】解:过点C作CD⊥AB,垂足为D,
由题意得:AB=(1)海里,
设CD=x海里,
在Rt△ACD中,∠CAD=90°﹣60°=30°,
∴ADx(海里),
在Rt△BCD中,∠CBD=90°﹣45°=45°,
∴BDx(海里),
∵AD﹣BD=AB,
∴x﹣x1,
解得:x=1,
∴CD=1海里,
∴渔船与灯塔C的最短距离是1海里,
故答案为:1.
【点评】本题考查了解直角三角形的应用﹣方向角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
12.(2024.武汉)如图是水槽水龙头的侧面图,矩形CDFG为水槽侧面,宽DF=50cm,深CD=15cm,排水口E位于DF的中点.在水槽边CD正上方安装水管BC,水龙头BA=10cm.按水龙头安装要求,水流需直接对准排水口确保水快速排入管道.测得∠ABC=127°,∠BAE=83°,则安装的水管BC的长为 8.4 cm.(精确到0.1cm,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,)
【考点】解直角三角形的应用;矩形的判定与性质.
【专题】解直角三角形及其应用;运算能力.
【答案】8.4.
【分析】过点A作AH⊥DF于H,过点B作BG′⊥AH于G′,证明四边形BDHG′是矩形,得到BD=G′H,DH=BG′,∠DBG=90°,再求出∠ABG′的度数,进而求出∠HAE的度数,解Rt△ABG′得到AG′,BG′的长,进而求出HE的长,再解Rt△AHE求出AH的长,进而求出BD的长即可得到答案.
【解答】解:如图所示,过点A作AH⊥DF于H,过点B作BG′⊥AH于G′,
由题意可得:四边形BDHG′是矩形,
∴BD=G′H,DH=BG′,∠DBG′=90°,
∵∠ABC=127°,
∴∠ABG′=∠ABC﹣∠DBG′=37°,
∴∠BAG′=90°﹣∠ABG′=53°,
∵∠BAE=83°,
∴∠HAE=∠BAE﹣∠BAG′=30°;
AG′=AB sin∠ABG′≈10×0.6=6(cm),
BG′=AB cos∠ABG′≈10×0.8=8(cm),
∴DH=8cm;
∵,
∴HE=DE﹣DH=17cm,
∴,
∴BD=G′H=AH﹣AG′=23.4cm,
∵CD=15cm,
∴BC=BD﹣CD=8.4cm.
故答案为:8.4.
【点评】本题主要考查了解直角三角形的实际应用,矩形的判定与性质,正确进行近计算是解题关键.
三.解答题(共3小题)
13.(2024.徐州)阅读下列材料,解答问题.
【背景】如图1,李叔家D与水果园E之间隔着一座小土坡,为方便浇水灌溉,从家里铺设的水管到果园,原来经过小土坡铺设的水管(DB﹣BA﹣AC﹣CE)由于风吹日晒,老化损坏,现在李叔准备从土坡下直接埋一条水管(D,B,C,E在同一直线上).
【问题】为了计算新水管的长度,需要测量B,C之间的距离;
要了解水管承受的压力,需要测量土坡的高度.
【工具】一把皮尺和一台测角仪,如图2.皮尺的功能是直接测量任意可到达的两点间的距离;测角仪的功能是在一固定位置测量可以看到的两个地点的夹角大小.
【测量】李叔用皮尺测量出原来土坡两边的长度AB=am,AC=bm,再用测角仪测得∠BAC=α.
解答问题:
(1)求BC的长度;(结果用含a,b,α的代数式表示)
(2)若测得a=20m,b=25m,α=120°,求出小土坡的高度.
【考点】解直角三角形的应用﹣仰角俯角问题;列代数式;全等三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】(1);
(2).
【分析】(1)过点B作BF⊥CA交CA延长线于点F,设∠BAF=β,在Rt△ABF中利用三角函数的定义求出BF和AF的长,得出CF的长,在Rt△BCF中利用勾股定理表示出BC的长,再根据平角的定义得到β=180°﹣α,即可求解;
(2)过点A作AG⊥BC于点G,结合(1)中的结论,代入数据求出BF和BC的长,再利用等面积法得到,求出AG的长,即可解答.
【解答】解:(1)过点B作BF⊥CA交CA延长线于点F,则∠F=90°,
设∠BAF=β,
∴,,
∴BF=ABsinβ=asinβ(m),AF=ABcosβ=acosβ(m),
∴CF=AF+AC=(acosβ+b)(m),
∵由勾股定理可得:BC2=BF2+CF2,
∴
,
∵∠BAF+∠BAC=180°,
∴β+α=180°,即β=180°﹣α,
∴,
∴BC的长度为.
(2)过点A作AG⊥BC于点G,
∵a=20m,b=25m,α=120°,
∴,,
∵,
∴a=20m,b=25m,α=120°时,小土坡的高度为:
,
答:高度为.
【点评】本题考查解直角三角形,正确进行计算是解题关键.
14.(2024.兴隆台区一模)实验是培养学生的创新能力的重要途径之一,如图是小红同学安装的化学实验装置,安装要求为试管略向下倾斜,试管夹应固定在距试管口的三分之一处,已知试管AB=24cm,,试管倾斜角α为10°.
(1)求酒精灯与铁架台的水平距离CD的长度;(精确到0.1cm)
(2)实验时,当导气管紧贴水槽MN,延长BM交CN的延长线于点F,且MN⊥CF,BH⊥CF(点C,D,H,N,F在一条直线上),经测得:DE=21.7cm,∠ABM=145°,求线段FH的长度.(精确到0.1cm)(参考数据:sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】(1)15.7cm;
(2)20.3cm.
【分析】(1)过E作EG⊥AC,根据三角函数求出EG,再根据矩形的性质即可得解;
(2)过B作BP⊥AC,交DE于P,根据三角函数求出EP,再根据矩形的性质和等腰三角形的性质即可得解.
【解答】解:(1)过E作EG⊥AC,垂足为点G,
∵,
∴BE=8cm,
∴AE=AB﹣BE=16cm,
在Rt△AEG中,∠AEG=10°,
∴EG=AE cos∠AEG≈15.7cm,
∵EG⊥AC,AC⊥CD,DE⊥CD,
∴∠EGC=∠C=∠CDE=90°,
∴四边形CDEG是矩形,
∴CD=EG=15.7cm,
答:CD的长度约为15.7cm.
(2)过B作BP⊥AC,交DE于P,
∵BP⊥AC,EG⊥AC,
∴EG∥BP,∠EPB=90°,
∴∠EBP=∠AEG=10°,
∵BP⊥AC,BH⊥CF,DE⊥CD,
∴∠BPD=∠BHC=∠HDP=90°,
∴四边形BHDP是矩形,
∴PD=BH,∠HBP=90°,
∵BE=8cm,∠EBP=10°,
∴EP=BE sin∠EBP=8×sin10°≈1.36cm,
∴PD=DE﹣EP=21.7﹣1.36≈20.3cm,
∴BH=PD=20.3cm,
∵=145°,
∴∠HBF=180°﹣∠ABM=180°﹣145°=45°,
∴∠HFB=∠HBF=45°,
∴HF=BH=20.3cm,
答:线段FH的长约为20.3cm.
【点评】本题考查解直角三角形的应用,通过作辅助线构造直角三角形,掌握直角三角形中的边角关系是解题的关键.
15.(2024.东港区二模)学校科研小组制作了一款机械手臂如图①所示,由上臂、中臂和底座三部分组成,其中上臂和中臂可自由转动,底座与水平地面垂直.在实际运用中要求三部分始终处于同一平面内,其示意图如图②所示,经测量,上臂AB=12cm,中臂BC=10cm,底座CD=4cm.
(1)若上臂AB与水平面平行,∠ABC=60°,计算点A到地面的距离(保留根号);
(2)在一次操作中,平台上有一高度为6cm的模具MN,如图③,点A恰好与点N重合,此时测得中臂与底座成143°夹角,请计算此时上臂与中臂夹角∠ABC的大小.
(sin37°≈0.61,cos37°≈0.8,tan37°≈0.75)
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】(1)点A到地面的距离为;
(2)97°.
【分析】(1)过点C作CP⊥AB,垂足为P,则∠BPC=90°,易证P,C,D三点共线,解直角三角形求出CP,即可求解;
(2)过点B作EF平行于地面,分别交MA,DC的延长线于点E,F,则四边形EFDM是矩形,解直角三角形求出CF=8cm,进而求出AE=EM﹣MN=6cm,利用正弦的定义求出∠ABE=30°,即可解答.
【解答】解:(1)过点C作CP⊥AB,垂足为P,则∠BPC=90°.
由题意可得:P,C,D三点共线,
∵∠ABC=60°,BC=10cm,
∴,
∴,
答:点A到地面的距离为;
(2)如图过点B作EF平行于地面,分别交MA,DC的延长线于点E,F,则四边形EFDM是矩形,
∵∠BCD=143°,
∴∠BCF=37°,∠CBF=53°,
∴,
∴CF=8cm,
∴EM=FD=12cm,
∴AE=EM﹣MN=6cm,
∵,
∴∠AEB=30°,
∴∠ABC=180°﹣30°﹣53°=97°.
【点评】本题考查了解直角三角形的应用,正确进行计算是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考冲刺核心考点 解直角三角形及其应用
一.选择题(共7小题)
1.(2024.江汉区)如图,已知A(﹣2,1)、B(0,0)、C(1,2)则tan∠BAC的值为( )
A. B.1 C. D.
2.(2024.通州区一模)如图,建筑物BC上有一旗杆AB,从与BC相距40m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,则旗杆AB的高度是( )
A. B.(40sin50°﹣40)m
C. D.(40tan50°﹣40)m
3.(2024.台江区)如图,将秋千绳索从与竖直方向夹角为α的位置OA1释放到OA处时,两次位置的高度差PA=h.则秋千绳索OA的长为( )
A. B. C. D.
4.(2025春 定海区)某河堤横断面如图所示,堤高BC=10米,迎水坡AB的坡比是(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是( )
A.米 B.20米 C.米 D.30米
5.(2024.郑州)一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力F1的方向与斜面垂直,摩擦力F2的方向与斜面平行.若斜面的坡角α=25°,则摩擦力F2与重力G方向的夹角β的度数为( )
A.155° B.125° C.115° D.65°
6.(2024.宝安区)港珠澳大桥是世界上最长的跨海大桥,被誉为“现代世界七大奇迹”的超级工程,它是我国从桥梁大国走向桥梁强国的里程碑之作.港珠澳大桥主桥为三座大跨度钢结构斜拉桥,其中九洲航道桥主塔造型取自“风帆”,寓意“扬帆起航”,某校九年级学生为了测量该主塔的高度,站在B处看塔顶A,仰角为60°,然后向后走190米,到达C处,此时看塔顶A,仰角为30°,则该主塔的高度是( )
A.95米 B.米 C.190米 D.米
7.(2024.南山区一模)图1是某市一地铁站入口的双翼闸机,双翼展开时示意图如图2所示,它是一个轴对称图形,AC=40cm,α=37°,则双翼边缘端点C与D之间的距离为( )cm
A.60﹣40sin37° B.60﹣2×40cos37°
C.60﹣2×40tan37° D.60﹣2×40sin37°
二.填空题(共5小题)
8.(2024.湖北)如图是小区内一小山的等高线示意图,小明同学计划利用这个等高线示意图计算AB的距离,他在点B处测得A处的俯角为30°,则AB= m.
9.(2024.平房区二模)已知,在△ABC中,∠ABC=60°,AC,AB=4,则BC= .
10.(2024.呼和浩特二模)如图,兴康社区附近有A、B、C三个快递中转站:B站在A站南偏西53°方向上,C站在B站的东北方向上,A站在C站的北偏东60°方向上且距离C站4km处,则B站到C站的距离为 km(精确到0.1km).(A、B、C、D在同一平面内,参考数据:1.41,,,,,
11.(2024.海勃湾区)如图,一渔船在海上A处测得灯塔C在它的北偏东60°方向,渔船向正东方向航行海里到达点B处,测得灯塔C在它的北偏东45°方向,若渔船继续向正东方向航行,则渔船与灯塔C的最短距离是 海里.
12.(2024.武汉)如图是水槽水龙头的侧面图,矩形CDFG为水槽侧面,宽DF=50cm,深CD=15cm,排水口E位于DF的中点.在水槽边CD正上方安装水管BC,水龙头BA=10cm.按水龙头安装要求,水流需直接对准排水口确保水快速排入管道.测得∠ABC=127°,∠BAE=83°,则安装的水管BC的长为 cm.(精确到0.1cm,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,)
三.解答题(共3小题)
13.(2024.徐州)阅读下列材料,解答问题.
【背景】如图1,李叔家D与水果园E之间隔着一座小土坡,为方便浇水灌溉,从家里铺设的水管到果园,原来经过小土坡铺设的水管(DB﹣BA﹣AC﹣CE)由于风吹日晒,老化损坏,现在李叔准备从土坡下直接埋一条水管(D,B,C,E在同一直线上).
【问题】为了计算新水管的长度,需要测量B,C之间的距离;
要了解水管承受的压力,需要测量土坡的高度.
【工具】一把皮尺和一台测角仪,如图2.皮尺的功能是直接测量任意可到达的两点间的距离;测角仪的功能是在一固定位置测量可以看到的两个地点的夹角大小.
【测量】李叔用皮尺测量出原来土坡两边的长度AB=am,AC=bm,再用测角仪测得∠BAC=α.
解答问题:
(1)求BC的长度;(结果用含a,b,α的代数式表示)
(2)若测得a=20m,b=25m,α=120°,求出小土坡的高度.
14.(2024.兴隆台区一模)实验是培养学生的创新能力的重要途径之一,如图是小红同学安装的化学实验装置,安装要求为试管略向下倾斜,试管夹应固定在距试管口的三分之一处,已知试管AB=24cm,,试管倾斜角α为10°.
(1)求酒精灯与铁架台的水平距离CD的长度;(精确到0.1cm)
(2)实验时,当导气管紧贴水槽MN,延长BM交CN的延长线于点F,且MN⊥CF,BH⊥CF(点C,D,H,N,F在一条直线上),经测得:DE=21.7cm,∠ABM=145°,求线段FH的长度.(精确到0.1cm)(参考数据:sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)
15.(2024.东港区二模)学校科研小组制作了一款机械手臂如图①所示,由上臂、中臂和底座三部分组成,其中上臂和中臂可自由转动,底座与水平地面垂直.在实际运用中要求三部分始终处于同一平面内,其示意图如图②所示,经测量,上臂AB=12cm,中臂BC=10cm,底座CD=4cm.
(1)若上臂AB与水平面平行,∠ABC=60°,计算点A到地面的距离(保留根号);
(2)在一次操作中,平台上有一高度为6cm的模具MN,如图③,点A恰好与点N重合,此时测得中臂与底座成143°夹角,请计算此时上臂与中臂夹角∠ABC的大小.
(sin37°≈0.61,cos37°≈0.8,tan37°≈0.75)
中考冲刺核心考点 解直角三角形及其应用
参考答案与试题解析
一.选择题(共7小题)
1.(2024.江汉区)如图,已知A(﹣2,1)、B(0,0)、C(1,2)则tan∠BAC的值为( )
A. B.1 C. D.
【考点】解直角三角形;坐标与图形性质.
【专题】平面直角坐标系;解直角三角形及其应用;运算能力.
【答案】B
【分析】根据题意,分别求出AB,BC,AC的长,再结合正切的定义即可解决问题.
【解答】解:由题知,
因为A(﹣2,1)、B(0,0)、C(1,2),
所以AB,
BC,
AC,
则AB2+BC2=AC2,
所以∠ABC=90°.
在Rt△ABC中,
tan∠BAC.
故选:B.
【点评】本题主要考查了坐标与图形性质及解直角三角形,熟知正切的定义是解题的关键.
2.(2024.通州区一模)如图,建筑物BC上有一旗杆AB,从与BC相距40m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,则旗杆AB的高度是( )
A. B.(40sin50°﹣40)m
C. D.(40tan50°﹣40)m
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】D
【分析】分别解直角三角形求出AC,BC的长,再用AC﹣BC进行求解即可.
【解答】解:∵AC=CD tan50°=40tan50°,
BC=CD tan45°=40,
∴AB=AC﹣BC=(40tan50°﹣40)m;
故选:D.
【点评】本题考查解直角三角形的应用,正确进行计算是解题关键.
3.(2024.台江区)如图,将秋千绳索从与竖直方向夹角为α的位置OA1释放到OA处时,两次位置的高度差PA=h.则秋千绳索OA的长为( )
A. B. C. D.
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;推理能力.
【答案】A
【分析】由题意可知,OA=OA1,再根据余弦的定义求解即可.
【解答】解:由题意可知,OA=OA1,
∵cosα,
∴OA1,
又∵OP=OA﹣PA=OA1﹣PA=OA1﹣h,
∴OA,
∴OA=OA1,
故选:A.
【点评】本题考查了解直角三角形的应用,熟记三角形函数的定义是解题的关键.
4.(2025春 定海区)某河堤横断面如图所示,堤高BC=10米,迎水坡AB的坡比是(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是( )
A.米 B.20米 C.米 D.30米
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】运算能力.
【答案】A
【分析】由堤高BC=10米,迎水坡AB的坡比,根据坡度的定义,即可求得AC的长.
【解答】解:∵迎水坡AB的坡比,
∴,
∵堤高BC=10米,
∴(米).
故选:A.
【点评】本题考查了解直角三角形的应用﹣坡度坡角问题,掌握坡比的概念是解题的关键.
5.(2024.郑州)一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力F1的方向与斜面垂直,摩擦力F2的方向与斜面平行.若斜面的坡角α=25°,则摩擦力F2与重力G方向的夹角β的度数为( )
A.155° B.125° C.115° D.65°
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】C
【分析】根据题意结合图形可知β是重力G与斜面形成的三角形的外角,从而可求得β的度数.
【解答】解:∵重力G的方向竖直向下,
∴重力G与水平方向夹角为90°,
由题意可得:
∴β=∠1=α+90°=115°,
故选:C.
【点评】本题考查了平行线的性质和三角形外角性质,正确进行计算是解题关键.
6.(2024.宝安区)港珠澳大桥是世界上最长的跨海大桥,被誉为“现代世界七大奇迹”的超级工程,它是我国从桥梁大国走向桥梁强国的里程碑之作.港珠澳大桥主桥为三座大跨度钢结构斜拉桥,其中九洲航道桥主塔造型取自“风帆”,寓意“扬帆起航”,某校九年级学生为了测量该主塔的高度,站在B处看塔顶A,仰角为60°,然后向后走190米,到达C处,此时看塔顶A,仰角为30°,则该主塔的高度是( )
A.95米 B.米 C.190米 D.米
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】B
【分析】该主塔为AD=x,在Rt△ABD中,利用正切函数的定义求得,同理,在Rt△ACD中,求得,根据CD﹣BD=190,列出方程求解即可.
【解答】解:如图,该主塔为AD=x,
由题意,得:∠ADC=90°,BC=190,∠ACD=30°,∠ABD=60°,
∵,
∴,
∵,
∴,
∵BC=CD﹣BD=190,
∴,
∴.
故选:B.
【点评】本题考查解直角三角形的实际应用,正确进行计算是解题关键.
7.(2024.南山区一模)图1是某市一地铁站入口的双翼闸机,双翼展开时示意图如图2所示,它是一个轴对称图形,AC=40cm,α=37°,则双翼边缘端点C与D之间的距离为( )cm
A.60﹣40sin37° B.60﹣2×40cos37°
C.60﹣2×40tan37° D.60﹣2×40sin37°
【考点】解直角三角形的应用;轴对称图形.
【专题】解直角三角形及其应用;应用意识.
【答案】D
【分析】作辅助线如图,由题意可得CE=DF,EF=60cm,解直角三角形ACE求出CE=40sin37° cm,然后根据CD=EF﹣2CE即可得出答案.
【解答】解:如图,作直线CD,交双翼闸机于点E、F,则CE⊥AE,DF⊥BF,
由题意可得CE=DF,EF=60cm,
在直角三角形ACE中,
CE=AC sin37°=40sin37°cm,
∴CD=EF﹣2CE=60﹣2×40sin37° (cm).
故选:D.
【点评】本题考查了解直角三角形的应用,正确理解题意、熟练掌握锐角三角函数的知识是解题的关键.
二.填空题(共5小题)
8.(2024.湖北)如图是小区内一小山的等高线示意图,小明同学计划利用这个等高线示意图计算AB的距离,他在点B处测得A处的俯角为30°,则AB= 100 m.
【考点】解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;应用意识.
【答案】100.
【分析】根据由等高线可知A、B两地的高度差为50米,然后点B处测得A处的俯角为30°求值即可.
【解答】解:作示意图如下:
由题意知:A、B两地的实际高度差为AH:550﹣500=50(m),∠B=30°,∠AHB=90°,
∴sinB,即sin30°,
解得:AB=100,
故答案为:100.
【点评】本题主要考查了解直角三角形的应用﹣仰角俯角问题,解答本题的关键是根据题意,作出直角三角形解决问题.
9.(2024.平房区二模)已知,在△ABC中,∠ABC=60°,AC,AB=4,则BC= 或 .
【考点】解直角三角形;勾股定理.
【专题】作图题;几何直观.
【答案】或.
【分析】如图,过点A作AH⊥BC于点H.解直角三角形求出CH,分两种情形求出BC即可.
【解答】解:如图,过点A作AH⊥BC于点H.
在Rt△ABH中,∠AHB=90°.AB=4,∠B=60°,
∴BH=AB cos60°=2,AHBH=2,
∴CH,
∴BC=BH+CH,
当点C在点H的左侧时,BC′=BH﹣HC′,
综上所述,BC的长为或.
故答案为:或.
【点评】本题考查解直角三角形,勾股定理,解题的关键是学会用分类讨论的思想思考问题.
10.(2024.呼和浩特二模)如图,兴康社区附近有A、B、C三个快递中转站:B站在A站南偏西53°方向上,C站在B站的东北方向上,A站在C站的北偏东60°方向上且距离C站4km处,则B站到C站的距离为 3.4 km(精确到0.1km).(A、B、C、D在同一平面内,参考数据:1.41,,,,,
【考点】解直角三角形的应用﹣方向角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】3.4.
【分析】过点C作CF⊥AD于点F,作CE⊥BD于点E,证明四边形CFDE是矩形,则CF=DE,DF=CE,求出AF=2,米,设BC=x,根据,列式计算即可求解即可.
【解答】解:过点C作CF⊥AD于点F,作CE⊥BD于点E,则∠CFD=∠CED=∠D=90°,
∴CF=DE,DF=CE,
在Rt△ACF中,∠ACF=30°,
∴,
,
∴,
设BC=x km,
在Rt△BCE中,
∴ km,
∴ km,
∵∠ABD=90°﹣53°=37°,
∴,
∴,
解得,
即B站到C站的距离为3.4km.
【点评】此题考查了解直角三角形的应用,正确进行计算是解题关键.
11.(2024.海勃湾区)如图,一渔船在海上A处测得灯塔C在它的北偏东60°方向,渔船向正东方向航行海里到达点B处,测得灯塔C在它的北偏东45°方向,若渔船继续向正东方向航行,则渔船与灯塔C的最短距离是 1 海里.
【考点】解直角三角形的应用﹣方向角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】1.
【分析】过点C作CD⊥AB,垂足为D,根据题意可得:AB=(1)海里,然后设CD=x海里,分别在Rt△ACD和Rt△BCD中,利用锐角三角函数的定义求出AD和BD的长,从而列出关于x的方程,进行计算即可解答.
【解答】解:过点C作CD⊥AB,垂足为D,
由题意得:AB=(1)海里,
设CD=x海里,
在Rt△ACD中,∠CAD=90°﹣60°=30°,
∴ADx(海里),
在Rt△BCD中,∠CBD=90°﹣45°=45°,
∴BDx(海里),
∵AD﹣BD=AB,
∴x﹣x1,
解得:x=1,
∴CD=1海里,
∴渔船与灯塔C的最短距离是1海里,
故答案为:1.
【点评】本题考查了解直角三角形的应用﹣方向角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
12.(2024.武汉)如图是水槽水龙头的侧面图,矩形CDFG为水槽侧面,宽DF=50cm,深CD=15cm,排水口E位于DF的中点.在水槽边CD正上方安装水管BC,水龙头BA=10cm.按水龙头安装要求,水流需直接对准排水口确保水快速排入管道.测得∠ABC=127°,∠BAE=83°,则安装的水管BC的长为 8.4 cm.(精确到0.1cm,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,)
【考点】解直角三角形的应用;矩形的判定与性质.
【专题】解直角三角形及其应用;运算能力.
【答案】8.4.
【分析】过点A作AH⊥DF于H,过点B作BG′⊥AH于G′,证明四边形BDHG′是矩形,得到BD=G′H,DH=BG′,∠DBG=90°,再求出∠ABG′的度数,进而求出∠HAE的度数,解Rt△ABG′得到AG′,BG′的长,进而求出HE的长,再解Rt△AHE求出AH的长,进而求出BD的长即可得到答案.
【解答】解:如图所示,过点A作AH⊥DF于H,过点B作BG′⊥AH于G′,
由题意可得:四边形BDHG′是矩形,
∴BD=G′H,DH=BG′,∠DBG′=90°,
∵∠ABC=127°,
∴∠ABG′=∠ABC﹣∠DBG′=37°,
∴∠BAG′=90°﹣∠ABG′=53°,
∵∠BAE=83°,
∴∠HAE=∠BAE﹣∠BAG′=30°;
AG′=AB sin∠ABG′≈10×0.6=6(cm),
BG′=AB cos∠ABG′≈10×0.8=8(cm),
∴DH=8cm;
∵,
∴HE=DE﹣DH=17cm,
∴,
∴BD=G′H=AH﹣AG′=23.4cm,
∵CD=15cm,
∴BC=BD﹣CD=8.4cm.
故答案为:8.4.
【点评】本题主要考查了解直角三角形的实际应用,矩形的判定与性质,正确进行近计算是解题关键.
三.解答题(共3小题)
13.(2024.徐州)阅读下列材料,解答问题.
【背景】如图1,李叔家D与水果园E之间隔着一座小土坡,为方便浇水灌溉,从家里铺设的水管到果园,原来经过小土坡铺设的水管(DB﹣BA﹣AC﹣CE)由于风吹日晒,老化损坏,现在李叔准备从土坡下直接埋一条水管(D,B,C,E在同一直线上).
【问题】为了计算新水管的长度,需要测量B,C之间的距离;
要了解水管承受的压力,需要测量土坡的高度.
【工具】一把皮尺和一台测角仪,如图2.皮尺的功能是直接测量任意可到达的两点间的距离;测角仪的功能是在一固定位置测量可以看到的两个地点的夹角大小.
【测量】李叔用皮尺测量出原来土坡两边的长度AB=am,AC=bm,再用测角仪测得∠BAC=α.
解答问题:
(1)求BC的长度;(结果用含a,b,α的代数式表示)
(2)若测得a=20m,b=25m,α=120°,求出小土坡的高度.
【考点】解直角三角形的应用﹣仰角俯角问题;列代数式;全等三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】(1);
(2).
【分析】(1)过点B作BF⊥CA交CA延长线于点F,设∠BAF=β,在Rt△ABF中利用三角函数的定义求出BF和AF的长,得出CF的长,在Rt△BCF中利用勾股定理表示出BC的长,再根据平角的定义得到β=180°﹣α,即可求解;
(2)过点A作AG⊥BC于点G,结合(1)中的结论,代入数据求出BF和BC的长,再利用等面积法得到,求出AG的长,即可解答.
【解答】解:(1)过点B作BF⊥CA交CA延长线于点F,则∠F=90°,
设∠BAF=β,
∴,,
∴BF=ABsinβ=asinβ(m),AF=ABcosβ=acosβ(m),
∴CF=AF+AC=(acosβ+b)(m),
∵由勾股定理可得:BC2=BF2+CF2,
∴
,
∵∠BAF+∠BAC=180°,
∴β+α=180°,即β=180°﹣α,
∴,
∴BC的长度为.
(2)过点A作AG⊥BC于点G,
∵a=20m,b=25m,α=120°,
∴,,
∵,
∴a=20m,b=25m,α=120°时,小土坡的高度为:
,
答:高度为.
【点评】本题考查解直角三角形,正确进行计算是解题关键.
14.(2024.兴隆台区一模)实验是培养学生的创新能力的重要途径之一,如图是小红同学安装的化学实验装置,安装要求为试管略向下倾斜,试管夹应固定在距试管口的三分之一处,已知试管AB=24cm,,试管倾斜角α为10°.
(1)求酒精灯与铁架台的水平距离CD的长度;(精确到0.1cm)
(2)实验时,当导气管紧贴水槽MN,延长BM交CN的延长线于点F,且MN⊥CF,BH⊥CF(点C,D,H,N,F在一条直线上),经测得:DE=21.7cm,∠ABM=145°,求线段FH的长度.(精确到0.1cm)(参考数据:sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)
【考点】解直角三角形的应用﹣坡度坡角问题.
【专题】解直角三角形及其应用;运算能力.
【答案】(1)15.7cm;
(2)20.3cm.
【分析】(1)过E作EG⊥AC,根据三角函数求出EG,再根据矩形的性质即可得解;
(2)过B作BP⊥AC,交DE于P,根据三角函数求出EP,再根据矩形的性质和等腰三角形的性质即可得解.
【解答】解:(1)过E作EG⊥AC,垂足为点G,
∵,
∴BE=8cm,
∴AE=AB﹣BE=16cm,
在Rt△AEG中,∠AEG=10°,
∴EG=AE cos∠AEG≈15.7cm,
∵EG⊥AC,AC⊥CD,DE⊥CD,
∴∠EGC=∠C=∠CDE=90°,
∴四边形CDEG是矩形,
∴CD=EG=15.7cm,
答:CD的长度约为15.7cm.
(2)过B作BP⊥AC,交DE于P,
∵BP⊥AC,EG⊥AC,
∴EG∥BP,∠EPB=90°,
∴∠EBP=∠AEG=10°,
∵BP⊥AC,BH⊥CF,DE⊥CD,
∴∠BPD=∠BHC=∠HDP=90°,
∴四边形BHDP是矩形,
∴PD=BH,∠HBP=90°,
∵BE=8cm,∠EBP=10°,
∴EP=BE sin∠EBP=8×sin10°≈1.36cm,
∴PD=DE﹣EP=21.7﹣1.36≈20.3cm,
∴BH=PD=20.3cm,
∵=145°,
∴∠HBF=180°﹣∠ABM=180°﹣145°=45°,
∴∠HFB=∠HBF=45°,
∴HF=BH=20.3cm,
答:线段FH的长约为20.3cm.
【点评】本题考查解直角三角形的应用,通过作辅助线构造直角三角形,掌握直角三角形中的边角关系是解题的关键.
15.(2024.东港区二模)学校科研小组制作了一款机械手臂如图①所示,由上臂、中臂和底座三部分组成,其中上臂和中臂可自由转动,底座与水平地面垂直.在实际运用中要求三部分始终处于同一平面内,其示意图如图②所示,经测量,上臂AB=12cm,中臂BC=10cm,底座CD=4cm.
(1)若上臂AB与水平面平行,∠ABC=60°,计算点A到地面的距离(保留根号);
(2)在一次操作中,平台上有一高度为6cm的模具MN,如图③,点A恰好与点N重合,此时测得中臂与底座成143°夹角,请计算此时上臂与中臂夹角∠ABC的大小.
(sin37°≈0.61,cos37°≈0.8,tan37°≈0.75)
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】(1)点A到地面的距离为;
(2)97°.
【分析】(1)过点C作CP⊥AB,垂足为P,则∠BPC=90°,易证P,C,D三点共线,解直角三角形求出CP,即可求解;
(2)过点B作EF平行于地面,分别交MA,DC的延长线于点E,F,则四边形EFDM是矩形,解直角三角形求出CF=8cm,进而求出AE=EM﹣MN=6cm,利用正弦的定义求出∠ABE=30°,即可解答.
【解答】解:(1)过点C作CP⊥AB,垂足为P,则∠BPC=90°.
由题意可得:P,C,D三点共线,
∵∠ABC=60°,BC=10cm,
∴,
∴,
答:点A到地面的距离为;
(2)如图过点B作EF平行于地面,分别交MA,DC的延长线于点E,F,则四边形EFDM是矩形,
∵∠BCD=143°,
∴∠BCF=37°,∠CBF=53°,
∴,
∴CF=8cm,
∴EM=FD=12cm,
∴AE=EM﹣MN=6cm,
∵,
∴∠AEB=30°,
∴∠ABC=180°﹣30°﹣53°=97°.
【点评】本题考查了解直角三角形的应用,正确进行计算是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
