【中考核心考点】2025年人教版中考数学考前冲刺 三视图(含解析)
文档属性
| 名称 | 【中考核心考点】2025年人教版中考数学考前冲刺 三视图(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-16 13:55:41 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
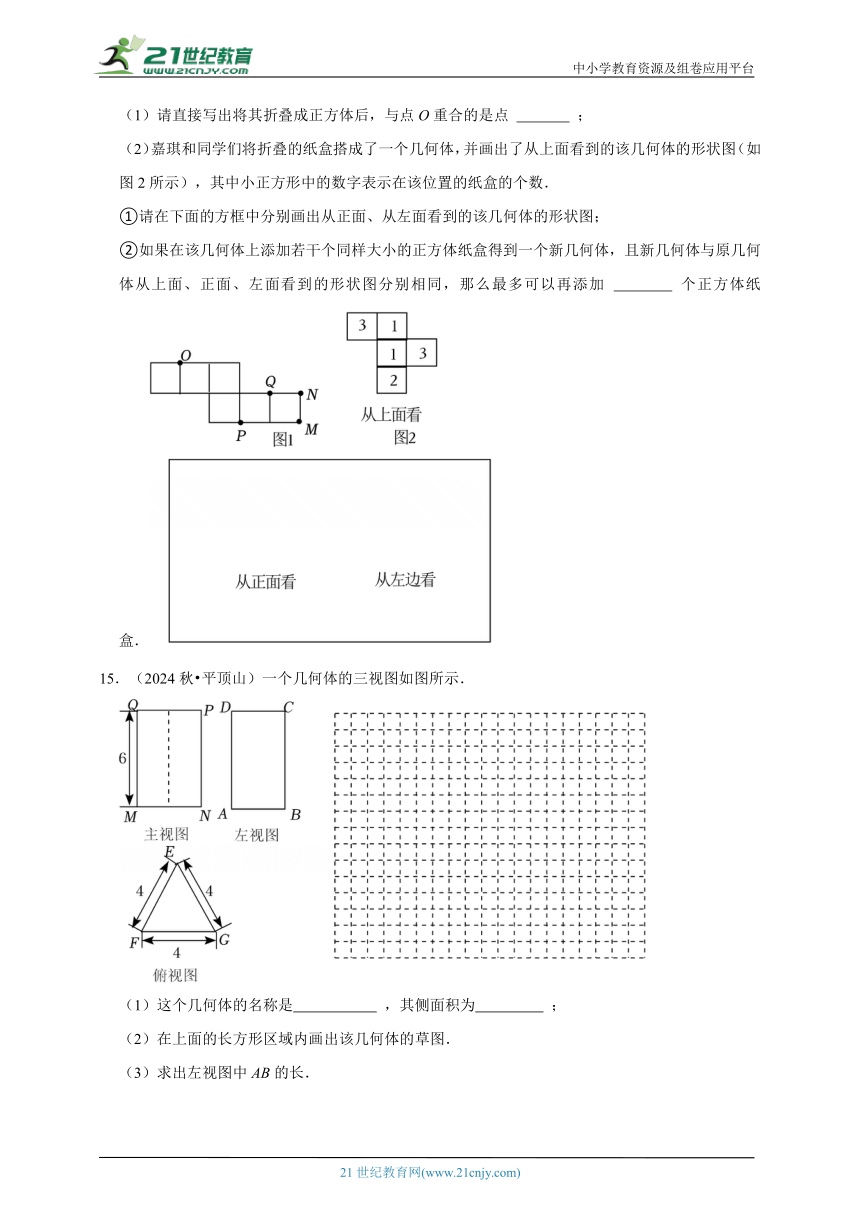
中考冲刺核心考点 三视图
一.选择题(共7小题)
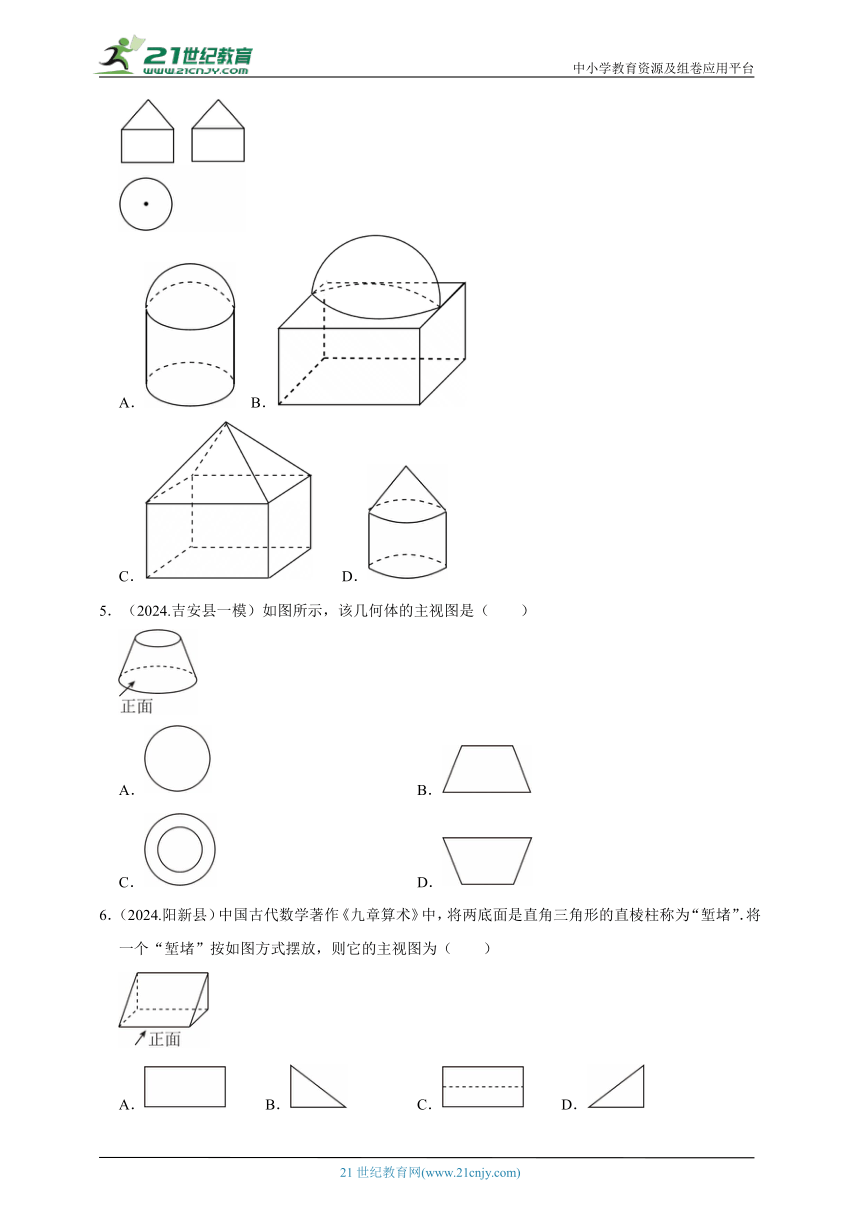
1.(2024.石家庄)如图是由五个小正方体组成的几何体,若要在图中序号所在的位置上添加一个小正方体,使得添加后该几何体的主视图和左视图均保持不变,则添加的位置应在( )
A.① B.② C.③ D.④
2.(2024.蜀山区一模)如图是生活中常用的“空心卷纸”,其俯视图和主视图分别是( )
A.①③ B.①④ C.②③ D.②④
3.(2024.市中区三模)漏斗是一种通过重力将液体或颗粒导入小口容器的实用工具,日常用于灌装油、调料,实验室中分离液体或过滤,工业上则用于分装原料,如图是一种常用不锈钢漏斗,其俯视图是( )
A. B. C. D.
4.(2024.平阴县二模)某几何体的三视图如图所示,则该几何体为( )
A. B.
C. D.
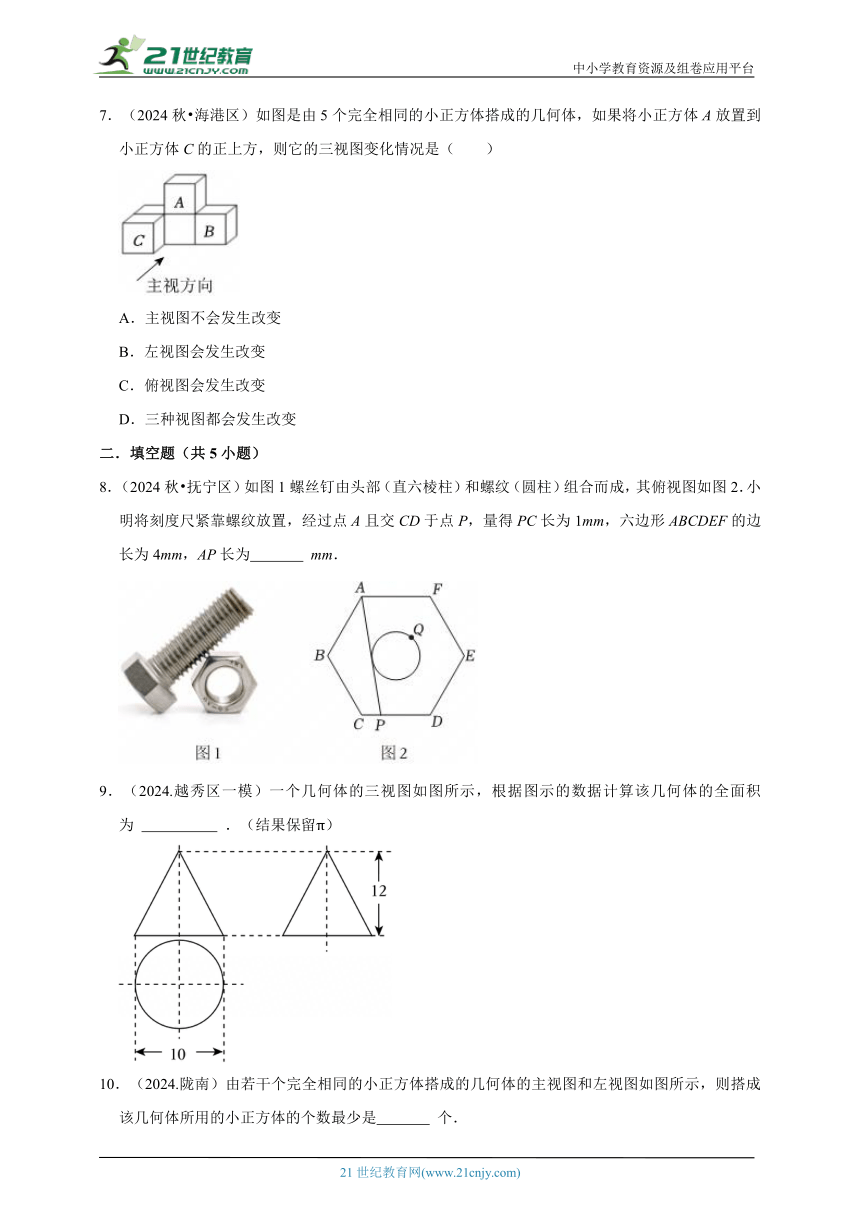
5.(2024.吉安县一模)如图所示,该几何体的主视图是( )
A. B.
C. D.
6.(2024.阳新县)中国古代数学著作《九章算术》中,将两底面是直角三角形的直棱柱称为“堑堵”.将一个“堑堵”按如图方式摆放,则它的主视图为( )
A. B. C. D.
7.(2024秋 海港区)如图是由5个完全相同的小正方体搭成的几何体,如果将小正方体A放置到小正方体C的正上方,则它的三视图变化情况是( )
A.主视图不会发生改变
B.左视图会发生改变
C.俯视图会发生改变
D.三种视图都会发生改变
二.填空题(共5小题)
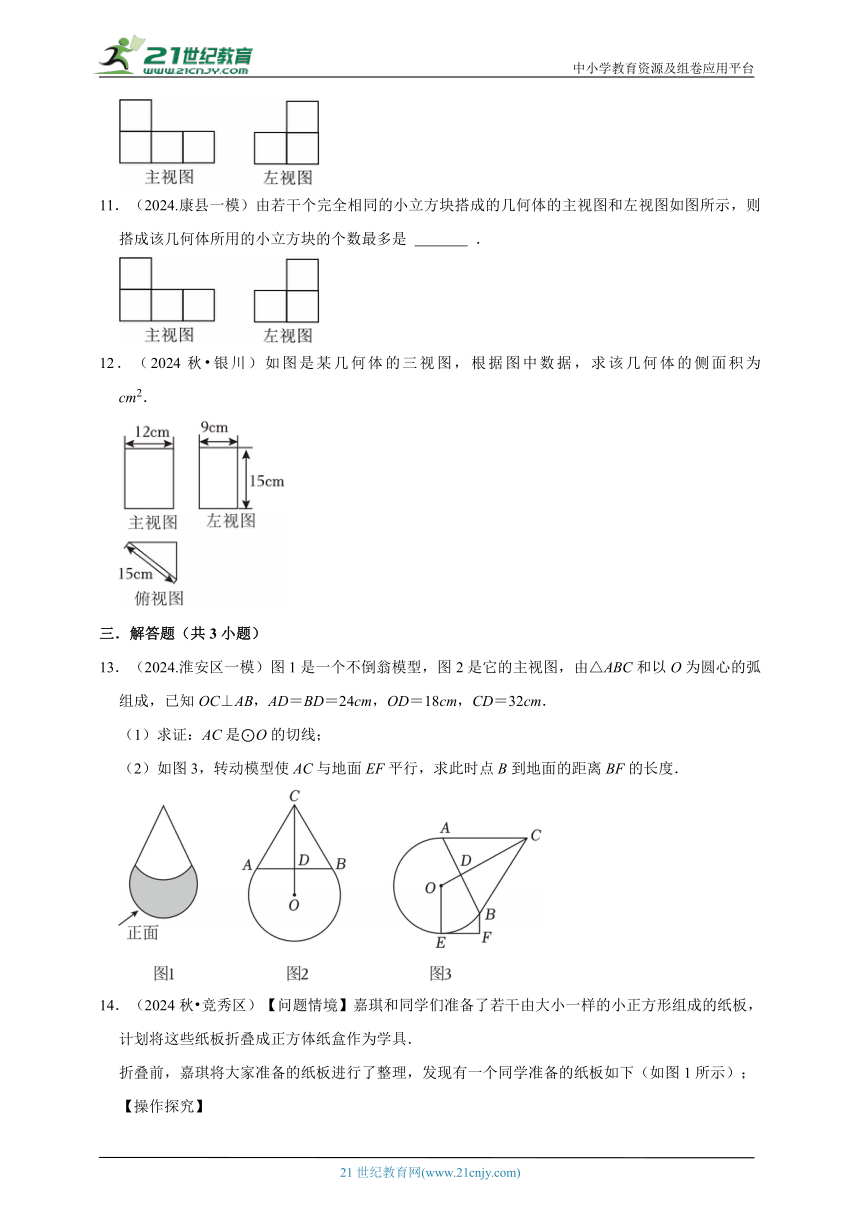
8.(2024秋 抚宁区)如图1螺丝钉由头部(直六棱柱)和螺纹(圆柱)组合而成,其俯视图如图2.小明将刻度尺紧靠螺纹放置,经过点A且交CD于点P,量得PC长为1mm,六边形ABCDEF的边长为4mm,AP长为 mm.
9.(2024.越秀区一模)一个几何体的三视图如图所示,根据图示的数据计算该几何体的全面积为 .(结果保留π)
10.(2024.陇南)由若干个完全相同的小正方体搭成的几何体的主视图和左视图如图所示,则搭成该几何体所用的小正方体的个数最少是 个.
11.(2024.康县一模)由若干个完全相同的小立方块搭成的几何体的主视图和左视图如图所示,则搭成该几何体所用的小立方块的个数最多是 .
12.(2024秋 银川)如图是某几何体的三视图,根据图中数据,求该几何体的侧面积为 cm2.
三.解答题(共3小题)
13.(2024.淮安区一模)图1是一个不倒翁模型,图2是它的主视图,由△ABC和以O为圆心的弧组成,已知OC⊥AB,AD=BD=24cm,OD=18cm,CD=32cm.
(1)求证:AC是⊙O的切线;
(2)如图3,转动模型使AC与地面EF平行,求此时点B到地面的距离BF的长度.
14.(2024秋 竞秀区)【问题情境】嘉琪和同学们准备了若干由大小一样的小正方形组成的纸板,计划将这些纸板折叠成正方体纸盒作为学具.
折叠前,嘉琪将大家准备的纸板进行了整理,发现有一个同学准备的纸板如下(如图1所示);
【操作探究】
(1)请直接写出将其折叠成正方体后,与点O重合的是点 ;
(2)嘉琪和同学们将折叠的纸盒搭成了一个几何体,并画出了从上面看到的该几何体的形状图(如图2所示),其中小正方形中的数字表示在该位置的纸盒的个数.
①请在下面的方框中分别画出从正面、从左面看到的该几何体的形状图;
②如果在该几何体上添加若干个同样大小的正方体纸盒得到一个新几何体,且新几何体与原几何体从上面、正面、左面看到的形状图分别相同,那么最多可以再添加 个正方体纸盒.
15.(2024秋 平顶山)一个几何体的三视图如图所示.
(1)这个几何体的名称是 ,其侧面积为 ;
(2)在上面的长方形区域内画出该几何体的草图.
(3)求出左视图中AB的长.
中考冲刺核心考点 三视图
参考答案与试题解析
一.选择题(共7小题)
1.(2024.石家庄)如图是由五个小正方体组成的几何体,若要在图中序号所在的位置上添加一个小正方体,使得添加后该几何体的主视图和左视图均保持不变,则添加的位置应在( )
A.① B.② C.③ D.④
【考点】简单组合体的三视图.
【专题】投影与视图.
【答案】B
【分析】结合每个选项的添加的位置,分析几何体的主视图和左视图的变化,即可作答.
【解答】解:A、若添加的位置在①,则该几何体的主视图不变,左视图变了,故该选项不符合题意;
B、若添加的位置在②,则该几何体的主视图和左视图都不变,故该选项符合题意;
C、若添加的位置在③,则该几何体的左视图不变,主视图变了,故该选项不符合题意;
D、若添加的位置在④,则该几何体的主视图和左视图都变了,故该选项不符合题意;
故选:B.
【点评】本题考查了几何体的三视图,明确左视图是从几何体的左面看到的图形,主视图是从几何体的正面看到的图形是解题的关键.
2.(2024.蜀山区一模)如图是生活中常用的“空心卷纸”,其俯视图和主视图分别是( )
A.①③ B.①④ C.②③ D.②④
【考点】简单组合体的三视图.
【专题】投影与视图;几何直观.
【答案】B
【分析】找到从上面和正面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.
【解答】解:俯视图和主视图分别是①④.
故选:B.
【点评】本题考查了简单组合体的三视图,俯视图是从物体的上面看得到的视图,主视图是从物体的正面看得到的视图,遮住的棱要画虚线.
3.(2024.市中区三模)漏斗是一种通过重力将液体或颗粒导入小口容器的实用工具,日常用于灌装油、调料,实验室中分离液体或过滤,工业上则用于分装原料,如图是一种常用不锈钢漏斗,其俯视图是( )
A.
B.
C.
D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】C
【分析】根据俯视图是从上往下看求解即可.
【解答】解:不锈钢漏斗的俯视图是.
故选:C.
【点评】本题主要考查了简单几何题的三视图,掌握几何体的空间结构特点是关键.
4.(2024.平阴县二模)某几何体的三视图如图所示,则该几何体为( )
A.
B.
C.
D.
【考点】由三视图判断几何体.
【专题】投影与视图;空间观念.
【答案】D
【分析】根据几何体的三视图的特点进行判断.
【解答】解:根据三视图的形状,可得该几何体为.
故选:D.
【点评】本题主要考查了由三视图判断几何体,掌握三视图的定义是关键.
5.(2024.吉安县一模)如图所示,该几何体的主视图是( )
A. B.
C. D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】B
【分析】根据从正面看到的图形叫主视图,可得出答案.
【解答】解:几何体的主视图是.
故选:B.
【点评】本题考查了简单组合体的三视图,掌握简单组合体三视图的画法和形状是关键.
6.(2024.阳新县)中国古代数学著作《九章算术》中,将两底面是直角三角形的直棱柱称为“堑堵”.将一个“堑堵”按如图方式摆放,则它的主视图为( )
A. B. C. D.
【考点】简单几何体的三视图.
【答案】A
【分析】主视图是从正面看到的图形,根据摆放方式即可找到从正面看到的图形.
【解答】解:根据摆放方式,由直棱柱的两底面是直角三角形可知,从正面看到的图形是长方形.
故选A.
【点评】本题考查了三视图的知识,主视图是从物体正面看到的视图.
7.(2024秋 海港区)如图是由5个完全相同的小正方体搭成的几何体,如果将小正方体A放置到小正方体C的正上方,则它的三视图变化情况是( )
A.主视图不会发生改变
B.左视图会发生改变
C.俯视图会发生改变
D.三种视图都会发生改变
【考点】简单组合体的三视图.
【专题】投影与视图;几何直观.
【答案】B
【分析】根据简单组合体的三视图的画法画出它们的三视图即可.
【解答】解:如果将小正方体A放置到小正方体C的正上方,则它的主视图和左视图会发生改变,俯视图不变.
故选:B.
【点评】本题考查了简单组合体的三视图,从上面看得到的图形俯视图,从正面看得到的图形是主视图,从左边看得到的图形是左视图.
二.填空题(共5小题)
8.(2024秋 抚宁区)如图1螺丝钉由头部(直六棱柱)和螺纹(圆柱)组合而成,其俯视图如图2.小明将刻度尺紧靠螺纹放置,经过点A且交CD于点P,量得PC长为1mm,六边形ABCDEF的边长为4mm,AP长为 7 mm.
【考点】由三视图判断几何体;垂径定理的应用.
【专题】与圆有关的计算;投影与视图;空间观念;运算能力;推理能力.
【答案】7.
【分析】根据正六边形的性质以及直角三角形的边角关系即可求出答案.
【解答】解:如图,连接OA、OB、AC,则OB⊥AC,
∵六边形ABCDEF是正六边形,
∴∠AOB=60°,AB=OA=OB=4mm,
∴ACOA×2(mm),
在Rt△ACP中,PC=1mm,ACmm,
∴AP7(mm),
故答案为:7.
【点评】本题考查由三视图判断几何体,垂径定理的应用,掌握正六边形的性质以及垂径定理是正确解答的关键.
9.(2024.越秀区一模)一个几何体的三视图如图所示,根据图示的数据计算该几何体的全面积为 90π .(结果保留π)
【考点】由三视图判断几何体.
【专题】投影与视图;空间观念.
【答案】90π.
【分析】根据圆锥侧面积公式首先求出圆锥的侧面积,再求出底面圆的面积,相加即可得出该几何体的全面积.
【解答】解:由图示可知,圆锥的高为12,底面圆的直径为10,
∴圆锥的母线为:,
∴圆锥的侧面积为:πrl=π×5×13=65π,
底面圆的面积为:πr2=25π,
∴该几何体的全面积为:65π+25π=90π.
故答案为:90π.
【点评】此题主要考查了由三视图判断几何体,圆锥侧面积公式,根据已知得母线长,再利用圆锥侧面积公式求出是解决问题的关键.
10.(2024.陇南)由若干个完全相同的小正方体搭成的几何体的主视图和左视图如图所示,则搭成该几何体所用的小正方体的个数最少是 4 个.
【考点】由三视图判断几何体.
【专题】投影与视图;空间观念.
【答案】见试题解答内容
【分析】先根据主视图和左视图得出该几何体为两层三列,再确定每层的最少个数即可.
【解答】解:由题意可知该几何体为两层三列,
最低层最少为3个,第二层为1个,
如图(一种最少的情况的俯视图):
∴最少由4个小正方体组成,
故答案为:4.
【点评】本题考查了根据几何体的三视图判断组成几何体的小正方体的个数,关键是根据主视图和左视图确定组合几何体的层数和列数.
11.(2024.康县一模)由若干个完全相同的小立方块搭成的几何体的主视图和左视图如图所示,则搭成该几何体所用的小立方块的个数最多是 7 .
【考点】由三视图判断几何体.
【专题】投影与视图;几何直观.
【答案】7.
【分析】根据所给出的图形可知这个几何体共有2层,3列,先看第一层正方体可能的最多个数,再看第二层正方体的可能的最多个数,相加即可.
【解答】解:根据主视图和左视图可得:
这个几何体有2层,3列,最底层最多有3×2=6个正方体,第二层有1个正方体.
故答案为:7.
【点评】此题考查了有三视图判断几何体,关键是根据主视图和左视图确定组合几何体的层数及列数.
12.(2024秋 银川)如图是某几何体的三视图,根据图中数据,求该几何体的侧面积为 540 cm2.
【考点】由三视图判断几何体;几何体的表面积.
【专题】投影与视图;空间观念;运算能力.
【答案】540.
【分析】根据三视图可以得出这个几何体应该是个三棱柱,再根据三棱柱的侧面是三个矩形解答即可.
【解答】解:由三视图可知,该几何体是一个三棱柱,侧面由长分别是15cm,12cm,9cm,高均为15cm的三个矩形组成,
故该几何体的侧面积为:(15+12+9)×15=540(cm2).
故答案为:540.
【点评】此题主要考查了由三视图判断几何体,能够根据几何体的三视图求解表面积是解题的关键.
三.解答题(共3小题)
13.(2024.淮安区一模)图1是一个不倒翁模型,图2是它的主视图,由△ABC和以O为圆心的弧组成,已知OC⊥AB,AD=BD=24cm,OD=18cm,CD=32cm.
(1)求证:AC是⊙O的切线;
(2)如图3,转动模型使AC与地面EF平行,求此时点B到地面的距离BF的长度.
【考点】由三视图判断几何体;勾股定理的应用;切线的判定与性质.
【专题】与圆有关的位置关系;图形的相似;运算能力;推理能力.
【答案】(1)见解答;(2)21.6.
【分析】(1)连接OA.证△ADO∽△CDA,得∠OAD=∠ACD,据此可知∠ACD+∠AOD=∠OAD+∠AOD=90°,从而得证;
(2)接OB,延长FB交AC于点H,由AC∥EF,∠BFE=90°知∠BHC=∠BFE=90°,结合,cm,cm,则,得BH的长度,继而可得答案.
【解答】解:(1)连接OA.
Rt△ADO与Rt△CDA中,∵∠ADO=∠CDA=90°,,
∴△ADO∽△CDA,
∴∠OAD=∠ACD,
∴∠ACD+∠AOD=∠OAD+∠AOD=90°,即∠OAC=90°,
∴OA⊥AC,
又∵OA是⊙O半径,
∴AC是⊙O的切线.
(2)连接OB,延长FB交AC于点H,
∵AC∥EF,∠BFE=90°,
∴∠BHC=∠BFE=90°,
∵S△ABC,AO30(cm),AC40cm,
∴,BH=38.4cm,
∴BF=FH﹣BH=60﹣38.4=21.6(cm).
【点评】本题主要考查相似三角形的判定与性质、切线的判定与性质,解题的关键是掌握切线的判定与性质.
14.(2024秋 竞秀区)【问题情境】嘉琪和同学们准备了若干由大小一样的小正方形组成的纸板,计划将这些纸板折叠成正方体纸盒作为学具.
折叠前,嘉琪将大家准备的纸板进行了整理,发现有一个同学准备的纸板如下(如图1所示);
【操作探究】
(1)请直接写出将其折叠成正方体后,与点O重合的是点 M ;
(2)嘉琪和同学们将折叠的纸盒搭成了一个几何体,并画出了从上面看到的该几何体的形状图(如图2所示),其中小正方形中的数字表示在该位置的纸盒的个数.
①请在下面的方框中分别画出从正面、从左面看到的该几何体的形状图;
②如果在该几何体上添加若干个同样大小的正方体纸盒得到一个新几何体,且新几何体与原几何体从上面、正面、左面看到的形状图分别相同,那么最多可以再添加 2 个正方体纸盒.
【考点】作图﹣三视图;展开图折叠成几何体;简单组合体的三视图;由三视图判断几何体.
【专题】展开与折叠;几何直观.
【答案】(1)M;
(2)①见解析;②2.
【分析】(1)将展开图折叠成正方体可得答案;
(2)根据从上面看到的图形画出从左面和正面看得到的图形即可;再从上面看的图形上增加小正方体的个数可得答案.
【解答】解:(1)如图,与点O重合的点是M.
故答案为:M;
(2)①从正面、从左面看到的该几何体的形状,如图;
②如图,添加2个正方体纸盒后从三个方向看正方体的形状图与原来的形状图一样.
故答案为:2.
【点评】本题主要考查了正方体的展开与折叠,掌握从三个方向看几何体的方法是解题的关键.
15.(2024秋 平顶山)一个几何体的三视图如图所示.
(1)这个几何体的名称是 正三棱柱 ,其侧面积为 72 ;
(2)在上面的长方形区域内画出该几何体的草图.
(3)求出左视图中AB的长.
【考点】由三视图判断几何体;几何体的表面积;等边三角形的判定与性质;勾股定理.
【专题】投影与视图;运算能力.
【答案】(1)正三棱柱;72;
(2)见解析;
(3).
【分析】(1)由三视图可知,该几何体为正三棱柱,再根据正三棱柱侧面积计算公式计算可得;
(2)根据题意画出该几何体即可;
(3)在△EFG中,作EH⊥FG于点H,根据勾股定理求出EH,即可得到AB.
【解答】解:(1)该几何体由主视图和左视图可判断为棱柱,由俯视图可判断为正三棱柱,
∴其侧面积为3×4×6=72,
故答案为:正三棱柱,72;
(2)如图,
(3)在△EFG中,作EH⊥FG于点H,
由条件可知△EFG是等边三角形,
∴,
∴,
∴.
【点评】本题考查了三视图,勾股定理,等边三角形的判定与性质,掌握知识点的应用是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考冲刺核心考点 三视图
一.选择题(共7小题)
1.(2024.石家庄)如图是由五个小正方体组成的几何体,若要在图中序号所在的位置上添加一个小正方体,使得添加后该几何体的主视图和左视图均保持不变,则添加的位置应在( )
A.① B.② C.③ D.④
2.(2024.蜀山区一模)如图是生活中常用的“空心卷纸”,其俯视图和主视图分别是( )
A.①③ B.①④ C.②③ D.②④
3.(2024.市中区三模)漏斗是一种通过重力将液体或颗粒导入小口容器的实用工具,日常用于灌装油、调料,实验室中分离液体或过滤,工业上则用于分装原料,如图是一种常用不锈钢漏斗,其俯视图是( )
A. B. C. D.
4.(2024.平阴县二模)某几何体的三视图如图所示,则该几何体为( )
A. B.
C. D.
5.(2024.吉安县一模)如图所示,该几何体的主视图是( )
A. B.
C. D.
6.(2024.阳新县)中国古代数学著作《九章算术》中,将两底面是直角三角形的直棱柱称为“堑堵”.将一个“堑堵”按如图方式摆放,则它的主视图为( )
A. B. C. D.
7.(2024秋 海港区)如图是由5个完全相同的小正方体搭成的几何体,如果将小正方体A放置到小正方体C的正上方,则它的三视图变化情况是( )
A.主视图不会发生改变
B.左视图会发生改变
C.俯视图会发生改变
D.三种视图都会发生改变
二.填空题(共5小题)
8.(2024秋 抚宁区)如图1螺丝钉由头部(直六棱柱)和螺纹(圆柱)组合而成,其俯视图如图2.小明将刻度尺紧靠螺纹放置,经过点A且交CD于点P,量得PC长为1mm,六边形ABCDEF的边长为4mm,AP长为 mm.
9.(2024.越秀区一模)一个几何体的三视图如图所示,根据图示的数据计算该几何体的全面积为 .(结果保留π)
10.(2024.陇南)由若干个完全相同的小正方体搭成的几何体的主视图和左视图如图所示,则搭成该几何体所用的小正方体的个数最少是 个.
11.(2024.康县一模)由若干个完全相同的小立方块搭成的几何体的主视图和左视图如图所示,则搭成该几何体所用的小立方块的个数最多是 .
12.(2024秋 银川)如图是某几何体的三视图,根据图中数据,求该几何体的侧面积为 cm2.
三.解答题(共3小题)
13.(2024.淮安区一模)图1是一个不倒翁模型,图2是它的主视图,由△ABC和以O为圆心的弧组成,已知OC⊥AB,AD=BD=24cm,OD=18cm,CD=32cm.
(1)求证:AC是⊙O的切线;
(2)如图3,转动模型使AC与地面EF平行,求此时点B到地面的距离BF的长度.
14.(2024秋 竞秀区)【问题情境】嘉琪和同学们准备了若干由大小一样的小正方形组成的纸板,计划将这些纸板折叠成正方体纸盒作为学具.
折叠前,嘉琪将大家准备的纸板进行了整理,发现有一个同学准备的纸板如下(如图1所示);
【操作探究】
(1)请直接写出将其折叠成正方体后,与点O重合的是点 ;
(2)嘉琪和同学们将折叠的纸盒搭成了一个几何体,并画出了从上面看到的该几何体的形状图(如图2所示),其中小正方形中的数字表示在该位置的纸盒的个数.
①请在下面的方框中分别画出从正面、从左面看到的该几何体的形状图;
②如果在该几何体上添加若干个同样大小的正方体纸盒得到一个新几何体,且新几何体与原几何体从上面、正面、左面看到的形状图分别相同,那么最多可以再添加 个正方体纸盒.
15.(2024秋 平顶山)一个几何体的三视图如图所示.
(1)这个几何体的名称是 ,其侧面积为 ;
(2)在上面的长方形区域内画出该几何体的草图.
(3)求出左视图中AB的长.
中考冲刺核心考点 三视图
参考答案与试题解析
一.选择题(共7小题)
1.(2024.石家庄)如图是由五个小正方体组成的几何体,若要在图中序号所在的位置上添加一个小正方体,使得添加后该几何体的主视图和左视图均保持不变,则添加的位置应在( )
A.① B.② C.③ D.④
【考点】简单组合体的三视图.
【专题】投影与视图.
【答案】B
【分析】结合每个选项的添加的位置,分析几何体的主视图和左视图的变化,即可作答.
【解答】解:A、若添加的位置在①,则该几何体的主视图不变,左视图变了,故该选项不符合题意;
B、若添加的位置在②,则该几何体的主视图和左视图都不变,故该选项符合题意;
C、若添加的位置在③,则该几何体的左视图不变,主视图变了,故该选项不符合题意;
D、若添加的位置在④,则该几何体的主视图和左视图都变了,故该选项不符合题意;
故选:B.
【点评】本题考查了几何体的三视图,明确左视图是从几何体的左面看到的图形,主视图是从几何体的正面看到的图形是解题的关键.
2.(2024.蜀山区一模)如图是生活中常用的“空心卷纸”,其俯视图和主视图分别是( )
A.①③ B.①④ C.②③ D.②④
【考点】简单组合体的三视图.
【专题】投影与视图;几何直观.
【答案】B
【分析】找到从上面和正面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.
【解答】解:俯视图和主视图分别是①④.
故选:B.
【点评】本题考查了简单组合体的三视图,俯视图是从物体的上面看得到的视图,主视图是从物体的正面看得到的视图,遮住的棱要画虚线.
3.(2024.市中区三模)漏斗是一种通过重力将液体或颗粒导入小口容器的实用工具,日常用于灌装油、调料,实验室中分离液体或过滤,工业上则用于分装原料,如图是一种常用不锈钢漏斗,其俯视图是( )
A.
B.
C.
D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】C
【分析】根据俯视图是从上往下看求解即可.
【解答】解:不锈钢漏斗的俯视图是.
故选:C.
【点评】本题主要考查了简单几何题的三视图,掌握几何体的空间结构特点是关键.
4.(2024.平阴县二模)某几何体的三视图如图所示,则该几何体为( )
A.
B.
C.
D.
【考点】由三视图判断几何体.
【专题】投影与视图;空间观念.
【答案】D
【分析】根据几何体的三视图的特点进行判断.
【解答】解:根据三视图的形状,可得该几何体为.
故选:D.
【点评】本题主要考查了由三视图判断几何体,掌握三视图的定义是关键.
5.(2024.吉安县一模)如图所示,该几何体的主视图是( )
A. B.
C. D.
【考点】简单组合体的三视图.
【专题】投影与视图;空间观念.
【答案】B
【分析】根据从正面看到的图形叫主视图,可得出答案.
【解答】解:几何体的主视图是.
故选:B.
【点评】本题考查了简单组合体的三视图,掌握简单组合体三视图的画法和形状是关键.
6.(2024.阳新县)中国古代数学著作《九章算术》中,将两底面是直角三角形的直棱柱称为“堑堵”.将一个“堑堵”按如图方式摆放,则它的主视图为( )
A. B. C. D.
【考点】简单几何体的三视图.
【答案】A
【分析】主视图是从正面看到的图形,根据摆放方式即可找到从正面看到的图形.
【解答】解:根据摆放方式,由直棱柱的两底面是直角三角形可知,从正面看到的图形是长方形.
故选A.
【点评】本题考查了三视图的知识,主视图是从物体正面看到的视图.
7.(2024秋 海港区)如图是由5个完全相同的小正方体搭成的几何体,如果将小正方体A放置到小正方体C的正上方,则它的三视图变化情况是( )
A.主视图不会发生改变
B.左视图会发生改变
C.俯视图会发生改变
D.三种视图都会发生改变
【考点】简单组合体的三视图.
【专题】投影与视图;几何直观.
【答案】B
【分析】根据简单组合体的三视图的画法画出它们的三视图即可.
【解答】解:如果将小正方体A放置到小正方体C的正上方,则它的主视图和左视图会发生改变,俯视图不变.
故选:B.
【点评】本题考查了简单组合体的三视图,从上面看得到的图形俯视图,从正面看得到的图形是主视图,从左边看得到的图形是左视图.
二.填空题(共5小题)
8.(2024秋 抚宁区)如图1螺丝钉由头部(直六棱柱)和螺纹(圆柱)组合而成,其俯视图如图2.小明将刻度尺紧靠螺纹放置,经过点A且交CD于点P,量得PC长为1mm,六边形ABCDEF的边长为4mm,AP长为 7 mm.
【考点】由三视图判断几何体;垂径定理的应用.
【专题】与圆有关的计算;投影与视图;空间观念;运算能力;推理能力.
【答案】7.
【分析】根据正六边形的性质以及直角三角形的边角关系即可求出答案.
【解答】解:如图,连接OA、OB、AC,则OB⊥AC,
∵六边形ABCDEF是正六边形,
∴∠AOB=60°,AB=OA=OB=4mm,
∴ACOA×2(mm),
在Rt△ACP中,PC=1mm,ACmm,
∴AP7(mm),
故答案为:7.
【点评】本题考查由三视图判断几何体,垂径定理的应用,掌握正六边形的性质以及垂径定理是正确解答的关键.
9.(2024.越秀区一模)一个几何体的三视图如图所示,根据图示的数据计算该几何体的全面积为 90π .(结果保留π)
【考点】由三视图判断几何体.
【专题】投影与视图;空间观念.
【答案】90π.
【分析】根据圆锥侧面积公式首先求出圆锥的侧面积,再求出底面圆的面积,相加即可得出该几何体的全面积.
【解答】解:由图示可知,圆锥的高为12,底面圆的直径为10,
∴圆锥的母线为:,
∴圆锥的侧面积为:πrl=π×5×13=65π,
底面圆的面积为:πr2=25π,
∴该几何体的全面积为:65π+25π=90π.
故答案为:90π.
【点评】此题主要考查了由三视图判断几何体,圆锥侧面积公式,根据已知得母线长,再利用圆锥侧面积公式求出是解决问题的关键.
10.(2024.陇南)由若干个完全相同的小正方体搭成的几何体的主视图和左视图如图所示,则搭成该几何体所用的小正方体的个数最少是 4 个.
【考点】由三视图判断几何体.
【专题】投影与视图;空间观念.
【答案】见试题解答内容
【分析】先根据主视图和左视图得出该几何体为两层三列,再确定每层的最少个数即可.
【解答】解:由题意可知该几何体为两层三列,
最低层最少为3个,第二层为1个,
如图(一种最少的情况的俯视图):
∴最少由4个小正方体组成,
故答案为:4.
【点评】本题考查了根据几何体的三视图判断组成几何体的小正方体的个数,关键是根据主视图和左视图确定组合几何体的层数和列数.
11.(2024.康县一模)由若干个完全相同的小立方块搭成的几何体的主视图和左视图如图所示,则搭成该几何体所用的小立方块的个数最多是 7 .
【考点】由三视图判断几何体.
【专题】投影与视图;几何直观.
【答案】7.
【分析】根据所给出的图形可知这个几何体共有2层,3列,先看第一层正方体可能的最多个数,再看第二层正方体的可能的最多个数,相加即可.
【解答】解:根据主视图和左视图可得:
这个几何体有2层,3列,最底层最多有3×2=6个正方体,第二层有1个正方体.
故答案为:7.
【点评】此题考查了有三视图判断几何体,关键是根据主视图和左视图确定组合几何体的层数及列数.
12.(2024秋 银川)如图是某几何体的三视图,根据图中数据,求该几何体的侧面积为 540 cm2.
【考点】由三视图判断几何体;几何体的表面积.
【专题】投影与视图;空间观念;运算能力.
【答案】540.
【分析】根据三视图可以得出这个几何体应该是个三棱柱,再根据三棱柱的侧面是三个矩形解答即可.
【解答】解:由三视图可知,该几何体是一个三棱柱,侧面由长分别是15cm,12cm,9cm,高均为15cm的三个矩形组成,
故该几何体的侧面积为:(15+12+9)×15=540(cm2).
故答案为:540.
【点评】此题主要考查了由三视图判断几何体,能够根据几何体的三视图求解表面积是解题的关键.
三.解答题(共3小题)
13.(2024.淮安区一模)图1是一个不倒翁模型,图2是它的主视图,由△ABC和以O为圆心的弧组成,已知OC⊥AB,AD=BD=24cm,OD=18cm,CD=32cm.
(1)求证:AC是⊙O的切线;
(2)如图3,转动模型使AC与地面EF平行,求此时点B到地面的距离BF的长度.
【考点】由三视图判断几何体;勾股定理的应用;切线的判定与性质.
【专题】与圆有关的位置关系;图形的相似;运算能力;推理能力.
【答案】(1)见解答;(2)21.6.
【分析】(1)连接OA.证△ADO∽△CDA,得∠OAD=∠ACD,据此可知∠ACD+∠AOD=∠OAD+∠AOD=90°,从而得证;
(2)接OB,延长FB交AC于点H,由AC∥EF,∠BFE=90°知∠BHC=∠BFE=90°,结合,cm,cm,则,得BH的长度,继而可得答案.
【解答】解:(1)连接OA.
Rt△ADO与Rt△CDA中,∵∠ADO=∠CDA=90°,,
∴△ADO∽△CDA,
∴∠OAD=∠ACD,
∴∠ACD+∠AOD=∠OAD+∠AOD=90°,即∠OAC=90°,
∴OA⊥AC,
又∵OA是⊙O半径,
∴AC是⊙O的切线.
(2)连接OB,延长FB交AC于点H,
∵AC∥EF,∠BFE=90°,
∴∠BHC=∠BFE=90°,
∵S△ABC,AO30(cm),AC40cm,
∴,BH=38.4cm,
∴BF=FH﹣BH=60﹣38.4=21.6(cm).
【点评】本题主要考查相似三角形的判定与性质、切线的判定与性质,解题的关键是掌握切线的判定与性质.
14.(2024秋 竞秀区)【问题情境】嘉琪和同学们准备了若干由大小一样的小正方形组成的纸板,计划将这些纸板折叠成正方体纸盒作为学具.
折叠前,嘉琪将大家准备的纸板进行了整理,发现有一个同学准备的纸板如下(如图1所示);
【操作探究】
(1)请直接写出将其折叠成正方体后,与点O重合的是点 M ;
(2)嘉琪和同学们将折叠的纸盒搭成了一个几何体,并画出了从上面看到的该几何体的形状图(如图2所示),其中小正方形中的数字表示在该位置的纸盒的个数.
①请在下面的方框中分别画出从正面、从左面看到的该几何体的形状图;
②如果在该几何体上添加若干个同样大小的正方体纸盒得到一个新几何体,且新几何体与原几何体从上面、正面、左面看到的形状图分别相同,那么最多可以再添加 2 个正方体纸盒.
【考点】作图﹣三视图;展开图折叠成几何体;简单组合体的三视图;由三视图判断几何体.
【专题】展开与折叠;几何直观.
【答案】(1)M;
(2)①见解析;②2.
【分析】(1)将展开图折叠成正方体可得答案;
(2)根据从上面看到的图形画出从左面和正面看得到的图形即可;再从上面看的图形上增加小正方体的个数可得答案.
【解答】解:(1)如图,与点O重合的点是M.
故答案为:M;
(2)①从正面、从左面看到的该几何体的形状,如图;
②如图,添加2个正方体纸盒后从三个方向看正方体的形状图与原来的形状图一样.
故答案为:2.
【点评】本题主要考查了正方体的展开与折叠,掌握从三个方向看几何体的方法是解题的关键.
15.(2024秋 平顶山)一个几何体的三视图如图所示.
(1)这个几何体的名称是 正三棱柱 ,其侧面积为 72 ;
(2)在上面的长方形区域内画出该几何体的草图.
(3)求出左视图中AB的长.
【考点】由三视图判断几何体;几何体的表面积;等边三角形的判定与性质;勾股定理.
【专题】投影与视图;运算能力.
【答案】(1)正三棱柱;72;
(2)见解析;
(3).
【分析】(1)由三视图可知,该几何体为正三棱柱,再根据正三棱柱侧面积计算公式计算可得;
(2)根据题意画出该几何体即可;
(3)在△EFG中,作EH⊥FG于点H,根据勾股定理求出EH,即可得到AB.
【解答】解:(1)该几何体由主视图和左视图可判断为棱柱,由俯视图可判断为正三棱柱,
∴其侧面积为3×4×6=72,
故答案为:正三棱柱,72;
(2)如图,
(3)在△EFG中,作EH⊥FG于点H,
由条件可知△EFG是等边三角形,
∴,
∴,
∴.
【点评】本题考查了三视图,勾股定理,等边三角形的判定与性质,掌握知识点的应用是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
