【中考押题预测】2025年中考数学核心考点考前冲刺 概率(含解析)
文档属性
| 名称 | 【中考押题预测】2025年中考数学核心考点考前冲刺 概率(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-16 14:08:18 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中考核心考点 概率
一.选择题(共10小题)
1.(2025 海陵区一模)小明和同学做“抛掷图钉试验”获得的数据如表:
抛掷次数 100 200 300 400 500 600 700 800 900 1000
钉尖不着地的频数 64 118 189 252 310 360 434 488 549 610
钉尖不着地的频率 0.64 0.59 0.63 0.63 0.62 0.60 0.62 0.61 0.61 0.61
下列说法正确的是( )
A.根据实验结果,“钉尖不着地”和“钉尖着地”具有等可能性
B.若抛掷图钉10000次,则“钉尖不着地”的次数大约有6100次
C.若抛掷图钉100次,则一定有61次“钉尖不着地”
D.若抛掷图钉10次,结果“钉尖不着地”8次,则“钉尖不着地”的概率为0.8
2.(2025春 高州市三模)如图,随意抛出的一枚硬币落在如图所示地板的某块方砖上(每一块方砖的大小相同),它停落在黑色方砖上的概率是( )
A. B. C. D.
3.(2025春 龙口市三模)十字路口的交通信号灯每分钟红灯亮25秒,绿灯亮30秒,黄灯亮5秒.当你抬头看信号灯时,是绿灯的概率是( )
A. B. C. D.
4.(2025 清原县一模)一个小球在如图所示的地面上自由滚动,小球停在阴影区域的概率为( )
A. B. C. D.
5.(2025春 海淀区)不透明的袋子中有红,黄,绿三个小球,这三个小球除颜色外无其他差别.从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,两次摸出的小球的颜色不同的概率是( )
A. B. C. D.
6.(2025春 贵阳)有四个图书架,每个图书架上整齐摆放着10本书,这些书除类别外其余都相同.若分别从每个图书架上随意抽取一本,抽到的书是文学类书籍这一事件为必然事件,应选的图书架是( )
A.0本文学类书籍10本传记类书籍 B.2本文学类书籍8本传记类书籍
C.9本文学类书籍1本传记类书籍 D.10本文学类书籍0本传记类书籍
7.(2025 盐田区二模)2025年是乙巳年,其中“乙”是天干,“巳”是地支.天干地支纪年法起源于古代中国的历法制定,用于记录年份、月份、日期等时间单位,由十个天干和十二个地支组成.天干包括甲、乙、丙、丁、戊、己、庚、辛、壬、癸.地支包括子、丑、寅、卯、辰、巳、午、未、申、酉、戍、亥.从“天干”中抽一个,抽到“乙”的概率是( )
A. B. C. D.
8.(2025 烟台一模)某小组做“用频率估计概率”的试验时,绘出的某一结果出现的频率分布折线图如图所示,则符合这一结果的试验可能是( )
A.抛一枚硬币,出现正面朝上
B.掷一个正六面体的骰子,出现3点朝上
C.任意画一个三角形,其内角和是360°
D.从一个装有2个黄色和1个白色乒乓球的不透明袋子中任取一球,取到的是白球
9.(2024秋 永宁县三模)数学课上,李老师与学生们做“用频率估计概率”的试验:不透明袋子中有4个白球、3个红球、2个黄球和1个黑球,这些球除颜色外无其他差别.从袋子中随机取出一个球,某一颜色的球出现的频率如图所示,则该种球的颜色最有可能是( )
A.黑球 B.红球 C.黄球 D.白球
10.(2025 高新区)一个不透明的袋子中有红球、白球共30个,这些球除颜色外都相同.将袋子中的球搅匀后,从中随意摸出一个球,记下它的颜色后再放回袋中.不断重复这个过程,共摸了50次球,发现有20次摸到红球.估计这个袋子中红球的数量为( )
A.12 B.16 C.18 D.20
二.填空题(共5小题)
11.(2025春 即墨区三模)小明同学抛一枚硬币10次,其中8次正面朝上,2次反面朝上,则第11次抛正面朝上的概率为 .
12.(2025春 南海区)小明将转盘分成n(n是正整数)个扇形,并使得各个扇形的面积都相等,然后他在这些扇形区域内分别标连接偶数数字2,4,6,...,2n(每个区域内标注1个数字,且各区域内标注的数字互不相同),转动转盘1次,当转盘停止转动时,若事件“指针所落区域标注的数字大于8”的概率是,则n的取值为 .
13.(2025 綦江区一模)在如图所示的电路中,随机闭合开关S1,S2,S3中的两个,能让红灯发光的概率是 .
14.(2025 成华区)二十四节气是中国古人智慧的结晶,它基本概括了一年中四季交替的准确时间以及大自然中一些物候等自然现象发生的规律.二十四节气中,春季的节气有:立春、雨水、惊蛰、春分、清明、谷雨;夏季的节气有:立夏、小满、芒种、夏至、小暑、大暑;秋季的节气有:立秋、处暑、白露、秋分、寒露、霜降;冬季的节气有:立冬、小雪、大雪、冬至、小寒、大寒.若从二十四个节气中随机抽一个节气,则抽到的节气在春季的概率为 .
15.(2025春 肥西县三模)在一个不透明的布袋里装有4个标号为1,2,3,4的小球,它们的材质、形状、大小完全相同,小慧从布袋里随机取出一个小球,记下数字为m,小莹从剩下的3个小球中随机取出一个小球,记下数字为n,这样确定了点A的坐标(m,n).则点A(m,n)在函数y=﹣2x+7的图象上的概率为 .
三.解答题(共5小题)
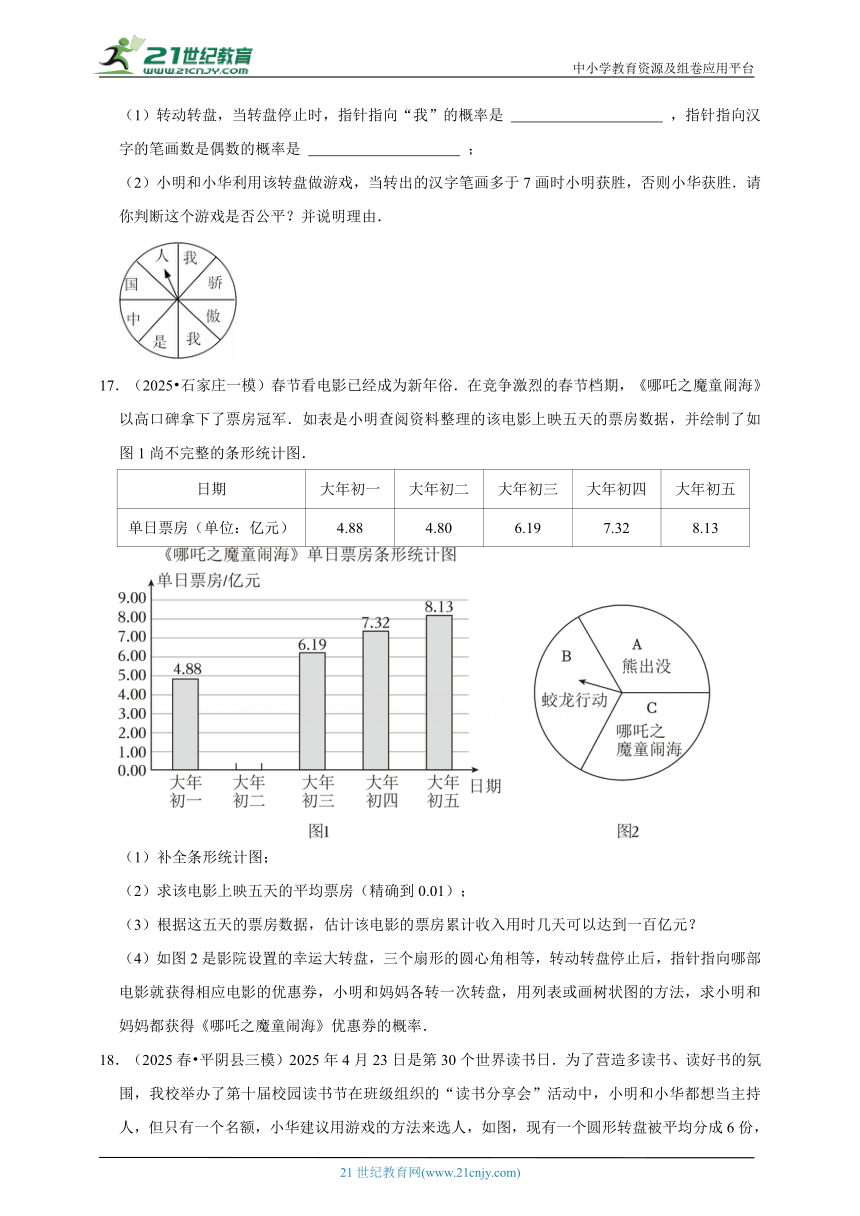
16.(2025春 高州市三模)如图,一个转盘被平均分成8等份,分别标有“我”“骄”“傲”“我”“是”“中”“国”“人”这8个汉字,转动转盘,当转盘停止后,指针指向的汉字即为转出的汉字.
(1)转动转盘,当转盘停止时,指针指向“我”的概率是 ,指针指向汉字的笔画数是偶数的概率是 ;
(2)小明和小华利用该转盘做游戏,当转出的汉字笔画多于7画时小明获胜,否则小华获胜.请你判断这个游戏是否公平?并说明理由.
17.(2025 石家庄一模)春节看电影已经成为新年俗.在竞争激烈的春节档期,《哪吒之魔童闹海》以高口碑拿下了票房冠军.如表是小明查阅资料整理的该电影上映五天的票房数据,并绘制了如图1尚不完整的条形统计图.
日期 大年初一 大年初二 大年初三 大年初四 大年初五
单日票房(单位:亿元) 4.88 4.80 6.19 7.32 8.13
(1)补全条形统计图;
(2)求该电影上映五天的平均票房(精确到0.01);
(3)根据这五天的票房数据,估计该电影的票房累计收入用时几天可以达到一百亿元?
(4)如图2是影院设置的幸运大转盘,三个扇形的圆心角相等,转动转盘停止后,指针指向哪部电影就获得相应电影的优惠券,小明和妈妈各转一次转盘,用列表或画树状图的方法,求小明和妈妈都获得《哪吒之魔童闹海》优惠券的概率.
18.(2025春 平阴县三模)2025年4月23日是第30个世界读书日.为了营造多读书、读好书的氛围,我校举办了第十届校园读书节在班级组织的“读书分享会”活动中,小明和小华都想当主持人,但只有一个名额,小华建议用游戏的方法来选人,如图,现有一个圆形转盘被平均分成6份,分别标有2、3、4、5、7、9这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字(若指针指向分界线,则重新转),求:
(1)转动转盘一次,转出的数字为4的概率是 .
(2)若小明转动两次后转到的数字分别是3和5,小明再转动一次,转出的数字与前两次转出的数字分别作为三条线段的长度(长度单位均相同),则这三条线段能构成等腰三角形的概率是 .
(3)自由转动转盘,若转出的数字是偶数,小明参加;若转出的数字大于4,小华参加;你认为这个游戏公平吗?请说明理由.
19.(2025春 清新区三模)在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 58 96 116 295 484 601
摸到白球的频率 0.58 0.64
0.59 0.605
(1)填写表格,并请估计:当n很大时,摸到白球的频率将会接近 ;
(2)假如你去摸一次,你摸到白球的概率是 ,摸到黑球的概率是 ;
(3)试估算口袋中白色的球有多少只?
20.(2025春 琼山区)为激发青少年崇尚科学、探索未知的热情,学校开展“科学小博士”知识竞赛.各班以小组为单位组织初赛,规定满分为10分,9分及以上为优秀.
数据整理:小夏将本班甲、乙两组同学(每组8人)初赛的成绩整理成如图的统计图.
数据分析:小夏对这两个小组的成绩进行了如下分析:
平均数(分) 中位数(分) 众数(分) 方差 优秀率
甲组 7.625 a 7 4.48 37.5%
乙组 7.625 7 b 0.73 c
请认真阅读上述信息,回答下列问题:
(1)填空:a= ;
(2)甲乙两组的这次初赛成绩中 组的初赛成绩更整齐;
(3)全校共有1600名学生参加了这次初赛,如果以甲乙两组的平均优秀率作为全校的优秀率,估计全校学生初赛成绩为优秀的大约有 人;
(4)已知甲乙两组初赛成绩是优秀的5名学生中有2名是女生、3名男生,若从5名学生中随机抽取2名学生在班上介绍学习经验,则恰好抽出一男一女的概率为 ;
(5)小祺认为甲、乙两组成绩的平均数相等,因此两个组成绩一样好.小夏认为甲组的成绩比乙组好,请结合表中的信息帮小夏说明理由(写出一条即可).
概率
参考答案与试题解析
一.选择题(共10小题)
1.(2025 海陵区一模)小明和同学做“抛掷图钉试验”获得的数据如表:
抛掷次数 100 200 300 400 500 600 700 800 900 1000
钉尖不着地的频数 64 118 189 252 310 360 434 488 549 610
钉尖不着地的频率 0.64 0.59 0.63 0.63 0.62 0.60 0.62 0.61 0.61 0.61
下列说法正确的是( )
A.根据实验结果,“钉尖不着地”和“钉尖着地”具有等可能性
B.若抛掷图钉10000次,则“钉尖不着地”的次数大约有6100次
C.若抛掷图钉100次,则一定有61次“钉尖不着地”
D.若抛掷图钉10次,结果“钉尖不着地”8次,则“钉尖不着地”的概率为0.8
【考点】利用频率估计概率.
【专题】概率及其应用;数据分析观念.
【答案】B
【分析】利用频率估计概率逐一判断即可.
【解答】解:A.根据实验结果,“钉尖不着地”和“钉尖着地”不具有等可能性,此选项错误;
B.若抛掷图钉10000次,则“钉尖不着地”的次数大约有6100次,此选项正确;
C.若抛掷图钉100次,则大约有61次“钉尖不着地”,此选项错误;
D.若抛掷图钉10次,结果“钉尖不着地”8次,由于实验次数较少,不能作为估计概率的情况,此选项错误;
故选:B.
【点评】本题主要考查利用频率估计概率,大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
2.(2025春 高州市三模)如图,随意抛出的一枚硬币落在如图所示地板的某块方砖上(每一块方砖的大小相同),它停落在黑色方砖上的概率是( )
A. B. C. D.
【考点】几何概率.
【专题】概率及其应用;数据分析观念.
【答案】C
【分析】用黑色方砖的面积除以方砖的总面积即可得到答案.
【解答】解:一共有9块方砖,其中黑色方砖有3块,
∴硬币停落在黑色方砖上的概率是,
故选:C.
【点评】本题考查了几何概率,解答本题的关键是熟练掌握概率的求法.
3.(2025春 龙口市三模)十字路口的交通信号灯每分钟红灯亮25秒,绿灯亮30秒,黄灯亮5秒.当你抬头看信号灯时,是绿灯的概率是( )
A. B. C. D.
【考点】概率公式.
【专题】概率及其应用;数据分析观念.
【答案】C
【分析】用绿灯亮的时间除以时间总数60即为所求的概率.
【解答】解:∵交通信号灯每分钟红灯亮25秒,绿灯亮30秒,黄灯亮5秒,
∴一共时间为:25+30+5=60(秒),其中绿灯亮30秒,
∴绿灯的概率是,
故选:C.
【点评】本题考查概率公式,熟练掌握概率公式是解题的关键.
4.(2025 清原县一模)一个小球在如图所示的地面上自由滚动,小球停在阴影区域的概率为( )
A. B. C. D.
【考点】几何概率.
【专题】概率及其应用;推理能力.
【答案】B
【分析】分别计算整个图形的面积和阴影部分面积,再根据概率公式求解即可.
【解答】解:整个图形面积=4×4=16,
阴影部分面积,
∴小球停在阴影区域的概率,
故选:B.
【点评】本题主要考查了几何概率公式,解题的关键是掌握几何概率公式:一般用阴影区域表示所求事件;然后计算阴影区域的面积在总面积中占的比例,这个比例即事件发生的概率.
5.(2025春 海淀区)不透明的袋子中有红,黄,绿三个小球,这三个小球除颜色外无其他差别.从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,两次摸出的小球的颜色不同的概率是( )
A. B. C. D.
【考点】列表法与树状图法;概率公式.
【专题】概率及其应用;数据分析观念.
【答案】A
【分析】画树状图,共有9种等可能的结果,其中两次摸出的小球的颜色不同的结果有6种,再由概率公式求解即可.
【解答】解:画树状图如下:
共有9种等可能的结果,其中两次摸出的小球的颜色不同的结果有6种,
∴两次摸出的小球的颜色不同的概率是,
故选:A.
【点评】此题考查了列表法或树状图法求概率.正确列出树状图是解题的关键.用到的知识点为:概率=所求情况数与总情况数之比.
6.(2025春 贵阳)有四个图书架,每个图书架上整齐摆放着10本书,这些书除类别外其余都相同.若分别从每个图书架上随意抽取一本,抽到的书是文学类书籍这一事件为必然事件,应选的图书架是( )
A.0本文学类书籍10本传记类书籍
B.2本文学类书籍8本传记类书籍
C.9本文学类书籍1本传记类书籍
D.10本文学类书籍0本传记类书籍
【考点】随机事件.
【专题】概率及其应用;应用意识.
【答案】D
【分析】必然事件:在一定条件下必然会发生的事件;不可能事件:一定不会发生的事件;随机事件:介于必然事件和不可能事件之间,可能发生也可能不发生的事件;由此即可求解.
【解答】解:选项A抽到的书是文学类书籍这一事件为不可能事件;选项B、C为随机事件;选项D为必然事件.
故选:D.
【点评】本题考查了随机事件,多边形内角和与外角,概率的意义,掌握随机事件,必然事件的概念是解题的关键.
7.(2025 盐田区二模)2025年是乙巳年,其中“乙”是天干,“巳”是地支.天干地支纪年法起源于古代中国的历法制定,用于记录年份、月份、日期等时间单位,由十个天干和十二个地支组成.天干包括甲、乙、丙、丁、戊、己、庚、辛、壬、癸.地支包括子、丑、寅、卯、辰、巳、午、未、申、酉、戍、亥.从“天干”中抽一个,抽到“乙”的概率是( )
A. B. C. D.
【考点】概率公式;用数字表示事件.
【专题】概率及其应用;应用意识.
【答案】B
【分析】根据天干中一共有10个,所以用抽到“乙”的一种情况除以总数即可.
【解答】解:抽到“乙”的概率是:1÷10,
故选:B.
【点评】本题考查了概率公式,解题的关键是掌握概率的计算方法.
8.(2025 烟台一模)某小组做“用频率估计概率”的试验时,绘出的某一结果出现的频率分布折线图如图所示,则符合这一结果的试验可能是( )
A.抛一枚硬币,出现正面朝上
B.掷一个正六面体的骰子,出现3点朝上
C.任意画一个三角形,其内角和是360°
D.从一个装有2个黄色和1个白色乒乓球的不透明袋子中任取一球,取到的是白球
【考点】利用频率估计概率;频数(率)分布折线图.
【专题】概率及其应用;运算能力.
【答案】D
【分析】根据统计图可知,试验结果在0.33附近波动,即其概率P≈0.33,计算四个选项的概率,约为0.33者即为正确答案.
【解答】解:A.抛一枚硬币,出现正面朝上的概率为,不符合题意;
B.掷一个正六面体的骰子,出现3点朝上的概率为,不符合题意;
C.任意画一个三角形,其内角和是360°的概率为0,不符合题意;
D.从一个装有2个黄色和1个白色乒乓球的不透明袋子中任取一球,取到的是白球的概率为,符合题意.
故选:D.
【点评】此题考查了利用频率估计概率,大量反复试验下频率稳定值即概率.用到的知识点为:频率=所求情况数与总情况数之比.同时此题在解答中要用到概率公式.
9.(2024秋 永宁县三模)数学课上,李老师与学生们做“用频率估计概率”的试验:不透明袋子中有4个白球、3个红球、2个黄球和1个黑球,这些球除颜色外无其他差别.从袋子中随机取出一个球,某一颜色的球出现的频率如图所示,则该种球的颜色最有可能是( )
A.黑球 B.红球 C.黄球 D.白球
【考点】利用频率估计概率.
【专题】概率及其应用;运算能力.
【答案】C
【分析】用频率估计概率,根据大量反复试验下频率的稳定值即为概率值得到抽到该球的概率为0.20,再分别计算出抽到四种颜色的球的概率即可得到答案.
【解答】解:观察统计图可知:该球的频率稳定在0.20左右,所以抽到该球的概率为0.20,
∵抽到白球的概率为0.4,
抽到红球的概率为0.3,
抽到黄球的概率为0.2,
抽到黑球的概率为0.1,
∴该种球的颜色最有可能是黄球.
故选:C.
【点评】本题考查l利用频率估计概率,理解频率、概率的意义和相互关系是正确解答的关键.
10.(2025 高新区)一个不透明的袋子中有红球、白球共30个,这些球除颜色外都相同.将袋子中的球搅匀后,从中随意摸出一个球,记下它的颜色后再放回袋中.不断重复这个过程,共摸了50次球,发现有20次摸到红球.估计这个袋子中红球的数量为( )
A.12 B.16 C.18 D.20
【考点】利用频率估计概率.
【专题】概率及其应用;运算能力.
【答案】A
【分析】首先求出摸到红球的频率,用频率去估计概率即可求出袋中红球约有多少个.
【解答】解:∵共摸了50次球,发现有20次摸到红球,
∴摸到红球的频率0.4,
∴估计摸到红球的概率为0.4,
∴估计这个袋子中红球的数量为30×0.4=12(个).
故选:A.
【点评】本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.用频率估计概率得到的是近似值,随实验次数的增多,值越来越精确.
二.填空题(共5小题)
11.(2025春 即墨区三模)小明同学抛一枚硬币10次,其中8次正面朝上,2次反面朝上,则第11次抛正面朝上的概率为 .
【考点】概率公式.
【专题】概率及其应用;数据分析观念.
【答案】.
【分析】根据抛硬币正面朝上与反面朝上出现的可能性即可求解.
【解答】解:抛一枚硬币,正面朝上与反面朝上出现的可能性相同,
所以抛正面朝上的概率为.
故答案为:.
【点评】本题考查了概率的意义,正确理解概率的意义是解题的关键.
12.(2025春 南海区)小明将转盘分成n(n是正整数)个扇形,并使得各个扇形的面积都相等,然后他在这些扇形区域内分别标连接偶数数字2,4,6,...,2n(每个区域内标注1个数字,且各区域内标注的数字互不相同),转动转盘1次,当转盘停止转动时,若事件“指针所落区域标注的数字大于8”的概率是,则n的取值为 24 .
【考点】概率公式.
【专题】概率及其应用;数据分析观念.
【答案】24.
【分析】用大于8的数字的个数n﹣4除以总个数=对应概率列出关于n的方程,解之可得.
【解答】解:∵“指针所落区域标注的数字大于8”的概率是,
∴,
解得:n=24,
故答案为:24.
【点评】本题主要考查几何概率,解题的关键是根据题意得出大于8的数字的个数及概率公式.
13.(2025 綦江区一模)在如图所示的电路中,随机闭合开关S1,S2,S3中的两个,能让红灯发光的概率是 .
【考点】列表法与树状图法;概率公式.
【专题】概率及其应用;数据分析观念.
【答案】.
【分析】利用树状图求概率即可得解.
【解答】解:随机闭合开关S1,S2,S3中的两个,作树状图如下:
共有6种等可能的结果,能让红灯发光的有2种情况,
∴能让红灯发光的概率为:.
故答案为:.
【点评】本题考查列表法与树状图法,概率公式,解答本题的关键是熟练掌握概率的求法:概率=所求情况数与总情况数之比,
14.(2025 成华区)二十四节气是中国古人智慧的结晶,它基本概括了一年中四季交替的准确时间以及大自然中一些物候等自然现象发生的规律.二十四节气中,春季的节气有:立春、雨水、惊蛰、春分、清明、谷雨;夏季的节气有:立夏、小满、芒种、夏至、小暑、大暑;秋季的节气有:立秋、处暑、白露、秋分、寒露、霜降;冬季的节气有:立冬、小雪、大雪、冬至、小寒、大寒.若从二十四个节气中随机抽一个节气,则抽到的节气在春季的概率为 .
【考点】概率公式.
【专题】概率及其应用;运算能力.
【答案】.
【分析】从二十四个节气中随机抽取一个节气,基本事件个数n=24,抽到的节气在春季包含的基本事件个数m=6,再根据概率公式计算即可.
【解答】解:∵从二十四个节气中随机抽取一个节气,基本事件个数n=24,抽到的节气在夏季包含的基本事件个数m=6,
∴抽到的节气在春季的概率为.
故答案为:.
【点评】本题主要考查了概率公式,熟记概率公式是解题的关键.
15.(2025春 肥西县三模)在一个不透明的布袋里装有4个标号为1,2,3,4的小球,它们的材质、形状、大小完全相同,小慧从布袋里随机取出一个小球,记下数字为m,小莹从剩下的3个小球中随机取出一个小球,记下数字为n,这样确定了点A的坐标(m,n).则点A(m,n)在函数y=﹣2x+7的图象上的概率为 .
【考点】列表法与树状图法;一次函数图象上点的坐标特征.
【专题】概率及其应用;数据分析观念.
【答案】.
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果,求得点A(m,n)在函数y=﹣2x+7的图象上的情况,再利用概率公式即可求得答案.
【解答】解:画树状图如下:
∴点A所有可能的坐标有(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3),共12种,
其中在函数y=﹣2x+7图象上的有2种,即(2,3),(3,1),
∴点在函A(m,n)数y=﹣2x+7图象上的概率为P.
【点评】此题考查了列表法与树状图法、概率公式的应用,用到的知识点为:概率=所求情况数与总情况数之比.
三.解答题(共5小题)
16.(2025春 高州市三模)如图,一个转盘被平均分成8等份,分别标有“我”“骄”“傲”“我”“是”“中”“国”“人”这8个汉字,转动转盘,当转盘停止后,指针指向的汉字即为转出的汉字.
(1)转动转盘,当转盘停止时,指针指向“我”的概率是 ,指针指向汉字的笔画数是偶数的概率是 ;
(2)小明和小华利用该转盘做游戏,当转出的汉字笔画多于7画时小明获胜,否则小华获胜.请你判断这个游戏是否公平?并说明理由.
【考点】游戏公平性;概率公式.
【专题】概率及其应用;数据分析观念.
【答案】(1);;
(2)公平,理由见解析.
【分析】(1)直接根据概率公式求解即可;
(2)分别计算出小明、小华获胜的概率,判断大小关系即可得出答案.
【解答】解:(1)转动转盘,当转盘停止时,指针指向“我”的概率是,
指针指向汉字的笔画数是偶数的有:人,傲,中,国,有4个,故指针指向汉字的笔画数是偶数的概率是,
故答案为:,;
(2)游戏公平;理由如下:
8个汉字中笔画多于7画的有:骄、傲、是、国,不多于7画的有:我、我、中、人,
∴小明获胜的概率为:,
小华获胜的概率为:,
∴小明获胜的概率=小华获胜的概率,
故游戏公平.
【点评】本题考查游戏公平性,概率公式,解答本题的关键是熟练掌握概率的求法:概率=所求情况数与总情况数之比.
17.(2025 石家庄一模)春节看电影已经成为新年俗.在竞争激烈的春节档期,《哪吒之魔童闹海》以高口碑拿下了票房冠军.如表是小明查阅资料整理的该电影上映五天的票房数据,并绘制了如图1尚不完整的条形统计图.
日期 大年初一 大年初二 大年初三 大年初四 大年初五
单日票房(单位:亿元) 4.88 4.80 6.19 7.32 8.13
(1)补全条形统计图;
(2)求该电影上映五天的平均票房(精确到0.01);
(3)根据这五天的票房数据,估计该电影的票房累计收入用时几天可以达到一百亿元?
(4)如图2是影院设置的幸运大转盘,三个扇形的圆心角相等,转动转盘停止后,指针指向哪部电影就获得相应电影的优惠券,小明和妈妈各转一次转盘,用列表或画树状图的方法,求小明和妈妈都获得《哪吒之魔童闹海》优惠券的概率.
【考点】列表法与树状图法;近似数和有效数字;用样本估计总体;扇形统计图;条形统计图;加权平均数;概率公式.
【专题】数据的收集与整理;统计的应用;概率及其应用;数据分析观念;运算能力.
【答案】(1)详见解答;
(2)6.26;
(3)16;
(4).
【分析】(1)根据统计表中的“大年初二”的单日票房数即可补全条形统计图;
(2)根据平均数的计算方法进行计算即可;
(3)根据单日票房的平均数进行计算即可;
(4)用树状图表示所有等可能出现的结果,再根据概率的定义进行计算即可.
【解答】解:(1)根据统计表中的“大年初二”的单日票房数补全统计图如图所示:
(2)该电影上映五天的平均票房为6.26,
答:该电影上映五天的平均票房约为6.26亿元;
(3)100÷6.26≈16(天),
答:根据这五天的票房数据,估计该电影的票房累计收入用时16天可以达到一百亿元;
(4)小明和妈妈各转一次转盘,指针指向各个区域的可能性如下:
共有9中等可能出现的结果,其中小明和妈妈都获得《哪吒之魔童闹海》的只有1种,
所以小明和妈妈都获得《哪吒之魔童闹海》的概率为.
【点评】本题考查列表法和树状图法,条形统计图、扇形统计图以及近似数与有效数字,掌握列表法和树状图法,条形统计图、扇形统计图以及近似数与有效数字的定义是正确解答的关键.
18.(2025春 平阴县三模)2025年4月23日是第30个世界读书日.为了营造多读书、读好书的氛围,我校举办了第十届校园读书节在班级组织的“读书分享会”活动中,小明和小华都想当主持人,但只有一个名额,小华建议用游戏的方法来选人,如图,现有一个圆形转盘被平均分成6份,分别标有2、3、4、5、7、9这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字(若指针指向分界线,则重新转),求:
(1)转动转盘一次,转出的数字为4的概率是 .
(2)若小明转动两次后转到的数字分别是3和5,小明再转动一次,转出的数字与前两次转出的数字分别作为三条线段的长度(长度单位均相同),则这三条线段能构成等腰三角形的概率是 .
(3)自由转动转盘,若转出的数字是偶数,小明参加;若转出的数字大于4,小华参加;你认为这个游戏公平吗?请说明理由.
【考点】游戏公平性;三角形三边关系;概率公式.
【专题】概率及其应用;数据分析观念.
【答案】(1);
(2);
(3)游戏不公平.理由见解答过程.
【分析】(1)直接根据概率公式求解即可;
(2)小明再转动一次,转出的数字共有6种等可能结果,其中与前两次转出的数字分别作为三条线段能构成等腰三角形的有3、5这2种结果,再根据概率公式求解即可;
(3)因为自由转动转盘共有6种等可能解雇,其中转出的数字是偶数的有2、4这2种结果,转出的数字大于4的有5、7、9这3种结果,再求出小明与小华参加的概率,继而可得答案.
【解答】解:(1)转动转盘一次,转出的数字为4的概率是,
故答案为:;
(2)小明再转动一次,转出的数字共有6种等可能结果,其中与前两次转出的数字分别作为三条线段能构成等腰三角形的有3、5这2种结果,
∴这三条线段能构成等腰三角形的概率是,
故答案为:;
(3)游戏不公平;理由如下:
共有6种等可能的结果,其中转出的数字是偶数的有2、4这2种结果,转出的数字大于4的有5、7、9这3种结果,
∴P(小明参加),P(小华参加),
∵,
∴游戏不公平.
【点评】本题考查游戏公平性,三角形三边关系,概率公式,熟练运用概率公式是解题的关键.
19.(2025春 清新区三模)在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 58 96 116 295 484 601
摸到白球的频率 0.58 0.64
0.59
0.59 0.605
0.601
(1)填写表格,并请估计:当n很大时,摸到白球的频率将会接近 0.60 ;
(2)假如你去摸一次,你摸到白球的概率是 0.60 ,摸到黑球的概率是 0.4 ;
(3)试估算口袋中白色的球有多少只?
【考点】利用频率估计概率.
【专题】概率及其应用;数据分析观念.
【答案】(1)表格见解析;0.59;0.601;0.60;
(2)0.60,0.4;
(3)12个.
【分析】(1)用摸到白球的次数除以摸球总数可得对应的摸到白球的频率,据此可计算并填写表格;观察表格中的统计数据,即可得出结论;
(2)根据摸到白球的频率,可以得出摸到白球的概率,进而可以求出摸到黑球的概率;
(3)根据口袋中黑、白两种颜色的球的概率即可求出口袋中黑、白两种颜色的球有多少个.
【解答】解:(1),
填写表格如下:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 58 96 116 295 484 601
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601
由表格数据知,当n增大时,摸到白球的频率将会接近0.60,
故答案为:0.59;0.601;0.60;
(2)∵当n很大时,摸到白球的频率将会接近0.60,
∴摸到白球的概率是0.6,
∴摸到黑球的概率是1﹣0.6=0.4;
故答案为:0.60,0.4;
(3)口袋中有白球是:20×0.6=12(只),
答:估算口袋中白色的球有12只.
【点评】本题主要考查了利用频率估计概率,解题的关键是正确理解频率和概率之间的关系.
20.(2025春 琼山区)为激发青少年崇尚科学、探索未知的热情,学校开展“科学小博士”知识竞赛.各班以小组为单位组织初赛,规定满分为10分,9分及以上为优秀.
数据整理:小夏将本班甲、乙两组同学(每组8人)初赛的成绩整理成如图的统计图.
数据分析:小夏对这两个小组的成绩进行了如下分析:
平均数(分) 中位数(分) 众数(分) 方差 优秀率
甲组 7.625 a 7 4.48 37.5%
乙组 7.625 7 b 0.73 c
请认真阅读上述信息,回答下列问题:
(1)填空:a= 7.5 ;
(2)甲乙两组的这次初赛成绩中 乙 组的初赛成绩更整齐;
(3)全校共有1600名学生参加了这次初赛,如果以甲乙两组的平均优秀率作为全校的优秀率,估计全校学生初赛成绩为优秀的大约有 500 人;
(4)已知甲乙两组初赛成绩是优秀的5名学生中有2名是女生、3名男生,若从5名学生中随机抽取2名学生在班上介绍学习经验,则恰好抽出一男一女的概率为 ;
(5)小祺认为甲、乙两组成绩的平均数相等,因此两个组成绩一样好.小夏认为甲组的成绩比乙组好,请结合表中的信息帮小夏说明理由(写出一条即可).
【考点】列表法与树状图法;用样本估计总体;加权平均数;中位数;众数;方差.
【专题】概率及其应用;数据分析观念.
【答案】(1)7.5;
(2)乙;
(3)500;
(4);
(5)见解析.
【分析】(1)根据中位数的定义和计算公式计算即可;
(2)从方差角度进行分析即可;
(3)先计算出乙组的优秀率,然后求出全校平均优秀率,最后用1600乘以全校平均优秀率即可;
(4)通过画树状图或列表罗列出所有等可能的情况,再从中找出符合条件的情况数,最后利用概率公式求解;
(5)从优秀率,中位数等角度中进行分析即可..
【解答】解:(1)根据中位数的定义和计算公式可得:,
故答案为:7.5;
(2)∵4.48>0.73,
∴乙组成绩波动较小,
∴乙组的初赛成绩更整齐,
故答案为:乙;
(3)乙组的优秀率为2÷8×100%=25%,
全校的平均优秀率为,
估计成绩为优秀的大约有1600×31.25%=500人,
故答案为:500;
(4)设女生为A,男生为B,
列表如下:
A A B B B
A (A,A) (A,B) (A,B) (A,B)
A (A,A) (A,B) (A,B) (A,B)
B (B,A) (B,A) (B,B) (B,B)
B (B,A) (B,A) (B,B) (B,B)
B (B,A) (B,A) (B,B) (B,B)
∴共有20种可能结果,恰好抽出一男一女的结果有12种,
∴P(两人同时看同一个直播节目).
故答案为:;
(5)乙组中7出现的次数最多,则众数b=7,
从优秀率看:甲组成绩的优秀率为37.5%,高于乙组成绩的优秀率25%,
∴从优秀率的角度看,甲组成绩比乙组好;
从中位数看,甲组成绩的中位数为7.5,高于乙组成绩的中位数7,
∴从中位数的角度看,甲组成绩比乙组好.
【点评】本题考查了方差,加权平均数,中位数和众数,概率等知识,熟练掌握以上知识点是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考核心考点 概率
一.选择题(共10小题)
1.(2025 海陵区一模)小明和同学做“抛掷图钉试验”获得的数据如表:
抛掷次数 100 200 300 400 500 600 700 800 900 1000
钉尖不着地的频数 64 118 189 252 310 360 434 488 549 610
钉尖不着地的频率 0.64 0.59 0.63 0.63 0.62 0.60 0.62 0.61 0.61 0.61
下列说法正确的是( )
A.根据实验结果,“钉尖不着地”和“钉尖着地”具有等可能性
B.若抛掷图钉10000次,则“钉尖不着地”的次数大约有6100次
C.若抛掷图钉100次,则一定有61次“钉尖不着地”
D.若抛掷图钉10次,结果“钉尖不着地”8次,则“钉尖不着地”的概率为0.8
2.(2025春 高州市三模)如图,随意抛出的一枚硬币落在如图所示地板的某块方砖上(每一块方砖的大小相同),它停落在黑色方砖上的概率是( )
A. B. C. D.
3.(2025春 龙口市三模)十字路口的交通信号灯每分钟红灯亮25秒,绿灯亮30秒,黄灯亮5秒.当你抬头看信号灯时,是绿灯的概率是( )
A. B. C. D.
4.(2025 清原县一模)一个小球在如图所示的地面上自由滚动,小球停在阴影区域的概率为( )
A. B. C. D.
5.(2025春 海淀区)不透明的袋子中有红,黄,绿三个小球,这三个小球除颜色外无其他差别.从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,两次摸出的小球的颜色不同的概率是( )
A. B. C. D.
6.(2025春 贵阳)有四个图书架,每个图书架上整齐摆放着10本书,这些书除类别外其余都相同.若分别从每个图书架上随意抽取一本,抽到的书是文学类书籍这一事件为必然事件,应选的图书架是( )
A.0本文学类书籍10本传记类书籍 B.2本文学类书籍8本传记类书籍
C.9本文学类书籍1本传记类书籍 D.10本文学类书籍0本传记类书籍
7.(2025 盐田区二模)2025年是乙巳年,其中“乙”是天干,“巳”是地支.天干地支纪年法起源于古代中国的历法制定,用于记录年份、月份、日期等时间单位,由十个天干和十二个地支组成.天干包括甲、乙、丙、丁、戊、己、庚、辛、壬、癸.地支包括子、丑、寅、卯、辰、巳、午、未、申、酉、戍、亥.从“天干”中抽一个,抽到“乙”的概率是( )
A. B. C. D.
8.(2025 烟台一模)某小组做“用频率估计概率”的试验时,绘出的某一结果出现的频率分布折线图如图所示,则符合这一结果的试验可能是( )
A.抛一枚硬币,出现正面朝上
B.掷一个正六面体的骰子,出现3点朝上
C.任意画一个三角形,其内角和是360°
D.从一个装有2个黄色和1个白色乒乓球的不透明袋子中任取一球,取到的是白球
9.(2024秋 永宁县三模)数学课上,李老师与学生们做“用频率估计概率”的试验:不透明袋子中有4个白球、3个红球、2个黄球和1个黑球,这些球除颜色外无其他差别.从袋子中随机取出一个球,某一颜色的球出现的频率如图所示,则该种球的颜色最有可能是( )
A.黑球 B.红球 C.黄球 D.白球
10.(2025 高新区)一个不透明的袋子中有红球、白球共30个,这些球除颜色外都相同.将袋子中的球搅匀后,从中随意摸出一个球,记下它的颜色后再放回袋中.不断重复这个过程,共摸了50次球,发现有20次摸到红球.估计这个袋子中红球的数量为( )
A.12 B.16 C.18 D.20
二.填空题(共5小题)
11.(2025春 即墨区三模)小明同学抛一枚硬币10次,其中8次正面朝上,2次反面朝上,则第11次抛正面朝上的概率为 .
12.(2025春 南海区)小明将转盘分成n(n是正整数)个扇形,并使得各个扇形的面积都相等,然后他在这些扇形区域内分别标连接偶数数字2,4,6,...,2n(每个区域内标注1个数字,且各区域内标注的数字互不相同),转动转盘1次,当转盘停止转动时,若事件“指针所落区域标注的数字大于8”的概率是,则n的取值为 .
13.(2025 綦江区一模)在如图所示的电路中,随机闭合开关S1,S2,S3中的两个,能让红灯发光的概率是 .
14.(2025 成华区)二十四节气是中国古人智慧的结晶,它基本概括了一年中四季交替的准确时间以及大自然中一些物候等自然现象发生的规律.二十四节气中,春季的节气有:立春、雨水、惊蛰、春分、清明、谷雨;夏季的节气有:立夏、小满、芒种、夏至、小暑、大暑;秋季的节气有:立秋、处暑、白露、秋分、寒露、霜降;冬季的节气有:立冬、小雪、大雪、冬至、小寒、大寒.若从二十四个节气中随机抽一个节气,则抽到的节气在春季的概率为 .
15.(2025春 肥西县三模)在一个不透明的布袋里装有4个标号为1,2,3,4的小球,它们的材质、形状、大小完全相同,小慧从布袋里随机取出一个小球,记下数字为m,小莹从剩下的3个小球中随机取出一个小球,记下数字为n,这样确定了点A的坐标(m,n).则点A(m,n)在函数y=﹣2x+7的图象上的概率为 .
三.解答题(共5小题)
16.(2025春 高州市三模)如图,一个转盘被平均分成8等份,分别标有“我”“骄”“傲”“我”“是”“中”“国”“人”这8个汉字,转动转盘,当转盘停止后,指针指向的汉字即为转出的汉字.
(1)转动转盘,当转盘停止时,指针指向“我”的概率是 ,指针指向汉字的笔画数是偶数的概率是 ;
(2)小明和小华利用该转盘做游戏,当转出的汉字笔画多于7画时小明获胜,否则小华获胜.请你判断这个游戏是否公平?并说明理由.
17.(2025 石家庄一模)春节看电影已经成为新年俗.在竞争激烈的春节档期,《哪吒之魔童闹海》以高口碑拿下了票房冠军.如表是小明查阅资料整理的该电影上映五天的票房数据,并绘制了如图1尚不完整的条形统计图.
日期 大年初一 大年初二 大年初三 大年初四 大年初五
单日票房(单位:亿元) 4.88 4.80 6.19 7.32 8.13
(1)补全条形统计图;
(2)求该电影上映五天的平均票房(精确到0.01);
(3)根据这五天的票房数据,估计该电影的票房累计收入用时几天可以达到一百亿元?
(4)如图2是影院设置的幸运大转盘,三个扇形的圆心角相等,转动转盘停止后,指针指向哪部电影就获得相应电影的优惠券,小明和妈妈各转一次转盘,用列表或画树状图的方法,求小明和妈妈都获得《哪吒之魔童闹海》优惠券的概率.
18.(2025春 平阴县三模)2025年4月23日是第30个世界读书日.为了营造多读书、读好书的氛围,我校举办了第十届校园读书节在班级组织的“读书分享会”活动中,小明和小华都想当主持人,但只有一个名额,小华建议用游戏的方法来选人,如图,现有一个圆形转盘被平均分成6份,分别标有2、3、4、5、7、9这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字(若指针指向分界线,则重新转),求:
(1)转动转盘一次,转出的数字为4的概率是 .
(2)若小明转动两次后转到的数字分别是3和5,小明再转动一次,转出的数字与前两次转出的数字分别作为三条线段的长度(长度单位均相同),则这三条线段能构成等腰三角形的概率是 .
(3)自由转动转盘,若转出的数字是偶数,小明参加;若转出的数字大于4,小华参加;你认为这个游戏公平吗?请说明理由.
19.(2025春 清新区三模)在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 58 96 116 295 484 601
摸到白球的频率 0.58 0.64
0.59 0.605
(1)填写表格,并请估计:当n很大时,摸到白球的频率将会接近 ;
(2)假如你去摸一次,你摸到白球的概率是 ,摸到黑球的概率是 ;
(3)试估算口袋中白色的球有多少只?
20.(2025春 琼山区)为激发青少年崇尚科学、探索未知的热情,学校开展“科学小博士”知识竞赛.各班以小组为单位组织初赛,规定满分为10分,9分及以上为优秀.
数据整理:小夏将本班甲、乙两组同学(每组8人)初赛的成绩整理成如图的统计图.
数据分析:小夏对这两个小组的成绩进行了如下分析:
平均数(分) 中位数(分) 众数(分) 方差 优秀率
甲组 7.625 a 7 4.48 37.5%
乙组 7.625 7 b 0.73 c
请认真阅读上述信息,回答下列问题:
(1)填空:a= ;
(2)甲乙两组的这次初赛成绩中 组的初赛成绩更整齐;
(3)全校共有1600名学生参加了这次初赛,如果以甲乙两组的平均优秀率作为全校的优秀率,估计全校学生初赛成绩为优秀的大约有 人;
(4)已知甲乙两组初赛成绩是优秀的5名学生中有2名是女生、3名男生,若从5名学生中随机抽取2名学生在班上介绍学习经验,则恰好抽出一男一女的概率为 ;
(5)小祺认为甲、乙两组成绩的平均数相等,因此两个组成绩一样好.小夏认为甲组的成绩比乙组好,请结合表中的信息帮小夏说明理由(写出一条即可).
概率
参考答案与试题解析
一.选择题(共10小题)
1.(2025 海陵区一模)小明和同学做“抛掷图钉试验”获得的数据如表:
抛掷次数 100 200 300 400 500 600 700 800 900 1000
钉尖不着地的频数 64 118 189 252 310 360 434 488 549 610
钉尖不着地的频率 0.64 0.59 0.63 0.63 0.62 0.60 0.62 0.61 0.61 0.61
下列说法正确的是( )
A.根据实验结果,“钉尖不着地”和“钉尖着地”具有等可能性
B.若抛掷图钉10000次,则“钉尖不着地”的次数大约有6100次
C.若抛掷图钉100次,则一定有61次“钉尖不着地”
D.若抛掷图钉10次,结果“钉尖不着地”8次,则“钉尖不着地”的概率为0.8
【考点】利用频率估计概率.
【专题】概率及其应用;数据分析观念.
【答案】B
【分析】利用频率估计概率逐一判断即可.
【解答】解:A.根据实验结果,“钉尖不着地”和“钉尖着地”不具有等可能性,此选项错误;
B.若抛掷图钉10000次,则“钉尖不着地”的次数大约有6100次,此选项正确;
C.若抛掷图钉100次,则大约有61次“钉尖不着地”,此选项错误;
D.若抛掷图钉10次,结果“钉尖不着地”8次,由于实验次数较少,不能作为估计概率的情况,此选项错误;
故选:B.
【点评】本题主要考查利用频率估计概率,大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
2.(2025春 高州市三模)如图,随意抛出的一枚硬币落在如图所示地板的某块方砖上(每一块方砖的大小相同),它停落在黑色方砖上的概率是( )
A. B. C. D.
【考点】几何概率.
【专题】概率及其应用;数据分析观念.
【答案】C
【分析】用黑色方砖的面积除以方砖的总面积即可得到答案.
【解答】解:一共有9块方砖,其中黑色方砖有3块,
∴硬币停落在黑色方砖上的概率是,
故选:C.
【点评】本题考查了几何概率,解答本题的关键是熟练掌握概率的求法.
3.(2025春 龙口市三模)十字路口的交通信号灯每分钟红灯亮25秒,绿灯亮30秒,黄灯亮5秒.当你抬头看信号灯时,是绿灯的概率是( )
A. B. C. D.
【考点】概率公式.
【专题】概率及其应用;数据分析观念.
【答案】C
【分析】用绿灯亮的时间除以时间总数60即为所求的概率.
【解答】解:∵交通信号灯每分钟红灯亮25秒,绿灯亮30秒,黄灯亮5秒,
∴一共时间为:25+30+5=60(秒),其中绿灯亮30秒,
∴绿灯的概率是,
故选:C.
【点评】本题考查概率公式,熟练掌握概率公式是解题的关键.
4.(2025 清原县一模)一个小球在如图所示的地面上自由滚动,小球停在阴影区域的概率为( )
A. B. C. D.
【考点】几何概率.
【专题】概率及其应用;推理能力.
【答案】B
【分析】分别计算整个图形的面积和阴影部分面积,再根据概率公式求解即可.
【解答】解:整个图形面积=4×4=16,
阴影部分面积,
∴小球停在阴影区域的概率,
故选:B.
【点评】本题主要考查了几何概率公式,解题的关键是掌握几何概率公式:一般用阴影区域表示所求事件;然后计算阴影区域的面积在总面积中占的比例,这个比例即事件发生的概率.
5.(2025春 海淀区)不透明的袋子中有红,黄,绿三个小球,这三个小球除颜色外无其他差别.从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,两次摸出的小球的颜色不同的概率是( )
A. B. C. D.
【考点】列表法与树状图法;概率公式.
【专题】概率及其应用;数据分析观念.
【答案】A
【分析】画树状图,共有9种等可能的结果,其中两次摸出的小球的颜色不同的结果有6种,再由概率公式求解即可.
【解答】解:画树状图如下:
共有9种等可能的结果,其中两次摸出的小球的颜色不同的结果有6种,
∴两次摸出的小球的颜色不同的概率是,
故选:A.
【点评】此题考查了列表法或树状图法求概率.正确列出树状图是解题的关键.用到的知识点为:概率=所求情况数与总情况数之比.
6.(2025春 贵阳)有四个图书架,每个图书架上整齐摆放着10本书,这些书除类别外其余都相同.若分别从每个图书架上随意抽取一本,抽到的书是文学类书籍这一事件为必然事件,应选的图书架是( )
A.0本文学类书籍10本传记类书籍
B.2本文学类书籍8本传记类书籍
C.9本文学类书籍1本传记类书籍
D.10本文学类书籍0本传记类书籍
【考点】随机事件.
【专题】概率及其应用;应用意识.
【答案】D
【分析】必然事件:在一定条件下必然会发生的事件;不可能事件:一定不会发生的事件;随机事件:介于必然事件和不可能事件之间,可能发生也可能不发生的事件;由此即可求解.
【解答】解:选项A抽到的书是文学类书籍这一事件为不可能事件;选项B、C为随机事件;选项D为必然事件.
故选:D.
【点评】本题考查了随机事件,多边形内角和与外角,概率的意义,掌握随机事件,必然事件的概念是解题的关键.
7.(2025 盐田区二模)2025年是乙巳年,其中“乙”是天干,“巳”是地支.天干地支纪年法起源于古代中国的历法制定,用于记录年份、月份、日期等时间单位,由十个天干和十二个地支组成.天干包括甲、乙、丙、丁、戊、己、庚、辛、壬、癸.地支包括子、丑、寅、卯、辰、巳、午、未、申、酉、戍、亥.从“天干”中抽一个,抽到“乙”的概率是( )
A. B. C. D.
【考点】概率公式;用数字表示事件.
【专题】概率及其应用;应用意识.
【答案】B
【分析】根据天干中一共有10个,所以用抽到“乙”的一种情况除以总数即可.
【解答】解:抽到“乙”的概率是:1÷10,
故选:B.
【点评】本题考查了概率公式,解题的关键是掌握概率的计算方法.
8.(2025 烟台一模)某小组做“用频率估计概率”的试验时,绘出的某一结果出现的频率分布折线图如图所示,则符合这一结果的试验可能是( )
A.抛一枚硬币,出现正面朝上
B.掷一个正六面体的骰子,出现3点朝上
C.任意画一个三角形,其内角和是360°
D.从一个装有2个黄色和1个白色乒乓球的不透明袋子中任取一球,取到的是白球
【考点】利用频率估计概率;频数(率)分布折线图.
【专题】概率及其应用;运算能力.
【答案】D
【分析】根据统计图可知,试验结果在0.33附近波动,即其概率P≈0.33,计算四个选项的概率,约为0.33者即为正确答案.
【解答】解:A.抛一枚硬币,出现正面朝上的概率为,不符合题意;
B.掷一个正六面体的骰子,出现3点朝上的概率为,不符合题意;
C.任意画一个三角形,其内角和是360°的概率为0,不符合题意;
D.从一个装有2个黄色和1个白色乒乓球的不透明袋子中任取一球,取到的是白球的概率为,符合题意.
故选:D.
【点评】此题考查了利用频率估计概率,大量反复试验下频率稳定值即概率.用到的知识点为:频率=所求情况数与总情况数之比.同时此题在解答中要用到概率公式.
9.(2024秋 永宁县三模)数学课上,李老师与学生们做“用频率估计概率”的试验:不透明袋子中有4个白球、3个红球、2个黄球和1个黑球,这些球除颜色外无其他差别.从袋子中随机取出一个球,某一颜色的球出现的频率如图所示,则该种球的颜色最有可能是( )
A.黑球 B.红球 C.黄球 D.白球
【考点】利用频率估计概率.
【专题】概率及其应用;运算能力.
【答案】C
【分析】用频率估计概率,根据大量反复试验下频率的稳定值即为概率值得到抽到该球的概率为0.20,再分别计算出抽到四种颜色的球的概率即可得到答案.
【解答】解:观察统计图可知:该球的频率稳定在0.20左右,所以抽到该球的概率为0.20,
∵抽到白球的概率为0.4,
抽到红球的概率为0.3,
抽到黄球的概率为0.2,
抽到黑球的概率为0.1,
∴该种球的颜色最有可能是黄球.
故选:C.
【点评】本题考查l利用频率估计概率,理解频率、概率的意义和相互关系是正确解答的关键.
10.(2025 高新区)一个不透明的袋子中有红球、白球共30个,这些球除颜色外都相同.将袋子中的球搅匀后,从中随意摸出一个球,记下它的颜色后再放回袋中.不断重复这个过程,共摸了50次球,发现有20次摸到红球.估计这个袋子中红球的数量为( )
A.12 B.16 C.18 D.20
【考点】利用频率估计概率.
【专题】概率及其应用;运算能力.
【答案】A
【分析】首先求出摸到红球的频率,用频率去估计概率即可求出袋中红球约有多少个.
【解答】解:∵共摸了50次球,发现有20次摸到红球,
∴摸到红球的频率0.4,
∴估计摸到红球的概率为0.4,
∴估计这个袋子中红球的数量为30×0.4=12(个).
故选:A.
【点评】本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.用频率估计概率得到的是近似值,随实验次数的增多,值越来越精确.
二.填空题(共5小题)
11.(2025春 即墨区三模)小明同学抛一枚硬币10次,其中8次正面朝上,2次反面朝上,则第11次抛正面朝上的概率为 .
【考点】概率公式.
【专题】概率及其应用;数据分析观念.
【答案】.
【分析】根据抛硬币正面朝上与反面朝上出现的可能性即可求解.
【解答】解:抛一枚硬币,正面朝上与反面朝上出现的可能性相同,
所以抛正面朝上的概率为.
故答案为:.
【点评】本题考查了概率的意义,正确理解概率的意义是解题的关键.
12.(2025春 南海区)小明将转盘分成n(n是正整数)个扇形,并使得各个扇形的面积都相等,然后他在这些扇形区域内分别标连接偶数数字2,4,6,...,2n(每个区域内标注1个数字,且各区域内标注的数字互不相同),转动转盘1次,当转盘停止转动时,若事件“指针所落区域标注的数字大于8”的概率是,则n的取值为 24 .
【考点】概率公式.
【专题】概率及其应用;数据分析观念.
【答案】24.
【分析】用大于8的数字的个数n﹣4除以总个数=对应概率列出关于n的方程,解之可得.
【解答】解:∵“指针所落区域标注的数字大于8”的概率是,
∴,
解得:n=24,
故答案为:24.
【点评】本题主要考查几何概率,解题的关键是根据题意得出大于8的数字的个数及概率公式.
13.(2025 綦江区一模)在如图所示的电路中,随机闭合开关S1,S2,S3中的两个,能让红灯发光的概率是 .
【考点】列表法与树状图法;概率公式.
【专题】概率及其应用;数据分析观念.
【答案】.
【分析】利用树状图求概率即可得解.
【解答】解:随机闭合开关S1,S2,S3中的两个,作树状图如下:
共有6种等可能的结果,能让红灯发光的有2种情况,
∴能让红灯发光的概率为:.
故答案为:.
【点评】本题考查列表法与树状图法,概率公式,解答本题的关键是熟练掌握概率的求法:概率=所求情况数与总情况数之比,
14.(2025 成华区)二十四节气是中国古人智慧的结晶,它基本概括了一年中四季交替的准确时间以及大自然中一些物候等自然现象发生的规律.二十四节气中,春季的节气有:立春、雨水、惊蛰、春分、清明、谷雨;夏季的节气有:立夏、小满、芒种、夏至、小暑、大暑;秋季的节气有:立秋、处暑、白露、秋分、寒露、霜降;冬季的节气有:立冬、小雪、大雪、冬至、小寒、大寒.若从二十四个节气中随机抽一个节气,则抽到的节气在春季的概率为 .
【考点】概率公式.
【专题】概率及其应用;运算能力.
【答案】.
【分析】从二十四个节气中随机抽取一个节气,基本事件个数n=24,抽到的节气在春季包含的基本事件个数m=6,再根据概率公式计算即可.
【解答】解:∵从二十四个节气中随机抽取一个节气,基本事件个数n=24,抽到的节气在夏季包含的基本事件个数m=6,
∴抽到的节气在春季的概率为.
故答案为:.
【点评】本题主要考查了概率公式,熟记概率公式是解题的关键.
15.(2025春 肥西县三模)在一个不透明的布袋里装有4个标号为1,2,3,4的小球,它们的材质、形状、大小完全相同,小慧从布袋里随机取出一个小球,记下数字为m,小莹从剩下的3个小球中随机取出一个小球,记下数字为n,这样确定了点A的坐标(m,n).则点A(m,n)在函数y=﹣2x+7的图象上的概率为 .
【考点】列表法与树状图法;一次函数图象上点的坐标特征.
【专题】概率及其应用;数据分析观念.
【答案】.
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果,求得点A(m,n)在函数y=﹣2x+7的图象上的情况,再利用概率公式即可求得答案.
【解答】解:画树状图如下:
∴点A所有可能的坐标有(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3),共12种,
其中在函数y=﹣2x+7图象上的有2种,即(2,3),(3,1),
∴点在函A(m,n)数y=﹣2x+7图象上的概率为P.
【点评】此题考查了列表法与树状图法、概率公式的应用,用到的知识点为:概率=所求情况数与总情况数之比.
三.解答题(共5小题)
16.(2025春 高州市三模)如图,一个转盘被平均分成8等份,分别标有“我”“骄”“傲”“我”“是”“中”“国”“人”这8个汉字,转动转盘,当转盘停止后,指针指向的汉字即为转出的汉字.
(1)转动转盘,当转盘停止时,指针指向“我”的概率是 ,指针指向汉字的笔画数是偶数的概率是 ;
(2)小明和小华利用该转盘做游戏,当转出的汉字笔画多于7画时小明获胜,否则小华获胜.请你判断这个游戏是否公平?并说明理由.
【考点】游戏公平性;概率公式.
【专题】概率及其应用;数据分析观念.
【答案】(1);;
(2)公平,理由见解析.
【分析】(1)直接根据概率公式求解即可;
(2)分别计算出小明、小华获胜的概率,判断大小关系即可得出答案.
【解答】解:(1)转动转盘,当转盘停止时,指针指向“我”的概率是,
指针指向汉字的笔画数是偶数的有:人,傲,中,国,有4个,故指针指向汉字的笔画数是偶数的概率是,
故答案为:,;
(2)游戏公平;理由如下:
8个汉字中笔画多于7画的有:骄、傲、是、国,不多于7画的有:我、我、中、人,
∴小明获胜的概率为:,
小华获胜的概率为:,
∴小明获胜的概率=小华获胜的概率,
故游戏公平.
【点评】本题考查游戏公平性,概率公式,解答本题的关键是熟练掌握概率的求法:概率=所求情况数与总情况数之比.
17.(2025 石家庄一模)春节看电影已经成为新年俗.在竞争激烈的春节档期,《哪吒之魔童闹海》以高口碑拿下了票房冠军.如表是小明查阅资料整理的该电影上映五天的票房数据,并绘制了如图1尚不完整的条形统计图.
日期 大年初一 大年初二 大年初三 大年初四 大年初五
单日票房(单位:亿元) 4.88 4.80 6.19 7.32 8.13
(1)补全条形统计图;
(2)求该电影上映五天的平均票房(精确到0.01);
(3)根据这五天的票房数据,估计该电影的票房累计收入用时几天可以达到一百亿元?
(4)如图2是影院设置的幸运大转盘,三个扇形的圆心角相等,转动转盘停止后,指针指向哪部电影就获得相应电影的优惠券,小明和妈妈各转一次转盘,用列表或画树状图的方法,求小明和妈妈都获得《哪吒之魔童闹海》优惠券的概率.
【考点】列表法与树状图法;近似数和有效数字;用样本估计总体;扇形统计图;条形统计图;加权平均数;概率公式.
【专题】数据的收集与整理;统计的应用;概率及其应用;数据分析观念;运算能力.
【答案】(1)详见解答;
(2)6.26;
(3)16;
(4).
【分析】(1)根据统计表中的“大年初二”的单日票房数即可补全条形统计图;
(2)根据平均数的计算方法进行计算即可;
(3)根据单日票房的平均数进行计算即可;
(4)用树状图表示所有等可能出现的结果,再根据概率的定义进行计算即可.
【解答】解:(1)根据统计表中的“大年初二”的单日票房数补全统计图如图所示:
(2)该电影上映五天的平均票房为6.26,
答:该电影上映五天的平均票房约为6.26亿元;
(3)100÷6.26≈16(天),
答:根据这五天的票房数据,估计该电影的票房累计收入用时16天可以达到一百亿元;
(4)小明和妈妈各转一次转盘,指针指向各个区域的可能性如下:
共有9中等可能出现的结果,其中小明和妈妈都获得《哪吒之魔童闹海》的只有1种,
所以小明和妈妈都获得《哪吒之魔童闹海》的概率为.
【点评】本题考查列表法和树状图法,条形统计图、扇形统计图以及近似数与有效数字,掌握列表法和树状图法,条形统计图、扇形统计图以及近似数与有效数字的定义是正确解答的关键.
18.(2025春 平阴县三模)2025年4月23日是第30个世界读书日.为了营造多读书、读好书的氛围,我校举办了第十届校园读书节在班级组织的“读书分享会”活动中,小明和小华都想当主持人,但只有一个名额,小华建议用游戏的方法来选人,如图,现有一个圆形转盘被平均分成6份,分别标有2、3、4、5、7、9这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字(若指针指向分界线,则重新转),求:
(1)转动转盘一次,转出的数字为4的概率是 .
(2)若小明转动两次后转到的数字分别是3和5,小明再转动一次,转出的数字与前两次转出的数字分别作为三条线段的长度(长度单位均相同),则这三条线段能构成等腰三角形的概率是 .
(3)自由转动转盘,若转出的数字是偶数,小明参加;若转出的数字大于4,小华参加;你认为这个游戏公平吗?请说明理由.
【考点】游戏公平性;三角形三边关系;概率公式.
【专题】概率及其应用;数据分析观念.
【答案】(1);
(2);
(3)游戏不公平.理由见解答过程.
【分析】(1)直接根据概率公式求解即可;
(2)小明再转动一次,转出的数字共有6种等可能结果,其中与前两次转出的数字分别作为三条线段能构成等腰三角形的有3、5这2种结果,再根据概率公式求解即可;
(3)因为自由转动转盘共有6种等可能解雇,其中转出的数字是偶数的有2、4这2种结果,转出的数字大于4的有5、7、9这3种结果,再求出小明与小华参加的概率,继而可得答案.
【解答】解:(1)转动转盘一次,转出的数字为4的概率是,
故答案为:;
(2)小明再转动一次,转出的数字共有6种等可能结果,其中与前两次转出的数字分别作为三条线段能构成等腰三角形的有3、5这2种结果,
∴这三条线段能构成等腰三角形的概率是,
故答案为:;
(3)游戏不公平;理由如下:
共有6种等可能的结果,其中转出的数字是偶数的有2、4这2种结果,转出的数字大于4的有5、7、9这3种结果,
∴P(小明参加),P(小华参加),
∵,
∴游戏不公平.
【点评】本题考查游戏公平性,三角形三边关系,概率公式,熟练运用概率公式是解题的关键.
19.(2025春 清新区三模)在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 58 96 116 295 484 601
摸到白球的频率 0.58 0.64
0.59
0.59 0.605
0.601
(1)填写表格,并请估计:当n很大时,摸到白球的频率将会接近 0.60 ;
(2)假如你去摸一次,你摸到白球的概率是 0.60 ,摸到黑球的概率是 0.4 ;
(3)试估算口袋中白色的球有多少只?
【考点】利用频率估计概率.
【专题】概率及其应用;数据分析观念.
【答案】(1)表格见解析;0.59;0.601;0.60;
(2)0.60,0.4;
(3)12个.
【分析】(1)用摸到白球的次数除以摸球总数可得对应的摸到白球的频率,据此可计算并填写表格;观察表格中的统计数据,即可得出结论;
(2)根据摸到白球的频率,可以得出摸到白球的概率,进而可以求出摸到黑球的概率;
(3)根据口袋中黑、白两种颜色的球的概率即可求出口袋中黑、白两种颜色的球有多少个.
【解答】解:(1),
填写表格如下:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 58 96 116 295 484 601
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601
由表格数据知,当n增大时,摸到白球的频率将会接近0.60,
故答案为:0.59;0.601;0.60;
(2)∵当n很大时,摸到白球的频率将会接近0.60,
∴摸到白球的概率是0.6,
∴摸到黑球的概率是1﹣0.6=0.4;
故答案为:0.60,0.4;
(3)口袋中有白球是:20×0.6=12(只),
答:估算口袋中白色的球有12只.
【点评】本题主要考查了利用频率估计概率,解题的关键是正确理解频率和概率之间的关系.
20.(2025春 琼山区)为激发青少年崇尚科学、探索未知的热情,学校开展“科学小博士”知识竞赛.各班以小组为单位组织初赛,规定满分为10分,9分及以上为优秀.
数据整理:小夏将本班甲、乙两组同学(每组8人)初赛的成绩整理成如图的统计图.
数据分析:小夏对这两个小组的成绩进行了如下分析:
平均数(分) 中位数(分) 众数(分) 方差 优秀率
甲组 7.625 a 7 4.48 37.5%
乙组 7.625 7 b 0.73 c
请认真阅读上述信息,回答下列问题:
(1)填空:a= 7.5 ;
(2)甲乙两组的这次初赛成绩中 乙 组的初赛成绩更整齐;
(3)全校共有1600名学生参加了这次初赛,如果以甲乙两组的平均优秀率作为全校的优秀率,估计全校学生初赛成绩为优秀的大约有 500 人;
(4)已知甲乙两组初赛成绩是优秀的5名学生中有2名是女生、3名男生,若从5名学生中随机抽取2名学生在班上介绍学习经验,则恰好抽出一男一女的概率为 ;
(5)小祺认为甲、乙两组成绩的平均数相等,因此两个组成绩一样好.小夏认为甲组的成绩比乙组好,请结合表中的信息帮小夏说明理由(写出一条即可).
【考点】列表法与树状图法;用样本估计总体;加权平均数;中位数;众数;方差.
【专题】概率及其应用;数据分析观念.
【答案】(1)7.5;
(2)乙;
(3)500;
(4);
(5)见解析.
【分析】(1)根据中位数的定义和计算公式计算即可;
(2)从方差角度进行分析即可;
(3)先计算出乙组的优秀率,然后求出全校平均优秀率,最后用1600乘以全校平均优秀率即可;
(4)通过画树状图或列表罗列出所有等可能的情况,再从中找出符合条件的情况数,最后利用概率公式求解;
(5)从优秀率,中位数等角度中进行分析即可..
【解答】解:(1)根据中位数的定义和计算公式可得:,
故答案为:7.5;
(2)∵4.48>0.73,
∴乙组成绩波动较小,
∴乙组的初赛成绩更整齐,
故答案为:乙;
(3)乙组的优秀率为2÷8×100%=25%,
全校的平均优秀率为,
估计成绩为优秀的大约有1600×31.25%=500人,
故答案为:500;
(4)设女生为A,男生为B,
列表如下:
A A B B B
A (A,A) (A,B) (A,B) (A,B)
A (A,A) (A,B) (A,B) (A,B)
B (B,A) (B,A) (B,B) (B,B)
B (B,A) (B,A) (B,B) (B,B)
B (B,A) (B,A) (B,B) (B,B)
∴共有20种可能结果,恰好抽出一男一女的结果有12种,
∴P(两人同时看同一个直播节目).
故答案为:;
(5)乙组中7出现的次数最多,则众数b=7,
从优秀率看:甲组成绩的优秀率为37.5%,高于乙组成绩的优秀率25%,
∴从优秀率的角度看,甲组成绩比乙组好;
从中位数看,甲组成绩的中位数为7.5,高于乙组成绩的中位数7,
∴从中位数的角度看,甲组成绩比乙组好.
【点评】本题考查了方差,加权平均数,中位数和众数,概率等知识,熟练掌握以上知识点是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
