【中考押题预测】2025年中考数学核心考点考前冲刺 数据收集与处理(含解析)
文档属性
| 名称 | 【中考押题预测】2025年中考数学核心考点考前冲刺 数据收集与处理(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-16 14:09:46 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中考核心考点 数据收集与处理
一.选择题(共10小题)
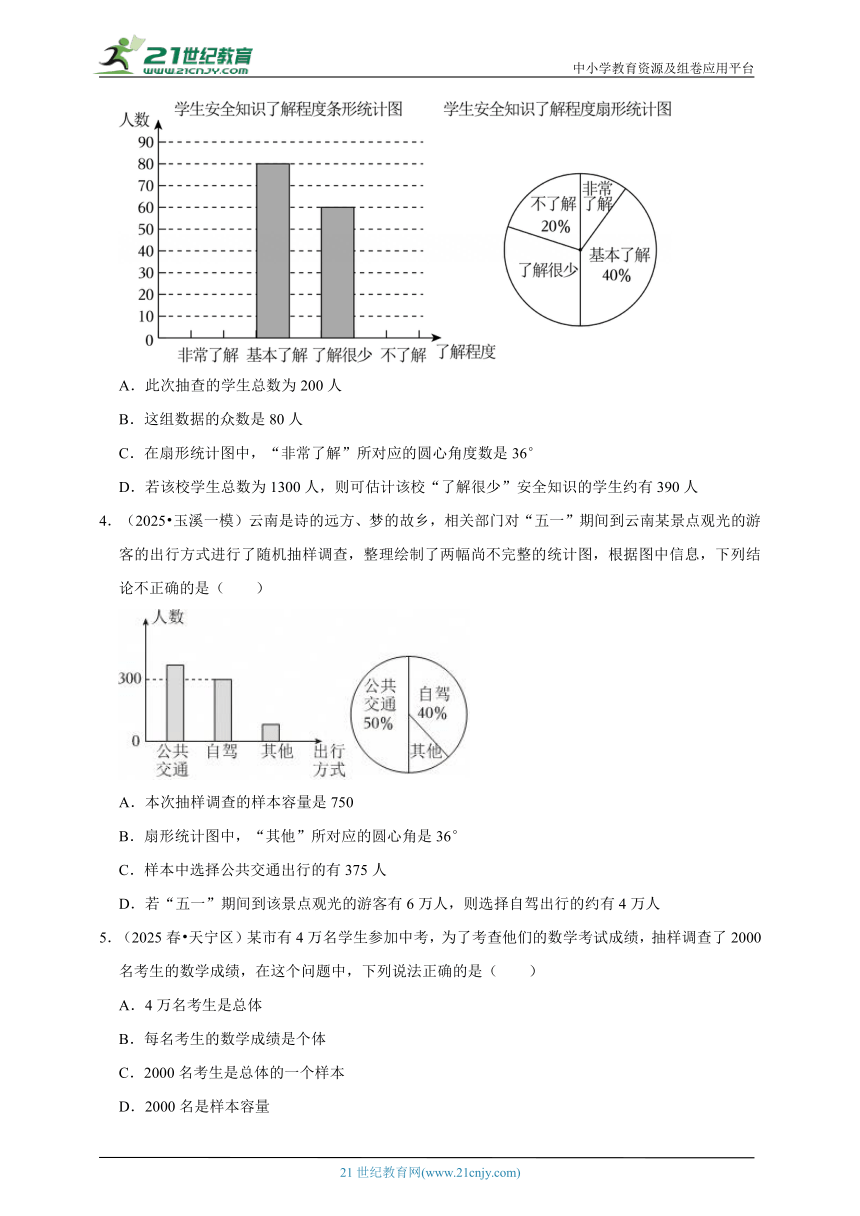
1.(2025春 北京三模)随着人工智能技术的不断突破,人形机器人行业备受关注,未来行业将持续保持高速发展.如图是某机构对2025~2030年全球人形机器人市场规模预测的数据:
根据预测数据,下列分析不正确的是( )
①2025~2030年全球人形机器人市场规模逐年增长;
②2025~2030年全球人形机器人市场规模增长率逐年增大;
③2025~2030年全球人形机器人市场总规模超6000亿元;
④若保持与2030年相同的年增长率,到2032年全球人形机器人市场规模将超1.5万亿元.
A.②③ B.②③④ C.①③④ D.只有②
2.(2025 高新区)下列采用的调查方式中,合适的是( )
A.调查观众对《哪吒2》的满意度,采用全面调查
B.对某批次的新能源电池使用寿命检测,采用全面调查
C.调查河南省中学生的睡眠时间,采用抽样调查
D.企业对招聘人员面试,采用抽样调查
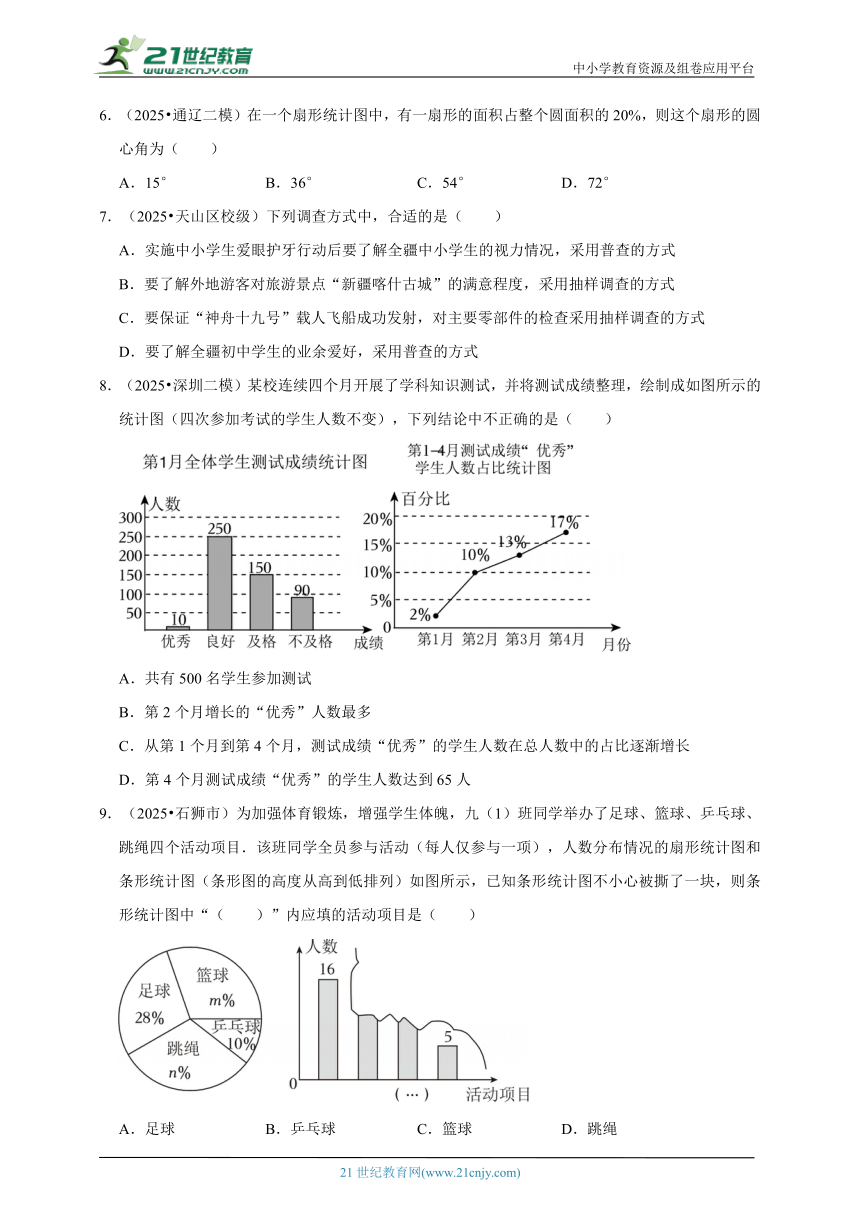
3.(2025 安徽)某学校为重点抓好学生“防溺水”安全教育,对部分学生就安全知识的了解程度进行了随机抽样调查,并绘制了如图所示的两幅统计图,请根据统计图中的信息,下列说法中不正确的是( )
A.此次抽查的学生总数为200人
B.这组数据的众数是80人
C.在扇形统计图中,“非常了解”所对应的圆心角度数是36°
D.若该校学生总数为1300人,则可估计该校“了解很少”安全知识的学生约有390人
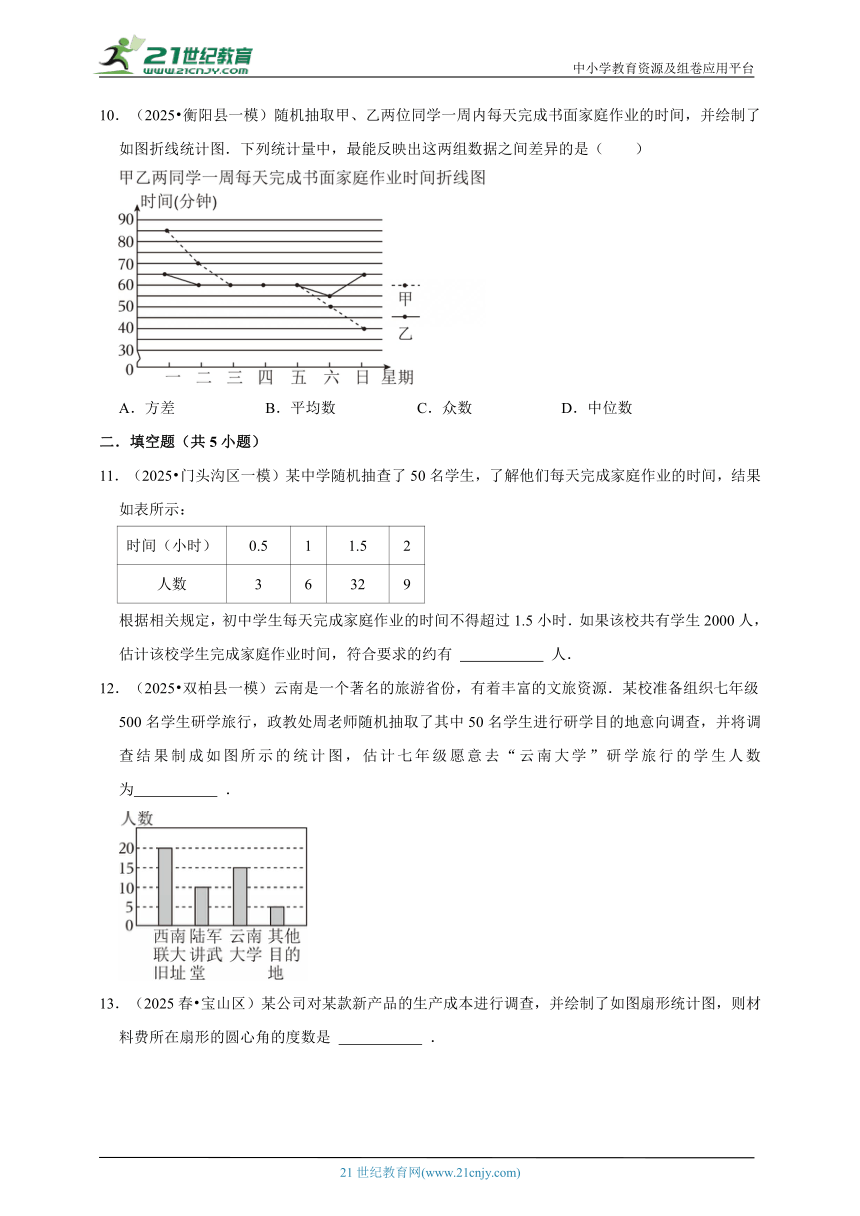
4.(2025 玉溪一模)云南是诗的远方、梦的故乡,相关部门对“五一”期间到云南某景点观光的游客的出行方式进行了随机抽样调查,整理绘制了两幅尚不完整的统计图,根据图中信息,下列结论不正确的是( )
A.本次抽样调查的样本容量是750
B.扇形统计图中,“其他”所对应的圆心角是36°
C.样本中选择公共交通出行的有375人
D.若“五一”期间到该景点观光的游客有6万人,则选择自驾出行的约有4万人
5.(2025春 天宁区)某市有4万名学生参加中考,为了考查他们的数学考试成绩,抽样调查了2000名考生的数学成绩,在这个问题中,下列说法正确的是( )
A.4万名考生是总体
B.每名考生的数学成绩是个体
C.2000名考生是总体的一个样本
D.2000名是样本容量
6.(2025 通辽二模)在一个扇形统计图中,有一扇形的面积占整个圆面积的20%,则这个扇形的圆心角为( )
A.15° B.36° C.54° D.72°
7.(2025 天山区校级)下列调查方式中,合适的是( )
A.实施中小学生爱眼护牙行动后要了解全疆中小学生的视力情况,采用普查的方式
B.要了解外地游客对旅游景点“新疆喀什古城”的满意程度,采用抽样调查的方式
C.要保证“神舟十九号”载人飞船成功发射,对主要零部件的检查采用抽样调查的方式
D.要了解全疆初中学生的业余爱好,采用普查的方式
8.(2025 深圳二模)某校连续四个月开展了学科知识测试,并将测试成绩整理,绘制成如图所示的统计图(四次参加考试的学生人数不变),下列结论中不正确的是( )
A.共有500名学生参加测试
B.第2个月增长的“优秀”人数最多
C.从第1个月到第4个月,测试成绩“优秀”的学生人数在总人数中的占比逐渐增长
D.第4个月测试成绩“优秀”的学生人数达到65人
9.(2025 石狮市)为加强体育锻炼,增强学生体魄,九(1)班同学举办了足球、篮球、乒乓球、跳绳四个活动项目.该班同学全员参与活动(每人仅参与一项),人数分布情况的扇形统计图和条形统计图(条形图的高度从高到低排列)如图所示,已知条形统计图不小心被撕了一块,则条形统计图中“( )”内应填的活动项目是( )
A.足球 B.乒乓球 C.篮球 D.跳绳
10.(2025 衡阳县一模)随机抽取甲、乙两位同学一周内每天完成书面家庭作业的时间,并绘制了如图折线统计图.下列统计量中,最能反映出这两组数据之间差异的是( )
A.方差 B.平均数 C.众数 D.中位数
二.填空题(共5小题)
11.(2025 门头沟区一模)某中学随机抽查了50名学生,了解他们每天完成家庭作业的时间,结果如表所示:
时间(小时) 0.5 1 1.5 2
人数 3 6 32 9
根据相关规定,初中学生每天完成家庭作业的时间不得超过1.5小时.如果该校共有学生2000人,估计该校学生完成家庭作业时间,符合要求的约有 人.
12.(2025 双柏县一模)云南是一个著名的旅游省份,有着丰富的文旅资源.某校准备组织七年级500名学生研学旅行,政教处周老师随机抽取了其中50名学生进行研学目的地意向调查,并将调查结果制成如图所示的统计图,估计七年级愿意去“云南大学”研学旅行的学生人数为 .
13.(2025春 宝山区)某公司对某款新产品的生产成本进行调查,并绘制了如图扇形统计图,则材料费所在扇形的圆心角的度数是 .
14.(2025 绥江县一模)如图是记录某足球队全年比赛结果(“胜”、“负”、“平”)的条形统计图和扇形统计图(不完整):根据图中信息,该足球队全年比赛胜了 场.
15.(2025 朝阳区一模)体育委员从全年级1000名学生中随机抽取了50名同学,统计了他们60秒跳绳的次数,并列出下面的频数分布表:
次数 80≤x<100 100≤x<120 120≤x<140 140≤x<160 160≤x≤180
频数 4 21 13 8 4
根据以上数据,估计该年级的1000名学生中60秒跳绳次数在100≤x<140范围的学生有 人.
三.解答题(共5小题)
16.(2025春 南湖区三模)某地政府为了旅游宣传,决定从甲、乙两家民宿中推选一家为“最美民宿”进行线上推广.现从两家的顾客中各随机抽取20名进行满意度调查打分(满分10分,只打整数分),并对分数进行整理、描述和分析,下面给出了部分信息.
(Ⅰ)甲民宿20名顾客的满意度分数为:
10,5,8,7,10,8,9,8,10,7,9,7,9,7,6,8,9,6,5,9;
(Ⅱ)乙民宿20名顾客的满意度分数条形统计图如图所示:
甲、乙民宿满意度分数统计表
民宿 平均分 众数 中位数 9分及9分以上人数所占百分比
甲 7.85 9 8 a%
乙 b 8 c 30%
(Ⅲ)甲、乙两家民宿的满意度分数的平均数、众数、中位数、9分及9分以上人数所占百分比如上表所示.
根据以上信息,解答下列问题:
(1)求出上述表中的a,b,c的值;
(2)春节假期期间,共有160人入住甲民宿,120人入住乙民宿,估计入住两家民宿的顾客能打9分及9分以上的人数共有多少人?
(3)根据以上表中信息,你会选择哪一家为“最美民宿”?用尽可能多的统计量说明理由.
17.(2025春 江阴市三模)某学校想了解学生家长对“双减”政策的认知情况,随机抽查了部分学生家长,将抽查的数据结果进行统计,并绘制出如图所示两幅不完整的统计图(A:不太了解,B:基本了解,C:比较了解,D:非常了解).根据图中提供的信息,解答下列问题:
(1)这次抽查的学生家长共有 人;
(2)在扇形统计图中,m的值为 ,C所在扇形的圆心角的度数为 ;
(3)请补全条形统计图;
(4)已知该学校共有3000名学生家长,估计对“双减”政策了解程度为“非常了解”的学生家长人数.
18.(2025春 仪征市三模)某中学科技兴趣小组为了解本校学生对我国航天科技的关注程度,在该校内进行了随机调查统计,将调查结果分为不关注、关注、比较关注、非常关注四类,回收、整理好全部调查问卷后,得到如图不完整的统计图.
(1)此次调查中接受调查的人数为 人;补全图1条形统计图;
(2)扇形统计图中“关注”对应扇形的圆心角为 °.
(3)该校共有1000人,根据调查结果估计该校“非堂关注”航天科技的人数多少人?
19.(2025 蜀山区二模)为进一步提升学生的安全意识,某校举办了安全知识竞赛,现从全校八、九年级学生中随机抽取20名学生竞赛成绩(百分制).数学兴趣小组对竞赛成绩进行统计分析,形成如下报告(不完整):
主题项目 校园安全知识竞赛成绩分析报告
数据收集 八年级学生成绩80,80,100,90,80, 70,70,80,70,90, 70,80,100,90,60, 80,90,80,90,90 九年级学生成绩 90,90,100,80,80, 60,70,80,60,100, 60,70,90,80,90, 90,90,70,100,90
数据整理与分析
八、九年级学生成绩分析表 统计量 年级平均数中位数众数方差八年级828080106九年级82n90166
任务1 ①补全条形统计图; ②求“扇形统计图”中80分所在扇形圆心角度数; ③直接写出成绩分析表中,九年级学生成绩的中位数n= .
任务2 该校九年级学生共1200人,请估计成绩不低于80分的人数;
任务3 根据上述统计数据,你认为哪个年级的成绩更好?请说明理由.
根据所给信息,请完成以上所有任务.
20.(2025 惠山区二模)在某校初三体育测试中(满分为40分),抽取部分学生的体育测试成绩,绘制了如下不完整的统计图,请根据图中的信息,解答下列问题:
(1)这次抽样一共抽取了 名学生,并补全条形统计图;
(2)扇形统计图中,“37分”所对应的圆心角为 度;
(3)已知该校初三年级共有1100名学生,根据抽样结果估计该校初三年级这次体育测试中成绩满分的学生人数.
数据收集与处理
参考答案与试题解析
一.选择题(共10小题)
1.(2025春 北京三模)随着人工智能技术的不断突破,人形机器人行业备受关注,未来行业将持续保持高速发展.如图是某机构对2025~2030年全球人形机器人市场规模预测的数据:
根据预测数据,下列分析不正确的是( )
①2025~2030年全球人形机器人市场规模逐年增长;
②2025~2030年全球人形机器人市场规模增长率逐年增大;
③2025~2030年全球人形机器人市场总规模超6000亿元;
④若保持与2030年相同的年增长率,到2032年全球人形机器人市场规模将超1.5万亿元.
A.②③ B.②③④ C.①③④ D.只有②
【考点】条形统计图.
【专题】统计的应用;数据分析观念.
【答案】C
【分析】根据条形统计图逐项分析即可.
【解答】解:根据场规模条形统计图可知,2025~2030年全球人形机器人市场规模逐年增长,故①正确;
根据增长率的折线统计图可知,2025~2030年全球人形机器人市场规模增长率逐年降低,故②错误;
根据场规模条形统计图可知,2025~2030年全球人形机器人市场总规模为:34+106+269+644+1517+3506=6076(亿元),故③正确;
2032年全球人形机器人市场规模为:3506×(1+131.1%)2≈18724.6(亿元),故④正确.
故选:C.
【点评】本题考查条形统计图,关键是从图中读取有效信息.
2.(2025 高新区)下列采用的调查方式中,合适的是( )
A.调查观众对《哪吒2》的满意度,采用全面调查
B.对某批次的新能源电池使用寿命检测,采用全面调查
C.调查河南省中学生的睡眠时间,采用抽样调查
D.企业对招聘人员面试,采用抽样调查
【考点】全面调查与抽样调查.
【专题】数据的收集与整理;数据分析观念.
【答案】C
【分析】根据抽样调查样本的代表性,可操作性结合具体问题情境综合进行判断即可.
【解答】解:A.为了调查观众对《哪吒2》的满意度,适合抽样调查,故本选项不符合题意;
B.了解一批灯泡的使用寿命,适合抽样调查,故本选项不符合题意;
C.了解江阴市中学生睡眠时间,适合抽样调查,故本选项符合题意;
D.企业对招聘人员面试,采用抽样调查,这样的抽样调查样本不具有代表性,故本选项不符合题意.
故选:C.
【点评】本题考查抽样调查的可靠性,理解抽样调查样本的代表性,可操作性是正确解答的关键.
3.(2025 安徽)某学校为重点抓好学生“防溺水”安全教育,对部分学生就安全知识的了解程度进行了随机抽样调查,并绘制了如图所示的两幅统计图,请根据统计图中的信息,下列说法中不正确的是( )
A.此次抽查的学生总数为200人
B.这组数据的众数是80人
C.在扇形统计图中,“非常了解”所对应的圆心角度数是36°
D.若该校学生总数为1300人,则可估计该校“了解很少”安全知识的学生约有390人
【考点】条形统计图;众数;用样本估计总体;扇形统计图.
【专题】统计的应用;应用意识.
【答案】C
【分析】由基本了解的有80人,占40%,可求得接受问卷调查的学生数;用总人数乘不了解的人数所占的百分比求出不了解的人数,再求出非常了解的人数,然后得出众数;用360°乘非常了解的人数所占的百分比即可求出所对应的圆心角度数;利用样本估计总体的方法,即可求得答案.
【解答】解:此次抽查的学生总数为80÷40%=200(人),
故A正确,不符合题意;
不了解的人数为200×20%=40(人),
非常了解的人数为200﹣80﹣60﹣40=20(人),
∴基本了解的人数最多,
∴这组数据的众数是80人,
故B正确,不符合题意;
∵360°×20%=72°,
∴“非常了解”所对应的圆心角度数是72°,
故C错误,符合题意;
∵1300390(人),
∴可估计该校“了解很少”安全知识的学生约有390人,
故D正确,不符合题意.
故选:C.
【点评】本题考查条形统计图、扇形统计图,了解和掌握两个统计图中数量之间的关系是正确解答的前提.
4.(2025 玉溪一模)云南是诗的远方、梦的故乡,相关部门对“五一”期间到云南某景点观光的游客的出行方式进行了随机抽样调查,整理绘制了两幅尚不完整的统计图,根据图中信息,下列结论不正确的是( )
A.本次抽样调查的样本容量是750
B.扇形统计图中,“其他”所对应的圆心角是36°
C.样本中选择公共交通出行的有375人
D.若“五一”期间到该景点观光的游客有6万人,则选择自驾出行的约有4万人
【考点】条形统计图;总体、个体、样本、样本容量;扇形统计图.
【专题】统计的应用;运算能力.
【答案】D
【分析】根据自驾人数及其对应的百分比可得样本容量,根据360°乘以“其他”所占的百分比求圆心角,用总人数乘以对应的百分比可得选择公共交通出行的人数,利用样本估计总体思想可得选择自驾方式出行的人数.
【解答】解:A.本次抽样调查的样本容量是300÷40%=750,此选项不符合题意;
B.扇形统计图中,“其他”所对应的圆心角是360°×(1﹣50%﹣40%)=36°,此选项不符合题意;
C.样本中选择公共交通出行的有750×50%=375(人),此选项不符合题意;
D.若“五一”期间到该景点观光的游客有6万人,则选择自驾出行的约有6×40%=2.4(万人),此选项符合题意.
故选:D.
【点评】本题考查了条形统计图和扇形统计图,熟悉样本、用样本估计总体是解题的关键.
5.(2025春 天宁区)某市有4万名学生参加中考,为了考查他们的数学考试成绩,抽样调查了2000名考生的数学成绩,在这个问题中,下列说法正确的是( )
A.4万名考生是总体
B.每名考生的数学成绩是个体
C.2000名考生是总体的一个样本
D.2000名是样本容量
【考点】总体、个体、样本、样本容量.
【专题】数据的收集与整理;数据分析观念.
【答案】B
【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目,我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象,从而找出总体、个体,再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【解答】解:根据个体,总体,样本,样本容量等知识逐项分析判断如下:
A、4万名学生的数学成绩是总体,故A不符合题意;
B、其中的每名考生的数学成绩是个体,故B符合题意;
C、2000名考生的数学成绩是总体的一个样本,故C不符合题意;
D、2000是样本容量,故D不符合题意;
故选:B.
【点评】本题考查了个体,总体,样本,样本容量等知识,解题的关键在于对知识的熟练掌握.
6.(2025 通辽二模)在一个扇形统计图中,有一扇形的面积占整个圆面积的20%,则这个扇形的圆心角为( )
A.15° B.36° C.54° D.72°
【考点】扇形统计图.
【专题】统计的应用;应用意识.
【答案】D
【分析】用360°乘以扇形的面积占整个圆面积的百分比即可得出答案.
【解答】解:这个扇形的圆心角为360°×20%=72°,
故选:D.
【点评】本题主要考查扇形统计图,扇形统计图是用整个圆表示总数用圆内各个扇形的大小表示各部分数量占总数的百分数.通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.用整个圆的面积表示总数(单位1),用圆的扇形面积表示各部分占总数的百分数.
7.(2025 天山区校级)下列调查方式中,合适的是( )
A.实施中小学生爱眼护牙行动后要了解全疆中小学生的视力情况,采用普查的方式
B.要了解外地游客对旅游景点“新疆喀什古城”的满意程度,采用抽样调查的方式
C.要保证“神舟十九号”载人飞船成功发射,对主要零部件的检查采用抽样调查的方式
D.要了解全疆初中学生的业余爱好,采用普查的方式
【考点】全面调查与抽样调查.
【专题】数据的收集与整理;数据分析观念.
【答案】B
【分析】根据抽样调查样本的代表性,可操作性结合具体问题情境综合进行判断即可.
【解答】解:A.实施中小学生爱眼护牙行动后要了解全疆中小学生的视力情,适合抽样调查,故本选项不符合题意;
B.要了解外地游客对旅游景点“新疆喀什古城”的满意程度,采用抽样调查的方式,节省人力、物力、财力,是合适的,故本选项符合题意;
C.要保证“神舟十九号”载人飞船成功发射,精确度要求高、事关重大,往往选用普查对主要零部件的检查采用适合调查,故本选项不符合题意;
D.了解全疆初中学生的业余爱好,进行一次全面的调查,费大量的人力物力是得不偿失的,采取抽样调查即可,故本选项不符合题意.
故选:B.
【点评】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
8.(2025 深圳二模)某校连续四个月开展了学科知识测试,并将测试成绩整理,绘制成如图所示的统计图(四次参加考试的学生人数不变),下列结论中不正确的是( )
A.共有500名学生参加测试
B.第2个月增长的“优秀”人数最多
C.从第1个月到第4个月,测试成绩“优秀”的学生人数在总人数中的占比逐渐增长
D.第4个月测试成绩“优秀”的学生人数达到65人
【考点】条形统计图;折线统计图.
【专题】统计的应用;应用意识.
【答案】D
【分析】根据条形统计图和折线统计图分别判断即可.
【解答】解:A.测试的学生人数为:10+250+150+90=500(名),原结论正确,故本选项不符合题意;
B.由折线统计图可知,第2月增长的“优秀”人数最多,原结论正确,故本选项不符合题意;
C.由折线统计图可知,从第1个月到第4个月,测试成绩“优秀”的学生人数在总人数中的占比逐周增长,原结论正确,故本选项不符合题意;
D.第4月测试成绩“优秀”的学生人数为:500×17%=85(人),原结论错误,故本选项符合题意.
故选:D.
【点评】本题考查的是条形统计图和折线统计图.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.注意读图获取信息、分析问题解决问题的能力.
9.(2025 石狮市)为加强体育锻炼,增强学生体魄,九(1)班同学举办了足球、篮球、乒乓球、跳绳四个活动项目.该班同学全员参与活动(每人仅参与一项),人数分布情况的扇形统计图和条形统计图(条形图的高度从高到低排列)如图所示,已知条形统计图不小心被撕了一块,则条形统计图中“( )”内应填的活动项目是( )
A.足球 B.乒乓球 C.篮球 D.跳绳
【考点】条形统计图;扇形统计图.
【专题】统计的应用;数据分析观念.
【答案】A
【分析】先求出总人数,再求出足球人数,继而得出另外两个项目的人数即可得出答案.
【解答】解:由扇形统计图知,总人数为5÷10%=50(人),
则足球人数为50×28%=14(人),
所以篮球或跳绳的人数为16人,
则另一种体育活动项目的人数为50﹣(14+16+5)=15(人),
所以人数从高到低排列,位于第三的是足球项自.
故选:A.
【点评】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.
10.(2025 衡阳县一模)随机抽取甲、乙两位同学一周内每天完成书面家庭作业的时间,并绘制了如图折线统计图.下列统计量中,最能反映出这两组数据之间差异的是( )
A.方差 B.平均数 C.众数 D.中位数
【考点】折线统计图;加权平均数;中位数;众数;方差;统计量的选择.
【专题】数据的收集与整理;应用意识.
【答案】A
【分析】根据统计图中的数据,可以判断哪个选项符合题意,本题得以解决.
【解答】解:由图可得,
60.7,
60.7,
故平均数不能反映出这两组数据之间差异,故选项B不符合题意;
甲和和乙的中位数和众数都相等,故不能反映出这两组数据之间差异,故选项C和D不符合题意;
由图象可得,甲的数据波动大,不稳定,乙数据波动小,比较稳定,能反映出这两组数据之间差异,故选项A符合题意;
故选:A.
【点评】本题考查折线统计图、中位数、众数、平均数、方差,解答本题的关键是明确题意,利用数形结合的思想解答.
二.填空题(共5小题)
11.(2025 门头沟区一模)某中学随机抽查了50名学生,了解他们每天完成家庭作业的时间,结果如表所示:
时间(小时) 0.5 1 1.5 2
人数 3 6 32 9
根据相关规定,初中学生每天完成家庭作业的时间不得超过1.5小时.如果该校共有学生2000人,估计该校学生完成家庭作业时间,符合要求的约有 1640 人.
【考点】用样本估计总体.
【专题】统计的应用;运算能力.
【答案】1640.
【分析】用总人数乘样本中每天完成家庭作业的时间不得超过1.5小时的人数所占比例即可.
【解答】解:估计该校学生完成家庭作业时间,符合要求的约有20001640(人).
故答案为:1640.
【点评】本题主要考查用样本估计总体,一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.
12.(2025 双柏县一模)云南是一个著名的旅游省份,有着丰富的文旅资源.某校准备组织七年级500名学生研学旅行,政教处周老师随机抽取了其中50名学生进行研学目的地意向调查,并将调查结果制成如图所示的统计图,估计七年级愿意去“云南大学”研学旅行的学生人数为 150人 .
【考点】用样本估计总体.
【专题】数据的收集与整理;数据分析观念.
【答案】150人.
【分析】用总人数乘样本中去“云南大学”的学生人数所占比例即可.
【解答】解:估计七年级愿意去“云南大学”研学旅行的学生人数为500150(人),
故选:150人.
【点评】本题主要考查用样本估计总体,一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.
13.(2025春 宝山区)某公司对某款新产品的生产成本进行调查,并绘制了如图扇形统计图,则材料费所在扇形的圆心角的度数是 144° .
【考点】扇形统计图.
【专题】统计的应用;应用意识.
【答案】144°.
【分析】用360°乘以材料费所占百分比即可.
【解答】解:由题意可得,材料费所在扇形的圆心角的度数是360°×(1﹣25%﹣35%)=144°.
故答案为:144°.
【点评】本题考查了扇形统计图,关键是求出材料费所占总数的百分数.
14.(2025 绥江县一模)如图是记录某足球队全年比赛结果(“胜”、“负”、“平”)的条形统计图和扇形统计图(不完整):根据图中信息,该足球队全年比赛胜了 30 场.
【考点】条形统计图;扇形统计图.
【专题】数据的收集与整理;统计的应用.
【答案】见试题解答内容
【分析】从两个统计图中可以得到“平”的有10场,占所有比赛结果的20%,从而可以求出表示=比赛的总场次,再根据“胜”的占比,可求出“胜”的场次.
【解答】解:10÷20%=50场,50×(1﹣20%﹣20%)=30场,
故答案为:30.
【点评】考查条形统计图、扇形统计图的意义和制作方法,从两个统计图中获取数量及数量之间的关系式正确解答的关键.
15.(2025 朝阳区一模)体育委员从全年级1000名学生中随机抽取了50名同学,统计了他们60秒跳绳的次数,并列出下面的频数分布表:
次数 80≤x<100 100≤x<120 120≤x<140 140≤x<160 160≤x≤180
频数 4 21 13 8 4
根据以上数据,估计该年级的1000名学生中60秒跳绳次数在100≤x<140范围的学生有 680 人.
【考点】频数(率)分布表;用样本估计总体.
【专题】数据的收集与整理;数据分析观念.
【答案】680.
【分析】用1000乘样本中60秒跳绳次数在100≤x<140范围的学生所占比例即可.
【解答】解:估计该年级的1000名学生中60秒跳绳次数在100≤x<140范围的学生有:
1000680(人),
故答案为:680.
【点评】本题考查频数分布表、用样本估计总体,解答本题的关键是正确列出算式.
三.解答题(共5小题)
16.(2025春 南湖区三模)某地政府为了旅游宣传,决定从甲、乙两家民宿中推选一家为“最美民宿”进行线上推广.现从两家的顾客中各随机抽取20名进行满意度调查打分(满分10分,只打整数分),并对分数进行整理、描述和分析,下面给出了部分信息.
(Ⅰ)甲民宿20名顾客的满意度分数为:
10,5,8,7,10,8,9,8,10,7,9,7,9,7,6,8,9,6,5,9;
(Ⅱ)乙民宿20名顾客的满意度分数条形统计图如图所示:
甲、乙民宿满意度分数统计表
民宿 平均分 众数 中位数 9分及9分以上人数所占百分比
甲 7.85 9 8 a%
乙 b 8 c 30%
(Ⅲ)甲、乙两家民宿的满意度分数的平均数、众数、中位数、9分及9分以上人数所占百分比如上表所示.
根据以上信息,解答下列问题:
(1)求出上述表中的a,b,c的值;
(2)春节假期期间,共有160人入住甲民宿,120人入住乙民宿,估计入住两家民宿的顾客能打9分及9分以上的人数共有多少人?
(3)根据以上表中信息,你会选择哪一家为“最美民宿”?用尽可能多的统计量说明理由.
【考点】条形统计图;加权平均数;中位数;众数;用样本估计总体.
【专题】统计的应用;数据分析观念;运算能力.
【答案】(1)a=40,b=7.75,c=8;
(2)100人;
(3)甲民宿,理由见解析.
【分析】(1)根据平均数和中位数的定义进行计算即可;
(2)根据甲民宿、乙民宿的顾客打9分及9分以上的人数所占的百分比估计总体中入住甲民宿、乙民宿的顾客打9分及9分以上的人数;
(3)根据平均数、众数和9分及9分以上的人数所占的百分比的大小比较得出答案.
【解答】解:(1)甲民宿9分及9分以上人数所占百分比a%100%=40%,
乙民宿的平均分b7.75(分),
将样本中20名顾客对乙民宿满意度分数从小到大排列后,处在中间位置的两个数的平均数为8,
因此中位数c=8;
答:a=40,b=7.75,c=8;
(2)160×40%+120×30%=64+36=100(人),
答:估计入住两家民宿的顾客能打9分及9分以上的人数共有100人;
(3)甲民宿,理由如下:
甲民宿顾客满意度分数的平均数、众数和9分及9分以上人数所占百分比都比乙的要大,因此选择甲民宿.
【点评】本题考查条形统计图,加权平均数、中位数、众数以及样本估计总体,掌握加权平均数、中位数、众数的计算方法是解决问题的关键.
17.(2025春 江阴市三模)某学校想了解学生家长对“双减”政策的认知情况,随机抽查了部分学生家长,将抽查的数据结果进行统计,并绘制出如图所示两幅不完整的统计图(A:不太了解,B:基本了解,C:比较了解,D:非常了解).根据图中提供的信息,解答下列问题:
(1)这次抽查的学生家长共有 50 人;
(2)在扇形统计图中,m的值为 40 ,C所在扇形的圆心角的度数为 144° ;
(3)请补全条形统计图;
(4)已知该学校共有3000名学生家长,估计对“双减”政策了解程度为“非常了解”的学生家长人数.
【考点】条形统计图;用样本估计总体;扇形统计图.
【专题】统计的应用;数据分析观念.
【答案】(1)50;
(2)40,144°;
(3)见解析;
(4)600人.
【分析】(1)根据A的人数除以占的百分比,得出调查总数即可;
(2)根据“比较了解”的有20人除以总人数即可得出m的值,用C的人数占被调查人数的比例乘以360°可得圆心角的度数;
(3)先用总人数乘以30%得出表示B的人数,将总人数减去A、B、C的人数即可得D的人数,补全条形统计图即可;
(4)用样本估算总体即可.
【解答】解:(1)这次抽样调查的家长有5÷10%=50(人),
故答案为:50;
(2)“比较了解”的有20人,
故100%=40%,
∴m=40,
“比较了解”部分所对应的圆心角是:360°×40%=144°,
故答案为:40,144°;
(3)表示“基本了解”的人数为:50×30%=15(人),表示“非常了解”的人数为:50﹣5﹣15﹣20=10(人),
补全图形如图:
(4)3000600(人),
答:估计对“双减”政策了解程度为“非常了解”的学生家长大约有600人.
【点评】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.
18.(2025春 仪征市三模)某中学科技兴趣小组为了解本校学生对我国航天科技的关注程度,在该校内进行了随机调查统计,将调查结果分为不关注、关注、比较关注、非常关注四类,回收、整理好全部调查问卷后,得到如图不完整的统计图.
(1)此次调查中接受调查的人数为 50 人;补全图1条形统计图;
(2)扇形统计图中“关注”对应扇形的圆心角为 43.2 °.
(3)该校共有1000人,根据调查结果估计该校“非堂关注”航天科技的人数多少人?
【考点】条形统计图;用样本估计总体;扇形统计图.
【专题】统计的应用;运算能力.
【答案】(1)50;
(2)43.2;
(3)320人.
【分析】(1)根据比较关注的人数和所占的百分比即可得出调查的总人数;用总人数减去其它调查的人数,求出非常关注的人数,从而补全条形统计图;
(2)360°乘以“关注”的比例即可得到“关注”对应扇形的圆心角度数;
(3)用1000乘样本中“非堂关注”航天科技的人数所占的百分比即可.
【解答】解:(1)此次调查中接受调查的人数为:24÷48%=50(人),
非常关注的人数有:50﹣4﹣6﹣24=16(人),
补全条形统计图如图所示:
故答案为:50;
(2)扇形统计图中“关注”对应扇形的圆心角为:360°43.2°;
故答案为:43.2;
(3)根据题意得:1000320(人),
答:估计该校“非堂关注”航天科技的人数为320人.
【点评】本题考查扇形统计图、条形统计图、用样本估计总体,从两个统计图中获取数量和数量之间的关系是解决问题的关键.
19.(2025 蜀山区二模)为进一步提升学生的安全意识,某校举办了安全知识竞赛,现从全校八、九年级学生中随机抽取20名学生竞赛成绩(百分制).数学兴趣小组对竞赛成绩进行统计分析,形成如下报告(不完整):
主题项目 校园安全知识竞赛成绩分析报告
数据收集 八年级学生成绩80,80,100,90,80, 70,70,80,70,90, 70,80,100,90,60, 80,90,80,90,90 九年级学生成绩 90,90,100,80,80, 60,70,80,60,100, 60,70,90,80,90, 90,90,70,100,90
数据整理与分析
八、九年级学生成绩分析表 统计量 年级平均数中位数众数方差八年级828080106九年级82n90166
任务1 ①补全条形统计图; ②求“扇形统计图”中80分所在扇形圆心角度数; ③直接写出成绩分析表中,九年级学生成绩的中位数n= 85 .
任务2 该校九年级学生共1200人,请估计成绩不低于80分的人数;
任务3 根据上述统计数据,你认为哪个年级的成绩更好?请说明理由.
根据所给信息,请完成以上所有任务.
【考点】条形统计图;中位数;众数;方差;用样本估计总体;扇形统计图.
【专题】数据的收集与整理;数据分析观念.
【答案】任务一:①见解答;②72°;③85;任务二:600人;任务三:八年级成绩更好,理由见解答(答案不唯一).
【分析】任务一:①根据所给数据找出80分人数,然后补全统计图;②先求出a值,再计算即可;③根据中位数的定义解答即可;
任务二:利用样本估计总体即可;
任务三:根据平均数和方差的意义解答即可.
【解答】解:任务一:①补全条形统计图,如图所示:
②“80分”所在扇形的圆心角的度数为:(1﹣15%﹣15%﹣15%﹣35%)×360°=72°;
③九年级学生成绩的中位数n85;
故答案为:85;
任务二:1200人×(1﹣15%﹣15%)=600(人),
答:估计成绩不低于80分的人数为600人;
任务三:我认为八年级成绩更好;
理由:由分析表可知两个年级的平均数相同,但八年级的方差小于九年级,所以八年级的成绩更稳定.
【点评】本题主要考查了中位数、众数、方差、统计图表、数据分析等内容,熟练掌握相关知识是解题的关键.
20.(2025 惠山区二模)在某校初三体育测试中(满分为40分),抽取部分学生的体育测试成绩,绘制了如下不完整的统计图,请根据图中的信息,解答下列问题:
(1)这次抽样一共抽取了 40 名学生,并补全条形统计图;
(2)扇形统计图中,“37分”所对应的圆心角为 45 度;
(3)已知该校初三年级共有1100名学生,根据抽样结果估计该校初三年级这次体育测试中成绩满分的学生人数.
【考点】条形统计图;用样本估计总体;扇形统计图.
【专题】统计的应用;数据分析观念.
【答案】(1)40;
(2)45;
(3)550人.
【分析】(1)根据“40分”的人数除以占比即可得出样本的容量,进而求“36分”的人数,补全统计图;
(2)根据“37分”的占比乘以360°即可求解;
(3)用样本估计总体,用初三年级共有1100名学生总人数乘以“40分”的比即可求解.
【解答】解:(1)本次调查的学生共有20÷50%=40(人),
“38分”的人数为40×15%=6(人),
“39分”的人数为40×15%=6(人),
“36分”的人数为40﹣5﹣6﹣6﹣20=3(人),
补全条形统计图如下:
故答案为:40;
(2)在扇形统计图中,“37分”对应的圆心角度数为360°45°,
故答案为:45;
(3)∵1100×50%×=550(人),
∴估计该校初三年级这次体育测试中成绩满分的学生人数约为550人.
【点评】本题主要考查了条形统计图和扇形统计图的综合运用,样本估计总体,读懂统计图从不同的统计图中得到必要的信息是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考核心考点 数据收集与处理
一.选择题(共10小题)
1.(2025春 北京三模)随着人工智能技术的不断突破,人形机器人行业备受关注,未来行业将持续保持高速发展.如图是某机构对2025~2030年全球人形机器人市场规模预测的数据:
根据预测数据,下列分析不正确的是( )
①2025~2030年全球人形机器人市场规模逐年增长;
②2025~2030年全球人形机器人市场规模增长率逐年增大;
③2025~2030年全球人形机器人市场总规模超6000亿元;
④若保持与2030年相同的年增长率,到2032年全球人形机器人市场规模将超1.5万亿元.
A.②③ B.②③④ C.①③④ D.只有②
2.(2025 高新区)下列采用的调查方式中,合适的是( )
A.调查观众对《哪吒2》的满意度,采用全面调查
B.对某批次的新能源电池使用寿命检测,采用全面调查
C.调查河南省中学生的睡眠时间,采用抽样调查
D.企业对招聘人员面试,采用抽样调查
3.(2025 安徽)某学校为重点抓好学生“防溺水”安全教育,对部分学生就安全知识的了解程度进行了随机抽样调查,并绘制了如图所示的两幅统计图,请根据统计图中的信息,下列说法中不正确的是( )
A.此次抽查的学生总数为200人
B.这组数据的众数是80人
C.在扇形统计图中,“非常了解”所对应的圆心角度数是36°
D.若该校学生总数为1300人,则可估计该校“了解很少”安全知识的学生约有390人
4.(2025 玉溪一模)云南是诗的远方、梦的故乡,相关部门对“五一”期间到云南某景点观光的游客的出行方式进行了随机抽样调查,整理绘制了两幅尚不完整的统计图,根据图中信息,下列结论不正确的是( )
A.本次抽样调查的样本容量是750
B.扇形统计图中,“其他”所对应的圆心角是36°
C.样本中选择公共交通出行的有375人
D.若“五一”期间到该景点观光的游客有6万人,则选择自驾出行的约有4万人
5.(2025春 天宁区)某市有4万名学生参加中考,为了考查他们的数学考试成绩,抽样调查了2000名考生的数学成绩,在这个问题中,下列说法正确的是( )
A.4万名考生是总体
B.每名考生的数学成绩是个体
C.2000名考生是总体的一个样本
D.2000名是样本容量
6.(2025 通辽二模)在一个扇形统计图中,有一扇形的面积占整个圆面积的20%,则这个扇形的圆心角为( )
A.15° B.36° C.54° D.72°
7.(2025 天山区校级)下列调查方式中,合适的是( )
A.实施中小学生爱眼护牙行动后要了解全疆中小学生的视力情况,采用普查的方式
B.要了解外地游客对旅游景点“新疆喀什古城”的满意程度,采用抽样调查的方式
C.要保证“神舟十九号”载人飞船成功发射,对主要零部件的检查采用抽样调查的方式
D.要了解全疆初中学生的业余爱好,采用普查的方式
8.(2025 深圳二模)某校连续四个月开展了学科知识测试,并将测试成绩整理,绘制成如图所示的统计图(四次参加考试的学生人数不变),下列结论中不正确的是( )
A.共有500名学生参加测试
B.第2个月增长的“优秀”人数最多
C.从第1个月到第4个月,测试成绩“优秀”的学生人数在总人数中的占比逐渐增长
D.第4个月测试成绩“优秀”的学生人数达到65人
9.(2025 石狮市)为加强体育锻炼,增强学生体魄,九(1)班同学举办了足球、篮球、乒乓球、跳绳四个活动项目.该班同学全员参与活动(每人仅参与一项),人数分布情况的扇形统计图和条形统计图(条形图的高度从高到低排列)如图所示,已知条形统计图不小心被撕了一块,则条形统计图中“( )”内应填的活动项目是( )
A.足球 B.乒乓球 C.篮球 D.跳绳
10.(2025 衡阳县一模)随机抽取甲、乙两位同学一周内每天完成书面家庭作业的时间,并绘制了如图折线统计图.下列统计量中,最能反映出这两组数据之间差异的是( )
A.方差 B.平均数 C.众数 D.中位数
二.填空题(共5小题)
11.(2025 门头沟区一模)某中学随机抽查了50名学生,了解他们每天完成家庭作业的时间,结果如表所示:
时间(小时) 0.5 1 1.5 2
人数 3 6 32 9
根据相关规定,初中学生每天完成家庭作业的时间不得超过1.5小时.如果该校共有学生2000人,估计该校学生完成家庭作业时间,符合要求的约有 人.
12.(2025 双柏县一模)云南是一个著名的旅游省份,有着丰富的文旅资源.某校准备组织七年级500名学生研学旅行,政教处周老师随机抽取了其中50名学生进行研学目的地意向调查,并将调查结果制成如图所示的统计图,估计七年级愿意去“云南大学”研学旅行的学生人数为 .
13.(2025春 宝山区)某公司对某款新产品的生产成本进行调查,并绘制了如图扇形统计图,则材料费所在扇形的圆心角的度数是 .
14.(2025 绥江县一模)如图是记录某足球队全年比赛结果(“胜”、“负”、“平”)的条形统计图和扇形统计图(不完整):根据图中信息,该足球队全年比赛胜了 场.
15.(2025 朝阳区一模)体育委员从全年级1000名学生中随机抽取了50名同学,统计了他们60秒跳绳的次数,并列出下面的频数分布表:
次数 80≤x<100 100≤x<120 120≤x<140 140≤x<160 160≤x≤180
频数 4 21 13 8 4
根据以上数据,估计该年级的1000名学生中60秒跳绳次数在100≤x<140范围的学生有 人.
三.解答题(共5小题)
16.(2025春 南湖区三模)某地政府为了旅游宣传,决定从甲、乙两家民宿中推选一家为“最美民宿”进行线上推广.现从两家的顾客中各随机抽取20名进行满意度调查打分(满分10分,只打整数分),并对分数进行整理、描述和分析,下面给出了部分信息.
(Ⅰ)甲民宿20名顾客的满意度分数为:
10,5,8,7,10,8,9,8,10,7,9,7,9,7,6,8,9,6,5,9;
(Ⅱ)乙民宿20名顾客的满意度分数条形统计图如图所示:
甲、乙民宿满意度分数统计表
民宿 平均分 众数 中位数 9分及9分以上人数所占百分比
甲 7.85 9 8 a%
乙 b 8 c 30%
(Ⅲ)甲、乙两家民宿的满意度分数的平均数、众数、中位数、9分及9分以上人数所占百分比如上表所示.
根据以上信息,解答下列问题:
(1)求出上述表中的a,b,c的值;
(2)春节假期期间,共有160人入住甲民宿,120人入住乙民宿,估计入住两家民宿的顾客能打9分及9分以上的人数共有多少人?
(3)根据以上表中信息,你会选择哪一家为“最美民宿”?用尽可能多的统计量说明理由.
17.(2025春 江阴市三模)某学校想了解学生家长对“双减”政策的认知情况,随机抽查了部分学生家长,将抽查的数据结果进行统计,并绘制出如图所示两幅不完整的统计图(A:不太了解,B:基本了解,C:比较了解,D:非常了解).根据图中提供的信息,解答下列问题:
(1)这次抽查的学生家长共有 人;
(2)在扇形统计图中,m的值为 ,C所在扇形的圆心角的度数为 ;
(3)请补全条形统计图;
(4)已知该学校共有3000名学生家长,估计对“双减”政策了解程度为“非常了解”的学生家长人数.
18.(2025春 仪征市三模)某中学科技兴趣小组为了解本校学生对我国航天科技的关注程度,在该校内进行了随机调查统计,将调查结果分为不关注、关注、比较关注、非常关注四类,回收、整理好全部调查问卷后,得到如图不完整的统计图.
(1)此次调查中接受调查的人数为 人;补全图1条形统计图;
(2)扇形统计图中“关注”对应扇形的圆心角为 °.
(3)该校共有1000人,根据调查结果估计该校“非堂关注”航天科技的人数多少人?
19.(2025 蜀山区二模)为进一步提升学生的安全意识,某校举办了安全知识竞赛,现从全校八、九年级学生中随机抽取20名学生竞赛成绩(百分制).数学兴趣小组对竞赛成绩进行统计分析,形成如下报告(不完整):
主题项目 校园安全知识竞赛成绩分析报告
数据收集 八年级学生成绩80,80,100,90,80, 70,70,80,70,90, 70,80,100,90,60, 80,90,80,90,90 九年级学生成绩 90,90,100,80,80, 60,70,80,60,100, 60,70,90,80,90, 90,90,70,100,90
数据整理与分析
八、九年级学生成绩分析表 统计量 年级平均数中位数众数方差八年级828080106九年级82n90166
任务1 ①补全条形统计图; ②求“扇形统计图”中80分所在扇形圆心角度数; ③直接写出成绩分析表中,九年级学生成绩的中位数n= .
任务2 该校九年级学生共1200人,请估计成绩不低于80分的人数;
任务3 根据上述统计数据,你认为哪个年级的成绩更好?请说明理由.
根据所给信息,请完成以上所有任务.
20.(2025 惠山区二模)在某校初三体育测试中(满分为40分),抽取部分学生的体育测试成绩,绘制了如下不完整的统计图,请根据图中的信息,解答下列问题:
(1)这次抽样一共抽取了 名学生,并补全条形统计图;
(2)扇形统计图中,“37分”所对应的圆心角为 度;
(3)已知该校初三年级共有1100名学生,根据抽样结果估计该校初三年级这次体育测试中成绩满分的学生人数.
数据收集与处理
参考答案与试题解析
一.选择题(共10小题)
1.(2025春 北京三模)随着人工智能技术的不断突破,人形机器人行业备受关注,未来行业将持续保持高速发展.如图是某机构对2025~2030年全球人形机器人市场规模预测的数据:
根据预测数据,下列分析不正确的是( )
①2025~2030年全球人形机器人市场规模逐年增长;
②2025~2030年全球人形机器人市场规模增长率逐年增大;
③2025~2030年全球人形机器人市场总规模超6000亿元;
④若保持与2030年相同的年增长率,到2032年全球人形机器人市场规模将超1.5万亿元.
A.②③ B.②③④ C.①③④ D.只有②
【考点】条形统计图.
【专题】统计的应用;数据分析观念.
【答案】C
【分析】根据条形统计图逐项分析即可.
【解答】解:根据场规模条形统计图可知,2025~2030年全球人形机器人市场规模逐年增长,故①正确;
根据增长率的折线统计图可知,2025~2030年全球人形机器人市场规模增长率逐年降低,故②错误;
根据场规模条形统计图可知,2025~2030年全球人形机器人市场总规模为:34+106+269+644+1517+3506=6076(亿元),故③正确;
2032年全球人形机器人市场规模为:3506×(1+131.1%)2≈18724.6(亿元),故④正确.
故选:C.
【点评】本题考查条形统计图,关键是从图中读取有效信息.
2.(2025 高新区)下列采用的调查方式中,合适的是( )
A.调查观众对《哪吒2》的满意度,采用全面调查
B.对某批次的新能源电池使用寿命检测,采用全面调查
C.调查河南省中学生的睡眠时间,采用抽样调查
D.企业对招聘人员面试,采用抽样调查
【考点】全面调查与抽样调查.
【专题】数据的收集与整理;数据分析观念.
【答案】C
【分析】根据抽样调查样本的代表性,可操作性结合具体问题情境综合进行判断即可.
【解答】解:A.为了调查观众对《哪吒2》的满意度,适合抽样调查,故本选项不符合题意;
B.了解一批灯泡的使用寿命,适合抽样调查,故本选项不符合题意;
C.了解江阴市中学生睡眠时间,适合抽样调查,故本选项符合题意;
D.企业对招聘人员面试,采用抽样调查,这样的抽样调查样本不具有代表性,故本选项不符合题意.
故选:C.
【点评】本题考查抽样调查的可靠性,理解抽样调查样本的代表性,可操作性是正确解答的关键.
3.(2025 安徽)某学校为重点抓好学生“防溺水”安全教育,对部分学生就安全知识的了解程度进行了随机抽样调查,并绘制了如图所示的两幅统计图,请根据统计图中的信息,下列说法中不正确的是( )
A.此次抽查的学生总数为200人
B.这组数据的众数是80人
C.在扇形统计图中,“非常了解”所对应的圆心角度数是36°
D.若该校学生总数为1300人,则可估计该校“了解很少”安全知识的学生约有390人
【考点】条形统计图;众数;用样本估计总体;扇形统计图.
【专题】统计的应用;应用意识.
【答案】C
【分析】由基本了解的有80人,占40%,可求得接受问卷调查的学生数;用总人数乘不了解的人数所占的百分比求出不了解的人数,再求出非常了解的人数,然后得出众数;用360°乘非常了解的人数所占的百分比即可求出所对应的圆心角度数;利用样本估计总体的方法,即可求得答案.
【解答】解:此次抽查的学生总数为80÷40%=200(人),
故A正确,不符合题意;
不了解的人数为200×20%=40(人),
非常了解的人数为200﹣80﹣60﹣40=20(人),
∴基本了解的人数最多,
∴这组数据的众数是80人,
故B正确,不符合题意;
∵360°×20%=72°,
∴“非常了解”所对应的圆心角度数是72°,
故C错误,符合题意;
∵1300390(人),
∴可估计该校“了解很少”安全知识的学生约有390人,
故D正确,不符合题意.
故选:C.
【点评】本题考查条形统计图、扇形统计图,了解和掌握两个统计图中数量之间的关系是正确解答的前提.
4.(2025 玉溪一模)云南是诗的远方、梦的故乡,相关部门对“五一”期间到云南某景点观光的游客的出行方式进行了随机抽样调查,整理绘制了两幅尚不完整的统计图,根据图中信息,下列结论不正确的是( )
A.本次抽样调查的样本容量是750
B.扇形统计图中,“其他”所对应的圆心角是36°
C.样本中选择公共交通出行的有375人
D.若“五一”期间到该景点观光的游客有6万人,则选择自驾出行的约有4万人
【考点】条形统计图;总体、个体、样本、样本容量;扇形统计图.
【专题】统计的应用;运算能力.
【答案】D
【分析】根据自驾人数及其对应的百分比可得样本容量,根据360°乘以“其他”所占的百分比求圆心角,用总人数乘以对应的百分比可得选择公共交通出行的人数,利用样本估计总体思想可得选择自驾方式出行的人数.
【解答】解:A.本次抽样调查的样本容量是300÷40%=750,此选项不符合题意;
B.扇形统计图中,“其他”所对应的圆心角是360°×(1﹣50%﹣40%)=36°,此选项不符合题意;
C.样本中选择公共交通出行的有750×50%=375(人),此选项不符合题意;
D.若“五一”期间到该景点观光的游客有6万人,则选择自驾出行的约有6×40%=2.4(万人),此选项符合题意.
故选:D.
【点评】本题考查了条形统计图和扇形统计图,熟悉样本、用样本估计总体是解题的关键.
5.(2025春 天宁区)某市有4万名学生参加中考,为了考查他们的数学考试成绩,抽样调查了2000名考生的数学成绩,在这个问题中,下列说法正确的是( )
A.4万名考生是总体
B.每名考生的数学成绩是个体
C.2000名考生是总体的一个样本
D.2000名是样本容量
【考点】总体、个体、样本、样本容量.
【专题】数据的收集与整理;数据分析观念.
【答案】B
【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目,我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象,从而找出总体、个体,再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【解答】解:根据个体,总体,样本,样本容量等知识逐项分析判断如下:
A、4万名学生的数学成绩是总体,故A不符合题意;
B、其中的每名考生的数学成绩是个体,故B符合题意;
C、2000名考生的数学成绩是总体的一个样本,故C不符合题意;
D、2000是样本容量,故D不符合题意;
故选:B.
【点评】本题考查了个体,总体,样本,样本容量等知识,解题的关键在于对知识的熟练掌握.
6.(2025 通辽二模)在一个扇形统计图中,有一扇形的面积占整个圆面积的20%,则这个扇形的圆心角为( )
A.15° B.36° C.54° D.72°
【考点】扇形统计图.
【专题】统计的应用;应用意识.
【答案】D
【分析】用360°乘以扇形的面积占整个圆面积的百分比即可得出答案.
【解答】解:这个扇形的圆心角为360°×20%=72°,
故选:D.
【点评】本题主要考查扇形统计图,扇形统计图是用整个圆表示总数用圆内各个扇形的大小表示各部分数量占总数的百分数.通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.用整个圆的面积表示总数(单位1),用圆的扇形面积表示各部分占总数的百分数.
7.(2025 天山区校级)下列调查方式中,合适的是( )
A.实施中小学生爱眼护牙行动后要了解全疆中小学生的视力情况,采用普查的方式
B.要了解外地游客对旅游景点“新疆喀什古城”的满意程度,采用抽样调查的方式
C.要保证“神舟十九号”载人飞船成功发射,对主要零部件的检查采用抽样调查的方式
D.要了解全疆初中学生的业余爱好,采用普查的方式
【考点】全面调查与抽样调查.
【专题】数据的收集与整理;数据分析观念.
【答案】B
【分析】根据抽样调查样本的代表性,可操作性结合具体问题情境综合进行判断即可.
【解答】解:A.实施中小学生爱眼护牙行动后要了解全疆中小学生的视力情,适合抽样调查,故本选项不符合题意;
B.要了解外地游客对旅游景点“新疆喀什古城”的满意程度,采用抽样调查的方式,节省人力、物力、财力,是合适的,故本选项符合题意;
C.要保证“神舟十九号”载人飞船成功发射,精确度要求高、事关重大,往往选用普查对主要零部件的检查采用适合调查,故本选项不符合题意;
D.了解全疆初中学生的业余爱好,进行一次全面的调查,费大量的人力物力是得不偿失的,采取抽样调查即可,故本选项不符合题意.
故选:B.
【点评】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
8.(2025 深圳二模)某校连续四个月开展了学科知识测试,并将测试成绩整理,绘制成如图所示的统计图(四次参加考试的学生人数不变),下列结论中不正确的是( )
A.共有500名学生参加测试
B.第2个月增长的“优秀”人数最多
C.从第1个月到第4个月,测试成绩“优秀”的学生人数在总人数中的占比逐渐增长
D.第4个月测试成绩“优秀”的学生人数达到65人
【考点】条形统计图;折线统计图.
【专题】统计的应用;应用意识.
【答案】D
【分析】根据条形统计图和折线统计图分别判断即可.
【解答】解:A.测试的学生人数为:10+250+150+90=500(名),原结论正确,故本选项不符合题意;
B.由折线统计图可知,第2月增长的“优秀”人数最多,原结论正确,故本选项不符合题意;
C.由折线统计图可知,从第1个月到第4个月,测试成绩“优秀”的学生人数在总人数中的占比逐周增长,原结论正确,故本选项不符合题意;
D.第4月测试成绩“优秀”的学生人数为:500×17%=85(人),原结论错误,故本选项符合题意.
故选:D.
【点评】本题考查的是条形统计图和折线统计图.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.注意读图获取信息、分析问题解决问题的能力.
9.(2025 石狮市)为加强体育锻炼,增强学生体魄,九(1)班同学举办了足球、篮球、乒乓球、跳绳四个活动项目.该班同学全员参与活动(每人仅参与一项),人数分布情况的扇形统计图和条形统计图(条形图的高度从高到低排列)如图所示,已知条形统计图不小心被撕了一块,则条形统计图中“( )”内应填的活动项目是( )
A.足球 B.乒乓球 C.篮球 D.跳绳
【考点】条形统计图;扇形统计图.
【专题】统计的应用;数据分析观念.
【答案】A
【分析】先求出总人数,再求出足球人数,继而得出另外两个项目的人数即可得出答案.
【解答】解:由扇形统计图知,总人数为5÷10%=50(人),
则足球人数为50×28%=14(人),
所以篮球或跳绳的人数为16人,
则另一种体育活动项目的人数为50﹣(14+16+5)=15(人),
所以人数从高到低排列,位于第三的是足球项自.
故选:A.
【点评】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.
10.(2025 衡阳县一模)随机抽取甲、乙两位同学一周内每天完成书面家庭作业的时间,并绘制了如图折线统计图.下列统计量中,最能反映出这两组数据之间差异的是( )
A.方差 B.平均数 C.众数 D.中位数
【考点】折线统计图;加权平均数;中位数;众数;方差;统计量的选择.
【专题】数据的收集与整理;应用意识.
【答案】A
【分析】根据统计图中的数据,可以判断哪个选项符合题意,本题得以解决.
【解答】解:由图可得,
60.7,
60.7,
故平均数不能反映出这两组数据之间差异,故选项B不符合题意;
甲和和乙的中位数和众数都相等,故不能反映出这两组数据之间差异,故选项C和D不符合题意;
由图象可得,甲的数据波动大,不稳定,乙数据波动小,比较稳定,能反映出这两组数据之间差异,故选项A符合题意;
故选:A.
【点评】本题考查折线统计图、中位数、众数、平均数、方差,解答本题的关键是明确题意,利用数形结合的思想解答.
二.填空题(共5小题)
11.(2025 门头沟区一模)某中学随机抽查了50名学生,了解他们每天完成家庭作业的时间,结果如表所示:
时间(小时) 0.5 1 1.5 2
人数 3 6 32 9
根据相关规定,初中学生每天完成家庭作业的时间不得超过1.5小时.如果该校共有学生2000人,估计该校学生完成家庭作业时间,符合要求的约有 1640 人.
【考点】用样本估计总体.
【专题】统计的应用;运算能力.
【答案】1640.
【分析】用总人数乘样本中每天完成家庭作业的时间不得超过1.5小时的人数所占比例即可.
【解答】解:估计该校学生完成家庭作业时间,符合要求的约有20001640(人).
故答案为:1640.
【点评】本题主要考查用样本估计总体,一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.
12.(2025 双柏县一模)云南是一个著名的旅游省份,有着丰富的文旅资源.某校准备组织七年级500名学生研学旅行,政教处周老师随机抽取了其中50名学生进行研学目的地意向调查,并将调查结果制成如图所示的统计图,估计七年级愿意去“云南大学”研学旅行的学生人数为 150人 .
【考点】用样本估计总体.
【专题】数据的收集与整理;数据分析观念.
【答案】150人.
【分析】用总人数乘样本中去“云南大学”的学生人数所占比例即可.
【解答】解:估计七年级愿意去“云南大学”研学旅行的学生人数为500150(人),
故选:150人.
【点评】本题主要考查用样本估计总体,一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.
13.(2025春 宝山区)某公司对某款新产品的生产成本进行调查,并绘制了如图扇形统计图,则材料费所在扇形的圆心角的度数是 144° .
【考点】扇形统计图.
【专题】统计的应用;应用意识.
【答案】144°.
【分析】用360°乘以材料费所占百分比即可.
【解答】解:由题意可得,材料费所在扇形的圆心角的度数是360°×(1﹣25%﹣35%)=144°.
故答案为:144°.
【点评】本题考查了扇形统计图,关键是求出材料费所占总数的百分数.
14.(2025 绥江县一模)如图是记录某足球队全年比赛结果(“胜”、“负”、“平”)的条形统计图和扇形统计图(不完整):根据图中信息,该足球队全年比赛胜了 30 场.
【考点】条形统计图;扇形统计图.
【专题】数据的收集与整理;统计的应用.
【答案】见试题解答内容
【分析】从两个统计图中可以得到“平”的有10场,占所有比赛结果的20%,从而可以求出表示=比赛的总场次,再根据“胜”的占比,可求出“胜”的场次.
【解答】解:10÷20%=50场,50×(1﹣20%﹣20%)=30场,
故答案为:30.
【点评】考查条形统计图、扇形统计图的意义和制作方法,从两个统计图中获取数量及数量之间的关系式正确解答的关键.
15.(2025 朝阳区一模)体育委员从全年级1000名学生中随机抽取了50名同学,统计了他们60秒跳绳的次数,并列出下面的频数分布表:
次数 80≤x<100 100≤x<120 120≤x<140 140≤x<160 160≤x≤180
频数 4 21 13 8 4
根据以上数据,估计该年级的1000名学生中60秒跳绳次数在100≤x<140范围的学生有 680 人.
【考点】频数(率)分布表;用样本估计总体.
【专题】数据的收集与整理;数据分析观念.
【答案】680.
【分析】用1000乘样本中60秒跳绳次数在100≤x<140范围的学生所占比例即可.
【解答】解:估计该年级的1000名学生中60秒跳绳次数在100≤x<140范围的学生有:
1000680(人),
故答案为:680.
【点评】本题考查频数分布表、用样本估计总体,解答本题的关键是正确列出算式.
三.解答题(共5小题)
16.(2025春 南湖区三模)某地政府为了旅游宣传,决定从甲、乙两家民宿中推选一家为“最美民宿”进行线上推广.现从两家的顾客中各随机抽取20名进行满意度调查打分(满分10分,只打整数分),并对分数进行整理、描述和分析,下面给出了部分信息.
(Ⅰ)甲民宿20名顾客的满意度分数为:
10,5,8,7,10,8,9,8,10,7,9,7,9,7,6,8,9,6,5,9;
(Ⅱ)乙民宿20名顾客的满意度分数条形统计图如图所示:
甲、乙民宿满意度分数统计表
民宿 平均分 众数 中位数 9分及9分以上人数所占百分比
甲 7.85 9 8 a%
乙 b 8 c 30%
(Ⅲ)甲、乙两家民宿的满意度分数的平均数、众数、中位数、9分及9分以上人数所占百分比如上表所示.
根据以上信息,解答下列问题:
(1)求出上述表中的a,b,c的值;
(2)春节假期期间,共有160人入住甲民宿,120人入住乙民宿,估计入住两家民宿的顾客能打9分及9分以上的人数共有多少人?
(3)根据以上表中信息,你会选择哪一家为“最美民宿”?用尽可能多的统计量说明理由.
【考点】条形统计图;加权平均数;中位数;众数;用样本估计总体.
【专题】统计的应用;数据分析观念;运算能力.
【答案】(1)a=40,b=7.75,c=8;
(2)100人;
(3)甲民宿,理由见解析.
【分析】(1)根据平均数和中位数的定义进行计算即可;
(2)根据甲民宿、乙民宿的顾客打9分及9分以上的人数所占的百分比估计总体中入住甲民宿、乙民宿的顾客打9分及9分以上的人数;
(3)根据平均数、众数和9分及9分以上的人数所占的百分比的大小比较得出答案.
【解答】解:(1)甲民宿9分及9分以上人数所占百分比a%100%=40%,
乙民宿的平均分b7.75(分),
将样本中20名顾客对乙民宿满意度分数从小到大排列后,处在中间位置的两个数的平均数为8,
因此中位数c=8;
答:a=40,b=7.75,c=8;
(2)160×40%+120×30%=64+36=100(人),
答:估计入住两家民宿的顾客能打9分及9分以上的人数共有100人;
(3)甲民宿,理由如下:
甲民宿顾客满意度分数的平均数、众数和9分及9分以上人数所占百分比都比乙的要大,因此选择甲民宿.
【点评】本题考查条形统计图,加权平均数、中位数、众数以及样本估计总体,掌握加权平均数、中位数、众数的计算方法是解决问题的关键.
17.(2025春 江阴市三模)某学校想了解学生家长对“双减”政策的认知情况,随机抽查了部分学生家长,将抽查的数据结果进行统计,并绘制出如图所示两幅不完整的统计图(A:不太了解,B:基本了解,C:比较了解,D:非常了解).根据图中提供的信息,解答下列问题:
(1)这次抽查的学生家长共有 50 人;
(2)在扇形统计图中,m的值为 40 ,C所在扇形的圆心角的度数为 144° ;
(3)请补全条形统计图;
(4)已知该学校共有3000名学生家长,估计对“双减”政策了解程度为“非常了解”的学生家长人数.
【考点】条形统计图;用样本估计总体;扇形统计图.
【专题】统计的应用;数据分析观念.
【答案】(1)50;
(2)40,144°;
(3)见解析;
(4)600人.
【分析】(1)根据A的人数除以占的百分比,得出调查总数即可;
(2)根据“比较了解”的有20人除以总人数即可得出m的值,用C的人数占被调查人数的比例乘以360°可得圆心角的度数;
(3)先用总人数乘以30%得出表示B的人数,将总人数减去A、B、C的人数即可得D的人数,补全条形统计图即可;
(4)用样本估算总体即可.
【解答】解:(1)这次抽样调查的家长有5÷10%=50(人),
故答案为:50;
(2)“比较了解”的有20人,
故100%=40%,
∴m=40,
“比较了解”部分所对应的圆心角是:360°×40%=144°,
故答案为:40,144°;
(3)表示“基本了解”的人数为:50×30%=15(人),表示“非常了解”的人数为:50﹣5﹣15﹣20=10(人),
补全图形如图:
(4)3000600(人),
答:估计对“双减”政策了解程度为“非常了解”的学生家长大约有600人.
【点评】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.
18.(2025春 仪征市三模)某中学科技兴趣小组为了解本校学生对我国航天科技的关注程度,在该校内进行了随机调查统计,将调查结果分为不关注、关注、比较关注、非常关注四类,回收、整理好全部调查问卷后,得到如图不完整的统计图.
(1)此次调查中接受调查的人数为 50 人;补全图1条形统计图;
(2)扇形统计图中“关注”对应扇形的圆心角为 43.2 °.
(3)该校共有1000人,根据调查结果估计该校“非堂关注”航天科技的人数多少人?
【考点】条形统计图;用样本估计总体;扇形统计图.
【专题】统计的应用;运算能力.
【答案】(1)50;
(2)43.2;
(3)320人.
【分析】(1)根据比较关注的人数和所占的百分比即可得出调查的总人数;用总人数减去其它调查的人数,求出非常关注的人数,从而补全条形统计图;
(2)360°乘以“关注”的比例即可得到“关注”对应扇形的圆心角度数;
(3)用1000乘样本中“非堂关注”航天科技的人数所占的百分比即可.
【解答】解:(1)此次调查中接受调查的人数为:24÷48%=50(人),
非常关注的人数有:50﹣4﹣6﹣24=16(人),
补全条形统计图如图所示:
故答案为:50;
(2)扇形统计图中“关注”对应扇形的圆心角为:360°43.2°;
故答案为:43.2;
(3)根据题意得:1000320(人),
答:估计该校“非堂关注”航天科技的人数为320人.
【点评】本题考查扇形统计图、条形统计图、用样本估计总体,从两个统计图中获取数量和数量之间的关系是解决问题的关键.
19.(2025 蜀山区二模)为进一步提升学生的安全意识,某校举办了安全知识竞赛,现从全校八、九年级学生中随机抽取20名学生竞赛成绩(百分制).数学兴趣小组对竞赛成绩进行统计分析,形成如下报告(不完整):
主题项目 校园安全知识竞赛成绩分析报告
数据收集 八年级学生成绩80,80,100,90,80, 70,70,80,70,90, 70,80,100,90,60, 80,90,80,90,90 九年级学生成绩 90,90,100,80,80, 60,70,80,60,100, 60,70,90,80,90, 90,90,70,100,90
数据整理与分析
八、九年级学生成绩分析表 统计量 年级平均数中位数众数方差八年级828080106九年级82n90166
任务1 ①补全条形统计图; ②求“扇形统计图”中80分所在扇形圆心角度数; ③直接写出成绩分析表中,九年级学生成绩的中位数n= 85 .
任务2 该校九年级学生共1200人,请估计成绩不低于80分的人数;
任务3 根据上述统计数据,你认为哪个年级的成绩更好?请说明理由.
根据所给信息,请完成以上所有任务.
【考点】条形统计图;中位数;众数;方差;用样本估计总体;扇形统计图.
【专题】数据的收集与整理;数据分析观念.
【答案】任务一:①见解答;②72°;③85;任务二:600人;任务三:八年级成绩更好,理由见解答(答案不唯一).
【分析】任务一:①根据所给数据找出80分人数,然后补全统计图;②先求出a值,再计算即可;③根据中位数的定义解答即可;
任务二:利用样本估计总体即可;
任务三:根据平均数和方差的意义解答即可.
【解答】解:任务一:①补全条形统计图,如图所示:
②“80分”所在扇形的圆心角的度数为:(1﹣15%﹣15%﹣15%﹣35%)×360°=72°;
③九年级学生成绩的中位数n85;
故答案为:85;
任务二:1200人×(1﹣15%﹣15%)=600(人),
答:估计成绩不低于80分的人数为600人;
任务三:我认为八年级成绩更好;
理由:由分析表可知两个年级的平均数相同,但八年级的方差小于九年级,所以八年级的成绩更稳定.
【点评】本题主要考查了中位数、众数、方差、统计图表、数据分析等内容,熟练掌握相关知识是解题的关键.
20.(2025 惠山区二模)在某校初三体育测试中(满分为40分),抽取部分学生的体育测试成绩,绘制了如下不完整的统计图,请根据图中的信息,解答下列问题:
(1)这次抽样一共抽取了 40 名学生,并补全条形统计图;
(2)扇形统计图中,“37分”所对应的圆心角为 45 度;
(3)已知该校初三年级共有1100名学生,根据抽样结果估计该校初三年级这次体育测试中成绩满分的学生人数.
【考点】条形统计图;用样本估计总体;扇形统计图.
【专题】统计的应用;数据分析观念.
【答案】(1)40;
(2)45;
(3)550人.
【分析】(1)根据“40分”的人数除以占比即可得出样本的容量,进而求“36分”的人数,补全统计图;
(2)根据“37分”的占比乘以360°即可求解;
(3)用样本估计总体,用初三年级共有1100名学生总人数乘以“40分”的比即可求解.
【解答】解:(1)本次调查的学生共有20÷50%=40(人),
“38分”的人数为40×15%=6(人),
“39分”的人数为40×15%=6(人),
“36分”的人数为40﹣5﹣6﹣6﹣20=3(人),
补全条形统计图如下:
故答案为:40;
(2)在扇形统计图中,“37分”对应的圆心角度数为360°45°,
故答案为:45;
(3)∵1100×50%×=550(人),
∴估计该校初三年级这次体育测试中成绩满分的学生人数约为550人.
【点评】本题主要考查了条形统计图和扇形统计图的综合运用,样本估计总体,读懂统计图从不同的统计图中得到必要的信息是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
