【中考押题预测】2025年中考数学核心考点考前冲刺 有理数(含解析)
文档属性
| 名称 | 【中考押题预测】2025年中考数学核心考点考前冲刺 有理数(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 224.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 16:06:47 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中考核心考点 有理数
一.选择题(共10小题)
1.(2025 扬州一模)我国古代著作《九章算术》在世界数学史上首次正式引入负数,若气温升高3℃时,气温变化记作+3℃,那么气温下降5℃时,气温变化记作( )
A.﹣8℃ B.﹣5℃ C.+5℃ D.+8℃
2.(2025春 永春县二模)若□=0,则□表示的数是( )
A.5 B. C. D.﹣5
3.(2025春 琼山区三模)下列各数中,与2025的和为0的是( )
A.2025 B.﹣2025 C. D.
4.(2025 长春一模)如图,在数轴上,点A、B分别表示数a、b,且a+b=0.若AB=4,则点A表示的数为( )
A.﹣2 B.0 C.2 D.﹣4
5.(2025春 瑶海区二模)数轴上A,B,C三点依次从左向右排列,表示的数分别为﹣2﹣x,2x﹣3和1,则x可能是( )
A.﹣2 B.﹣1 C.0 D.1
6.(2025 沂源县一模)DeepSeek团队在人工智能研发过程中坚持自主创新.实验数括显示,他们的模型训练效率达到了惊人的2.4×1015次浮点运算/秒.若某次连续训练持续了1.2×104秒,则总共完成了多少次浮点运算( )
A.2.48×1019 B.2.88×1018 C.2.88×1019 D.2.88×1020
7.(2025 辽阳一模)当气体的温度降低到一定程度的时候就会变成液体,人们把这种变化过程叫做液化.初中物理就介绍了下面几种常见气体液化时的温度(标准大气压):
气体 氧气 氨气 氢气 氮气
液化温度/℃ ﹣183 ﹣33.5 ﹣253 ﹣196
其中液化温度最低的气体是( )
A.氧气 B.氨气 C.氢气 D.氮气
8.(2025 文山州二模)《九章算术》中注有“今两算得失相反,要令正负以名之”.意思是:今有两数若其意义相反,则分别叫做正数和负数.若升高30米记作+30米,那么﹣5米表示( )
A.上升5米 B.下降35米 C.上升25米 D.下降5米
9.(2025 海淀区一模)为进一步提高义务教育质量,某地区今年义务教育财政预算支出比去年上调了5%.已知该地区去年的义务教育财政预算支出约为3.8×1010元,则今年的义务教育财政预算支出约为( )
A.3.8×1010元 B.5.7×1010元
C.3.99×1010元 D.3.99×1011元
10.(2025 孝义市一模)约公元820年,中亚细亚数学家阿尔一花拉子米写了一本代数书,重点论述怎样解方程.这本书的拉丁文译本取名为《对消与还原》,其中,“对消”指的是“合并同类项”,“还原”指的是“移项”.我国古代数学著作《九章算术》的“方程”章,更早使用了“对消”和“还原”的方法;体现的数学思想是( )
A.分类思想 B.数形结合思想
C.转化思想 D.公理化思想
二.填空题(共5小题)
11.(2025春 江北区二模)规定:对于任意有理数a与b,满足,如5*3=3×5﹣3=12,.若有理数x满足x*3=15,则x的值为 .
12.(2025春 长寿区二模)为了丰富学生课外小组活动,培养学生动手操作能力,王老师让学生把6m长的彩绳剪成2m或1m的彩绳(允许只剪成其中一种长度),用来做手工编织,在不造成浪费的前提下,你有 种不同的剪法.
13.(2025 房山区一模)某工厂需要生产三种产品A,B,C,每种产品的生产分为两个阶段:第一阶段是制作,第二阶段是包装,每种产品在每个阶段所需的时间(单位:小时)如表所示:
A B C
制作 10 8 12
包装 6 10 8
若由一名工人单独完成三种产品的生产、那么总共需要 小时;若由两位工人合作完成这三种产品的生产,每个阶段由一个人单独完成,每种产品制作完才可以包装,那么完成这三种产品的生产最少需要 小时.
14.(2025春 思明区二模)学校组织学生参加木艺艺术品加工劳动实践活动,已知某木艺艺术品加工完成共需A、B、C、D、E、F、G七道工序,加工要求如下:①工序C、D须在工序A完成后进行,工序E须在工序B、D都完成后进行,工序F须在工序C、D都完成后进行;②一道工序只能由一名学生完成,此工序完成后该学生才能进行其他工序;③各道工序所需时间如下表所示:
工序 A B C D E F G
所需时间/分钟 9 9 7 9 7 10 2
若由两名学生合作完成此木艺艺术品的加工,则最少需要的时间是 分钟.
15.(2025 湖南)小华有一个密码小宝箱,他忘记6位数密码的一部分8904□2,且密码每一个数字和其他数字都不重复.现在小华想要打开他的宝箱,最多需要尝试 次.
三.解答题(共5小题)
16.(2025春 锡山区二模)定义:使a﹣b=ab﹣1成立的一对有理数a,b称为“共生有理数对”,记作(a,b).例如:因为﹣2﹣1=﹣2×1﹣1,所以(﹣2,1)是“共生有理数对”.
(1)判断数对是否为“共生有理数对”,并说明理由;
(2)若5是“共生有理数对”中的一个有理数,则这个“共生有理数对”为 ;
(3)若数对(m,n)是“共生有理数对”,且m=n+2,求(﹣2)mn的值.
17.(2025春 新华区二模)对于任意四个有理数a、b、c、d,可以组成两个有理数对(a,b)与(c,d),我们规定:(a,b)*(c,d)=a2+c2﹣bd.例如:(1,2)*(3,4)=12+32﹣2×4=2.
(1)求(﹣3,2)*(2,﹣1)的值;
(2)若2x+y=10,且(3x+y,2x2+3y2)*(x﹣3y,3)=80,求xy的值.
18.(2025 定海区一模)综合与实践
有趣的“乘法运算”
小明在学完《整式的乘法》后对一类特殊的乘法运算进行了探究.
【算法界定】这里的“乘法运算”指的是末位数字相同,首位数字和为十的两位数相乘.
【算法介绍】两数首位数字相乘再加上末位的数字作为“前积”,末位数字的平方作为“后积”,前积乘以100加上后积就是得数.
例:14×94=100×(1×9+4)+42=1316,前积是13,后积是16
(1)26×86=100×(2×8+6)+62=2236,前积是 ,后积是 ;
【初探算法】仿照例题,写出下面两数相乘的运算过程及结果.
(2)25×85= = ;
【推理算法】记两位数分别是和,且a+b=10,其中.
(3)请写出算法介绍中的运算规律,并加以证明.
19.(2025春 青秀区二模)【知识背景】
某学校开展科技节活动,在操场搭建一个科技展台,并安排了施工小组按设计图制作展板.
【步骤实施】请同学们完成以下四个任务.
任务一 截取一个边长为20dm的正方形ABCD,则这个正方形ABCD的面积为 dm2.
任务二 用4个相同的小正方形拼成一个面积为40dm2的大正方形EFGH,小正方形的边长为 dm2.
任务三 另有一块面积为225dm2的正方形板材,要从这块板材裁出一块面积为105dm2的长方形PQMN,使长方形的长与宽的比为5:3,问能否裁出?请说明理由.
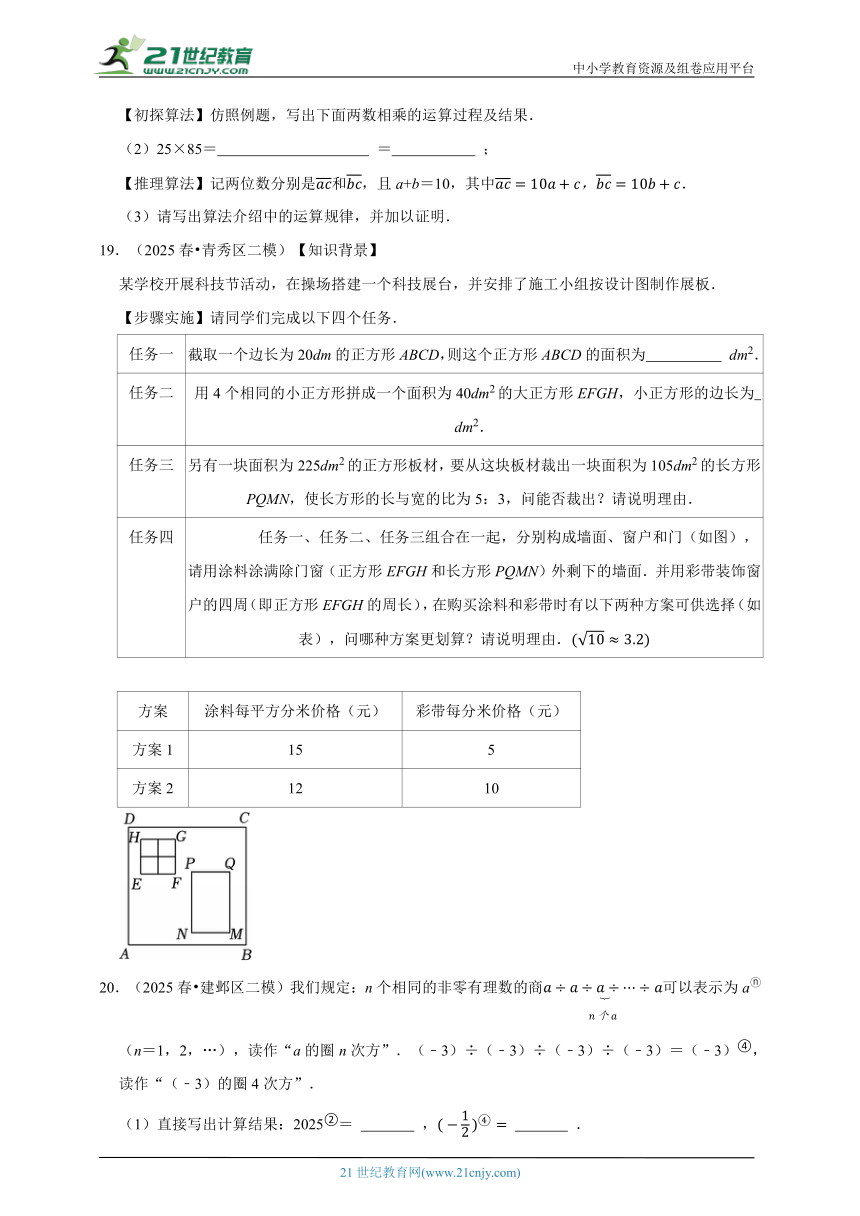
任务四
任务一、任务二、任务三组合在一起,分别构成墙面、窗户和门(如图),请用涂料涂满除门窗(正方形EFGH和长方形PQMN)外剩下的墙面.并用彩带装饰窗户的四周(即正方形EFGH的周长),在购买涂料和彩带时有以下两种方案可供选择(如表),问哪种方案更划算?请说明理由.
方案 涂料每平方分米价格(元) 彩带每分米价格(元)
方案1 15 5
方案2 12 10
20.(2025春 建邺区二模)我们规定:n个相同的非零有理数的商可以表示为a (n=1,2,…),读作“a的圈n次方”.(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)=(﹣3)④,读作“(﹣3)的圈4次方”.
(1)直接写出计算结果:2025②= , .
(2)若n为任意正整数,下列结论:①任何非零整数的圈n次方小于或等于本身;②负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数;③互为相反数的两个数的圈n次方互为相反数;④互为倒数的两个数的圈n次方互为倒数;⑤圈n次方等于它本身的数是1或﹣1.其中所有正确结论的序号是 .
(3)试说明a ÷a =am﹣n(m,n为正整数,且m>n).
中考核心考点 有理数
参考答案与试题解析
一.选择题(共10小题)
1.(2025 扬州一模)我国古代著作《九章算术》在世界数学史上首次正式引入负数,若气温升高3℃时,气温变化记作+3℃,那么气温下降5℃时,气温变化记作( )
A.﹣8℃ B.﹣5℃ C.+5℃ D.+8℃
【考点】正数和负数.
【专题】实数;运算能力.
【答案】B
【分析】在一对具有相反意义的量中,规定其中一个为正,则另一个就用负表示.据此求解即可.
【解答】解:根据题意,气温下降5℃时,气温变化记作﹣5℃.
故选:B.
【点评】本题考查了正负数在现实生活的应用,熟练掌握正负数的意义是解答本题的关键.
2.(2025春 永春县二模)若□=0,则□表示的数是( )
A.5 B. C. D.﹣5
【考点】有理数的加法.
【专题】实数;运算能力.
【答案】B
【分析】根据加减法是互逆运算,列式计算.
【解答】解:∵0﹣(),
故选:B.
【点评】本题考查了有理数的加法,理解加减法是互逆运算是解题的关键.
3.(2025春 琼山区三模)下列各数中,与2025的和为0的是( )
A.2025 B.﹣2025 C. D.
【考点】相反数.
【专题】实数;运算能力.
【答案】B
【分析】根据题意列式0﹣2025求值即可.
【解答】解:根据有理数减法运算法则得:0﹣2025=﹣2025,
故答案为:B.
【点评】本题考查有理数的减法计算法则:减去一个数等于加上这个数的相反数是关键.
4.(2025 长春一模)如图,在数轴上,点A、B分别表示数a、b,且a+b=0.若AB=4,则点A表示的数为( )
A.﹣2 B.0 C.2 D.﹣4
【考点】数轴.
【专题】实数;运算能力.
【答案】A
【分析】根据AB=4得到点A和点B到原点的距离之和为4,根据相反数的性质可知点A和点B分别位于原点两侧,到原点的距离相等,即可得到答案.
【解答】解:∵点A和点B到原点的距离之和为4,a+b=0,
∴点A到原点的距离为2个单位,且在原点左侧,
即点A表示的数为﹣2.
故选:A.
【点评】本题主要考查相反数的定义和性质、数轴上两点之间的距离等知识.熟练掌握以上知识点是关键.
5.(2025春 瑶海区二模)数轴上A,B,C三点依次从左向右排列,表示的数分别为﹣2﹣x,2x﹣3和1,则x可能是( )
A.﹣2 B.﹣1 C.0 D.1
【考点】数轴.
【专题】实数;运算能力.
【答案】D
【分析】根据数轴上点从左到右数逐渐增大的性质,列出不等式组,求解x的取值范围,再对照选项判断.
【解答】解:因为三点依次从左向右排列,所以﹣2﹣x<2x﹣3且2x﹣3<1.
解不等式﹣2﹣x<2x﹣3:得,
解不等式2x﹣3<1:解得x<2,
∴x的取值范围是,
故选:D.
【点评】本题考查了数轴上数的大小关系与不等式的求解,解题的关键是根据数轴上点的左右顺序列出不等式组并求解.
6.(2025 沂源县一模)DeepSeek团队在人工智能研发过程中坚持自主创新.实验数括显示,他们的模型训练效率达到了惊人的2.4×1015次浮点运算/秒.若某次连续训练持续了1.2×104秒,则总共完成了多少次浮点运算( )
A.2.48×1019 B.2.88×1018 C.2.88×1019 D.2.88×1020
【考点】科学记数法—表示较大的数.
【专题】实数;运算能力.
【答案】C
【分析】根据有理数的运算法则求解.
【解答】解:2.4×1015×1.2×104=2.88×1019,
故选:C.
【点评】本题考查了科学记数法,掌握有理数的运算法则是解题的关键.
7.(2025 辽阳一模)当气体的温度降低到一定程度的时候就会变成液体,人们把这种变化过程叫做液化.初中物理就介绍了下面几种常见气体液化时的温度(标准大气压):
气体 氧气 氨气 氢气 氮气
液化温度/℃ ﹣183 ﹣33.5 ﹣253 ﹣196
其中液化温度最低的气体是( )
A.氧气 B.氨气 C.氢气 D.氮气
【考点】有理数大小比较;正数和负数.
【专题】实数;数感.
【答案】C
【分析】先将液化温度从低到高排序,然后找出最低温度.
【解答】解:∵﹣253℃<﹣196℃<﹣183℃<﹣33.5℃,∴液化温度最低的气体是氢气.
故选:C.
【点评】本题考查了有理数比较大小,掌握比较有理数大小的方法是关键.
8.(2025 文山州二模)《九章算术》中注有“今两算得失相反,要令正负以名之”.意思是:今有两数若其意义相反,则分别叫做正数和负数.若升高30米记作+30米,那么﹣5米表示( )
A.上升5米 B.下降35米 C.上升25米 D.下降5米
【考点】正数和负数;数学常识.
【专题】实数;符号意识.
【答案】D
【分析】利用正数和负数的意义,数字常识解答.
【解答】解:升高30米记作+30米,那么﹣5米表示下降5米.
故选:D.
【点评】本题考查了正数和负数,数字常识,解题的关键是掌握正数和负数的意义,数字常识.
9.(2025 海淀区一模)为进一步提高义务教育质量,某地区今年义务教育财政预算支出比去年上调了5%.已知该地区去年的义务教育财政预算支出约为3.8×1010元,则今年的义务教育财政预算支出约为( )
A.3.8×1010元 B.5.7×1010元
C.3.99×1010元 D.3.99×1011元
【考点】科学记数法—表示较大的数.
【专题】实数;数感.
【答案】C
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:3.8×1010×(1+5%)=3.99×1010,
故选:C.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
10.(2025 孝义市一模)约公元820年,中亚细亚数学家阿尔一花拉子米写了一本代数书,重点论述怎样解方程.这本书的拉丁文译本取名为《对消与还原》,其中,“对消”指的是“合并同类项”,“还原”指的是“移项”.我国古代数学著作《九章算术》的“方程”章,更早使用了“对消”和“还原”的方法;体现的数学思想是( )
A.分类思想 B.数形结合思想
C.转化思想 D.公理化思想
【考点】数学常识.
【专题】推理填空题;推理能力.
【答案】C
【分析】由“对消”和“还原”的方法,即“合并同类项”,“移项”,即可得体现的数学思想是转化思想.
【解答】解:“对消”和“还原”的方法,即“合并同类项”,“移项”,体现的数学思想是转化思想.
故选:C.
【点评】本题主要考查了数学思想,解题关键是正确判断.
二.填空题(共5小题)
11.(2025春 江北区二模)规定:对于任意有理数a与b,满足,如5*3=3×5﹣3=12,.若有理数x满足x*3=15,则x的值为 6 .
【考点】有理数的混合运算.
【专题】新定义;运算能力.
【答案】6.
【分析】根据新定义的运算进行列方程,再解方程即可.
【解答】解:由新定义可得:①当x≥3时,
3x﹣3=15,
解得:x= 6;
②当x<3时,
x﹣3×3=15,
解得:x= 24(舍去).
故答案为:6.
【点评】本题考查了有理数的混合运算,解题的关键是根据新定义的运算进行解答.
12.(2025春 长寿区二模)为了丰富学生课外小组活动,培养学生动手操作能力,王老师让学生把6m长的彩绳剪成2m或1m的彩绳(允许只剪成其中一种长度),用来做手工编织,在不造成浪费的前提下,你有 4 种不同的剪法.
【考点】有理数的加法.
【专题】计算题;运算能力.
【答案】4.
【分析】根据题意列出方程,再解方程即可.
【解答】解:设截成2m的彩绳x根,1m的彩绳y根,
由题意可得2x+y=6,
因为不造成浪费,
∴x,y是正整数,
x=0,y=6;
x=1,y=4;
x=2,y=2;
x=3,y=0.
则共有4种不同截法,
故答案为:4.
【点评】本题考查了有理数的加法,解题的关键是根据题意列出方程.
13.(2025 房山区一模)某工厂需要生产三种产品A,B,C,每种产品的生产分为两个阶段:第一阶段是制作,第二阶段是包装,每种产品在每个阶段所需的时间(单位:小时)如表所示:
A B C
制作 10 8 12
包装 6 10 8
若由一名工人单独完成三种产品的生产、那么总共需要 54 小时;若由两位工人合作完成这三种产品的生产,每个阶段由一个人单独完成,每种产品制作完才可以包装,那么完成这三种产品的生产最少需要 26 小时.
【考点】有理数的混合运算.
【专题】实数;运算能力.
【答案】54,26.
【分析】本题主要考查对生产时间的计算,第一问是单人完成生产的总时间计算,直接将三种产品制作和包装时间累加即可;第二问是两人合作的最短时间计算,关键在于合理分配任务,让两人的工作时间尽可能均衡且不出现等待时间.
【解答】解:一名工人单独完成,总时间为三种产品制作时间与包装时间之和,即(10+8+12)+(6+10+8)=30+24=54小时.
设两名工人为甲、乙.
为使时间最短,安排甲按B、A、C顺序制作产品,乙负责包装.
甲制作产品B用时8小时,此时乙等待8小时候开始包装B,用时10小时,
甲接着制作产品A用时10小时,此时乙包装B还剩10﹣8=2小时,甲制作A过程中乙完成B包装后开始包装A,乙包装A用时6小时,在甲制作A的10小时内乙可完成A包装;
甲再制作产品C用时12小时,乙包装C用时8小时.
整个过程总用时为甲制作产品BAC的时间加上乙包装产品C的时间,即8+10+12﹣(10﹣8))﹣(6)+8=26小时.
故答案为:54,26.
【点评】本题将实际生产场景转化为数学计算问题,既考查了基本的加法运算能力,又对逻辑规划能力有一定要求.第一问较为基础,是简单的时间求和.第二问难度提升,需要思考如何合理安排任务流程以达到最短时间,这种问题有助于培养学生的统筹规划思维,在实际生产生活中也有很强的应用价值,可引导学生将数学知识与实际应用相结合.
14.(2025春 思明区二模)学校组织学生参加木艺艺术品加工劳动实践活动,已知某木艺艺术品加工完成共需A、B、C、D、E、F、G七道工序,加工要求如下:①工序C、D须在工序A完成后进行,工序E须在工序B、D都完成后进行,工序F须在工序C、D都完成后进行;②一道工序只能由一名学生完成,此工序完成后该学生才能进行其他工序;③各道工序所需时间如下表所示:
工序 A B C D E F G
所需时间/分钟 9 9 7 9 7 10 2
若由两名学生合作完成此木艺艺术品的加工,则最少需要的时间是 28 分钟.
【考点】有理数的混合运算.
【专题】实数;运算能力.
【答案】28.
【分析】假设这两名学生为甲、乙,推导出甲学生做工序A,乙学生做工序B,需要9分钟,然后甲学生做工序D,同时乙学生做工序C,乙学生工序C完成后接着做工序G,最后甲学生做工序E,乙学生同时做工序F,据此进一步解答.
【解答】解:假设这两名学生为甲,乙,
∵工序C、D须在工序A完成后进行,工序E须在工序B、D都完成后进行,且工序A,B都需要9分钟完成,
∴甲学生做工序A,乙学生做工序B,需要9分钟,
然后甲学生做工序D,同时乙学生做工序C,
乙学生工序C完成后接着做工序G,
此时需要9分钟,
最后甲学生做工序E,乙学生同时做工序F,
此时需要10分钟,
则9+9+10=28(分钟),
即若由两名学生合作完成此木艺艺术品的加工,则最少需要28分钟.
故答案为:28.
【点评】本题考查有理数的运算,结合题意进行正确的推理是解题的关键.
15.(2025 湖南)小华有一个密码小宝箱,他忘记6位数密码的一部分8904□2,且密码每一个数字和其他数字都不重复.现在小华想要打开他的宝箱,最多需要尝试 5 次.
【考点】有理数的混合运算.
【专题】推理填空题;推理能力.
【答案】5.
【分析】根据题意即可找到可以填的数字.
【解答】解:根据密码每一个数字和其他数字都不重复,
所以方框里只能填:1,3,5,6,7,
故答案为:5.
【点评】本题考查了有理数的混合运算,解题的关键是根据题意找到可以填的数字.
三.解答题(共5小题)
16.(2025春 锡山区二模)定义:使a﹣b=ab﹣1成立的一对有理数a,b称为“共生有理数对”,记作(a,b).例如:因为﹣2﹣1=﹣2×1﹣1,所以(﹣2,1)是“共生有理数对”.
(1)判断数对是否为“共生有理数对”,并说明理由;
(2)若5是“共生有理数对”中的一个有理数,则这个“共生有理数对”为 (5,1)或(﹣1,5) ;
(3)若数对(m,n)是“共生有理数对”,且m=n+2,求(﹣2)mn的值.
【考点】有理数的混合运算.
【专题】实数;运算能力.
【答案】(1)不是;(2)(5,1)或(﹣1,5);(3)﹣8.
【分析】(1)代入定义式,看等式是否成立即可;
(2)设这个共生数对为(5,a)或(a,5),代入定义式,求出a,表示出数对即可;
(3)数对(m,n)是“共生有理数对”,所以m﹣n=mn﹣1,因为m=n+2,两式联立求出mn=3,求出结果即可.
【解答】解:(1),
,
,
数对不是“共生有理数对”.
(2)设这个共生数对为(5,a)或(a,5).
当数对为(5,a)时,
5﹣a=5a﹣1,
可得:a=1;
这个数对时(5,1);
当数对为(a,5)时,
a﹣5=5a﹣1,
解得:a=﹣1,
这个数对时(﹣1,5).
故答案为:(5,1)或(﹣1,5).
(3)因为(m,n)是“共生有理数对”,
所以m﹣n=mn﹣1,
因为m=n+2,
所以n+2﹣n=mn﹣1,
得:mn=3,
(﹣2)mn=(﹣2)3=﹣8.
【点评】本题考查了有理数的混合运算,解决本题的关键是按照“共生有理数对”的公式计算.
17.(2025春 新华区二模)对于任意四个有理数a、b、c、d,可以组成两个有理数对(a,b)与(c,d),我们规定:(a,b)*(c,d)=a2+c2﹣bd.例如:(1,2)*(3,4)=12+32﹣2×4=2.
(1)求(﹣3,2)*(2,﹣1)的值;
(2)若2x+y=10,且(3x+y,2x2+3y2)*(x﹣3y,3)=80,求xy的值.
【考点】有理数的混合运算.
【专题】计算题;整式;运算能力.
【答案】(1)15;(2)5.
【分析】(1)因为(a,b)*(c,d)=a2+c2﹣bd,所以(﹣3,2)*(2,﹣1)=(﹣3)2+22﹣2×(﹣1),求出结果即可;
(2)因为(a,b)*(c,d)=a2+c2﹣bd,(3x+y,2x2+3y2)*(x﹣3y,3)=80,所以即(3x+y)2+(x﹣3y)2﹣3(2x2+3y2)=80,
得4x2+y2=80,因为2x+y=10,所以sxy=(2x+y)2﹣(4x2+y2)=20,求出xy=5.
【解答】解:(1)(﹣3,2)*(2,﹣1)
=(﹣3)2+22﹣2×(﹣1)
=9+4+2
=15;
(2)因为(3x+y,2x2+3y2)*(x﹣3y,3)=80,
即(3x+y)2+(x﹣3y)2﹣3(2x2+3y2)=80,
得4x2+y2=80,
因为2x+y=10,
所以(2x+y)2﹣(4x2+y2)
=4x2+y2+4xy﹣4x2﹣y2
=4xy,
4xy=102﹣80=20,
xy=5.
【点评】本题考查了有理数的混合运算,解决本题的关键是根据示例的运算法则计算.
18.(2025 定海区一模)综合与实践
有趣的“乘法运算”
小明在学完《整式的乘法》后对一类特殊的乘法运算进行了探究.
【算法界定】这里的“乘法运算”指的是末位数字相同,首位数字和为十的两位数相乘.
【算法介绍】两数首位数字相乘再加上末位的数字作为“前积”,末位数字的平方作为“后积”,前积乘以100加上后积就是得数.
例:14×94=100×(1×9+4)+42=1316,前积是13,后积是16
(1)26×86=100×(2×8+6)+62=2236,前积是 22 ,后积是 36 ;
【初探算法】仿照例题,写出下面两数相乘的运算过程及结果.
(2)25×85= 100(2×8+5)+52 = 2125 ;
【推理算法】记两位数分别是和,且a+b=10,其中.
(3)请写出算法介绍中的运算规律,并加以证明.
【考点】有理数的混合运算.
【专题】阅读型;规律型;实数;运算能力;推理能力.
【答案】(1)22;36;(2)100×(2×8+5)+52;2125;(3)算法介绍中的运算规律为:记两位数分别是和,且a+b=10,其中,那么100(ab+c)+c2.证明见解析.
【分析】(1)利用题干中的示例的方法解答即可;
(2)仿照例题的解答过程运算即可;
(3)利用多项式乘以多项式的法则运算即可.
【解答】解:(1)∵26×86=100×(2×8+6)+62=2236,
∴前积是22,后积是36.
故答案为:22;36;
(2)25×85=100×(2×8+5)+52=2125.
故答案为:100×(2×8+5)+52;2125;
(3)算法介绍中的运算规律为:记两位数分别是和,且a+b=10,其中,那么100(ab+c)+c2.
证明:∵,
∴
=(10a+c)(10b+c)
=100ab+10(a+b)c+c2,
∵a+b=10,
∴
=100ab+100c+c2
=100(ab+c)+c2.
【点评】本题主要考查了有理数的混合运算,数字变化的规律,本题是阅读型题目,熟练掌握题干中的方法并熟练应用是解题的关键.
19.(2025春 青秀区二模)【知识背景】
某学校开展科技节活动,在操场搭建一个科技展台,并安排了施工小组按设计图制作展板.
【步骤实施】请同学们完成以下四个任务.
任务一 截取一个边长为20dm的正方形ABCD,则这个正方形ABCD的面积为 400 dm2.
任务二 用4个相同的小正方形拼成一个面积为40dm2的大正方形EFGH,小正方形的边长为 dm2.
任务三 另有一块面积为225dm2的正方形板材,要从这块板材裁出一块面积为105dm2的长方形PQMN,使长方形的长与宽的比为5:3,问能否裁出?请说明理由.
任务四
任务一、任务二、任务三组合在一起,分别构成墙面、窗户和门(如图),请用涂料涂满除门窗(正方形EFGH和长方形PQMN)外剩下的墙面.并用彩带装饰窗户的四周(即正方形EFGH的周长),在购买涂料和彩带时有以下两种方案可供选择(如表),问哪种方案更划算?请说明理由.
方案 涂料每平方分米价格(元) 彩带每分米价格(元)
方案1 15 5
方案2 12 10
【考点】有理数的混合运算;算术平方根.
【专题】实数;矩形 菱形 正方形;运算能力;推理能力.
【答案】任务一:400;任务二:;任务三:能够裁出.理由见解析;任务四:方案2更划算,理由见解析.
【分析】任务一.利用正方形的面积公式解答即可;
任务二.利用正方形的面积公式和算术平方根的意义解答即可;
任务三.设长方形的长为5x dm,则宽为3x dm,利用长方形的面积公式求得长方形的长,通过比较与正方形的边长的大小得出结论;
任务四.通过计算两个方案的费用,比较大小即可得出结论.
【解答】解:任务一:∵正方形ABCD的边长为20dm,
∴这个正方形ABCD的面积为400dm2.
故答案为:400;
任务二:∵4个相同的小正方形拼成一个面积为40dm2的大正方形EFGH,
∴每个小正方形的面积为10dm2,
∴小正方形的边长为dm.
故答案为:;
任务三:能够裁出.理由:
∵长方形的长与宽的比为5:3,
∴设长方形的长为5x dm,则宽为3x dm,
∵长方形的面积为105dm2,
∴5x 3x=105,
∵x>0,
∴x,
∴长方形的长为5dm,则宽为3dm,
∵正方形的面积为225dm2,
∴正方形的边长为15dm,
∵5,15,
∴515,
∴能够裁出.
任务四:方案2更划算,理由:
由题意:除门窗(正方形EFGH和长方形PQMN)外剩下的墙面面积为:400﹣40﹣105=255(dm2),
正方形EFGH的周长为88×3.2=25.6(dm),
利用方案1的费用为:255×15+25.6×5=3825+128=3953(元),
利用方案2的费用为:255×12+25.6×10=3060+256=3316(元).
∵3953>3316,
∴方案2更划算.
【点评】本题主要考查了正方形的性质,有理数的混合运算,算术平方根的应用,熟练掌握上述法则与性质是解题的关键.
20.(2025春 建邺区二模)我们规定:n个相同的非零有理数的商可以表示为a (n=1,2,…),读作“a的圈n次方”.(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)=(﹣3)④,读作“(﹣3)的圈4次方”.
(1)直接写出计算结果:2025②= 1 , 4 .
(2)若n为任意正整数,下列结论:①任何非零整数的圈n次方小于或等于本身;②负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数;③互为相反数的两个数的圈n次方互为相反数;④互为倒数的两个数的圈n次方互为倒数;⑤圈n次方等于它本身的数是1或﹣1.其中所有正确结论的序号是 ②④ .
(3)试说明a ÷a =am﹣n(m,n为正整数,且m>n).
【考点】有理数的乘方;正数和负数;有理数;有理数的除法.
【专题】实数;运算能力.
【答案】(1)1,4;
(2)②④;
(3)见解答.
【分析】(1)根据新规定求解;
(2)根据新规定求解;
(3)根据新规定和同底数幂的运算证明.
【解答】解:(1)∵2025②=2025÷2025=1, () =4,
故答案为:1,4;
(2)①∵(﹣1)÷(﹣1)=1>﹣1,
故①是错误的;
②奇数个负数相除还是负数,偶数个负数相除是正数,
故②是正确的;
③∵(﹣2)÷(﹣2)=1,2÷2=1,
故③是错误的;
④∵a ,() =an﹣2,
故④是正确的;
⑤圈n次方等于它本身的数是1,
故⑤是错误的;
故答案为:②④.
(3)证明:原式am﹣n.
【点评】本题考查了新运算,理解新运算和掌握幂的运算法则是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考核心考点 有理数
一.选择题(共10小题)
1.(2025 扬州一模)我国古代著作《九章算术》在世界数学史上首次正式引入负数,若气温升高3℃时,气温变化记作+3℃,那么气温下降5℃时,气温变化记作( )
A.﹣8℃ B.﹣5℃ C.+5℃ D.+8℃
2.(2025春 永春县二模)若□=0,则□表示的数是( )
A.5 B. C. D.﹣5
3.(2025春 琼山区三模)下列各数中,与2025的和为0的是( )
A.2025 B.﹣2025 C. D.
4.(2025 长春一模)如图,在数轴上,点A、B分别表示数a、b,且a+b=0.若AB=4,则点A表示的数为( )
A.﹣2 B.0 C.2 D.﹣4
5.(2025春 瑶海区二模)数轴上A,B,C三点依次从左向右排列,表示的数分别为﹣2﹣x,2x﹣3和1,则x可能是( )
A.﹣2 B.﹣1 C.0 D.1
6.(2025 沂源县一模)DeepSeek团队在人工智能研发过程中坚持自主创新.实验数括显示,他们的模型训练效率达到了惊人的2.4×1015次浮点运算/秒.若某次连续训练持续了1.2×104秒,则总共完成了多少次浮点运算( )
A.2.48×1019 B.2.88×1018 C.2.88×1019 D.2.88×1020
7.(2025 辽阳一模)当气体的温度降低到一定程度的时候就会变成液体,人们把这种变化过程叫做液化.初中物理就介绍了下面几种常见气体液化时的温度(标准大气压):
气体 氧气 氨气 氢气 氮气
液化温度/℃ ﹣183 ﹣33.5 ﹣253 ﹣196
其中液化温度最低的气体是( )
A.氧气 B.氨气 C.氢气 D.氮气
8.(2025 文山州二模)《九章算术》中注有“今两算得失相反,要令正负以名之”.意思是:今有两数若其意义相反,则分别叫做正数和负数.若升高30米记作+30米,那么﹣5米表示( )
A.上升5米 B.下降35米 C.上升25米 D.下降5米
9.(2025 海淀区一模)为进一步提高义务教育质量,某地区今年义务教育财政预算支出比去年上调了5%.已知该地区去年的义务教育财政预算支出约为3.8×1010元,则今年的义务教育财政预算支出约为( )
A.3.8×1010元 B.5.7×1010元
C.3.99×1010元 D.3.99×1011元
10.(2025 孝义市一模)约公元820年,中亚细亚数学家阿尔一花拉子米写了一本代数书,重点论述怎样解方程.这本书的拉丁文译本取名为《对消与还原》,其中,“对消”指的是“合并同类项”,“还原”指的是“移项”.我国古代数学著作《九章算术》的“方程”章,更早使用了“对消”和“还原”的方法;体现的数学思想是( )
A.分类思想 B.数形结合思想
C.转化思想 D.公理化思想
二.填空题(共5小题)
11.(2025春 江北区二模)规定:对于任意有理数a与b,满足,如5*3=3×5﹣3=12,.若有理数x满足x*3=15,则x的值为 .
12.(2025春 长寿区二模)为了丰富学生课外小组活动,培养学生动手操作能力,王老师让学生把6m长的彩绳剪成2m或1m的彩绳(允许只剪成其中一种长度),用来做手工编织,在不造成浪费的前提下,你有 种不同的剪法.
13.(2025 房山区一模)某工厂需要生产三种产品A,B,C,每种产品的生产分为两个阶段:第一阶段是制作,第二阶段是包装,每种产品在每个阶段所需的时间(单位:小时)如表所示:
A B C
制作 10 8 12
包装 6 10 8
若由一名工人单独完成三种产品的生产、那么总共需要 小时;若由两位工人合作完成这三种产品的生产,每个阶段由一个人单独完成,每种产品制作完才可以包装,那么完成这三种产品的生产最少需要 小时.
14.(2025春 思明区二模)学校组织学生参加木艺艺术品加工劳动实践活动,已知某木艺艺术品加工完成共需A、B、C、D、E、F、G七道工序,加工要求如下:①工序C、D须在工序A完成后进行,工序E须在工序B、D都完成后进行,工序F须在工序C、D都完成后进行;②一道工序只能由一名学生完成,此工序完成后该学生才能进行其他工序;③各道工序所需时间如下表所示:
工序 A B C D E F G
所需时间/分钟 9 9 7 9 7 10 2
若由两名学生合作完成此木艺艺术品的加工,则最少需要的时间是 分钟.
15.(2025 湖南)小华有一个密码小宝箱,他忘记6位数密码的一部分8904□2,且密码每一个数字和其他数字都不重复.现在小华想要打开他的宝箱,最多需要尝试 次.
三.解答题(共5小题)
16.(2025春 锡山区二模)定义:使a﹣b=ab﹣1成立的一对有理数a,b称为“共生有理数对”,记作(a,b).例如:因为﹣2﹣1=﹣2×1﹣1,所以(﹣2,1)是“共生有理数对”.
(1)判断数对是否为“共生有理数对”,并说明理由;
(2)若5是“共生有理数对”中的一个有理数,则这个“共生有理数对”为 ;
(3)若数对(m,n)是“共生有理数对”,且m=n+2,求(﹣2)mn的值.
17.(2025春 新华区二模)对于任意四个有理数a、b、c、d,可以组成两个有理数对(a,b)与(c,d),我们规定:(a,b)*(c,d)=a2+c2﹣bd.例如:(1,2)*(3,4)=12+32﹣2×4=2.
(1)求(﹣3,2)*(2,﹣1)的值;
(2)若2x+y=10,且(3x+y,2x2+3y2)*(x﹣3y,3)=80,求xy的值.
18.(2025 定海区一模)综合与实践
有趣的“乘法运算”
小明在学完《整式的乘法》后对一类特殊的乘法运算进行了探究.
【算法界定】这里的“乘法运算”指的是末位数字相同,首位数字和为十的两位数相乘.
【算法介绍】两数首位数字相乘再加上末位的数字作为“前积”,末位数字的平方作为“后积”,前积乘以100加上后积就是得数.
例:14×94=100×(1×9+4)+42=1316,前积是13,后积是16
(1)26×86=100×(2×8+6)+62=2236,前积是 ,后积是 ;
【初探算法】仿照例题,写出下面两数相乘的运算过程及结果.
(2)25×85= = ;
【推理算法】记两位数分别是和,且a+b=10,其中.
(3)请写出算法介绍中的运算规律,并加以证明.
19.(2025春 青秀区二模)【知识背景】
某学校开展科技节活动,在操场搭建一个科技展台,并安排了施工小组按设计图制作展板.
【步骤实施】请同学们完成以下四个任务.
任务一 截取一个边长为20dm的正方形ABCD,则这个正方形ABCD的面积为 dm2.
任务二 用4个相同的小正方形拼成一个面积为40dm2的大正方形EFGH,小正方形的边长为 dm2.
任务三 另有一块面积为225dm2的正方形板材,要从这块板材裁出一块面积为105dm2的长方形PQMN,使长方形的长与宽的比为5:3,问能否裁出?请说明理由.
任务四
任务一、任务二、任务三组合在一起,分别构成墙面、窗户和门(如图),请用涂料涂满除门窗(正方形EFGH和长方形PQMN)外剩下的墙面.并用彩带装饰窗户的四周(即正方形EFGH的周长),在购买涂料和彩带时有以下两种方案可供选择(如表),问哪种方案更划算?请说明理由.
方案 涂料每平方分米价格(元) 彩带每分米价格(元)
方案1 15 5
方案2 12 10
20.(2025春 建邺区二模)我们规定:n个相同的非零有理数的商可以表示为a (n=1,2,…),读作“a的圈n次方”.(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)=(﹣3)④,读作“(﹣3)的圈4次方”.
(1)直接写出计算结果:2025②= , .
(2)若n为任意正整数,下列结论:①任何非零整数的圈n次方小于或等于本身;②负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数;③互为相反数的两个数的圈n次方互为相反数;④互为倒数的两个数的圈n次方互为倒数;⑤圈n次方等于它本身的数是1或﹣1.其中所有正确结论的序号是 .
(3)试说明a ÷a =am﹣n(m,n为正整数,且m>n).
中考核心考点 有理数
参考答案与试题解析
一.选择题(共10小题)
1.(2025 扬州一模)我国古代著作《九章算术》在世界数学史上首次正式引入负数,若气温升高3℃时,气温变化记作+3℃,那么气温下降5℃时,气温变化记作( )
A.﹣8℃ B.﹣5℃ C.+5℃ D.+8℃
【考点】正数和负数.
【专题】实数;运算能力.
【答案】B
【分析】在一对具有相反意义的量中,规定其中一个为正,则另一个就用负表示.据此求解即可.
【解答】解:根据题意,气温下降5℃时,气温变化记作﹣5℃.
故选:B.
【点评】本题考查了正负数在现实生活的应用,熟练掌握正负数的意义是解答本题的关键.
2.(2025春 永春县二模)若□=0,则□表示的数是( )
A.5 B. C. D.﹣5
【考点】有理数的加法.
【专题】实数;运算能力.
【答案】B
【分析】根据加减法是互逆运算,列式计算.
【解答】解:∵0﹣(),
故选:B.
【点评】本题考查了有理数的加法,理解加减法是互逆运算是解题的关键.
3.(2025春 琼山区三模)下列各数中,与2025的和为0的是( )
A.2025 B.﹣2025 C. D.
【考点】相反数.
【专题】实数;运算能力.
【答案】B
【分析】根据题意列式0﹣2025求值即可.
【解答】解:根据有理数减法运算法则得:0﹣2025=﹣2025,
故答案为:B.
【点评】本题考查有理数的减法计算法则:减去一个数等于加上这个数的相反数是关键.
4.(2025 长春一模)如图,在数轴上,点A、B分别表示数a、b,且a+b=0.若AB=4,则点A表示的数为( )
A.﹣2 B.0 C.2 D.﹣4
【考点】数轴.
【专题】实数;运算能力.
【答案】A
【分析】根据AB=4得到点A和点B到原点的距离之和为4,根据相反数的性质可知点A和点B分别位于原点两侧,到原点的距离相等,即可得到答案.
【解答】解:∵点A和点B到原点的距离之和为4,a+b=0,
∴点A到原点的距离为2个单位,且在原点左侧,
即点A表示的数为﹣2.
故选:A.
【点评】本题主要考查相反数的定义和性质、数轴上两点之间的距离等知识.熟练掌握以上知识点是关键.
5.(2025春 瑶海区二模)数轴上A,B,C三点依次从左向右排列,表示的数分别为﹣2﹣x,2x﹣3和1,则x可能是( )
A.﹣2 B.﹣1 C.0 D.1
【考点】数轴.
【专题】实数;运算能力.
【答案】D
【分析】根据数轴上点从左到右数逐渐增大的性质,列出不等式组,求解x的取值范围,再对照选项判断.
【解答】解:因为三点依次从左向右排列,所以﹣2﹣x<2x﹣3且2x﹣3<1.
解不等式﹣2﹣x<2x﹣3:得,
解不等式2x﹣3<1:解得x<2,
∴x的取值范围是,
故选:D.
【点评】本题考查了数轴上数的大小关系与不等式的求解,解题的关键是根据数轴上点的左右顺序列出不等式组并求解.
6.(2025 沂源县一模)DeepSeek团队在人工智能研发过程中坚持自主创新.实验数括显示,他们的模型训练效率达到了惊人的2.4×1015次浮点运算/秒.若某次连续训练持续了1.2×104秒,则总共完成了多少次浮点运算( )
A.2.48×1019 B.2.88×1018 C.2.88×1019 D.2.88×1020
【考点】科学记数法—表示较大的数.
【专题】实数;运算能力.
【答案】C
【分析】根据有理数的运算法则求解.
【解答】解:2.4×1015×1.2×104=2.88×1019,
故选:C.
【点评】本题考查了科学记数法,掌握有理数的运算法则是解题的关键.
7.(2025 辽阳一模)当气体的温度降低到一定程度的时候就会变成液体,人们把这种变化过程叫做液化.初中物理就介绍了下面几种常见气体液化时的温度(标准大气压):
气体 氧气 氨气 氢气 氮气
液化温度/℃ ﹣183 ﹣33.5 ﹣253 ﹣196
其中液化温度最低的气体是( )
A.氧气 B.氨气 C.氢气 D.氮气
【考点】有理数大小比较;正数和负数.
【专题】实数;数感.
【答案】C
【分析】先将液化温度从低到高排序,然后找出最低温度.
【解答】解:∵﹣253℃<﹣196℃<﹣183℃<﹣33.5℃,∴液化温度最低的气体是氢气.
故选:C.
【点评】本题考查了有理数比较大小,掌握比较有理数大小的方法是关键.
8.(2025 文山州二模)《九章算术》中注有“今两算得失相反,要令正负以名之”.意思是:今有两数若其意义相反,则分别叫做正数和负数.若升高30米记作+30米,那么﹣5米表示( )
A.上升5米 B.下降35米 C.上升25米 D.下降5米
【考点】正数和负数;数学常识.
【专题】实数;符号意识.
【答案】D
【分析】利用正数和负数的意义,数字常识解答.
【解答】解:升高30米记作+30米,那么﹣5米表示下降5米.
故选:D.
【点评】本题考查了正数和负数,数字常识,解题的关键是掌握正数和负数的意义,数字常识.
9.(2025 海淀区一模)为进一步提高义务教育质量,某地区今年义务教育财政预算支出比去年上调了5%.已知该地区去年的义务教育财政预算支出约为3.8×1010元,则今年的义务教育财政预算支出约为( )
A.3.8×1010元 B.5.7×1010元
C.3.99×1010元 D.3.99×1011元
【考点】科学记数法—表示较大的数.
【专题】实数;数感.
【答案】C
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:3.8×1010×(1+5%)=3.99×1010,
故选:C.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
10.(2025 孝义市一模)约公元820年,中亚细亚数学家阿尔一花拉子米写了一本代数书,重点论述怎样解方程.这本书的拉丁文译本取名为《对消与还原》,其中,“对消”指的是“合并同类项”,“还原”指的是“移项”.我国古代数学著作《九章算术》的“方程”章,更早使用了“对消”和“还原”的方法;体现的数学思想是( )
A.分类思想 B.数形结合思想
C.转化思想 D.公理化思想
【考点】数学常识.
【专题】推理填空题;推理能力.
【答案】C
【分析】由“对消”和“还原”的方法,即“合并同类项”,“移项”,即可得体现的数学思想是转化思想.
【解答】解:“对消”和“还原”的方法,即“合并同类项”,“移项”,体现的数学思想是转化思想.
故选:C.
【点评】本题主要考查了数学思想,解题关键是正确判断.
二.填空题(共5小题)
11.(2025春 江北区二模)规定:对于任意有理数a与b,满足,如5*3=3×5﹣3=12,.若有理数x满足x*3=15,则x的值为 6 .
【考点】有理数的混合运算.
【专题】新定义;运算能力.
【答案】6.
【分析】根据新定义的运算进行列方程,再解方程即可.
【解答】解:由新定义可得:①当x≥3时,
3x﹣3=15,
解得:x= 6;
②当x<3时,
x﹣3×3=15,
解得:x= 24(舍去).
故答案为:6.
【点评】本题考查了有理数的混合运算,解题的关键是根据新定义的运算进行解答.
12.(2025春 长寿区二模)为了丰富学生课外小组活动,培养学生动手操作能力,王老师让学生把6m长的彩绳剪成2m或1m的彩绳(允许只剪成其中一种长度),用来做手工编织,在不造成浪费的前提下,你有 4 种不同的剪法.
【考点】有理数的加法.
【专题】计算题;运算能力.
【答案】4.
【分析】根据题意列出方程,再解方程即可.
【解答】解:设截成2m的彩绳x根,1m的彩绳y根,
由题意可得2x+y=6,
因为不造成浪费,
∴x,y是正整数,
x=0,y=6;
x=1,y=4;
x=2,y=2;
x=3,y=0.
则共有4种不同截法,
故答案为:4.
【点评】本题考查了有理数的加法,解题的关键是根据题意列出方程.
13.(2025 房山区一模)某工厂需要生产三种产品A,B,C,每种产品的生产分为两个阶段:第一阶段是制作,第二阶段是包装,每种产品在每个阶段所需的时间(单位:小时)如表所示:
A B C
制作 10 8 12
包装 6 10 8
若由一名工人单独完成三种产品的生产、那么总共需要 54 小时;若由两位工人合作完成这三种产品的生产,每个阶段由一个人单独完成,每种产品制作完才可以包装,那么完成这三种产品的生产最少需要 26 小时.
【考点】有理数的混合运算.
【专题】实数;运算能力.
【答案】54,26.
【分析】本题主要考查对生产时间的计算,第一问是单人完成生产的总时间计算,直接将三种产品制作和包装时间累加即可;第二问是两人合作的最短时间计算,关键在于合理分配任务,让两人的工作时间尽可能均衡且不出现等待时间.
【解答】解:一名工人单独完成,总时间为三种产品制作时间与包装时间之和,即(10+8+12)+(6+10+8)=30+24=54小时.
设两名工人为甲、乙.
为使时间最短,安排甲按B、A、C顺序制作产品,乙负责包装.
甲制作产品B用时8小时,此时乙等待8小时候开始包装B,用时10小时,
甲接着制作产品A用时10小时,此时乙包装B还剩10﹣8=2小时,甲制作A过程中乙完成B包装后开始包装A,乙包装A用时6小时,在甲制作A的10小时内乙可完成A包装;
甲再制作产品C用时12小时,乙包装C用时8小时.
整个过程总用时为甲制作产品BAC的时间加上乙包装产品C的时间,即8+10+12﹣(10﹣8))﹣(6)+8=26小时.
故答案为:54,26.
【点评】本题将实际生产场景转化为数学计算问题,既考查了基本的加法运算能力,又对逻辑规划能力有一定要求.第一问较为基础,是简单的时间求和.第二问难度提升,需要思考如何合理安排任务流程以达到最短时间,这种问题有助于培养学生的统筹规划思维,在实际生产生活中也有很强的应用价值,可引导学生将数学知识与实际应用相结合.
14.(2025春 思明区二模)学校组织学生参加木艺艺术品加工劳动实践活动,已知某木艺艺术品加工完成共需A、B、C、D、E、F、G七道工序,加工要求如下:①工序C、D须在工序A完成后进行,工序E须在工序B、D都完成后进行,工序F须在工序C、D都完成后进行;②一道工序只能由一名学生完成,此工序完成后该学生才能进行其他工序;③各道工序所需时间如下表所示:
工序 A B C D E F G
所需时间/分钟 9 9 7 9 7 10 2
若由两名学生合作完成此木艺艺术品的加工,则最少需要的时间是 28 分钟.
【考点】有理数的混合运算.
【专题】实数;运算能力.
【答案】28.
【分析】假设这两名学生为甲、乙,推导出甲学生做工序A,乙学生做工序B,需要9分钟,然后甲学生做工序D,同时乙学生做工序C,乙学生工序C完成后接着做工序G,最后甲学生做工序E,乙学生同时做工序F,据此进一步解答.
【解答】解:假设这两名学生为甲,乙,
∵工序C、D须在工序A完成后进行,工序E须在工序B、D都完成后进行,且工序A,B都需要9分钟完成,
∴甲学生做工序A,乙学生做工序B,需要9分钟,
然后甲学生做工序D,同时乙学生做工序C,
乙学生工序C完成后接着做工序G,
此时需要9分钟,
最后甲学生做工序E,乙学生同时做工序F,
此时需要10分钟,
则9+9+10=28(分钟),
即若由两名学生合作完成此木艺艺术品的加工,则最少需要28分钟.
故答案为:28.
【点评】本题考查有理数的运算,结合题意进行正确的推理是解题的关键.
15.(2025 湖南)小华有一个密码小宝箱,他忘记6位数密码的一部分8904□2,且密码每一个数字和其他数字都不重复.现在小华想要打开他的宝箱,最多需要尝试 5 次.
【考点】有理数的混合运算.
【专题】推理填空题;推理能力.
【答案】5.
【分析】根据题意即可找到可以填的数字.
【解答】解:根据密码每一个数字和其他数字都不重复,
所以方框里只能填:1,3,5,6,7,
故答案为:5.
【点评】本题考查了有理数的混合运算,解题的关键是根据题意找到可以填的数字.
三.解答题(共5小题)
16.(2025春 锡山区二模)定义:使a﹣b=ab﹣1成立的一对有理数a,b称为“共生有理数对”,记作(a,b).例如:因为﹣2﹣1=﹣2×1﹣1,所以(﹣2,1)是“共生有理数对”.
(1)判断数对是否为“共生有理数对”,并说明理由;
(2)若5是“共生有理数对”中的一个有理数,则这个“共生有理数对”为 (5,1)或(﹣1,5) ;
(3)若数对(m,n)是“共生有理数对”,且m=n+2,求(﹣2)mn的值.
【考点】有理数的混合运算.
【专题】实数;运算能力.
【答案】(1)不是;(2)(5,1)或(﹣1,5);(3)﹣8.
【分析】(1)代入定义式,看等式是否成立即可;
(2)设这个共生数对为(5,a)或(a,5),代入定义式,求出a,表示出数对即可;
(3)数对(m,n)是“共生有理数对”,所以m﹣n=mn﹣1,因为m=n+2,两式联立求出mn=3,求出结果即可.
【解答】解:(1),
,
,
数对不是“共生有理数对”.
(2)设这个共生数对为(5,a)或(a,5).
当数对为(5,a)时,
5﹣a=5a﹣1,
可得:a=1;
这个数对时(5,1);
当数对为(a,5)时,
a﹣5=5a﹣1,
解得:a=﹣1,
这个数对时(﹣1,5).
故答案为:(5,1)或(﹣1,5).
(3)因为(m,n)是“共生有理数对”,
所以m﹣n=mn﹣1,
因为m=n+2,
所以n+2﹣n=mn﹣1,
得:mn=3,
(﹣2)mn=(﹣2)3=﹣8.
【点评】本题考查了有理数的混合运算,解决本题的关键是按照“共生有理数对”的公式计算.
17.(2025春 新华区二模)对于任意四个有理数a、b、c、d,可以组成两个有理数对(a,b)与(c,d),我们规定:(a,b)*(c,d)=a2+c2﹣bd.例如:(1,2)*(3,4)=12+32﹣2×4=2.
(1)求(﹣3,2)*(2,﹣1)的值;
(2)若2x+y=10,且(3x+y,2x2+3y2)*(x﹣3y,3)=80,求xy的值.
【考点】有理数的混合运算.
【专题】计算题;整式;运算能力.
【答案】(1)15;(2)5.
【分析】(1)因为(a,b)*(c,d)=a2+c2﹣bd,所以(﹣3,2)*(2,﹣1)=(﹣3)2+22﹣2×(﹣1),求出结果即可;
(2)因为(a,b)*(c,d)=a2+c2﹣bd,(3x+y,2x2+3y2)*(x﹣3y,3)=80,所以即(3x+y)2+(x﹣3y)2﹣3(2x2+3y2)=80,
得4x2+y2=80,因为2x+y=10,所以sxy=(2x+y)2﹣(4x2+y2)=20,求出xy=5.
【解答】解:(1)(﹣3,2)*(2,﹣1)
=(﹣3)2+22﹣2×(﹣1)
=9+4+2
=15;
(2)因为(3x+y,2x2+3y2)*(x﹣3y,3)=80,
即(3x+y)2+(x﹣3y)2﹣3(2x2+3y2)=80,
得4x2+y2=80,
因为2x+y=10,
所以(2x+y)2﹣(4x2+y2)
=4x2+y2+4xy﹣4x2﹣y2
=4xy,
4xy=102﹣80=20,
xy=5.
【点评】本题考查了有理数的混合运算,解决本题的关键是根据示例的运算法则计算.
18.(2025 定海区一模)综合与实践
有趣的“乘法运算”
小明在学完《整式的乘法》后对一类特殊的乘法运算进行了探究.
【算法界定】这里的“乘法运算”指的是末位数字相同,首位数字和为十的两位数相乘.
【算法介绍】两数首位数字相乘再加上末位的数字作为“前积”,末位数字的平方作为“后积”,前积乘以100加上后积就是得数.
例:14×94=100×(1×9+4)+42=1316,前积是13,后积是16
(1)26×86=100×(2×8+6)+62=2236,前积是 22 ,后积是 36 ;
【初探算法】仿照例题,写出下面两数相乘的运算过程及结果.
(2)25×85= 100(2×8+5)+52 = 2125 ;
【推理算法】记两位数分别是和,且a+b=10,其中.
(3)请写出算法介绍中的运算规律,并加以证明.
【考点】有理数的混合运算.
【专题】阅读型;规律型;实数;运算能力;推理能力.
【答案】(1)22;36;(2)100×(2×8+5)+52;2125;(3)算法介绍中的运算规律为:记两位数分别是和,且a+b=10,其中,那么100(ab+c)+c2.证明见解析.
【分析】(1)利用题干中的示例的方法解答即可;
(2)仿照例题的解答过程运算即可;
(3)利用多项式乘以多项式的法则运算即可.
【解答】解:(1)∵26×86=100×(2×8+6)+62=2236,
∴前积是22,后积是36.
故答案为:22;36;
(2)25×85=100×(2×8+5)+52=2125.
故答案为:100×(2×8+5)+52;2125;
(3)算法介绍中的运算规律为:记两位数分别是和,且a+b=10,其中,那么100(ab+c)+c2.
证明:∵,
∴
=(10a+c)(10b+c)
=100ab+10(a+b)c+c2,
∵a+b=10,
∴
=100ab+100c+c2
=100(ab+c)+c2.
【点评】本题主要考查了有理数的混合运算,数字变化的规律,本题是阅读型题目,熟练掌握题干中的方法并熟练应用是解题的关键.
19.(2025春 青秀区二模)【知识背景】
某学校开展科技节活动,在操场搭建一个科技展台,并安排了施工小组按设计图制作展板.
【步骤实施】请同学们完成以下四个任务.
任务一 截取一个边长为20dm的正方形ABCD,则这个正方形ABCD的面积为 400 dm2.
任务二 用4个相同的小正方形拼成一个面积为40dm2的大正方形EFGH,小正方形的边长为 dm2.
任务三 另有一块面积为225dm2的正方形板材,要从这块板材裁出一块面积为105dm2的长方形PQMN,使长方形的长与宽的比为5:3,问能否裁出?请说明理由.
任务四
任务一、任务二、任务三组合在一起,分别构成墙面、窗户和门(如图),请用涂料涂满除门窗(正方形EFGH和长方形PQMN)外剩下的墙面.并用彩带装饰窗户的四周(即正方形EFGH的周长),在购买涂料和彩带时有以下两种方案可供选择(如表),问哪种方案更划算?请说明理由.
方案 涂料每平方分米价格(元) 彩带每分米价格(元)
方案1 15 5
方案2 12 10
【考点】有理数的混合运算;算术平方根.
【专题】实数;矩形 菱形 正方形;运算能力;推理能力.
【答案】任务一:400;任务二:;任务三:能够裁出.理由见解析;任务四:方案2更划算,理由见解析.
【分析】任务一.利用正方形的面积公式解答即可;
任务二.利用正方形的面积公式和算术平方根的意义解答即可;
任务三.设长方形的长为5x dm,则宽为3x dm,利用长方形的面积公式求得长方形的长,通过比较与正方形的边长的大小得出结论;
任务四.通过计算两个方案的费用,比较大小即可得出结论.
【解答】解:任务一:∵正方形ABCD的边长为20dm,
∴这个正方形ABCD的面积为400dm2.
故答案为:400;
任务二:∵4个相同的小正方形拼成一个面积为40dm2的大正方形EFGH,
∴每个小正方形的面积为10dm2,
∴小正方形的边长为dm.
故答案为:;
任务三:能够裁出.理由:
∵长方形的长与宽的比为5:3,
∴设长方形的长为5x dm,则宽为3x dm,
∵长方形的面积为105dm2,
∴5x 3x=105,
∵x>0,
∴x,
∴长方形的长为5dm,则宽为3dm,
∵正方形的面积为225dm2,
∴正方形的边长为15dm,
∵5,15,
∴515,
∴能够裁出.
任务四:方案2更划算,理由:
由题意:除门窗(正方形EFGH和长方形PQMN)外剩下的墙面面积为:400﹣40﹣105=255(dm2),
正方形EFGH的周长为88×3.2=25.6(dm),
利用方案1的费用为:255×15+25.6×5=3825+128=3953(元),
利用方案2的费用为:255×12+25.6×10=3060+256=3316(元).
∵3953>3316,
∴方案2更划算.
【点评】本题主要考查了正方形的性质,有理数的混合运算,算术平方根的应用,熟练掌握上述法则与性质是解题的关键.
20.(2025春 建邺区二模)我们规定:n个相同的非零有理数的商可以表示为a (n=1,2,…),读作“a的圈n次方”.(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)=(﹣3)④,读作“(﹣3)的圈4次方”.
(1)直接写出计算结果:2025②= 1 , 4 .
(2)若n为任意正整数,下列结论:①任何非零整数的圈n次方小于或等于本身;②负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数;③互为相反数的两个数的圈n次方互为相反数;④互为倒数的两个数的圈n次方互为倒数;⑤圈n次方等于它本身的数是1或﹣1.其中所有正确结论的序号是 ②④ .
(3)试说明a ÷a =am﹣n(m,n为正整数,且m>n).
【考点】有理数的乘方;正数和负数;有理数;有理数的除法.
【专题】实数;运算能力.
【答案】(1)1,4;
(2)②④;
(3)见解答.
【分析】(1)根据新规定求解;
(2)根据新规定求解;
(3)根据新规定和同底数幂的运算证明.
【解答】解:(1)∵2025②=2025÷2025=1, () =4,
故答案为:1,4;
(2)①∵(﹣1)÷(﹣1)=1>﹣1,
故①是错误的;
②奇数个负数相除还是负数,偶数个负数相除是正数,
故②是正确的;
③∵(﹣2)÷(﹣2)=1,2÷2=1,
故③是错误的;
④∵a ,() =an﹣2,
故④是正确的;
⑤圈n次方等于它本身的数是1,
故⑤是错误的;
故答案为:②④.
(3)证明:原式am﹣n.
【点评】本题考查了新运算,理解新运算和掌握幂的运算法则是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
