【中考押题预测】2025年中考数学核心考点考前冲刺 圆(含解析)
文档属性
| 名称 | 【中考押题预测】2025年中考数学核心考点考前冲刺 圆(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 16:07:41 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中考核心考点 圆
一.选择题(共10小题)
1.(2025 蜀山区二模)如图,CD为⊙O的直径,弦AB交CD于点E,点C为中点,若的度数为60°,点O到AD的距离为2,则OE的长为( )
A. B. C.3 D.2
2.(2025 綦江区一模)如图,在矩形ABCD中,AB=4,BC=4,连接AC,以点C为圆心,CD为半径作弧交BC于点E,连接AE.则图中阴影部分的面积为( )
A. B. C. D.
3.(2025春 肥西县二模)一个扇形的半径为4,弧长等于3π,则扇形的圆心角度数为( )
A.120° B.135° C.150° D.270°
4.(2025 黄埔区一模)如图,CD是⊙O的直径,AB是弦,CD⊥AB于E,DE=2,AB=8,则AC的长为( )
A.8 B.10 C.4 D.4
5.(2025 南安市)我国伟大的数学家刘徽于公元263年撰《九章算术注》中指出,“周三径一”不是圆周率值,实际上是圆内接正六边形周长和直径的比值(如图1).刘徽发现,圆内接正多边形边数无限增加时,多边形的周长就无限逼近圆周长,从而创立“割圆术”,为计算圆周率建立起相当严密的理论和完善的算法.如图2,六边形ABCDEF是圆内接正六边形,把每段弧二等分,可以作出一个圆内接正十二边形,点G为CD的中点,连接BG,CF,BG交CF于点P,若,则PG的长为( )
A. B. C. D.
6.(2025春 大足区二模)如图,在矩形ABCD中,AB=1,AD=2,以点D为圆心,AD长为半径画弧交BC于点E,连接DE,则图中阴影部分的面积为( )
A. B. C. D.
7.(2025 岳池县)如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AB=2,将Rt△ABC绕点C顺时针旋转90°后得到Rt△DEC,点B经过的路径为,将线段AB绕点A顺时针旋转60°后,点B恰好落在CE上的点F处,点B经过的路径为,则图中阴影部分的面积是( )
A. B. C. D.
8.(2025 雁塔区)如图,AD是⊙O的直径,AB是⊙O的弦,半径OC⊥AB,连接CD,交OB于点E,∠BOC=42°,则∠OED的度数是( )
A.63° B.61° C.53° D.65°
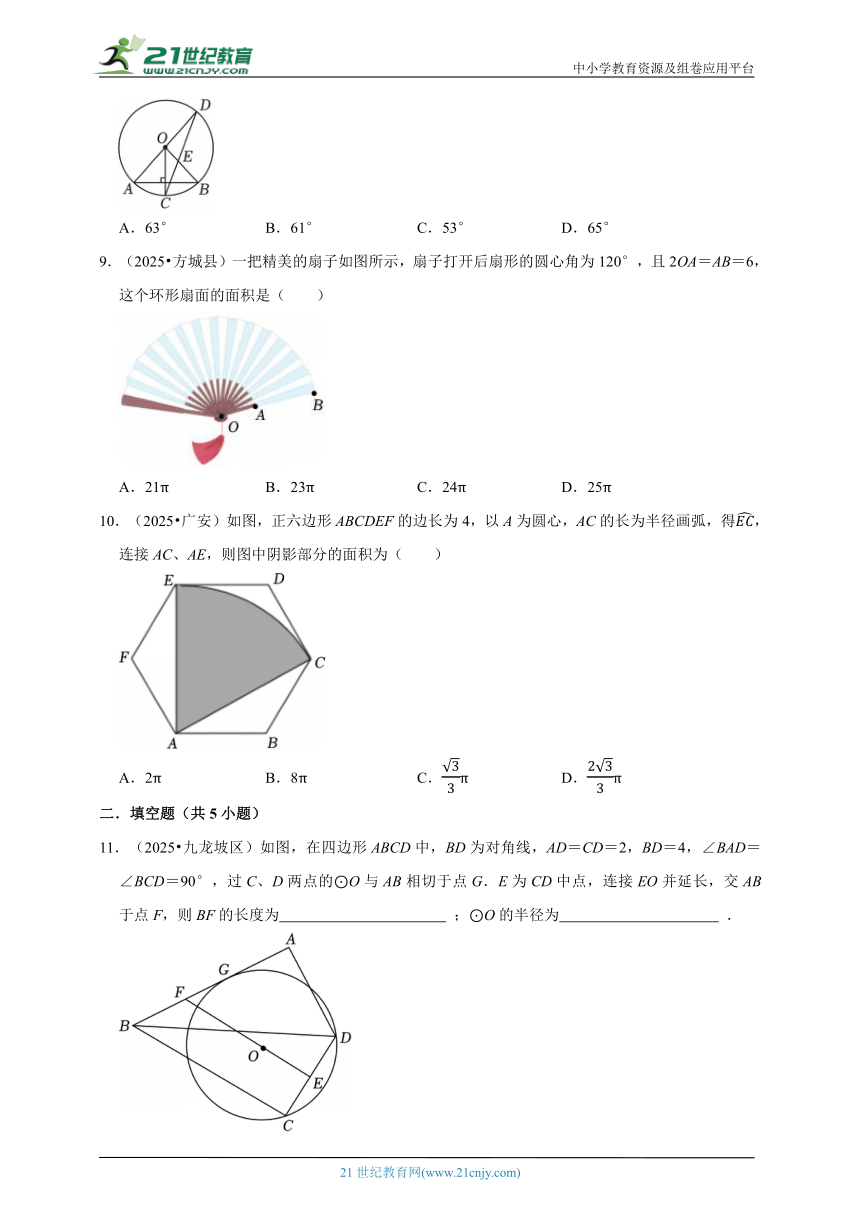
9.(2025 方城县)一把精美的扇子如图所示,扇子打开后扇形的圆心角为120°,且2OA=AB=6,这个环形扇面的面积是( )
A.21π B.23π C.24π D.25π
10.(2025 广安)如图,正六边形ABCDEF的边长为4,以A为圆心,AC的长为半径画弧,得,连接AC、AE,则图中阴影部分的面积为( )
A.2π B.8π C.π D.π
二.填空题(共5小题)
11.(2025 九龙坡区)如图,在四边形ABCD中,BD为对角线,AD=CD=2,BD=4,∠BAD=∠BCD=90°,过C、D两点的⊙O与AB相切于点G.E为CD中点,连接EO并延长,交AB于点F,则BF的长度为 ;⊙O的半径为 .
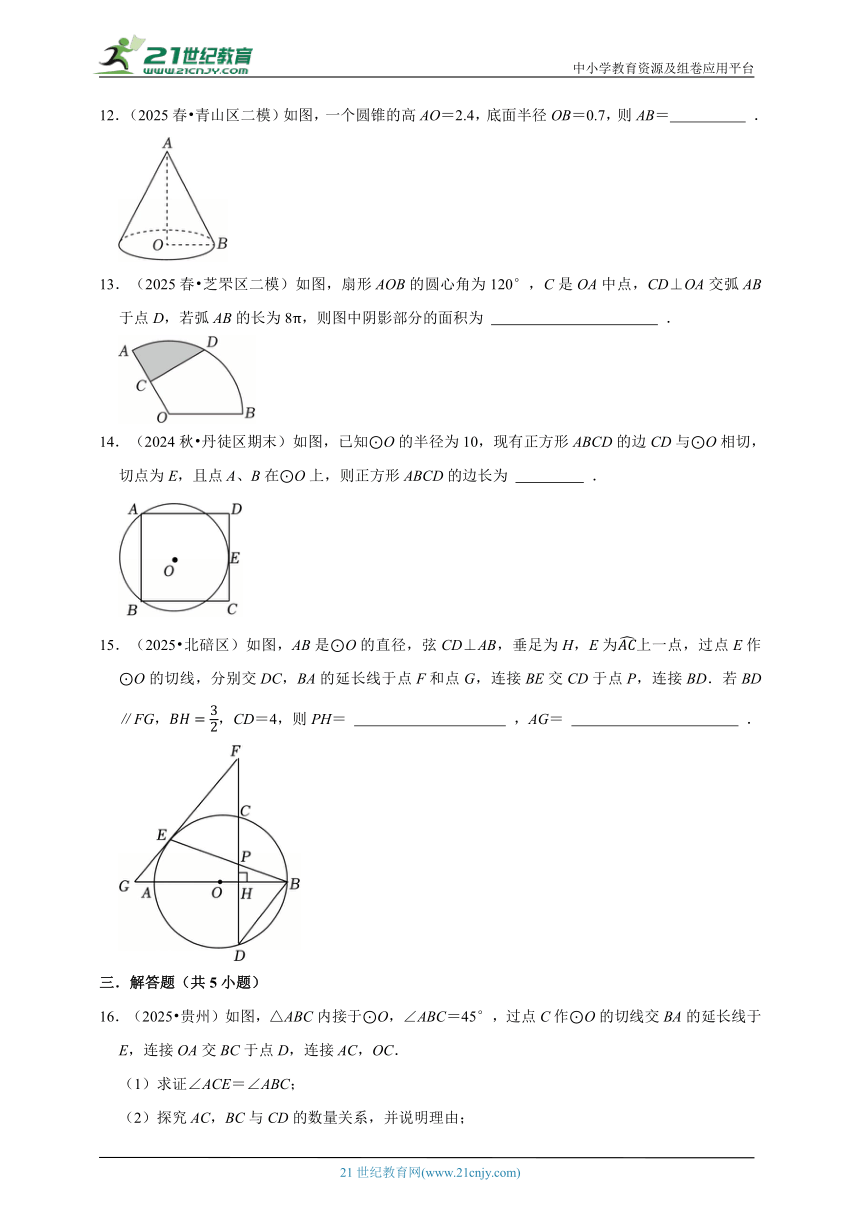
12.(2025春 青山区二模)如图,一个圆锥的高AO=2.4,底面半径OB=0.7,则AB= .
13.(2025春 芝罘区二模)如图,扇形AOB的圆心角为120°,C是OA中点,CD⊥OA交弧AB于点D,若弧AB的长为8π,则图中阴影部分的面积为 .
14.(2024秋 丹徒区期末)如图,已知⊙O的半径为10,现有正方形ABCD的边CD与⊙O相切,切点为E,且点A、B在⊙O上,则正方形ABCD的边长为 .
15.(2025 北碚区)如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,E为上一点,过点E作⊙O的切线,分别交DC,BA的延长线于点F和点G,连接BE交CD于点P,连接BD.若BD∥FG,,CD=4,则PH= ,AG= .
三.解答题(共5小题)
16.(2025 贵州)如图,△ABC内接于⊙O,∠ABC=45°,过点C作⊙O的切线交BA的延长线于E,连接OA交BC于点D,连接AC,OC.
(1)求证∠ACE=∠ABC;
(2)探究AC,BC与CD的数量关系,并说明理由;
(3)若tan∠DCO,CE=6,求⊙O的半径.
17.(2025 温江区二模)如图,在Rt△ABC中,∠B=90°,⊙O与边BC相切于点D,与AB,AC分别相交于点E,F,AD与OE相交于点G.
(1)求证:∠C=∠ADE;
(2)若CF=4,sinC,求⊙O的半径和DG的长.
18.(2025 蜀山区二模)如图,BC是⊙O的直径,AB,AD与⊙O相切于点B,D,过点C作CE∥AD分别交AB,AO于E,F两点,连接CD.
(1)求证:四边形ADCF是平行四边形;
(2)若⊙O的半径为,AD=5,求AE的长.
19.(2025 滨江区一模)已知,AB,CD是⊙O的弦,CD⊥AB于点E,且,连接BC,AD.
(1)如图1,若AB是⊙O的直径,求∠C的度数.
(2)如图2,求证:①CD=CB.
②AE+AD=BE.
20.(2025 双城区一模)△ABC内接于⊙O,F为上一点,连接OF、CF,OF交弦AB于点D,若∠ACF=∠BCF.
(1)如图1,求证:;
(2)如图2,连接AO,若AB=AC,求证:AO⊥BC.
(3)在(2)的条件下,延长FO交⊙O于点E,过点F作FN⊥AC垂足为N,过点E作EM⊥AC垂足为M,若AN=3cm,MN=20cm,求DF的长.
中考核心考点 圆
参考答案与试题解析
一.选择题(共10小题)
1.(2025 蜀山区二模)如图,CD为⊙O的直径,弦AB交CD于点E,点C为中点,若的度数为60°,点O到AD的距离为2,则OE的长为( )
A. B. C.3 D.2
【考点】圆心角、弧、弦的关系;垂径定理.
【专题】圆的有关概念及性质;推理能力.
【答案】D
【分析】连接AO,过O作OH⊥AD于H,得到OH=2,由垂径定理推出CD⊥AB,由圆心角、弧、弦的关系定理得到∠AOC=60°,由圆周角定理求出∠ODH=30°,由含30度角的直角三角形的性质得到OHOD,OEOA,得到OE=OH=2.
【解答】解:连接AO,过O作OH⊥AD于H,
∵点O到AD的距离为2,
∴OH=2,
∵CD为⊙O的直径,C为中点,
∴CD⊥AB,
∵的度数为60°,C为中点,
∴∠AOC=60°,
∴∠ODH∠AOC=30°,
∵∠OHD=90°,
∴OHOD,
∵∠OAE=90°﹣60°=30°,
∴OEOA,
∵OA=OD,
∴OE=OH=2.
故选:D.
【点评】本题考查圆心角、弧、弦的关系,垂径定理,含30度角的直角三角形,关键是由含30度角的直角三角形的性质推出OHOD,OEOA.
2.(2025 綦江区一模)如图,在矩形ABCD中,AB=4,BC=4,连接AC,以点C为圆心,CD为半径作弧交BC于点E,连接AE.则图中阴影部分的面积为( )
A. B. C. D.
【考点】扇形面积的计算;矩形的性质.
【专题】矩形 菱形 正方形;几何直观;推理能力.
【答案】A
【分析】利用特殊角的三角函数求出∠ACB=30°,再根据矩形的性质求出∠ACD的度数,最后利用阴影部分面积S=S△ACE+S扇形DCE﹣2S扇形ECF求解即可.
【解答】解:∵四边形ABCD是矩形,
∴∠ABC=∠BCD=90°,
在直角三角形ABC中,AB=4,,
∴,
∴∠ACB=∠ECF=30°,
∴∠ACD=∠BCD﹣∠ACB=90°﹣30°=60°.
∴阴影部分面积S=S△ACE+S扇形DCE﹣2S扇形ECF
.
故选:A.
【点评】本题考查了矩形的性质,扇形的面积公式,熟练掌握扇形的面积公式是解题的关键.
3.(2025春 肥西县二模)一个扇形的半径为4,弧长等于3π,则扇形的圆心角度数为( )
A.120° B.135° C.150° D.270°
【考点】弧长的计算.
【专题】与圆有关的计算;运算能力.
【答案】B
【分析】设扇形的圆心角度数为n°,根据弧长公式列关于n的方程并求解即可.
【解答】解:设扇形的圆心角度数为n°,
根据题意,得2π×4=3π,
解得n=135,
∴扇形的圆心角度数为135°.
故选:B.
【点评】本题考查弧长的计算,掌握弧长计算公式是解题的关键.
4.(2025 黄埔区一模)如图,CD是⊙O的直径,AB是弦,CD⊥AB于E,DE=2,AB=8,则AC的长为( )
A.8 B.10 C.4 D.4
【考点】垂径定理;勾股定理.
【专题】等腰三角形与直角三角形;圆的有关概念及性质;运算能力.
【答案】C
【分析】连接OA,设⊙O的半径为R,则OA=R,OE=R﹣2,根据垂径定理求出AE=BE=4,根据勾股定理求出OA2=OE2+AE2,得出R2=(R﹣2)2+42,求出R,再求出CE,最后根据勾股定理求出AC即可.
【解答】解:连接OA,设⊙O的半径为R,则OA=R,OE=R﹣2,
∵CD⊥AB,CD过圆心O,AB=8,
∴AE=BE=4,∠AEC=90°,
由勾股定理得:OA2=OE2+AE2,
即R2=(R﹣2)2+42,
解得:R=5,
即OA=OC=5,OE=5﹣2=3,
∴CE=OC+OE=5+3=8,
∴AC4,
故选:C.
【点评】本题考查了垂径定理和勾股定理,能熟记垂直于弦的直径平分这条弦是解此题的关键.
5.(2025 南安市)我国伟大的数学家刘徽于公元263年撰《九章算术注》中指出,“周三径一”不是圆周率值,实际上是圆内接正六边形周长和直径的比值(如图1).刘徽发现,圆内接正多边形边数无限增加时,多边形的周长就无限逼近圆周长,从而创立“割圆术”,为计算圆周率建立起相当严密的理论和完善的算法.如图2,六边形ABCDEF是圆内接正六边形,把每段弧二等分,可以作出一个圆内接正十二边形,点G为CD的中点,连接BG,CF,BG交CF于点P,若,则PG的长为( )
A. B. C. D.
【考点】正多边形和圆;确定圆的条件.
【专题】正多边形与圆;几何直观;运算能力;推理能力.
【答案】B
【分析】设正六边形ABCDEF的外接圆的圆心为O,连接OA、OB、OG、OD,则∠COF=3×60°=180°,所以圆心O在CF上,由点G为的中点,得∠COG=∠DOG∠COD=30°,可求得∠GCP=75°,由△BOC是等边三角形,得∠OCB=60°,则∠CBG∠COG=15°,所以∠GPC=∠GCP=75°,则PG=CG,作PI⊥CF交BC于点I,则∠PIC=30°,所以∠IPB=∠CBG=15°,则CI=2CP1,BI=PICP,于是得CO=BC,再证明△CGP∽△COG,得,则PG=CG,于是得到问题的答案.
【解答】解:如图2,设正六边形ABCDEF的外接圆的圆心为O,连接OA、OB、OG、OD,
∵∠AOF=∠AOB=∠BOC=∠COD360°=60°,
∴∠COF=3×60°=180°,∠CGP∠BOC=30°,
∴圆心O在CF上,
∵点G为的中点,
∴∠COG=∠DOG∠COD=30°,
∵OC=OG,
∴∠GCP=∠OGC(180°﹣30°)=75°,
∵OB=OC,∠BOC=60°,
∴△BOC是等边三角形,
∴∠OCB=60°,
∵∠CBG∠COG=15°,
∴∠GPC=∠OCB+∠CBG=75°=∠GCP,
∴PG=CG,
作PI⊥CF交BC于点I,则∠CPI=90°,
∴∠PIC=90°﹣60°=30°,CP,
∴∠IPB=∠PIC﹣∠CBG=15°=∠CBG,CI=2CP=2×()1,
∴BI=PICP(),
∴CO=BC1,
∵∠CGP=∠COG,∠PCG=∠GPO,
∴△CGP∽△COG,
∴,
∴PG=CG,
故选:B.
【点评】此题重点考查正多边形与圆、圆周角定理、等边三角形的判定与性质、直角三角形中30°角所对的直角边等于斜边的一半、勾股定理、相似三角形的判定与性质等知识,正确地作出所需要的辅助线是解题的关键.
6.(2025春 大足区二模)如图,在矩形ABCD中,AB=1,AD=2,以点D为圆心,AD长为半径画弧交BC于点E,连接DE,则图中阴影部分的面积为( )
A. B. C. D.
【考点】扇形面积的计算;矩形的性质.
【专题】与圆有关的计算;运算能力.
【答案】C
【分析】根据条件,先求出∠ADE=∠DEC=30°,再利用扇形的面积公式计算即可.
【解答】解:∵矩形ABCD中,AB=1,AD=2,以点D为圆心,AD长为半径画弧交BC于点E,连接DE,
∴CD=1,DE=2,∠C=90°,
∴∠DEC=30°,
∵AD∥BC,
∴∠ADE=∠DEC=30°,
∴S阴影.
故选:C.
【点评】本题考查了扇形面积的计算、矩形的性质,熟练掌握扇形面积公式是解答本题的关键.
7.(2025 岳池县)如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AB=2,将Rt△ABC绕点C顺时针旋转90°后得到Rt△DEC,点B经过的路径为,将线段AB绕点A顺时针旋转60°后,点B恰好落在CE上的点F处,点B经过的路径为,则图中阴影部分的面积是( )
A. B. C. D.
【考点】扇形面积的计算;旋转的性质;含30度角的直角三角形;勾股定理;圆周角定理.
【专题】等腰三角形与直角三角形;与圆有关的计算;运算能力.
【答案】D
【分析】根据直角三角形的性质和勾股定理可以求得AC和AB的长,再观察图形可知,S阴影=S△ABC+S扇形CBE﹣S扇形ABF,然后代入数据计算即可.
【解答】解:∵∠ACB=90°,∠A=60°,AB=2,
∴∠ABC=30°,
∴AC=1,BC
由图可得,
S阴影=S△ABC+S扇形CBE﹣S扇形ABF
π
π,
故选:D.
【点评】本题考查扇形面积的计算、勾股定理、直角三角形的性质,解答本题的关键是明确题意,利用数形结合的思想解答.
8.(2025 雁塔区)如图,AD是⊙O的直径,AB是⊙O的弦,半径OC⊥AB,连接CD,交OB于点E,∠BOC=42°,则∠OED的度数是( )
A.63° B.61° C.53° D.65°
【考点】圆周角定理;垂径定理;圆心角、弧、弦的关系.
【专题】与圆有关的计算;几何直观;推理能力.
【答案】A
【分析】由垂径定理可得,由定理可得∠AOC=∠BOC=42°,,求出∠DOE=96°,再由三角形内角和定理计算即可得解.
【解答】解:∵AD是⊙O的直径,AB是⊙O的弦,半径OC⊥AB,∠BOC=42°,
∴,
∴∠AOC=∠BOC=42°,
∴,∠DOE=180°﹣∠AOC﹣∠BOC=96°,
∴∠OED=180°﹣∠D﹣∠DOE=63°,
故选:A.
【点评】本题考查了圆周角定理,垂径定理,圆心角、弧、弦的关系,解答本题的关键是熟练掌握圆周角定理与垂径定理.
9.(2025 方城县)一把精美的扇子如图所示,扇子打开后扇形的圆心角为120°,且2OA=AB=6,这个环形扇面的面积是( )
A.21π B.23π C.24π D.25π
【考点】扇形面积的计算;圆环.
【专题】运算能力.
【答案】C
【分析】根据题意,用大扇形的面积减去小扇形的面积即可解决问题.
【解答】解:由题知,
因为2OA=AB=6,
所以OA=3,
所以OB=9,
则大扇形的面积为:;
小扇形的面积为:,
所以这个环形扇面的面积是27π﹣3π=24π.
故选:C.
【点评】本题主要考查了扇形面积的计算及圆环,熟知扇形的面积公式是解题的关键.
10.(2025 广安)如图,正六边形ABCDEF的边长为4,以A为圆心,AC的长为半径画弧,得,连接AC、AE,则图中阴影部分的面积为( )
A.2π B.8π C.π D.π
【考点】正多边形和圆;扇形面积的计算.
【专题】正多边形与圆;与圆有关的计算;解直角三角形及其应用;运算能力;推理能力.
【答案】B
【分析】根据正六边形的性质,等腰三角形的性质以及直角三角形的边角关系求出扇形的半径、圆心角度数,由扇形面积的计算公式进行计算即可.
【解答】解:∵六边形ABCDEF是正六边形,
∴AB=BC=4,∠ABC120°=∠BAF,
∴∠BAC=∠BCA=30°,
同理∠FAE=30°,
∴∠EAC=120°﹣30°﹣30°=60°,
过点B作BM⊥AC 于点M,则AM=MCAC,∠ABM=60°,
在Rt△ABM 中,AB=4,∠ABM=60°,
∴AMAB=2,
∴AC=2AM=4,
∴S阴影=S扇形8π,
故选:B.
【点评】本题考查正多边形和圆,扇形面积的计算,掌握正六边形的性质,等腰三角形的性质,直角三角形的边角关系以及扇形面积的计算公式是正确解答的关键.
二.填空题(共5小题)
11.(2025 九龙坡区)如图,在四边形ABCD中,BD为对角线,AD=CD=2,BD=4,∠BAD=∠BCD=90°,过C、D两点的⊙O与AB相切于点G.E为CD中点,连接EO并延长,交AB于点F,则BF的长度为 ;⊙O的半径为 .
【考点】切线的性质;垂径定理;圆周角定理.
【专题】方程思想;等腰三角形与直角三角形;矩形 菱形 正方形;与圆有关的位置关系;运算能力;推理能力;应用意识.
【答案】,.
【分析】作FH⊥BC于点H,如图1所示,由垂径定理推论可得OE⊥CD.进而可得四边形CEFH为矩形,CE=FH1.由已知可得∠ABD=∠CBD=30°,BC.BF.连接OG、OD,设BD交EF于点H,由切线性质可得∠FGO=90°.∠BFH=30°,所以BH,HC=BC﹣BH,EF=HC,再导角证明△BJF为等腰三角形,所以BF=JF.设JO=x,则OF=FJ+JOx,半径GO=sin60°×OF(x)=1OD,OE=EF﹣FO(x).在Rt△ODE中,由勾股定理可得()2+1=(1)2,解得x或(不合题意,舍去),故GO=1().
【解答】解:作FH⊥BC于点H,如图1所示,
∵E为CD中点,OE为过圆心的直线,
∴由垂径定理推论可得OE⊥CD.
∵∠BAD=∠BCD=90°,
∴四边形CEFH为矩形,CE=FH1.
∵AD=CD=2,BD=4,
∴∠ABD=∠CBD=30°,BC.
∴BF.
连接OG、OD,设BD交EF于点H,如图1所示,
由切线性质可得∠FGO=90°.
∵∠BFH=30°,
∴BH,
∴HC=BC﹣BH.
∵四边形CEFH为矩形,
∴EF=HC.
∵∠JDE=60°,∠JED=90°,
∴∠DJE=30°=∠FJB,
∵∠FBD=30°,
∴BF=JF.
设JO=x,则OF=FJ+JOx,
∵∠BFH=30°,∠HFE=90°,
∴∠GFO=60°,
故半径GO=sin60°×OF(x)=1OD,
OE=EF﹣FO(x).
在Rt△ODE中,由勾股定理可得:OE2+DE2=OD2,
即()2+1=(1)2,整理得,
解得x或(不合题意,舍去),
故GO=1().
故答案为:,.
【点评】本题考查了直角三角形的性质,勾股定理,解直角三角形,垂径定理的推论,矩形的判定与性质,切线的性质,熟练掌握以上内容并能作出恰当的辅助线是解题关键.
12.(2025春 青山区二模)如图,一个圆锥的高AO=2.4,底面半径OB=0.7,则AB= 2.5 .
【考点】圆锥的计算.
【专题】运算能力.
【答案】2.5.
【分析】根据勾股定理进行计算即可.
【解答】解:由题知,
因为圆锥的高AO=2.4,底面半径OB=0.7,
所以AB2.5.
故答案为:2.5.
【点评】本题主要考查了圆锥的计算,熟知勾股定理是解题的关键.
13.(2025春 芝罘区二模)如图,扇形AOB的圆心角为120°,C是OA中点,CD⊥OA交弧AB于点D,若弧AB的长为8π,则图中阴影部分的面积为 .
【考点】扇形面积的计算;线段垂直平分线的性质;弧长的计算.
【专题】与圆有关的计算;运算能力.
【答案】.
【分析】连接OD,设OA=OB=OD=r,根据弧长公式列出方程求出r的值,再解Rt△COD求出∠COD的度数,进而求出CD的长,最后根据S阴影=S扇形AOD﹣S△OCD列式计算即可.
【解答】解:如图所示,连接OD,设OA=OB=OD=r,
由条件可知,
∴r=12,
∴OA=OD=12,
∵C是OA中点,
∴,
∴,
∴∠COD=60°,
∴,
∴S阴影=S扇形AOD﹣S△OCD
,
故答案为:.
【点评】本题主要考查了求不规则图形面积,弧长公式,解直角三角形,熟练掌握原式知识点是关键.
14.(2024秋 丹徒区期末)如图,已知⊙O的半径为10,现有正方形ABCD的边CD与⊙O相切,切点为E,且点A、B在⊙O上,则正方形ABCD的边长为 16 .
【考点】切线的性质;正方形的性质.
【专题】矩形 菱形 正方形;与圆有关的位置关系;运算能力;推理能力.
【答案】16.
【分析】连接并延长EO交AB于点F,连接OB,由切线的性质得CD⊥OE,可证明四边AFED是矩形,则OF⊥AB,所以AF=BFAB,设正方形ABCD的边长为m,则EF=AD=AB=m,BFm,而OB=OE=10,所以OF=m﹣10,由勾股定理得(m﹣10)2102,求得m=16,于是得到问题的答案.
【解答】解:连接并延长EO交AB于点F,连接OB,
∵CD与⊙O相切于点E,
∴CD⊥OE,
∵四边形ABCD是正方形,
∴∠A=∠D=∠DEF=90°,
∴四边AFED是矩形,
∴∠AFE=90°,
∴OF⊥AB,
∴AF=BFAB,
设正方形ABCD的边长为m,则EF=AD=AB=m,BFm,
∵⊙O的半径为10,
∴OB=OE=10,
∴OF=m﹣10,
∵∠OFB=90°,
∴OF2+BF2=OB2,
∴(m﹣10)2102,
解得m=16或m=0(不符合题意,舍去),
∴正方形ABCD的边长为16,
故答案为:16.
【点评】此题重点考查正方形的性质、切线的性质、垂径定理、勾股定理等知识,正确地作出辅助线是解题的关键.
15.(2025 北碚区)如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,E为上一点,过点E作⊙O的切线,分别交DC,BA的延长线于点F和点G,连接BE交CD于点P,连接BD.若BD∥FG,,CD=4,则PH= ,AG= .
【考点】切线的性质;勾股定理;垂径定理;圆周角定理.
【专题】几何图形;与圆有关的位置关系;推理能力.
【答案】,.
【分析】连接OE、OD、AE,如图,设⊙O的半径为r,则OH=r,根据垂径定理得到CH=DH=2,则利用勾股定理计算得BD,利用勾股定理得到方程(r)2+22=r2,解方程得r,再根据切线的性质得到∠OEG=90°,接着证明Rt△OEG∽Rt△DHB,利用相似三角形的性质得到OG,GE,所以AG,然后证明△GEA∽△GBE,则,最后证明△BPH∽△BAE得到,所以PHBH.
【解答】解:连接OE、OD、AE,如图,设⊙O的半径为r,则OH=r,
∵AB⊥CD,
∴CH=DHCD=2,在Rt△OHD中,(r)2+22=r2,
解得r,
在Rt△BDH中,∵BH,DH=2,
∴BD,∵
GF为⊙O的切线,
∴OE⊥GF,
∴∠OEG=90°,
∵BD∥FG,
∴∠G=∠DBH,
∴Rt△OEG∽Rt△DHB,
∴,即,
解得OG,GE,
∴AG=OG﹣OA,
∵AB为直径,
∴∠AEB=90°,
∵∠GEA+∠AEO=90°,∠AEO+∠OEB=90°,
∴∠GEA=∠OEB,
∵OB=OE,
∴∠OEB=∠OBE,
∴∠GEA=∠OBE,
∵∠EGA=∠BGE,
∴△GEA∽△GBE,
∴,
∵∠HBP=∠EBA,∠BHP=∠BEA,
∴△BPH∽△BAE,
∴,
∴,
∴BH.
故答案为:,.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了垂径定理、圆周角定理和勾股定理.
三.解答题(共5小题)
16.(2025 贵州)如图,△ABC内接于⊙O,∠ABC=45°,过点C作⊙O的切线交BA的延长线于E,连接OA交BC于点D,连接AC,OC.
(1)求证∠ACE=∠ABC;
(2)探究AC,BC与CD的数量关系,并说明理由;
(3)若tan∠DCO,CE=6,求⊙O的半径.
【考点】圆的综合题.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;圆的有关概念及性质;与圆有关的位置关系;图形的相似;解直角三角形及其应用;运算能力;推理能力.
【答案】(1)证明见解析;(2)AC,BC与CD的数量关系为AC2=CD BC,理由见解析;(3)4.
【分析】(1)利用晕这就对了,等腰直角三角形的性质,圆的切线的性质定理和直角三角形的性质解答即可;
(2)利用相似三角形的判定与性质解答即可;
(3)过点A作AF⊥EC于点F,过点B作BG⊥OA于点G,利用直角三角形的边角关系定理得到tan∠DCO,设OD=x,则OC=3x,利用正方形的判定与性质得到OA=OC=AF=FC=3x,AC=3x,AD=OA﹣OD=2x,利用(2)的结论求得BD,利用直角三角形的边角关系定理求得BG,AG,再利用相似三角形的判定与性质求得EF,最后利用EC=EF+CF列出方程求得x值,则⊙O的半径=OC=3x=4.
【解答】(1)证明:∵∠AOC=2∠ABC,∠ABC=45°,
∴∠AOC=90°,
∵OA=OC,
∴∠OAC=∠OCA=45°.
∵CE是⊙O的切线,
∴OC⊥CE,
∴∠OCE=90°,
∴∠ACE=90°﹣∠OCA=45°,
∴∠ACE=∠ABC;
(2)解:AC,BC与CD的数量关系为AC2=CD BC,理由:
由(1)知:∠ACE=∠ABC,∠OAC=∠OCA,
∴∠OAC=∠ABC,
∵∠ACD=∠BCA,
∴△ACD∽△BCA,
∴,
∴AC2=CD BC.
(3)解:过点A作AF⊥EC于点F,过点B作BG⊥OA于点G,如图,
∵tan∠DCO,∠AOC=90°,
∴tan∠DCO,
设OD=x,则OC=3x,
∴CDx.
由(1)知:∠AOC=90°,OC⊥EC,
∵AF⊥EC,
∴四边形AOCF为矩形,
∵OA=OC,
∴四边形AOCF为正方形,
∴OA=OC=AF=FC=3x,
∴AC=3x,AD=OA﹣OD=2x.
由(2)知:AC2=CD BC,
∴,
∴BCx,
∴BD=BC﹣CDx,
∵∠BGD=∠AOC=90°,
∴BG∥OC,
∴∠DBG=∠DCO,
∴tan∠DBG=tan∠DCO,
∵tan∠DBG,
∴,
设DG=k,则BG=3k,
∴BD,
∴k,
∴BGx,AG=AD﹣DGx.
∵四边形AOCF为正方形,
∴OA∥CE,
∴∠BAG=∠E,
∵∠BGA=∠EFA=90°,
∴△BGA∽△AFE,
∴,
∴,
∴EFx,
∴EC=EF+CF3x=6,
∴x.
∴⊙O的半径=OC=3x=4.
【点评】本题主要考查了圆的有关性质,圆周角定理,圆的切线的性质定理,直角三角形的性质,勾股定理,直角三角形的边角关系定理,等腰直角三角形的性质,相似三角形的判定与性质,连接经过切点的半径是解决此类问题常添加的辅助线.
17.(2025 温江区二模)如图,在Rt△ABC中,∠B=90°,⊙O与边BC相切于点D,与AB,AC分别相交于点E,F,AD与OE相交于点G.
(1)求证:∠C=∠ADE;
(2)若CF=4,sinC,求⊙O的半径和DG的长.
【考点】切线的性质;解直角三角形;圆周角定理.
【专题】圆的有关概念及性质;与圆有关的位置关系;解直角三角形及其应用;几何直观;运算能力;推理能力.
【答案】(1)证明见解答过程;
(2)⊙O的半径为6;DG.
【分析】(1)连接OD,根据切线性质得∠ODB=90°,则∠BDE+∠ODA+∠ADE=90°,由弦切角定理得∠BDE=∠BAD,根据OA=OD得∠ODA=∠OAD,进而得∠BAC+∠ADE=90°,然后根据∠C+∠BAC=90°即可得出结论;
(2)延长OE交CB的延长线于点P,过点O作OH∥BC交AD于点H,在Rt△ODC中,根据sinC,设OD=3k,OC=5k,则CD=4k,进而得OA=OD=OF=3k,CF=2k,根据CF=4,得k=2,则⊙O的半径为6;再求出OC=5k=10,CD=4k=8,AC=16,证明△ODC和△ABC相似,利用相似三角形性质得AB,CB,BD,则AD,证明∠P=∠C得△OPC是等腰三角形,则PD=CD=8,再证明△AOH和△ACD相似,利用相似三角形性质得AH,OH=3,则DH=AD﹣AH,然后证明△OH和△PDG相似得,设HG=3x,DG=8x,则DH=HG+DG=11x=3√5,由此求出x即可得出DG的长.
【解答】(1)证明:连接OD,如图1所示:
∵⊙O与边BC相切于点D,
∴OD⊥BC,
∴∠ODB=90°,
即∠BDE+∠ODA+∠ADE=90°,
由弦切角定理得:∠BDE=∠BAD,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠BAD+∠OAD+∠ADE=90°,
即∠BAC+∠ADE=90°,
在Rt△ABC中,∠C+∠BAC=90°,
∴∠C=∠ADE;
(2)延长OE交CB的延长线于点P,过点O作OH∥BC交AD于点H,如图2所示:
∵OD⊥BC,
∴在Rt△ODC中,sinC,
设OD=3k,OC=5k,
由勾股定理得:CD4k,
∴OA=OD=OF=3k,
∴CF=OC﹣OF=5k﹣3k=2k,
∵CF=4,
∴2k=4,
解得:k=2,
∴OA=OD=OF=3k=6,
故⊙O的半径为6;
∵OC=5k=10,CD=4k=8,
∴AC=OA+OC=6+10=16,
∵OD⊥BC,∠ABC=90°,
∴∠ODC=∠ABC=90°,
∴OD∥AB,
∴△ODC∽△ABC,
∴,
∴,
∴AB,CB,
∴BD=CB﹣CD,
在Rt△ABD中,由勾股定理得:AD,
在Rt△PBE中,∠P+∠PEB=90°,
∴∠PEB=∠AEO,
∴∠P+∠AEO=90°,
∵OE=OA,
∴∠AEO=∠BAC,
∴∠P+∠BAC=90°,
又∵∠C+∠BAC=90°,
∴∠P=∠C,
∴△OPC是等腰三角形,
∵OD⊥BC,
∴PD=CD=8,
∵OH∥BC,
∴△AOH∽△ACD,
∴,
由,得AH AC=AD OA,
∴,
∴AH,
由,得:OH AC=CD OA,
∴OH×16=8×6,
∴OH=3,
∴DH=AD﹣AH,
∵OH∥BC,
∴△OHG∽△PDG,
∴,
设HG=3x,DG=8x,
∴DH=HG+DG=11x,
∴,
∴DG=8x.
【点评】此题主要考查了切线的性质,圆周角定理,解直角三角形,理解切线的性质,圆周角定理,熟练掌握锐角三角函数的定义,相似三角形的判定和性质是解决问题的关键,正确地添加辅助线,构造相似三角形是解决问题的难点.
18.(2025 蜀山区二模)如图,BC是⊙O的直径,AB,AD与⊙O相切于点B,D,过点C作CE∥AD分别交AB,AO于E,F两点,连接CD.
(1)求证:四边形ADCF是平行四边形;
(2)若⊙O的半径为,AD=5,求AE的长.
【考点】圆的综合题.
【专题】线段、角、相交线与平行线;图形的全等;等腰三角形与直角三角形;多边形与平行四边形;圆的有关概念及性质;与圆有关的位置关系;运算能力;推理能力.
【答案】(1)证明见解析;(2)AE的长为2.
【分析】(1)连接OD,利用切线的性质定理和全等三角形的判定与性质得到∠AOB=∠AODBOD,利用圆周角定理得到∠AOB=∠BCD,再利用平行线的判定定理和平行四边形的判定定理解答即可;
(2)利用(1)的结论和全等三角形的性质定理得到∠BAO=∠DAO,AB=AD=5,利用平行线的性质和等腰三角形的判定定理得到AE=EF,利用平行四边形的性质定理得到FC=AD=5,设AE=EF=x,则BE=AB﹣AE=5﹣x,EC=EF+FC=5+x,利用勾股定理列出方程解答即可得出结论.
【解答】(1)证明:连接OD,如图,
∵AB,AD与⊙O相切于点B,D,
∴OB⊥AB,OD⊥AD,
∴∠ABO=∠ADO=90°,
在Rt△ABO和Rt△ADO中,
,
∴Rt△ABO≌Rt△ADO(HL),
∴∠AOB=∠AODBOD,
∵∠BCDAOD,
∴∠AOB=∠BCD,
∴AO∥CD,
∵CE∥AD,
∴四边形ADCF是平行四边形;
(2)解:由(1)知:Rt△ABO≌Rt△ADO,
∴∠BAO=∠DAO,AB=AD=5,
∵CE∥AD,
∴∠AFE=∠DAO,
∴∠AFE=∠BAO,
∴AE=EF,
∵四边形ADCF是平行四边形,
∴FC=AD=5,
设AE=EF=x,则BE=AB﹣AE=5﹣x,EC=EF+FC=5+x,
∵⊙O的半径为,
∴BC=2.
∵∠ABC=90°,
∴BE2+BC2=EC2,
∴,
∴x=2.
∴AE的长为2.
【点评】本题主要考查了圆的有关性质,圆周角定理,圆的切线的性质定理,全等三角形的判定与性质,平行线的性质,平行四边形的判定与性质,等腰三角形的判定与性质,直角三角形的性质,勾股定理,连接经过切点的半径是解决此类问题常添加的辅助线.
19.(2025 滨江区一模)已知,AB,CD是⊙O的弦,CD⊥AB于点E,且,连接BC,AD.
(1)如图1,若AB是⊙O的直径,求∠C的度数.
(2)如图2,求证:①CD=CB.
②AE+AD=BE.
【考点】圆的综合题.
【专题】图形的全等;等腰三角形与直角三角形;圆的有关概念及性质;运算能力;推理能力.
【答案】(1)60°;(2)①证明见解析;②证明见解析.
【分析】(1)连接AC,利用圆周角定理解答即可;
(2)①取的中点F,连接AC,AF,CF,利用圆周角定理得到∠ACE+∠CAE=90°,可得CF为⊙O的直径,再利用垂径定理解答即可得出结论;
②在BE上取一点F,使EF=AE,连接DF并延长交BC于点G,利用相等的垂直平分线的性质,垂直的定义和圆周角定理得到∠BGF=∠CGD=∠BEC=∠AED=90°,利用全等三角形的判定与性质和等式的性质得到BG=DE,最后再利用全等三角形的判定与性质解答即可得出结论.
【解答】(1)解:连接AC,如图,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵,
∴∠BCD=2∠ACD,
∴∠BCDBCD=90°,
∴∠BCD=60°.
∴∠C的度数为60°;
(2)证明:①取的中点F,连接AC,AF,CF,如图,
则.
∵,
∴,
∴∠ACD=∠DCF=∠BAF,
∵CD⊥AB,
∴∠AEC=90°,
∴∠ACE+∠CAE=90°,
∴∠CAE+∠BAF=90°,
∴∠CAF=90°,
∴CF为⊙O的直径,
∵,
∴,
∴CD=CB;
②在BE上取一点F,使EF=AE,连接DF并延长交BC于点G,如图,
∵EF=AE,CD⊥AB,
∴CD垂直平分AF,
∴AD=DF,
∴∠A=∠AFD,
∵∠AFD=∠BFG,
∴∠BFG=∠A,
∵∠A+∠ADC=90°,∠ADC=∠B,
∴∠B+∠BFG=90°,
∴∠BGF=90°,
∴∠BGF=∠CGD=∠BEC=∠AED=90°.
在△CDG和△CBE中,
,
∴△CDG≌△CBE(AAS),
∴CG=CE,
∴CB﹣CG=CD﹣CE,
∴BG=DE.
在△ADE和△BFG中,
,
∴△ADE≌△BFG(ASA),
∴AD=BF.
∵BE=EF+BF,
∴AE+AD=BE.
【点评】本题主要考查了圆的有关性质,圆周角定理,垂径定理,直角三角形的性质,等腰三角形的性质,全等三角形的判定与性质,添加适当的辅助线构造全等三角形是解题的关键.
20.(2025 双城区一模)△ABC内接于⊙O,F为上一点,连接OF、CF,OF交弦AB于点D,若∠ACF=∠BCF.
(1)如图1,求证:;
(2)如图2,连接AO,若AB=AC,求证:AO⊥BC.
(3)在(2)的条件下,延长FO交⊙O于点E,过点F作FN⊥AC垂足为N,过点E作EM⊥AC垂足为M,若AN=3cm,MN=20cm,求DF的长.
【考点】圆的综合题.
【专题】线段、角、相交线与平行线;图形的全等;等腰三角形与直角三角形;圆的有关概念及性质;图形的相似;解直角三角形及其应用;运算能力;推理能力.
【答案】(1)证明见解析;(2)证明见解析;(3).
【分析】(1)连接OA,OB,利用圆周角定理解答即可;
(2)连接OC,OB,利用全等三角形的判定与性质得到∠CAO=∠BAO,再利用等腰三角形的三线合一的性质解答即可;
(3)过点O作OH⊥AC于H,利用垂径定理得到AH=CH,利用平行线的判定定理和平行线分线段成比例定理MH=HN,利用等式的性质得到AN=CM=3cm;连接AE,BE,OB,过E作EG⊥BC于点G,利用圆周角定理和全等三角形的判定与性质得到EG=EM,连接EC,利用全等三角形的判定与性质求得AC=26cm,BC=BG﹣CG=20cm;延长AO交BC于点P,利用勾股定理求得AP,设OB=OA=r,则OP=24﹣r,利用勾股定理求得r值,OD则.
【解答】(1)证明:连接OA,OB,如图,
∵,
∴∠AOF=2∠ACF,
∵,
∠BOF=2∠BCF,
∵∠ACF=∠BCF
∴∠AOF=∠BOF,
∴;
(2)证明:连接OC,OB,如图,
在△AOC和△AOB中,
,
∴△AOC≌△AOB(SSS),
∴∠CAO=∠BAO,
∴AO⊥BC;
(3)解:过点O作OH⊥AC于H,如图,
∵OH⊥AC,
∴AH=CH,
∵EM⊥AC,OH⊥AC,FN⊥AC,
∴EM∥OH∥FN,
∴,
∵OE=OF,
∴MH=HN.
∴CH﹣MH=AH﹣NH,
即AN=CM=3cm.
连接AE,BE,OB,过E作EG⊥BC于点G,
由(1)知:∠AOF=∠BOF,
∵OA=OB,
∴OD⊥AB,
∴EF是AB的垂直平分线.
∴AE=BE,
∵,
∴∠EAC=∠EBC.
在△AEM和△BEG中,
,
∴△AEM≌△BEG(AAS),
∴EG=EM,
连接EC,
在Rt△ECG和Rt△ECM中,
,
∴Rt△ECG≌Rt△ECM(HL),
∴CG=CM=3cm.
∵MN=20cm,
∴BG=AM=23cm.
∴AC=26cm,BC=BG﹣CG=20cm,
延长AO交BC于点P,
由(2)知:AO⊥BC,
∴∠APC=90°,
∴cm.
∴AP24(cm),
设OB=OA=r,则OP=24﹣r,
在Rt△BPO中,
∵OP2+BP2=OB2,
∴(24﹣r)2+102=r2,
∴,
∴OBcm.
∵EF是AB的垂直平分线,
∴AD=BDAB13cm,
∴OD,
∴.
【点评】本题主要考查了圆的有关性质,圆周角定理,垂径定理,等腰三角形的判定与性质,全等三角形的判定与性质,直角三角形的性质,勾股定理,平行线的判定与性质,平行线分线段成比例定理,添加适当的辅助线构造全等三角形是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考核心考点 圆
一.选择题(共10小题)
1.(2025 蜀山区二模)如图,CD为⊙O的直径,弦AB交CD于点E,点C为中点,若的度数为60°,点O到AD的距离为2,则OE的长为( )
A. B. C.3 D.2
2.(2025 綦江区一模)如图,在矩形ABCD中,AB=4,BC=4,连接AC,以点C为圆心,CD为半径作弧交BC于点E,连接AE.则图中阴影部分的面积为( )
A. B. C. D.
3.(2025春 肥西县二模)一个扇形的半径为4,弧长等于3π,则扇形的圆心角度数为( )
A.120° B.135° C.150° D.270°
4.(2025 黄埔区一模)如图,CD是⊙O的直径,AB是弦,CD⊥AB于E,DE=2,AB=8,则AC的长为( )
A.8 B.10 C.4 D.4
5.(2025 南安市)我国伟大的数学家刘徽于公元263年撰《九章算术注》中指出,“周三径一”不是圆周率值,实际上是圆内接正六边形周长和直径的比值(如图1).刘徽发现,圆内接正多边形边数无限增加时,多边形的周长就无限逼近圆周长,从而创立“割圆术”,为计算圆周率建立起相当严密的理论和完善的算法.如图2,六边形ABCDEF是圆内接正六边形,把每段弧二等分,可以作出一个圆内接正十二边形,点G为CD的中点,连接BG,CF,BG交CF于点P,若,则PG的长为( )
A. B. C. D.
6.(2025春 大足区二模)如图,在矩形ABCD中,AB=1,AD=2,以点D为圆心,AD长为半径画弧交BC于点E,连接DE,则图中阴影部分的面积为( )
A. B. C. D.
7.(2025 岳池县)如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AB=2,将Rt△ABC绕点C顺时针旋转90°后得到Rt△DEC,点B经过的路径为,将线段AB绕点A顺时针旋转60°后,点B恰好落在CE上的点F处,点B经过的路径为,则图中阴影部分的面积是( )
A. B. C. D.
8.(2025 雁塔区)如图,AD是⊙O的直径,AB是⊙O的弦,半径OC⊥AB,连接CD,交OB于点E,∠BOC=42°,则∠OED的度数是( )
A.63° B.61° C.53° D.65°
9.(2025 方城县)一把精美的扇子如图所示,扇子打开后扇形的圆心角为120°,且2OA=AB=6,这个环形扇面的面积是( )
A.21π B.23π C.24π D.25π
10.(2025 广安)如图,正六边形ABCDEF的边长为4,以A为圆心,AC的长为半径画弧,得,连接AC、AE,则图中阴影部分的面积为( )
A.2π B.8π C.π D.π
二.填空题(共5小题)
11.(2025 九龙坡区)如图,在四边形ABCD中,BD为对角线,AD=CD=2,BD=4,∠BAD=∠BCD=90°,过C、D两点的⊙O与AB相切于点G.E为CD中点,连接EO并延长,交AB于点F,则BF的长度为 ;⊙O的半径为 .
12.(2025春 青山区二模)如图,一个圆锥的高AO=2.4,底面半径OB=0.7,则AB= .
13.(2025春 芝罘区二模)如图,扇形AOB的圆心角为120°,C是OA中点,CD⊥OA交弧AB于点D,若弧AB的长为8π,则图中阴影部分的面积为 .
14.(2024秋 丹徒区期末)如图,已知⊙O的半径为10,现有正方形ABCD的边CD与⊙O相切,切点为E,且点A、B在⊙O上,则正方形ABCD的边长为 .
15.(2025 北碚区)如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,E为上一点,过点E作⊙O的切线,分别交DC,BA的延长线于点F和点G,连接BE交CD于点P,连接BD.若BD∥FG,,CD=4,则PH= ,AG= .
三.解答题(共5小题)
16.(2025 贵州)如图,△ABC内接于⊙O,∠ABC=45°,过点C作⊙O的切线交BA的延长线于E,连接OA交BC于点D,连接AC,OC.
(1)求证∠ACE=∠ABC;
(2)探究AC,BC与CD的数量关系,并说明理由;
(3)若tan∠DCO,CE=6,求⊙O的半径.
17.(2025 温江区二模)如图,在Rt△ABC中,∠B=90°,⊙O与边BC相切于点D,与AB,AC分别相交于点E,F,AD与OE相交于点G.
(1)求证:∠C=∠ADE;
(2)若CF=4,sinC,求⊙O的半径和DG的长.
18.(2025 蜀山区二模)如图,BC是⊙O的直径,AB,AD与⊙O相切于点B,D,过点C作CE∥AD分别交AB,AO于E,F两点,连接CD.
(1)求证:四边形ADCF是平行四边形;
(2)若⊙O的半径为,AD=5,求AE的长.
19.(2025 滨江区一模)已知,AB,CD是⊙O的弦,CD⊥AB于点E,且,连接BC,AD.
(1)如图1,若AB是⊙O的直径,求∠C的度数.
(2)如图2,求证:①CD=CB.
②AE+AD=BE.
20.(2025 双城区一模)△ABC内接于⊙O,F为上一点,连接OF、CF,OF交弦AB于点D,若∠ACF=∠BCF.
(1)如图1,求证:;
(2)如图2,连接AO,若AB=AC,求证:AO⊥BC.
(3)在(2)的条件下,延长FO交⊙O于点E,过点F作FN⊥AC垂足为N,过点E作EM⊥AC垂足为M,若AN=3cm,MN=20cm,求DF的长.
中考核心考点 圆
参考答案与试题解析
一.选择题(共10小题)
1.(2025 蜀山区二模)如图,CD为⊙O的直径,弦AB交CD于点E,点C为中点,若的度数为60°,点O到AD的距离为2,则OE的长为( )
A. B. C.3 D.2
【考点】圆心角、弧、弦的关系;垂径定理.
【专题】圆的有关概念及性质;推理能力.
【答案】D
【分析】连接AO,过O作OH⊥AD于H,得到OH=2,由垂径定理推出CD⊥AB,由圆心角、弧、弦的关系定理得到∠AOC=60°,由圆周角定理求出∠ODH=30°,由含30度角的直角三角形的性质得到OHOD,OEOA,得到OE=OH=2.
【解答】解:连接AO,过O作OH⊥AD于H,
∵点O到AD的距离为2,
∴OH=2,
∵CD为⊙O的直径,C为中点,
∴CD⊥AB,
∵的度数为60°,C为中点,
∴∠AOC=60°,
∴∠ODH∠AOC=30°,
∵∠OHD=90°,
∴OHOD,
∵∠OAE=90°﹣60°=30°,
∴OEOA,
∵OA=OD,
∴OE=OH=2.
故选:D.
【点评】本题考查圆心角、弧、弦的关系,垂径定理,含30度角的直角三角形,关键是由含30度角的直角三角形的性质推出OHOD,OEOA.
2.(2025 綦江区一模)如图,在矩形ABCD中,AB=4,BC=4,连接AC,以点C为圆心,CD为半径作弧交BC于点E,连接AE.则图中阴影部分的面积为( )
A. B. C. D.
【考点】扇形面积的计算;矩形的性质.
【专题】矩形 菱形 正方形;几何直观;推理能力.
【答案】A
【分析】利用特殊角的三角函数求出∠ACB=30°,再根据矩形的性质求出∠ACD的度数,最后利用阴影部分面积S=S△ACE+S扇形DCE﹣2S扇形ECF求解即可.
【解答】解:∵四边形ABCD是矩形,
∴∠ABC=∠BCD=90°,
在直角三角形ABC中,AB=4,,
∴,
∴∠ACB=∠ECF=30°,
∴∠ACD=∠BCD﹣∠ACB=90°﹣30°=60°.
∴阴影部分面积S=S△ACE+S扇形DCE﹣2S扇形ECF
.
故选:A.
【点评】本题考查了矩形的性质,扇形的面积公式,熟练掌握扇形的面积公式是解题的关键.
3.(2025春 肥西县二模)一个扇形的半径为4,弧长等于3π,则扇形的圆心角度数为( )
A.120° B.135° C.150° D.270°
【考点】弧长的计算.
【专题】与圆有关的计算;运算能力.
【答案】B
【分析】设扇形的圆心角度数为n°,根据弧长公式列关于n的方程并求解即可.
【解答】解:设扇形的圆心角度数为n°,
根据题意,得2π×4=3π,
解得n=135,
∴扇形的圆心角度数为135°.
故选:B.
【点评】本题考查弧长的计算,掌握弧长计算公式是解题的关键.
4.(2025 黄埔区一模)如图,CD是⊙O的直径,AB是弦,CD⊥AB于E,DE=2,AB=8,则AC的长为( )
A.8 B.10 C.4 D.4
【考点】垂径定理;勾股定理.
【专题】等腰三角形与直角三角形;圆的有关概念及性质;运算能力.
【答案】C
【分析】连接OA,设⊙O的半径为R,则OA=R,OE=R﹣2,根据垂径定理求出AE=BE=4,根据勾股定理求出OA2=OE2+AE2,得出R2=(R﹣2)2+42,求出R,再求出CE,最后根据勾股定理求出AC即可.
【解答】解:连接OA,设⊙O的半径为R,则OA=R,OE=R﹣2,
∵CD⊥AB,CD过圆心O,AB=8,
∴AE=BE=4,∠AEC=90°,
由勾股定理得:OA2=OE2+AE2,
即R2=(R﹣2)2+42,
解得:R=5,
即OA=OC=5,OE=5﹣2=3,
∴CE=OC+OE=5+3=8,
∴AC4,
故选:C.
【点评】本题考查了垂径定理和勾股定理,能熟记垂直于弦的直径平分这条弦是解此题的关键.
5.(2025 南安市)我国伟大的数学家刘徽于公元263年撰《九章算术注》中指出,“周三径一”不是圆周率值,实际上是圆内接正六边形周长和直径的比值(如图1).刘徽发现,圆内接正多边形边数无限增加时,多边形的周长就无限逼近圆周长,从而创立“割圆术”,为计算圆周率建立起相当严密的理论和完善的算法.如图2,六边形ABCDEF是圆内接正六边形,把每段弧二等分,可以作出一个圆内接正十二边形,点G为CD的中点,连接BG,CF,BG交CF于点P,若,则PG的长为( )
A. B. C. D.
【考点】正多边形和圆;确定圆的条件.
【专题】正多边形与圆;几何直观;运算能力;推理能力.
【答案】B
【分析】设正六边形ABCDEF的外接圆的圆心为O,连接OA、OB、OG、OD,则∠COF=3×60°=180°,所以圆心O在CF上,由点G为的中点,得∠COG=∠DOG∠COD=30°,可求得∠GCP=75°,由△BOC是等边三角形,得∠OCB=60°,则∠CBG∠COG=15°,所以∠GPC=∠GCP=75°,则PG=CG,作PI⊥CF交BC于点I,则∠PIC=30°,所以∠IPB=∠CBG=15°,则CI=2CP1,BI=PICP,于是得CO=BC,再证明△CGP∽△COG,得,则PG=CG,于是得到问题的答案.
【解答】解:如图2,设正六边形ABCDEF的外接圆的圆心为O,连接OA、OB、OG、OD,
∵∠AOF=∠AOB=∠BOC=∠COD360°=60°,
∴∠COF=3×60°=180°,∠CGP∠BOC=30°,
∴圆心O在CF上,
∵点G为的中点,
∴∠COG=∠DOG∠COD=30°,
∵OC=OG,
∴∠GCP=∠OGC(180°﹣30°)=75°,
∵OB=OC,∠BOC=60°,
∴△BOC是等边三角形,
∴∠OCB=60°,
∵∠CBG∠COG=15°,
∴∠GPC=∠OCB+∠CBG=75°=∠GCP,
∴PG=CG,
作PI⊥CF交BC于点I,则∠CPI=90°,
∴∠PIC=90°﹣60°=30°,CP,
∴∠IPB=∠PIC﹣∠CBG=15°=∠CBG,CI=2CP=2×()1,
∴BI=PICP(),
∴CO=BC1,
∵∠CGP=∠COG,∠PCG=∠GPO,
∴△CGP∽△COG,
∴,
∴PG=CG,
故选:B.
【点评】此题重点考查正多边形与圆、圆周角定理、等边三角形的判定与性质、直角三角形中30°角所对的直角边等于斜边的一半、勾股定理、相似三角形的判定与性质等知识,正确地作出所需要的辅助线是解题的关键.
6.(2025春 大足区二模)如图,在矩形ABCD中,AB=1,AD=2,以点D为圆心,AD长为半径画弧交BC于点E,连接DE,则图中阴影部分的面积为( )
A. B. C. D.
【考点】扇形面积的计算;矩形的性质.
【专题】与圆有关的计算;运算能力.
【答案】C
【分析】根据条件,先求出∠ADE=∠DEC=30°,再利用扇形的面积公式计算即可.
【解答】解:∵矩形ABCD中,AB=1,AD=2,以点D为圆心,AD长为半径画弧交BC于点E,连接DE,
∴CD=1,DE=2,∠C=90°,
∴∠DEC=30°,
∵AD∥BC,
∴∠ADE=∠DEC=30°,
∴S阴影.
故选:C.
【点评】本题考查了扇形面积的计算、矩形的性质,熟练掌握扇形面积公式是解答本题的关键.
7.(2025 岳池县)如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AB=2,将Rt△ABC绕点C顺时针旋转90°后得到Rt△DEC,点B经过的路径为,将线段AB绕点A顺时针旋转60°后,点B恰好落在CE上的点F处,点B经过的路径为,则图中阴影部分的面积是( )
A. B. C. D.
【考点】扇形面积的计算;旋转的性质;含30度角的直角三角形;勾股定理;圆周角定理.
【专题】等腰三角形与直角三角形;与圆有关的计算;运算能力.
【答案】D
【分析】根据直角三角形的性质和勾股定理可以求得AC和AB的长,再观察图形可知,S阴影=S△ABC+S扇形CBE﹣S扇形ABF,然后代入数据计算即可.
【解答】解:∵∠ACB=90°,∠A=60°,AB=2,
∴∠ABC=30°,
∴AC=1,BC
由图可得,
S阴影=S△ABC+S扇形CBE﹣S扇形ABF
π
π,
故选:D.
【点评】本题考查扇形面积的计算、勾股定理、直角三角形的性质,解答本题的关键是明确题意,利用数形结合的思想解答.
8.(2025 雁塔区)如图,AD是⊙O的直径,AB是⊙O的弦,半径OC⊥AB,连接CD,交OB于点E,∠BOC=42°,则∠OED的度数是( )
A.63° B.61° C.53° D.65°
【考点】圆周角定理;垂径定理;圆心角、弧、弦的关系.
【专题】与圆有关的计算;几何直观;推理能力.
【答案】A
【分析】由垂径定理可得,由定理可得∠AOC=∠BOC=42°,,求出∠DOE=96°,再由三角形内角和定理计算即可得解.
【解答】解:∵AD是⊙O的直径,AB是⊙O的弦,半径OC⊥AB,∠BOC=42°,
∴,
∴∠AOC=∠BOC=42°,
∴,∠DOE=180°﹣∠AOC﹣∠BOC=96°,
∴∠OED=180°﹣∠D﹣∠DOE=63°,
故选:A.
【点评】本题考查了圆周角定理,垂径定理,圆心角、弧、弦的关系,解答本题的关键是熟练掌握圆周角定理与垂径定理.
9.(2025 方城县)一把精美的扇子如图所示,扇子打开后扇形的圆心角为120°,且2OA=AB=6,这个环形扇面的面积是( )
A.21π B.23π C.24π D.25π
【考点】扇形面积的计算;圆环.
【专题】运算能力.
【答案】C
【分析】根据题意,用大扇形的面积减去小扇形的面积即可解决问题.
【解答】解:由题知,
因为2OA=AB=6,
所以OA=3,
所以OB=9,
则大扇形的面积为:;
小扇形的面积为:,
所以这个环形扇面的面积是27π﹣3π=24π.
故选:C.
【点评】本题主要考查了扇形面积的计算及圆环,熟知扇形的面积公式是解题的关键.
10.(2025 广安)如图,正六边形ABCDEF的边长为4,以A为圆心,AC的长为半径画弧,得,连接AC、AE,则图中阴影部分的面积为( )
A.2π B.8π C.π D.π
【考点】正多边形和圆;扇形面积的计算.
【专题】正多边形与圆;与圆有关的计算;解直角三角形及其应用;运算能力;推理能力.
【答案】B
【分析】根据正六边形的性质,等腰三角形的性质以及直角三角形的边角关系求出扇形的半径、圆心角度数,由扇形面积的计算公式进行计算即可.
【解答】解:∵六边形ABCDEF是正六边形,
∴AB=BC=4,∠ABC120°=∠BAF,
∴∠BAC=∠BCA=30°,
同理∠FAE=30°,
∴∠EAC=120°﹣30°﹣30°=60°,
过点B作BM⊥AC 于点M,则AM=MCAC,∠ABM=60°,
在Rt△ABM 中,AB=4,∠ABM=60°,
∴AMAB=2,
∴AC=2AM=4,
∴S阴影=S扇形8π,
故选:B.
【点评】本题考查正多边形和圆,扇形面积的计算,掌握正六边形的性质,等腰三角形的性质,直角三角形的边角关系以及扇形面积的计算公式是正确解答的关键.
二.填空题(共5小题)
11.(2025 九龙坡区)如图,在四边形ABCD中,BD为对角线,AD=CD=2,BD=4,∠BAD=∠BCD=90°,过C、D两点的⊙O与AB相切于点G.E为CD中点,连接EO并延长,交AB于点F,则BF的长度为 ;⊙O的半径为 .
【考点】切线的性质;垂径定理;圆周角定理.
【专题】方程思想;等腰三角形与直角三角形;矩形 菱形 正方形;与圆有关的位置关系;运算能力;推理能力;应用意识.
【答案】,.
【分析】作FH⊥BC于点H,如图1所示,由垂径定理推论可得OE⊥CD.进而可得四边形CEFH为矩形,CE=FH1.由已知可得∠ABD=∠CBD=30°,BC.BF.连接OG、OD,设BD交EF于点H,由切线性质可得∠FGO=90°.∠BFH=30°,所以BH,HC=BC﹣BH,EF=HC,再导角证明△BJF为等腰三角形,所以BF=JF.设JO=x,则OF=FJ+JOx,半径GO=sin60°×OF(x)=1OD,OE=EF﹣FO(x).在Rt△ODE中,由勾股定理可得()2+1=(1)2,解得x或(不合题意,舍去),故GO=1().
【解答】解:作FH⊥BC于点H,如图1所示,
∵E为CD中点,OE为过圆心的直线,
∴由垂径定理推论可得OE⊥CD.
∵∠BAD=∠BCD=90°,
∴四边形CEFH为矩形,CE=FH1.
∵AD=CD=2,BD=4,
∴∠ABD=∠CBD=30°,BC.
∴BF.
连接OG、OD,设BD交EF于点H,如图1所示,
由切线性质可得∠FGO=90°.
∵∠BFH=30°,
∴BH,
∴HC=BC﹣BH.
∵四边形CEFH为矩形,
∴EF=HC.
∵∠JDE=60°,∠JED=90°,
∴∠DJE=30°=∠FJB,
∵∠FBD=30°,
∴BF=JF.
设JO=x,则OF=FJ+JOx,
∵∠BFH=30°,∠HFE=90°,
∴∠GFO=60°,
故半径GO=sin60°×OF(x)=1OD,
OE=EF﹣FO(x).
在Rt△ODE中,由勾股定理可得:OE2+DE2=OD2,
即()2+1=(1)2,整理得,
解得x或(不合题意,舍去),
故GO=1().
故答案为:,.
【点评】本题考查了直角三角形的性质,勾股定理,解直角三角形,垂径定理的推论,矩形的判定与性质,切线的性质,熟练掌握以上内容并能作出恰当的辅助线是解题关键.
12.(2025春 青山区二模)如图,一个圆锥的高AO=2.4,底面半径OB=0.7,则AB= 2.5 .
【考点】圆锥的计算.
【专题】运算能力.
【答案】2.5.
【分析】根据勾股定理进行计算即可.
【解答】解:由题知,
因为圆锥的高AO=2.4,底面半径OB=0.7,
所以AB2.5.
故答案为:2.5.
【点评】本题主要考查了圆锥的计算,熟知勾股定理是解题的关键.
13.(2025春 芝罘区二模)如图,扇形AOB的圆心角为120°,C是OA中点,CD⊥OA交弧AB于点D,若弧AB的长为8π,则图中阴影部分的面积为 .
【考点】扇形面积的计算;线段垂直平分线的性质;弧长的计算.
【专题】与圆有关的计算;运算能力.
【答案】.
【分析】连接OD,设OA=OB=OD=r,根据弧长公式列出方程求出r的值,再解Rt△COD求出∠COD的度数,进而求出CD的长,最后根据S阴影=S扇形AOD﹣S△OCD列式计算即可.
【解答】解:如图所示,连接OD,设OA=OB=OD=r,
由条件可知,
∴r=12,
∴OA=OD=12,
∵C是OA中点,
∴,
∴,
∴∠COD=60°,
∴,
∴S阴影=S扇形AOD﹣S△OCD
,
故答案为:.
【点评】本题主要考查了求不规则图形面积,弧长公式,解直角三角形,熟练掌握原式知识点是关键.
14.(2024秋 丹徒区期末)如图,已知⊙O的半径为10,现有正方形ABCD的边CD与⊙O相切,切点为E,且点A、B在⊙O上,则正方形ABCD的边长为 16 .
【考点】切线的性质;正方形的性质.
【专题】矩形 菱形 正方形;与圆有关的位置关系;运算能力;推理能力.
【答案】16.
【分析】连接并延长EO交AB于点F,连接OB,由切线的性质得CD⊥OE,可证明四边AFED是矩形,则OF⊥AB,所以AF=BFAB,设正方形ABCD的边长为m,则EF=AD=AB=m,BFm,而OB=OE=10,所以OF=m﹣10,由勾股定理得(m﹣10)2102,求得m=16,于是得到问题的答案.
【解答】解:连接并延长EO交AB于点F,连接OB,
∵CD与⊙O相切于点E,
∴CD⊥OE,
∵四边形ABCD是正方形,
∴∠A=∠D=∠DEF=90°,
∴四边AFED是矩形,
∴∠AFE=90°,
∴OF⊥AB,
∴AF=BFAB,
设正方形ABCD的边长为m,则EF=AD=AB=m,BFm,
∵⊙O的半径为10,
∴OB=OE=10,
∴OF=m﹣10,
∵∠OFB=90°,
∴OF2+BF2=OB2,
∴(m﹣10)2102,
解得m=16或m=0(不符合题意,舍去),
∴正方形ABCD的边长为16,
故答案为:16.
【点评】此题重点考查正方形的性质、切线的性质、垂径定理、勾股定理等知识,正确地作出辅助线是解题的关键.
15.(2025 北碚区)如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,E为上一点,过点E作⊙O的切线,分别交DC,BA的延长线于点F和点G,连接BE交CD于点P,连接BD.若BD∥FG,,CD=4,则PH= ,AG= .
【考点】切线的性质;勾股定理;垂径定理;圆周角定理.
【专题】几何图形;与圆有关的位置关系;推理能力.
【答案】,.
【分析】连接OE、OD、AE,如图,设⊙O的半径为r,则OH=r,根据垂径定理得到CH=DH=2,则利用勾股定理计算得BD,利用勾股定理得到方程(r)2+22=r2,解方程得r,再根据切线的性质得到∠OEG=90°,接着证明Rt△OEG∽Rt△DHB,利用相似三角形的性质得到OG,GE,所以AG,然后证明△GEA∽△GBE,则,最后证明△BPH∽△BAE得到,所以PHBH.
【解答】解:连接OE、OD、AE,如图,设⊙O的半径为r,则OH=r,
∵AB⊥CD,
∴CH=DHCD=2,在Rt△OHD中,(r)2+22=r2,
解得r,
在Rt△BDH中,∵BH,DH=2,
∴BD,∵
GF为⊙O的切线,
∴OE⊥GF,
∴∠OEG=90°,
∵BD∥FG,
∴∠G=∠DBH,
∴Rt△OEG∽Rt△DHB,
∴,即,
解得OG,GE,
∴AG=OG﹣OA,
∵AB为直径,
∴∠AEB=90°,
∵∠GEA+∠AEO=90°,∠AEO+∠OEB=90°,
∴∠GEA=∠OEB,
∵OB=OE,
∴∠OEB=∠OBE,
∴∠GEA=∠OBE,
∵∠EGA=∠BGE,
∴△GEA∽△GBE,
∴,
∵∠HBP=∠EBA,∠BHP=∠BEA,
∴△BPH∽△BAE,
∴,
∴,
∴BH.
故答案为:,.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了垂径定理、圆周角定理和勾股定理.
三.解答题(共5小题)
16.(2025 贵州)如图,△ABC内接于⊙O,∠ABC=45°,过点C作⊙O的切线交BA的延长线于E,连接OA交BC于点D,连接AC,OC.
(1)求证∠ACE=∠ABC;
(2)探究AC,BC与CD的数量关系,并说明理由;
(3)若tan∠DCO,CE=6,求⊙O的半径.
【考点】圆的综合题.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;圆的有关概念及性质;与圆有关的位置关系;图形的相似;解直角三角形及其应用;运算能力;推理能力.
【答案】(1)证明见解析;(2)AC,BC与CD的数量关系为AC2=CD BC,理由见解析;(3)4.
【分析】(1)利用晕这就对了,等腰直角三角形的性质,圆的切线的性质定理和直角三角形的性质解答即可;
(2)利用相似三角形的判定与性质解答即可;
(3)过点A作AF⊥EC于点F,过点B作BG⊥OA于点G,利用直角三角形的边角关系定理得到tan∠DCO,设OD=x,则OC=3x,利用正方形的判定与性质得到OA=OC=AF=FC=3x,AC=3x,AD=OA﹣OD=2x,利用(2)的结论求得BD,利用直角三角形的边角关系定理求得BG,AG,再利用相似三角形的判定与性质求得EF,最后利用EC=EF+CF列出方程求得x值,则⊙O的半径=OC=3x=4.
【解答】(1)证明:∵∠AOC=2∠ABC,∠ABC=45°,
∴∠AOC=90°,
∵OA=OC,
∴∠OAC=∠OCA=45°.
∵CE是⊙O的切线,
∴OC⊥CE,
∴∠OCE=90°,
∴∠ACE=90°﹣∠OCA=45°,
∴∠ACE=∠ABC;
(2)解:AC,BC与CD的数量关系为AC2=CD BC,理由:
由(1)知:∠ACE=∠ABC,∠OAC=∠OCA,
∴∠OAC=∠ABC,
∵∠ACD=∠BCA,
∴△ACD∽△BCA,
∴,
∴AC2=CD BC.
(3)解:过点A作AF⊥EC于点F,过点B作BG⊥OA于点G,如图,
∵tan∠DCO,∠AOC=90°,
∴tan∠DCO,
设OD=x,则OC=3x,
∴CDx.
由(1)知:∠AOC=90°,OC⊥EC,
∵AF⊥EC,
∴四边形AOCF为矩形,
∵OA=OC,
∴四边形AOCF为正方形,
∴OA=OC=AF=FC=3x,
∴AC=3x,AD=OA﹣OD=2x.
由(2)知:AC2=CD BC,
∴,
∴BCx,
∴BD=BC﹣CDx,
∵∠BGD=∠AOC=90°,
∴BG∥OC,
∴∠DBG=∠DCO,
∴tan∠DBG=tan∠DCO,
∵tan∠DBG,
∴,
设DG=k,则BG=3k,
∴BD,
∴k,
∴BGx,AG=AD﹣DGx.
∵四边形AOCF为正方形,
∴OA∥CE,
∴∠BAG=∠E,
∵∠BGA=∠EFA=90°,
∴△BGA∽△AFE,
∴,
∴,
∴EFx,
∴EC=EF+CF3x=6,
∴x.
∴⊙O的半径=OC=3x=4.
【点评】本题主要考查了圆的有关性质,圆周角定理,圆的切线的性质定理,直角三角形的性质,勾股定理,直角三角形的边角关系定理,等腰直角三角形的性质,相似三角形的判定与性质,连接经过切点的半径是解决此类问题常添加的辅助线.
17.(2025 温江区二模)如图,在Rt△ABC中,∠B=90°,⊙O与边BC相切于点D,与AB,AC分别相交于点E,F,AD与OE相交于点G.
(1)求证:∠C=∠ADE;
(2)若CF=4,sinC,求⊙O的半径和DG的长.
【考点】切线的性质;解直角三角形;圆周角定理.
【专题】圆的有关概念及性质;与圆有关的位置关系;解直角三角形及其应用;几何直观;运算能力;推理能力.
【答案】(1)证明见解答过程;
(2)⊙O的半径为6;DG.
【分析】(1)连接OD,根据切线性质得∠ODB=90°,则∠BDE+∠ODA+∠ADE=90°,由弦切角定理得∠BDE=∠BAD,根据OA=OD得∠ODA=∠OAD,进而得∠BAC+∠ADE=90°,然后根据∠C+∠BAC=90°即可得出结论;
(2)延长OE交CB的延长线于点P,过点O作OH∥BC交AD于点H,在Rt△ODC中,根据sinC,设OD=3k,OC=5k,则CD=4k,进而得OA=OD=OF=3k,CF=2k,根据CF=4,得k=2,则⊙O的半径为6;再求出OC=5k=10,CD=4k=8,AC=16,证明△ODC和△ABC相似,利用相似三角形性质得AB,CB,BD,则AD,证明∠P=∠C得△OPC是等腰三角形,则PD=CD=8,再证明△AOH和△ACD相似,利用相似三角形性质得AH,OH=3,则DH=AD﹣AH,然后证明△OH和△PDG相似得,设HG=3x,DG=8x,则DH=HG+DG=11x=3√5,由此求出x即可得出DG的长.
【解答】(1)证明:连接OD,如图1所示:
∵⊙O与边BC相切于点D,
∴OD⊥BC,
∴∠ODB=90°,
即∠BDE+∠ODA+∠ADE=90°,
由弦切角定理得:∠BDE=∠BAD,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠BAD+∠OAD+∠ADE=90°,
即∠BAC+∠ADE=90°,
在Rt△ABC中,∠C+∠BAC=90°,
∴∠C=∠ADE;
(2)延长OE交CB的延长线于点P,过点O作OH∥BC交AD于点H,如图2所示:
∵OD⊥BC,
∴在Rt△ODC中,sinC,
设OD=3k,OC=5k,
由勾股定理得:CD4k,
∴OA=OD=OF=3k,
∴CF=OC﹣OF=5k﹣3k=2k,
∵CF=4,
∴2k=4,
解得:k=2,
∴OA=OD=OF=3k=6,
故⊙O的半径为6;
∵OC=5k=10,CD=4k=8,
∴AC=OA+OC=6+10=16,
∵OD⊥BC,∠ABC=90°,
∴∠ODC=∠ABC=90°,
∴OD∥AB,
∴△ODC∽△ABC,
∴,
∴,
∴AB,CB,
∴BD=CB﹣CD,
在Rt△ABD中,由勾股定理得:AD,
在Rt△PBE中,∠P+∠PEB=90°,
∴∠PEB=∠AEO,
∴∠P+∠AEO=90°,
∵OE=OA,
∴∠AEO=∠BAC,
∴∠P+∠BAC=90°,
又∵∠C+∠BAC=90°,
∴∠P=∠C,
∴△OPC是等腰三角形,
∵OD⊥BC,
∴PD=CD=8,
∵OH∥BC,
∴△AOH∽△ACD,
∴,
由,得AH AC=AD OA,
∴,
∴AH,
由,得:OH AC=CD OA,
∴OH×16=8×6,
∴OH=3,
∴DH=AD﹣AH,
∵OH∥BC,
∴△OHG∽△PDG,
∴,
设HG=3x,DG=8x,
∴DH=HG+DG=11x,
∴,
∴DG=8x.
【点评】此题主要考查了切线的性质,圆周角定理,解直角三角形,理解切线的性质,圆周角定理,熟练掌握锐角三角函数的定义,相似三角形的判定和性质是解决问题的关键,正确地添加辅助线,构造相似三角形是解决问题的难点.
18.(2025 蜀山区二模)如图,BC是⊙O的直径,AB,AD与⊙O相切于点B,D,过点C作CE∥AD分别交AB,AO于E,F两点,连接CD.
(1)求证:四边形ADCF是平行四边形;
(2)若⊙O的半径为,AD=5,求AE的长.
【考点】圆的综合题.
【专题】线段、角、相交线与平行线;图形的全等;等腰三角形与直角三角形;多边形与平行四边形;圆的有关概念及性质;与圆有关的位置关系;运算能力;推理能力.
【答案】(1)证明见解析;(2)AE的长为2.
【分析】(1)连接OD,利用切线的性质定理和全等三角形的判定与性质得到∠AOB=∠AODBOD,利用圆周角定理得到∠AOB=∠BCD,再利用平行线的判定定理和平行四边形的判定定理解答即可;
(2)利用(1)的结论和全等三角形的性质定理得到∠BAO=∠DAO,AB=AD=5,利用平行线的性质和等腰三角形的判定定理得到AE=EF,利用平行四边形的性质定理得到FC=AD=5,设AE=EF=x,则BE=AB﹣AE=5﹣x,EC=EF+FC=5+x,利用勾股定理列出方程解答即可得出结论.
【解答】(1)证明:连接OD,如图,
∵AB,AD与⊙O相切于点B,D,
∴OB⊥AB,OD⊥AD,
∴∠ABO=∠ADO=90°,
在Rt△ABO和Rt△ADO中,
,
∴Rt△ABO≌Rt△ADO(HL),
∴∠AOB=∠AODBOD,
∵∠BCDAOD,
∴∠AOB=∠BCD,
∴AO∥CD,
∵CE∥AD,
∴四边形ADCF是平行四边形;
(2)解:由(1)知:Rt△ABO≌Rt△ADO,
∴∠BAO=∠DAO,AB=AD=5,
∵CE∥AD,
∴∠AFE=∠DAO,
∴∠AFE=∠BAO,
∴AE=EF,
∵四边形ADCF是平行四边形,
∴FC=AD=5,
设AE=EF=x,则BE=AB﹣AE=5﹣x,EC=EF+FC=5+x,
∵⊙O的半径为,
∴BC=2.
∵∠ABC=90°,
∴BE2+BC2=EC2,
∴,
∴x=2.
∴AE的长为2.
【点评】本题主要考查了圆的有关性质,圆周角定理,圆的切线的性质定理,全等三角形的判定与性质,平行线的性质,平行四边形的判定与性质,等腰三角形的判定与性质,直角三角形的性质,勾股定理,连接经过切点的半径是解决此类问题常添加的辅助线.
19.(2025 滨江区一模)已知,AB,CD是⊙O的弦,CD⊥AB于点E,且,连接BC,AD.
(1)如图1,若AB是⊙O的直径,求∠C的度数.
(2)如图2,求证:①CD=CB.
②AE+AD=BE.
【考点】圆的综合题.
【专题】图形的全等;等腰三角形与直角三角形;圆的有关概念及性质;运算能力;推理能力.
【答案】(1)60°;(2)①证明见解析;②证明见解析.
【分析】(1)连接AC,利用圆周角定理解答即可;
(2)①取的中点F,连接AC,AF,CF,利用圆周角定理得到∠ACE+∠CAE=90°,可得CF为⊙O的直径,再利用垂径定理解答即可得出结论;
②在BE上取一点F,使EF=AE,连接DF并延长交BC于点G,利用相等的垂直平分线的性质,垂直的定义和圆周角定理得到∠BGF=∠CGD=∠BEC=∠AED=90°,利用全等三角形的判定与性质和等式的性质得到BG=DE,最后再利用全等三角形的判定与性质解答即可得出结论.
【解答】(1)解:连接AC,如图,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵,
∴∠BCD=2∠ACD,
∴∠BCDBCD=90°,
∴∠BCD=60°.
∴∠C的度数为60°;
(2)证明:①取的中点F,连接AC,AF,CF,如图,
则.
∵,
∴,
∴∠ACD=∠DCF=∠BAF,
∵CD⊥AB,
∴∠AEC=90°,
∴∠ACE+∠CAE=90°,
∴∠CAE+∠BAF=90°,
∴∠CAF=90°,
∴CF为⊙O的直径,
∵,
∴,
∴CD=CB;
②在BE上取一点F,使EF=AE,连接DF并延长交BC于点G,如图,
∵EF=AE,CD⊥AB,
∴CD垂直平分AF,
∴AD=DF,
∴∠A=∠AFD,
∵∠AFD=∠BFG,
∴∠BFG=∠A,
∵∠A+∠ADC=90°,∠ADC=∠B,
∴∠B+∠BFG=90°,
∴∠BGF=90°,
∴∠BGF=∠CGD=∠BEC=∠AED=90°.
在△CDG和△CBE中,
,
∴△CDG≌△CBE(AAS),
∴CG=CE,
∴CB﹣CG=CD﹣CE,
∴BG=DE.
在△ADE和△BFG中,
,
∴△ADE≌△BFG(ASA),
∴AD=BF.
∵BE=EF+BF,
∴AE+AD=BE.
【点评】本题主要考查了圆的有关性质,圆周角定理,垂径定理,直角三角形的性质,等腰三角形的性质,全等三角形的判定与性质,添加适当的辅助线构造全等三角形是解题的关键.
20.(2025 双城区一模)△ABC内接于⊙O,F为上一点,连接OF、CF,OF交弦AB于点D,若∠ACF=∠BCF.
(1)如图1,求证:;
(2)如图2,连接AO,若AB=AC,求证:AO⊥BC.
(3)在(2)的条件下,延长FO交⊙O于点E,过点F作FN⊥AC垂足为N,过点E作EM⊥AC垂足为M,若AN=3cm,MN=20cm,求DF的长.
【考点】圆的综合题.
【专题】线段、角、相交线与平行线;图形的全等;等腰三角形与直角三角形;圆的有关概念及性质;图形的相似;解直角三角形及其应用;运算能力;推理能力.
【答案】(1)证明见解析;(2)证明见解析;(3).
【分析】(1)连接OA,OB,利用圆周角定理解答即可;
(2)连接OC,OB,利用全等三角形的判定与性质得到∠CAO=∠BAO,再利用等腰三角形的三线合一的性质解答即可;
(3)过点O作OH⊥AC于H,利用垂径定理得到AH=CH,利用平行线的判定定理和平行线分线段成比例定理MH=HN,利用等式的性质得到AN=CM=3cm;连接AE,BE,OB,过E作EG⊥BC于点G,利用圆周角定理和全等三角形的判定与性质得到EG=EM,连接EC,利用全等三角形的判定与性质求得AC=26cm,BC=BG﹣CG=20cm;延长AO交BC于点P,利用勾股定理求得AP,设OB=OA=r,则OP=24﹣r,利用勾股定理求得r值,OD则.
【解答】(1)证明:连接OA,OB,如图,
∵,
∴∠AOF=2∠ACF,
∵,
∠BOF=2∠BCF,
∵∠ACF=∠BCF
∴∠AOF=∠BOF,
∴;
(2)证明:连接OC,OB,如图,
在△AOC和△AOB中,
,
∴△AOC≌△AOB(SSS),
∴∠CAO=∠BAO,
∴AO⊥BC;
(3)解:过点O作OH⊥AC于H,如图,
∵OH⊥AC,
∴AH=CH,
∵EM⊥AC,OH⊥AC,FN⊥AC,
∴EM∥OH∥FN,
∴,
∵OE=OF,
∴MH=HN.
∴CH﹣MH=AH﹣NH,
即AN=CM=3cm.
连接AE,BE,OB,过E作EG⊥BC于点G,
由(1)知:∠AOF=∠BOF,
∵OA=OB,
∴OD⊥AB,
∴EF是AB的垂直平分线.
∴AE=BE,
∵,
∴∠EAC=∠EBC.
在△AEM和△BEG中,
,
∴△AEM≌△BEG(AAS),
∴EG=EM,
连接EC,
在Rt△ECG和Rt△ECM中,
,
∴Rt△ECG≌Rt△ECM(HL),
∴CG=CM=3cm.
∵MN=20cm,
∴BG=AM=23cm.
∴AC=26cm,BC=BG﹣CG=20cm,
延长AO交BC于点P,
由(2)知:AO⊥BC,
∴∠APC=90°,
∴cm.
∴AP24(cm),
设OB=OA=r,则OP=24﹣r,
在Rt△BPO中,
∵OP2+BP2=OB2,
∴(24﹣r)2+102=r2,
∴,
∴OBcm.
∵EF是AB的垂直平分线,
∴AD=BDAB13cm,
∴OD,
∴.
【点评】本题主要考查了圆的有关性质,圆周角定理,垂径定理,等腰三角形的判定与性质,全等三角形的判定与性质,直角三角形的性质,勾股定理,平行线的判定与性质,平行线分线段成比例定理,添加适当的辅助线构造全等三角形是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
