【中考押题预测】2025年中考数学核心考点考前冲刺 整式(含解析)
文档属性
| 名称 | 【中考押题预测】2025年中考数学核心考点考前冲刺 整式(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 813.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 16:14:54 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中考核心考点 整式
一.选择题(共10小题)
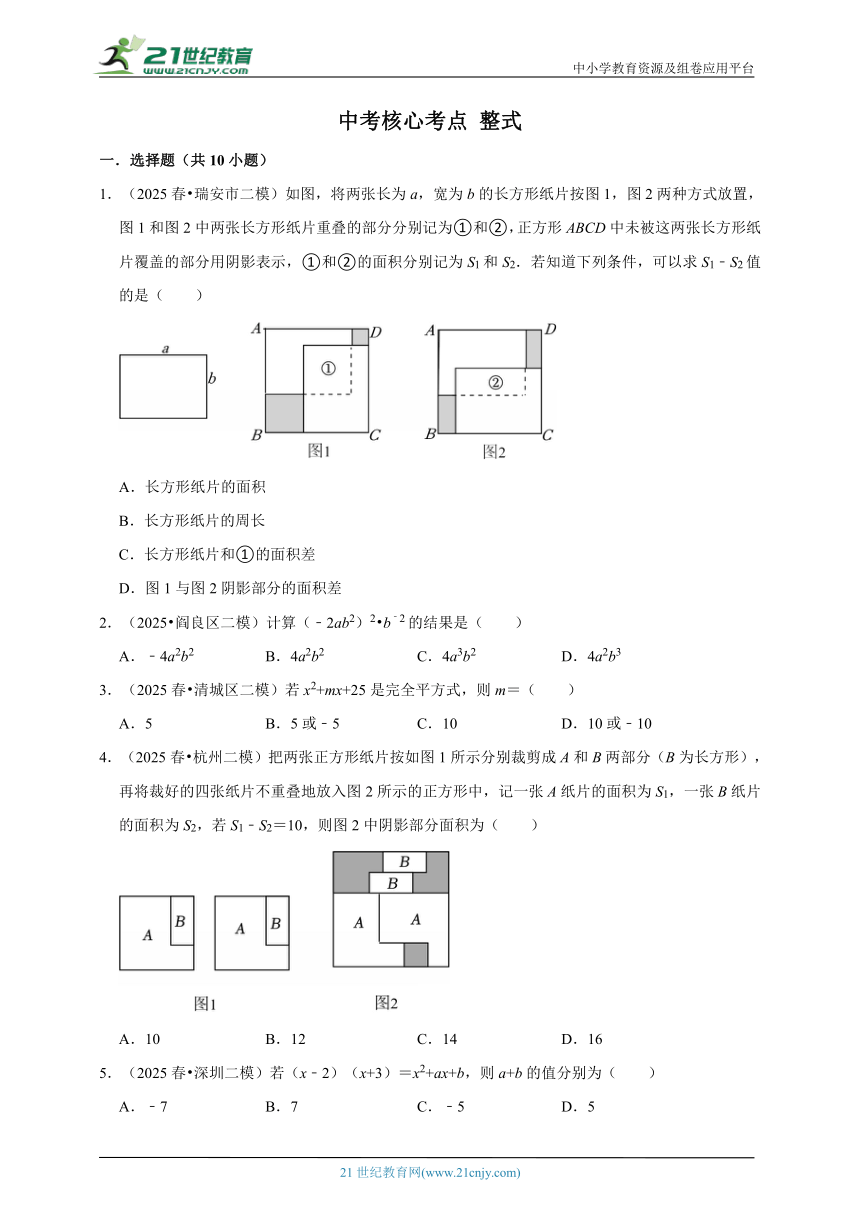
1.(2025春 瑞安市二模)如图,将两张长为a,宽为b的长方形纸片按图1,图2两种方式放置,图1和图2中两张长方形纸片重叠的部分分别记为①和②,正方形ABCD中未被这两张长方形纸片覆盖的部分用阴影表示,①和②的面积分别记为S1和S2.若知道下列条件,可以求S1﹣S2值的是( )
A.长方形纸片的面积
B.长方形纸片的周长
C.长方形纸片和①的面积差
D.图1与图2阴影部分的面积差
2.(2025 阎良区二模)计算(﹣2ab2)2 b﹣2的结果是( )
A.﹣4a2b2 B.4a2b2 C.4a3b2 D.4a2b3
3.(2025春 清城区二模)若x2+mx+25是完全平方式,则m=( )
A.5 B.5或﹣5 C.10 D.10或﹣10
4.(2025春 杭州二模)把两张正方形纸片按如图1所示分别裁剪成A和B两部分(B为长方形),再将裁好的四张纸片不重叠地放入图2所示的正方形中,记一张A纸片的面积为S1,一张B纸片的面积为S2,若S1﹣S2=10,则图2中阴影部分面积为( )
A.10 B.12 C.14 D.16
5.(2025春 深圳二模)若(x﹣2)(x+3)=x2+ax+b,则a+b的值分别为( )
A.﹣7 B.7 C.﹣5 D.5
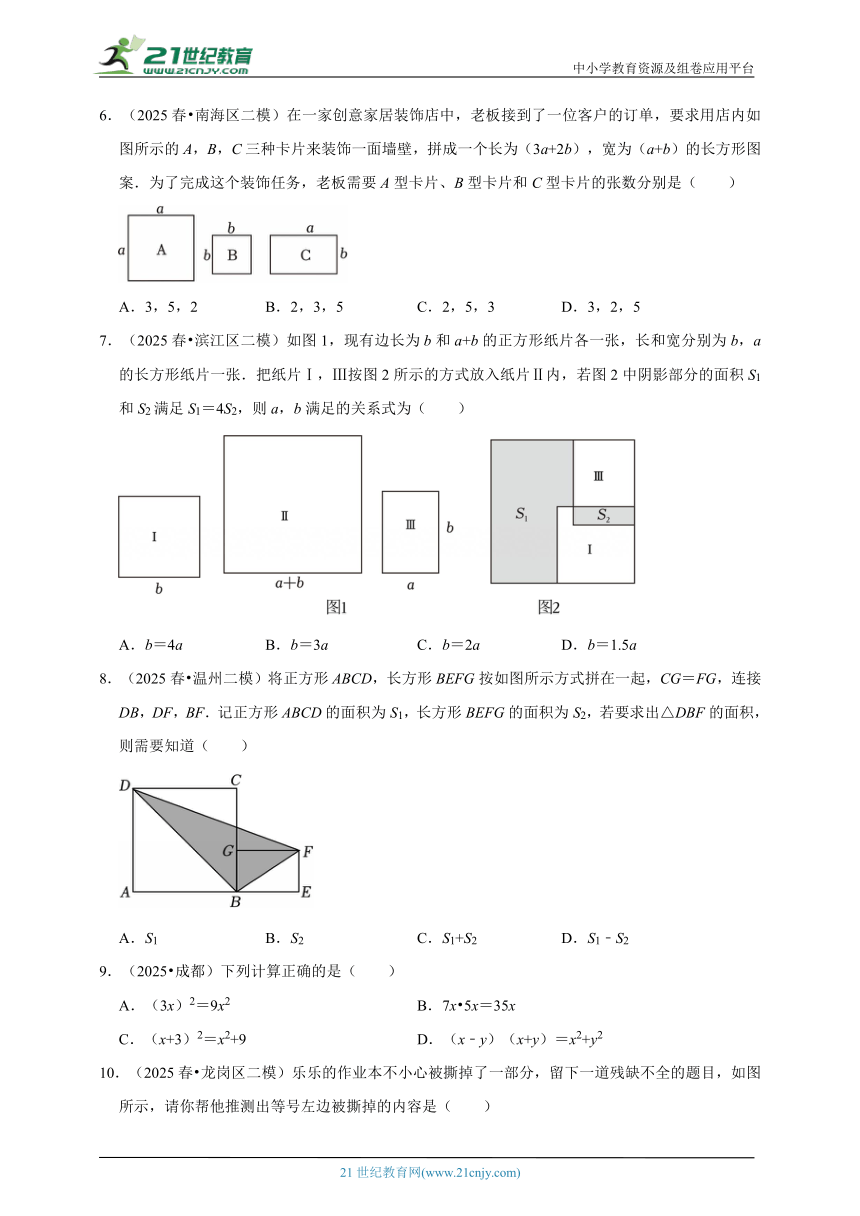
6.(2025春 南海区二模)在一家创意家居装饰店中,老板接到了一位客户的订单,要求用店内如图所示的A,B,C三种卡片来装饰一面墙壁,拼成一个长为(3a+2b),宽为(a+b)的长方形图案.为了完成这个装饰任务,老板需要A型卡片、B型卡片和C型卡片的张数分别是( )
A.3,5,2 B.2,3,5 C.2,5,3 D.3,2,5
7.(2025春 滨江区二模)如图1,现有边长为b和a+b的正方形纸片各一张,长和宽分别为b,a的长方形纸片一张.把纸片Ⅰ,Ⅲ按图2所示的方式放入纸片Ⅱ内,若图2中阴影部分的面积S1和S2满足S1=4S2,则a,b满足的关系式为( )
A.b=4a B.b=3a C.b=2a D.b=1.5a
8.(2025春 温州二模)将正方形ABCD,长方形BEFG按如图所示方式拼在一起,CG=FG,连接DB,DF,BF.记正方形ABCD的面积为S1,长方形BEFG的面积为S2,若要求出△DBF的面积,则需要知道( )
A.S1 B.S2 C.S1+S2 D.S1﹣S2
9.(2025 成都)下列计算正确的是( )
A.(3x)2=9x2 B.7x 5x=35x
C.(x+3)2=x2+9 D.(x﹣y)(x+y)=x2+y2
10.(2025春 龙岗区二模)乐乐的作业本不小心被撕掉了一部分,留下一道残缺不全的题目,如图所示,请你帮他推测出等号左边被撕掉的内容是( )
A.(x2﹣2x+6) B.(x2﹣3x2+6)
C.(x2﹣3x+6) D.(x2﹣3x﹣6)
二.填空题(共5小题)
11.(2025 阎良区二模)《几何原本》是古希腊数学家欧几里得的一部数学巨著,他在第二卷“几何与代数”中,阐述了数与形是一家,即通过“以数解形”和“以形助数”,可以把代数公式与几何图形相互转化.如图可以得到(a+b)2=a2+2ab+b2,基于此,若ab=6,a+b=5,则a2+b2的值为 .
12.(2025春 靖江市二模)若m,n,k满足m2+n2+k2=8,则(m+n)2+(n+k)2+(m+k)2的最小值为 .
13.(2025春 九龙坡区二模)一个各数位数字互不相等且均不为0三位正整数,若百位数字与个位数字之和减去4等于十位数字,则称这个三位数为“至善数”,例如:631,因为6+1﹣4=3,则称631是“至善数”;则最大的“至善数”与最小的“至善数”之差是 ;若正整数,记F(t)=c﹣2a.且,是两个不同的“至善数”(1≤y≤8,1≤n≤9,1≤m,z≤9且y,z,m,n均为整数),且F(t1)+2F(t2)+4n能被17整除,t2的值是 .
14.(2025春 梅县区二模)如图,两个正方形的边长分别为a、b,若a+b=10,ab=20,则图中阴影部分的面积为 .
15.(2025春 蜀山区二模)如图,将两张周长为10,面积为4的长方形纸片按图1,图2两种方式放置,正方形ABCD中未被这两张长方形纸片覆盖部分用阴影表示,图1和图2中阴影部分的面积分别记为S1和S2.则S1﹣S2= .
三.解答题(共5小题)
16.(2025春 清新区二模)先化简,再求值:[(x﹣2y)2+(x﹣2y)(x+2y)﹣3x(x﹣2y)]÷2x,其中,.
17.(2025春 海州区二模)如图1是一个长为2m、宽为2n的长方形.沿图中虚线用剪刀均匀分成四块全等小长方形,然后按图2形状拼成一个正方形.
(1)观察图2,直接写出代数式(m+n)2,(m﹣n)2,mn之间的关系: ;
(2)利用(1)的结论和公式变形,尝试解决以下问题:
①已知x+y=7,xy=6,则x﹣y的值为 ;
②已知(2024﹣x)(x﹣2025)=﹣6,求(2024﹣x)2+(x﹣2025)2的值;
(3)两个正方形ABCD、AEFG如图3摆放.边长分别为x,y,若x2+y2=34,BE=2,求图中阴影部分的面积.
18.(2025 扬州一模)某数学兴趣小组研究如下等式:38×32=1216,53×57=3021,71×79=5609,84×86=7224.观察发现以上等式均是“两位数乘以两位数,十位数字相同,个位数字之和是10,且积有一定的规律”.
(1)根据上述的运算规律,直接写出结果:58×52= ;752= ;
(2)设其中一个数的十位数字为a,个位数字为b(a>0,b>0).
①请用含a,b的等式表示这个运算规律,并用所学的数学知识证明;
②上述等式中,分别将左边两个乘数的十位和个位数字调换位置,得到新的两个两位数相乘(如:38×32调换为83×23).若记新的两个两位数的乘积为m,①中的运算结果为n,若|m﹣n|一定能被一个两位数整除,试求这个两位数的最大值.
19.(2025春 扬州二模)阅读:在计算(x﹣1)(xn+xn﹣1+xn﹣2+…+x+1)的过程中,我们可以先从简单的、特殊的情形入手,再到复杂的、一般的问题,通过观察、归纳、总结,形成解决一类问题的一般方法,数学中把这样的过程叫做特殊到一般.如下所示:
(1)【观察】①(x﹣1)(x+1)= ;
②(x﹣1)(x2+x+1)= :
③(x﹣1)(x3+x2+x+1)= ;………
(2)【猜想】由此可得:(x﹣1)(xn+xn﹣1+xn﹣2+…+x+1)= ;
(3)【应用】请运用上面的结论,解决下列问题:计算:52024+52023+52022+52021+…+5+1的值.
20.(2025春 包河区二模)两个边长分别为a和b的正方形如图放置(如图①),其未叠合部分(阴影)面积为S1;若在图①中大正方形的右下角再摆放一个边长为b的小正方形(如图②),两个小正方形叠合部分(阴影)面积为S2.
(1)用含a、b的代数式分别表示S1、S2;
(2)若a+b=4、ab=5,求S1+S2;
(3)图③也是由两个边长分别为a和b的正方形放置构成.用a、b的代数式表示图③中阴影部分的面积S3;并当S1+S2=32时,求S3的值.
中考核心考点 整式
参考答案与试题解析
一.选择题(共10小题)
1.(2025春 瑞安市二模)如图,将两张长为a,宽为b的长方形纸片按图1,图2两种方式放置,图1和图2中两张长方形纸片重叠的部分分别记为①和②,正方形ABCD中未被这两张长方形纸片覆盖的部分用阴影表示,①和②的面积分别记为S1和S2.若知道下列条件,可以求S1﹣S2值的是( )
A.长方形纸片的面积
B.长方形纸片的周长
C.长方形纸片和①的面积差
D.图1与图2阴影部分的面积差
【考点】整式的混合运算;列代数式.
【专题】整式;运算能力.
【答案】D
【分析】用字母表示长度,列代数式,运用整式的运算进行验证.
【解答】解:如图,设矩形的两边长分别是a、b;阴影部分的长分别为下x、y;
则a+x=b+y,即a﹣b=y﹣x,
∴图1阴影部分面积为x2+y2,图2阴影部分面积为2xy;
∴x2+y2﹣2xy=(x﹣y)2=(a﹣b)2;
又因为①的面积是(b﹣x)(a﹣y)②的面积是(a﹣x)(b﹣y);
(b﹣x)(a﹣y)﹣(a﹣x)(b﹣y)=(a﹣b)(y﹣x)=(a﹣b)2;
故选:D.
【点评】本题整式的混合运算的运用,熟记运算法则是解题的关键.
2.(2025 阎良区二模)计算(﹣2ab2)2 b﹣2的结果是( )
A.﹣4a2b2 B.4a2b2 C.4a3b2 D.4a2b3
【考点】单项式乘单项式;负整数指数幂;幂的乘方与积的乘方.
【专题】整式;运算能力.
【答案】B
【分析】先计算积的乘方,再计算同底数幂的乘法即可.
【解答】解:原式=4a2b4 b﹣2
=4a2b4﹣2
=4a2b2.
故选:B.
【点评】本题考查了积的乘方,同底数幂的乘法,单项式乘单项式,负整数指数幂的含义,正确掌握相关运算法则是解题关键.
3.(2025春 清城区二模)若x2+mx+25是完全平方式,则m=( )
A.5 B.5或﹣5 C.10 D.10或﹣10
【考点】完全平方式.
【专题】整式;运算能力.
【答案】D
【分析】先根据平方项确定出这两个数,再根据完全平方公式:(a±b)2=a2±2ab+b2.利用乘积二倍项列式求解即可.
【解答】解:∵x2+mx+25=x2+mx+52是完全平方式,
∴这两个数是x和5,
∴mx=±2×5 x,
∴m=±10,
故选:D.
【点评】本题考查完全平方公式,两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式,根据平方项确定出这两个数是求解的关键.
4.(2025春 杭州二模)把两张正方形纸片按如图1所示分别裁剪成A和B两部分(B为长方形),再将裁好的四张纸片不重叠地放入图2所示的正方形中,记一张A纸片的面积为S1,一张B纸片的面积为S2,若S1﹣S2=10,则图2中阴影部分面积为( )
A.10 B.12 C.14 D.16
【考点】整式的混合运算.
【专题】整式;运算能力.
【答案】C
【分析】设图1正方形纸片边长为a,B部分的宽为b,长为c,根据图1和图2得出a=3b和c=2b,再利用S1﹣S2=10得到b2=2,再表示出,代入计算即可.
【解答】解:将B向左推,可得如图,
设图1正方形纸片边长为a,B部分的宽为b,长为c,
根据图2是正方形,得a+(a﹣b)=a+2b,
即a=3b,
由图(2)两个A的位置,可得c+b=a即c=2b,
∴图2正方形边长为a+2b=5b.
∴PQ=5b﹣a﹣(a﹣c)=5b﹣3b﹣b=b,HQ=3b﹣2b=b.
∵S1﹣S2=10,
∴a2﹣bc﹣bc=10.
∴b2=2.
∴.
故选:C.
【点评】本题考查了整式的混合运算,熟练掌握整式混合运算的顺序和法则是解题的关键.
5.(2025春 深圳二模)若(x﹣2)(x+3)=x2+ax+b,则a+b的值分别为( )
A.﹣7 B.7 C.﹣5 D.5
【考点】多项式乘多项式.
【专题】整式;运算能力.
【答案】C
【分析】先根据多项式乘多项式法则展开,合并同类项,求出a、b值,再代入求出即可.
【解答】解:∵(x﹣2)(x+3)=x2+x﹣6,(x﹣2)(x+3)=x2+ax+b,
∴a=1,n=﹣6,
∴a+b=﹣5,
故选:C.
【点评】本题考查了多项式乘以多项式法则,能正确根据多项式乘以多项式法则展开是解此题的关键.
6.(2025春 南海区二模)在一家创意家居装饰店中,老板接到了一位客户的订单,要求用店内如图所示的A,B,C三种卡片来装饰一面墙壁,拼成一个长为(3a+2b),宽为(a+b)的长方形图案.为了完成这个装饰任务,老板需要A型卡片、B型卡片和C型卡片的张数分别是( )
A.3,5,2 B.2,3,5 C.2,5,3 D.3,2,5
【考点】多项式乘多项式.
【专题】整式;应用意识.
【答案】D
【分析】根据长方形的面积公式可知该墙壁面积S=3a2+2b2+5ab,即可得出答案.
【解答】解:∵长方形的长为(3a+2b),宽为(a+b),
∴长方形的面积S=(3a+2b)(a+b)=3a2+2b2+5ab,
∴需要A型卡片、B型卡片和C型卡片的张数分别3、2、5张.
故选:D.
【点评】本题主要考查了多项式的乘法的应用,熟练掌握多项式乘以多项式法则是解题关键.
7.(2025春 滨江区二模)如图1,现有边长为b和a+b的正方形纸片各一张,长和宽分别为b,a的长方形纸片一张.把纸片Ⅰ,Ⅲ按图2所示的方式放入纸片Ⅱ内,若图2中阴影部分的面积S1和S2满足S1=4S2,则a,b满足的关系式为( )
A.b=4a B.b=3a C.b=2a D.b=1.5a
【考点】整式的混合运算.
【专题】整式;运算能力.
【答案】C
【分析】根据题意可得S1=(a+b)2﹣b2﹣a2=2ab,S2=(b﹣a)a=ab﹣a2,利用S1=4S2可得b=2a即可.
【解答】解:由题意可得:S1=(a+b)2﹣b2﹣a2=2ab,S2=(b﹣a)a=ab﹣a2,
∵S1=4S2,
∴2ab=4(ab﹣a2),
2ab=4ab﹣4a2,
∵a≠0,
∴b=2a,
故选:C.
【点评】本题考查了整式的混合运算,熟练掌握s1和s2面积的组成是关键.
8.(2025春 温州二模)将正方形ABCD,长方形BEFG按如图所示方式拼在一起,CG=FG,连接DB,DF,BF.记正方形ABCD的面积为S1,长方形BEFG的面积为S2,若要求出△DBF的面积,则需要知道( )
A.S1 B.S2 C.S1+S2 D.S1﹣S2
【考点】整式的混合运算.
【专题】整式;矩形 菱形 正方形;运算能力.
【答案】A
【分析】延长DC和EF交于点H,连接CF,利用等底同高的两个三角形面积相等可得S△DBF=S△DBCS1即可得到结论.
【解答】解:如图,延长DC和EF交于点H,连接CF,
∵CG=FG,
∴四边形CGFH是正方形,
∵四边形ABCD和四边形CGFH都是正方形,
∴∠DBC=∠FCG=45°,
∴CF∥BD,
∴S△DBF=S△DBCS1.
故选:A.
【点评】本题考查了正方形的性质、整式的混合运算,熟练掌握等底同高的两个三角形面积相等是关键.
9.(2025 成都)下列计算正确的是( )
A.(3x)2=9x2 B.7x 5x=35x
C.(x+3)2=x2+9 D.(x﹣y)(x+y)=x2+y2
【考点】整式的混合运算.
【专题】整式;运算能力.
【答案】A
【分析】各项计算得到结果,即可作出判断.
【解答】解:A、原式=9x2,故符合题意;
B、原式=35x2,故不符合题意;
C、原式=x2+6x+9,故不符合题意;
D、原式=x2﹣y2,故不符合题意,
故选:A.
【点评】此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.
10.(2025春 龙岗区二模)乐乐的作业本不小心被撕掉了一部分,留下一道残缺不全的题目,如图所示,请你帮他推测出等号左边被撕掉的内容是( )
A.(x2﹣2x+6) B.(x2﹣3x2+6)
C.(x2﹣3x+6) D.(x2﹣3x﹣6)
【考点】整式的除法.
【专题】整式;运算能力.
【答案】C
【分析】根据题意得到(x3﹣3x2+6x)÷x,计算即可得到等号左边被撕掉的内容.
【解答】解:根据题意可知,(x3﹣3x2+6x)÷x=x2﹣3x+6.
故选:C.
【点评】此题考查了整式的除法,掌握整式的除法的运算法则是关键.
二.填空题(共5小题)
11.(2025 阎良区二模)《几何原本》是古希腊数学家欧几里得的一部数学巨著,他在第二卷“几何与代数”中,阐述了数与形是一家,即通过“以数解形”和“以形助数”,可以把代数公式与几何图形相互转化.如图可以得到(a+b)2=a2+2ab+b2,基于此,若ab=6,a+b=5,则a2+b2的值为 13 .
【考点】完全平方公式.
【专题】整式;运算能力.
【答案】13.
【分析】直接利用完全平方公式变形计算即可.
【解答】解:由条件可知(a+b)2=a2+2ab+b2=a2+b2+2×6=25,
∴a2+b2=13;
故答案为:13.
【点评】本题考查利用完全平方公式变形计算,熟练掌握完全平方公式是解题的关键.
12.(2025春 靖江市二模)若m,n,k满足m2+n2+k2=8,则(m+n)2+(n+k)2+(m+k)2的最小值为 8 .
【考点】完全平方公式.
【专题】运算能力.
【答案】8.
【分析】根据m2+n2+k2=8,代入(m+n)2+(n+k)2+(m+k)2=2m2+2n2+2k2+2mn+2nk+2mk,得(m+n)2+(n+k)2+(m+k)2=16+2(mn+nk+mk),根据(m+n+k)2=8+2(mn+nk+mk),得mn+nk+mk,mn+nk+mk要想取得最小值(m+n+k)2取最小值即可解答.
【解答】解:原式=(m2+2mn+n2)+(n2+2nk+k2)+(m2+2mk+k2)
=2m2+2n2+2k2+2mn+2nk+2mk,
∵m2+n2+k2=8,
∴2m2+2n2+2k2+2mn+2nk+2mk=16+2(mn+nk+mk),
∵(m+n+k)2=m2+n2+k2+2(mn+nk+mk)=8+2(mn+nk+mk),
∴mn+nk+mk,
∴16+2(mn+nk+mk)=8+(m+n+k)2,
当(m+n+k)2取得最小值0时,16+2(mn+nk+mk)取得最小值8,
即(m+n)2+(n+k)2+(m+k)2取得最小值8,
故答案为:8.
【点评】本题的考查了完全平方公式,掌握完全平方公式是解题的关键.
13.(2025春 九龙坡区二模)一个各数位数字互不相等且均不为0三位正整数,若百位数字与个位数字之和减去4等于十位数字,则称这个三位数为“至善数”,例如:631,因为6+1﹣4=3,则称631是“至善数”;则最大的“至善数”与最小的“至善数”之差是 858 ;若正整数,记F(t)=c﹣2a.且,是两个不同的“至善数”(1≤y≤8,1≤n≤9,1≤m,z≤9且y,z,m,n均为整数),且F(t1)+2F(t2)+4n能被17整除,t2的值是 631,543,367 .
【考点】整式的加减;列代数式.
【专题】整式;运算能力.
【答案】858;631,543,367.
【分析】根据最大的“至善数”可得a=9,b=8,进而根据定义求得c,同理求得最小的“至善数”的a=1,b=2,再求得c的值,求两数的差,即可求解.,是两个不同的“至善数”,可得方程组;再根据F(t1)+2F(t2)+4n列代数式,最后根据F(t1)+2F(t2)+4n能被17整除进行分类讨论,即可得答案.
【解答】解:由条件可知a+c﹣4=b,则c=b﹣a+4,
最大的“至善数”可得a=9,b=8,则c=3,则最大的“至善数”为983,
最小的“至善数”的a=1,b=2,则c=5,则最小的“至善数”为125,
983﹣125=858,
由条件可知,
得2+z=m+n,即z=m+n﹣2,y=z﹣2=m+n﹣4,
∴F(t1)+2F(t2)+4n
=z﹣2×2+2(n﹣2m)+4n
=z﹣4﹣4m+6n
=m+n﹣2﹣4﹣4m+6n
=﹣3m+7n﹣6.
∵1≤y≤8,1≤m≤9,1≤n≤9,
∴﹣26≤﹣3m+7n﹣6≤54.
∵﹣3m+7n﹣6能被17整除,
∴﹣3m+7n﹣6=﹣17或0或17或34或51.
①当﹣3m+7n﹣6=﹣17时,
∴,
当m=6时,n=1,y=m+n﹣4=3,z=m+n﹣2=6+1﹣2=5,
∴,
②当﹣3m+7n﹣6=0时,,
当m=5时,n=3,y=m+n﹣4=4,z=y+2=6,
∴,
③当﹣3m+7n﹣6=17时,,
当m=4时,n=5,y=m+n﹣4=5,z=y+2=7,
∴(舍去),
④当﹣3m+7n﹣6=34时,,
当m=3时,n=7,y=m+n﹣4=6,z=y+2=8,
∴,
⑤当﹣3m+7n﹣6=51时,,
当m=2时,n=9,y=m+n﹣4=7,z=y+2=9,
∴,(相同,舍去),
故答案为:858;631,543,367.
【点评】本题考查了二元一次方程组的应用,新定义、数的整除等知识,分类讨论是解题的关键
14.(2025春 梅县区二模)如图,两个正方形的边长分别为a、b,若a+b=10,ab=20,则图中阴影部分的面积为 20 .
【考点】完全平方公式的几何背景.
【专题】整式;运算能力.
【答案】20.
【分析】用含有a、b的代数式表示阴影部分的面积,再根据完全平方公式进行代数式的变形,进而求出答案.
【解答】解:阴影部分的面积为,
当a+b=10,ab=20时,
原式(100﹣60)=20.
故答案为:20.
【点评】本题考查完全平方公式的应用,正确的表示阴影部分的面积和适当的变形,是得到正确答案的关键.
15.(2025春 蜀山区二模)如图,将两张周长为10,面积为4的长方形纸片按图1,图2两种方式放置,正方形ABCD中未被这两张长方形纸片覆盖部分用阴影表示,图1和图2中阴影部分的面积分别记为S1和S2.则S1﹣S2= 9 .
【考点】整式的混合运算.
【专题】整式;运算能力;推理能力.
【答案】9.
【分析】先求出a、b值,再根据图示列出S1=(x﹣1)2+(x﹣4)2,S2=2(x﹣1)(x﹣4),代入S1﹣S2计算即可.
【解答】解:根据题意得,解得,
设正方形ABCD的边长为x,
S1=(x﹣1)2+(x﹣4)2,S2=2(x﹣1)(x﹣4),
∴S1﹣S2=(x﹣1)2+(x﹣4)2﹣2(x﹣1)(x﹣4)=(x﹣1﹣x+4)2=9.
故答案为:9.
【点评】本题考查了整式的混合运算,根据图示列出S1=(x﹣1)2+(x﹣4)2,S2=2(x﹣1)(x﹣4),是关键.
三.解答题(共5小题)
16.(2025春 清新区二模)先化简,再求值:[(x﹣2y)2+(x﹣2y)(x+2y)﹣3x(x﹣2y)]÷2x,其中,.
【考点】整式的混合运算—化简求值.
【专题】整式;运算能力.
【答案】,.
【分析】根据整式的混合运算法则化简,再将x、y代入即可解答.
【解答】解:[(x﹣2y)2+(x﹣2y)(x+2y)﹣3x(x﹣2y)]÷2x
=(x2﹣4xy+4y2+x2﹣4y2﹣3x2+6xy)÷2x
=(﹣x2+2xy)÷2x
;
当,时,原式
【点评】本题考查了整式的混合运算和化简求值,掌握整式的混合运算法则是解题的关键.
17.(2025春 海州区二模)如图1是一个长为2m、宽为2n的长方形.沿图中虚线用剪刀均匀分成四块全等小长方形,然后按图2形状拼成一个正方形.
(1)观察图2,直接写出代数式(m+n)2,(m﹣n)2,mn之间的关系: (m+n)2=(m﹣n)2+4mn ;
(2)利用(1)的结论和公式变形,尝试解决以下问题:
①已知x+y=7,xy=6,则x﹣y的值为 ±5 ;
②已知(2024﹣x)(x﹣2025)=﹣6,求(2024﹣x)2+(x﹣2025)2的值;
(3)两个正方形ABCD、AEFG如图3摆放.边长分别为x,y,若x2+y2=34,BE=2,求图中阴影部分的面积.
【考点】完全平方公式.
【专题】整式;运算能力.
【答案】(1)(m+n)2=(m﹣n)2+4mn;
(2)±5,13;
(3)8.
【分析】(1)根据大正方形的面积等于小正方形的面积加上4个小长方形的面积,即可作答.
(2)①直接把数值代入(x+y)2=(x﹣y)2+4xy进行计算,即可作答.
②根据(2024﹣x)2+(x﹣2025)2=[(2024﹣x)+(x﹣2025)]2﹣2(2024﹣x)(x﹣2025),然后代入数值化简计算,即可作答.
(3)由题意可知x﹣y=2,,,即可求出S阴影=x+y.结合x2+y2=34,可求出xy=15,最后根据(x+y)2=x2+y2+2xy求解即可.
【解答】解:(1)依题意,(m+n)2=(m﹣n)2+4mn;
故答案为:(m+n)2=(m﹣n)2+4mn;
(2)①与(1)同理得(x+y)2=(x﹣y)2+4xy,
∵x+y=7,xy=6,
∴49=(x﹣y)2+4×6,
∴(x﹣y)2=25,
∴x﹣y=±5;
故答案为:±5;
②∵(2024﹣x)(x﹣2025)=﹣6,
∴(2024﹣x)2+(x﹣2025)2
=[(2024﹣x)+(x﹣2025)]2﹣2(2024﹣x)(x﹣2025)
=(﹣1)2﹣2×(﹣6)
=1+12
=13.
(3)∵BE=2,
∴x﹣y=2.
由图可知△CDF的底为x,高为2,
∴.
△BEF的底为2,高为y,
∴,
∴S阴影=S△CDF+S△BEF=x+y.
∵22+2xy=34,
∴xy=15,
∴(x+y)2=x2+y2+2xy=34+2×15=64,
∴x+y=8(舍去负值),
∴阴影部分面积和为8.
【点评】本题考查完全平方公式的变形求值,完全平方公式在几何图形中的应用,利用数形结合的思想是解题关键.
18.(2025 扬州一模)某数学兴趣小组研究如下等式:38×32=1216,53×57=3021,71×79=5609,84×86=7224.观察发现以上等式均是“两位数乘以两位数,十位数字相同,个位数字之和是10,且积有一定的规律”.
(1)根据上述的运算规律,直接写出结果:58×52= 3016 ;752= 5625 ;
(2)设其中一个数的十位数字为a,个位数字为b(a>0,b>0).
①请用含a,b的等式表示这个运算规律,并用所学的数学知识证明;
②上述等式中,分别将左边两个乘数的十位和个位数字调换位置,得到新的两个两位数相乘(如:38×32调换为83×23).若记新的两个两位数的乘积为m,①中的运算结果为n,若|m﹣n|一定能被一个两位数整除,试求这个两位数的最大值.
【考点】整式的加减.
【专题】整式;运算能力.
【答案】(1)3016;5625;
(2)①详见解析;②99.
【分析】(1)根据上述的运算规律计算,即可求解;
(2)①根据题意可得这两个两位数分别为10a+b,10a+10﹣b,从而得到这个运算规律为(10a+b)(10a+10﹣b)=100a(a+1)+b(10﹣b),然后分别计算等式的左右两边,即可;②由①得:n=100a2+100a+10b﹣b2,可得新的两个两位数分别为10b+a,10(10﹣b)+a,进而得到m=(10b+a)[10(10﹣b)+a],然后计算出m﹣n,再进一步求解即可.
【解答】解:(1)根据题意得:58×52=(5×6)×100+8×2=3016,
752=(7×8)×100+5×5=5625;
故答案为:3016;5625;
(2)①∵其中一个数的十位数字为a,个位数字为b(a>0,b>0),
∴另一个数的十位数字为a,个位数字为10﹣b,
∴这两个两位数分别为10a+b,10a+10﹣b,
根据题意得:这个运算规律为(10a+b)(10a+10﹣b)=100a(a+1)+b(10﹣b),
证明:左边=100a2+10ab+100a+10b﹣10ab﹣b2
=100a2+100a+10b﹣b2
右边=100a2+100a+10b﹣b2,
∴左边=右边;
②由①得:n=100a2+100a+10b﹣b2,
由条件可知新的两个两位数分别为10b+a,10(10﹣b)+a,
∴m=(10b+a)[10(10﹣b)+a]
=(10b+a)(100﹣10b+a)
=1000b+100a﹣100b2﹣10ab+10ab+a2
=1000b﹣100b2+100a+a2,
∴m﹣n=(1000b﹣100b2+100a+a2)﹣(100a2+100a+10b﹣b2)
=﹣99a2﹣99b2+990b
=﹣99(a2+b2+10b),
∴a2+b2+10b为整数,
∴m﹣n能被99整除,
∴这个两位数的最大值为99.
【点评】本题主要考查了整式的混合运算,因式分解的应用,明确题意,准确得到规律是解题的关键.
19.(2025春 扬州二模)阅读:在计算(x﹣1)(xn+xn﹣1+xn﹣2+…+x+1)的过程中,我们可以先从简单的、特殊的情形入手,再到复杂的、一般的问题,通过观察、归纳、总结,形成解决一类问题的一般方法,数学中把这样的过程叫做特殊到一般.如下所示:
(1)【观察】①(x﹣1)(x+1)= x2﹣1 ;
②(x﹣1)(x2+x+1)= x3﹣1 :
③(x﹣1)(x3+x2+x+1)= x4﹣1 ;………
(2)【猜想】由此可得:(x﹣1)(xn+xn﹣1+xn﹣2+…+x+1)= xn+1﹣1 ;
(3)【应用】请运用上面的结论,解决下列问题:计算:52024+52023+52022+52021+…+5+1的值.
【考点】多项式乘多项式;规律型:数字的变化类.
【专题】运算能力.
【答案】(1)x2﹣1;x3﹣1;x4﹣1;
(2)xn+1﹣1;
(3).
【分析】(1)利用平方差公式和多项式乘以多项式计算即可;
(2)利用(1)中变化规律进而得出答案;
(3)设x=5,n=2024,则(5﹣1)(52024+52023+52022+ +5+1)=52025﹣1,即可求解.
【解答】解:(1)(x﹣1)(x+1)=x2﹣1;
(x﹣1)(x2+x+1)=x(x2+x+1)﹣(x2+x+1)=x3﹣1;
(x﹣1)(x3+x2+x+1)=x(x3+x2+x+1)﹣(x3+x2+x+1)=x4﹣1,
故答案为:x2﹣1;x3﹣1;x4﹣1;
(2)由(1)得,(x﹣1)(xn+xn﹣1+xn﹣2+ +x+1)=xn+1﹣1,
故答案为:xn+1﹣1;
(3)设x=5,n=2024,
根据(x﹣1)(xn+xn﹣1+xn﹣2+ +x+1)=xn+1﹣1
则(5﹣1)(52024+52023+52022+ +5+1)=52025﹣1,
∴.
【点评】此题主要考查了平方差公式、多项式乘以多项式以及数字变化规律,正确得出式子之间的变化规律是解题关键.
20.(2025春 包河区二模)两个边长分别为a和b的正方形如图放置(如图①),其未叠合部分(阴影)面积为S1;若在图①中大正方形的右下角再摆放一个边长为b的小正方形(如图②),两个小正方形叠合部分(阴影)面积为S2.
(1)用含a、b的代数式分别表示S1、S2;
(2)若a+b=4、ab=5,求S1+S2;
(3)图③也是由两个边长分别为a和b的正方形放置构成.用a、b的代数式表示图③中阴影部分的面积S3;并当S1+S2=32时,求S3的值.
【考点】整式的混合运算;完全平方公式的几何背景.
【专题】整式;运算能力.
【答案】(1)S1=a2﹣b2,S2=2b2﹣ab;
(2)1;
(3)16.
【分析】(1)由图中正方形和长方形的面积关系,可得答案;
(2)根据(1)中的结论,将a+b=4,ab=5,代入进行计算即可;
(3)表示出S3,再变形整体代入求值即可.
【解答】解:(1)由图可得,S1=a2﹣b2,S2=a(a﹣b)+2b2﹣a2=2b2﹣ab;
(2)∵a+b=4,ab=5,
∴S1+S2
=a2﹣b2+2b2﹣ab
=a2+b2﹣ab
=(a+b)2﹣3ab
=42﹣3×5
=1;
(3),
∵S1+S2=a2+b2﹣ab=32,
∴S332=16.
【点评】本题考查了整式的混合运算,完全平方公式,数形结合、恰当进行代数式变形是解答本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考核心考点 整式
一.选择题(共10小题)
1.(2025春 瑞安市二模)如图,将两张长为a,宽为b的长方形纸片按图1,图2两种方式放置,图1和图2中两张长方形纸片重叠的部分分别记为①和②,正方形ABCD中未被这两张长方形纸片覆盖的部分用阴影表示,①和②的面积分别记为S1和S2.若知道下列条件,可以求S1﹣S2值的是( )
A.长方形纸片的面积
B.长方形纸片的周长
C.长方形纸片和①的面积差
D.图1与图2阴影部分的面积差
2.(2025 阎良区二模)计算(﹣2ab2)2 b﹣2的结果是( )
A.﹣4a2b2 B.4a2b2 C.4a3b2 D.4a2b3
3.(2025春 清城区二模)若x2+mx+25是完全平方式,则m=( )
A.5 B.5或﹣5 C.10 D.10或﹣10
4.(2025春 杭州二模)把两张正方形纸片按如图1所示分别裁剪成A和B两部分(B为长方形),再将裁好的四张纸片不重叠地放入图2所示的正方形中,记一张A纸片的面积为S1,一张B纸片的面积为S2,若S1﹣S2=10,则图2中阴影部分面积为( )
A.10 B.12 C.14 D.16
5.(2025春 深圳二模)若(x﹣2)(x+3)=x2+ax+b,则a+b的值分别为( )
A.﹣7 B.7 C.﹣5 D.5
6.(2025春 南海区二模)在一家创意家居装饰店中,老板接到了一位客户的订单,要求用店内如图所示的A,B,C三种卡片来装饰一面墙壁,拼成一个长为(3a+2b),宽为(a+b)的长方形图案.为了完成这个装饰任务,老板需要A型卡片、B型卡片和C型卡片的张数分别是( )
A.3,5,2 B.2,3,5 C.2,5,3 D.3,2,5
7.(2025春 滨江区二模)如图1,现有边长为b和a+b的正方形纸片各一张,长和宽分别为b,a的长方形纸片一张.把纸片Ⅰ,Ⅲ按图2所示的方式放入纸片Ⅱ内,若图2中阴影部分的面积S1和S2满足S1=4S2,则a,b满足的关系式为( )
A.b=4a B.b=3a C.b=2a D.b=1.5a
8.(2025春 温州二模)将正方形ABCD,长方形BEFG按如图所示方式拼在一起,CG=FG,连接DB,DF,BF.记正方形ABCD的面积为S1,长方形BEFG的面积为S2,若要求出△DBF的面积,则需要知道( )
A.S1 B.S2 C.S1+S2 D.S1﹣S2
9.(2025 成都)下列计算正确的是( )
A.(3x)2=9x2 B.7x 5x=35x
C.(x+3)2=x2+9 D.(x﹣y)(x+y)=x2+y2
10.(2025春 龙岗区二模)乐乐的作业本不小心被撕掉了一部分,留下一道残缺不全的题目,如图所示,请你帮他推测出等号左边被撕掉的内容是( )
A.(x2﹣2x+6) B.(x2﹣3x2+6)
C.(x2﹣3x+6) D.(x2﹣3x﹣6)
二.填空题(共5小题)
11.(2025 阎良区二模)《几何原本》是古希腊数学家欧几里得的一部数学巨著,他在第二卷“几何与代数”中,阐述了数与形是一家,即通过“以数解形”和“以形助数”,可以把代数公式与几何图形相互转化.如图可以得到(a+b)2=a2+2ab+b2,基于此,若ab=6,a+b=5,则a2+b2的值为 .
12.(2025春 靖江市二模)若m,n,k满足m2+n2+k2=8,则(m+n)2+(n+k)2+(m+k)2的最小值为 .
13.(2025春 九龙坡区二模)一个各数位数字互不相等且均不为0三位正整数,若百位数字与个位数字之和减去4等于十位数字,则称这个三位数为“至善数”,例如:631,因为6+1﹣4=3,则称631是“至善数”;则最大的“至善数”与最小的“至善数”之差是 ;若正整数,记F(t)=c﹣2a.且,是两个不同的“至善数”(1≤y≤8,1≤n≤9,1≤m,z≤9且y,z,m,n均为整数),且F(t1)+2F(t2)+4n能被17整除,t2的值是 .
14.(2025春 梅县区二模)如图,两个正方形的边长分别为a、b,若a+b=10,ab=20,则图中阴影部分的面积为 .
15.(2025春 蜀山区二模)如图,将两张周长为10,面积为4的长方形纸片按图1,图2两种方式放置,正方形ABCD中未被这两张长方形纸片覆盖部分用阴影表示,图1和图2中阴影部分的面积分别记为S1和S2.则S1﹣S2= .
三.解答题(共5小题)
16.(2025春 清新区二模)先化简,再求值:[(x﹣2y)2+(x﹣2y)(x+2y)﹣3x(x﹣2y)]÷2x,其中,.
17.(2025春 海州区二模)如图1是一个长为2m、宽为2n的长方形.沿图中虚线用剪刀均匀分成四块全等小长方形,然后按图2形状拼成一个正方形.
(1)观察图2,直接写出代数式(m+n)2,(m﹣n)2,mn之间的关系: ;
(2)利用(1)的结论和公式变形,尝试解决以下问题:
①已知x+y=7,xy=6,则x﹣y的值为 ;
②已知(2024﹣x)(x﹣2025)=﹣6,求(2024﹣x)2+(x﹣2025)2的值;
(3)两个正方形ABCD、AEFG如图3摆放.边长分别为x,y,若x2+y2=34,BE=2,求图中阴影部分的面积.
18.(2025 扬州一模)某数学兴趣小组研究如下等式:38×32=1216,53×57=3021,71×79=5609,84×86=7224.观察发现以上等式均是“两位数乘以两位数,十位数字相同,个位数字之和是10,且积有一定的规律”.
(1)根据上述的运算规律,直接写出结果:58×52= ;752= ;
(2)设其中一个数的十位数字为a,个位数字为b(a>0,b>0).
①请用含a,b的等式表示这个运算规律,并用所学的数学知识证明;
②上述等式中,分别将左边两个乘数的十位和个位数字调换位置,得到新的两个两位数相乘(如:38×32调换为83×23).若记新的两个两位数的乘积为m,①中的运算结果为n,若|m﹣n|一定能被一个两位数整除,试求这个两位数的最大值.
19.(2025春 扬州二模)阅读:在计算(x﹣1)(xn+xn﹣1+xn﹣2+…+x+1)的过程中,我们可以先从简单的、特殊的情形入手,再到复杂的、一般的问题,通过观察、归纳、总结,形成解决一类问题的一般方法,数学中把这样的过程叫做特殊到一般.如下所示:
(1)【观察】①(x﹣1)(x+1)= ;
②(x﹣1)(x2+x+1)= :
③(x﹣1)(x3+x2+x+1)= ;………
(2)【猜想】由此可得:(x﹣1)(xn+xn﹣1+xn﹣2+…+x+1)= ;
(3)【应用】请运用上面的结论,解决下列问题:计算:52024+52023+52022+52021+…+5+1的值.
20.(2025春 包河区二模)两个边长分别为a和b的正方形如图放置(如图①),其未叠合部分(阴影)面积为S1;若在图①中大正方形的右下角再摆放一个边长为b的小正方形(如图②),两个小正方形叠合部分(阴影)面积为S2.
(1)用含a、b的代数式分别表示S1、S2;
(2)若a+b=4、ab=5,求S1+S2;
(3)图③也是由两个边长分别为a和b的正方形放置构成.用a、b的代数式表示图③中阴影部分的面积S3;并当S1+S2=32时,求S3的值.
中考核心考点 整式
参考答案与试题解析
一.选择题(共10小题)
1.(2025春 瑞安市二模)如图,将两张长为a,宽为b的长方形纸片按图1,图2两种方式放置,图1和图2中两张长方形纸片重叠的部分分别记为①和②,正方形ABCD中未被这两张长方形纸片覆盖的部分用阴影表示,①和②的面积分别记为S1和S2.若知道下列条件,可以求S1﹣S2值的是( )
A.长方形纸片的面积
B.长方形纸片的周长
C.长方形纸片和①的面积差
D.图1与图2阴影部分的面积差
【考点】整式的混合运算;列代数式.
【专题】整式;运算能力.
【答案】D
【分析】用字母表示长度,列代数式,运用整式的运算进行验证.
【解答】解:如图,设矩形的两边长分别是a、b;阴影部分的长分别为下x、y;
则a+x=b+y,即a﹣b=y﹣x,
∴图1阴影部分面积为x2+y2,图2阴影部分面积为2xy;
∴x2+y2﹣2xy=(x﹣y)2=(a﹣b)2;
又因为①的面积是(b﹣x)(a﹣y)②的面积是(a﹣x)(b﹣y);
(b﹣x)(a﹣y)﹣(a﹣x)(b﹣y)=(a﹣b)(y﹣x)=(a﹣b)2;
故选:D.
【点评】本题整式的混合运算的运用,熟记运算法则是解题的关键.
2.(2025 阎良区二模)计算(﹣2ab2)2 b﹣2的结果是( )
A.﹣4a2b2 B.4a2b2 C.4a3b2 D.4a2b3
【考点】单项式乘单项式;负整数指数幂;幂的乘方与积的乘方.
【专题】整式;运算能力.
【答案】B
【分析】先计算积的乘方,再计算同底数幂的乘法即可.
【解答】解:原式=4a2b4 b﹣2
=4a2b4﹣2
=4a2b2.
故选:B.
【点评】本题考查了积的乘方,同底数幂的乘法,单项式乘单项式,负整数指数幂的含义,正确掌握相关运算法则是解题关键.
3.(2025春 清城区二模)若x2+mx+25是完全平方式,则m=( )
A.5 B.5或﹣5 C.10 D.10或﹣10
【考点】完全平方式.
【专题】整式;运算能力.
【答案】D
【分析】先根据平方项确定出这两个数,再根据完全平方公式:(a±b)2=a2±2ab+b2.利用乘积二倍项列式求解即可.
【解答】解:∵x2+mx+25=x2+mx+52是完全平方式,
∴这两个数是x和5,
∴mx=±2×5 x,
∴m=±10,
故选:D.
【点评】本题考查完全平方公式,两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式,根据平方项确定出这两个数是求解的关键.
4.(2025春 杭州二模)把两张正方形纸片按如图1所示分别裁剪成A和B两部分(B为长方形),再将裁好的四张纸片不重叠地放入图2所示的正方形中,记一张A纸片的面积为S1,一张B纸片的面积为S2,若S1﹣S2=10,则图2中阴影部分面积为( )
A.10 B.12 C.14 D.16
【考点】整式的混合运算.
【专题】整式;运算能力.
【答案】C
【分析】设图1正方形纸片边长为a,B部分的宽为b,长为c,根据图1和图2得出a=3b和c=2b,再利用S1﹣S2=10得到b2=2,再表示出,代入计算即可.
【解答】解:将B向左推,可得如图,
设图1正方形纸片边长为a,B部分的宽为b,长为c,
根据图2是正方形,得a+(a﹣b)=a+2b,
即a=3b,
由图(2)两个A的位置,可得c+b=a即c=2b,
∴图2正方形边长为a+2b=5b.
∴PQ=5b﹣a﹣(a﹣c)=5b﹣3b﹣b=b,HQ=3b﹣2b=b.
∵S1﹣S2=10,
∴a2﹣bc﹣bc=10.
∴b2=2.
∴.
故选:C.
【点评】本题考查了整式的混合运算,熟练掌握整式混合运算的顺序和法则是解题的关键.
5.(2025春 深圳二模)若(x﹣2)(x+3)=x2+ax+b,则a+b的值分别为( )
A.﹣7 B.7 C.﹣5 D.5
【考点】多项式乘多项式.
【专题】整式;运算能力.
【答案】C
【分析】先根据多项式乘多项式法则展开,合并同类项,求出a、b值,再代入求出即可.
【解答】解:∵(x﹣2)(x+3)=x2+x﹣6,(x﹣2)(x+3)=x2+ax+b,
∴a=1,n=﹣6,
∴a+b=﹣5,
故选:C.
【点评】本题考查了多项式乘以多项式法则,能正确根据多项式乘以多项式法则展开是解此题的关键.
6.(2025春 南海区二模)在一家创意家居装饰店中,老板接到了一位客户的订单,要求用店内如图所示的A,B,C三种卡片来装饰一面墙壁,拼成一个长为(3a+2b),宽为(a+b)的长方形图案.为了完成这个装饰任务,老板需要A型卡片、B型卡片和C型卡片的张数分别是( )
A.3,5,2 B.2,3,5 C.2,5,3 D.3,2,5
【考点】多项式乘多项式.
【专题】整式;应用意识.
【答案】D
【分析】根据长方形的面积公式可知该墙壁面积S=3a2+2b2+5ab,即可得出答案.
【解答】解:∵长方形的长为(3a+2b),宽为(a+b),
∴长方形的面积S=(3a+2b)(a+b)=3a2+2b2+5ab,
∴需要A型卡片、B型卡片和C型卡片的张数分别3、2、5张.
故选:D.
【点评】本题主要考查了多项式的乘法的应用,熟练掌握多项式乘以多项式法则是解题关键.
7.(2025春 滨江区二模)如图1,现有边长为b和a+b的正方形纸片各一张,长和宽分别为b,a的长方形纸片一张.把纸片Ⅰ,Ⅲ按图2所示的方式放入纸片Ⅱ内,若图2中阴影部分的面积S1和S2满足S1=4S2,则a,b满足的关系式为( )
A.b=4a B.b=3a C.b=2a D.b=1.5a
【考点】整式的混合运算.
【专题】整式;运算能力.
【答案】C
【分析】根据题意可得S1=(a+b)2﹣b2﹣a2=2ab,S2=(b﹣a)a=ab﹣a2,利用S1=4S2可得b=2a即可.
【解答】解:由题意可得:S1=(a+b)2﹣b2﹣a2=2ab,S2=(b﹣a)a=ab﹣a2,
∵S1=4S2,
∴2ab=4(ab﹣a2),
2ab=4ab﹣4a2,
∵a≠0,
∴b=2a,
故选:C.
【点评】本题考查了整式的混合运算,熟练掌握s1和s2面积的组成是关键.
8.(2025春 温州二模)将正方形ABCD,长方形BEFG按如图所示方式拼在一起,CG=FG,连接DB,DF,BF.记正方形ABCD的面积为S1,长方形BEFG的面积为S2,若要求出△DBF的面积,则需要知道( )
A.S1 B.S2 C.S1+S2 D.S1﹣S2
【考点】整式的混合运算.
【专题】整式;矩形 菱形 正方形;运算能力.
【答案】A
【分析】延长DC和EF交于点H,连接CF,利用等底同高的两个三角形面积相等可得S△DBF=S△DBCS1即可得到结论.
【解答】解:如图,延长DC和EF交于点H,连接CF,
∵CG=FG,
∴四边形CGFH是正方形,
∵四边形ABCD和四边形CGFH都是正方形,
∴∠DBC=∠FCG=45°,
∴CF∥BD,
∴S△DBF=S△DBCS1.
故选:A.
【点评】本题考查了正方形的性质、整式的混合运算,熟练掌握等底同高的两个三角形面积相等是关键.
9.(2025 成都)下列计算正确的是( )
A.(3x)2=9x2 B.7x 5x=35x
C.(x+3)2=x2+9 D.(x﹣y)(x+y)=x2+y2
【考点】整式的混合运算.
【专题】整式;运算能力.
【答案】A
【分析】各项计算得到结果,即可作出判断.
【解答】解:A、原式=9x2,故符合题意;
B、原式=35x2,故不符合题意;
C、原式=x2+6x+9,故不符合题意;
D、原式=x2﹣y2,故不符合题意,
故选:A.
【点评】此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.
10.(2025春 龙岗区二模)乐乐的作业本不小心被撕掉了一部分,留下一道残缺不全的题目,如图所示,请你帮他推测出等号左边被撕掉的内容是( )
A.(x2﹣2x+6) B.(x2﹣3x2+6)
C.(x2﹣3x+6) D.(x2﹣3x﹣6)
【考点】整式的除法.
【专题】整式;运算能力.
【答案】C
【分析】根据题意得到(x3﹣3x2+6x)÷x,计算即可得到等号左边被撕掉的内容.
【解答】解:根据题意可知,(x3﹣3x2+6x)÷x=x2﹣3x+6.
故选:C.
【点评】此题考查了整式的除法,掌握整式的除法的运算法则是关键.
二.填空题(共5小题)
11.(2025 阎良区二模)《几何原本》是古希腊数学家欧几里得的一部数学巨著,他在第二卷“几何与代数”中,阐述了数与形是一家,即通过“以数解形”和“以形助数”,可以把代数公式与几何图形相互转化.如图可以得到(a+b)2=a2+2ab+b2,基于此,若ab=6,a+b=5,则a2+b2的值为 13 .
【考点】完全平方公式.
【专题】整式;运算能力.
【答案】13.
【分析】直接利用完全平方公式变形计算即可.
【解答】解:由条件可知(a+b)2=a2+2ab+b2=a2+b2+2×6=25,
∴a2+b2=13;
故答案为:13.
【点评】本题考查利用完全平方公式变形计算,熟练掌握完全平方公式是解题的关键.
12.(2025春 靖江市二模)若m,n,k满足m2+n2+k2=8,则(m+n)2+(n+k)2+(m+k)2的最小值为 8 .
【考点】完全平方公式.
【专题】运算能力.
【答案】8.
【分析】根据m2+n2+k2=8,代入(m+n)2+(n+k)2+(m+k)2=2m2+2n2+2k2+2mn+2nk+2mk,得(m+n)2+(n+k)2+(m+k)2=16+2(mn+nk+mk),根据(m+n+k)2=8+2(mn+nk+mk),得mn+nk+mk,mn+nk+mk要想取得最小值(m+n+k)2取最小值即可解答.
【解答】解:原式=(m2+2mn+n2)+(n2+2nk+k2)+(m2+2mk+k2)
=2m2+2n2+2k2+2mn+2nk+2mk,
∵m2+n2+k2=8,
∴2m2+2n2+2k2+2mn+2nk+2mk=16+2(mn+nk+mk),
∵(m+n+k)2=m2+n2+k2+2(mn+nk+mk)=8+2(mn+nk+mk),
∴mn+nk+mk,
∴16+2(mn+nk+mk)=8+(m+n+k)2,
当(m+n+k)2取得最小值0时,16+2(mn+nk+mk)取得最小值8,
即(m+n)2+(n+k)2+(m+k)2取得最小值8,
故答案为:8.
【点评】本题的考查了完全平方公式,掌握完全平方公式是解题的关键.
13.(2025春 九龙坡区二模)一个各数位数字互不相等且均不为0三位正整数,若百位数字与个位数字之和减去4等于十位数字,则称这个三位数为“至善数”,例如:631,因为6+1﹣4=3,则称631是“至善数”;则最大的“至善数”与最小的“至善数”之差是 858 ;若正整数,记F(t)=c﹣2a.且,是两个不同的“至善数”(1≤y≤8,1≤n≤9,1≤m,z≤9且y,z,m,n均为整数),且F(t1)+2F(t2)+4n能被17整除,t2的值是 631,543,367 .
【考点】整式的加减;列代数式.
【专题】整式;运算能力.
【答案】858;631,543,367.
【分析】根据最大的“至善数”可得a=9,b=8,进而根据定义求得c,同理求得最小的“至善数”的a=1,b=2,再求得c的值,求两数的差,即可求解.,是两个不同的“至善数”,可得方程组;再根据F(t1)+2F(t2)+4n列代数式,最后根据F(t1)+2F(t2)+4n能被17整除进行分类讨论,即可得答案.
【解答】解:由条件可知a+c﹣4=b,则c=b﹣a+4,
最大的“至善数”可得a=9,b=8,则c=3,则最大的“至善数”为983,
最小的“至善数”的a=1,b=2,则c=5,则最小的“至善数”为125,
983﹣125=858,
由条件可知,
得2+z=m+n,即z=m+n﹣2,y=z﹣2=m+n﹣4,
∴F(t1)+2F(t2)+4n
=z﹣2×2+2(n﹣2m)+4n
=z﹣4﹣4m+6n
=m+n﹣2﹣4﹣4m+6n
=﹣3m+7n﹣6.
∵1≤y≤8,1≤m≤9,1≤n≤9,
∴﹣26≤﹣3m+7n﹣6≤54.
∵﹣3m+7n﹣6能被17整除,
∴﹣3m+7n﹣6=﹣17或0或17或34或51.
①当﹣3m+7n﹣6=﹣17时,
∴,
当m=6时,n=1,y=m+n﹣4=3,z=m+n﹣2=6+1﹣2=5,
∴,
②当﹣3m+7n﹣6=0时,,
当m=5时,n=3,y=m+n﹣4=4,z=y+2=6,
∴,
③当﹣3m+7n﹣6=17时,,
当m=4时,n=5,y=m+n﹣4=5,z=y+2=7,
∴(舍去),
④当﹣3m+7n﹣6=34时,,
当m=3时,n=7,y=m+n﹣4=6,z=y+2=8,
∴,
⑤当﹣3m+7n﹣6=51时,,
当m=2时,n=9,y=m+n﹣4=7,z=y+2=9,
∴,(相同,舍去),
故答案为:858;631,543,367.
【点评】本题考查了二元一次方程组的应用,新定义、数的整除等知识,分类讨论是解题的关键
14.(2025春 梅县区二模)如图,两个正方形的边长分别为a、b,若a+b=10,ab=20,则图中阴影部分的面积为 20 .
【考点】完全平方公式的几何背景.
【专题】整式;运算能力.
【答案】20.
【分析】用含有a、b的代数式表示阴影部分的面积,再根据完全平方公式进行代数式的变形,进而求出答案.
【解答】解:阴影部分的面积为,
当a+b=10,ab=20时,
原式(100﹣60)=20.
故答案为:20.
【点评】本题考查完全平方公式的应用,正确的表示阴影部分的面积和适当的变形,是得到正确答案的关键.
15.(2025春 蜀山区二模)如图,将两张周长为10,面积为4的长方形纸片按图1,图2两种方式放置,正方形ABCD中未被这两张长方形纸片覆盖部分用阴影表示,图1和图2中阴影部分的面积分别记为S1和S2.则S1﹣S2= 9 .
【考点】整式的混合运算.
【专题】整式;运算能力;推理能力.
【答案】9.
【分析】先求出a、b值,再根据图示列出S1=(x﹣1)2+(x﹣4)2,S2=2(x﹣1)(x﹣4),代入S1﹣S2计算即可.
【解答】解:根据题意得,解得,
设正方形ABCD的边长为x,
S1=(x﹣1)2+(x﹣4)2,S2=2(x﹣1)(x﹣4),
∴S1﹣S2=(x﹣1)2+(x﹣4)2﹣2(x﹣1)(x﹣4)=(x﹣1﹣x+4)2=9.
故答案为:9.
【点评】本题考查了整式的混合运算,根据图示列出S1=(x﹣1)2+(x﹣4)2,S2=2(x﹣1)(x﹣4),是关键.
三.解答题(共5小题)
16.(2025春 清新区二模)先化简,再求值:[(x﹣2y)2+(x﹣2y)(x+2y)﹣3x(x﹣2y)]÷2x,其中,.
【考点】整式的混合运算—化简求值.
【专题】整式;运算能力.
【答案】,.
【分析】根据整式的混合运算法则化简,再将x、y代入即可解答.
【解答】解:[(x﹣2y)2+(x﹣2y)(x+2y)﹣3x(x﹣2y)]÷2x
=(x2﹣4xy+4y2+x2﹣4y2﹣3x2+6xy)÷2x
=(﹣x2+2xy)÷2x
;
当,时,原式
【点评】本题考查了整式的混合运算和化简求值,掌握整式的混合运算法则是解题的关键.
17.(2025春 海州区二模)如图1是一个长为2m、宽为2n的长方形.沿图中虚线用剪刀均匀分成四块全等小长方形,然后按图2形状拼成一个正方形.
(1)观察图2,直接写出代数式(m+n)2,(m﹣n)2,mn之间的关系: (m+n)2=(m﹣n)2+4mn ;
(2)利用(1)的结论和公式变形,尝试解决以下问题:
①已知x+y=7,xy=6,则x﹣y的值为 ±5 ;
②已知(2024﹣x)(x﹣2025)=﹣6,求(2024﹣x)2+(x﹣2025)2的值;
(3)两个正方形ABCD、AEFG如图3摆放.边长分别为x,y,若x2+y2=34,BE=2,求图中阴影部分的面积.
【考点】完全平方公式.
【专题】整式;运算能力.
【答案】(1)(m+n)2=(m﹣n)2+4mn;
(2)±5,13;
(3)8.
【分析】(1)根据大正方形的面积等于小正方形的面积加上4个小长方形的面积,即可作答.
(2)①直接把数值代入(x+y)2=(x﹣y)2+4xy进行计算,即可作答.
②根据(2024﹣x)2+(x﹣2025)2=[(2024﹣x)+(x﹣2025)]2﹣2(2024﹣x)(x﹣2025),然后代入数值化简计算,即可作答.
(3)由题意可知x﹣y=2,,,即可求出S阴影=x+y.结合x2+y2=34,可求出xy=15,最后根据(x+y)2=x2+y2+2xy求解即可.
【解答】解:(1)依题意,(m+n)2=(m﹣n)2+4mn;
故答案为:(m+n)2=(m﹣n)2+4mn;
(2)①与(1)同理得(x+y)2=(x﹣y)2+4xy,
∵x+y=7,xy=6,
∴49=(x﹣y)2+4×6,
∴(x﹣y)2=25,
∴x﹣y=±5;
故答案为:±5;
②∵(2024﹣x)(x﹣2025)=﹣6,
∴(2024﹣x)2+(x﹣2025)2
=[(2024﹣x)+(x﹣2025)]2﹣2(2024﹣x)(x﹣2025)
=(﹣1)2﹣2×(﹣6)
=1+12
=13.
(3)∵BE=2,
∴x﹣y=2.
由图可知△CDF的底为x,高为2,
∴.
△BEF的底为2,高为y,
∴,
∴S阴影=S△CDF+S△BEF=x+y.
∵22+2xy=34,
∴xy=15,
∴(x+y)2=x2+y2+2xy=34+2×15=64,
∴x+y=8(舍去负值),
∴阴影部分面积和为8.
【点评】本题考查完全平方公式的变形求值,完全平方公式在几何图形中的应用,利用数形结合的思想是解题关键.
18.(2025 扬州一模)某数学兴趣小组研究如下等式:38×32=1216,53×57=3021,71×79=5609,84×86=7224.观察发现以上等式均是“两位数乘以两位数,十位数字相同,个位数字之和是10,且积有一定的规律”.
(1)根据上述的运算规律,直接写出结果:58×52= 3016 ;752= 5625 ;
(2)设其中一个数的十位数字为a,个位数字为b(a>0,b>0).
①请用含a,b的等式表示这个运算规律,并用所学的数学知识证明;
②上述等式中,分别将左边两个乘数的十位和个位数字调换位置,得到新的两个两位数相乘(如:38×32调换为83×23).若记新的两个两位数的乘积为m,①中的运算结果为n,若|m﹣n|一定能被一个两位数整除,试求这个两位数的最大值.
【考点】整式的加减.
【专题】整式;运算能力.
【答案】(1)3016;5625;
(2)①详见解析;②99.
【分析】(1)根据上述的运算规律计算,即可求解;
(2)①根据题意可得这两个两位数分别为10a+b,10a+10﹣b,从而得到这个运算规律为(10a+b)(10a+10﹣b)=100a(a+1)+b(10﹣b),然后分别计算等式的左右两边,即可;②由①得:n=100a2+100a+10b﹣b2,可得新的两个两位数分别为10b+a,10(10﹣b)+a,进而得到m=(10b+a)[10(10﹣b)+a],然后计算出m﹣n,再进一步求解即可.
【解答】解:(1)根据题意得:58×52=(5×6)×100+8×2=3016,
752=(7×8)×100+5×5=5625;
故答案为:3016;5625;
(2)①∵其中一个数的十位数字为a,个位数字为b(a>0,b>0),
∴另一个数的十位数字为a,个位数字为10﹣b,
∴这两个两位数分别为10a+b,10a+10﹣b,
根据题意得:这个运算规律为(10a+b)(10a+10﹣b)=100a(a+1)+b(10﹣b),
证明:左边=100a2+10ab+100a+10b﹣10ab﹣b2
=100a2+100a+10b﹣b2
右边=100a2+100a+10b﹣b2,
∴左边=右边;
②由①得:n=100a2+100a+10b﹣b2,
由条件可知新的两个两位数分别为10b+a,10(10﹣b)+a,
∴m=(10b+a)[10(10﹣b)+a]
=(10b+a)(100﹣10b+a)
=1000b+100a﹣100b2﹣10ab+10ab+a2
=1000b﹣100b2+100a+a2,
∴m﹣n=(1000b﹣100b2+100a+a2)﹣(100a2+100a+10b﹣b2)
=﹣99a2﹣99b2+990b
=﹣99(a2+b2+10b),
∴a2+b2+10b为整数,
∴m﹣n能被99整除,
∴这个两位数的最大值为99.
【点评】本题主要考查了整式的混合运算,因式分解的应用,明确题意,准确得到规律是解题的关键.
19.(2025春 扬州二模)阅读:在计算(x﹣1)(xn+xn﹣1+xn﹣2+…+x+1)的过程中,我们可以先从简单的、特殊的情形入手,再到复杂的、一般的问题,通过观察、归纳、总结,形成解决一类问题的一般方法,数学中把这样的过程叫做特殊到一般.如下所示:
(1)【观察】①(x﹣1)(x+1)= x2﹣1 ;
②(x﹣1)(x2+x+1)= x3﹣1 :
③(x﹣1)(x3+x2+x+1)= x4﹣1 ;………
(2)【猜想】由此可得:(x﹣1)(xn+xn﹣1+xn﹣2+…+x+1)= xn+1﹣1 ;
(3)【应用】请运用上面的结论,解决下列问题:计算:52024+52023+52022+52021+…+5+1的值.
【考点】多项式乘多项式;规律型:数字的变化类.
【专题】运算能力.
【答案】(1)x2﹣1;x3﹣1;x4﹣1;
(2)xn+1﹣1;
(3).
【分析】(1)利用平方差公式和多项式乘以多项式计算即可;
(2)利用(1)中变化规律进而得出答案;
(3)设x=5,n=2024,则(5﹣1)(52024+52023+52022+ +5+1)=52025﹣1,即可求解.
【解答】解:(1)(x﹣1)(x+1)=x2﹣1;
(x﹣1)(x2+x+1)=x(x2+x+1)﹣(x2+x+1)=x3﹣1;
(x﹣1)(x3+x2+x+1)=x(x3+x2+x+1)﹣(x3+x2+x+1)=x4﹣1,
故答案为:x2﹣1;x3﹣1;x4﹣1;
(2)由(1)得,(x﹣1)(xn+xn﹣1+xn﹣2+ +x+1)=xn+1﹣1,
故答案为:xn+1﹣1;
(3)设x=5,n=2024,
根据(x﹣1)(xn+xn﹣1+xn﹣2+ +x+1)=xn+1﹣1
则(5﹣1)(52024+52023+52022+ +5+1)=52025﹣1,
∴.
【点评】此题主要考查了平方差公式、多项式乘以多项式以及数字变化规律,正确得出式子之间的变化规律是解题关键.
20.(2025春 包河区二模)两个边长分别为a和b的正方形如图放置(如图①),其未叠合部分(阴影)面积为S1;若在图①中大正方形的右下角再摆放一个边长为b的小正方形(如图②),两个小正方形叠合部分(阴影)面积为S2.
(1)用含a、b的代数式分别表示S1、S2;
(2)若a+b=4、ab=5,求S1+S2;
(3)图③也是由两个边长分别为a和b的正方形放置构成.用a、b的代数式表示图③中阴影部分的面积S3;并当S1+S2=32时,求S3的值.
【考点】整式的混合运算;完全平方公式的几何背景.
【专题】整式;运算能力.
【答案】(1)S1=a2﹣b2,S2=2b2﹣ab;
(2)1;
(3)16.
【分析】(1)由图中正方形和长方形的面积关系,可得答案;
(2)根据(1)中的结论,将a+b=4,ab=5,代入进行计算即可;
(3)表示出S3,再变形整体代入求值即可.
【解答】解:(1)由图可得,S1=a2﹣b2,S2=a(a﹣b)+2b2﹣a2=2b2﹣ab;
(2)∵a+b=4,ab=5,
∴S1+S2
=a2﹣b2+2b2﹣ab
=a2+b2﹣ab
=(a+b)2﹣3ab
=42﹣3×5
=1;
(3),
∵S1+S2=a2+b2﹣ab=32,
∴S332=16.
【点评】本题考查了整式的混合运算,完全平方公式,数形结合、恰当进行代数式变形是解答本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
