【中考押题预测】2025年中考数学核心考点考前冲刺 图形的对称(含解析)
文档属性
| 名称 | 【中考押题预测】2025年中考数学核心考点考前冲刺 图形的对称(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 16:20:14 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中考核心考点 图形的对称
一.选择题(共10小题)
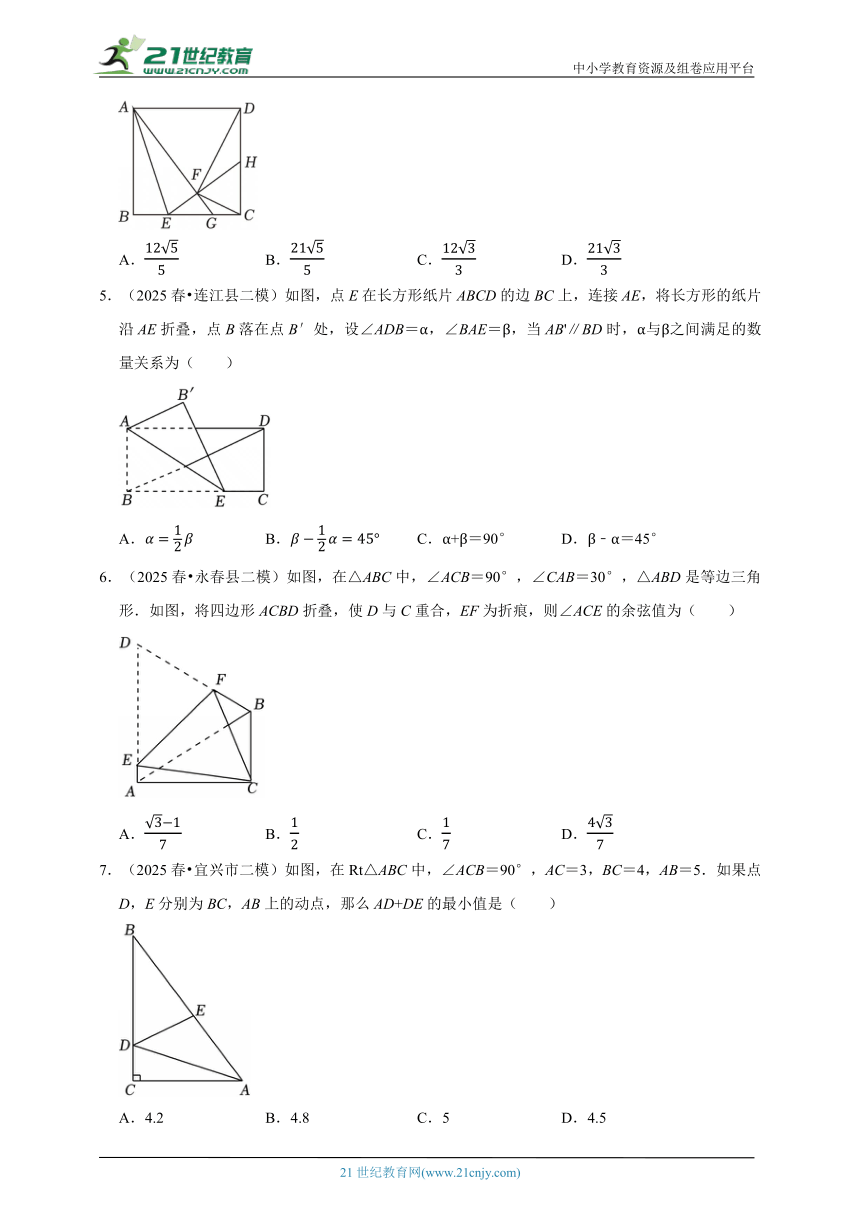
1.(2025春 江阴市二模)如图,正方形ABCD中,E是AB上一点,将△DAE沿DE翻折得△DFE,点A的对应点是点F,直线AF与DE交于点H,与∠CDF的平分线交于点G,连接BG,下列说法:①DH=GH;②∠AGB=45°;③若连接CG,则CG⊥AG;④若正方形边长为2,E为AB的中点,则点C到直线AG的距离为1.其中正确的是( )
A.①③ B.①②③ C.①③④ D.②④
2.(2025春 长安区二模)如图,在△ABC中,∠BAC=60°,AD是∠BAC的平分线,,若点P是AD上一动点,作PN⊥AC于点N,则PC+PN的最小值是( )
A. B. C. D.
3.(2025春 鼓楼区二模)如图,将长方形纸条沿直线EF折叠,点A落在A′处,点D落在D′处,A′E交CD于点G.若∠AEF=40°,则∠A′GC=( )
A.100° B.120° C.140° D.160°
4.(2025春 江北区二模)如图,在正方形ABCD中,点E是边CB的一点且BE:EC=1:2,连接AE,将AB沿AE折叠至正方形内部,得到线段AF,延长AF交BC于点G,延长EF交DC于点H,若AB=6,连接CF,DF,则DF的长为( )
A. B. C. D.
5.(2025春 连江县二模)如图,点E在长方形纸片ABCD的边BC上,连接AE,将长方形的纸片沿AE折叠,点B落在点B′处,设∠ADB=α,∠BAE=β,当AB'∥BD时,α与β之间满足的数量关系为( )
A. B. C.α+β=90° D.β﹣α=45°
6.(2025春 永春县二模)如图,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形.如图,将四边形ACBD折叠,使D与C重合,EF为折痕,则∠ACE的余弦值为( )
A. B. C. D.
7.(2025春 宜兴市二模)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5.如果点D,E分别为BC,AB上的动点,那么AD+DE的最小值是( )
A.4.2 B.4.8 C.5 D.4.5
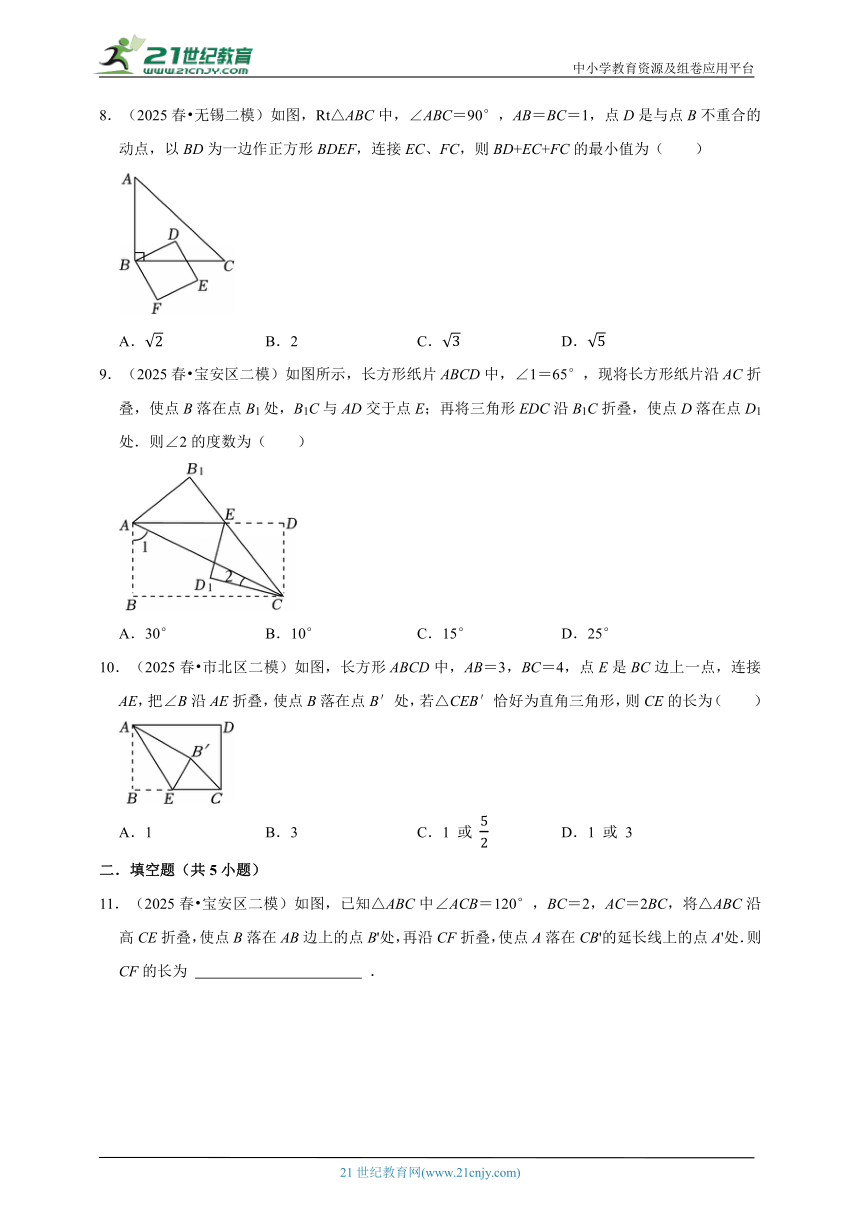
8.(2025春 无锡二模)如图,Rt△ABC中,∠ABC=90°,AB=BC=1,点D是与点B不重合的动点,以BD为一边作正方形BDEF,连接EC、FC,则BD+EC+FC的最小值为( )
A. B.2 C. D.
9.(2025春 宝安区二模)如图所示,长方形纸片ABCD中,∠1=65°,现将长方形纸片沿AC折叠,使点B落在点B1处,B1C与AD交于点E;再将三角形EDC沿B1C折叠,使点D落在点D1处.则∠2的度数为( )
A.30° B.10° C.15° D.25°
10.(2025春 市北区二模)如图,长方形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,若△CEB′恰好为直角三角形,则CE的长为( )
A.1 B.3 C.1 或 D.1 或 3
二.填空题(共5小题)
11.(2025春 宝安区二模)如图,已知△ABC中∠ACB=120°,BC=2,AC=2BC,将△ABC沿高CE折叠,使点B落在AB边上的点B'处,再沿CF折叠,使点A落在CB'的延长线上的点A'处.则CF的长为 .
12.(2025春 广州二模)如图,等边三角形ABC中,BD⊥AC于点D,点E、F分别是BC、DC上的动点,沿EF所在直线折叠△CEF,使点C落在BD上的点C'处,AB=16,当△BEC'是直角三角形时,DF的值为 .
13.(2025春 宁海县二模)如图,在等腰Rt△ABC中,∠A=90°,BD平分∠ABC,BE平分∠DBC,M,N分别为射线BE,BC上的动点,若BD=8,则CM+MN的最小值为 .
14.(2025春 西安)小明从A点出发,走到水平直线l上P点,再回到到B点,若A、B到水平直线l的距离分别是2,1,AB两点之间水平距离是4,则PA+PB最小值为 .
15.(2025 温江区二模)如图,在菱形ABCD中,AB=4,∠B=60°,M是BC的中点,点P是CD上一动点,连接PA,PM,则PA+PM的最小值为 .
三.解答题(共5小题)
16.(2025春 江阴市二模)如图,直角三角形ABC中,∠ACB=90°,AC=6,BC=8,AB=10,用无刻度的直尺和圆规完成下列作图.
(1)作边AB的中点D;
(2)作∠ABC的平分线BE,交AC边于点E;
(3)作点C关于直线BE的对称点F;
(4)直接写出DF的长为 .
17.(2025春 武汉二模)(1)王芳同学把两个边长为1的正方形分别沿对角线剪开,将所得的4个直角三角形按如图(1)拼在一起,就得到了一个边长为 的大正方形.
(2)图(2)是由5个边长为1的小正方形组成的图形,这个图形按图(3)的方式剪裁,拼成图(4).
①拼成的正方形图(4)的面积为 ,边长为 ;
②仿照上面的做法,将图(5)中这十个小正方形组成的图形,拼成一个大正方形,请在图(5)中画出裁剪方法,并求出拼成的正方形边长 ;
③能否在图(5)拼成的正方形中裁剪出一个边长为1:3面积为9的长方形?若能,求它的长、宽;若不能,请说明理由.
18.(2025春 宜兴市二模)如图,已知长方形OABC的顶点A在x轴上,顶点C在y轴上,OA=8,OC=4,D、E分别为OA、BC上的两点,将长方形OABC沿直线DE折叠后,点A刚好与点C重合,点B落在点F处,再将其打开、展平.
(1)点D的坐标是 ,点E的坐标是 ,点F的坐标是 ;
(2)设动点P从点D出发,以1个单位长度/秒的速度沿折线D→A→B→C向终点C运动,运动时间为t秒,当S△PDE时,求t的值.
19.(2025春 越秀区二模)如图,直角坐标系中的网格由单位为1的正方形构成.
(1)写出A、B、C的坐标;
(2)若以A、B、C及点D为顶点的四边形为 ABCD,画出 ABCD,并直接写出D点的坐标.
(3)在x轴上是否存在一点P,使AP+DP的值最小.若存在,请在图中找出这个点,请求出最小值;若不存在,请说明理由.
20.(2025春 和平区二模)如图1,Rt△ABC中,∠ACB=90°,AC=5,AB=13.
(1)如图2,点E是边BC上一点,△ABC沿着AE折叠,点C恰好与斜边AB上点D重合,求CE的长;
(2)如图3,点F为斜边上AB上动点,连接CF,在点F的运动过程中,若△BCF为等腰三角形,请直接写出AF的长.
中考核心考点 图形的对称
参考答案与试题解析
一.选择题(共10小题)
1.(2025春 江阴市二模)如图,正方形ABCD中,E是AB上一点,将△DAE沿DE翻折得△DFE,点A的对应点是点F,直线AF与DE交于点H,与∠CDF的平分线交于点G,连接BG,下列说法:①DH=GH;②∠AGB=45°;③若连接CG,则CG⊥AG;④若正方形边长为2,E为AB的中点,则点C到直线AG的距离为1.其中正确的是( )
A.①③ B.①②③ C.①③④ D.②④
【考点】翻折变换(折叠问题);解直角三角形;全等三角形的判定与性质;正方形的性质.
【专题】图形的全等;矩形 菱形 正方形;展开与折叠;几何直观;运算能力;推理能力.
【答案】B
【分析】先由折叠的性质可得∠AHD=90°,再由角平 分线的定义可得∠FDG=∠CDG,进而证明∠HDG=45°,则△DHG是等腰直角三角,即可判断①;证明A、D、G、B四点共圆,即可判断 ②;证明A、B、G、C四点共圆,即可判断③;由②可知∠DGH=45°,再说明△DFG≌△DCG,可得∠CGF=90°,即CG就是点C到直线AG的距离,根据锐角三角函数求出AH,DH,即可得出答案,判断④.
【解答】解:根据翻折可知∠ADE=∠EDF,点A和点F关于DE对称,
∴∠AHD=90°.
∵DG是∠CDF的平分线,
∴∠FDG=∠CDG.
∵四边形ABCD是正方形,
∴∠ADC=∠DAE=∠ABC=90°,AB=AD,
∴∠HDG=45°,
∴∠DGH=∠HDG=45°,
∴DH=GH.
故①正确;
如图1,连接BD,
∵四边形是正方形,∠DGH=45°,
∴∠ABD=∠AGD=∠ADB=45°,
∴A、D、G、B四点共圆,
∴∠AGB=∠ADB=45°,
故②正确;
如图1,连接AC,
∵∠ACB=∠AGB=45°,
∴A、B、G、C四点共圆,
∴∠AGC=∠ABC=90°,
∴CG⊥AG,
故③正确;
由②可知∠DGH=45°,
在△DFG和△DCG中,
,
∴△DFG≌△DCG(SAS),
∴∠DGF=∠CGD=45°,
∴∠CGF=90°,即CG就是点C到直线AG的距离.
∵AD=2,AE=1,
∴DE,
∴sin∠ADE,cos∠ADE,
在Rt△ADH中,sin∠ADH,cos∠ADH,
∴AH,,
∴FHHG,
∴CG=FG,
故④不正确.
综上所述,正确的是①②③,
故选:B.
【点评】本题主要考查了翻折变换(折叠问题),全等三角形的判定与性质,正方形的性质,解直角三角形,合理构造全等三角形是解题的关键.
2.(2025春 长安区二模)如图,在△ABC中,∠BAC=60°,AD是∠BAC的平分线,,若点P是AD上一动点,作PN⊥AC于点N,则PC+PN的最小值是( )
A. B. C. D.
【考点】轴对称﹣最短路线问题;角平分线的定义.
【专题】线段、角、相交线与平行线;平移、旋转与对称;几何直观;推理能力.
【答案】D
【分析】作CE⊥AB于点E,则CE的长就是PN+PC的最小值,在直角△ACE中利用三角函数求解.
【解答】解:作CE⊥AB于点E.连接PE,
∵AD是∠BAC的平分线,
∴PN=PE,
∴PN+PC=PE+PC≥EC,
当CE⊥AB时,PN+PC最短,即为CE的长度,
在直角△ACE中,CE=AC sin∠BAC.
故选:D.
【点评】本题考查了轴对称﹣最短路线问题,角平分线的定义,根据角的平分线的性质理解CE的长是PN+PC的最小值是解答本题的关键.
3.(2025春 鼓楼区二模)如图,将长方形纸条沿直线EF折叠,点A落在A′处,点D落在D′处,A′E交CD于点G.若∠AEF=40°,则∠A′GC=( )
A.100° B.120° C.140° D.160°
【考点】翻折变换(折叠问题);平行线的性质;矩形的性质.
【专题】平移、旋转与对称;运算能力.
【答案】A
【分析】利用翻折变换的性质以及平行线的性质求解.
【解答】解:由翻折变换的性质可知∠AEF=∠A′EF=40°,
∴∠GEB=180﹣°﹣40°﹣40°=100°,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠A′GC=∠GEB=100°.
故选:A.
【点评】本题考查翻折变换,平行线的性质,矩形的性质,解题的关键是掌握翻折变换的性质.
4.(2025春 江北区二模)如图,在正方形ABCD中,点E是边CB的一点且BE:EC=1:2,连接AE,将AB沿AE折叠至正方形内部,得到线段AF,延长AF交BC于点G,延长EF交DC于点H,若AB=6,连接CF,DF,则DF的长为( )
A. B. C. D.
【考点】翻折变换(折叠问题);正方形的性质.
【专题】矩形 菱形 正方形;平移、旋转与对称;运算能力.
【答案】A
【分析】如图,连接AH交DF于点O.证明Rt△AHD≌Rt△AHF(HL),推出DH=HF,设DH=HF=x,利用勾股定理构建方程求出x可得结论.
【解答】解:如图,连接AH交DF于点O.
∵四边形ABCD是正方形,
∴AB=BC=AD=6,∠B=∠ADC=∠BCD=90°,
∵BE:EC=1:2,
∴BE=2,EC=4,
由翻折变换的性质可知AB=AF,BE=EF=2,∠B=∠AFE=∠AFH=90°,
∴AD=AF,
∵∠ADH=∠AFH,AH=AH,
∴Rt△AHD≌Rt△AHF(HL),
∴DH=HF,设DH=HF=x,
在Rt△ECH中,则有(2+x)2=42+(6﹣x)2,
解得x=3,
∴DH=3,
∴AH3,
∵AD=AF,HD=HF,
∴AH垂直平分线段DF,
∴OD=OF,
∴DF=2.
故选:A.
【点评】本题考查翻折变换,正方形的性质,全等三角形的判定和性质,勾股定理,解题的关键是掌握翻折变换的性质.
5.(2025春 连江县二模)如图,点E在长方形纸片ABCD的边BC上,连接AE,将长方形的纸片沿AE折叠,点B落在点B′处,设∠ADB=α,∠BAE=β,当AB'∥BD时,α与β之间满足的数量关系为( )
A. B. C.α+β=90° D.β﹣α=45°
【考点】翻折变换(折叠问题);矩形的性质.
【专题】矩形 菱形 正方形;平移、旋转与对称;运算能力.
【答案】B
【分析】利用矩形的性质,平行线的性质,翻折变换的性质求解即可.
【解答】解:∵四边形ABCD是矩形,
∴∠BAD=90°,
∴∠EAD=90°﹣β,
∵AB′∥BD,
∴∠DAB′=∠ADB=α,
∵∠EAB=∠EAB′=β,
∴β=α+90°﹣β,
∴βα=45°.
故选:B.
【点评】本题考查翻折变换,矩形的性质,解题的关键是掌握相关知识解决问题.
6.(2025春 永春县二模)如图,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形.如图,将四边形ACBD折叠,使D与C重合,EF为折痕,则∠ACE的余弦值为( )
A. B. C. D.
【考点】翻折变换(折叠问题);解直角三角形;等边三角形的性质;勾股定理.
【专题】等腰三角形与直角三角形;平移、旋转与对称;解直角三角形及其应用;运算能力;推理能力.
【答案】D
【分析】设AB=2a,由含30°角的直角三角形的性质和勾股定理求得BC、AC的值,再由等边三角形的性质证得∠EAC=90°,然后由折叠的性质知DE=CE,设DE=CE=x,由勾股定理求出EC的长,最后由锐角三角函数的定义即可得出结果.
【解答】解:设AB=2a,
∵△ABC中,∠ACB=90°,∠BAC=30°,
∴BC=a,ACa,
∵△ABD是等边三角形,
∴AD=AB=2a,∠DAB=60°,
∴∠EAC=60°+30°=90°,
由折叠的性质得:DE=EC,
设DE=EC=x,则AE=2a﹣x,
在Rt△AEC中,由勾股定理得:AE2+AC2=EC2,
即(2a﹣x)2+(a)2=x2,
解得:xa,
∴ECa,
∴cos∠ACE,
故选:D.
【点评】本题考查了折叠的性质、等边三角形的性质、勾股定理、锐角三角函数的定义等知识,熟练掌握折叠的性质和勾股定理是解题的关键.
7.(2025春 宜兴市二模)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5.如果点D,E分别为BC,AB上的动点,那么AD+DE的最小值是( )
A.4.2 B.4.8 C.5 D.4.5
【考点】轴对称﹣最短路线问题.
【专题】平移、旋转与对称;推理能力.
【答案】B
【分析】延长AC到点M,使CM=AC,则BC是线段AM的垂直平分线,连接BM,过点M作ME′⊥AB交D′,连接AD′,根据线段垂直平分线的性质可得:AD′+D′E′=MD′+D′E′,根据垂线段最短,可知当ME′⊥AB时,AD′+D′E′的值最小,利用三角形的面积公式求出ME′的长度即为AD′+D′E′的最小值.
【解答】解:如图所示,延长AC到点M,使CM=AC,连接BM,过点M作ME′⊥AB交D′,连接AD′,点 D′即为使得AD+DE取最小值的点,
由条件可知BC是AM的垂直平分线,AM=2AC=6,
∴AD′=D′M,
∴AD′+D′E′=MD′+D′E′,
∴,
,
解得:ME′=4.8.
故选:B.
【点评】本题考查了线段垂直平分线的性质,熟练掌握该知识点是关键.
8.(2025春 无锡二模)如图,Rt△ABC中,∠ABC=90°,AB=BC=1,点D是与点B不重合的动点,以BD为一边作正方形BDEF,连接EC、FC,则BD+EC+FC的最小值为( )
A. B.2 C. D.
【考点】轴对称﹣最短路线问题;全等三角形的判定与性质;勾股定理;等腰直角三角形;正方形的性质.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;平移、旋转与对称;几何直观;推理能力.
【答案】A
【分析】根据正方形的性质和全等三角形的判定和性质得出AD=CF,进而解答即可.
【解答】解:Rt△ABC中,∠ABC=90°,AB=BC=1,如图,连接AD,CF,CE,
∵四边形BDEF是正方形,
∴BD=BF,∠DBF=90°,
∴∠ABC﹣∠DBC=∠DBF﹣∠DBC,即∠ABD=∠CBF,
在△ABD与△CBF中,
,
∴△ABD≌△CBF(SAS),
∴AD=CF,
∵BD+EC+FC=DE+EC+AD,
当A、D、E、C在同一直线上时,BD+EC+FC最小即为AC,
∵Rt△ABC中,∠ABC=90°,AB=BC=1,
∴AC,
∴BD+EC+FC最小即为,
故选:A.
【点评】本题考查轴对称﹣最短路线问题,全等三角形的判定与性质定理,勾股定理,等腰直角三角形正方形的性质,解答本题的关键是根据SAS证明△ABD与△CBF全等.
9.(2025春 宝安区二模)如图所示,长方形纸片ABCD中,∠1=65°,现将长方形纸片沿AC折叠,使点B落在点B1处,B1C与AD交于点E;再将三角形EDC沿B1C折叠,使点D落在点D1处.则∠2的度数为( )
A.30° B.10° C.15° D.25°
【考点】翻折变换(折叠问题);平行线的性质;矩形的性质.
【专题】线段、角、相交线与平行线;矩形 菱形 正方形;展开与折叠;几何直观;推理能力.
【答案】C
【分析】求出∠ACB=90°﹣65°=25°,由折叠大的性质得到∠ACB1=∠ACB=25°,∠DCE=∠D1CE,求出∠DCE=40°,即可得到∠2的度数.
【解答】解:∵四边形ABCD是长方形,
∴∠B=∠BCD=90°,
∴∠ACB=90°﹣∠1=90°﹣65°=25°,
由折叠大的性质得到:∠ACB1=∠ACB=25°,∠DCE=∠D1CE,
∴∠DCE=∠BCD﹣∠ACB﹣ACB1=90°﹣25°﹣25°=40°,
∴∠2=∠D1CE﹣∠ACB1=40°﹣25°=15°.
故选:C.
【点评】本题考查了翻折变换(折叠问题),平行线的性质,矩形的性质,熟练掌握平行线的性质是解题的关键.
10.(2025春 市北区二模)如图,长方形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,若△CEB′恰好为直角三角形,则CE的长为( )
A.1 B.3 C.1 或 D.1 或 3
【考点】翻折变换(折叠问题);勾股定理;矩形的性质.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;平移、旋转与对称;推理能力.
【答案】C
【分析】分为两种情况,当∠CB′E=90°和∠CEB′=90°时,将图形画出,利用折叠性质和勾股定理求解即可.
【解答】解:如图,当∠CB′E=90°时,
在矩形ABCD中,,
∵把∠B沿AE折叠,使点B落在点B′处,
∴∠B=∠AB′E=90°,AB′=AB=3,B′E=BE,则点B′在AC上,
∴B′C=AC﹣AB′=2,
设BE=x,则:CE=4﹣x,B′E=BE=x
在Rt△B′CE中,由勾股定理可得:x2+22=(4﹣x)2,
解得:,
∴,则,
如图,当∠CEB′=90°时,
∴∠BEB′=90°,
∵把∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠ABE=90°,B′E=BE,
∴四边形ABEB′为正方形,
∴BE=B′E=AB=3,则CE=1,
综上,或1,
故选:C.
【点评】本题考查折叠的性质,矩形的性质,勾股定理等知识点,解题的关键是分两种情况考虑,画出对应图形.
二.填空题(共5小题)
11.(2025春 宝安区二模)如图,已知△ABC中∠ACB=120°,BC=2,AC=2BC,将△ABC沿高CE折叠,使点B落在AB边上的点B'处,再沿CF折叠,使点A落在CB'的延长线上的点A'处.则CF的长为 .
【考点】翻折变换(折叠问题).
【专题】平移、旋转与对称;解直角三角形及其应用;运算能力.
【答案】.
【分析】如图,过点A作AJ⊥BC交BC的延长线于点J.证明CF=2CE,利用面积法求出CE即可.
【解答】解:如图,过点A作AJ⊥BC交BC的延长线于点J.
∵BC=2,AC=2BC,
∴AC=4,
∵∠ACB=120°,
∴∠ACJ=60°,
∵∠J=90°,
∴∠JAC=30°,
∴CJAC=2,
∴AJ2,
∴BJ=4,
∴AB2,
由翻折变换的性质可知CE⊥BB′,∠BCE=∠ECB′,∠ACF=∠A′CF,
∴∠FCE∠ACB=60°,
∴∠CFE=30°,
∴CF=2CE,
∵ BC AJ AB CE,
∴CE,
∴CF=2CE.
故答案为:.
【点评】本题考查翻折变换,含30度的直角三角形,解题的关键是掌握翻折变换的性质.
12.(2025春 广州二模)如图,等边三角形ABC中,BD⊥AC于点D,点E、F分别是BC、DC上的动点,沿EF所在直线折叠△CEF,使点C落在BD上的点C'处,AB=16,当△BEC'是直角三角形时,DF的值为 24﹣8或 .
【考点】翻折变换(折叠问题);等边三角形的性质;勾股定理.
【专题】等腰三角形与直角三角形;平移、旋转与对称;运算能力.
【答案】24﹣8或.
【分析】由等边三角形的性质可得∠DBC=30°,分∠BEC'=90°,∠BC'E=90°两种情况讨论,由直角三角形的性质可求BC'的长.
【解答】解:∵△ABC是等边三角形,BD⊥AC,
∴∠DBC=30°,
∵折叠,
∴CE=C'E,
若∠BEC'=90°,且∠C'BE=30°,
∴BEC'E,BC'=2C'E,
且BE+CE=BC=16,
∴CE+CE=16,
∴CE=88=C'E,
∴BC'=16﹣16,BE=24﹣8.
若∠BC'E=90°,∠C'BE=30°,
∴BE=2C'E,BC'C'E,
且BE+CE=BC=16,
∴CEC'E,
∴BE,
故答案为:24﹣8或.
【点评】本题考查了翻折变换,等边三角形的性质,折叠的性质,熟练运用折叠的性质是本题的关键.
13.(2025春 宁海县二模)如图,在等腰Rt△ABC中,∠A=90°,BD平分∠ABC,BE平分∠DBC,M,N分别为射线BE,BC上的动点,若BD=8,则CM+MN的最小值为 4 .
【考点】轴对称﹣最短路线问题;角平分线的性质;勾股定理;等腰直角三角形.
【专题】等腰三角形与直角三角形;平移、旋转与对称;几何直观;推理能力.
【答案】4.
【分析】如图,作N关于BE的对称点N′,则MN=MN′,当C,M,N′三点共线时最短即CN′,当CN′⊥BF时最短,过点C作CF⊥BD,交BD的延长线于点F,即N′与F点重合时最短,过点D作DG⊥BC于点G,根据等面积法求得CF,即可求解.
【解答】解:如图,作N关于BE的对称点N′,过点C作CF⊥BD,交BD的延长线于点F,过点D作DG⊥BC于点G,
∴MN=MN′,当C,M,N′三点共线时CM+MN最小即CN′,
∵当CN′⊥BF时,CN′最短,
∴CF即为所求,
∵DG⊥BC,Rt△ABC是等腰直角三角形,
∴△DGC是等腰直角三角形,
∴,
∵BD平分∠ABC,
∴DA=DG,
∵AC=AB,
设AD=a,则,
在直角三角形ABD中,,
由勾股定理得:BD2=AD2+AB2,
∴,
解得,
∴,
∵,
∴
=4,
故答案为:4.
【点评】本题考查了轴对称﹣最短路线问题,角平分线的性质,勾股定理,等腰直角三角形,作出辅助线是解题的关键.
14.(2025春 西安)小明从A点出发,走到水平直线l上P点,再回到到B点,若A、B到水平直线l的距离分别是2,1,AB两点之间水平距离是4,则PA+PB最小值为 5 .
【考点】轴对称﹣最短路线问题.
【专题】等腰三角形与直角三角形;平移、旋转与对称;推理能力;应用意识.
【答案】5.
【分析】首先作A关于直线l的对称点A′,连接A′B交直线l于点P,此时AP+PB最小;然后可得AP+PB的最小值=A′B,再利用勾股定理求解,即可求得答案.
【解答】解:A、B到水平直线l的距离分别是2,1,AB两点之间水平距离是4,如图,作A关于直线l的对称点A′,连接A′B交直线l于点P,此时AP+PB最小;
由题意得:PA=PA′,
∴AP+PB=PA′+PA=A′B,
过点B作BC⊥AA′于点C,
则OA′=OA=2,OC=1,BC=4,
∴A′C=OA′+OC=2+1=3,
∴,
∴AP+PB最小值=5.
故答案为:5.
【点评】本题考查了轴对称﹣最短路线问题,勾股定理,解答本题的关键是准确找到点P的位置.
15.(2025 温江区二模)如图,在菱形ABCD中,AB=4,∠B=60°,M是BC的中点,点P是CD上一动点,连接PA,PM,则PA+PM的最小值为 4 .
【考点】轴对称﹣最短路线问题;等边三角形的判定与性质;菱形的性质.
【专题】矩形 菱形 正方形;平移、旋转与对称;几何直观;推理能力.
【答案】4.
【分析】根据题意,作点A关于CD的对称点N,然后根据两点之间线段最短,可知AN就是PA+PM的最小值,推导出△ABM≌△ADE(AAS),求得AM=AE=2,进而推导出AN的值.
【解答】解:如图,作点M关于CD的对称点N,连接AN,交CD于点E,则AN就是PA+PM的最小值,连接AM,AC,
∴AN⊥CD,AN=2AE,
在菱形ABCD 中,AB=4,∠ABC=60°,
∴AB=BC=AD,∠B=∠D,
∴△ABC是等边三角形,
∵M是BC的中点,
∴AM⊥BC,
∴△ABM≌△ADE(AAS),AMAB=2,
∴AE=AM=2,
∴AN=4,
故答案为:4.
【点评】本题考查轴对称﹣最短路线问题,等边三角形的判定与性质,菱形的性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
三.解答题(共5小题)
16.(2025春 江阴市二模)如图,直角三角形ABC中,∠ACB=90°,AC=6,BC=8,AB=10,用无刻度的直尺和圆规完成下列作图.
(1)作边AB的中点D;
(2)作∠ABC的平分线BE,交AC边于点E;
(3)作点C关于直线BE的对称点F;
(4)直接写出DF的长为 3 .
【考点】作图﹣轴对称变换;角平分线的性质;线段垂直平分线的性质.
【专题】作图题;推理能力.
【答案】(1)见解答;
(2)见解答;
(3)见解答;
(4)3.
【分析】(1)作AB的中垂线即可;
(2)根据作角的平分线的基本作法作图;
(3)根据等腰三角形的性质作图;
(4)根据中点的定义及线段的和差求解.
【解答】解:(1)如图:D即为所求;
(2)BE即为所求;
(3)点F即为所求;
(4)∵D为AB的中点,
∴BDAB=5,
由作图得:BF=BC=8,
∴DF=BF﹣BD=3,
故答案为:3.
【点评】本题考查了轴对称变换,掌握常见的基本作图和等腰三角形的性质是解题的关键.
17.(2025春 武汉二模)(1)王芳同学把两个边长为1的正方形分别沿对角线剪开,将所得的4个直角三角形按如图(1)拼在一起,就得到了一个边长为 的大正方形.
(2)图(2)是由5个边长为1的小正方形组成的图形,这个图形按图(3)的方式剪裁,拼成图(4).
①拼成的正方形图(4)的面积为 5 ,边长为 ;
②仿照上面的做法,将图(5)中这十个小正方形组成的图形,拼成一个大正方形,请在图(5)中画出裁剪方法,并求出拼成的正方形边长 ;
③能否在图(5)拼成的正方形中裁剪出一个边长为1:3面积为9的长方形?若能,求它的长、宽;若不能,请说明理由.
【考点】图形的剪拼;正方形的性质.
【专题】作图题;几何直观.
【答案】(1);
(2)①5,;②见解析,;③不能,理由见解析.
【分析】(1)利用数形结合的思想解决问题;
(2)①理由数形结合的思想解决问题;
②作一个边长为的正方形即可;
③不能,设长方形的边长分别为x,3x.构建方程求出x,即可判断.
【解答】解:(1)王芳同学把两个边长为1的正方形分别沿对角线剪开,将所得的4个直角三角形按如图(1)拼在一起,就得到了一个边长为的大正方形.
故答案为:;
(2)图(2)是由5个边长为1的小正方形组成的图形,这个图形按图(3)的方式剪裁,拼成图(4).
①拼成的正方形图(4)的面积为5,边长为;
故答案为:5,;
②图形如图所示拼成的正方形边长;
故答案为:;
③不能.
理由:设长方形的边长分别为x,3x.
则有3x2=9,
∴x,
∵3x=3,
∴不能裁剪出一个边长为1:3面积为9的长方形.
【点评】本题考查图形的拼剪,正方形的性质,解题的关键是理解题意,灵活运用所学知识解决问题.
18.(2025春 宜兴市二模)如图,已知长方形OABC的顶点A在x轴上,顶点C在y轴上,OA=8,OC=4,D、E分别为OA、BC上的两点,将长方形OABC沿直线DE折叠后,点A刚好与点C重合,点B落在点F处,再将其打开、展平.
(1)点D的坐标是 (3,0) ,点E的坐标是 (5,4) ,点F的坐标是 (,) ;
(2)设动点P从点D出发,以1个单位长度/秒的速度沿折线D→A→B→C向终点C运动,运动时间为t秒,当S△PDE时,求t的值.
【考点】翻折变换(折叠问题);三角形的面积;矩形的性质;坐标与图形变化﹣对称.
【专题】矩形 菱形 正方形;平移、旋转与对称;运算能力.
【答案】(1)(3,0),(5,4),(,);
(2)t的值为2.5或9.5或14.5.
【分析】(1)设OD=m,则AD=8m,利用勾股定理求出m,可得点D坐标,再证明CD=CE=5,可得点E坐标,作FH⊥BC于点H,利用面积法求出FH,可得点F的坐标;
(2)分四种情形分别求解即可.
【解答】解:(1)∵OA=8,OC=4,
∴B(8,4),
设OD=m,则AD=8m,
根据翻折的性质可得CD=AD=16﹣m,∠ADE=∠CDE,
∵OC2+OD2=CD2,
∴42+m2=(8﹣m)2,
解得m=3,
∴D(3,0),CD=AD=8﹣m=5,
∵BC∥OA,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD=5,
∴E(5,4),
过点F作FH⊥CE于点H.
∵△CEF的面积CF×EFCE×FH,
∴FH,
∴CH,
∴F(,).
故答案为:(3,0),(5,4),(,);
(2)当点P在线段DA上,DP时,满足条件,
此时t=2.5.
当点P在AB上,△PDE的面积的最小值3×4=6>5,不满足条件,
当点P在线段BE上,BP=0.5时,满足条件,此时t=5+4+0.5=9.5.
当点P在线段EC上时,EP=2.5时,满足条件,此时t=5+4+5.5=14.5.
综上所述,满足条件的t的值为2.5或9.5或14.5.
【点评】本题考查翻折变换,矩形的性质,三角形的面积,坐标与图形变化﹣对称,解题的关键是掌握相关知识解决问题.
19.(2025春 越秀区二模)如图,直角坐标系中的网格由单位为1的正方形构成.
(1)写出A、B、C的坐标;
(2)若以A、B、C及点D为顶点的四边形为 ABCD,画出 ABCD,并直接写出D点的坐标.
(3)在x轴上是否存在一点P,使AP+DP的值最小.若存在,请在图中找出这个点,请求出最小值;若不存在,请说明理由.
【考点】轴对称﹣最短路线问题;坐标与图形性质;勾股定理;平行四边形的判定与性质.
【专题】作图题;几何直观.
【答案】(1)A(2,3),B(﹣2,0),C(0,﹣1);
(2)见解析,D(4,2);
(3)见解析,.
【分析】(1)根据A,B,C的位置写出坐标即可;
(2)根据平行四边形的判定画出平行四边形ABCD即可;
(3)作点D关于x轴的对称点D′,连接AD′交x轴于点P,连接PD,求出AD′即可.
【解答】解:(1)A(2,3),B(﹣2,0),C(0,﹣1);
(2)如图,四边形ABCD即为所求,D(4,2);
(3)如图,点P即为所求,PA+PD的最小值=AD′.
【点评】本题考查轴对称﹣最短问题,坐标与图形性质,勾股定理,平行四边形的判定和性质,解题的关键是理解题意,灵活运用所学知识解决问题.
20.(2025春 和平区二模)如图1,Rt△ABC中,∠ACB=90°,AC=5,AB=13.
(1)如图2,点E是边BC上一点,△ABC沿着AE折叠,点C恰好与斜边AB上点D重合,求CE的长;
(2)如图3,点F为斜边上AB上动点,连接CF,在点F的运动过程中,若△BCF为等腰三角形,请直接写出AF的长.
【考点】翻折变换(折叠问题);等腰三角形的性质;勾股定理.
【专题】等腰三角形与直角三角形;平移、旋转与对称;推理能力.
【答案】(1);
(2)1或.
【分析】(1)根据勾股定理可得BC=12,设CE=x,则BE=BC﹣CE=12﹣x,由翻折可得DE=CE=x,AD=AC=5,∠EDA=∠C=90°,所以BD=AB﹣AD=8,然后利用勾股定理列出方程即可解决问题;
(2)分两种情况:①当BC=BF=12时,②当CF=BF时,利用等腰三角形的性质即可解决问题.
【解答】解:(1)Rt△ABC中,∠ACB=90°,
∵AC=5,AB=13,
∴BC12,
设CE=x,则BE=BC﹣CE=12﹣x,
由翻折可知:DE=CE=x,AD=AC=5,∠EDA=∠C=90°,
∴BD=AB﹣AD=13﹣5=8,
在Rt△BDE中,根据勾股定理得:
BE2=BD2+DE2,
∴(12﹣x)2=82+x2,
解得x,
∴CE;
(2)若△BCF为等腰三角形,分两种情况:
①当BC=BF=12时,
∴AF=AB﹣BF=13﹣12=1;
②当CF=BF时,
∴∠B=∠FCB,
∵∠B+∠A=∠FCB+∠FCA=90°,
∴∠FCA=∠A,
∴CF=AF,
∴CF=AF=BF,
∵AF=AB﹣BF=13﹣AF,
∴AF.
综上所述:AF的长为1或.
【点评】本题考查了翻折变换,等腰三角形的判定与性质,勾股定理,解决本题的关键是掌握翻折的性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考核心考点 图形的对称
一.选择题(共10小题)
1.(2025春 江阴市二模)如图,正方形ABCD中,E是AB上一点,将△DAE沿DE翻折得△DFE,点A的对应点是点F,直线AF与DE交于点H,与∠CDF的平分线交于点G,连接BG,下列说法:①DH=GH;②∠AGB=45°;③若连接CG,则CG⊥AG;④若正方形边长为2,E为AB的中点,则点C到直线AG的距离为1.其中正确的是( )
A.①③ B.①②③ C.①③④ D.②④
2.(2025春 长安区二模)如图,在△ABC中,∠BAC=60°,AD是∠BAC的平分线,,若点P是AD上一动点,作PN⊥AC于点N,则PC+PN的最小值是( )
A. B. C. D.
3.(2025春 鼓楼区二模)如图,将长方形纸条沿直线EF折叠,点A落在A′处,点D落在D′处,A′E交CD于点G.若∠AEF=40°,则∠A′GC=( )
A.100° B.120° C.140° D.160°
4.(2025春 江北区二模)如图,在正方形ABCD中,点E是边CB的一点且BE:EC=1:2,连接AE,将AB沿AE折叠至正方形内部,得到线段AF,延长AF交BC于点G,延长EF交DC于点H,若AB=6,连接CF,DF,则DF的长为( )
A. B. C. D.
5.(2025春 连江县二模)如图,点E在长方形纸片ABCD的边BC上,连接AE,将长方形的纸片沿AE折叠,点B落在点B′处,设∠ADB=α,∠BAE=β,当AB'∥BD时,α与β之间满足的数量关系为( )
A. B. C.α+β=90° D.β﹣α=45°
6.(2025春 永春县二模)如图,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形.如图,将四边形ACBD折叠,使D与C重合,EF为折痕,则∠ACE的余弦值为( )
A. B. C. D.
7.(2025春 宜兴市二模)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5.如果点D,E分别为BC,AB上的动点,那么AD+DE的最小值是( )
A.4.2 B.4.8 C.5 D.4.5
8.(2025春 无锡二模)如图,Rt△ABC中,∠ABC=90°,AB=BC=1,点D是与点B不重合的动点,以BD为一边作正方形BDEF,连接EC、FC,则BD+EC+FC的最小值为( )
A. B.2 C. D.
9.(2025春 宝安区二模)如图所示,长方形纸片ABCD中,∠1=65°,现将长方形纸片沿AC折叠,使点B落在点B1处,B1C与AD交于点E;再将三角形EDC沿B1C折叠,使点D落在点D1处.则∠2的度数为( )
A.30° B.10° C.15° D.25°
10.(2025春 市北区二模)如图,长方形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,若△CEB′恰好为直角三角形,则CE的长为( )
A.1 B.3 C.1 或 D.1 或 3
二.填空题(共5小题)
11.(2025春 宝安区二模)如图,已知△ABC中∠ACB=120°,BC=2,AC=2BC,将△ABC沿高CE折叠,使点B落在AB边上的点B'处,再沿CF折叠,使点A落在CB'的延长线上的点A'处.则CF的长为 .
12.(2025春 广州二模)如图,等边三角形ABC中,BD⊥AC于点D,点E、F分别是BC、DC上的动点,沿EF所在直线折叠△CEF,使点C落在BD上的点C'处,AB=16,当△BEC'是直角三角形时,DF的值为 .
13.(2025春 宁海县二模)如图,在等腰Rt△ABC中,∠A=90°,BD平分∠ABC,BE平分∠DBC,M,N分别为射线BE,BC上的动点,若BD=8,则CM+MN的最小值为 .
14.(2025春 西安)小明从A点出发,走到水平直线l上P点,再回到到B点,若A、B到水平直线l的距离分别是2,1,AB两点之间水平距离是4,则PA+PB最小值为 .
15.(2025 温江区二模)如图,在菱形ABCD中,AB=4,∠B=60°,M是BC的中点,点P是CD上一动点,连接PA,PM,则PA+PM的最小值为 .
三.解答题(共5小题)
16.(2025春 江阴市二模)如图,直角三角形ABC中,∠ACB=90°,AC=6,BC=8,AB=10,用无刻度的直尺和圆规完成下列作图.
(1)作边AB的中点D;
(2)作∠ABC的平分线BE,交AC边于点E;
(3)作点C关于直线BE的对称点F;
(4)直接写出DF的长为 .
17.(2025春 武汉二模)(1)王芳同学把两个边长为1的正方形分别沿对角线剪开,将所得的4个直角三角形按如图(1)拼在一起,就得到了一个边长为 的大正方形.
(2)图(2)是由5个边长为1的小正方形组成的图形,这个图形按图(3)的方式剪裁,拼成图(4).
①拼成的正方形图(4)的面积为 ,边长为 ;
②仿照上面的做法,将图(5)中这十个小正方形组成的图形,拼成一个大正方形,请在图(5)中画出裁剪方法,并求出拼成的正方形边长 ;
③能否在图(5)拼成的正方形中裁剪出一个边长为1:3面积为9的长方形?若能,求它的长、宽;若不能,请说明理由.
18.(2025春 宜兴市二模)如图,已知长方形OABC的顶点A在x轴上,顶点C在y轴上,OA=8,OC=4,D、E分别为OA、BC上的两点,将长方形OABC沿直线DE折叠后,点A刚好与点C重合,点B落在点F处,再将其打开、展平.
(1)点D的坐标是 ,点E的坐标是 ,点F的坐标是 ;
(2)设动点P从点D出发,以1个单位长度/秒的速度沿折线D→A→B→C向终点C运动,运动时间为t秒,当S△PDE时,求t的值.
19.(2025春 越秀区二模)如图,直角坐标系中的网格由单位为1的正方形构成.
(1)写出A、B、C的坐标;
(2)若以A、B、C及点D为顶点的四边形为 ABCD,画出 ABCD,并直接写出D点的坐标.
(3)在x轴上是否存在一点P,使AP+DP的值最小.若存在,请在图中找出这个点,请求出最小值;若不存在,请说明理由.
20.(2025春 和平区二模)如图1,Rt△ABC中,∠ACB=90°,AC=5,AB=13.
(1)如图2,点E是边BC上一点,△ABC沿着AE折叠,点C恰好与斜边AB上点D重合,求CE的长;
(2)如图3,点F为斜边上AB上动点,连接CF,在点F的运动过程中,若△BCF为等腰三角形,请直接写出AF的长.
中考核心考点 图形的对称
参考答案与试题解析
一.选择题(共10小题)
1.(2025春 江阴市二模)如图,正方形ABCD中,E是AB上一点,将△DAE沿DE翻折得△DFE,点A的对应点是点F,直线AF与DE交于点H,与∠CDF的平分线交于点G,连接BG,下列说法:①DH=GH;②∠AGB=45°;③若连接CG,则CG⊥AG;④若正方形边长为2,E为AB的中点,则点C到直线AG的距离为1.其中正确的是( )
A.①③ B.①②③ C.①③④ D.②④
【考点】翻折变换(折叠问题);解直角三角形;全等三角形的判定与性质;正方形的性质.
【专题】图形的全等;矩形 菱形 正方形;展开与折叠;几何直观;运算能力;推理能力.
【答案】B
【分析】先由折叠的性质可得∠AHD=90°,再由角平 分线的定义可得∠FDG=∠CDG,进而证明∠HDG=45°,则△DHG是等腰直角三角,即可判断①;证明A、D、G、B四点共圆,即可判断 ②;证明A、B、G、C四点共圆,即可判断③;由②可知∠DGH=45°,再说明△DFG≌△DCG,可得∠CGF=90°,即CG就是点C到直线AG的距离,根据锐角三角函数求出AH,DH,即可得出答案,判断④.
【解答】解:根据翻折可知∠ADE=∠EDF,点A和点F关于DE对称,
∴∠AHD=90°.
∵DG是∠CDF的平分线,
∴∠FDG=∠CDG.
∵四边形ABCD是正方形,
∴∠ADC=∠DAE=∠ABC=90°,AB=AD,
∴∠HDG=45°,
∴∠DGH=∠HDG=45°,
∴DH=GH.
故①正确;
如图1,连接BD,
∵四边形是正方形,∠DGH=45°,
∴∠ABD=∠AGD=∠ADB=45°,
∴A、D、G、B四点共圆,
∴∠AGB=∠ADB=45°,
故②正确;
如图1,连接AC,
∵∠ACB=∠AGB=45°,
∴A、B、G、C四点共圆,
∴∠AGC=∠ABC=90°,
∴CG⊥AG,
故③正确;
由②可知∠DGH=45°,
在△DFG和△DCG中,
,
∴△DFG≌△DCG(SAS),
∴∠DGF=∠CGD=45°,
∴∠CGF=90°,即CG就是点C到直线AG的距离.
∵AD=2,AE=1,
∴DE,
∴sin∠ADE,cos∠ADE,
在Rt△ADH中,sin∠ADH,cos∠ADH,
∴AH,,
∴FHHG,
∴CG=FG,
故④不正确.
综上所述,正确的是①②③,
故选:B.
【点评】本题主要考查了翻折变换(折叠问题),全等三角形的判定与性质,正方形的性质,解直角三角形,合理构造全等三角形是解题的关键.
2.(2025春 长安区二模)如图,在△ABC中,∠BAC=60°,AD是∠BAC的平分线,,若点P是AD上一动点,作PN⊥AC于点N,则PC+PN的最小值是( )
A. B. C. D.
【考点】轴对称﹣最短路线问题;角平分线的定义.
【专题】线段、角、相交线与平行线;平移、旋转与对称;几何直观;推理能力.
【答案】D
【分析】作CE⊥AB于点E,则CE的长就是PN+PC的最小值,在直角△ACE中利用三角函数求解.
【解答】解:作CE⊥AB于点E.连接PE,
∵AD是∠BAC的平分线,
∴PN=PE,
∴PN+PC=PE+PC≥EC,
当CE⊥AB时,PN+PC最短,即为CE的长度,
在直角△ACE中,CE=AC sin∠BAC.
故选:D.
【点评】本题考查了轴对称﹣最短路线问题,角平分线的定义,根据角的平分线的性质理解CE的长是PN+PC的最小值是解答本题的关键.
3.(2025春 鼓楼区二模)如图,将长方形纸条沿直线EF折叠,点A落在A′处,点D落在D′处,A′E交CD于点G.若∠AEF=40°,则∠A′GC=( )
A.100° B.120° C.140° D.160°
【考点】翻折变换(折叠问题);平行线的性质;矩形的性质.
【专题】平移、旋转与对称;运算能力.
【答案】A
【分析】利用翻折变换的性质以及平行线的性质求解.
【解答】解:由翻折变换的性质可知∠AEF=∠A′EF=40°,
∴∠GEB=180﹣°﹣40°﹣40°=100°,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠A′GC=∠GEB=100°.
故选:A.
【点评】本题考查翻折变换,平行线的性质,矩形的性质,解题的关键是掌握翻折变换的性质.
4.(2025春 江北区二模)如图,在正方形ABCD中,点E是边CB的一点且BE:EC=1:2,连接AE,将AB沿AE折叠至正方形内部,得到线段AF,延长AF交BC于点G,延长EF交DC于点H,若AB=6,连接CF,DF,则DF的长为( )
A. B. C. D.
【考点】翻折变换(折叠问题);正方形的性质.
【专题】矩形 菱形 正方形;平移、旋转与对称;运算能力.
【答案】A
【分析】如图,连接AH交DF于点O.证明Rt△AHD≌Rt△AHF(HL),推出DH=HF,设DH=HF=x,利用勾股定理构建方程求出x可得结论.
【解答】解:如图,连接AH交DF于点O.
∵四边形ABCD是正方形,
∴AB=BC=AD=6,∠B=∠ADC=∠BCD=90°,
∵BE:EC=1:2,
∴BE=2,EC=4,
由翻折变换的性质可知AB=AF,BE=EF=2,∠B=∠AFE=∠AFH=90°,
∴AD=AF,
∵∠ADH=∠AFH,AH=AH,
∴Rt△AHD≌Rt△AHF(HL),
∴DH=HF,设DH=HF=x,
在Rt△ECH中,则有(2+x)2=42+(6﹣x)2,
解得x=3,
∴DH=3,
∴AH3,
∵AD=AF,HD=HF,
∴AH垂直平分线段DF,
∴OD=OF,
∴DF=2.
故选:A.
【点评】本题考查翻折变换,正方形的性质,全等三角形的判定和性质,勾股定理,解题的关键是掌握翻折变换的性质.
5.(2025春 连江县二模)如图,点E在长方形纸片ABCD的边BC上,连接AE,将长方形的纸片沿AE折叠,点B落在点B′处,设∠ADB=α,∠BAE=β,当AB'∥BD时,α与β之间满足的数量关系为( )
A. B. C.α+β=90° D.β﹣α=45°
【考点】翻折变换(折叠问题);矩形的性质.
【专题】矩形 菱形 正方形;平移、旋转与对称;运算能力.
【答案】B
【分析】利用矩形的性质,平行线的性质,翻折变换的性质求解即可.
【解答】解:∵四边形ABCD是矩形,
∴∠BAD=90°,
∴∠EAD=90°﹣β,
∵AB′∥BD,
∴∠DAB′=∠ADB=α,
∵∠EAB=∠EAB′=β,
∴β=α+90°﹣β,
∴βα=45°.
故选:B.
【点评】本题考查翻折变换,矩形的性质,解题的关键是掌握相关知识解决问题.
6.(2025春 永春县二模)如图,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形.如图,将四边形ACBD折叠,使D与C重合,EF为折痕,则∠ACE的余弦值为( )
A. B. C. D.
【考点】翻折变换(折叠问题);解直角三角形;等边三角形的性质;勾股定理.
【专题】等腰三角形与直角三角形;平移、旋转与对称;解直角三角形及其应用;运算能力;推理能力.
【答案】D
【分析】设AB=2a,由含30°角的直角三角形的性质和勾股定理求得BC、AC的值,再由等边三角形的性质证得∠EAC=90°,然后由折叠的性质知DE=CE,设DE=CE=x,由勾股定理求出EC的长,最后由锐角三角函数的定义即可得出结果.
【解答】解:设AB=2a,
∵△ABC中,∠ACB=90°,∠BAC=30°,
∴BC=a,ACa,
∵△ABD是等边三角形,
∴AD=AB=2a,∠DAB=60°,
∴∠EAC=60°+30°=90°,
由折叠的性质得:DE=EC,
设DE=EC=x,则AE=2a﹣x,
在Rt△AEC中,由勾股定理得:AE2+AC2=EC2,
即(2a﹣x)2+(a)2=x2,
解得:xa,
∴ECa,
∴cos∠ACE,
故选:D.
【点评】本题考查了折叠的性质、等边三角形的性质、勾股定理、锐角三角函数的定义等知识,熟练掌握折叠的性质和勾股定理是解题的关键.
7.(2025春 宜兴市二模)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5.如果点D,E分别为BC,AB上的动点,那么AD+DE的最小值是( )
A.4.2 B.4.8 C.5 D.4.5
【考点】轴对称﹣最短路线问题.
【专题】平移、旋转与对称;推理能力.
【答案】B
【分析】延长AC到点M,使CM=AC,则BC是线段AM的垂直平分线,连接BM,过点M作ME′⊥AB交D′,连接AD′,根据线段垂直平分线的性质可得:AD′+D′E′=MD′+D′E′,根据垂线段最短,可知当ME′⊥AB时,AD′+D′E′的值最小,利用三角形的面积公式求出ME′的长度即为AD′+D′E′的最小值.
【解答】解:如图所示,延长AC到点M,使CM=AC,连接BM,过点M作ME′⊥AB交D′,连接AD′,点 D′即为使得AD+DE取最小值的点,
由条件可知BC是AM的垂直平分线,AM=2AC=6,
∴AD′=D′M,
∴AD′+D′E′=MD′+D′E′,
∴,
,
解得:ME′=4.8.
故选:B.
【点评】本题考查了线段垂直平分线的性质,熟练掌握该知识点是关键.
8.(2025春 无锡二模)如图,Rt△ABC中,∠ABC=90°,AB=BC=1,点D是与点B不重合的动点,以BD为一边作正方形BDEF,连接EC、FC,则BD+EC+FC的最小值为( )
A. B.2 C. D.
【考点】轴对称﹣最短路线问题;全等三角形的判定与性质;勾股定理;等腰直角三角形;正方形的性质.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;平移、旋转与对称;几何直观;推理能力.
【答案】A
【分析】根据正方形的性质和全等三角形的判定和性质得出AD=CF,进而解答即可.
【解答】解:Rt△ABC中,∠ABC=90°,AB=BC=1,如图,连接AD,CF,CE,
∵四边形BDEF是正方形,
∴BD=BF,∠DBF=90°,
∴∠ABC﹣∠DBC=∠DBF﹣∠DBC,即∠ABD=∠CBF,
在△ABD与△CBF中,
,
∴△ABD≌△CBF(SAS),
∴AD=CF,
∵BD+EC+FC=DE+EC+AD,
当A、D、E、C在同一直线上时,BD+EC+FC最小即为AC,
∵Rt△ABC中,∠ABC=90°,AB=BC=1,
∴AC,
∴BD+EC+FC最小即为,
故选:A.
【点评】本题考查轴对称﹣最短路线问题,全等三角形的判定与性质定理,勾股定理,等腰直角三角形正方形的性质,解答本题的关键是根据SAS证明△ABD与△CBF全等.
9.(2025春 宝安区二模)如图所示,长方形纸片ABCD中,∠1=65°,现将长方形纸片沿AC折叠,使点B落在点B1处,B1C与AD交于点E;再将三角形EDC沿B1C折叠,使点D落在点D1处.则∠2的度数为( )
A.30° B.10° C.15° D.25°
【考点】翻折变换(折叠问题);平行线的性质;矩形的性质.
【专题】线段、角、相交线与平行线;矩形 菱形 正方形;展开与折叠;几何直观;推理能力.
【答案】C
【分析】求出∠ACB=90°﹣65°=25°,由折叠大的性质得到∠ACB1=∠ACB=25°,∠DCE=∠D1CE,求出∠DCE=40°,即可得到∠2的度数.
【解答】解:∵四边形ABCD是长方形,
∴∠B=∠BCD=90°,
∴∠ACB=90°﹣∠1=90°﹣65°=25°,
由折叠大的性质得到:∠ACB1=∠ACB=25°,∠DCE=∠D1CE,
∴∠DCE=∠BCD﹣∠ACB﹣ACB1=90°﹣25°﹣25°=40°,
∴∠2=∠D1CE﹣∠ACB1=40°﹣25°=15°.
故选:C.
【点评】本题考查了翻折变换(折叠问题),平行线的性质,矩形的性质,熟练掌握平行线的性质是解题的关键.
10.(2025春 市北区二模)如图,长方形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,若△CEB′恰好为直角三角形,则CE的长为( )
A.1 B.3 C.1 或 D.1 或 3
【考点】翻折变换(折叠问题);勾股定理;矩形的性质.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;平移、旋转与对称;推理能力.
【答案】C
【分析】分为两种情况,当∠CB′E=90°和∠CEB′=90°时,将图形画出,利用折叠性质和勾股定理求解即可.
【解答】解:如图,当∠CB′E=90°时,
在矩形ABCD中,,
∵把∠B沿AE折叠,使点B落在点B′处,
∴∠B=∠AB′E=90°,AB′=AB=3,B′E=BE,则点B′在AC上,
∴B′C=AC﹣AB′=2,
设BE=x,则:CE=4﹣x,B′E=BE=x
在Rt△B′CE中,由勾股定理可得:x2+22=(4﹣x)2,
解得:,
∴,则,
如图,当∠CEB′=90°时,
∴∠BEB′=90°,
∵把∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠ABE=90°,B′E=BE,
∴四边形ABEB′为正方形,
∴BE=B′E=AB=3,则CE=1,
综上,或1,
故选:C.
【点评】本题考查折叠的性质,矩形的性质,勾股定理等知识点,解题的关键是分两种情况考虑,画出对应图形.
二.填空题(共5小题)
11.(2025春 宝安区二模)如图,已知△ABC中∠ACB=120°,BC=2,AC=2BC,将△ABC沿高CE折叠,使点B落在AB边上的点B'处,再沿CF折叠,使点A落在CB'的延长线上的点A'处.则CF的长为 .
【考点】翻折变换(折叠问题).
【专题】平移、旋转与对称;解直角三角形及其应用;运算能力.
【答案】.
【分析】如图,过点A作AJ⊥BC交BC的延长线于点J.证明CF=2CE,利用面积法求出CE即可.
【解答】解:如图,过点A作AJ⊥BC交BC的延长线于点J.
∵BC=2,AC=2BC,
∴AC=4,
∵∠ACB=120°,
∴∠ACJ=60°,
∵∠J=90°,
∴∠JAC=30°,
∴CJAC=2,
∴AJ2,
∴BJ=4,
∴AB2,
由翻折变换的性质可知CE⊥BB′,∠BCE=∠ECB′,∠ACF=∠A′CF,
∴∠FCE∠ACB=60°,
∴∠CFE=30°,
∴CF=2CE,
∵ BC AJ AB CE,
∴CE,
∴CF=2CE.
故答案为:.
【点评】本题考查翻折变换,含30度的直角三角形,解题的关键是掌握翻折变换的性质.
12.(2025春 广州二模)如图,等边三角形ABC中,BD⊥AC于点D,点E、F分别是BC、DC上的动点,沿EF所在直线折叠△CEF,使点C落在BD上的点C'处,AB=16,当△BEC'是直角三角形时,DF的值为 24﹣8或 .
【考点】翻折变换(折叠问题);等边三角形的性质;勾股定理.
【专题】等腰三角形与直角三角形;平移、旋转与对称;运算能力.
【答案】24﹣8或.
【分析】由等边三角形的性质可得∠DBC=30°,分∠BEC'=90°,∠BC'E=90°两种情况讨论,由直角三角形的性质可求BC'的长.
【解答】解:∵△ABC是等边三角形,BD⊥AC,
∴∠DBC=30°,
∵折叠,
∴CE=C'E,
若∠BEC'=90°,且∠C'BE=30°,
∴BEC'E,BC'=2C'E,
且BE+CE=BC=16,
∴CE+CE=16,
∴CE=88=C'E,
∴BC'=16﹣16,BE=24﹣8.
若∠BC'E=90°,∠C'BE=30°,
∴BE=2C'E,BC'C'E,
且BE+CE=BC=16,
∴CEC'E,
∴BE,
故答案为:24﹣8或.
【点评】本题考查了翻折变换,等边三角形的性质,折叠的性质,熟练运用折叠的性质是本题的关键.
13.(2025春 宁海县二模)如图,在等腰Rt△ABC中,∠A=90°,BD平分∠ABC,BE平分∠DBC,M,N分别为射线BE,BC上的动点,若BD=8,则CM+MN的最小值为 4 .
【考点】轴对称﹣最短路线问题;角平分线的性质;勾股定理;等腰直角三角形.
【专题】等腰三角形与直角三角形;平移、旋转与对称;几何直观;推理能力.
【答案】4.
【分析】如图,作N关于BE的对称点N′,则MN=MN′,当C,M,N′三点共线时最短即CN′,当CN′⊥BF时最短,过点C作CF⊥BD,交BD的延长线于点F,即N′与F点重合时最短,过点D作DG⊥BC于点G,根据等面积法求得CF,即可求解.
【解答】解:如图,作N关于BE的对称点N′,过点C作CF⊥BD,交BD的延长线于点F,过点D作DG⊥BC于点G,
∴MN=MN′,当C,M,N′三点共线时CM+MN最小即CN′,
∵当CN′⊥BF时,CN′最短,
∴CF即为所求,
∵DG⊥BC,Rt△ABC是等腰直角三角形,
∴△DGC是等腰直角三角形,
∴,
∵BD平分∠ABC,
∴DA=DG,
∵AC=AB,
设AD=a,则,
在直角三角形ABD中,,
由勾股定理得:BD2=AD2+AB2,
∴,
解得,
∴,
∵,
∴
=4,
故答案为:4.
【点评】本题考查了轴对称﹣最短路线问题,角平分线的性质,勾股定理,等腰直角三角形,作出辅助线是解题的关键.
14.(2025春 西安)小明从A点出发,走到水平直线l上P点,再回到到B点,若A、B到水平直线l的距离分别是2,1,AB两点之间水平距离是4,则PA+PB最小值为 5 .
【考点】轴对称﹣最短路线问题.
【专题】等腰三角形与直角三角形;平移、旋转与对称;推理能力;应用意识.
【答案】5.
【分析】首先作A关于直线l的对称点A′,连接A′B交直线l于点P,此时AP+PB最小;然后可得AP+PB的最小值=A′B,再利用勾股定理求解,即可求得答案.
【解答】解:A、B到水平直线l的距离分别是2,1,AB两点之间水平距离是4,如图,作A关于直线l的对称点A′,连接A′B交直线l于点P,此时AP+PB最小;
由题意得:PA=PA′,
∴AP+PB=PA′+PA=A′B,
过点B作BC⊥AA′于点C,
则OA′=OA=2,OC=1,BC=4,
∴A′C=OA′+OC=2+1=3,
∴,
∴AP+PB最小值=5.
故答案为:5.
【点评】本题考查了轴对称﹣最短路线问题,勾股定理,解答本题的关键是准确找到点P的位置.
15.(2025 温江区二模)如图,在菱形ABCD中,AB=4,∠B=60°,M是BC的中点,点P是CD上一动点,连接PA,PM,则PA+PM的最小值为 4 .
【考点】轴对称﹣最短路线问题;等边三角形的判定与性质;菱形的性质.
【专题】矩形 菱形 正方形;平移、旋转与对称;几何直观;推理能力.
【答案】4.
【分析】根据题意,作点A关于CD的对称点N,然后根据两点之间线段最短,可知AN就是PA+PM的最小值,推导出△ABM≌△ADE(AAS),求得AM=AE=2,进而推导出AN的值.
【解答】解:如图,作点M关于CD的对称点N,连接AN,交CD于点E,则AN就是PA+PM的最小值,连接AM,AC,
∴AN⊥CD,AN=2AE,
在菱形ABCD 中,AB=4,∠ABC=60°,
∴AB=BC=AD,∠B=∠D,
∴△ABC是等边三角形,
∵M是BC的中点,
∴AM⊥BC,
∴△ABM≌△ADE(AAS),AMAB=2,
∴AE=AM=2,
∴AN=4,
故答案为:4.
【点评】本题考查轴对称﹣最短路线问题,等边三角形的判定与性质,菱形的性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
三.解答题(共5小题)
16.(2025春 江阴市二模)如图,直角三角形ABC中,∠ACB=90°,AC=6,BC=8,AB=10,用无刻度的直尺和圆规完成下列作图.
(1)作边AB的中点D;
(2)作∠ABC的平分线BE,交AC边于点E;
(3)作点C关于直线BE的对称点F;
(4)直接写出DF的长为 3 .
【考点】作图﹣轴对称变换;角平分线的性质;线段垂直平分线的性质.
【专题】作图题;推理能力.
【答案】(1)见解答;
(2)见解答;
(3)见解答;
(4)3.
【分析】(1)作AB的中垂线即可;
(2)根据作角的平分线的基本作法作图;
(3)根据等腰三角形的性质作图;
(4)根据中点的定义及线段的和差求解.
【解答】解:(1)如图:D即为所求;
(2)BE即为所求;
(3)点F即为所求;
(4)∵D为AB的中点,
∴BDAB=5,
由作图得:BF=BC=8,
∴DF=BF﹣BD=3,
故答案为:3.
【点评】本题考查了轴对称变换,掌握常见的基本作图和等腰三角形的性质是解题的关键.
17.(2025春 武汉二模)(1)王芳同学把两个边长为1的正方形分别沿对角线剪开,将所得的4个直角三角形按如图(1)拼在一起,就得到了一个边长为 的大正方形.
(2)图(2)是由5个边长为1的小正方形组成的图形,这个图形按图(3)的方式剪裁,拼成图(4).
①拼成的正方形图(4)的面积为 5 ,边长为 ;
②仿照上面的做法,将图(5)中这十个小正方形组成的图形,拼成一个大正方形,请在图(5)中画出裁剪方法,并求出拼成的正方形边长 ;
③能否在图(5)拼成的正方形中裁剪出一个边长为1:3面积为9的长方形?若能,求它的长、宽;若不能,请说明理由.
【考点】图形的剪拼;正方形的性质.
【专题】作图题;几何直观.
【答案】(1);
(2)①5,;②见解析,;③不能,理由见解析.
【分析】(1)利用数形结合的思想解决问题;
(2)①理由数形结合的思想解决问题;
②作一个边长为的正方形即可;
③不能,设长方形的边长分别为x,3x.构建方程求出x,即可判断.
【解答】解:(1)王芳同学把两个边长为1的正方形分别沿对角线剪开,将所得的4个直角三角形按如图(1)拼在一起,就得到了一个边长为的大正方形.
故答案为:;
(2)图(2)是由5个边长为1的小正方形组成的图形,这个图形按图(3)的方式剪裁,拼成图(4).
①拼成的正方形图(4)的面积为5,边长为;
故答案为:5,;
②图形如图所示拼成的正方形边长;
故答案为:;
③不能.
理由:设长方形的边长分别为x,3x.
则有3x2=9,
∴x,
∵3x=3,
∴不能裁剪出一个边长为1:3面积为9的长方形.
【点评】本题考查图形的拼剪,正方形的性质,解题的关键是理解题意,灵活运用所学知识解决问题.
18.(2025春 宜兴市二模)如图,已知长方形OABC的顶点A在x轴上,顶点C在y轴上,OA=8,OC=4,D、E分别为OA、BC上的两点,将长方形OABC沿直线DE折叠后,点A刚好与点C重合,点B落在点F处,再将其打开、展平.
(1)点D的坐标是 (3,0) ,点E的坐标是 (5,4) ,点F的坐标是 (,) ;
(2)设动点P从点D出发,以1个单位长度/秒的速度沿折线D→A→B→C向终点C运动,运动时间为t秒,当S△PDE时,求t的值.
【考点】翻折变换(折叠问题);三角形的面积;矩形的性质;坐标与图形变化﹣对称.
【专题】矩形 菱形 正方形;平移、旋转与对称;运算能力.
【答案】(1)(3,0),(5,4),(,);
(2)t的值为2.5或9.5或14.5.
【分析】(1)设OD=m,则AD=8m,利用勾股定理求出m,可得点D坐标,再证明CD=CE=5,可得点E坐标,作FH⊥BC于点H,利用面积法求出FH,可得点F的坐标;
(2)分四种情形分别求解即可.
【解答】解:(1)∵OA=8,OC=4,
∴B(8,4),
设OD=m,则AD=8m,
根据翻折的性质可得CD=AD=16﹣m,∠ADE=∠CDE,
∵OC2+OD2=CD2,
∴42+m2=(8﹣m)2,
解得m=3,
∴D(3,0),CD=AD=8﹣m=5,
∵BC∥OA,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD=5,
∴E(5,4),
过点F作FH⊥CE于点H.
∵△CEF的面积CF×EFCE×FH,
∴FH,
∴CH,
∴F(,).
故答案为:(3,0),(5,4),(,);
(2)当点P在线段DA上,DP时,满足条件,
此时t=2.5.
当点P在AB上,△PDE的面积的最小值3×4=6>5,不满足条件,
当点P在线段BE上,BP=0.5时,满足条件,此时t=5+4+0.5=9.5.
当点P在线段EC上时,EP=2.5时,满足条件,此时t=5+4+5.5=14.5.
综上所述,满足条件的t的值为2.5或9.5或14.5.
【点评】本题考查翻折变换,矩形的性质,三角形的面积,坐标与图形变化﹣对称,解题的关键是掌握相关知识解决问题.
19.(2025春 越秀区二模)如图,直角坐标系中的网格由单位为1的正方形构成.
(1)写出A、B、C的坐标;
(2)若以A、B、C及点D为顶点的四边形为 ABCD,画出 ABCD,并直接写出D点的坐标.
(3)在x轴上是否存在一点P,使AP+DP的值最小.若存在,请在图中找出这个点,请求出最小值;若不存在,请说明理由.
【考点】轴对称﹣最短路线问题;坐标与图形性质;勾股定理;平行四边形的判定与性质.
【专题】作图题;几何直观.
【答案】(1)A(2,3),B(﹣2,0),C(0,﹣1);
(2)见解析,D(4,2);
(3)见解析,.
【分析】(1)根据A,B,C的位置写出坐标即可;
(2)根据平行四边形的判定画出平行四边形ABCD即可;
(3)作点D关于x轴的对称点D′,连接AD′交x轴于点P,连接PD,求出AD′即可.
【解答】解:(1)A(2,3),B(﹣2,0),C(0,﹣1);
(2)如图,四边形ABCD即为所求,D(4,2);
(3)如图,点P即为所求,PA+PD的最小值=AD′.
【点评】本题考查轴对称﹣最短问题,坐标与图形性质,勾股定理,平行四边形的判定和性质,解题的关键是理解题意,灵活运用所学知识解决问题.
20.(2025春 和平区二模)如图1,Rt△ABC中,∠ACB=90°,AC=5,AB=13.
(1)如图2,点E是边BC上一点,△ABC沿着AE折叠,点C恰好与斜边AB上点D重合,求CE的长;
(2)如图3,点F为斜边上AB上动点,连接CF,在点F的运动过程中,若△BCF为等腰三角形,请直接写出AF的长.
【考点】翻折变换(折叠问题);等腰三角形的性质;勾股定理.
【专题】等腰三角形与直角三角形;平移、旋转与对称;推理能力.
【答案】(1);
(2)1或.
【分析】(1)根据勾股定理可得BC=12,设CE=x,则BE=BC﹣CE=12﹣x,由翻折可得DE=CE=x,AD=AC=5,∠EDA=∠C=90°,所以BD=AB﹣AD=8,然后利用勾股定理列出方程即可解决问题;
(2)分两种情况:①当BC=BF=12时,②当CF=BF时,利用等腰三角形的性质即可解决问题.
【解答】解:(1)Rt△ABC中,∠ACB=90°,
∵AC=5,AB=13,
∴BC12,
设CE=x,则BE=BC﹣CE=12﹣x,
由翻折可知:DE=CE=x,AD=AC=5,∠EDA=∠C=90°,
∴BD=AB﹣AD=13﹣5=8,
在Rt△BDE中,根据勾股定理得:
BE2=BD2+DE2,
∴(12﹣x)2=82+x2,
解得x,
∴CE;
(2)若△BCF为等腰三角形,分两种情况:
①当BC=BF=12时,
∴AF=AB﹣BF=13﹣12=1;
②当CF=BF时,
∴∠B=∠FCB,
∵∠B+∠A=∠FCB+∠FCA=90°,
∴∠FCA=∠A,
∴CF=AF,
∴CF=AF=BF,
∵AF=AB﹣BF=13﹣AF,
∴AF.
综上所述:AF的长为1或.
【点评】本题考查了翻折变换,等腰三角形的判定与性质,勾股定理,解决本题的关键是掌握翻折的性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
