【中考押题预测】2025年中考数学核心考点考前冲刺 图形的相似(含解析)
文档属性
| 名称 | 【中考押题预测】2025年中考数学核心考点考前冲刺 图形的相似(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-16 14:11:15 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
中考核心考点 图形的相似
一.选择题(共10小题)
1.(2025春 江阴市二模)如图,在正方形ABCD中,AB=5,E为边CD上一动点(不与端点重合),AE交BD于点F,过点F作FH⊥AE交BC于点H,过点H作HG⊥BD于点G,连接AH,HE.给出下列结论:①AF=HE;②∠HAE=45°;③;④,其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
2.(2025 綦江区一模)如图,四边形ABCD与四边形EFGH位似,位似中心是O,若OA:AE=1:2,且四边形ABCD的周长为5,则四边形EFGH的周长为( )
A.10 B.15 C.20 D.45
3.(2025 姑苏区一模)如图,在菱形ABCD中,E为边BC上一点,且DE=CD,BD与AE交于点F.下列结论:①AE=BD,②AE平分∠BED,③AD2=AF AE,④BE BC=BF BD,其中正确的是( )
A.①②③④ B.①②④ C.①③④ D.①②③
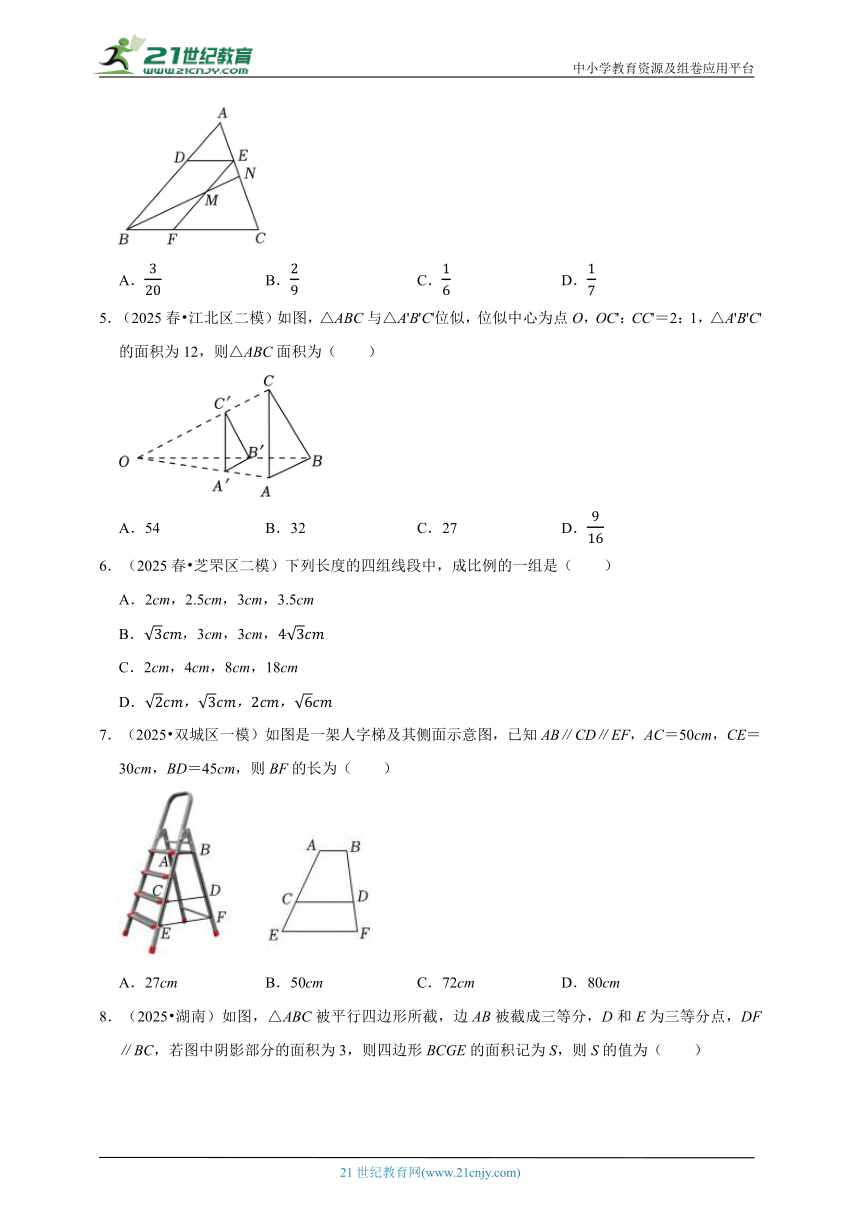
4.(2025春 莱州市二模)如图,点D,E,F分别在△ABC的边上,,DE∥BC,EF∥AB,点M是EF的中点,连接BM并延长交AC于点N,则的值是( )
A. B. C. D.
5.(2025春 江北区二模)如图,△ABC与△A'B'C'位似,位似中心为点O,OC':CC'=2:1,△A'B'C'的面积为12,则△ABC面积为( )
A.54 B.32 C.27 D.
6.(2025春 芝罘区二模)下列长度的四组线段中,成比例的一组是( )
A.2cm,2.5cm,3cm,3.5cm
B.,3cm,3cm,
C.2cm,4cm,8cm,18cm
D.
7.(2025 双城区一模)如图是一架人字梯及其侧面示意图,已知AB∥CD∥EF,AC=50cm,CE=30cm,BD=45cm,则BF的长为( )
A.27cm B.50cm C.72cm D.80cm
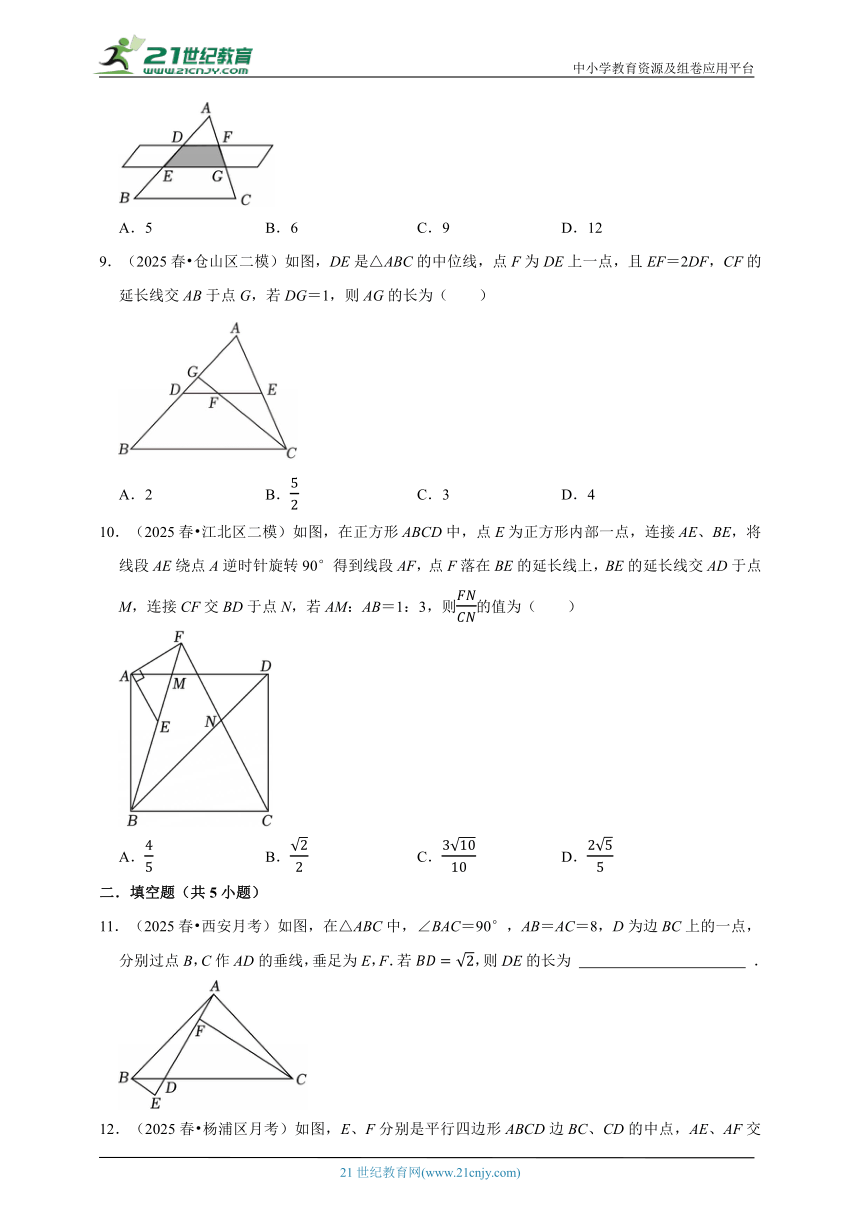
8.(2025 湖南)如图,△ABC被平行四边形所截,边AB被截成三等分,D和E为三等分点,DF∥BC,若图中阴影部分的面积为3,则四边形BCGE的面积记为S,则S的值为( )
A.5 B.6 C.9 D.12
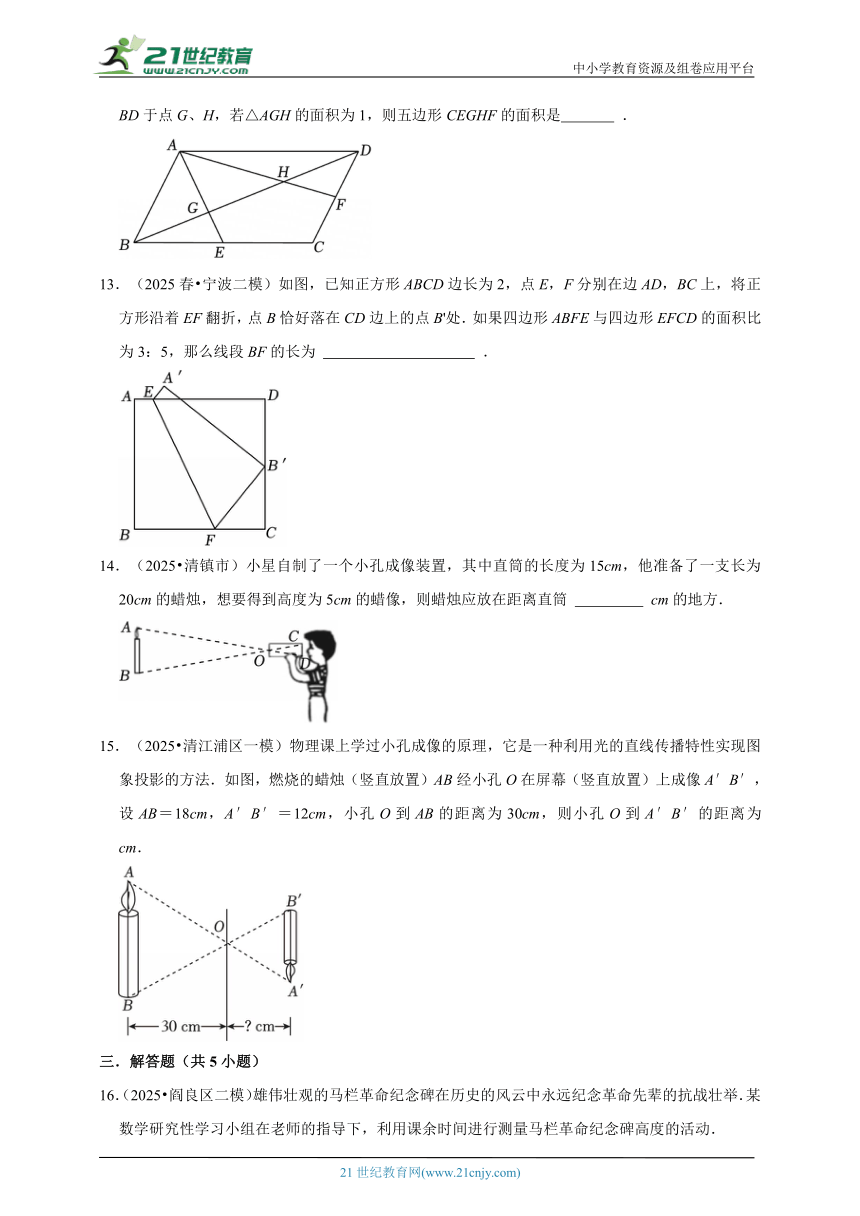
9.(2025春 仓山区二模)如图,DE是△ABC的中位线,点F为DE上一点,且EF=2DF,CF的延长线交AB于点G,若DG=1,则AG的长为( )
A.2 B. C.3 D.4
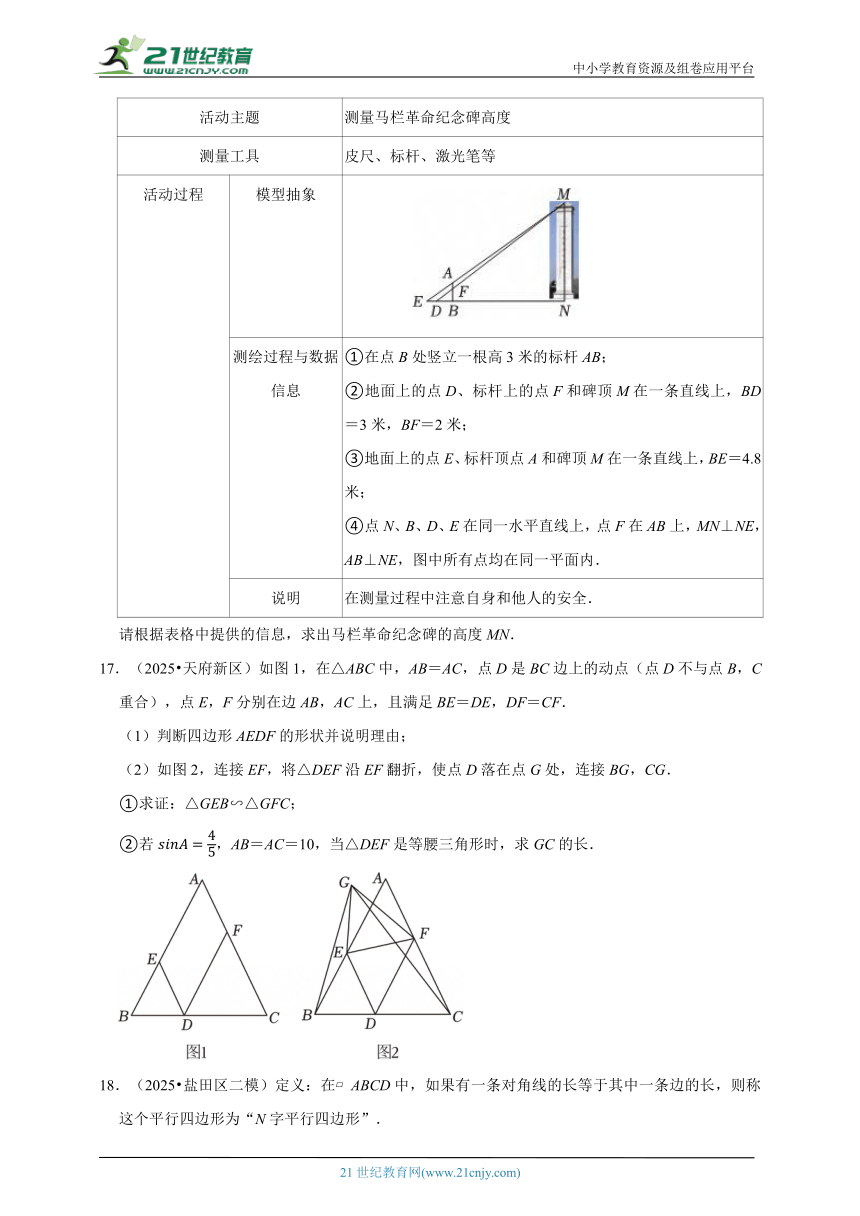
10.(2025春 江北区二模)如图,在正方形ABCD中,点E为正方形内部一点,连接AE、BE,将线段AE绕点A逆时针旋转90°得到线段AF,点F落在BE的延长线上,BE的延长线交AD于点M,连接CF交BD于点N,若AM:AB=1:3,则的值为( )
A. B. C. D.
二.填空题(共5小题)
11.(2025春 西安月考)如图,在△ABC中,∠BAC=90°,AB=AC=8,D为边BC上的一点,分别过点B,C作AD的垂线,垂足为E,F.若,则DE的长为 .
12.(2025春 杨浦区月考)如图,E、F分别是平行四边形ABCD边BC、CD的中点,AE、AF交BD于点G、H,若△AGH的面积为1,则五边形CEGHF的面积是 .
13.(2025春 宁波二模)如图,已知正方形ABCD边长为2,点E,F分别在边AD,BC上,将正方形沿着EF翻折,点B恰好落在CD边上的点B'处.如果四边形ABFE与四边形EFCD的面积比为3:5,那么线段BF的长为 .
14.(2025 清镇市)小星自制了一个小孔成像装置,其中直筒的长度为15cm,他准备了一支长为20cm的蜡烛,想要得到高度为5cm的蜡像,则蜡烛应放在距离直筒 cm的地方.
15.(2025 清江浦区一模)物理课上学过小孔成像的原理,它是一种利用光的直线传播特性实现图象投影的方法.如图,燃烧的蜡烛(竖直放置)AB经小孔O在屏幕(竖直放置)上成像A′B′,设AB=18cm,A′B′=12cm,小孔O到AB的距离为30cm,则小孔O到A′B′的距离为 cm.
三.解答题(共5小题)
16.(2025 阎良区二模)雄伟壮观的马栏革命纪念碑在历史的风云中永远纪念革命先辈的抗战壮举.某数学研究性学习小组在老师的指导下,利用课余时间进行测量马栏革命纪念碑高度的活动.
活动主题 测量马栏革命纪念碑高度
测量工具 皮尺、标杆、激光笔等
活动过程 模型抽象
测绘过程与数据信息 ①在点B处竖立一根高3米的标杆AB; ②地面上的点D、标杆上的点F和碑顶M在一条直线上,BD=3米,BF=2米; ③地面上的点E、标杆顶点A和碑顶M在一条直线上,BE=4.8米; ④点N、B、D、E在同一水平直线上,点F在AB上,MN⊥NE,AB⊥NE,图中所有点均在同一平面内.
说明 在测量过程中注意自身和他人的安全.
请根据表格中提供的信息,求出马栏革命纪念碑的高度MN.
17.(2025 天府新区)如图1,在△ABC中,AB=AC,点D是BC边上的动点(点D不与点B,C重合),点E,F分别在边AB,AC上,且满足BE=DE,DF=CF.
(1)判断四边形AEDF的形状并说明理由;
(2)如图2,连接EF,将△DEF沿EF翻折,使点D落在点G处,连接BG,CG.
①求证:△GEB∽△GFC;
②若,AB=AC=10,当△DEF是等腰三角形时,求GC的长.
18.(2025 盐田区二模)定义:在 ABCD中,如果有一条对角线的长等于其中一条边的长,则称这个平行四边形为“N字平行四边形”.
(1)下面的图形中是“N字平行四边形”的有: ;
A.正方形
B.矩形
C.有一个角是60°的菱形
D.有一个角是60°的平行四边形
E.有一个角是45°的平行四边形
(2)在“N字平行四边形”中,∠A=45°,AB>BC,则 ;
(3)如图1,在“N字平行四边形ABCD”中,∠B=75°,AB=AC=8,点F是AB边上一点,FG∥AC,FG与DC的延长线交于点G,若 AFGC为“N字平行四边形”,求AF的值;
(4)如图2,在矩形ABCD中,点E、F分别是BC边和AD边上的点,四边形BEDF为“N字平行四边形”,若AB=2AF,求的值.
19.(2025春 莱州市二模)【教材呈现】下面是华师版教材九年级上册52页的部分内容:
我们可以发现,当两条直线与一组平行线相交时,所截得的线段存在一定的比例关系:.这就是如下的基本事实: 两条直线被一组平行线所截,所得的对应线段成比例.(简称“平行线分线段成比例”)
【问题原型】如图①,在矩形ABCD中,点E为边AB的中点,过E作EF∥AD交边DC于点F,点P、Q分别在矩形的边AD、BC上,连结PQ交EF于点M.求证:PM=QM.
【结论应用】如图②,在【问题原型】的基础上,点R在边BC上(不与点Q重合),连结PR交EF于点N.
(1)若MN=4,则线段QR的长为 ;
(2)当点Q与点B重合,点R与点C重合时,如图③,若BC=10,且△PMN周长的最小值为12,则边AB的长为 .
20.(2024秋 秦皇岛三模)综合与实践
【问题情境】
数学活动课上,老师让同学们准备了一些等边三角形纸片、正方形纸片和等腰直角三角形纸片,通过折、拼的方式探索其中蕴含的数学知识.
【数学思考】
(1)希望小组选用等边三角形纸片进行折叠,并提出问题:如图①,将等边三角形ABC沿直线DE折叠,点A恰好落在边BC上的点F处,折痕分别交AB,AC于D,E两点.求证:;
(2)善思小组选用正方形纸片进行折叠,并提出问题:如图②,将正方形ABCD沿直线EF折叠,点A恰好落在边BC的中点G处,点D落在点H处,折痕分别交AB,CD于E,F两点,设GH,CD交于点I.若AB=8,求GI的长;
【拓展探究】
(3)智慧小组将两个不同的等腰直角三角形拼在一起,并提出问题:如图③,△ABC与△ADE都是等腰直角三角形,点D在边BC上,∠BAC=∠DAE=90°,DE交AC于点F.若BD=1,CD=3,请直接写出图中阴影部分的面积.
中考核心考点 图形的相似
参考答案与试题解析
一.选择题(共10小题)
1.(2025春 江阴市二模)如图,在正方形ABCD中,AB=5,E为边CD上一动点(不与端点重合),AE交BD于点F,过点F作FH⊥AE交BC于点H,过点H作HG⊥BD于点G,连接AH,HE.给出下列结论:①AF=HE;②∠HAE=45°;③;④,其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
【考点】相似三角形的判定与性质;全等三角形的判定与性质;正方形的性质.
【专题】矩形 菱形 正方形;图形的相似;运算能力;推理能力.
【答案】B
【分析】①作辅助线,延长HF交AD于点L,连接CF,通过证明△ADF≌△CDF,可得:AF=CF,故需证明FC=FH,可证:AF=FH;AF<EH,据此得征;
②由FH⊥AE,AF=FH,可得:∠HAE=45°,据此得证;
③利用条件证明△AFO≌△FHG,可得FG=AO,可得结论;
④若FH=2,则AHFH=4,AH<AB,这与直角三角形斜边大于直角边矛盾,据此判断即可.
【解答】解:①连接FC,延长HF交AD于点L,如图1,
∵BD为正方形ABCD的对角线,
∴∠ADB=∠CDF=45°.
∵AD=CD,DF=DF,
∴△ADF≌△CDF(SAS).
∴FC=AF,∠ECF=∠DAF.
∵∠ALH+∠LAF=90°,
∴∠LHC+∠DAF=90°.
∵∠ECF=∠DAF,
∴∠FHC=∠FCH,
∴FH=FC.
∴FH=AF,
∵FH⊥AE,
∴FH<EH,
∴AF<EH,故①错误;
②∵FH⊥AE,FH=AF,
∴∠HAE=45°,故②正确;
③连接AC,交BD于点O,
∴BD⊥AC,
在△AFO和△FHG中,
,
∴△AFO≌△FHG(AAS),
∴FG=AO,
∵AOACAB,
∴FG,故③正确;
④若FH=2,则AHFH=4,
∴AH<AB,这与直角三角形斜边大于直角边矛盾.
故④错误.
综上所述,②③正确.
故选:B.
【点评】本题考查正方形的性质,全等三角形的判定和性质,等腰直角三角形的判定和性质等知识,熟练添加辅助线是解题的关键.
2.(2025 綦江区一模)如图,四边形ABCD与四边形EFGH位似,位似中心是O,若OA:AE=1:2,且四边形ABCD的周长为5,则四边形EFGH的周长为( )
A.10 B.15 C.20 D.45
【考点】位似变换.
【专题】图形的相似;几何直观;推理能力.
【答案】B
【分析】根据相似比等于位似比可得:四边形ABCD的周长:四边形EFGH的周长=1:3,据此解答即可得解.
【解答】解:∵四边形ABCD与四边形EFGH位似,位似中心是O,OA:AE=1:2,
∴OA:OE=1:3,四边形ABCD与四边形EFGH的相似比为1:3,
∴四边形ABCD的周长:四边形EFGH的周长=1:3,
∵四边形ABCD的周长为5,
∴四边形EFGH的周长为3×5=15,
故选:B.
【点评】本题考查了位似变换,掌握位似图形的性质是解题的关键.
3.(2025 姑苏区一模)如图,在菱形ABCD中,E为边BC上一点,且DE=CD,BD与AE交于点F.下列结论:①AE=BD,②AE平分∠BED,③AD2=AF AE,④BE BC=BF BD,其中正确的是( )
A.①②③④ B.①②④ C.①③④ D.①②③
【考点】相似三角形的判定与性质;全等三角形的判定与性质;菱形的性质.
【专题】矩形 菱形 正方形;图形的相似;推理能力.
【答案】A
【分析】①正确.证明四边形ABED是等腰梯形可得结论;
②正确.证明∠AEB=∠AED即可;
③正确.证明△ADF∽△AED即可;
④正确.证明△BEF∽△BDC即可.
【解答】解:∵四边形ABCD是菱形,
∴AD∥BC,AB=CD,
∵DE=CD,
∴DE=AB,
∴四边形ABED是等腰梯形,
∴AE=BD,故①正确;
∵AD∥BC,
∴∠AEB=∠DAE,
∵DA=DC=DE,
∴∠DAE=∠DEA,
∴∠DEA=∠AEB,
∴AE平分∠BED,故②正确;
∵四边形ABCD是菱形,
∴∠ADB=∠BDC,∠ADC=∠ABE,
∵四边形ABED是等腰梯形,
∴∠ABE=∠BED=∠DC,
∵∠AED=∠AEB,
∴∠ADF=∠AED,
∵∠DAF=∠DAE,
∴△ADF∽△AED,
∴,
∴AD2=AF AE,故③正确;
∵∠BEF=∠BDC,∠EBF=∠DBC,
∴△BEF∽△BDC,
∴,
∴BE BC=BF BD,故④正确.
故选:A.
【点评】本题考查相似三角形的判定和性质,菱形的性质,等腰梯形的判定和性质,解题的关键是理解题意,灵活运用所学知识解决问题.
4.(2025春 莱州市二模)如图,点D,E,F分别在△ABC的边上,,DE∥BC,EF∥AB,点M是EF的中点,连接BM并延长交AC于点N,则的值是( )
A. B. C. D.
【考点】平行线分线段成比例.
【专题】线段、角、相交线与平行线;运算能力.
【答案】A
【分析】过点F作FG∥BN交AC于点G,可证EN=GN.同理,可得,EC=3AE,;由FG∥BN,得,于是GC=3NG;设EN=NG=a,则GC=3a,EC=5a,,从而得.
【解答】解:过点F作FG∥BN交AC于点G,
∴,
∴EN=GN,
∵DE∥BC,
∴.
∴EC=3AE.
∵EF∥AB,
∴.
∵FG∥BN,
∴.
∴GC=3NG.
设EN=NG=a,则GC=3a,
∴EC=EN+NG+GC=5a
∴EC=3AE=5a.
∴.
∴.
∴.
故选:A.
【点评】本题考查平行线分线段成比例定理;由平行线得到线段间的数量关系是解题的关键.
5.(2025春 江北区二模)如图,△ABC与△A'B'C'位似,位似中心为点O,OC':CC'=2:1,△A'B'C'的面积为12,则△ABC面积为( )
A.54 B.32 C.27 D.
【考点】位似变换.
【专题】图形的相似;几何直观;推理能力.
【答案】C
【分析】根据可得,即可得出,再结合S△A′B′C′=12可得答案.
【解答】解:∵△ABC与△A'B'C'位似,位似中心为点O,OC':CC'=2:1,
∴,
∴.
∵S△A′B′C′=12,
∴S△ABC=27.
故选:C.
【点评】本题主要考查了位似变换,解答本题的关键是熟练掌握位似图形的性质.
6.(2025春 芝罘区二模)下列长度的四组线段中,成比例的一组是( )
A.2cm,2.5cm,3cm,3.5cm
B.,3cm,3cm,
C.2cm,4cm,8cm,18cm
D.
【考点】比例线段.
【专题】线段、角、相交线与平行线;运算能力.
【答案】D
【分析】根据比例线段的概念,让最小的和最大的相乘,另外两条相乘,看它们的积是否相等即可得出答案.
【解答】解:A.∵2×3.5≠3×2.5,∴四条线段不成比例,故不符合题意;
B.∵43×3,∴四条线段不成比例,故不符合题意;
C.∵2×18≠4×8,∴四条线段不成比例,故不符合题意;
D.∵2=2,∴四条线段成比例,故符合题意;
故选:D.
【点评】此题考查了比例线段,理解成比例线段的概念,注意在线段两两相乘的时候,要让最小的和最大的相乘,另外两条相乘,看它们的积是否相等进行判断.
7.(2025 双城区一模)如图是一架人字梯及其侧面示意图,已知AB∥CD∥EF,AC=50cm,CE=30cm,BD=45cm,则BF的长为( )
A.27cm B.50cm C.72cm D.80cm
【考点】平行线分线段成比例.
【专题】线段、角、相交线与平行线;几何直观;推理能力.
【答案】C
【分析】先根据平行线等分线段定理列比例式求得DF=27cm.BF=BD+DF=72cm,再运用线段的和差求解即可.
【解答】解:已知AB∥CD∥EF,AC=50cm,CE=30cm,BD=45cm,
∴,
∴,
解得:DF=27cm.
∴BF=BD+DF=72cm,
∴BF=BD+DF=72cm,
故选:C.
【点评】本题主要考查了平行线分线段成比例,根据平行线等分定理列比例式成为解题的关键.
8.(2025 湖南)如图,△ABC被平行四边形所截,边AB被截成三等分,D和E为三等分点,DF∥BC,若图中阴影部分的面积为3,则四边形BCGE的面积记为S,则S的值为( )
A.5 B.6 C.9 D.12
【考点】相似三角形的判定与性质;平行四边形的性质.
【专题】图形的相似;运算能力.
【答案】A
【分析】由题意易得DF∥EG∥BC,则有△ADF∽△AEG∽△ABC,然后根据相似三角形的性质可进行求解.
【解答】解:由题意可知:DF∥EG∥BC,
∴△ADF∽△AEG∽△ABC,
∵AD=DE=EF,
∴,,
∴()2,()2,
∵阴影部分的面积是3,
∴S△AEGS四边形EFGH=4,
∴S△ABCS△AEG=9,
∴S四边形BCGF=S△ABC﹣S△AEG=5;
故选:A.
【点评】本题主要考查相似三角形的性质与判定,平行四边形的性质,熟练掌握相似三角形的性质与判定是解题的关键.
9.(2025春 仓山区二模)如图,DE是△ABC的中位线,点F为DE上一点,且EF=2DF,CF的延长线交AB于点G,若DG=1,则AG的长为( )
A.2 B. C.3 D.4
【考点】相似三角形的判定与性质;三角形中位线定理.
【专题】图形的相似;几何直观;推理能力.
【答案】D
【分析】过点E作EM∥AB交CG于点M,证明△FEM∽△FDG,△CME∽△CGA,根据相似三角形的性质以及中位线的性质,即可求解.
【解答】解:EF=2DF,DG=1,如图,过点E作EM∥AB交CG于点M,
∴△FEM∽△FDG,
∴,
∴EM=2,
∵DE是△ABC的中位线,
∴AC=2EC,
∵EM∥AB,
∴△CME∽△CGA,
∴,
∴AG=2EM=4,
故选:D.
【点评】本题考查了相似三角形的判定与性质,三角形中位线定理,解答本题的关键是熟练掌握相似三角形的性质.
10.(2025春 江北区二模)如图,在正方形ABCD中,点E为正方形内部一点,连接AE、BE,将线段AE绕点A逆时针旋转90°得到线段AF,点F落在BE的延长线上,BE的延长线交AD于点M,连接CF交BD于点N,若AM:AB=1:3,则的值为( )
A. B. C. D.
【考点】相似三角形的判定与性质;全等三角形的判定与性质;正方形的性质;旋转的性质.
【专题】图形的全等;矩形 菱形 正方形;平移、旋转与对称;图形的相似;几何直观;运算能力;推理能力.
【答案】A
【分析】连接DF,过点F作FH∥AD,交BD的延长线于点H,先证明△AFD≌△AEB,得到∠ABM=∠FDM,∠AEB=∠AFD,进而推出△DFM为直角三角形,利用tan∠MDF=tan∠ABM,得到,设AM=x,AB=3x,MF=a,DF=3a,进而得到,求出,证明△BMD∽△BFH,求出FH的长,再证明△FNH∽△CNB,得到,即可.
【解答】解:连接DF,过点F作FH∥AD,交BD的延长线于点H,
∵四边形ABCD是正方形,
∴AB=BC=AD,∠BAM=90°,AD∥BC,
∴FH∥BC,
由旋转的性质得:AF=AE,∠EAF=90°,
∴∠AEF=∠AFE=45°,∠BAE=∠DAF=90°﹣∠DAE,
∴∠BEA=180°﹣∠AEF=135°,
在△AFD和△AEB中,
,
△AFD≌△AEB(SAS),
∴∠ABM=∠FDM,∠AEB=∠AFD=135°,
∴∠DFM=135°﹣45°=90°,tan∠MDF=tan∠ABM,
∴,
设AM=x,AB=3x,MF=a,DF=3a,则:,
∴,
∴,
∴,
∵FH∥AD,
∴△BMD∽△BFH,
∴,
∴,
∵FH∥BC,
∴△FNH∽△CNB,
∴;
故选:A.
【点评】本题考查正方形的性质,旋转的性质,全等三角形的判定和性质,相似三角形的判定和性质,解直角三角形等知识点,解题的关键是添加辅助线构造全等和相似三角形.
二.填空题(共5小题)
11.(2025春 西安月考)如图,在△ABC中,∠BAC=90°,AB=AC=8,D为边BC上的一点,分别过点B,C作AD的垂线,垂足为E,F.若,则DE的长为 .
【考点】相似三角形的判定与性质;全等三角形的判定与性质;勾股定理.
【专题】图形的全等;等腰三角形与直角三角形;图形的相似;几何直观;推理能力.
【答案】.
【分析】由勾股定理得,即得,设DE=x,则,由△BDE∽△CDF得,可得,再证明△ABE≌△CAF(AAS)得,最后由AF2+CF2=AC2得,即可求解.
【解答】解:在直角三角形ABC中,∠BAC=90°,AB=AC=8,
由勾股定理得:,
∵,
∴,
∵BE⊥AE,CF⊥AD,
∴∠E=∠AFC=∠CFD=90°,
设DE=x,
在直角三角形BDE中,由勾股定理得:,
∵∠E=∠CFD=90°,∠BDE=∠CDF,
∴△BDE∽△CDF,
∴,
∴,
∴,
∵∠BAE+∠CAF=90°,∠ACF+∠CAF=90°,
∴∠BAE=∠ACF,
在△ABE和△CAF中,
,
∴△ABE≌△CAF(AAS),
∴,
在直角三角形ACF中,由勾股定理得:AF2+CF2=AC2,
∴,
解得,
∴DE的长为,
故答案为:.
【点评】本题考查了相似三角形的判定与性质,全等三角形的判定与性质,勾股定理,掌握以上知识点是解题的关键.
12.(2025春 杨浦区月考)如图,E、F分别是平行四边形ABCD边BC、CD的中点,AE、AF交BD于点G、H,若△AGH的面积为1,则五边形CEGHF的面积是 2 .
【考点】相似三角形的判定与性质;三角形中位线定理;平行四边形的性质.
【专题】多边形与平行四边形;图形的相似;几何直观;推理能力.
【答案】2.
【分析】连接AC交BD于点O,由平行四边形的性质证明△ADG∽△EBG,△ABH∽△FDH,进而推出BG=GH=DH,得到S△ABG=S△AGH=S△ADH=1,即可求解.
【解答】解:E、F分别是平行四边形ABCD边BC、CD的中点,AE、AF交BD于点G、H,如图,连接AC交BD于点O,
∴AD∥BC,AB∥CD,AD=BC,AB=CD,,
S△ABE=S△ACE,S△ACF=S△ADF,
∴,
∵AD∥BC,AB∥CD,
∴△ADG∽△EBG,△ABH∽△FDH,
∴,,
∴DG=2BG,BH=2DH,
∴BG=GH=DH,
∴S△ABG=S△AGH=S△ADH=1,
∴S△ABD=3,
∴,
∴S四边形AECF=3,
∴五边形CEGHF的面积是S五边形CEGHF=S四边形AECF﹣S△AGH=2,
故答案为:2
【点评】本题考查了相似三角形的判定与性质,三角形中位线定理,平行四边形的性质,掌握相似三角形的性质是解题关键.
13.(2025春 宁波二模)如图,已知正方形ABCD边长为2,点E,F分别在边AD,BC上,将正方形沿着EF翻折,点B恰好落在CD边上的点B'处.如果四边形ABFE与四边形EFCD的面积比为3:5,那么线段BF的长为 .
【考点】相似三角形的判定与性质;比的应用;正方形的性质;翻折变换(折叠问题).
【专题】矩形 菱形 正方形;图形的相似;运算能力.
【答案】.
【分析】连接BB',过点F作FH⊥AD,设CF=x,则DH=x,BF=2﹣x,根据已知条件,分别表示出AE、EH、HD,证明△EHF≌△B'CB,得出EH=B'C2x,在Rt△B'FC中,根据勾股定理建立方程即可解答.
【解答】解:如图,连接BB',过点F作FH⊥AD,
∵已知正方形ABCD的边长为2,四边形ABFE与四边形EFCD的面积比为3:5,
∴S四边形ABFE=,
设CF=x,则DH=x,BF=2﹣x,
∴S四边形ABFE4,
即 (AE+2﹣x)×2,
解得AE=x,
∴DE=2﹣AEx,
∴EH=ED﹣HDx﹣x2x,
由折叠的性质可得BB'⊥EF,
∴∠1+∠2=∠BGF=90°,
∵∠2+∠3=90°,
∴∠1=∠3,
又FH=BC=2,∠EHF=∠C,
∴△EHF≌△B'CB(ASA),
∴EH=B'C2x,
在Rt△B'FC中,B'F2=B'C2+CF2,
∴(2﹣x)2=x2+(2x)2,
解得x1=x2,
∴BF=2
故答案为:.
【点评】本题主要考查了正方形的性质,全等三角形的判定与性质,勾股定理,轴对称的性质,熟练掌握正方形的性质是解题的关键.
14.(2025 清镇市)小星自制了一个小孔成像装置,其中直筒的长度为15cm,他准备了一支长为20cm的蜡烛,想要得到高度为5cm的蜡像,则蜡烛应放在距离直筒 60 cm的地方.
【考点】相似三角形的应用.
【专题】图形的相似;应用意识.
【答案】60.
【分析】先根据题意得出相似三角形,再利用三角形相似的性质得到相似比,然后根据比例性质计算.
【解答】解:由题意知:AB=20cm,OF=15cm,CD=5cm,如图,作OE⊥AB于点E,
∵AB∥CD,EF⊥AB,
∴EF⊥CD,
∴△OAB∽△ODC,
∴,
∴,
解得OE=60.
∴蜡烛应放在距离纸筒60cm的地方,
故答案为:60.
【点评】本题考查的是相似三角形的应用,熟知相似三角形的对应边成比例是解答此题的关键.
15.(2025 清江浦区一模)物理课上学过小孔成像的原理,它是一种利用光的直线传播特性实现图象投影的方法.如图,燃烧的蜡烛(竖直放置)AB经小孔O在屏幕(竖直放置)上成像A′B′,设AB=18cm,A′B′=12cm,小孔O到AB的距离为30cm,则小孔O到A′B′的距离为 20 cm.
【考点】相似三角形的应用;平行投影.
【专题】图形的相似;运算能力.
【答案】20.
【分析】过点O作OC⊥AB,垂足为C,过点O作OD⊥A′B′,垂足为D,根据题意可得:AB∥A′B′,从而可得∠OAB=∠OA′B′,∠OBA=∠OB′A′,进而可得△OAB∽△OA′B′,然后利用相似三角形的性质进行计算,即可解答.
【解答】解:过点O作OC⊥AB,垂足为C,过点O作OD⊥A′B′,垂足为D,
由题意得:AB∥A′B′,
∴∠OAB=∠OA′B′,∠OBA=∠OB′A′,
∴△OAB∽△OA′B′,
∴,
∴,
解得:OD=20,
∴小孔O到A′B′的距离为20cm,
故答案为:20.
【点评】本题考查了相似三角形的应用,平行投影,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
三.解答题(共5小题)
16.(2025 阎良区二模)雄伟壮观的马栏革命纪念碑在历史的风云中永远纪念革命先辈的抗战壮举.某数学研究性学习小组在老师的指导下,利用课余时间进行测量马栏革命纪念碑高度的活动.
活动主题 测量马栏革命纪念碑高度
测量工具 皮尺、标杆、激光笔等
活动过程 模型抽象
测绘过程与数据信息 ①在点B处竖立一根高3米的标杆AB; ②地面上的点D、标杆上的点F和碑顶M在一条直线上,BD=3米,BF=2米; ③地面上的点E、标杆顶点A和碑顶M在一条直线上,BE=4.8米; ④点N、B、D、E在同一水平直线上,点F在AB上,MN⊥NE,AB⊥NE,图中所有点均在同一平面内.
说明 在测量过程中注意自身和他人的安全.
请根据表格中提供的信息,求出马栏革命纪念碑的高度MN.
【考点】相似三角形的应用.
【专题】图形的相似;几何直观;推理能力.
【答案】18米.
【分析】由题意可得,根据相似三角形的判定和性质定理即可得结论.
【解答】解:由题意可得:∠ABE=∠MNE=90°,∠FDB=∠NDM,∠E=∠E,AB=3米,BD=3米,BF=2米,BE=4.8米,
∴△BDF∽△NDM,△ABE∽△MNE,
∴,,
∴,,
∴,BN=1.6MN﹣4.8,
∴,
∴MN=18米.
答:马栏革命纪念碑的高度MN为18米.
【点评】本题主要考查了相似三角形的应用,熟练掌握相似三角形的判定和性质定理是正确解答此题的关键.
17.(2025 天府新区)如图1,在△ABC中,AB=AC,点D是BC边上的动点(点D不与点B,C重合),点E,F分别在边AB,AC上,且满足BE=DE,DF=CF.
(1)判断四边形AEDF的形状并说明理由;
(2)如图2,连接EF,将△DEF沿EF翻折,使点D落在点G处,连接BG,CG.
①求证:△GEB∽△GFC;
②若,AB=AC=10,当△DEF是等腰三角形时,求GC的长.
【考点】相似形综合题.
【专题】几何综合题;三角形;图形的相似;几何直观;运算能力;推理能力.
【答案】(1)四边形AEDF是平行四边形,证明见解答;
(2)①证明见解答;
②10或或.
【分析】(1)由等边对等角可得∠B=∠C,∠B=∠EDB,∠C=∠FDC,继而得到∠B=∠EDB=∠C=∠FDC,再由三角形内角和定理得到∠A=∠BED=∠DFC,然后得到DE∥AF,DF∥AE,即可证明四边形AEDF是平行四边形;
(2)①由翻折可知EG=ED,FG=FD,再结合已知条件可得到,再令∠BED=α,∠DEF=β,由翻折可知∠GEF=∠DEF=β,∠GFE=∠EFD=180°﹣α﹣β,继而得到∠BEG=∠CFG,即可证明△GEB∽△GFC;
②分三种情况进行讨论:DE=DF,DE=EF,DF=EF,通过角度之间的转换得到边相等,进而求出GC的长.
【解答】(1)解:∵AB=AC,
∴∠B=∠C,
又∵BE=DE,DF=CF,
∴∠B=∠EDB,∠C=∠FDC,
∴∠B=∠EDB=∠C=∠FDC,
∵∠A=180°﹣(∠B+∠C),∠BED=180°﹣(∠B+∠EDB),∠DFC=180°﹣(∠C+∠FDC),
∴∠A=∠BED=∠DFC,
∴DE∥AF,DF∥AE,
∴四边形AEDF是平行四边形;
(2)①证明:由翻折可知EG=ED,FG=FD,
∵BE=DE,FD=FC,
∴EG=BE,FG=FC,
∴,
令∠BED=α,∠DEF=β,
∵DF∥AE,DE∥AF,
∴∠EDF=∠DFC=α,
∴∠EFD=180°﹣α﹣β,
由翻折可知∠GEF=∠DEF=β,∠GFE=∠EFD=180°﹣α﹣β,
∴∠BEG=360°﹣α﹣2β,∠GFC=α+2(180°﹣α﹣β )=360°﹣α﹣2β,
∴∠BEG=∠GFC,
又∵,
∴△GEB∽△GFC,
②解:∵△DEF是等腰三角形,
∴可以分为三种情况,分别是:DE=DF,DF=EF,DE=EF,
第一种情况:DE=DF,
当DE=DF时,△BED≌△DFC,
∴BD=CD,
∵四边形AEDF是平行四边形,
∴点E、F、D分别是AB、AC、BC的中点,此时点G与点A重合,
∴GC=AC=10;
第二种情况:DF=EF,
当DF=EF时,β=α,
∴∠GEB=360°﹣3α,
∴,
∵,
∴,
∵∠BGC=∠EGF=∠EDF=α,
∴∠BGC=∠GBC,
∴GC=BC,
过点B作BH⊥AC,交AC于点H,如图,
在Rt△ABH中,,
∴,
∴AH=6,
∴CH=4,
在Rt△BHC中,,
∴;
第三种情况:DE=EF,
∵△GEB∽△GFC,
∴∠BGE=∠CGF,
∴∠BGC=∠BGE+∠EGC=∠CGF+∠EGC=∠EGF=∠A=∠BED=α,
当DE=EF时,∠GFE=∠EFD=∠EDF=α,
∴∠GFC=3α,
∴,
∴,
∴∠BGC=∠GCB,
∴BC=BG,
过点B作BM⊥GC,交GC于点M,如图,
在Rt△BMC中,,
∴,
∴,
∴,
综上,GC的长为10或或.
【点评】本题考查了相似形的综合应用,主要考查等腰三角形的性质,平行四边形的判定,相似三角形的判定,三角函数,勾股定理等知识,用到了分类讨论的数学思想方法,熟记相关的性质和判定,会通过角度之间的转换得到边相等是解题的关键.
18.(2025 盐田区二模)定义:在 ABCD中,如果有一条对角线的长等于其中一条边的长,则称这个平行四边形为“N字平行四边形”.
(1)下面的图形中是“N字平行四边形”的有: C ;
A.正方形
B.矩形
C.有一个角是60°的菱形
D.有一个角是60°的平行四边形
E.有一个角是45°的平行四边形
(2)在“N字平行四边形”中,∠A=45°,AB>BC,则 ;
(3)如图1,在“N字平行四边形ABCD”中,∠B=75°,AB=AC=8,点F是AB边上一点,FG∥AC,FG与DC的延长线交于点G,若 AFGC为“N字平行四边形”,求AF的值;
(4)如图2,在矩形ABCD中,点E、F分别是BC边和AD边上的点,四边形BEDF为“N字平行四边形”,若AB=2AF,求的值.
【考点】相似形综合题.
【专题】几何综合题;推理能力.
【答案】(1)C;
(2);
(3);
(4)或.
【分析】(1)根据选项逐一判断即可;
(2)画出图形,证明△ABD是等腰直角三角形即可得解;
(3)由题易得∠ACG=∠ACB+∠BCG=150°,则 AFGC为“N字平行四边形”,只能分为两种情况:①当CF=AF时,∠FCA=∠FAC=30°,②当CF=AC时,∠CAF=∠AFC=30°,再分别求解即可;
(4)过点E作EM⊥BF于点M,过点F作FN⊥BE于点N,分两种情况:①当FB=FE时,②当EB=EF时,分别画出图形求解即可.
【解答】(1)解:正方形的对角线是边长的倍,故A选项不是;
矩形的对角线是直角三角形的斜边比边长大,故B选项不是;
有一个角是60°的菱形必定包含等边三角形,
会有一条对角线等于边长,故C选项是;
有一个角是60°的平行四边形和有一个角是45°的平行四边形并不必然出现对角线等于边长,故D、E选项均不是;
故选:C;
(2)解:如图,
∵ ABCD是“N字平行四边形”,
∴DA=DB,
∵∠A=45°,
∴∠ABD=45°,
∴△ABD是等腰直角三角形,
∴,
∴,
故答案为:;
(3)证明:连接AG,CF,
∵在N字 ABCD中,∠B=75°,AB=AC=8,
∴∠B=∠ACB=75°,∠BAC=30°.
∵AB∥DG,
∴∠B=∠BCG=75°,
∴∠ACG=∠ACB+∠BCG=150°,
由大角对大边可得AG>AC,AG>GC,
若 AFGC为“N字平行四边形”,只能分为以下几种情况:
①当CF=AF时,∠FCA=∠FAC=30°,
过点F作FH⊥AC于点H,可得点H为AC的中点,AF=2HF,,
又∵AC=8,
∴,
∴,;
②当CF=AC时,∠CAF=∠AFC=30°,此时,∠ACF=120°>∠ACB矛盾.
综上,若 AFGC为N字平行四边形,;
(4)过点E作EM⊥BF于点M,过点F作FN⊥BE于点N,
∵四边形ABCD为矩形,
∴AD=BC,∠A=∠C=90°,AB=DC=FN,
∵四边形BEDF为平行四边形,
∴FD=BE,FB=DE,
∴AF=AD﹣FD,CE=BC﹣BE,即AF=CE.
∵四边形BEDF为N字平行四边形,
又∵BD>BE,BD>DE,
∴有以下两种情况:
①当FB=FE时,
∵FN⊥BE,
∴N为BE的中点,
∴BN=NE.
在矩形ABNF中,AF=BN,
又∵AF=CE,
∴BN=NE=CE=AF,
∴BC=BN+NE+CE=3AF,
∵AB=2AF,
∴;
②当EB=EF时,
∵EM⊥BF,
∴M为BF的中点,,
设AF=t,则AB=2t,,,
∵EM⊥BF,
∴∠EMB=90°,
∵AD∥BC,
∴∠AFB=∠MBE,
∴Rt△BAF∽Rt△EMB,
∴AF:AB:BF=MB:ME:BE=1:2:,
由可得,
∴,
∴;
综上,或.
【点评】本题主要考查了平行四边形的性质、等腰三角形的性质、勾股定理、相似三角形的判定和性质等内容,熟练掌握相关知识是解题的关键.
19.(2025春 莱州市二模)【教材呈现】下面是华师版教材九年级上册52页的部分内容:
我们可以发现,当两条直线与一组平行线相交时,所截得的线段存在一定的比例关系:.这就是如下的基本事实: 两条直线被一组平行线所截,所得的对应线段成比例.(简称“平行线分线段成比例”)
【问题原型】如图①,在矩形ABCD中,点E为边AB的中点,过E作EF∥AD交边DC于点F,点P、Q分别在矩形的边AD、BC上,连结PQ交EF于点M.求证:PM=QM.
【结论应用】如图②,在【问题原型】的基础上,点R在边BC上(不与点Q重合),连结PR交EF于点N.
(1)若MN=4,则线段QR的长为 8 ;
(2)当点Q与点B重合,点R与点C重合时,如图③,若BC=10,且△PMN周长的最小值为12,则边AB的长为 2 .
【考点】平行线分线段成比例;三角形中位线定理;轴对称﹣最短路线问题.
【专题】矩形 菱形 正方形;平移、旋转与对称;运算能力;推理能力.
【答案】[问题原型]见解析;[结论应用](1)8;(2).
【分析】[问题原型]根据平行线分线段成比例即可得证;
[结论应用](1)根据平行线分线段成比例得出,,进而得到MN是△PQR的中位线,即可求解;
(2)根据(1)的结论得出MN是是△PQR的中位线,当P为中点时得出△PBC的周长的最小值为24,进而勾股定理即可求解.
【解答】[问题原型]证明:∵点E为边AB的中点,
∴AE=BE,
在矩形ABCD中,AD∥BC,
∵EF∥AD,
∴AD∥EF∥BC,
∴,
∴PM=QM,
[结论应用](1)解:根据题意可得AD∥EF∥BC
∴,,
∴QR=2MN=8,
故答案为:8.
(2)解:如图所示,
作点C关于AD的对称点,连接PG,BG,DG,
∴PB+PC=PB+PG≥BG,
当P在BG上时,取得最小值,
又∵PD∥BC,D是CG的中点,
∴PD是BC的中位线,
∴P是AD的中点,则PB=PG=PC,
即当P顶点是AD 中点时,三角形PBC的面积取得最小值,
∵根据(1)的结论得出MN是是△PQR的中位线,BC=10,且△PMN周长的最小值为12,
∴△PBC的周长为24,
∴,PB+PC=24﹣10=14,
∴PB=7,
∴.
故答案为:2.
【点评】本题考查了平行线分线段成比例,中位线的性质与判定,轴对称的性质求线段的最小值,熟练掌握以上知识是解题的关键.
20.(2024秋 秦皇岛三模)综合与实践
【问题情境】
数学活动课上,老师让同学们准备了一些等边三角形纸片、正方形纸片和等腰直角三角形纸片,通过折、拼的方式探索其中蕴含的数学知识.
【数学思考】
(1)希望小组选用等边三角形纸片进行折叠,并提出问题:如图①,将等边三角形ABC沿直线DE折叠,点A恰好落在边BC上的点F处,折痕分别交AB,AC于D,E两点.求证:;
(2)善思小组选用正方形纸片进行折叠,并提出问题:如图②,将正方形ABCD沿直线EF折叠,点A恰好落在边BC的中点G处,点D落在点H处,折痕分别交AB,CD于E,F两点,设GH,CD交于点I.若AB=8,求GI的长;
【拓展探究】
(3)智慧小组将两个不同的等腰直角三角形拼在一起,并提出问题:如图③,△ABC与△ADE都是等腰直角三角形,点D在边BC上,∠BAC=∠DAE=90°,DE交AC于点F.若BD=1,CD=3,请直接写出图中阴影部分的面积.
【考点】相似形综合题.
【专题】几何综合题;运算能力;推理能力.
【答案】(1)见解析;
(2)GI;
(3).
【分析】(1)根据等边三角形的性质得到∠A=∠B=∠C=60°,根据折叠的性质得到FD=AD,FE=AE,∠DFE=∠A=60°,求得∠BDF=∠CFE,根据相似三角形的性质即可得到结论;
(2)根据正方形的性质得到∠A=∠B=∠C=90°,AB=BC=8,根据折叠的性质得到GE=AE,∠EGH=∠A=90°,根据相似三角形的性质得到BG=CGBC=4,设AE=EG=x,则BE=8﹣x,根据勾股定理得到EG=5,BE=3,于是得到GI;
(3)根据等腰直角三角形的性质得到∠BAC=∠DAE=90°,AB=AC,AD=AE,∠B=∠C=∠ADE=∠E=45°,根据相似三角形的性质得到BC=BD+CD=4,设AB=AC=x,根据勾股定理得到AB=AC=2,求得CF,得到AF=AC﹣CF=2,过D作DP⊥AC于P,根据相似三角形的性质得到DP,于是得到S△ADFAF DP.
【解答】(1)证明:∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∵将等边三角形ABC沿直线DE折叠,点A恰好落在边BC上的点F处,
∴FD=AD,FE=AE,∠DFE=∠A=60°,
∵∠BDF=180°﹣∠B﹣∠BFD=120°﹣∠BFD,∠CFE=180°﹣∠DFE﹣∠BFD=120°﹣∠BFD,
∴∠BDF=∠CFE,
∵∠B=∠C=60°,
∴△BDF∽△CFE,
∴,
∵DF=AD,FE=AE,
∴;
(2)解:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=90°,AB=BC=8,
∵将正方形ABCD沿直线EF折叠,点A恰好落在边BC的中点G处,点D落在点H处,
∴GE=AE,∠EGH=∠A=90°,
∵∠BEG=90°﹣∠BGE,∠CGI=180°﹣∠EGH﹣∠BGE=90°﹣∠BGE,
∴∠BEG=∠CGI,
∵∠B=∠C=90°,
∴△BEG∽△CGI.
∴,
∵点G是BC的中点,
∴BG=CGBC=4,
设AE=EG=x,则BE=8﹣x,
在Rt△BEG中,BE2+BG2=EG2,
∴(8﹣x)2+42=x2,
∴x=5,
∴EG=5,BE=3,
∵,
∴,
∴GI;
(3)∵△ABC与△ADE是等腰直角三角形,
∴∠BAC=∠DAE=90°,AB=AC,AD=AE,∠B=∠C=∠ADE=∠E=45°,
∵∠BAD=180°﹣∠B﹣∠ADB=135°﹣∠ADB,∠CDF=180°﹣∠ADE﹣∠ADB=135°﹣∠ADB,
∴∠BAD=∠CDF,
∵∠B=∠C=45°,
∴△ABD∽△DCF,
∴,
∵BD=1,CD=3,
∴BC=BD+CD=4,
设AB=AC=x,
∵AB2+AC2=BC2,
∴x2+x2=42,
解得x1=2,x2=﹣2(舍去),
∴AB=AC=2,
∵,
∴,
∴CF,
∴AF=AC﹣CF=2,
过D作DP⊥AC于P,
∴∠DPC=90°=∠BAC,
∵∠C=∠C=45°,
∴△DPC∽△BAC,
∴,
∴,
∴DP,
∴S△ADFAF DP.
【点评】本题是相似形的综合题,考查了相似三角形的判定和性质,勾股定理等腰直角三角形的判定和性质,正方形的性质,熟练掌握相似三角形的判定和性质定理是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考核心考点 图形的相似
一.选择题(共10小题)
1.(2025春 江阴市二模)如图,在正方形ABCD中,AB=5,E为边CD上一动点(不与端点重合),AE交BD于点F,过点F作FH⊥AE交BC于点H,过点H作HG⊥BD于点G,连接AH,HE.给出下列结论:①AF=HE;②∠HAE=45°;③;④,其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
2.(2025 綦江区一模)如图,四边形ABCD与四边形EFGH位似,位似中心是O,若OA:AE=1:2,且四边形ABCD的周长为5,则四边形EFGH的周长为( )
A.10 B.15 C.20 D.45
3.(2025 姑苏区一模)如图,在菱形ABCD中,E为边BC上一点,且DE=CD,BD与AE交于点F.下列结论:①AE=BD,②AE平分∠BED,③AD2=AF AE,④BE BC=BF BD,其中正确的是( )
A.①②③④ B.①②④ C.①③④ D.①②③
4.(2025春 莱州市二模)如图,点D,E,F分别在△ABC的边上,,DE∥BC,EF∥AB,点M是EF的中点,连接BM并延长交AC于点N,则的值是( )
A. B. C. D.
5.(2025春 江北区二模)如图,△ABC与△A'B'C'位似,位似中心为点O,OC':CC'=2:1,△A'B'C'的面积为12,则△ABC面积为( )
A.54 B.32 C.27 D.
6.(2025春 芝罘区二模)下列长度的四组线段中,成比例的一组是( )
A.2cm,2.5cm,3cm,3.5cm
B.,3cm,3cm,
C.2cm,4cm,8cm,18cm
D.
7.(2025 双城区一模)如图是一架人字梯及其侧面示意图,已知AB∥CD∥EF,AC=50cm,CE=30cm,BD=45cm,则BF的长为( )
A.27cm B.50cm C.72cm D.80cm
8.(2025 湖南)如图,△ABC被平行四边形所截,边AB被截成三等分,D和E为三等分点,DF∥BC,若图中阴影部分的面积为3,则四边形BCGE的面积记为S,则S的值为( )
A.5 B.6 C.9 D.12
9.(2025春 仓山区二模)如图,DE是△ABC的中位线,点F为DE上一点,且EF=2DF,CF的延长线交AB于点G,若DG=1,则AG的长为( )
A.2 B. C.3 D.4
10.(2025春 江北区二模)如图,在正方形ABCD中,点E为正方形内部一点,连接AE、BE,将线段AE绕点A逆时针旋转90°得到线段AF,点F落在BE的延长线上,BE的延长线交AD于点M,连接CF交BD于点N,若AM:AB=1:3,则的值为( )
A. B. C. D.
二.填空题(共5小题)
11.(2025春 西安月考)如图,在△ABC中,∠BAC=90°,AB=AC=8,D为边BC上的一点,分别过点B,C作AD的垂线,垂足为E,F.若,则DE的长为 .
12.(2025春 杨浦区月考)如图,E、F分别是平行四边形ABCD边BC、CD的中点,AE、AF交BD于点G、H,若△AGH的面积为1,则五边形CEGHF的面积是 .
13.(2025春 宁波二模)如图,已知正方形ABCD边长为2,点E,F分别在边AD,BC上,将正方形沿着EF翻折,点B恰好落在CD边上的点B'处.如果四边形ABFE与四边形EFCD的面积比为3:5,那么线段BF的长为 .
14.(2025 清镇市)小星自制了一个小孔成像装置,其中直筒的长度为15cm,他准备了一支长为20cm的蜡烛,想要得到高度为5cm的蜡像,则蜡烛应放在距离直筒 cm的地方.
15.(2025 清江浦区一模)物理课上学过小孔成像的原理,它是一种利用光的直线传播特性实现图象投影的方法.如图,燃烧的蜡烛(竖直放置)AB经小孔O在屏幕(竖直放置)上成像A′B′,设AB=18cm,A′B′=12cm,小孔O到AB的距离为30cm,则小孔O到A′B′的距离为 cm.
三.解答题(共5小题)
16.(2025 阎良区二模)雄伟壮观的马栏革命纪念碑在历史的风云中永远纪念革命先辈的抗战壮举.某数学研究性学习小组在老师的指导下,利用课余时间进行测量马栏革命纪念碑高度的活动.
活动主题 测量马栏革命纪念碑高度
测量工具 皮尺、标杆、激光笔等
活动过程 模型抽象
测绘过程与数据信息 ①在点B处竖立一根高3米的标杆AB; ②地面上的点D、标杆上的点F和碑顶M在一条直线上,BD=3米,BF=2米; ③地面上的点E、标杆顶点A和碑顶M在一条直线上,BE=4.8米; ④点N、B、D、E在同一水平直线上,点F在AB上,MN⊥NE,AB⊥NE,图中所有点均在同一平面内.
说明 在测量过程中注意自身和他人的安全.
请根据表格中提供的信息,求出马栏革命纪念碑的高度MN.
17.(2025 天府新区)如图1,在△ABC中,AB=AC,点D是BC边上的动点(点D不与点B,C重合),点E,F分别在边AB,AC上,且满足BE=DE,DF=CF.
(1)判断四边形AEDF的形状并说明理由;
(2)如图2,连接EF,将△DEF沿EF翻折,使点D落在点G处,连接BG,CG.
①求证:△GEB∽△GFC;
②若,AB=AC=10,当△DEF是等腰三角形时,求GC的长.
18.(2025 盐田区二模)定义:在 ABCD中,如果有一条对角线的长等于其中一条边的长,则称这个平行四边形为“N字平行四边形”.
(1)下面的图形中是“N字平行四边形”的有: ;
A.正方形
B.矩形
C.有一个角是60°的菱形
D.有一个角是60°的平行四边形
E.有一个角是45°的平行四边形
(2)在“N字平行四边形”中,∠A=45°,AB>BC,则 ;
(3)如图1,在“N字平行四边形ABCD”中,∠B=75°,AB=AC=8,点F是AB边上一点,FG∥AC,FG与DC的延长线交于点G,若 AFGC为“N字平行四边形”,求AF的值;
(4)如图2,在矩形ABCD中,点E、F分别是BC边和AD边上的点,四边形BEDF为“N字平行四边形”,若AB=2AF,求的值.
19.(2025春 莱州市二模)【教材呈现】下面是华师版教材九年级上册52页的部分内容:
我们可以发现,当两条直线与一组平行线相交时,所截得的线段存在一定的比例关系:.这就是如下的基本事实: 两条直线被一组平行线所截,所得的对应线段成比例.(简称“平行线分线段成比例”)
【问题原型】如图①,在矩形ABCD中,点E为边AB的中点,过E作EF∥AD交边DC于点F,点P、Q分别在矩形的边AD、BC上,连结PQ交EF于点M.求证:PM=QM.
【结论应用】如图②,在【问题原型】的基础上,点R在边BC上(不与点Q重合),连结PR交EF于点N.
(1)若MN=4,则线段QR的长为 ;
(2)当点Q与点B重合,点R与点C重合时,如图③,若BC=10,且△PMN周长的最小值为12,则边AB的长为 .
20.(2024秋 秦皇岛三模)综合与实践
【问题情境】
数学活动课上,老师让同学们准备了一些等边三角形纸片、正方形纸片和等腰直角三角形纸片,通过折、拼的方式探索其中蕴含的数学知识.
【数学思考】
(1)希望小组选用等边三角形纸片进行折叠,并提出问题:如图①,将等边三角形ABC沿直线DE折叠,点A恰好落在边BC上的点F处,折痕分别交AB,AC于D,E两点.求证:;
(2)善思小组选用正方形纸片进行折叠,并提出问题:如图②,将正方形ABCD沿直线EF折叠,点A恰好落在边BC的中点G处,点D落在点H处,折痕分别交AB,CD于E,F两点,设GH,CD交于点I.若AB=8,求GI的长;
【拓展探究】
(3)智慧小组将两个不同的等腰直角三角形拼在一起,并提出问题:如图③,△ABC与△ADE都是等腰直角三角形,点D在边BC上,∠BAC=∠DAE=90°,DE交AC于点F.若BD=1,CD=3,请直接写出图中阴影部分的面积.
中考核心考点 图形的相似
参考答案与试题解析
一.选择题(共10小题)
1.(2025春 江阴市二模)如图,在正方形ABCD中,AB=5,E为边CD上一动点(不与端点重合),AE交BD于点F,过点F作FH⊥AE交BC于点H,过点H作HG⊥BD于点G,连接AH,HE.给出下列结论:①AF=HE;②∠HAE=45°;③;④,其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
【考点】相似三角形的判定与性质;全等三角形的判定与性质;正方形的性质.
【专题】矩形 菱形 正方形;图形的相似;运算能力;推理能力.
【答案】B
【分析】①作辅助线,延长HF交AD于点L,连接CF,通过证明△ADF≌△CDF,可得:AF=CF,故需证明FC=FH,可证:AF=FH;AF<EH,据此得征;
②由FH⊥AE,AF=FH,可得:∠HAE=45°,据此得证;
③利用条件证明△AFO≌△FHG,可得FG=AO,可得结论;
④若FH=2,则AHFH=4,AH<AB,这与直角三角形斜边大于直角边矛盾,据此判断即可.
【解答】解:①连接FC,延长HF交AD于点L,如图1,
∵BD为正方形ABCD的对角线,
∴∠ADB=∠CDF=45°.
∵AD=CD,DF=DF,
∴△ADF≌△CDF(SAS).
∴FC=AF,∠ECF=∠DAF.
∵∠ALH+∠LAF=90°,
∴∠LHC+∠DAF=90°.
∵∠ECF=∠DAF,
∴∠FHC=∠FCH,
∴FH=FC.
∴FH=AF,
∵FH⊥AE,
∴FH<EH,
∴AF<EH,故①错误;
②∵FH⊥AE,FH=AF,
∴∠HAE=45°,故②正确;
③连接AC,交BD于点O,
∴BD⊥AC,
在△AFO和△FHG中,
,
∴△AFO≌△FHG(AAS),
∴FG=AO,
∵AOACAB,
∴FG,故③正确;
④若FH=2,则AHFH=4,
∴AH<AB,这与直角三角形斜边大于直角边矛盾.
故④错误.
综上所述,②③正确.
故选:B.
【点评】本题考查正方形的性质,全等三角形的判定和性质,等腰直角三角形的判定和性质等知识,熟练添加辅助线是解题的关键.
2.(2025 綦江区一模)如图,四边形ABCD与四边形EFGH位似,位似中心是O,若OA:AE=1:2,且四边形ABCD的周长为5,则四边形EFGH的周长为( )
A.10 B.15 C.20 D.45
【考点】位似变换.
【专题】图形的相似;几何直观;推理能力.
【答案】B
【分析】根据相似比等于位似比可得:四边形ABCD的周长:四边形EFGH的周长=1:3,据此解答即可得解.
【解答】解:∵四边形ABCD与四边形EFGH位似,位似中心是O,OA:AE=1:2,
∴OA:OE=1:3,四边形ABCD与四边形EFGH的相似比为1:3,
∴四边形ABCD的周长:四边形EFGH的周长=1:3,
∵四边形ABCD的周长为5,
∴四边形EFGH的周长为3×5=15,
故选:B.
【点评】本题考查了位似变换,掌握位似图形的性质是解题的关键.
3.(2025 姑苏区一模)如图,在菱形ABCD中,E为边BC上一点,且DE=CD,BD与AE交于点F.下列结论:①AE=BD,②AE平分∠BED,③AD2=AF AE,④BE BC=BF BD,其中正确的是( )
A.①②③④ B.①②④ C.①③④ D.①②③
【考点】相似三角形的判定与性质;全等三角形的判定与性质;菱形的性质.
【专题】矩形 菱形 正方形;图形的相似;推理能力.
【答案】A
【分析】①正确.证明四边形ABED是等腰梯形可得结论;
②正确.证明∠AEB=∠AED即可;
③正确.证明△ADF∽△AED即可;
④正确.证明△BEF∽△BDC即可.
【解答】解:∵四边形ABCD是菱形,
∴AD∥BC,AB=CD,
∵DE=CD,
∴DE=AB,
∴四边形ABED是等腰梯形,
∴AE=BD,故①正确;
∵AD∥BC,
∴∠AEB=∠DAE,
∵DA=DC=DE,
∴∠DAE=∠DEA,
∴∠DEA=∠AEB,
∴AE平分∠BED,故②正确;
∵四边形ABCD是菱形,
∴∠ADB=∠BDC,∠ADC=∠ABE,
∵四边形ABED是等腰梯形,
∴∠ABE=∠BED=∠DC,
∵∠AED=∠AEB,
∴∠ADF=∠AED,
∵∠DAF=∠DAE,
∴△ADF∽△AED,
∴,
∴AD2=AF AE,故③正确;
∵∠BEF=∠BDC,∠EBF=∠DBC,
∴△BEF∽△BDC,
∴,
∴BE BC=BF BD,故④正确.
故选:A.
【点评】本题考查相似三角形的判定和性质,菱形的性质,等腰梯形的判定和性质,解题的关键是理解题意,灵活运用所学知识解决问题.
4.(2025春 莱州市二模)如图,点D,E,F分别在△ABC的边上,,DE∥BC,EF∥AB,点M是EF的中点,连接BM并延长交AC于点N,则的值是( )
A. B. C. D.
【考点】平行线分线段成比例.
【专题】线段、角、相交线与平行线;运算能力.
【答案】A
【分析】过点F作FG∥BN交AC于点G,可证EN=GN.同理,可得,EC=3AE,;由FG∥BN,得,于是GC=3NG;设EN=NG=a,则GC=3a,EC=5a,,从而得.
【解答】解:过点F作FG∥BN交AC于点G,
∴,
∴EN=GN,
∵DE∥BC,
∴.
∴EC=3AE.
∵EF∥AB,
∴.
∵FG∥BN,
∴.
∴GC=3NG.
设EN=NG=a,则GC=3a,
∴EC=EN+NG+GC=5a
∴EC=3AE=5a.
∴.
∴.
∴.
故选:A.
【点评】本题考查平行线分线段成比例定理;由平行线得到线段间的数量关系是解题的关键.
5.(2025春 江北区二模)如图,△ABC与△A'B'C'位似,位似中心为点O,OC':CC'=2:1,△A'B'C'的面积为12,则△ABC面积为( )
A.54 B.32 C.27 D.
【考点】位似变换.
【专题】图形的相似;几何直观;推理能力.
【答案】C
【分析】根据可得,即可得出,再结合S△A′B′C′=12可得答案.
【解答】解:∵△ABC与△A'B'C'位似,位似中心为点O,OC':CC'=2:1,
∴,
∴.
∵S△A′B′C′=12,
∴S△ABC=27.
故选:C.
【点评】本题主要考查了位似变换,解答本题的关键是熟练掌握位似图形的性质.
6.(2025春 芝罘区二模)下列长度的四组线段中,成比例的一组是( )
A.2cm,2.5cm,3cm,3.5cm
B.,3cm,3cm,
C.2cm,4cm,8cm,18cm
D.
【考点】比例线段.
【专题】线段、角、相交线与平行线;运算能力.
【答案】D
【分析】根据比例线段的概念,让最小的和最大的相乘,另外两条相乘,看它们的积是否相等即可得出答案.
【解答】解:A.∵2×3.5≠3×2.5,∴四条线段不成比例,故不符合题意;
B.∵43×3,∴四条线段不成比例,故不符合题意;
C.∵2×18≠4×8,∴四条线段不成比例,故不符合题意;
D.∵2=2,∴四条线段成比例,故符合题意;
故选:D.
【点评】此题考查了比例线段,理解成比例线段的概念,注意在线段两两相乘的时候,要让最小的和最大的相乘,另外两条相乘,看它们的积是否相等进行判断.
7.(2025 双城区一模)如图是一架人字梯及其侧面示意图,已知AB∥CD∥EF,AC=50cm,CE=30cm,BD=45cm,则BF的长为( )
A.27cm B.50cm C.72cm D.80cm
【考点】平行线分线段成比例.
【专题】线段、角、相交线与平行线;几何直观;推理能力.
【答案】C
【分析】先根据平行线等分线段定理列比例式求得DF=27cm.BF=BD+DF=72cm,再运用线段的和差求解即可.
【解答】解:已知AB∥CD∥EF,AC=50cm,CE=30cm,BD=45cm,
∴,
∴,
解得:DF=27cm.
∴BF=BD+DF=72cm,
∴BF=BD+DF=72cm,
故选:C.
【点评】本题主要考查了平行线分线段成比例,根据平行线等分定理列比例式成为解题的关键.
8.(2025 湖南)如图,△ABC被平行四边形所截,边AB被截成三等分,D和E为三等分点,DF∥BC,若图中阴影部分的面积为3,则四边形BCGE的面积记为S,则S的值为( )
A.5 B.6 C.9 D.12
【考点】相似三角形的判定与性质;平行四边形的性质.
【专题】图形的相似;运算能力.
【答案】A
【分析】由题意易得DF∥EG∥BC,则有△ADF∽△AEG∽△ABC,然后根据相似三角形的性质可进行求解.
【解答】解:由题意可知:DF∥EG∥BC,
∴△ADF∽△AEG∽△ABC,
∵AD=DE=EF,
∴,,
∴()2,()2,
∵阴影部分的面积是3,
∴S△AEGS四边形EFGH=4,
∴S△ABCS△AEG=9,
∴S四边形BCGF=S△ABC﹣S△AEG=5;
故选:A.
【点评】本题主要考查相似三角形的性质与判定,平行四边形的性质,熟练掌握相似三角形的性质与判定是解题的关键.
9.(2025春 仓山区二模)如图,DE是△ABC的中位线,点F为DE上一点,且EF=2DF,CF的延长线交AB于点G,若DG=1,则AG的长为( )
A.2 B. C.3 D.4
【考点】相似三角形的判定与性质;三角形中位线定理.
【专题】图形的相似;几何直观;推理能力.
【答案】D
【分析】过点E作EM∥AB交CG于点M,证明△FEM∽△FDG,△CME∽△CGA,根据相似三角形的性质以及中位线的性质,即可求解.
【解答】解:EF=2DF,DG=1,如图,过点E作EM∥AB交CG于点M,
∴△FEM∽△FDG,
∴,
∴EM=2,
∵DE是△ABC的中位线,
∴AC=2EC,
∵EM∥AB,
∴△CME∽△CGA,
∴,
∴AG=2EM=4,
故选:D.
【点评】本题考查了相似三角形的判定与性质,三角形中位线定理,解答本题的关键是熟练掌握相似三角形的性质.
10.(2025春 江北区二模)如图,在正方形ABCD中,点E为正方形内部一点,连接AE、BE,将线段AE绕点A逆时针旋转90°得到线段AF,点F落在BE的延长线上,BE的延长线交AD于点M,连接CF交BD于点N,若AM:AB=1:3,则的值为( )
A. B. C. D.
【考点】相似三角形的判定与性质;全等三角形的判定与性质;正方形的性质;旋转的性质.
【专题】图形的全等;矩形 菱形 正方形;平移、旋转与对称;图形的相似;几何直观;运算能力;推理能力.
【答案】A
【分析】连接DF,过点F作FH∥AD,交BD的延长线于点H,先证明△AFD≌△AEB,得到∠ABM=∠FDM,∠AEB=∠AFD,进而推出△DFM为直角三角形,利用tan∠MDF=tan∠ABM,得到,设AM=x,AB=3x,MF=a,DF=3a,进而得到,求出,证明△BMD∽△BFH,求出FH的长,再证明△FNH∽△CNB,得到,即可.
【解答】解:连接DF,过点F作FH∥AD,交BD的延长线于点H,
∵四边形ABCD是正方形,
∴AB=BC=AD,∠BAM=90°,AD∥BC,
∴FH∥BC,
由旋转的性质得:AF=AE,∠EAF=90°,
∴∠AEF=∠AFE=45°,∠BAE=∠DAF=90°﹣∠DAE,
∴∠BEA=180°﹣∠AEF=135°,
在△AFD和△AEB中,
,
△AFD≌△AEB(SAS),
∴∠ABM=∠FDM,∠AEB=∠AFD=135°,
∴∠DFM=135°﹣45°=90°,tan∠MDF=tan∠ABM,
∴,
设AM=x,AB=3x,MF=a,DF=3a,则:,
∴,
∴,
∴,
∵FH∥AD,
∴△BMD∽△BFH,
∴,
∴,
∵FH∥BC,
∴△FNH∽△CNB,
∴;
故选:A.
【点评】本题考查正方形的性质,旋转的性质,全等三角形的判定和性质,相似三角形的判定和性质,解直角三角形等知识点,解题的关键是添加辅助线构造全等和相似三角形.
二.填空题(共5小题)
11.(2025春 西安月考)如图,在△ABC中,∠BAC=90°,AB=AC=8,D为边BC上的一点,分别过点B,C作AD的垂线,垂足为E,F.若,则DE的长为 .
【考点】相似三角形的判定与性质;全等三角形的判定与性质;勾股定理.
【专题】图形的全等;等腰三角形与直角三角形;图形的相似;几何直观;推理能力.
【答案】.
【分析】由勾股定理得,即得,设DE=x,则,由△BDE∽△CDF得,可得,再证明△ABE≌△CAF(AAS)得,最后由AF2+CF2=AC2得,即可求解.
【解答】解:在直角三角形ABC中,∠BAC=90°,AB=AC=8,
由勾股定理得:,
∵,
∴,
∵BE⊥AE,CF⊥AD,
∴∠E=∠AFC=∠CFD=90°,
设DE=x,
在直角三角形BDE中,由勾股定理得:,
∵∠E=∠CFD=90°,∠BDE=∠CDF,
∴△BDE∽△CDF,
∴,
∴,
∴,
∵∠BAE+∠CAF=90°,∠ACF+∠CAF=90°,
∴∠BAE=∠ACF,
在△ABE和△CAF中,
,
∴△ABE≌△CAF(AAS),
∴,
在直角三角形ACF中,由勾股定理得:AF2+CF2=AC2,
∴,
解得,
∴DE的长为,
故答案为:.
【点评】本题考查了相似三角形的判定与性质,全等三角形的判定与性质,勾股定理,掌握以上知识点是解题的关键.
12.(2025春 杨浦区月考)如图,E、F分别是平行四边形ABCD边BC、CD的中点,AE、AF交BD于点G、H,若△AGH的面积为1,则五边形CEGHF的面积是 2 .
【考点】相似三角形的判定与性质;三角形中位线定理;平行四边形的性质.
【专题】多边形与平行四边形;图形的相似;几何直观;推理能力.
【答案】2.
【分析】连接AC交BD于点O,由平行四边形的性质证明△ADG∽△EBG,△ABH∽△FDH,进而推出BG=GH=DH,得到S△ABG=S△AGH=S△ADH=1,即可求解.
【解答】解:E、F分别是平行四边形ABCD边BC、CD的中点,AE、AF交BD于点G、H,如图,连接AC交BD于点O,
∴AD∥BC,AB∥CD,AD=BC,AB=CD,,
S△ABE=S△ACE,S△ACF=S△ADF,
∴,
∵AD∥BC,AB∥CD,
∴△ADG∽△EBG,△ABH∽△FDH,
∴,,
∴DG=2BG,BH=2DH,
∴BG=GH=DH,
∴S△ABG=S△AGH=S△ADH=1,
∴S△ABD=3,
∴,
∴S四边形AECF=3,
∴五边形CEGHF的面积是S五边形CEGHF=S四边形AECF﹣S△AGH=2,
故答案为:2
【点评】本题考查了相似三角形的判定与性质,三角形中位线定理,平行四边形的性质,掌握相似三角形的性质是解题关键.
13.(2025春 宁波二模)如图,已知正方形ABCD边长为2,点E,F分别在边AD,BC上,将正方形沿着EF翻折,点B恰好落在CD边上的点B'处.如果四边形ABFE与四边形EFCD的面积比为3:5,那么线段BF的长为 .
【考点】相似三角形的判定与性质;比的应用;正方形的性质;翻折变换(折叠问题).
【专题】矩形 菱形 正方形;图形的相似;运算能力.
【答案】.
【分析】连接BB',过点F作FH⊥AD,设CF=x,则DH=x,BF=2﹣x,根据已知条件,分别表示出AE、EH、HD,证明△EHF≌△B'CB,得出EH=B'C2x,在Rt△B'FC中,根据勾股定理建立方程即可解答.
【解答】解:如图,连接BB',过点F作FH⊥AD,
∵已知正方形ABCD的边长为2,四边形ABFE与四边形EFCD的面积比为3:5,
∴S四边形ABFE=,
设CF=x,则DH=x,BF=2﹣x,
∴S四边形ABFE4,
即 (AE+2﹣x)×2,
解得AE=x,
∴DE=2﹣AEx,
∴EH=ED﹣HDx﹣x2x,
由折叠的性质可得BB'⊥EF,
∴∠1+∠2=∠BGF=90°,
∵∠2+∠3=90°,
∴∠1=∠3,
又FH=BC=2,∠EHF=∠C,
∴△EHF≌△B'CB(ASA),
∴EH=B'C2x,
在Rt△B'FC中,B'F2=B'C2+CF2,
∴(2﹣x)2=x2+(2x)2,
解得x1=x2,
∴BF=2
故答案为:.
【点评】本题主要考查了正方形的性质,全等三角形的判定与性质,勾股定理,轴对称的性质,熟练掌握正方形的性质是解题的关键.
14.(2025 清镇市)小星自制了一个小孔成像装置,其中直筒的长度为15cm,他准备了一支长为20cm的蜡烛,想要得到高度为5cm的蜡像,则蜡烛应放在距离直筒 60 cm的地方.
【考点】相似三角形的应用.
【专题】图形的相似;应用意识.
【答案】60.
【分析】先根据题意得出相似三角形,再利用三角形相似的性质得到相似比,然后根据比例性质计算.
【解答】解:由题意知:AB=20cm,OF=15cm,CD=5cm,如图,作OE⊥AB于点E,
∵AB∥CD,EF⊥AB,
∴EF⊥CD,
∴△OAB∽△ODC,
∴,
∴,
解得OE=60.
∴蜡烛应放在距离纸筒60cm的地方,
故答案为:60.
【点评】本题考查的是相似三角形的应用,熟知相似三角形的对应边成比例是解答此题的关键.
15.(2025 清江浦区一模)物理课上学过小孔成像的原理,它是一种利用光的直线传播特性实现图象投影的方法.如图,燃烧的蜡烛(竖直放置)AB经小孔O在屏幕(竖直放置)上成像A′B′,设AB=18cm,A′B′=12cm,小孔O到AB的距离为30cm,则小孔O到A′B′的距离为 20 cm.
【考点】相似三角形的应用;平行投影.
【专题】图形的相似;运算能力.
【答案】20.
【分析】过点O作OC⊥AB,垂足为C,过点O作OD⊥A′B′,垂足为D,根据题意可得:AB∥A′B′,从而可得∠OAB=∠OA′B′,∠OBA=∠OB′A′,进而可得△OAB∽△OA′B′,然后利用相似三角形的性质进行计算,即可解答.
【解答】解:过点O作OC⊥AB,垂足为C,过点O作OD⊥A′B′,垂足为D,
由题意得:AB∥A′B′,
∴∠OAB=∠OA′B′,∠OBA=∠OB′A′,
∴△OAB∽△OA′B′,
∴,
∴,
解得:OD=20,
∴小孔O到A′B′的距离为20cm,
故答案为:20.
【点评】本题考查了相似三角形的应用,平行投影,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
三.解答题(共5小题)
16.(2025 阎良区二模)雄伟壮观的马栏革命纪念碑在历史的风云中永远纪念革命先辈的抗战壮举.某数学研究性学习小组在老师的指导下,利用课余时间进行测量马栏革命纪念碑高度的活动.
活动主题 测量马栏革命纪念碑高度
测量工具 皮尺、标杆、激光笔等
活动过程 模型抽象
测绘过程与数据信息 ①在点B处竖立一根高3米的标杆AB; ②地面上的点D、标杆上的点F和碑顶M在一条直线上,BD=3米,BF=2米; ③地面上的点E、标杆顶点A和碑顶M在一条直线上,BE=4.8米; ④点N、B、D、E在同一水平直线上,点F在AB上,MN⊥NE,AB⊥NE,图中所有点均在同一平面内.
说明 在测量过程中注意自身和他人的安全.
请根据表格中提供的信息,求出马栏革命纪念碑的高度MN.
【考点】相似三角形的应用.
【专题】图形的相似;几何直观;推理能力.
【答案】18米.
【分析】由题意可得,根据相似三角形的判定和性质定理即可得结论.
【解答】解:由题意可得:∠ABE=∠MNE=90°,∠FDB=∠NDM,∠E=∠E,AB=3米,BD=3米,BF=2米,BE=4.8米,
∴△BDF∽△NDM,△ABE∽△MNE,
∴,,
∴,,
∴,BN=1.6MN﹣4.8,
∴,
∴MN=18米.
答:马栏革命纪念碑的高度MN为18米.
【点评】本题主要考查了相似三角形的应用,熟练掌握相似三角形的判定和性质定理是正确解答此题的关键.
17.(2025 天府新区)如图1,在△ABC中,AB=AC,点D是BC边上的动点(点D不与点B,C重合),点E,F分别在边AB,AC上,且满足BE=DE,DF=CF.
(1)判断四边形AEDF的形状并说明理由;
(2)如图2,连接EF,将△DEF沿EF翻折,使点D落在点G处,连接BG,CG.
①求证:△GEB∽△GFC;
②若,AB=AC=10,当△DEF是等腰三角形时,求GC的长.
【考点】相似形综合题.
【专题】几何综合题;三角形;图形的相似;几何直观;运算能力;推理能力.
【答案】(1)四边形AEDF是平行四边形,证明见解答;
(2)①证明见解答;
②10或或.
【分析】(1)由等边对等角可得∠B=∠C,∠B=∠EDB,∠C=∠FDC,继而得到∠B=∠EDB=∠C=∠FDC,再由三角形内角和定理得到∠A=∠BED=∠DFC,然后得到DE∥AF,DF∥AE,即可证明四边形AEDF是平行四边形;
(2)①由翻折可知EG=ED,FG=FD,再结合已知条件可得到,再令∠BED=α,∠DEF=β,由翻折可知∠GEF=∠DEF=β,∠GFE=∠EFD=180°﹣α﹣β,继而得到∠BEG=∠CFG,即可证明△GEB∽△GFC;
②分三种情况进行讨论:DE=DF,DE=EF,DF=EF,通过角度之间的转换得到边相等,进而求出GC的长.
【解答】(1)解:∵AB=AC,
∴∠B=∠C,
又∵BE=DE,DF=CF,
∴∠B=∠EDB,∠C=∠FDC,
∴∠B=∠EDB=∠C=∠FDC,
∵∠A=180°﹣(∠B+∠C),∠BED=180°﹣(∠B+∠EDB),∠DFC=180°﹣(∠C+∠FDC),
∴∠A=∠BED=∠DFC,
∴DE∥AF,DF∥AE,
∴四边形AEDF是平行四边形;
(2)①证明:由翻折可知EG=ED,FG=FD,
∵BE=DE,FD=FC,
∴EG=BE,FG=FC,
∴,
令∠BED=α,∠DEF=β,
∵DF∥AE,DE∥AF,
∴∠EDF=∠DFC=α,
∴∠EFD=180°﹣α﹣β,
由翻折可知∠GEF=∠DEF=β,∠GFE=∠EFD=180°﹣α﹣β,
∴∠BEG=360°﹣α﹣2β,∠GFC=α+2(180°﹣α﹣β )=360°﹣α﹣2β,
∴∠BEG=∠GFC,
又∵,
∴△GEB∽△GFC,
②解:∵△DEF是等腰三角形,
∴可以分为三种情况,分别是:DE=DF,DF=EF,DE=EF,
第一种情况:DE=DF,
当DE=DF时,△BED≌△DFC,
∴BD=CD,
∵四边形AEDF是平行四边形,
∴点E、F、D分别是AB、AC、BC的中点,此时点G与点A重合,
∴GC=AC=10;
第二种情况:DF=EF,
当DF=EF时,β=α,
∴∠GEB=360°﹣3α,
∴,
∵,
∴,
∵∠BGC=∠EGF=∠EDF=α,
∴∠BGC=∠GBC,
∴GC=BC,
过点B作BH⊥AC,交AC于点H,如图,
在Rt△ABH中,,
∴,
∴AH=6,
∴CH=4,
在Rt△BHC中,,
∴;
第三种情况:DE=EF,
∵△GEB∽△GFC,
∴∠BGE=∠CGF,
∴∠BGC=∠BGE+∠EGC=∠CGF+∠EGC=∠EGF=∠A=∠BED=α,
当DE=EF时,∠GFE=∠EFD=∠EDF=α,
∴∠GFC=3α,
∴,
∴,
∴∠BGC=∠GCB,
∴BC=BG,
过点B作BM⊥GC,交GC于点M,如图,
在Rt△BMC中,,
∴,
∴,
∴,
综上,GC的长为10或或.
【点评】本题考查了相似形的综合应用,主要考查等腰三角形的性质,平行四边形的判定,相似三角形的判定,三角函数,勾股定理等知识,用到了分类讨论的数学思想方法,熟记相关的性质和判定,会通过角度之间的转换得到边相等是解题的关键.
18.(2025 盐田区二模)定义:在 ABCD中,如果有一条对角线的长等于其中一条边的长,则称这个平行四边形为“N字平行四边形”.
(1)下面的图形中是“N字平行四边形”的有: C ;
A.正方形
B.矩形
C.有一个角是60°的菱形
D.有一个角是60°的平行四边形
E.有一个角是45°的平行四边形
(2)在“N字平行四边形”中,∠A=45°,AB>BC,则 ;
(3)如图1,在“N字平行四边形ABCD”中,∠B=75°,AB=AC=8,点F是AB边上一点,FG∥AC,FG与DC的延长线交于点G,若 AFGC为“N字平行四边形”,求AF的值;
(4)如图2,在矩形ABCD中,点E、F分别是BC边和AD边上的点,四边形BEDF为“N字平行四边形”,若AB=2AF,求的值.
【考点】相似形综合题.
【专题】几何综合题;推理能力.
【答案】(1)C;
(2);
(3);
(4)或.
【分析】(1)根据选项逐一判断即可;
(2)画出图形,证明△ABD是等腰直角三角形即可得解;
(3)由题易得∠ACG=∠ACB+∠BCG=150°,则 AFGC为“N字平行四边形”,只能分为两种情况:①当CF=AF时,∠FCA=∠FAC=30°,②当CF=AC时,∠CAF=∠AFC=30°,再分别求解即可;
(4)过点E作EM⊥BF于点M,过点F作FN⊥BE于点N,分两种情况:①当FB=FE时,②当EB=EF时,分别画出图形求解即可.
【解答】(1)解:正方形的对角线是边长的倍,故A选项不是;
矩形的对角线是直角三角形的斜边比边长大,故B选项不是;
有一个角是60°的菱形必定包含等边三角形,
会有一条对角线等于边长,故C选项是;
有一个角是60°的平行四边形和有一个角是45°的平行四边形并不必然出现对角线等于边长,故D、E选项均不是;
故选:C;
(2)解:如图,
∵ ABCD是“N字平行四边形”,
∴DA=DB,
∵∠A=45°,
∴∠ABD=45°,
∴△ABD是等腰直角三角形,
∴,
∴,
故答案为:;
(3)证明:连接AG,CF,
∵在N字 ABCD中,∠B=75°,AB=AC=8,
∴∠B=∠ACB=75°,∠BAC=30°.
∵AB∥DG,
∴∠B=∠BCG=75°,
∴∠ACG=∠ACB+∠BCG=150°,
由大角对大边可得AG>AC,AG>GC,
若 AFGC为“N字平行四边形”,只能分为以下几种情况:
①当CF=AF时,∠FCA=∠FAC=30°,
过点F作FH⊥AC于点H,可得点H为AC的中点,AF=2HF,,
又∵AC=8,
∴,
∴,;
②当CF=AC时,∠CAF=∠AFC=30°,此时,∠ACF=120°>∠ACB矛盾.
综上,若 AFGC为N字平行四边形,;
(4)过点E作EM⊥BF于点M,过点F作FN⊥BE于点N,
∵四边形ABCD为矩形,
∴AD=BC,∠A=∠C=90°,AB=DC=FN,
∵四边形BEDF为平行四边形,
∴FD=BE,FB=DE,
∴AF=AD﹣FD,CE=BC﹣BE,即AF=CE.
∵四边形BEDF为N字平行四边形,
又∵BD>BE,BD>DE,
∴有以下两种情况:
①当FB=FE时,
∵FN⊥BE,
∴N为BE的中点,
∴BN=NE.
在矩形ABNF中,AF=BN,
又∵AF=CE,
∴BN=NE=CE=AF,
∴BC=BN+NE+CE=3AF,
∵AB=2AF,
∴;
②当EB=EF时,
∵EM⊥BF,
∴M为BF的中点,,
设AF=t,则AB=2t,,,
∵EM⊥BF,
∴∠EMB=90°,
∵AD∥BC,
∴∠AFB=∠MBE,
∴Rt△BAF∽Rt△EMB,
∴AF:AB:BF=MB:ME:BE=1:2:,
由可得,
∴,
∴;
综上,或.
【点评】本题主要考查了平行四边形的性质、等腰三角形的性质、勾股定理、相似三角形的判定和性质等内容,熟练掌握相关知识是解题的关键.
19.(2025春 莱州市二模)【教材呈现】下面是华师版教材九年级上册52页的部分内容:
我们可以发现,当两条直线与一组平行线相交时,所截得的线段存在一定的比例关系:.这就是如下的基本事实: 两条直线被一组平行线所截,所得的对应线段成比例.(简称“平行线分线段成比例”)
【问题原型】如图①,在矩形ABCD中,点E为边AB的中点,过E作EF∥AD交边DC于点F,点P、Q分别在矩形的边AD、BC上,连结PQ交EF于点M.求证:PM=QM.
【结论应用】如图②,在【问题原型】的基础上,点R在边BC上(不与点Q重合),连结PR交EF于点N.
(1)若MN=4,则线段QR的长为 8 ;
(2)当点Q与点B重合,点R与点C重合时,如图③,若BC=10,且△PMN周长的最小值为12,则边AB的长为 2 .
【考点】平行线分线段成比例;三角形中位线定理;轴对称﹣最短路线问题.
【专题】矩形 菱形 正方形;平移、旋转与对称;运算能力;推理能力.
【答案】[问题原型]见解析;[结论应用](1)8;(2).
【分析】[问题原型]根据平行线分线段成比例即可得证;
[结论应用](1)根据平行线分线段成比例得出,,进而得到MN是△PQR的中位线,即可求解;
(2)根据(1)的结论得出MN是是△PQR的中位线,当P为中点时得出△PBC的周长的最小值为24,进而勾股定理即可求解.
【解答】[问题原型]证明:∵点E为边AB的中点,
∴AE=BE,
在矩形ABCD中,AD∥BC,
∵EF∥AD,
∴AD∥EF∥BC,
∴,
∴PM=QM,
[结论应用](1)解:根据题意可得AD∥EF∥BC
∴,,
∴QR=2MN=8,
故答案为:8.
(2)解:如图所示,
作点C关于AD的对称点,连接PG,BG,DG,
∴PB+PC=PB+PG≥BG,
当P在BG上时,取得最小值,
又∵PD∥BC,D是CG的中点,
∴PD是BC的中位线,
∴P是AD的中点,则PB=PG=PC,
即当P顶点是AD 中点时,三角形PBC的面积取得最小值,
∵根据(1)的结论得出MN是是△PQR的中位线,BC=10,且△PMN周长的最小值为12,
∴△PBC的周长为24,
∴,PB+PC=24﹣10=14,
∴PB=7,
∴.
故答案为:2.
【点评】本题考查了平行线分线段成比例,中位线的性质与判定,轴对称的性质求线段的最小值,熟练掌握以上知识是解题的关键.
20.(2024秋 秦皇岛三模)综合与实践
【问题情境】
数学活动课上,老师让同学们准备了一些等边三角形纸片、正方形纸片和等腰直角三角形纸片,通过折、拼的方式探索其中蕴含的数学知识.
【数学思考】
(1)希望小组选用等边三角形纸片进行折叠,并提出问题:如图①,将等边三角形ABC沿直线DE折叠,点A恰好落在边BC上的点F处,折痕分别交AB,AC于D,E两点.求证:;
(2)善思小组选用正方形纸片进行折叠,并提出问题:如图②,将正方形ABCD沿直线EF折叠,点A恰好落在边BC的中点G处,点D落在点H处,折痕分别交AB,CD于E,F两点,设GH,CD交于点I.若AB=8,求GI的长;
【拓展探究】
(3)智慧小组将两个不同的等腰直角三角形拼在一起,并提出问题:如图③,△ABC与△ADE都是等腰直角三角形,点D在边BC上,∠BAC=∠DAE=90°,DE交AC于点F.若BD=1,CD=3,请直接写出图中阴影部分的面积.
【考点】相似形综合题.
【专题】几何综合题;运算能力;推理能力.
【答案】(1)见解析;
(2)GI;
(3).
【分析】(1)根据等边三角形的性质得到∠A=∠B=∠C=60°,根据折叠的性质得到FD=AD,FE=AE,∠DFE=∠A=60°,求得∠BDF=∠CFE,根据相似三角形的性质即可得到结论;
(2)根据正方形的性质得到∠A=∠B=∠C=90°,AB=BC=8,根据折叠的性质得到GE=AE,∠EGH=∠A=90°,根据相似三角形的性质得到BG=CGBC=4,设AE=EG=x,则BE=8﹣x,根据勾股定理得到EG=5,BE=3,于是得到GI;
(3)根据等腰直角三角形的性质得到∠BAC=∠DAE=90°,AB=AC,AD=AE,∠B=∠C=∠ADE=∠E=45°,根据相似三角形的性质得到BC=BD+CD=4,设AB=AC=x,根据勾股定理得到AB=AC=2,求得CF,得到AF=AC﹣CF=2,过D作DP⊥AC于P,根据相似三角形的性质得到DP,于是得到S△ADFAF DP.
【解答】(1)证明:∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∵将等边三角形ABC沿直线DE折叠,点A恰好落在边BC上的点F处,
∴FD=AD,FE=AE,∠DFE=∠A=60°,
∵∠BDF=180°﹣∠B﹣∠BFD=120°﹣∠BFD,∠CFE=180°﹣∠DFE﹣∠BFD=120°﹣∠BFD,
∴∠BDF=∠CFE,
∵∠B=∠C=60°,
∴△BDF∽△CFE,
∴,
∵DF=AD,FE=AE,
∴;
(2)解:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=90°,AB=BC=8,
∵将正方形ABCD沿直线EF折叠,点A恰好落在边BC的中点G处,点D落在点H处,
∴GE=AE,∠EGH=∠A=90°,
∵∠BEG=90°﹣∠BGE,∠CGI=180°﹣∠EGH﹣∠BGE=90°﹣∠BGE,
∴∠BEG=∠CGI,
∵∠B=∠C=90°,
∴△BEG∽△CGI.
∴,
∵点G是BC的中点,
∴BG=CGBC=4,
设AE=EG=x,则BE=8﹣x,
在Rt△BEG中,BE2+BG2=EG2,
∴(8﹣x)2+42=x2,
∴x=5,
∴EG=5,BE=3,
∵,
∴,
∴GI;
(3)∵△ABC与△ADE是等腰直角三角形,
∴∠BAC=∠DAE=90°,AB=AC,AD=AE,∠B=∠C=∠ADE=∠E=45°,
∵∠BAD=180°﹣∠B﹣∠ADB=135°﹣∠ADB,∠CDF=180°﹣∠ADE﹣∠ADB=135°﹣∠ADB,
∴∠BAD=∠CDF,
∵∠B=∠C=45°,
∴△ABD∽△DCF,
∴,
∵BD=1,CD=3,
∴BC=BD+CD=4,
设AB=AC=x,
∵AB2+AC2=BC2,
∴x2+x2=42,
解得x1=2,x2=﹣2(舍去),
∴AB=AC=2,
∵,
∴,
∴CF,
∴AF=AC﹣CF=2,
过D作DP⊥AC于P,
∴∠DPC=90°=∠BAC,
∵∠C=∠C=45°,
∴△DPC∽△BAC,
∴,
∴,
∴DP,
∴S△ADFAF DP.
【点评】本题是相似形的综合题,考查了相似三角形的判定和性质,勾股定理等腰直角三角形的判定和性质,正方形的性质,熟练掌握相似三角形的判定和性质定理是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
