【中考押题预测】2025年中考数学核心考点考前冲刺 图形的旋转(含解析)
文档属性
| 名称 | 【中考押题预测】2025年中考数学核心考点考前冲刺 图形的旋转(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-16 14:10:55 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中考核心考点 图形的旋转
一.选择题(共10小题)
1.(2025春 江阴市二模)如图,正方形ABCD的边长为,点E在边AB上(不与A,B重合),将△ADE沿直线DE折叠,点A落在点A1处,连接A1B,将A1B绕点B顺时针旋转90°得到A2B,连接A1A,A1C,A2C.给出下列四个结论:①△ABA1≌△CBA2;②∠ADE+∠A1CB=45°;③点P是直线DE上动点,则CP+A1P的最小值为;④当∠ADE=30°时,△A1BE的面积为.其中正确的结论有几个( )
A.1个 B.2个 C.3个 D.4个
2.(2025春 市北区二模)如图,时钟的时针从上午8时转动到上午10时,时针绕表盘中心旋转的旋转角为( )
A.30° B.50° C.60° D.70°
3.(2025春 太原二模)《哪吒2》作为国漫佳作,在服饰、场景和道具等细节上,深度融入中国传统纹样,将丰富的文化内涵展现得淋漓尽致.下面纹样中文字上方的图案是中心对称图形的是( )
A. B.
C. D.
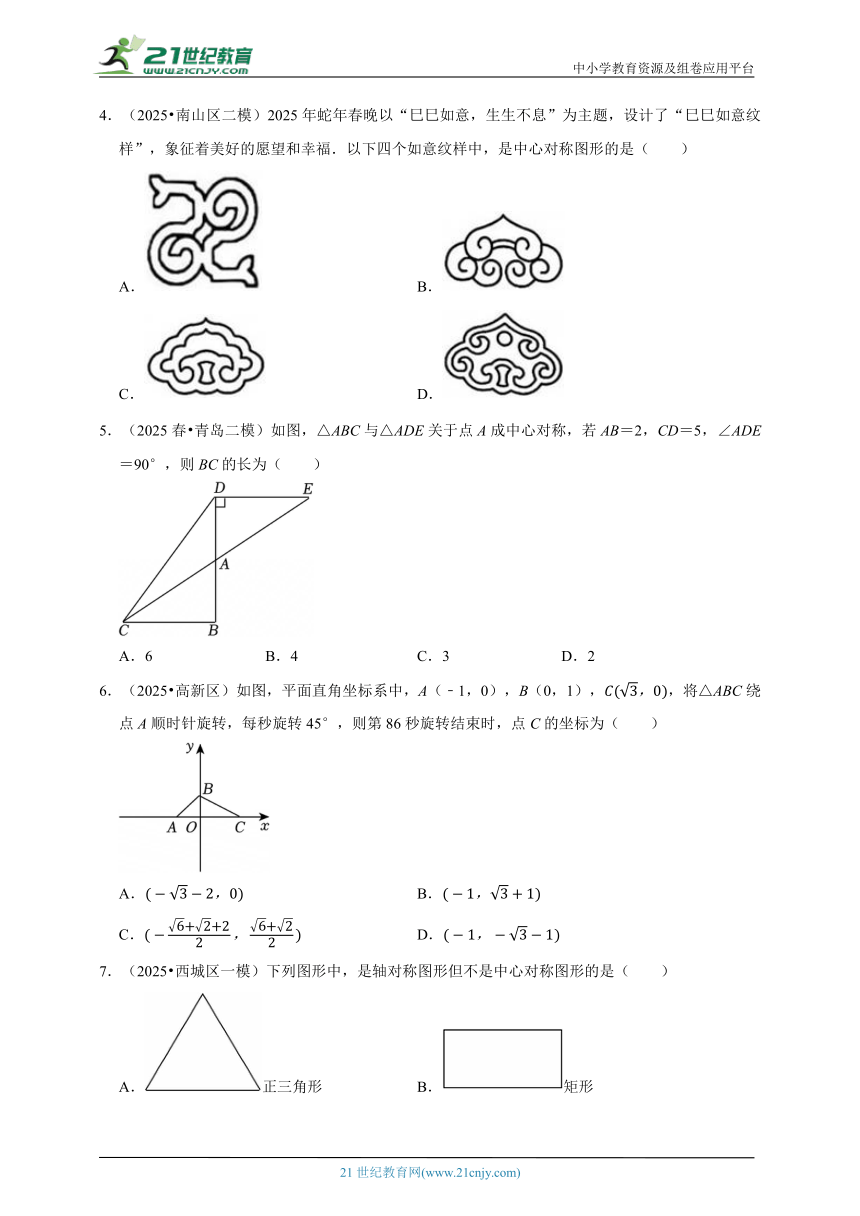
4.(2025 南山区二模)2025年蛇年春晚以“巳巳如意,生生不息”为主题,设计了“巳巳如意纹样”,象征着美好的愿望和幸福.以下四个如意纹样中,是中心对称图形的是( )
A. B.
C. D.
5.(2025春 青岛二模)如图,△ABC与△ADE关于点A成中心对称,若AB=2,CD=5,∠ADE=90°,则BC的长为( )
A.6 B.4 C.3 D.2
6.(2025 高新区)如图,平面直角坐标系中,A(﹣1,0),B(0,1),,将△ABC绕点A顺时针旋转,每秒旋转45°,则第86秒旋转结束时,点C的坐标为( )
A. B.
C. D.
7.(2025 西城区一模)下列图形中,是轴对称图形但不是中心对称图形的是( )
A.正三角形 B.矩形
C.圆 D.菱形
8.(2025 西城区一模)如图,等边△ABC的边长为1,将边AC,BA,CB分别绕点A,B,C逆时针旋转α(0°<α<180°)得到线段AC1,BA1,CB1,连接A1B1,A1C1,B1C1.对△A1B1C1给出下面三个结论:
①对任意α都有△A1B1C1是等边三角形;
②存在唯一一点到点A1,B1,C1的距离相等;
③当α=120°时,△A1B1C1的周长是.
上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
9.(2025春 南京二模)如图,在Rt△ABC中,∠C=90°.将△ABC绕点A逆时针旋转得到△AB'C'.若BC′∥AB,∠B'AC=16°,则旋转角α(0°<α<90°)的度数为( )
A.16° B.32° C.36° D.37°
10.(2025春 苏州二模)如图,△DEF是由△ABC绕着点O顺时针旋转得到的,以下说法不一定正确的是( )
A.∠COF=∠BOE B.∠BAC=∠EDF C.OC=OF D.BC=DF
二.填空题(共5小题)
11.(2025春 莲湖区三模)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,D是直角边AC上的一个动点,连接BD,以BD为边向外作等边△BDE,连接CE.在点D运动的过程中,线段CE的长的最小值为 .
12.(2025春 杨浦区三模)如图,在等腰△ABC中,底边BC的中点是D,底角的正切值是,将该等腰三角形绕其腰AC上的中点M顺时针旋转,使旋转后的点D与A重合,得到△A′B′C′,若旋转后的底边B′C′与BC交于点N,则cos∠ANB= .
13.(2025春 天山区三模)如图,点O为直线AB上一点,一副三角板如图摆放,其中∠C=∠DOC=45°,∠M=30°,∠N=60°.将直角三角板MON绕点O旋转一周,当∠AOM的度数是 时,直线MN与直线OC互相平行.
14.(2025 綦江区一模)如图,在平面直角坐标系中,A(6,0),B(0,8),连接AB,将线段AB绕点A顺时针旋转90°得到线段AC,连接OC,则线段OC的长度为 .
15.(2025 高新区)平面内,对于图形M与点P,给出如下定义:图形M绕点P逆时针旋转90°得到图形N,若图形N与图形M有重叠,则称图形M关于点P“逆垂相关”.如图,在平面直角坐标系xOy中,线段AB的端点分别是A(0,3),B(1,0).若以C(3,0)为圆心,r为半径的⊙C上存在点P,使线段AB关于点P“逆垂相关”,则r的取值范围是 .
三.解答题(共5小题)
16.(2025春 西城区三模)在平面直角坐标系xOy中,图形G和图形W的“中位形”的定义如下:点P是图形G上任意一点,点Q是图形W上任意一点,取PO中点M,取QO中点N,由所有线段MN所组成的图形叫做图形G和图形W的“中位形”.(当两个点重合时,连接这两点的线段和线段的中点都视为此点)
已知点A(4,0)、点B(0,2).
(1)点A和点B的“中位形”的长度是 ;
(2)已知点H(a,0),若点H和线段AB的“中位形”面积为2,求a的值.
(3)已知点E(10,0)、点F(0,﹣10),以线段AB为边作两条对角线都在坐标轴上的菱形ABCD.将菱形ABCD沿着直线y=x平移得到菱形A′B′C′D′,设菱形A′B′C′D′的对角线交点坐标为(t,t).若线段EF和菱形A′B′C′D′的“中位形”与菱形ABCD有公共点,直接写出t的取值范围.
17.(2025 沙坪坝区)在Rt△ABC中,∠BAC=90°,AB=AC,点D是平面内一点,连接AD,将点A绕点D顺时针旋转90°得点E,连接AE,DE.
(1)如图1,点D在△ABC的内部,连接CD,点E恰好在CD上.若AE=CE,求∠DAB的度数;
(2)如图2,点D在点A的右上方,连接BE,CE,点D恰好在CE上,延长DA交BE于点F,点G是AC的中点,连接FG,求证:;
(3)如图3,连接EC,∠AEC=90°,将线段AD沿AC所在直线翻折至△ABC所在平面内得到线段AM,点M为点D的对应点,连接BM,当BM取得最大值时,请直接写出此时的值.
18.(2025 历下区二模)在△ABC中,∠A=90°,AB=AC,点D在边AC上(点D不与点A,点C重合),连接BD并将BD绕点D逆时针旋转90°得到DE.
(1)如图1,连接CE.
①CE与BC的位置关系为 ,∠ABD与∠CED的数量关系是 ;
②请用等式表示BC,CD和CE的数量关系,并说明理由;
(2)如图2,将△ABD沿BD翻折,得到△A′BD,连接A′E,若A′E的最小值为2,求AB的长.
19.(2025春 重庆二模)在平面直角坐标系中,点O为原点,点B(0,﹣4)是y轴负半轴上一点,将点B向右平移6个单位得到点A.
(1)点A的坐标为 ;
(2)如图2,动点F从点A出发,以每秒2个单位长度的速度沿AB方向运动,当点F运动到点B时,停止运动.设点F运动时间为t秒,用含t的式子表示F点的坐标;当t为何值时,△OBF的面积为6?求出此时点F的坐标;
(3)过点F作直线EF交x轴正半轴于E,交线段OA于D,若∠EOD,∠AFD的平分线相交于点N,∠ODF=α,请用含α的式子表示∠ONF的大小,并说明理由.
20.(2025春 沙坪坝区三模)综合与实践.
问题情境:
如图,在△ABC中,∠ACB=90°,AC=BC,点D在△ABC所在的平面内运动.探究图形间存在的关系.
特例探究:
(1)如图1,当点D在边AB上运动,连接CD,以CD为边在其右侧作等腰直角三角形CDE,连接BE,发现BE⊥AB,请说明理由;
求异探究:
(2)如图2,点E为AC的中点,点F为AB的中点,△AEF为等腰直角三角形,点D在△ABC外部时,连接ED,以ED为边在其右侧作等腰直角三角形EDH,连接DF和CH,判断DF与CH的关系,并证明;
拓展应用:
(3)如图3,当点D在直线AC上时,连接BD,在线段BD绕点B逆时针旋转90°得到线段BE,连接AE.若CD=6,AE=10,求△ABD的面积.
中考核心考点 图形的旋转
参考答案与试题解析
一.选择题(共10小题)
1.(2025春 江阴市二模)如图,正方形ABCD的边长为,点E在边AB上(不与A,B重合),将△ADE沿直线DE折叠,点A落在点A1处,连接A1B,将A1B绕点B顺时针旋转90°得到A2B,连接A1A,A1C,A2C.给出下列四个结论:①△ABA1≌△CBA2;②∠ADE+∠A1CB=45°;③点P是直线DE上动点,则CP+A1P的最小值为;④当∠ADE=30°时,△A1BE的面积为.其中正确的结论有几个( )
A.1个 B.2个 C.3个 D.4个
【考点】旋转的性质;三角形的面积;全等三角形的判定;正方形的性质;轴对称﹣最短路线问题;翻折变换(折叠问题).
【专题】平移、旋转与对称;推理能力.
【答案】B
【分析】根据SAS证明三角形全等即可①正确;过点D作DT⊥CA1于点T,证明∠ADE+∠CDT=45°,∠CDT=∠BCA1即可判断②正确;连接PA,AC.因为A,A1关于DE对称,推出PA=PA1,推出,可得结论③错误;过点A1作A1H⊥AB于点H,求出EB,A1H,可得结论④错误.
【解答】解:∵四边形ABCD是正方形,
∴BA=BC,∠ABC=90°,
∵∠A1BA2=∠ABC=90°,
∴∠ABA1=∠CBA2,
∵BA1=BA2,
∴△ABA1 △CBA2(SAS),故①正确;
过点D作DT⊥CA1于点T,
∵CD=DA1,
∴∠CDT=∠A1DT,
∵∠ADE=∠A1DE,∠ADC=90°,
∴∠ADE+∠CDT=45°,
∵∠CDT+∠DCT=90°,∠DCT+∠BCA1=90°,
∴∠CDT=∠BCA1,
∴∠ADE+∠BCA1=45°,故②正确;
连接PA,AC,
∵A,A1关于DE对称,
∴PA=PA1,
∴,
∴PA1+PC的最小值为,故③错误;
过点A1作A1H⊥AB于点H,
∵∠ADE=30°,
∴,
∴,
∵∠A1EB=60°,
∴,
∴,故④错误;
故选:B.
【点评】本题是四边形综合题,考查正方形的性质,解直角三角形,翻折变换,全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题.
2.(2025春 市北区二模)如图,时钟的时针从上午8时转动到上午10时,时针绕表盘中心旋转的旋转角为( )
A.30° B.50° C.60° D.70°
【考点】生活中的旋转现象.
【专题】平移、旋转与对称;应用意识.
【答案】C
【分析】将圆心角360°分为12份求出2份即可得到答案.
【解答】解:将圆心角360°分为12份求出2份的度数为:360°÷12×2=60°,
故选:C.
【点评】本题考查钟面圆心角的求法,解题的关键是知道钟面刻度将圆心角分为了12份.
3.(2025春 太原二模)《哪吒2》作为国漫佳作,在服饰、场景和道具等细节上,深度融入中国传统纹样,将丰富的文化内涵展现得淋漓尽致.下面纹样中文字上方的图案是中心对称图形的是( )
A. B.
C. D.
【考点】中心对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】D
【分析】根据中心对称图形的概念对各选项分析判断即可得解.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.
【解答】解:选项A、B、C中的图案都不能找到一个点,使图形绕某一点旋转180°后与原来的图形重合,所以不是中心对称图形.
选项D中的图案能找到一个点,使图形绕某一点旋转180°后与原来的图形重合,所以是中心对称图形.
故选:D.
【点评】本题考查了中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180度后与原图重合.
4.(2025 南山区二模)2025年蛇年春晚以“巳巳如意,生生不息”为主题,设计了“巳巳如意纹样”,象征着美好的愿望和幸福.以下四个如意纹样中,是中心对称图形的是( )
A. B.
C. D.
【考点】中心对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】A
【分析】根据中心对称图形的概念判断.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.
【解答】解:选项B、C、D中的图形都不能找到一个点,使图形绕某一点旋转180°后与原来的图形重合,所以不是中心对称图形.
选项A中的图形能找到一个点,使图形绕某一点旋转180°后与原来的图形重合,所以是中心对称图形.
故选:A.
【点评】本题考查的是中心对称图形,中心对称图形是要寻找对称中心,旋转180度后与自身重合.
5.(2025春 青岛二模)如图,△ABC与△ADE关于点A成中心对称,若AB=2,CD=5,∠ADE=90°,则BC的长为( )
A.6 B.4 C.3 D.2
【考点】中心对称.
【专题】平移、旋转与对称;解直角三角形及其应用;运算能力.
【答案】C
【分析】根据中心对称的性质可得AD=AB=2,∠BCD=∠ADE=90°,据此可得BD=4,再根据勾股定理计算即可.
【解答】解:∵△ABC与△ADE关于点A成中心对称,
∴AD=AB=2,∠BCD=∠ADE=90°,
∴BD=AD+AB=4,
∴BC3.
故选:C.
【点评】本题考查了中心对称以及勾股定理,掌握中心对称的性质是解答本题的关键.
6.(2025 高新区)如图,平面直角坐标系中,A(﹣1,0),B(0,1),,将△ABC绕点A顺时针旋转,每秒旋转45°,则第86秒旋转结束时,点C的坐标为( )
A. B.
C. D.
【考点】坐标与图形变化﹣旋转.
【专题】规律型;平移、旋转与对称;几何直观.
【答案】B
【分析】由题意得,每旋转8秒△ABC回到原来位置,则第86秒旋转结束时△ABC的位置与第6秒旋转结束时△ABC的位置相同,结合旋转的性质可得答案.
【解答】解:∵△ABC绕点A顺时针旋转,每秒旋转45°,
∴每旋转8秒△ABC回到原来位置.
∵86=8×10+6,
∴第86秒旋转结束时△ABC的位置与第6秒旋转结束时△ABC的位置相同.
如图,第6秒旋转结束时△ABC旋转到△AB6C6的位置,
∵6×45°=270°,
∴AC6⊥x轴.
∵A(﹣1,0),,
∴AC.
由旋转得,AC6=AC,
∴C6(﹣1,),
∴第86秒旋转结束时,点C的坐标为(﹣1,).
故选:B.
【点评】本题考查坐标与图形变化﹣旋转,熟练掌握旋转的性质是解答本题的关键.
7.(2025 西城区一模)下列图形中,是轴对称图形但不是中心对称图形的是( )
A.正三角形 B.矩形
C.圆 D.菱形
【考点】中心对称图形;轴对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】A
【分析】根据轴对称图形和中心对称图形的概念,对各选项分析判断即可得解.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
【解答】解:A.是轴对称图形,但不是中心对称图形,故符合题意;
B.既是轴对称图形,又是中心对称图形,故不符合题意;
C.既是轴对称图形,又是中心对称图形,故不符合题意;
D.既是轴对称图形,又是中心对称图形,故不符合题意;
故选:A.
【点评】本题主要查了轴对称图形和中心对称图形.熟练掌握两者定义是关键.
8.(2025 西城区一模)如图,等边△ABC的边长为1,将边AC,BA,CB分别绕点A,B,C逆时针旋转α(0°<α<180°)得到线段AC1,BA1,CB1,连接A1B1,A1C1,B1C1.对△A1B1C1给出下面三个结论:
①对任意α都有△A1B1C1是等边三角形;
②存在唯一一点到点A1,B1,C1的距离相等;
③当α=120°时,△A1B1C1的周长是.
上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
【考点】旋转的性质;等边三角形的判定与性质.
【专题】平移、旋转与对称;推理能力.
【答案】D
【分析】先证△BAA1≌△CBB1(SAS),再证△AA1C1≌△BB1A1≌△CC1B1,据此一一判断选项即可.
【解答】解:连接AA1、BB1、CC1,
∵△ABC是等边三角形,
∴AB=AC,
∴BA1=AC1,
在△BAA1和△CBB1中,
,
∴△BAA1≌△CBB1(SAS),
∴AA1=BB1,∠BAA1=∠BCB1,
同理可得AA1=BB1=CC1,∠BAA1=∠BCB1=∠CAC1,
∴∠A1AC1=∠B1BA1,
在△AA1C1和△BB1A1中,
,
∴△AA1C1≌△BB1A1(SAS),
同理可证△AA1C1≌△BB1A1≌△CC1B1,
∴A1B1=A1C1=B1C1,
故△A1B1C1是等边三角形,故①对;
∵△A1B1C1是等边三角形,
∴△ABC外心O也为△A1B1C1外心,
∴存在一点到点A,C1的距离相等,故②对;
当α=120°时,则A1、B、C共线,
∴A1B=1,BC1=2,
如图,过C1作C1G⊥A1B于点G,
则∠C1BG=60°,
∴BG=BC1 cos60°=1,C1G=BC1 sin60°,
∴A1G=2,
∴A1C1,
∴,故③对,
故选:D.
【点评】本题主要考查了旋转的性质、全等三角形的判定和性质、解直角三角形、勾股定理等内容,熟练掌握相关知识是解题的关键.
9.(2025春 南京二模)如图,在Rt△ABC中,∠C=90°.将△ABC绕点A逆时针旋转得到△AB'C'.若BC′∥AB,∠B'AC=16°,则旋转角α(0°<α<90°)的度数为( )
A.16° B.32° C.36° D.37°
【考点】旋转的性质;平行线的性质;直角三角形的性质.
【专题】线段、角、相交线与平行线;等腰三角形与直角三角形;平移、旋转与对称;几何直观;推理能力.
【答案】D
【分析】由旋转的性质得到∠BAB′=∠CAC′,由BC′∥AB得到∠BAB′=∠CAC′(90°﹣16°)=37°,据此解答即可.
【解答】解答解:将△ABC绕点A逆时针旋转得到△AB'C',
∴∠BAB′=∠CAC′,
∵BC′∥AB,∠C=90°,
∴∠BAC=90°,
∵∠B'AC=16°,
∴∠BAB′=∠CAC′(90°﹣16°)=37°,
∴旋转角α(0°<α<90°)的度数为37°,
故选:D.
【点评】本题主要考查了旋转的性质,平行线的性质,直角三角形的性质,解答本题的关键是熟练掌握旋转的性质.
10.(2025春 苏州二模)如图,△DEF是由△ABC绕着点O顺时针旋转得到的,以下说法不一定正确的是( )
A.∠COF=∠BOE B.∠BAC=∠EDF C.OC=OF D.BC=DF
【考点】旋转的性质.
【专题】平移、旋转与对称;数感;推理能力.
【答案】D
【分析】根据旋转的性质逐一判断即可.
【解答】解:∵△DEF是由△ABC绕着点O旋转得到的,
由旋转的性质得:∠COF=∠BOE,∠BAC=∠EDF,OC=OF,BC=EF,
故A,B,C选项正确,不符合题意;
由已知条件无法得到BC=DF,
故D选项错误,符合题意,
故选:D.
【点评】本题考查了旋转的性质,熟记旋转前后对应边、对应角相等是解题的关键.
二.填空题(共5小题)
11.(2025春 莲湖区三模)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,D是直角边AC上的一个动点,连接BD,以BD为边向外作等边△BDE,连接CE.在点D运动的过程中,线段CE的长的最小值为 1 .
【考点】旋转的性质;垂线段最短;三角形三边关系;全等三角形的判定与性质;等边三角形的性质;含30度角的直角三角形.
【专题】图形的全等;等腰三角形与直角三角形;平移、旋转与对称;几何直观;推理能力.
【答案】1.
【分析】延长BC到点F,使得CF=BC,连接AF,EF,由∠C=90°,∠BAC=30°,AB=4,可得:,∠ABF=60°,证明△ABF是等边三角形,得到∠AFB=60°,结合△BDE是等边三角形,可证明△FBE≌△ABD,得到∠BFE=∠BAD=30°,推出∠AFE=90°,得到点E在经过点F且与AF垂直的射线FE上运动,作CH⊥FE交射线FE于点H,则∠CHE=90°,得到,由CE≥CH可得CE≥1,即可求解.
【解答】解:在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,如图,延长BC到点F,使得CF=BC,连接AF,EF,
∴,∠ABF=90°﹣∠BAC=60°,
∴BF=2BC=4,
∴AB=BF,
∴△ABF是等边三角形,
∴∠AFB=60°,
∵△BDE是等边三角形,
∴BE=BD,∠DBE=60°,
∴∠FBE=∠ABD=60°﹣∠DBF,
在△FBE和△ABD中,
,
∴△FBE≌△ABD(SAS),
∴∠BFE=∠BAD=30°,
∴∠AFE=∠AFB+∠BFE=90°,
∴点E在经过点F且与AF垂直的射线FE上运动,作CH⊥FE交射线FE于点H,则∠CHE=90°,
∴,
∵CE≥CH,
∴CE≥1,
∴CE的最小值为1,
故答案为:1.
【点评】本题考查了旋转的性质,垂线段最短,三角形三边关系,全等三角形的判定与性质,等边三角形的性质,含30度角的直角三角形,解题的关键是掌握相关知识,并正确作出辅助线.
12.(2025春 杨浦区三模)如图,在等腰△ABC中,底边BC的中点是D,底角的正切值是,将该等腰三角形绕其腰AC上的中点M顺时针旋转,使旋转后的点D与A重合,得到△A′B′C′,若旋转后的底边B′C′与BC交于点N,则cos∠ANB= .
【考点】旋转的性质;解直角三角形;等腰三角形的性质.
【专题】统计与概率;平移、旋转与对称;几何直观;推理能力.
【答案】.
【分析】根据题意连接AD,A′A,再得到∠B=∠C,再利用旋转性质可得∠ANB=∠MAN+∠C=2∠C,再利用正切值可设A′A=2x,C′D=6x,再取A′A中点E,连接ME,过点A′作A′F⊥AM于F,继而得到本题答案.
【解答】解:在等腰△ABC中,底边BC的中点是D,底角的正切值是,如图,连接AD,A′A,
,
∴∠B=∠C,
将该等腰三角形绕其腰AC上的中点M顺时针旋转,使旋转后的点D与A重合,得到△A′B′C′,
∴,∠C=∠C′,
∴∠MAC′=∠C=∠C′,
∴∠ANB=∠MAN+∠C=2∠C,
∵,
∴,
设A′A=2x,C′A=6x,
∴,,
∴,
取A′A中点E,连接ME,过点A′作A′F⊥AM于F,
则,
∵,
∴,
∴,
∴,
故答案为:.
【点评】本题考查旋转的性质,等腰三角形的性质,解直角三角形,解答本题的关键是熟练掌握旋转的性质.
13.(2025春 天山区三模)如图,点O为直线AB上一点,一副三角板如图摆放,其中∠C=∠DOC=45°,∠M=30°,∠N=60°.将直角三角板MON绕点O旋转一周,当∠AOM的度数是 75°或105° 时,直线MN与直线OC互相平行.
【考点】旋转的性质;平行线的判定;平行线的性质.
【专题】线段、角、相交线与平行线;平移、旋转与对称;推理能力.
【答案】75°或105°.
【分析】根据MN在OC左边或右边分别画出图形,利用平行线的性质得到∠COM的度数,再求出∠AOM的度数即可.
【解答】解:当MN在OC右边时,如图,
∵MN∥OC,
∴∠M=∠COM=30°,
∵∠DOC=∠C=45°,
∴∠AOM=∠COM+∠DOC=75°;
当MN在OC左边时,如图,
∵MN∥OC,
∴∠M+∠COM=180°,
∵∠M=30°,
∴∠COM=150°,
∵∠DOC=∠C=45°,
∴∠AOM=∠COM﹣∠DOC=105°;
综上所述,当∠AOM的度数是75°或105°时,直线MN与直线OC互相平行,
故答案为:75°或105°.
【点评】本题考查平行线的性质和判定,旋转的性质,熟练掌握旋转的性质是解题的关键.
14.(2025 綦江区一模)如图,在平面直角坐标系中,A(6,0),B(0,8),连接AB,将线段AB绕点A顺时针旋转90°得到线段AC,连接OC,则线段OC的长度为 .
【考点】坐标与图形变化﹣旋转;全等三角形的判定与性质;勾股定理.
【专题】等腰三角形与直角三角形;平移、旋转与对称;几何直观;推理能力.
【答案】.
【分析】过点C作x轴的垂线,证得△AOB≌△CMA(AAS),推导出AO=CM,BO=AM,得到OM=14,CM=6.在Rt△COM中,利用勾股定理求得OC即可.
【解答】解:将线段AB绕点A顺时针旋转90°得到线段AC,如图,过点C作x轴的垂线,垂足为M,
∴∠BAC=90°,∠BOA=∠CMA=90°,AB=AC,
∴∠BAO+∠CAM=90°,∠BAO+∠OBA=90°,
∴∠CAM=∠OBA,
在△AOB和△CMA中,
,
∴△AOB≌△CMA(AAS),
∴AO=CM,BO=AM,
又∵A(6,0),B(0,8),
∴CM=AO=6,AM=BO=8,
∴OM=14,CM=6.
在Rt△COM中,由勾股定理得:.
故答案为:.
【点评】本题考查坐标与图形变化﹣旋转,勾股定理,全等三角形的判定与性质,通过全等三角形求出OM=14,CM=6是解题的关键.
15.(2025 高新区)平面内,对于图形M与点P,给出如下定义:图形M绕点P逆时针旋转90°得到图形N,若图形N与图形M有重叠,则称图形M关于点P“逆垂相关”.如图,在平面直角坐标系xOy中,线段AB的端点分别是A(0,3),B(1,0).若以C(3,0)为圆心,r为半径的⊙C上存在点P,使线段AB关于点P“逆垂相关”,则r的取值范围是 r≤3 .
【考点】旋转的性质.
【专题】新定义;推理能力.
【答案】r≤3.
【分析】以AB为边分别往两侧作正方形,由题意可得点P在正方形AP3BP4内,据此求出半径最大值和最小值即可.
【解答】解:如图,
由题可设线段AB关于点P“逆垂相关”为线段A'B',
则线段AB与A'B'要有交点,
旋转后必有AB⊥A'B',
①当点P在P1处,即在点A时,B在B1处;
②当点P在P2处,即在点B时,A在A1处;
③当点P在P3处,A在B处,B在B3处;
④当点P在P4处,A在A4处,B在A处;
要让AB与A'B'有交点,则P在正方形AP3BP4内,
由题可得A(0,3),B3(4,1),C(3,0),
∴P3(2,2),P4(﹣1,1),
∴r1=AC=3,r2=CP4,
∵,
∴rmax=3;
很明显,当CP5⊥BP3时,r最小,
在Rt△CBP5中,BC=2,
∴CP5,即rmin;
∴r≤3;
故答案为:r≤3.
【点评】本题主要考查了以圆和旋转为背景的新定义,正确理解题意是解题的关键.
三.解答题(共5小题)
16.(2025春 西城区三模)在平面直角坐标系xOy中,图形G和图形W的“中位形”的定义如下:点P是图形G上任意一点,点Q是图形W上任意一点,取PO中点M,取QO中点N,由所有线段MN所组成的图形叫做图形G和图形W的“中位形”.(当两个点重合时,连接这两点的线段和线段的中点都视为此点)
已知点A(4,0)、点B(0,2).
(1)点A和点B的“中位形”的长度是 ;
(2)已知点H(a,0),若点H和线段AB的“中位形”面积为2,求a的值.
(3)已知点E(10,0)、点F(0,﹣10),以线段AB为边作两条对角线都在坐标轴上的菱形ABCD.将菱形ABCD沿着直线y=x平移得到菱形A′B′C′D′,设菱形A′B′C′D′的对角线交点坐标为(t,t).若线段EF和菱形A′B′C′D′的“中位形”与菱形ABCD有公共点,直接写出t的取值范围.
【考点】几何变换综合题.
【专题】新定义;一次函数及其应用;矩形 菱形 正方形;运算能力;推理能力.
【答案】(1);
(2)a=﹣4或12;
(3)﹣10≤t≤60.
【分析】(1)求△OAB的OA和OB的中点形成中位线的长即可;
(2)线段AB的“中位形”的线段的端点为M(2,0),N(0,1),点H的“中位形”H′(),根据S△MNH′得出a的值;
(3)可表示出菱形A′B′C′D′的“中位”图形菱形A″B″C″D″的点C″(),B″(),EF的“中位”图形E′F′,其中E′(5,0),F(0,﹣5),可求出直线AF′的解析式为:y,直线DE′的解析式为:y,求得当AF过点C″和DE′过B″时t的结果,进而得出结果.
【解答】解:(1)∵∠AOB=90°,OA=4,OB=2,
∴AB=2,
∵M是OA的中点,N是OB的中点,
∴MN,
故答案为:;
(2)如图1,
∵MN是线段AB的“中位形”,
∴M(2,0),N(0,1),
∵点H的“中位形”H′(),
∴MH′=||,
由S△MNH′得,
,
∴a=﹣4或12;
(3)如图2,
∵菱形A′B′C′D′的对角线交点坐标为(t,t),
∴菱形A′B′C′D′的“中位”图形菱形A″B″C″D″的点C″(),B″(),
EF的“中位”图形E′F′,其中E′(5,0),F(0,﹣5)
∵A(4,0),D(0,﹣2),
∴直线AF′的解析式为:y,直线DE的解析式为:y,
当AF′过点C″时,
,
∴t=60,
当DE′过点B″时,
,
∴t=﹣10,
∴﹣10≤t≤60.
【点评】本题在新定义的基础上,考查了三角形中位线的性质,求一次函数的解析式,菱形的性质等知识,解决问题的关键是数形结合.
17.(2025 沙坪坝区)在Rt△ABC中,∠BAC=90°,AB=AC,点D是平面内一点,连接AD,将点A绕点D顺时针旋转90°得点E,连接AE,DE.
(1)如图1,点D在△ABC的内部,连接CD,点E恰好在CD上.若AE=CE,求∠DAB的度数;
(2)如图2,点D在点A的右上方,连接BE,CE,点D恰好在CE上,延长DA交BE于点F,点G是AC的中点,连接FG,求证:;
(3)如图3,连接EC,∠AEC=90°,将线段AD沿AC所在直线翻折至△ABC所在平面内得到线段AM,点M为点D的对应点,连接BM,当BM取得最大值时,请直接写出此时的值.
【考点】几何变换综合题.
【专题】三角形;推理能力.
【答案】(1)22.5°.
(2)证明见解答.
(3).
【分析】(1)首先判定△ABC和△ADE是等腰直角三角形,然后根据外角的性质求出∠ECA=22.5°,再从∠BAC中由角的和差关系求出∠DAB的大小.
(2)通过辅助线构造△ACD∽△BCH,接着推出BH=AE,进而证明△BFH≌△EFA,从而得到AF=FH,则FG是△AHG的中位线,再结合CHCD即可证明结论.
(3)先由定弦定角模型求出点E的运动轨迹,然后根据瓜豆模型中主从动点的运动轨迹关系判定出点D的运动轨迹,从而由轴对称的性质得出点M的运动轨迹,再由等腰直角三角形的性质及中位线的性质在Rt△BQI中求出BM关于AB的表达式,最终求出答案.
【解答】解:(1)根据题意可知△ABC和△ADE是等腰直角三角形.
∴∠DAE=∠DEA=45°.
∵AE=CE,
∴∠ECA=∠EAC22.5°,
∵∠DAB=∠BAC﹣∠DAE﹣∠EAC=90°﹣45°﹣22.5°=22.5°.
(2)证明:延长DF至点H,使DH=CD,连接BH,CH,则△DCH是等腰直角三角形.
∴∠DCH=∠DHC=∠ACB=45°,
∴∠ACD=∠BCH=45°﹣∠ACH.
又∵.
∴△ACD∽△BCH.
∴BHAD=AE,∠BHC=∠ADC=90°,
∵∠EAH=180°﹣∠EAD=135°,∠AHB=∠BHC+∠DHC=135°,
∴∠EAH=∠AHB,
又∵∠AFE=∠HFB,
∴△BFH≌△EFA(AAS),
∴AF=FH,
∵AG=GC,
∴FGCHCD.
∴CDFG.
(3)如图,点F、G分别为AC、AB的中点,过点F作BC的垂线交BA延长线于点H,交BC于点I.
易得△BHI为等腰直角三角形.
∵FG为△ABC的中位线,
∴FG∥BC,FGBCAB.
根据题意,∠AEC=90°,由定弦定角辅助圆模型可知主动点E的运动轨迹是以AC为直径的⊙F上,因此从动点D的运动轨迹在以GF为直径的⊙P上.
而根据轴对称的性质,点D关于AC的对称点M的运动轨迹在以FH为直径的⊙Q上,
∴FG=FH,AG=AH.
∴AQ为△GFH的中位线.
∴AQ∥FG,
由平行线分线段成比例可得F、Q两点分别是线段HI的三等分点,则QI=FH=FG.
在Rt△BQI中,BI=HIFHAB,QI=FGAB,则BQAB.
∴BM=BQ+MQABAB.
∴.
【点评】本题考查了等腰直角三角形的性质,相似三角形和全等三角形的判定和性质,轴对称的性质,勾股定理,定弦定角辅助圆模型,瓜豆模型等知识点.构造全等三角形证明相关线段和角相等,以及熟练掌握瓜豆模型是解答本题的关键.
18.(2025 历下区二模)在△ABC中,∠A=90°,AB=AC,点D在边AC上(点D不与点A,点C重合),连接BD并将BD绕点D逆时针旋转90°得到DE.
(1)如图1,连接CE.
①CE与BC的位置关系为 CE⊥BC ,∠ABD与∠CED的数量关系是 ∠ABD+∠CED=45° ;
②请用等式表示BC,CD和CE的数量关系,并说明理由;
(2)如图2,将△ABD沿BD翻折,得到△A′BD,连接A′E,若A′E的最小值为2,求AB的长.
【考点】几何变换综合题.
【专题】几何变换;几何直观;推理能力;模型思想.
【答案】(1)①CE⊥BC,∠ABD+∠CED=45°;
②BC=CE,理由见解析;
(2).
【分析】(1)①由题意可得△BAC与△BDE为等腰直角三角形,再证明△ABD∽△CBE,利用相似三角形的性质导角可得CE⊥BC,∠ABD+∠CED=45°;
②在BC上取点F,使BF=CE,连接DF,如图2所示,证明△BDF≌△EDC(SAS),可得DC=DF,又∠DCF=45°,可得△DFC为等腰直角三角形,CF,从而BC=BF+CF=CE;
(2)如图2所示,连接BE,将△BA'E沿BE翻折至△BFE,则BA'=BF=BA,A'E=FE,由翻折可知∠ABD=∠A'BD,∠A'BE=∠FBE,导角可知∠ABF=2(∠A'BD+∠A'BE)=90°,故四边形ABFC为正方形,
由(1)知∠BCE=90°,故E在过点C的BC的垂线上运动.当A′E的最小值为2时,即FE最小为2,即当FE⊥CE时,FE最小为2,此时EF2,故BC=4,从而AB.
【解答】解:(1)①如图1所示,连接BE,
由题意可得△BAC与△BDE为等腰直角三角形,
∴∠ABC=∠DBE=45°,从而∠ABD=∠CBE,
,
∴,
∴△ABD∽△CBE,
∴∠BCE=∠BAD=90°,
∵∠BDE=∠BCE=90°,
∴∠DBC=∠CED,
∵∠ABD+∠DBC=45°,
∴∠ABD+∠CED=45°.
故答案为:CE⊥BC,∠ABD+∠CED=45°.
②证明:BC=CE,理由如下:
在BC上取点F,使BF=CE,连接DF,如图2所示,
在△BDF和△EDC中,
,
∴△BDF≌△EDC(SAS),
∴DC=DF,
∵∠DCF=45°,
∴△DFC为等腰直角三角形,CF,
∴BC=BF+CF=CE,
(2)法一(翻折构造法):如图2所示,连接BE,将△BA'E沿BE翻折至△BFE,
则BA'=BF=BA,A'E=FE,
由翻折可知∠ABD=∠A'BD,∠A'BE=∠FBE,
又∵∠DBE=45°=∠A'BD+∠A'BE,
∴∠ABF=2(∠A'BD+∠A'BE)=90°,
故四边形ABFC为正方形,
又由(1)知∠BCE=90°,
故E在过点C的BC的垂线上运动.
当A′E的最小值为2时,即FE最小为2,
即当FE⊥CE时,FE最小为2,
此时EF2,故BC=4,
从而AB.
法二(构造相似):如图3所示,
取BC中点M,连接MD、AM、连接BE,
由题意可知△ABM和△BDE为等腰直角三角形,ABBA',
BE.
由折叠可知∠ABD=∠A'BD=∠DBM+∠MBA',
由(1)可知∠ABD=∠CBE=∠MBA'+∠A'BE,
∴∠DBM+∠MBA'=∠MBA'+∠A'BE,
∴∠DBM=∠A'BE,
又∵,
∴△BMD∽△BA'E.
∴A'EMD,
当A'E最小为2时,MD最小为,
此时MD⊥AC,D为AC中点,
由中位线定理可知AB=2DM.
法三(构造一线三垂直):
过E点作EG⊥DA'的延长线于点G,如图4所示,
易证△BDA'≌△DEG(AAS),
则设GE=DA'=a,BA'=AB=DG=b,
则A'G=DG﹣DA'=b﹣a,
则由勾股定理得A'E2=A'G2+GE2=(b﹣a)2+a2=b2﹣2ab+2a2,
把a看成未知数,b看成常数,
故A'E2=2a2﹣2ab+b2=2(a)2,
当a时,A'E2取得最小值为,
A'E最小为2,
即4,故b,
故AB.
法四(旋转﹣两动化一动):
将△DA'E绕点D顺时针旋转90°得△DHB,如图5所示,
故DH=DA',BH=A'E,
则易知△DHA'为等腰直角三角形,
∴∠DA'H=45°,∠HA'B=45°,
∵B点为定点,BA'为定长,H点在与BA'成45°角的射线上运动,
故当BH⊥A'H时,BH最小,最小为2,
此时△BHA'为等腰直角三角形,
从而知BA',
故AB.
法五(对称法结合瓜豆原理):
作点E关于BD的对称点E',连接BE',可得△BE'D为等腰直角三角形,
以AB为腰向左构造等腰直角三角形ABC',连接C'E',如图6所示,
∴BC',BE',即.
∵∠C'BA=∠E'BD=45°,
∴∠C'BE'=∠ABD,
∴△C'BE'∽△ABD,
∴∠BC'E'=∠BAD=90°=∠C'BC,
故C'E'∥BC,即E'直线C'E'上运动.
由对称性可知△DAE'≌△DA'E,
∴AE'=A'E,
当A'E最小为2时,AE'最小也为2,
故当AE'⊥C'E'时最小为2,
此时△C'E'A为等腰直角三角形,
AC',
由于△ABC'也为等腰直角三角形,
故AB=AC'.
【点评】本题考查了旋转变换的性质,等腰直角三角形的判定与性质,相似三角形的判定与性质,全等三角形的判定与性质,勾股定理,轴对称变换的性质,以及转化的数学思想,熟练掌握以上内容并灵活运用作出恰当的辅助线是解题关键.
19.(2025春 重庆二模)在平面直角坐标系中,点O为原点,点B(0,﹣4)是y轴负半轴上一点,将点B向右平移6个单位得到点A.
(1)点A的坐标为 (6,﹣4) ;
(2)如图2,动点F从点A出发,以每秒2个单位长度的速度沿AB方向运动,当点F运动到点B时,停止运动.设点F运动时间为t秒,用含t的式子表示F点的坐标;当t为何值时,△OBF的面积为6?求出此时点F的坐标;
(3)过点F作直线EF交x轴正半轴于E,交线段OA于D,若∠EOD,∠AFD的平分线相交于点N,∠ODF=α,请用含α的式子表示∠ONF的大小,并说明理由.
【考点】几何变换综合题.
【专题】代数几何综合题;几何直观;运算能力;推理能力.
【答案】(1)(6,﹣4);
(2)F点的坐标为(6﹣2t,﹣4);此时点F的坐标为(3,﹣4);
(3)∠ONFα,理由见解析.
【分析】(1)由平移的性质即可得到点A的坐标;
(2)利用平移的性质求得F点的坐标;利用三角形面积公式可求出答案;
(3)过点N作MN∥x轴,平行线的性质及角平分线的定义可得出∠MNO=∠NOE∠EOD,∠MNF=∠NFA∠AFD,再利用三角形外角性质,即可得出∠ONF的度数.
【解答】解:(1)∵将点B(0,﹣4)向右平移6个单位得到点A的坐标为(6,﹣4).
故答案为:(6,﹣4);
(2)由题意得AB=6,AF=2t,
∴BF=6﹣2t,
∴F点的坐标为(6﹣2t,﹣4);
∴,
解得,
此时点F的坐标为(3,﹣4);
(3),理由如下:
过点N作MN∥x轴,如图,
∴∠MNO=∠NOE,
∵ON是∠EOD的角平分线,
∴∠MNO=∠NOE∠EOD,
∵AB∥x轴,
∴MN∥AB,
∴∠MNF=∠NFA,
∵FN是∠AFD的角平分线,
∴∠MNF=∠NFA∠AFD,
∵AB∥x轴,
∴∠OED=∠AFD,
∵∠ODF=α,
∴∠ODF=∠EOD+∠OED=∠EOD+∠AFD=α,
∴∠ONF=∠MNO+∠MNF(∠EOD+∠AFD)α.
【点评】本题考查了坐标变换—平移,平行线的性质,三角形的外角性质,角平分线的定义等知识,灵活运用这些性质解决问题是本题的关键.
20.(2025春 沙坪坝区三模)综合与实践.
问题情境:
如图,在△ABC中,∠ACB=90°,AC=BC,点D在△ABC所在的平面内运动.探究图形间存在的关系.
特例探究:
(1)如图1,当点D在边AB上运动,连接CD,以CD为边在其右侧作等腰直角三角形CDE,连接BE,发现BE⊥AB,请说明理由;
求异探究:
(2)如图2,点E为AC的中点,点F为AB的中点,△AEF为等腰直角三角形,点D在△ABC外部时,连接ED,以ED为边在其右侧作等腰直角三角形EDH,连接DF和CH,判断DF与CH的关系,并证明;
拓展应用:
(3)如图3,当点D在直线AC上时,连接BD,在线段BD绕点B逆时针旋转90°得到线段BE,连接AE.若CD=6,AE=10,求△ABD的面积.
【考点】几何变换综合题.
【专题】代数几何综合题;几何直观;运算能力;推理能力.
【答案】(1)见解析;
(2)DF=CH,DF⊥CH,见解析;
(3)△ABD的面积为4或176.
【分析】(1)根据旋转的性质可得CD=CE,∠DCE=90°=∠ACB,进而证明△ACD≌△BCE(SAS),得出∠CBE=∠A=45°,可得∠ABE=∠ABC+∠CBE=90°,即可得证;
(2)连接AD,CF,先证明△DAE≌△HFE(SAS)可得∠EAD=∠EFH,AD=FH,进而证明△ADF≌△FHC(SAS),根据全等三角形的性质即可得解;
(3)分两种情况讨论,当点D在AC的延长线上时,过点B作FB⊥AB,交AD的延长线于点F,得出△ACB是等腰直角三角形,证明△ABE≌△FBD(SAS),得出FD=AE=10,BC=CF=CA=16,AD=22,利用三角形面积公式可求解;当点D在CA的延长线上时,同理可求解.
【解答】(1)证明:在△ABC中,∠ACB=90°,AC=BC,当点D在边AB上运动,连接CD,以CD为边在其右侧作等腰直角三角形CDE,
∴∠A=∠ABC=45°,
∵将线段CD绕点C逆时针旋转90°得到CE,
∴CD=CE,∠DCE=90°=∠ACB,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴∠CBE=∠A=45°,
∴∠ABE=∠ABC+∠CBE=90°,
∴BE⊥AB;
(2)解:DF=CH,DF⊥CH;理由如下:
点E为AC的中点,点F为AB的中点,△AEF为等腰直角三角形,点D在△ABC外部时,连接ED,以ED为边在其右侧作等腰直角三角形EDH,如图2所示,连接AD,CF,
∴ED=EH,∠DEH=90°,
∵∠ACB=90°,AC=BC,
∴∠CAB=∠ABC=45°,
∵点E和F分别为AC和AB的中点,
∴EF∥BC,EF∥BC,EFBCAC=AE,则∠AEF=90°,
∴∠AED=∠FEH,
∴△DAE≌△HFE(SAS),
∴∠EAD=∠EFH,AD=FH,
∵CF⊥AB,∠ACB=90°,CA=CB,
∴,
又∵EF⊥AC,
∴∠EFC=45°,
∴∠EFC=∠EAF=45°,
∴∠EAD﹣∠EAF=∠EFH﹣∠EFC,即∠FAD=∠CFH,
在△ADF和△FHC中,
,
∴△ADF≌△FHC(SAS),
∴DF=CH,∠AFD=∠FCH,
∵∠ACB=90°,AC=BC,点F为AB的中点,
∴AF=CF=BF,∠AFC=90°,
∴∠AFD+∠CFG=90°,
∴∠FCH+∠CFG=90°,
∴∠FGC=90°,
∴DF⊥CH;
(3)解:当点D在AC的延长线上时,如图3所示,过点B作FB⊥AB,交AD的延长线于点F,
∵△ACB是等腰直角三角形,
∴∠CAB=45°,
∵FB⊥AB,
∴△ABF是等腰直角三角形,
∴BA=BF,
∵将线段BD绕点B逆时针旋转90°得到线段BE,
∴DB=EB,∠DBE=90°,
∴∠FBD=90°﹣∠ABD=∠ABE,
∴△ABE≌△FBD(SAS),
∴FD=AE=10,
∵∠ACB=90°,BA=FB,
∴BC=CF=CA=CD+DF=16,AD=CA+CD=22,
∴△ABD的面积为;
当点D在CA的延长线上时,如图4所示,过点B作FB⊥AB,交AD的延长线于点F,
同理△ABF是等腰直角三角形,
△ABE≌△FBD(SAS),
∴FD=AE=10,
∵∠ACB=90°,BA=FB,
∴BC=CF=CA=DF﹣CD=4,AD=CD﹣CA=2,
∴△ABD的面积为;
综上,△ABD的面积为4或176.
【点评】本题考查了全等三角形的性质与判定,等腰直角三角形的性质与判定,旋转的性质;熟练掌握旋转的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考核心考点 图形的旋转
一.选择题(共10小题)
1.(2025春 江阴市二模)如图,正方形ABCD的边长为,点E在边AB上(不与A,B重合),将△ADE沿直线DE折叠,点A落在点A1处,连接A1B,将A1B绕点B顺时针旋转90°得到A2B,连接A1A,A1C,A2C.给出下列四个结论:①△ABA1≌△CBA2;②∠ADE+∠A1CB=45°;③点P是直线DE上动点,则CP+A1P的最小值为;④当∠ADE=30°时,△A1BE的面积为.其中正确的结论有几个( )
A.1个 B.2个 C.3个 D.4个
2.(2025春 市北区二模)如图,时钟的时针从上午8时转动到上午10时,时针绕表盘中心旋转的旋转角为( )
A.30° B.50° C.60° D.70°
3.(2025春 太原二模)《哪吒2》作为国漫佳作,在服饰、场景和道具等细节上,深度融入中国传统纹样,将丰富的文化内涵展现得淋漓尽致.下面纹样中文字上方的图案是中心对称图形的是( )
A. B.
C. D.
4.(2025 南山区二模)2025年蛇年春晚以“巳巳如意,生生不息”为主题,设计了“巳巳如意纹样”,象征着美好的愿望和幸福.以下四个如意纹样中,是中心对称图形的是( )
A. B.
C. D.
5.(2025春 青岛二模)如图,△ABC与△ADE关于点A成中心对称,若AB=2,CD=5,∠ADE=90°,则BC的长为( )
A.6 B.4 C.3 D.2
6.(2025 高新区)如图,平面直角坐标系中,A(﹣1,0),B(0,1),,将△ABC绕点A顺时针旋转,每秒旋转45°,则第86秒旋转结束时,点C的坐标为( )
A. B.
C. D.
7.(2025 西城区一模)下列图形中,是轴对称图形但不是中心对称图形的是( )
A.正三角形 B.矩形
C.圆 D.菱形
8.(2025 西城区一模)如图,等边△ABC的边长为1,将边AC,BA,CB分别绕点A,B,C逆时针旋转α(0°<α<180°)得到线段AC1,BA1,CB1,连接A1B1,A1C1,B1C1.对△A1B1C1给出下面三个结论:
①对任意α都有△A1B1C1是等边三角形;
②存在唯一一点到点A1,B1,C1的距离相等;
③当α=120°时,△A1B1C1的周长是.
上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
9.(2025春 南京二模)如图,在Rt△ABC中,∠C=90°.将△ABC绕点A逆时针旋转得到△AB'C'.若BC′∥AB,∠B'AC=16°,则旋转角α(0°<α<90°)的度数为( )
A.16° B.32° C.36° D.37°
10.(2025春 苏州二模)如图,△DEF是由△ABC绕着点O顺时针旋转得到的,以下说法不一定正确的是( )
A.∠COF=∠BOE B.∠BAC=∠EDF C.OC=OF D.BC=DF
二.填空题(共5小题)
11.(2025春 莲湖区三模)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,D是直角边AC上的一个动点,连接BD,以BD为边向外作等边△BDE,连接CE.在点D运动的过程中,线段CE的长的最小值为 .
12.(2025春 杨浦区三模)如图,在等腰△ABC中,底边BC的中点是D,底角的正切值是,将该等腰三角形绕其腰AC上的中点M顺时针旋转,使旋转后的点D与A重合,得到△A′B′C′,若旋转后的底边B′C′与BC交于点N,则cos∠ANB= .
13.(2025春 天山区三模)如图,点O为直线AB上一点,一副三角板如图摆放,其中∠C=∠DOC=45°,∠M=30°,∠N=60°.将直角三角板MON绕点O旋转一周,当∠AOM的度数是 时,直线MN与直线OC互相平行.
14.(2025 綦江区一模)如图,在平面直角坐标系中,A(6,0),B(0,8),连接AB,将线段AB绕点A顺时针旋转90°得到线段AC,连接OC,则线段OC的长度为 .
15.(2025 高新区)平面内,对于图形M与点P,给出如下定义:图形M绕点P逆时针旋转90°得到图形N,若图形N与图形M有重叠,则称图形M关于点P“逆垂相关”.如图,在平面直角坐标系xOy中,线段AB的端点分别是A(0,3),B(1,0).若以C(3,0)为圆心,r为半径的⊙C上存在点P,使线段AB关于点P“逆垂相关”,则r的取值范围是 .
三.解答题(共5小题)
16.(2025春 西城区三模)在平面直角坐标系xOy中,图形G和图形W的“中位形”的定义如下:点P是图形G上任意一点,点Q是图形W上任意一点,取PO中点M,取QO中点N,由所有线段MN所组成的图形叫做图形G和图形W的“中位形”.(当两个点重合时,连接这两点的线段和线段的中点都视为此点)
已知点A(4,0)、点B(0,2).
(1)点A和点B的“中位形”的长度是 ;
(2)已知点H(a,0),若点H和线段AB的“中位形”面积为2,求a的值.
(3)已知点E(10,0)、点F(0,﹣10),以线段AB为边作两条对角线都在坐标轴上的菱形ABCD.将菱形ABCD沿着直线y=x平移得到菱形A′B′C′D′,设菱形A′B′C′D′的对角线交点坐标为(t,t).若线段EF和菱形A′B′C′D′的“中位形”与菱形ABCD有公共点,直接写出t的取值范围.
17.(2025 沙坪坝区)在Rt△ABC中,∠BAC=90°,AB=AC,点D是平面内一点,连接AD,将点A绕点D顺时针旋转90°得点E,连接AE,DE.
(1)如图1,点D在△ABC的内部,连接CD,点E恰好在CD上.若AE=CE,求∠DAB的度数;
(2)如图2,点D在点A的右上方,连接BE,CE,点D恰好在CE上,延长DA交BE于点F,点G是AC的中点,连接FG,求证:;
(3)如图3,连接EC,∠AEC=90°,将线段AD沿AC所在直线翻折至△ABC所在平面内得到线段AM,点M为点D的对应点,连接BM,当BM取得最大值时,请直接写出此时的值.
18.(2025 历下区二模)在△ABC中,∠A=90°,AB=AC,点D在边AC上(点D不与点A,点C重合),连接BD并将BD绕点D逆时针旋转90°得到DE.
(1)如图1,连接CE.
①CE与BC的位置关系为 ,∠ABD与∠CED的数量关系是 ;
②请用等式表示BC,CD和CE的数量关系,并说明理由;
(2)如图2,将△ABD沿BD翻折,得到△A′BD,连接A′E,若A′E的最小值为2,求AB的长.
19.(2025春 重庆二模)在平面直角坐标系中,点O为原点,点B(0,﹣4)是y轴负半轴上一点,将点B向右平移6个单位得到点A.
(1)点A的坐标为 ;
(2)如图2,动点F从点A出发,以每秒2个单位长度的速度沿AB方向运动,当点F运动到点B时,停止运动.设点F运动时间为t秒,用含t的式子表示F点的坐标;当t为何值时,△OBF的面积为6?求出此时点F的坐标;
(3)过点F作直线EF交x轴正半轴于E,交线段OA于D,若∠EOD,∠AFD的平分线相交于点N,∠ODF=α,请用含α的式子表示∠ONF的大小,并说明理由.
20.(2025春 沙坪坝区三模)综合与实践.
问题情境:
如图,在△ABC中,∠ACB=90°,AC=BC,点D在△ABC所在的平面内运动.探究图形间存在的关系.
特例探究:
(1)如图1,当点D在边AB上运动,连接CD,以CD为边在其右侧作等腰直角三角形CDE,连接BE,发现BE⊥AB,请说明理由;
求异探究:
(2)如图2,点E为AC的中点,点F为AB的中点,△AEF为等腰直角三角形,点D在△ABC外部时,连接ED,以ED为边在其右侧作等腰直角三角形EDH,连接DF和CH,判断DF与CH的关系,并证明;
拓展应用:
(3)如图3,当点D在直线AC上时,连接BD,在线段BD绕点B逆时针旋转90°得到线段BE,连接AE.若CD=6,AE=10,求△ABD的面积.
中考核心考点 图形的旋转
参考答案与试题解析
一.选择题(共10小题)
1.(2025春 江阴市二模)如图,正方形ABCD的边长为,点E在边AB上(不与A,B重合),将△ADE沿直线DE折叠,点A落在点A1处,连接A1B,将A1B绕点B顺时针旋转90°得到A2B,连接A1A,A1C,A2C.给出下列四个结论:①△ABA1≌△CBA2;②∠ADE+∠A1CB=45°;③点P是直线DE上动点,则CP+A1P的最小值为;④当∠ADE=30°时,△A1BE的面积为.其中正确的结论有几个( )
A.1个 B.2个 C.3个 D.4个
【考点】旋转的性质;三角形的面积;全等三角形的判定;正方形的性质;轴对称﹣最短路线问题;翻折变换(折叠问题).
【专题】平移、旋转与对称;推理能力.
【答案】B
【分析】根据SAS证明三角形全等即可①正确;过点D作DT⊥CA1于点T,证明∠ADE+∠CDT=45°,∠CDT=∠BCA1即可判断②正确;连接PA,AC.因为A,A1关于DE对称,推出PA=PA1,推出,可得结论③错误;过点A1作A1H⊥AB于点H,求出EB,A1H,可得结论④错误.
【解答】解:∵四边形ABCD是正方形,
∴BA=BC,∠ABC=90°,
∵∠A1BA2=∠ABC=90°,
∴∠ABA1=∠CBA2,
∵BA1=BA2,
∴△ABA1 △CBA2(SAS),故①正确;
过点D作DT⊥CA1于点T,
∵CD=DA1,
∴∠CDT=∠A1DT,
∵∠ADE=∠A1DE,∠ADC=90°,
∴∠ADE+∠CDT=45°,
∵∠CDT+∠DCT=90°,∠DCT+∠BCA1=90°,
∴∠CDT=∠BCA1,
∴∠ADE+∠BCA1=45°,故②正确;
连接PA,AC,
∵A,A1关于DE对称,
∴PA=PA1,
∴,
∴PA1+PC的最小值为,故③错误;
过点A1作A1H⊥AB于点H,
∵∠ADE=30°,
∴,
∴,
∵∠A1EB=60°,
∴,
∴,故④错误;
故选:B.
【点评】本题是四边形综合题,考查正方形的性质,解直角三角形,翻折变换,全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题.
2.(2025春 市北区二模)如图,时钟的时针从上午8时转动到上午10时,时针绕表盘中心旋转的旋转角为( )
A.30° B.50° C.60° D.70°
【考点】生活中的旋转现象.
【专题】平移、旋转与对称;应用意识.
【答案】C
【分析】将圆心角360°分为12份求出2份即可得到答案.
【解答】解:将圆心角360°分为12份求出2份的度数为:360°÷12×2=60°,
故选:C.
【点评】本题考查钟面圆心角的求法,解题的关键是知道钟面刻度将圆心角分为了12份.
3.(2025春 太原二模)《哪吒2》作为国漫佳作,在服饰、场景和道具等细节上,深度融入中国传统纹样,将丰富的文化内涵展现得淋漓尽致.下面纹样中文字上方的图案是中心对称图形的是( )
A. B.
C. D.
【考点】中心对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】D
【分析】根据中心对称图形的概念对各选项分析判断即可得解.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.
【解答】解:选项A、B、C中的图案都不能找到一个点,使图形绕某一点旋转180°后与原来的图形重合,所以不是中心对称图形.
选项D中的图案能找到一个点,使图形绕某一点旋转180°后与原来的图形重合,所以是中心对称图形.
故选:D.
【点评】本题考查了中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180度后与原图重合.
4.(2025 南山区二模)2025年蛇年春晚以“巳巳如意,生生不息”为主题,设计了“巳巳如意纹样”,象征着美好的愿望和幸福.以下四个如意纹样中,是中心对称图形的是( )
A. B.
C. D.
【考点】中心对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】A
【分析】根据中心对称图形的概念判断.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.
【解答】解:选项B、C、D中的图形都不能找到一个点,使图形绕某一点旋转180°后与原来的图形重合,所以不是中心对称图形.
选项A中的图形能找到一个点,使图形绕某一点旋转180°后与原来的图形重合,所以是中心对称图形.
故选:A.
【点评】本题考查的是中心对称图形,中心对称图形是要寻找对称中心,旋转180度后与自身重合.
5.(2025春 青岛二模)如图,△ABC与△ADE关于点A成中心对称,若AB=2,CD=5,∠ADE=90°,则BC的长为( )
A.6 B.4 C.3 D.2
【考点】中心对称.
【专题】平移、旋转与对称;解直角三角形及其应用;运算能力.
【答案】C
【分析】根据中心对称的性质可得AD=AB=2,∠BCD=∠ADE=90°,据此可得BD=4,再根据勾股定理计算即可.
【解答】解:∵△ABC与△ADE关于点A成中心对称,
∴AD=AB=2,∠BCD=∠ADE=90°,
∴BD=AD+AB=4,
∴BC3.
故选:C.
【点评】本题考查了中心对称以及勾股定理,掌握中心对称的性质是解答本题的关键.
6.(2025 高新区)如图,平面直角坐标系中,A(﹣1,0),B(0,1),,将△ABC绕点A顺时针旋转,每秒旋转45°,则第86秒旋转结束时,点C的坐标为( )
A. B.
C. D.
【考点】坐标与图形变化﹣旋转.
【专题】规律型;平移、旋转与对称;几何直观.
【答案】B
【分析】由题意得,每旋转8秒△ABC回到原来位置,则第86秒旋转结束时△ABC的位置与第6秒旋转结束时△ABC的位置相同,结合旋转的性质可得答案.
【解答】解:∵△ABC绕点A顺时针旋转,每秒旋转45°,
∴每旋转8秒△ABC回到原来位置.
∵86=8×10+6,
∴第86秒旋转结束时△ABC的位置与第6秒旋转结束时△ABC的位置相同.
如图,第6秒旋转结束时△ABC旋转到△AB6C6的位置,
∵6×45°=270°,
∴AC6⊥x轴.
∵A(﹣1,0),,
∴AC.
由旋转得,AC6=AC,
∴C6(﹣1,),
∴第86秒旋转结束时,点C的坐标为(﹣1,).
故选:B.
【点评】本题考查坐标与图形变化﹣旋转,熟练掌握旋转的性质是解答本题的关键.
7.(2025 西城区一模)下列图形中,是轴对称图形但不是中心对称图形的是( )
A.正三角形 B.矩形
C.圆 D.菱形
【考点】中心对称图形;轴对称图形.
【专题】平移、旋转与对称;几何直观.
【答案】A
【分析】根据轴对称图形和中心对称图形的概念,对各选项分析判断即可得解.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
【解答】解:A.是轴对称图形,但不是中心对称图形,故符合题意;
B.既是轴对称图形,又是中心对称图形,故不符合题意;
C.既是轴对称图形,又是中心对称图形,故不符合题意;
D.既是轴对称图形,又是中心对称图形,故不符合题意;
故选:A.
【点评】本题主要查了轴对称图形和中心对称图形.熟练掌握两者定义是关键.
8.(2025 西城区一模)如图,等边△ABC的边长为1,将边AC,BA,CB分别绕点A,B,C逆时针旋转α(0°<α<180°)得到线段AC1,BA1,CB1,连接A1B1,A1C1,B1C1.对△A1B1C1给出下面三个结论:
①对任意α都有△A1B1C1是等边三角形;
②存在唯一一点到点A1,B1,C1的距离相等;
③当α=120°时,△A1B1C1的周长是.
上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
【考点】旋转的性质;等边三角形的判定与性质.
【专题】平移、旋转与对称;推理能力.
【答案】D
【分析】先证△BAA1≌△CBB1(SAS),再证△AA1C1≌△BB1A1≌△CC1B1,据此一一判断选项即可.
【解答】解:连接AA1、BB1、CC1,
∵△ABC是等边三角形,
∴AB=AC,
∴BA1=AC1,
在△BAA1和△CBB1中,
,
∴△BAA1≌△CBB1(SAS),
∴AA1=BB1,∠BAA1=∠BCB1,
同理可得AA1=BB1=CC1,∠BAA1=∠BCB1=∠CAC1,
∴∠A1AC1=∠B1BA1,
在△AA1C1和△BB1A1中,
,
∴△AA1C1≌△BB1A1(SAS),
同理可证△AA1C1≌△BB1A1≌△CC1B1,
∴A1B1=A1C1=B1C1,
故△A1B1C1是等边三角形,故①对;
∵△A1B1C1是等边三角形,
∴△ABC外心O也为△A1B1C1外心,
∴存在一点到点A,C1的距离相等,故②对;
当α=120°时,则A1、B、C共线,
∴A1B=1,BC1=2,
如图,过C1作C1G⊥A1B于点G,
则∠C1BG=60°,
∴BG=BC1 cos60°=1,C1G=BC1 sin60°,
∴A1G=2,
∴A1C1,
∴,故③对,
故选:D.
【点评】本题主要考查了旋转的性质、全等三角形的判定和性质、解直角三角形、勾股定理等内容,熟练掌握相关知识是解题的关键.
9.(2025春 南京二模)如图,在Rt△ABC中,∠C=90°.将△ABC绕点A逆时针旋转得到△AB'C'.若BC′∥AB,∠B'AC=16°,则旋转角α(0°<α<90°)的度数为( )
A.16° B.32° C.36° D.37°
【考点】旋转的性质;平行线的性质;直角三角形的性质.
【专题】线段、角、相交线与平行线;等腰三角形与直角三角形;平移、旋转与对称;几何直观;推理能力.
【答案】D
【分析】由旋转的性质得到∠BAB′=∠CAC′,由BC′∥AB得到∠BAB′=∠CAC′(90°﹣16°)=37°,据此解答即可.
【解答】解答解:将△ABC绕点A逆时针旋转得到△AB'C',
∴∠BAB′=∠CAC′,
∵BC′∥AB,∠C=90°,
∴∠BAC=90°,
∵∠B'AC=16°,
∴∠BAB′=∠CAC′(90°﹣16°)=37°,
∴旋转角α(0°<α<90°)的度数为37°,
故选:D.
【点评】本题主要考查了旋转的性质,平行线的性质,直角三角形的性质,解答本题的关键是熟练掌握旋转的性质.
10.(2025春 苏州二模)如图,△DEF是由△ABC绕着点O顺时针旋转得到的,以下说法不一定正确的是( )
A.∠COF=∠BOE B.∠BAC=∠EDF C.OC=OF D.BC=DF
【考点】旋转的性质.
【专题】平移、旋转与对称;数感;推理能力.
【答案】D
【分析】根据旋转的性质逐一判断即可.
【解答】解:∵△DEF是由△ABC绕着点O旋转得到的,
由旋转的性质得:∠COF=∠BOE,∠BAC=∠EDF,OC=OF,BC=EF,
故A,B,C选项正确,不符合题意;
由已知条件无法得到BC=DF,
故D选项错误,符合题意,
故选:D.
【点评】本题考查了旋转的性质,熟记旋转前后对应边、对应角相等是解题的关键.
二.填空题(共5小题)
11.(2025春 莲湖区三模)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,D是直角边AC上的一个动点,连接BD,以BD为边向外作等边△BDE,连接CE.在点D运动的过程中,线段CE的长的最小值为 1 .
【考点】旋转的性质;垂线段最短;三角形三边关系;全等三角形的判定与性质;等边三角形的性质;含30度角的直角三角形.
【专题】图形的全等;等腰三角形与直角三角形;平移、旋转与对称;几何直观;推理能力.
【答案】1.
【分析】延长BC到点F,使得CF=BC,连接AF,EF,由∠C=90°,∠BAC=30°,AB=4,可得:,∠ABF=60°,证明△ABF是等边三角形,得到∠AFB=60°,结合△BDE是等边三角形,可证明△FBE≌△ABD,得到∠BFE=∠BAD=30°,推出∠AFE=90°,得到点E在经过点F且与AF垂直的射线FE上运动,作CH⊥FE交射线FE于点H,则∠CHE=90°,得到,由CE≥CH可得CE≥1,即可求解.
【解答】解:在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,如图,延长BC到点F,使得CF=BC,连接AF,EF,
∴,∠ABF=90°﹣∠BAC=60°,
∴BF=2BC=4,
∴AB=BF,
∴△ABF是等边三角形,
∴∠AFB=60°,
∵△BDE是等边三角形,
∴BE=BD,∠DBE=60°,
∴∠FBE=∠ABD=60°﹣∠DBF,
在△FBE和△ABD中,
,
∴△FBE≌△ABD(SAS),
∴∠BFE=∠BAD=30°,
∴∠AFE=∠AFB+∠BFE=90°,
∴点E在经过点F且与AF垂直的射线FE上运动,作CH⊥FE交射线FE于点H,则∠CHE=90°,
∴,
∵CE≥CH,
∴CE≥1,
∴CE的最小值为1,
故答案为:1.
【点评】本题考查了旋转的性质,垂线段最短,三角形三边关系,全等三角形的判定与性质,等边三角形的性质,含30度角的直角三角形,解题的关键是掌握相关知识,并正确作出辅助线.
12.(2025春 杨浦区三模)如图,在等腰△ABC中,底边BC的中点是D,底角的正切值是,将该等腰三角形绕其腰AC上的中点M顺时针旋转,使旋转后的点D与A重合,得到△A′B′C′,若旋转后的底边B′C′与BC交于点N,则cos∠ANB= .
【考点】旋转的性质;解直角三角形;等腰三角形的性质.
【专题】统计与概率;平移、旋转与对称;几何直观;推理能力.
【答案】.
【分析】根据题意连接AD,A′A,再得到∠B=∠C,再利用旋转性质可得∠ANB=∠MAN+∠C=2∠C,再利用正切值可设A′A=2x,C′D=6x,再取A′A中点E,连接ME,过点A′作A′F⊥AM于F,继而得到本题答案.
【解答】解:在等腰△ABC中,底边BC的中点是D,底角的正切值是,如图,连接AD,A′A,
,
∴∠B=∠C,
将该等腰三角形绕其腰AC上的中点M顺时针旋转,使旋转后的点D与A重合,得到△A′B′C′,
∴,∠C=∠C′,
∴∠MAC′=∠C=∠C′,
∴∠ANB=∠MAN+∠C=2∠C,
∵,
∴,
设A′A=2x,C′A=6x,
∴,,
∴,
取A′A中点E,连接ME,过点A′作A′F⊥AM于F,
则,
∵,
∴,
∴,
∴,
故答案为:.
【点评】本题考查旋转的性质,等腰三角形的性质,解直角三角形,解答本题的关键是熟练掌握旋转的性质.
13.(2025春 天山区三模)如图,点O为直线AB上一点,一副三角板如图摆放,其中∠C=∠DOC=45°,∠M=30°,∠N=60°.将直角三角板MON绕点O旋转一周,当∠AOM的度数是 75°或105° 时,直线MN与直线OC互相平行.
【考点】旋转的性质;平行线的判定;平行线的性质.
【专题】线段、角、相交线与平行线;平移、旋转与对称;推理能力.
【答案】75°或105°.
【分析】根据MN在OC左边或右边分别画出图形,利用平行线的性质得到∠COM的度数,再求出∠AOM的度数即可.
【解答】解:当MN在OC右边时,如图,
∵MN∥OC,
∴∠M=∠COM=30°,
∵∠DOC=∠C=45°,
∴∠AOM=∠COM+∠DOC=75°;
当MN在OC左边时,如图,
∵MN∥OC,
∴∠M+∠COM=180°,
∵∠M=30°,
∴∠COM=150°,
∵∠DOC=∠C=45°,
∴∠AOM=∠COM﹣∠DOC=105°;
综上所述,当∠AOM的度数是75°或105°时,直线MN与直线OC互相平行,
故答案为:75°或105°.
【点评】本题考查平行线的性质和判定,旋转的性质,熟练掌握旋转的性质是解题的关键.
14.(2025 綦江区一模)如图,在平面直角坐标系中,A(6,0),B(0,8),连接AB,将线段AB绕点A顺时针旋转90°得到线段AC,连接OC,则线段OC的长度为 .
【考点】坐标与图形变化﹣旋转;全等三角形的判定与性质;勾股定理.
【专题】等腰三角形与直角三角形;平移、旋转与对称;几何直观;推理能力.
【答案】.
【分析】过点C作x轴的垂线,证得△AOB≌△CMA(AAS),推导出AO=CM,BO=AM,得到OM=14,CM=6.在Rt△COM中,利用勾股定理求得OC即可.
【解答】解:将线段AB绕点A顺时针旋转90°得到线段AC,如图,过点C作x轴的垂线,垂足为M,
∴∠BAC=90°,∠BOA=∠CMA=90°,AB=AC,
∴∠BAO+∠CAM=90°,∠BAO+∠OBA=90°,
∴∠CAM=∠OBA,
在△AOB和△CMA中,
,
∴△AOB≌△CMA(AAS),
∴AO=CM,BO=AM,
又∵A(6,0),B(0,8),
∴CM=AO=6,AM=BO=8,
∴OM=14,CM=6.
在Rt△COM中,由勾股定理得:.
故答案为:.
【点评】本题考查坐标与图形变化﹣旋转,勾股定理,全等三角形的判定与性质,通过全等三角形求出OM=14,CM=6是解题的关键.
15.(2025 高新区)平面内,对于图形M与点P,给出如下定义:图形M绕点P逆时针旋转90°得到图形N,若图形N与图形M有重叠,则称图形M关于点P“逆垂相关”.如图,在平面直角坐标系xOy中,线段AB的端点分别是A(0,3),B(1,0).若以C(3,0)为圆心,r为半径的⊙C上存在点P,使线段AB关于点P“逆垂相关”,则r的取值范围是 r≤3 .
【考点】旋转的性质.
【专题】新定义;推理能力.
【答案】r≤3.
【分析】以AB为边分别往两侧作正方形,由题意可得点P在正方形AP3BP4内,据此求出半径最大值和最小值即可.
【解答】解:如图,
由题可设线段AB关于点P“逆垂相关”为线段A'B',
则线段AB与A'B'要有交点,
旋转后必有AB⊥A'B',
①当点P在P1处,即在点A时,B在B1处;
②当点P在P2处,即在点B时,A在A1处;
③当点P在P3处,A在B处,B在B3处;
④当点P在P4处,A在A4处,B在A处;
要让AB与A'B'有交点,则P在正方形AP3BP4内,
由题可得A(0,3),B3(4,1),C(3,0),
∴P3(2,2),P4(﹣1,1),
∴r1=AC=3,r2=CP4,
∵,
∴rmax=3;
很明显,当CP5⊥BP3时,r最小,
在Rt△CBP5中,BC=2,
∴CP5,即rmin;
∴r≤3;
故答案为:r≤3.
【点评】本题主要考查了以圆和旋转为背景的新定义,正确理解题意是解题的关键.
三.解答题(共5小题)
16.(2025春 西城区三模)在平面直角坐标系xOy中,图形G和图形W的“中位形”的定义如下:点P是图形G上任意一点,点Q是图形W上任意一点,取PO中点M,取QO中点N,由所有线段MN所组成的图形叫做图形G和图形W的“中位形”.(当两个点重合时,连接这两点的线段和线段的中点都视为此点)
已知点A(4,0)、点B(0,2).
(1)点A和点B的“中位形”的长度是 ;
(2)已知点H(a,0),若点H和线段AB的“中位形”面积为2,求a的值.
(3)已知点E(10,0)、点F(0,﹣10),以线段AB为边作两条对角线都在坐标轴上的菱形ABCD.将菱形ABCD沿着直线y=x平移得到菱形A′B′C′D′,设菱形A′B′C′D′的对角线交点坐标为(t,t).若线段EF和菱形A′B′C′D′的“中位形”与菱形ABCD有公共点,直接写出t的取值范围.
【考点】几何变换综合题.
【专题】新定义;一次函数及其应用;矩形 菱形 正方形;运算能力;推理能力.
【答案】(1);
(2)a=﹣4或12;
(3)﹣10≤t≤60.
【分析】(1)求△OAB的OA和OB的中点形成中位线的长即可;
(2)线段AB的“中位形”的线段的端点为M(2,0),N(0,1),点H的“中位形”H′(),根据S△MNH′得出a的值;
(3)可表示出菱形A′B′C′D′的“中位”图形菱形A″B″C″D″的点C″(),B″(),EF的“中位”图形E′F′,其中E′(5,0),F(0,﹣5),可求出直线AF′的解析式为:y,直线DE′的解析式为:y,求得当AF过点C″和DE′过B″时t的结果,进而得出结果.
【解答】解:(1)∵∠AOB=90°,OA=4,OB=2,
∴AB=2,
∵M是OA的中点,N是OB的中点,
∴MN,
故答案为:;
(2)如图1,
∵MN是线段AB的“中位形”,
∴M(2,0),N(0,1),
∵点H的“中位形”H′(),
∴MH′=||,
由S△MNH′得,
,
∴a=﹣4或12;
(3)如图2,
∵菱形A′B′C′D′的对角线交点坐标为(t,t),
∴菱形A′B′C′D′的“中位”图形菱形A″B″C″D″的点C″(),B″(),
EF的“中位”图形E′F′,其中E′(5,0),F(0,﹣5)
∵A(4,0),D(0,﹣2),
∴直线AF′的解析式为:y,直线DE的解析式为:y,
当AF′过点C″时,
,
∴t=60,
当DE′过点B″时,
,
∴t=﹣10,
∴﹣10≤t≤60.
【点评】本题在新定义的基础上,考查了三角形中位线的性质,求一次函数的解析式,菱形的性质等知识,解决问题的关键是数形结合.
17.(2025 沙坪坝区)在Rt△ABC中,∠BAC=90°,AB=AC,点D是平面内一点,连接AD,将点A绕点D顺时针旋转90°得点E,连接AE,DE.
(1)如图1,点D在△ABC的内部,连接CD,点E恰好在CD上.若AE=CE,求∠DAB的度数;
(2)如图2,点D在点A的右上方,连接BE,CE,点D恰好在CE上,延长DA交BE于点F,点G是AC的中点,连接FG,求证:;
(3)如图3,连接EC,∠AEC=90°,将线段AD沿AC所在直线翻折至△ABC所在平面内得到线段AM,点M为点D的对应点,连接BM,当BM取得最大值时,请直接写出此时的值.
【考点】几何变换综合题.
【专题】三角形;推理能力.
【答案】(1)22.5°.
(2)证明见解答.
(3).
【分析】(1)首先判定△ABC和△ADE是等腰直角三角形,然后根据外角的性质求出∠ECA=22.5°,再从∠BAC中由角的和差关系求出∠DAB的大小.
(2)通过辅助线构造△ACD∽△BCH,接着推出BH=AE,进而证明△BFH≌△EFA,从而得到AF=FH,则FG是△AHG的中位线,再结合CHCD即可证明结论.
(3)先由定弦定角模型求出点E的运动轨迹,然后根据瓜豆模型中主从动点的运动轨迹关系判定出点D的运动轨迹,从而由轴对称的性质得出点M的运动轨迹,再由等腰直角三角形的性质及中位线的性质在Rt△BQI中求出BM关于AB的表达式,最终求出答案.
【解答】解:(1)根据题意可知△ABC和△ADE是等腰直角三角形.
∴∠DAE=∠DEA=45°.
∵AE=CE,
∴∠ECA=∠EAC22.5°,
∵∠DAB=∠BAC﹣∠DAE﹣∠EAC=90°﹣45°﹣22.5°=22.5°.
(2)证明:延长DF至点H,使DH=CD,连接BH,CH,则△DCH是等腰直角三角形.
∴∠DCH=∠DHC=∠ACB=45°,
∴∠ACD=∠BCH=45°﹣∠ACH.
又∵.
∴△ACD∽△BCH.
∴BHAD=AE,∠BHC=∠ADC=90°,
∵∠EAH=180°﹣∠EAD=135°,∠AHB=∠BHC+∠DHC=135°,
∴∠EAH=∠AHB,
又∵∠AFE=∠HFB,
∴△BFH≌△EFA(AAS),
∴AF=FH,
∵AG=GC,
∴FGCHCD.
∴CDFG.
(3)如图,点F、G分别为AC、AB的中点,过点F作BC的垂线交BA延长线于点H,交BC于点I.
易得△BHI为等腰直角三角形.
∵FG为△ABC的中位线,
∴FG∥BC,FGBCAB.
根据题意,∠AEC=90°,由定弦定角辅助圆模型可知主动点E的运动轨迹是以AC为直径的⊙F上,因此从动点D的运动轨迹在以GF为直径的⊙P上.
而根据轴对称的性质,点D关于AC的对称点M的运动轨迹在以FH为直径的⊙Q上,
∴FG=FH,AG=AH.
∴AQ为△GFH的中位线.
∴AQ∥FG,
由平行线分线段成比例可得F、Q两点分别是线段HI的三等分点,则QI=FH=FG.
在Rt△BQI中,BI=HIFHAB,QI=FGAB,则BQAB.
∴BM=BQ+MQABAB.
∴.
【点评】本题考查了等腰直角三角形的性质,相似三角形和全等三角形的判定和性质,轴对称的性质,勾股定理,定弦定角辅助圆模型,瓜豆模型等知识点.构造全等三角形证明相关线段和角相等,以及熟练掌握瓜豆模型是解答本题的关键.
18.(2025 历下区二模)在△ABC中,∠A=90°,AB=AC,点D在边AC上(点D不与点A,点C重合),连接BD并将BD绕点D逆时针旋转90°得到DE.
(1)如图1,连接CE.
①CE与BC的位置关系为 CE⊥BC ,∠ABD与∠CED的数量关系是 ∠ABD+∠CED=45° ;
②请用等式表示BC,CD和CE的数量关系,并说明理由;
(2)如图2,将△ABD沿BD翻折,得到△A′BD,连接A′E,若A′E的最小值为2,求AB的长.
【考点】几何变换综合题.
【专题】几何变换;几何直观;推理能力;模型思想.
【答案】(1)①CE⊥BC,∠ABD+∠CED=45°;
②BC=CE,理由见解析;
(2).
【分析】(1)①由题意可得△BAC与△BDE为等腰直角三角形,再证明△ABD∽△CBE,利用相似三角形的性质导角可得CE⊥BC,∠ABD+∠CED=45°;
②在BC上取点F,使BF=CE,连接DF,如图2所示,证明△BDF≌△EDC(SAS),可得DC=DF,又∠DCF=45°,可得△DFC为等腰直角三角形,CF,从而BC=BF+CF=CE;
(2)如图2所示,连接BE,将△BA'E沿BE翻折至△BFE,则BA'=BF=BA,A'E=FE,由翻折可知∠ABD=∠A'BD,∠A'BE=∠FBE,导角可知∠ABF=2(∠A'BD+∠A'BE)=90°,故四边形ABFC为正方形,
由(1)知∠BCE=90°,故E在过点C的BC的垂线上运动.当A′E的最小值为2时,即FE最小为2,即当FE⊥CE时,FE最小为2,此时EF2,故BC=4,从而AB.
【解答】解:(1)①如图1所示,连接BE,
由题意可得△BAC与△BDE为等腰直角三角形,
∴∠ABC=∠DBE=45°,从而∠ABD=∠CBE,
,
∴,
∴△ABD∽△CBE,
∴∠BCE=∠BAD=90°,
∵∠BDE=∠BCE=90°,
∴∠DBC=∠CED,
∵∠ABD+∠DBC=45°,
∴∠ABD+∠CED=45°.
故答案为:CE⊥BC,∠ABD+∠CED=45°.
②证明:BC=CE,理由如下:
在BC上取点F,使BF=CE,连接DF,如图2所示,
在△BDF和△EDC中,
,
∴△BDF≌△EDC(SAS),
∴DC=DF,
∵∠DCF=45°,
∴△DFC为等腰直角三角形,CF,
∴BC=BF+CF=CE,
(2)法一(翻折构造法):如图2所示,连接BE,将△BA'E沿BE翻折至△BFE,
则BA'=BF=BA,A'E=FE,
由翻折可知∠ABD=∠A'BD,∠A'BE=∠FBE,
又∵∠DBE=45°=∠A'BD+∠A'BE,
∴∠ABF=2(∠A'BD+∠A'BE)=90°,
故四边形ABFC为正方形,
又由(1)知∠BCE=90°,
故E在过点C的BC的垂线上运动.
当A′E的最小值为2时,即FE最小为2,
即当FE⊥CE时,FE最小为2,
此时EF2,故BC=4,
从而AB.
法二(构造相似):如图3所示,
取BC中点M,连接MD、AM、连接BE,
由题意可知△ABM和△BDE为等腰直角三角形,ABBA',
BE.
由折叠可知∠ABD=∠A'BD=∠DBM+∠MBA',
由(1)可知∠ABD=∠CBE=∠MBA'+∠A'BE,
∴∠DBM+∠MBA'=∠MBA'+∠A'BE,
∴∠DBM=∠A'BE,
又∵,
∴△BMD∽△BA'E.
∴A'EMD,
当A'E最小为2时,MD最小为,
此时MD⊥AC,D为AC中点,
由中位线定理可知AB=2DM.
法三(构造一线三垂直):
过E点作EG⊥DA'的延长线于点G,如图4所示,
易证△BDA'≌△DEG(AAS),
则设GE=DA'=a,BA'=AB=DG=b,
则A'G=DG﹣DA'=b﹣a,
则由勾股定理得A'E2=A'G2+GE2=(b﹣a)2+a2=b2﹣2ab+2a2,
把a看成未知数,b看成常数,
故A'E2=2a2﹣2ab+b2=2(a)2,
当a时,A'E2取得最小值为,
A'E最小为2,
即4,故b,
故AB.
法四(旋转﹣两动化一动):
将△DA'E绕点D顺时针旋转90°得△DHB,如图5所示,
故DH=DA',BH=A'E,
则易知△DHA'为等腰直角三角形,
∴∠DA'H=45°,∠HA'B=45°,
∵B点为定点,BA'为定长,H点在与BA'成45°角的射线上运动,
故当BH⊥A'H时,BH最小,最小为2,
此时△BHA'为等腰直角三角形,
从而知BA',
故AB.
法五(对称法结合瓜豆原理):
作点E关于BD的对称点E',连接BE',可得△BE'D为等腰直角三角形,
以AB为腰向左构造等腰直角三角形ABC',连接C'E',如图6所示,
∴BC',BE',即.
∵∠C'BA=∠E'BD=45°,
∴∠C'BE'=∠ABD,
∴△C'BE'∽△ABD,
∴∠BC'E'=∠BAD=90°=∠C'BC,
故C'E'∥BC,即E'直线C'E'上运动.
由对称性可知△DAE'≌△DA'E,
∴AE'=A'E,
当A'E最小为2时,AE'最小也为2,
故当AE'⊥C'E'时最小为2,
此时△C'E'A为等腰直角三角形,
AC',
由于△ABC'也为等腰直角三角形,
故AB=AC'.
【点评】本题考查了旋转变换的性质,等腰直角三角形的判定与性质,相似三角形的判定与性质,全等三角形的判定与性质,勾股定理,轴对称变换的性质,以及转化的数学思想,熟练掌握以上内容并灵活运用作出恰当的辅助线是解题关键.
19.(2025春 重庆二模)在平面直角坐标系中,点O为原点,点B(0,﹣4)是y轴负半轴上一点,将点B向右平移6个单位得到点A.
(1)点A的坐标为 (6,﹣4) ;
(2)如图2,动点F从点A出发,以每秒2个单位长度的速度沿AB方向运动,当点F运动到点B时,停止运动.设点F运动时间为t秒,用含t的式子表示F点的坐标;当t为何值时,△OBF的面积为6?求出此时点F的坐标;
(3)过点F作直线EF交x轴正半轴于E,交线段OA于D,若∠EOD,∠AFD的平分线相交于点N,∠ODF=α,请用含α的式子表示∠ONF的大小,并说明理由.
【考点】几何变换综合题.
【专题】代数几何综合题;几何直观;运算能力;推理能力.
【答案】(1)(6,﹣4);
(2)F点的坐标为(6﹣2t,﹣4);此时点F的坐标为(3,﹣4);
(3)∠ONFα,理由见解析.
【分析】(1)由平移的性质即可得到点A的坐标;
(2)利用平移的性质求得F点的坐标;利用三角形面积公式可求出答案;
(3)过点N作MN∥x轴,平行线的性质及角平分线的定义可得出∠MNO=∠NOE∠EOD,∠MNF=∠NFA∠AFD,再利用三角形外角性质,即可得出∠ONF的度数.
【解答】解:(1)∵将点B(0,﹣4)向右平移6个单位得到点A的坐标为(6,﹣4).
故答案为:(6,﹣4);
(2)由题意得AB=6,AF=2t,
∴BF=6﹣2t,
∴F点的坐标为(6﹣2t,﹣4);
∴,
解得,
此时点F的坐标为(3,﹣4);
(3),理由如下:
过点N作MN∥x轴,如图,
∴∠MNO=∠NOE,
∵ON是∠EOD的角平分线,
∴∠MNO=∠NOE∠EOD,
∵AB∥x轴,
∴MN∥AB,
∴∠MNF=∠NFA,
∵FN是∠AFD的角平分线,
∴∠MNF=∠NFA∠AFD,
∵AB∥x轴,
∴∠OED=∠AFD,
∵∠ODF=α,
∴∠ODF=∠EOD+∠OED=∠EOD+∠AFD=α,
∴∠ONF=∠MNO+∠MNF(∠EOD+∠AFD)α.
【点评】本题考查了坐标变换—平移,平行线的性质,三角形的外角性质,角平分线的定义等知识,灵活运用这些性质解决问题是本题的关键.
20.(2025春 沙坪坝区三模)综合与实践.
问题情境:
如图,在△ABC中,∠ACB=90°,AC=BC,点D在△ABC所在的平面内运动.探究图形间存在的关系.
特例探究:
(1)如图1,当点D在边AB上运动,连接CD,以CD为边在其右侧作等腰直角三角形CDE,连接BE,发现BE⊥AB,请说明理由;
求异探究:
(2)如图2,点E为AC的中点,点F为AB的中点,△AEF为等腰直角三角形,点D在△ABC外部时,连接ED,以ED为边在其右侧作等腰直角三角形EDH,连接DF和CH,判断DF与CH的关系,并证明;
拓展应用:
(3)如图3,当点D在直线AC上时,连接BD,在线段BD绕点B逆时针旋转90°得到线段BE,连接AE.若CD=6,AE=10,求△ABD的面积.
【考点】几何变换综合题.
【专题】代数几何综合题;几何直观;运算能力;推理能力.
【答案】(1)见解析;
(2)DF=CH,DF⊥CH,见解析;
(3)△ABD的面积为4或176.
【分析】(1)根据旋转的性质可得CD=CE,∠DCE=90°=∠ACB,进而证明△ACD≌△BCE(SAS),得出∠CBE=∠A=45°,可得∠ABE=∠ABC+∠CBE=90°,即可得证;
(2)连接AD,CF,先证明△DAE≌△HFE(SAS)可得∠EAD=∠EFH,AD=FH,进而证明△ADF≌△FHC(SAS),根据全等三角形的性质即可得解;
(3)分两种情况讨论,当点D在AC的延长线上时,过点B作FB⊥AB,交AD的延长线于点F,得出△ACB是等腰直角三角形,证明△ABE≌△FBD(SAS),得出FD=AE=10,BC=CF=CA=16,AD=22,利用三角形面积公式可求解;当点D在CA的延长线上时,同理可求解.
【解答】(1)证明:在△ABC中,∠ACB=90°,AC=BC,当点D在边AB上运动,连接CD,以CD为边在其右侧作等腰直角三角形CDE,
∴∠A=∠ABC=45°,
∵将线段CD绕点C逆时针旋转90°得到CE,
∴CD=CE,∠DCE=90°=∠ACB,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴∠CBE=∠A=45°,
∴∠ABE=∠ABC+∠CBE=90°,
∴BE⊥AB;
(2)解:DF=CH,DF⊥CH;理由如下:
点E为AC的中点,点F为AB的中点,△AEF为等腰直角三角形,点D在△ABC外部时,连接ED,以ED为边在其右侧作等腰直角三角形EDH,如图2所示,连接AD,CF,
∴ED=EH,∠DEH=90°,
∵∠ACB=90°,AC=BC,
∴∠CAB=∠ABC=45°,
∵点E和F分别为AC和AB的中点,
∴EF∥BC,EF∥BC,EFBCAC=AE,则∠AEF=90°,
∴∠AED=∠FEH,
∴△DAE≌△HFE(SAS),
∴∠EAD=∠EFH,AD=FH,
∵CF⊥AB,∠ACB=90°,CA=CB,
∴,
又∵EF⊥AC,
∴∠EFC=45°,
∴∠EFC=∠EAF=45°,
∴∠EAD﹣∠EAF=∠EFH﹣∠EFC,即∠FAD=∠CFH,
在△ADF和△FHC中,
,
∴△ADF≌△FHC(SAS),
∴DF=CH,∠AFD=∠FCH,
∵∠ACB=90°,AC=BC,点F为AB的中点,
∴AF=CF=BF,∠AFC=90°,
∴∠AFD+∠CFG=90°,
∴∠FCH+∠CFG=90°,
∴∠FGC=90°,
∴DF⊥CH;
(3)解:当点D在AC的延长线上时,如图3所示,过点B作FB⊥AB,交AD的延长线于点F,
∵△ACB是等腰直角三角形,
∴∠CAB=45°,
∵FB⊥AB,
∴△ABF是等腰直角三角形,
∴BA=BF,
∵将线段BD绕点B逆时针旋转90°得到线段BE,
∴DB=EB,∠DBE=90°,
∴∠FBD=90°﹣∠ABD=∠ABE,
∴△ABE≌△FBD(SAS),
∴FD=AE=10,
∵∠ACB=90°,BA=FB,
∴BC=CF=CA=CD+DF=16,AD=CA+CD=22,
∴△ABD的面积为;
当点D在CA的延长线上时,如图4所示,过点B作FB⊥AB,交AD的延长线于点F,
同理△ABF是等腰直角三角形,
△ABE≌△FBD(SAS),
∴FD=AE=10,
∵∠ACB=90°,BA=FB,
∴BC=CF=CA=DF﹣CD=4,AD=CD﹣CA=2,
∴△ABD的面积为;
综上,△ABD的面积为4或176.
【点评】本题考查了全等三角形的性质与判定,等腰直角三角形的性质与判定,旋转的性质;熟练掌握旋转的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
