(小升初择校分班考)小升初分班考高频考点预测卷-2024-2025学年六年级下册数学苏教版(含答案解析)
文档属性
| 名称 | (小升初择校分班考)小升初分班考高频考点预测卷-2024-2025学年六年级下册数学苏教版(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 170.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 05:29:30 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024-2025学年六年级下册数学小升初分班考高频考点预测卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题(共10小题,共10分)
1.下面各数中的“6”表示6个十分之一的是( )
A.164 B.5.67 C.8.062 D.21.946
2.一个电影院楼下有697个座位,楼上有208个座位。这个电影院能同时容纳1000人看电影吗?解决这个问题适合选择( )
A.口算 B.估算 C.笔算 D.计算器计算
3.一个长方体金鱼缸(如图所示),长40厘米,宽30厘米,高35厘米。它右侧面的玻璃打碎了,要重新配一块。重新配的玻璃是( )平方厘米。
A.1200 B.1050 C.1400 D.2100
4.一台收割机小时收割公顷小麦,这台收割机收割1公顷需要( )小时。
A. B. C. D.
5.从两根长4厘米和两根长9厘米的小棒中,选出3根围成一个等腰三角形,这个等腰三角形的周长是( )厘米。
A.12 B.17 C.27 D.22
6.下面各题中的两种量成正比例的是( )
A.长方形面积一定,长和宽 B.圆的半径和面积
C.订阅《小学生数学报》的总价和数量 D.,x和y
7.一个三角形的三个内角的度数比是1:2:6,这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.等腰三角形 D.钝角三角形
8.下面的数中,( )是2的倍数,也是3的倍数。
A.45 B.100 C.132 D.225
9.两个正方体的棱长之比是1:3,它们的体积之比是( )
A.1:3 B.1:9 C.1:27 D.1:81
10.一根铁丝,剪去,还剩下米,则( )
A.剪去的长 B.剩下的长 C.剪去的和剩下的一样长 D.无法确定
二.填空题(共14小题,共22分)
11.我国有丰富的石油资源,基础储量大约是三十二亿三千九百六十八万吨,横线上的数写作 ,省略“亿”后面的尾数大约是 亿。
12.直线上的点x表示的数是 ,点y表示的数写成分数是 。
13.如果m﹣n=1(m和n是不等于0的自然数),那么m和n的最大公因数是 。
14.如图所示,涂色部分面积与空白部分面积的最简整数比是 。
15.一个圆柱形木料底面直径是6厘米。如果沿着直径和高把它平均分成两块(如图1所示),那么表面积比原来增加96平方厘米,这个圆柱的高是 厘米;如果把这个圆柱平均截成3段(如图2所示),那么表面积比原来增加 平方厘米。
16.2.06升= 毫升 800平方米= 公顷
17.找规律,接着填写:3×4﹣1=11,33×34﹣11=1111,333×334﹣111=111111,3333×3334﹣1111= 。
18.从袋子里任意摸一个球(如图所示),摸到 球的可能性大;如果要使摸到黑球和白球的可能性相等,你的方法是 。
19.苹果的单价是8.5元/千克,桃子的单价是6.5元/千克。爸爸买了a千克苹果和b千克桃子,一共要付______ 元。
20.一个圆锥形沙堆,底面积是30平方米,高是1.5米。如果把这堆沙均匀地填在一个长7.5米、宽4米的长方体沙坑里,那么沙坑里沙子的厚度是 米。
21.李叔叔想买一部价值2500元的手机,他到6月18日去买,可以节省 元。
22.张阿姨买一台冰箱,原价5200元,打 折后,只花了4160元;李叔叔种了一批树,成活率是92%,成活了46棵,未成活的有 棵。
23.和都是假分数,的分数单位是 ;如果M是一个质数,那么这里的M是 。
24.用边长1cm的小正方形拼成长方形(如图)。像这样,用5个小正方形拼成的长方形的周长是 厘米,用a个小正方形拼成的长方形的周长是 厘米。
三.计算题(共3小题,共26分)
25.口算。(共8分)
726﹣398= 0.72+0.8=
5.7÷0.19= 0.25×99+25%=
26.求x的值。(共9分)
3x﹣1.8×2=2.4
27.脱式计算,能简算的要简算。(共9分)
0.12 [(1﹣90%)]
四.操作题(共1小题,共6分)
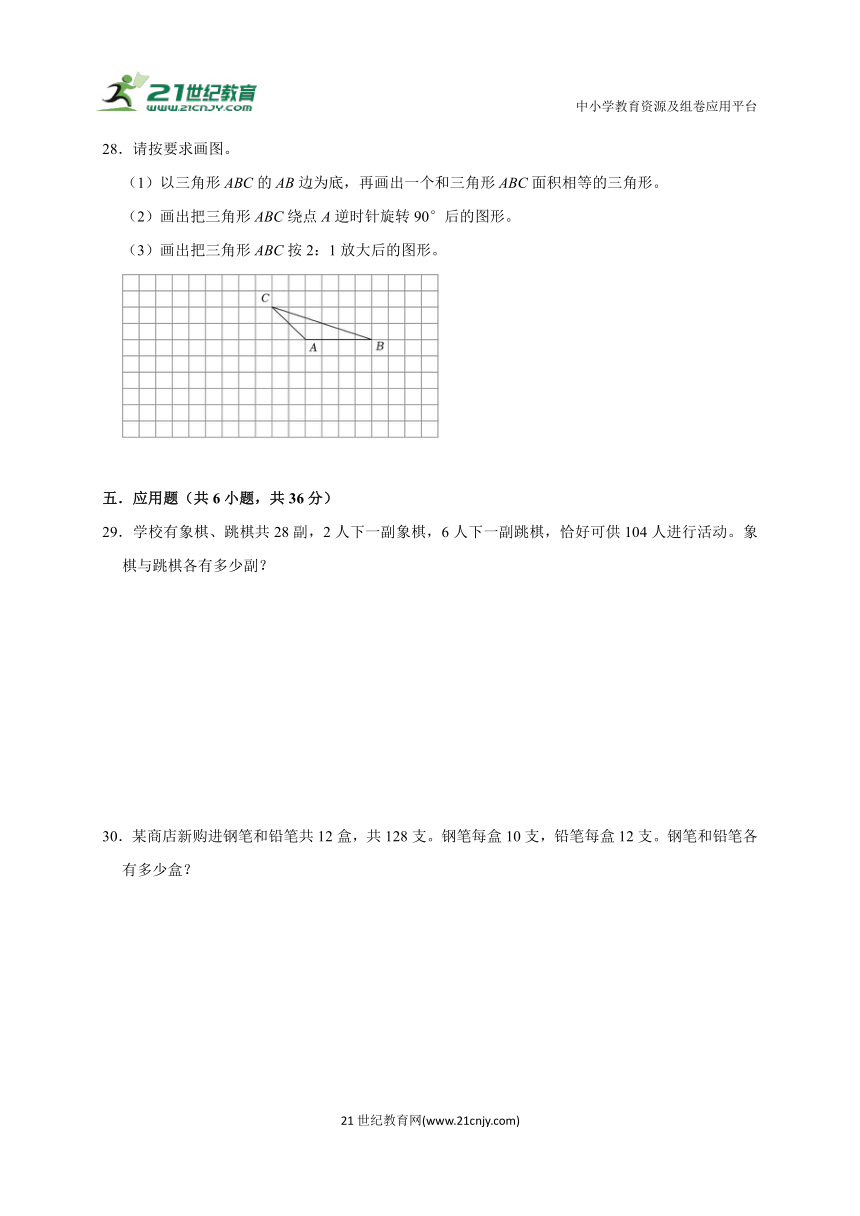
28.请按要求画图。
(1)以三角形ABC的AB边为底,再画出一个和三角形ABC面积相等的三角形。
(2)画出把三角形ABC绕点A逆时针旋转90°后的图形。
(3)画出把三角形ABC按2:1放大后的图形。
五.应用题(共6小题,共36分)
29.学校有象棋、跳棋共28副,2人下一副象棋,6人下一副跳棋,恰好可供104人进行活动。象棋与跳棋各有多少副?
30.某商店新购进钢笔和铅笔共12盒,共128支。钢笔每盒10支,铅笔每盒12支。钢笔和铅笔各有多少盒?
31.科技馆“七色彩虹”项目的门票20元/张,优惠政策有两种:满50张可以购买团体票,团体票打六折;购买学生票打五折。如果六(4)班44名学生和8名老师都参加“七色彩虹”项目,怎样购票更划算?(请通过计算说明)
32.六年级3班42名同学采集标本共120件,男生平均每人采集2.5件,女生平均每人采集3件。六年级3班女生有多少人?
33.为了方便参加“球形屏幕观影”项目,44名同学们分为8个小组,每个老师负责一组,男老师负责的小组每组有6名学生,女教师负责的小组每组有4名学生,正好安排完。你知道男教师、女教师各有多少人?
34.李强在市民图书馆借了一本历史故事书,如果每天看16页,15天能全部看完。如果要在规定期限内准时归还,而不必交延时服务费,李强每天至少要看几页?
市民图书馆借阅规定 1借阅期限:10天。 2超过10天的,从第11天起,每天每册收取0.5元延时服务费。
参考答案与试题解析
一.选择题(共10小题,共10分)
1.B
【分析】“6”在十分位上,表示6个十分之一。
【解析】解:A.164,“6”在十位上,表示6个十;
B.5.67,“6”在十分位上,表示6个十分之一;
C.8.062,“6”在百分位上,表示6个百分之一;
D.21.946,“6”在千分位上,表示6个千分之一。
“6”表示6个十分之一的是5.67。
故选:B。
【点评】本题考查了小数的意义。
2.B
【分析】根据题意,把电影院楼下的座位数和楼上的座位数分别看成和它接近的整百数,再相加,即可求出这个电影院大约能容纳的人数,再与1000人比较即可。
【解析】解:697≈700
208≈200
700+200=900(人)
900人<1000人,能同时容纳1000人看电影。
故选:B。
【点评】此题考查整数的估算。估算时把一个数看作与它接近的整千、整百、整十的数,再进行计算。
3.B
【分析】依据题意结合图示可知,有侧面是一个长是35厘米,宽是30厘米的长方形,利用长方形的面积=长×宽,结合题中数据计算即可。
【解析】解:重新配的玻璃的面积是:35×30=1050(平方厘米)。
故选:B。
【点评】本题考查的是长方体的表面积的应用。
4.A
【分析】小时收割公顷小麦,求收割1公顷需要多少小时,就是用除以即可解答。
【解析】解:
(小时)
答:这台收割机收割1公顷需要小时。
故选:A。
【点评】这种类型的题目属于基本的分数除法应用题,利用基本数量关系解决问题。
5.D
【分析】根据三角形的三边关系可知:三角形的三边必须满足:任意两边之和大于第三边,才能围成三角形,由此只能选出1根4厘米和2根9厘米的小棒,根据三角形的周长定义即可解答。
【解析】解:选出围成一个等腰三角形的3根小棒的长度分别是:4厘米、9厘米、9厘米,
所以这个三角形的周长是:9+9+4=22(厘米)
答:围成的等腰三角形的周长是22厘米。
故选:D。
【点评】此题考查了三角形的三边关系以及三角形的周长的计算方法的灵活应用。
6.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解析】解:A.长方形面积=长×宽,长方形面积一定,是乘积一定,所以长和宽成反比例。
B.因为圆的面积S=πr2,(r为圆的半径),所以圆的面积÷半径的平方=π,π是一定的,即圆的半径的平方和面积成正比例关系,但圆的半径和面积不成比例。
C.订阅《小学生数学报》的总价÷数量=单价(一定),商一定,所以订阅《小学生数学报》的总价和数量成正比例关系。
D. ,xy=6×9,x和y的乘积一定,所以x和y成反比例。
故选:C。
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,还是对应的其它量一定,再作判断即可。
7.D
【分析】三角形的内角和为180°,进一步直接利用按比例分配求得份数最大的角,进而根据三角形的分类进行判断即可。
【解析】解:1+2+6=9
180120(度)
答:这个三角形一定是钝角三角形。
故选:D。
【点评】此题主要利用三角形的内角和与按比例分配来解答问题。
8.C
【分析】根据2 的倍数特征,B、C合适,再根据3的倍数特征,C合适。
【解析】解:根据2和3的倍数特征,只有132符合题意。
故选:C。
【点评】本题考查的是2和3的倍数特征,2的倍数特征:个位是0、2、4、6、8的;3的倍数特征:各位数字和是3的倍数。
9.C
【分析】正方体的体积等于棱长的立方,所以他们的体积比等于他们棱长的立方比。
【解析】解:因为正方体的棱长之比是1:3,
所以它们的体积之比是13:33,也就是1:27。
故选:C。
【点评】根据正方体的体积公式和比的知识解决此问题。
10.A
【分析】把一根铁丝看作单位“1”,平均分成3份,其中的2份表示剪去的,那么还剩下(3﹣2)份,据此比较即可。
【解析】解:根据分析可知,一根铁丝,剪去,还剩下1,,所以剪去的长。
故选:A。
【点评】本题考查了分数大小比较的应用。
二.填空题(共14小题,共24分)
11.3239680000,32。
【分析】根据整数的写法,从高位到低位,一级一级地写,哪一个数位上一个计数单位也没有,就在那个数位上写0,即可写出此数;
省略“亿”后面的尾数就是四舍五入到亿位,就是把亿位后的千万位上的数进行四舍五入,再在数的后面写上“亿”字。
【解析】解:三十二亿三千九百六十八万写作:3239680000,3239680000≈32亿。
故答案为:3239680000,32。
【点评】本题主要考查整数的写法和求近似数,分级写或借助数位表写数能较好地避免写错数的情况,求近似数时要注意带计数单位。
12.﹣1,。
【分析】根据图示,数轴上的0到﹣2之间平均分成4份,每份是1,结合正负数知识即可知道直线上的点x表示的数是﹣1;
数轴上的0到1之间平均分成5份,每份用分数表示是,据此解答即可。
【解析】解:直线上的点x表示的数是﹣1,点y表示的数写成分数是。
故答案为:﹣1,。
【点评】本题考查了数轴的认识,结合正负数知识解答即可。
13.1。
【分析】相邻的两个非0自然数互质,两个数互质,则最大公因数是1。
【解析】解:如果m﹣n=1(m和n是不为0的自然数),那么m和n的最大公因数是1。
故答案为:1。
【点评】本题主要考查求两个数的最大公因数的方法。
14.2:3。
【分析】根据长方形面积=长×宽,三角形面积=底×高÷2,分别求出它们的面积,再写出它们的比并化简,即可解答。
【解析】解:5×2=10
4×2÷2
=8÷2
=4
10﹣4=6
4:6=2:3
答:涂色部分面积与空白部分面积的最简整数比是2:3。
故答案为:2:3。
【点评】本题考查的是比的意义,理解和应用比的意义是解答关键。
15.8,113.04。
【分析】一个圆柱形木料底面直径是6厘米。如果沿着直径和高把它平均分成两块(如图1所示),那么表面积比原来增加两个长是圆柱底面直径,宽是圆柱的高的长方形面积,用96除以2,求出一个长方形面积,再除以6,求出长方形的宽,就是圆柱的高,如果把这个圆柱平均截成3段(如图2所示),那么表面积比原来增加4个圆柱底面面积,根据圆的面积=×半径×半径,求出一个圆柱底面面积,再乘4,即可解答。
【解析】解:96÷2÷6
=48÷6
=8(厘米)
3.14×(6÷2)×(6÷2)×4
=28.26×4
=113.04(平方厘米)
答:这个圆柱的高是8厘米;如果把这个圆柱平均截成3段(如图2所示),那么表面积比原来增加113.04平方厘米。
故答案为:8,113.04。
【点评】本题考查的是圆柱的底面积、侧面积、表面积,熟记公式是解答关键。
16.2060,0.08。
【分析】高级单位升化低级单位毫升乘进率1000。
低级单位平方米化高级单位公顷除以进率10000。
【解析】解:2.06升=2060毫升
800平方米=0.08公顷
故答案为:2060,0.08。
【点评】此题考查了体积(容积)的单位换算、面积的单位换算。单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率。
17.11111111。
【分析】观察题中算式可知:乘加算式中第一个因数是n个3,第二个因数是(n﹣1)个3和一共4,减数是1,结果等于2n个1。由此解答本题。
【解析】解:3333×3334﹣1111=11111111。
故答案为:11111111。
【点评】解决本题的关键是找出题中的规律,利用规律去解答。
18.白;再往袋子里放2个黑球(答案不唯一)。
【分析】根据白球和黑球的数量进行分析解答。
【解析】解:白球有4个,黑球有2个,所以摸到白球的可能性大;
如果要使摸到黑球和白球的可能性相等,则黑球和白球的数量应相等,可以再往袋子里放2个黑球(答案不唯一)。
故答案为:白;再往袋子里放2个黑球(答案不唯一)。
【点评】此题考查可能性的大小。
19.(8.5a+6.5b)。
【分析】苹果的单价是8.5元/千克,买了a千克苹果,根据单价×数量=总价,列式是8.5×a=8.5a买了a千克苹果,桃子的总价求法同苹果的总价。再把苹果和桃子的钱数加起来即可。
【解析】解:8.5×a+6.5×b=(8.5a+6.5b)元
答:一共要付(8.5a+6.5b)元。
故答案为:(8.5a+6.5b)。
【点评】本题考查了用字母表示单价、数量、总价的关系。
20.0.5。
【分析】依据题意可知,利用圆锥的体积=底面积×高÷3,长方体的体积=长×宽×高,结合题中数据计算即可。
【解析】解:30×1.5÷3÷(7.5×4)
=15÷30
=0.5(米)
答:沙坑里沙子的厚度是0.5米。
故答案为:0.5。
【点评】本题考查的是圆锥、长方体的体积公式的应用。
21.300。
【分析】商品打八八折,就是按照原价的88%出售,可以节省原价的(1﹣88%),用2500×(1﹣88%)计算。
【解析】解:2500×(1﹣88%)
=2500×12%
=300(元)
答:可以节省300元。
故答案为:300。
【点评】本题考查了百分数乘法的意义及折扣的知识。
22.见试题解答内容
【分析】用打折后的钱数除以原件即可求出打几折;先用成活的数量除以92%求出种树总数量;然后用总数量乘(1﹣92%)就是未成活数量。
【解析】解:4160÷5200×100%
=0.8×100%
=80%
80%=八折
46÷92%×(1﹣92%)
=50×8%
=4(棵)
故答案为:八;4。
【点评】此题应了解“折数”的概念,以及对简单的百分数应用题的掌握。
23.;11。
【分析】先根据分数单位的意义确定出的分数单位,然后根据假分数的意义先确定M的值,然后找出其中的质数即可。
【解析】解:的分数单位是。
是假分数,则M≥8;是假分数,则M≤12,所以8≤M≤12,M可以是8、9、10、11、12,如果M是一个质数,那么这里的M是11。
答:的分数单位是;如果M是一个质数,那么这里的M是 11。
故答案为:;11。
【点评】解答本题需熟练掌握假分数的意义,熟记20以内的质数,灵活解答。
24.12,(2a+2)。
【分析】单独一个正方形的周长是4厘米,每多一个正方形周长就增加2厘米,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,然后结合规律解答。
【解析】解:2个正方形拼成长方形的周长=4+(2﹣1)×2=6(厘米)
3个正方形拼成长方形的周长=4+(3﹣1)×2=8(厘米)
4个正方形拼成长方形的周长=4+(4﹣1)×2=10(厘米)
5个正方形拼成长方形的周长=4+(5﹣1)×2=12(厘米)
.......
由此得出规律:用a个正方形拼成长方形的周长=4+(a﹣1)×2=(2a+2)厘米
故答案为:12,(2a+2)。
【点评】此题属于数与形结合的规律,考查的目的是通过特例分析从而归纳总结出一般结论的能力,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,然后利用规律解决问题。
三.计算题(共3小题,共26分)
25.328,,1.52,,30,,,25。
【分析】根据整数减法,小数加法和除法,以及分数加减乘除法的计算方法求解;0.25×99+25%根据乘法分配律计算。
【解析】解:
726﹣398=328 0.72+0.8=1.52
5.7÷0.19=30 0.25×99+25%=25
【点评】本题考查了简单的计算,计算时要细心,注意平时积累经验,提高计算的水平。
26.x=2;x;x。
【分析】(1)先计算1.8×2,根据等式的基本性质,方程两边同时加上3.6;再同时除以3即可;
(2)先计算左面的算式,等式两边再同时除以;
(3)根据比例的基本性质,两个内项的积等于两个外项的积,化成普通方程,等式两边再同时除以即可。
【解析】解:3x﹣1.8×2=2.4
3x=6
x=2
x
x
x
x
【点评】此题主要考查了解比例问题,要熟练掌握,注意比例的基本性质的应用。
27.;34;3.048。
【分析】第一道题:先把小数化成分数,再根据分数连乘的计算方法计算即可;
第二道题:先算小括号里面的减法,再算中括号里面的除法,最后算括号外面的乘法;
第三道题:应用乘法分配律计算比较简便。
【解析】解:
[(1﹣90%)]
=34
=1.6+2﹣0.552
=3.048
【点评】熟练掌握乘法分配律和小数化成分数、分数连乘的计算方法以及四则混合运算的运算顺序,是解答本题的关键。
四.操作题(共1小题,共6分)
28.(以三角形ABC的AB边为底,再画出一个和三角形ABC面积相等的三角形,画法不唯一)。
【分析】(1)等底、等高的三角形面积相等,以AB为底,以点C所在行上的任意一点(或以AB下面2格的直线上任意一点)所画的三角形都与三角形ABC的面积相等(画法不唯一)。
(2)根据旋转的特征,三角形ABC绕点A逆时针旋转90°,点A的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(3)三角形ABC看作底为3格,高为2格三角形,根据图形放大的意义,把这个图形对应的底边、高均放大到原来的2倍,对应角大小不变,所得到的图形就是原图形按2:1放大后的图形。
【解析】解:根据题意画图如下:
(以三角形ABC的AB边为底,再画出一个和三角形ABC面积相等的三角形,画法不唯一)。
【点评】此题考查的知识点:三角形面积的计算、作旋转一定度数后的图形、图形的放大与缩小。
五.应用题(共6小题,共36分)
29.象棋有16副;跳棋有12副。
【分析】全是象棋时,少算了的人数与一副跳棋和一副象棋需要人数之差的商就是跳棋的副数,然后再进一步解答即可。
【解析】解:(104﹣2×28)÷(6﹣2)
=48÷4
=12(副)
28﹣12=16(副)
答:象棋有16副;跳棋有12副。
【点评】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
30.钢笔有8盒,铅笔有4盒。
【分析】假设全部是铅笔,则共有12×12=144(支),比实际的少算了144﹣128=16(支),因为把每盒钢笔当做铅笔多算了12﹣10=2(支),所以钢笔有16÷2=8(盒),则铅笔有12﹣8=4(盒),据此解答。
【解析】解:钢笔:(12×12﹣128)÷(12﹣10)
=16÷2
=8(盒)
铅笔:12﹣8=4(盒)
答:钢笔有8盒,铅笔有4盒。
【点评】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
31.44名学生购买学生票,8名老师正常购票。
【分析】根据总价=单价×数量,分别求出两种优惠政策下,购票需要的钱数各是多少,再比较大小,判断出选择哪种方案购票最合算即可。
【解析】解:(44+8)×20×60%
=52×20×0.6
=624(元)
20×8+44×20×50%
=160+440
=600(元)
600<624
答:44名学生购买学生票,8名老师正常购票更划算。
【点评】此题主要考查了最优化问题,解答此题的关键是熟练掌握单价、总价、数量的关系,分别求出两种优惠政策下,购票需要的钱数各是多少。
32.30人。
【分析】根据题干,设女生有x人,则男生就是(42﹣x)人,再利用等量关系:男生人数×2.5+女生人数×3=采集的标本总件数120,据此列出方程即可解答问题。
【解析】解:设女生有x人,则男生就是(42﹣x)人。
3x+2.5×(42﹣x)=120
3x+105﹣2.5x=120
0.5x=15
x=30
答:六年级3班女生有30人。
【点评】此题含有两个未知数,可以先设出其中一个为x,另一个用x来表示,再利用等量关系列出方程即可解决问题。
33.男教师有6人;女教师有2人。
【分析】假设都是男教师则共有学生6×8=48(人),比实际多了48﹣44=4(人),然后除以男、女老师负责的每组的人数差,求出女老师负责的组数,即女老师的人数,然后进一步解答即可。
【解析】解:(6×8﹣44)÷(6﹣4)
=4÷2
=2(人)
8﹣2=6(人)
答:男教师有6人;女教师有2人。
【点评】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
34.24页。
【分析】要想能准时归还而不交延时服务费,就必须10天看完这本书,所以要先求出这本书一共有多少页,就是求15个16页是多少,用乘法计算,即16×15;然后用总页数除以10天,就是她每天要看的页数,由此求解。
【解析】解:16×15÷10
=240÷10
=24(页)
答:李强每天至少要看24页。
【点评】本题主要考查了整数乘除法的意义和实际应用,要熟练掌握。
21世纪教育网(www.21cnjy.com)
2024-2025学年六年级下册数学小升初分班考高频考点预测卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题(共10小题,共10分)
1.下面各数中的“6”表示6个十分之一的是( )
A.164 B.5.67 C.8.062 D.21.946
2.一个电影院楼下有697个座位,楼上有208个座位。这个电影院能同时容纳1000人看电影吗?解决这个问题适合选择( )
A.口算 B.估算 C.笔算 D.计算器计算
3.一个长方体金鱼缸(如图所示),长40厘米,宽30厘米,高35厘米。它右侧面的玻璃打碎了,要重新配一块。重新配的玻璃是( )平方厘米。
A.1200 B.1050 C.1400 D.2100
4.一台收割机小时收割公顷小麦,这台收割机收割1公顷需要( )小时。
A. B. C. D.
5.从两根长4厘米和两根长9厘米的小棒中,选出3根围成一个等腰三角形,这个等腰三角形的周长是( )厘米。
A.12 B.17 C.27 D.22
6.下面各题中的两种量成正比例的是( )
A.长方形面积一定,长和宽 B.圆的半径和面积
C.订阅《小学生数学报》的总价和数量 D.,x和y
7.一个三角形的三个内角的度数比是1:2:6,这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.等腰三角形 D.钝角三角形
8.下面的数中,( )是2的倍数,也是3的倍数。
A.45 B.100 C.132 D.225
9.两个正方体的棱长之比是1:3,它们的体积之比是( )
A.1:3 B.1:9 C.1:27 D.1:81
10.一根铁丝,剪去,还剩下米,则( )
A.剪去的长 B.剩下的长 C.剪去的和剩下的一样长 D.无法确定
二.填空题(共14小题,共22分)
11.我国有丰富的石油资源,基础储量大约是三十二亿三千九百六十八万吨,横线上的数写作 ,省略“亿”后面的尾数大约是 亿。
12.直线上的点x表示的数是 ,点y表示的数写成分数是 。
13.如果m﹣n=1(m和n是不等于0的自然数),那么m和n的最大公因数是 。
14.如图所示,涂色部分面积与空白部分面积的最简整数比是 。
15.一个圆柱形木料底面直径是6厘米。如果沿着直径和高把它平均分成两块(如图1所示),那么表面积比原来增加96平方厘米,这个圆柱的高是 厘米;如果把这个圆柱平均截成3段(如图2所示),那么表面积比原来增加 平方厘米。
16.2.06升= 毫升 800平方米= 公顷
17.找规律,接着填写:3×4﹣1=11,33×34﹣11=1111,333×334﹣111=111111,3333×3334﹣1111= 。
18.从袋子里任意摸一个球(如图所示),摸到 球的可能性大;如果要使摸到黑球和白球的可能性相等,你的方法是 。
19.苹果的单价是8.5元/千克,桃子的单价是6.5元/千克。爸爸买了a千克苹果和b千克桃子,一共要付______ 元。
20.一个圆锥形沙堆,底面积是30平方米,高是1.5米。如果把这堆沙均匀地填在一个长7.5米、宽4米的长方体沙坑里,那么沙坑里沙子的厚度是 米。
21.李叔叔想买一部价值2500元的手机,他到6月18日去买,可以节省 元。
22.张阿姨买一台冰箱,原价5200元,打 折后,只花了4160元;李叔叔种了一批树,成活率是92%,成活了46棵,未成活的有 棵。
23.和都是假分数,的分数单位是 ;如果M是一个质数,那么这里的M是 。
24.用边长1cm的小正方形拼成长方形(如图)。像这样,用5个小正方形拼成的长方形的周长是 厘米,用a个小正方形拼成的长方形的周长是 厘米。
三.计算题(共3小题,共26分)
25.口算。(共8分)
726﹣398= 0.72+0.8=
5.7÷0.19= 0.25×99+25%=
26.求x的值。(共9分)
3x﹣1.8×2=2.4
27.脱式计算,能简算的要简算。(共9分)
0.12 [(1﹣90%)]
四.操作题(共1小题,共6分)
28.请按要求画图。
(1)以三角形ABC的AB边为底,再画出一个和三角形ABC面积相等的三角形。
(2)画出把三角形ABC绕点A逆时针旋转90°后的图形。
(3)画出把三角形ABC按2:1放大后的图形。
五.应用题(共6小题,共36分)
29.学校有象棋、跳棋共28副,2人下一副象棋,6人下一副跳棋,恰好可供104人进行活动。象棋与跳棋各有多少副?
30.某商店新购进钢笔和铅笔共12盒,共128支。钢笔每盒10支,铅笔每盒12支。钢笔和铅笔各有多少盒?
31.科技馆“七色彩虹”项目的门票20元/张,优惠政策有两种:满50张可以购买团体票,团体票打六折;购买学生票打五折。如果六(4)班44名学生和8名老师都参加“七色彩虹”项目,怎样购票更划算?(请通过计算说明)
32.六年级3班42名同学采集标本共120件,男生平均每人采集2.5件,女生平均每人采集3件。六年级3班女生有多少人?
33.为了方便参加“球形屏幕观影”项目,44名同学们分为8个小组,每个老师负责一组,男老师负责的小组每组有6名学生,女教师负责的小组每组有4名学生,正好安排完。你知道男教师、女教师各有多少人?
34.李强在市民图书馆借了一本历史故事书,如果每天看16页,15天能全部看完。如果要在规定期限内准时归还,而不必交延时服务费,李强每天至少要看几页?
市民图书馆借阅规定 1借阅期限:10天。 2超过10天的,从第11天起,每天每册收取0.5元延时服务费。
参考答案与试题解析
一.选择题(共10小题,共10分)
1.B
【分析】“6”在十分位上,表示6个十分之一。
【解析】解:A.164,“6”在十位上,表示6个十;
B.5.67,“6”在十分位上,表示6个十分之一;
C.8.062,“6”在百分位上,表示6个百分之一;
D.21.946,“6”在千分位上,表示6个千分之一。
“6”表示6个十分之一的是5.67。
故选:B。
【点评】本题考查了小数的意义。
2.B
【分析】根据题意,把电影院楼下的座位数和楼上的座位数分别看成和它接近的整百数,再相加,即可求出这个电影院大约能容纳的人数,再与1000人比较即可。
【解析】解:697≈700
208≈200
700+200=900(人)
900人<1000人,能同时容纳1000人看电影。
故选:B。
【点评】此题考查整数的估算。估算时把一个数看作与它接近的整千、整百、整十的数,再进行计算。
3.B
【分析】依据题意结合图示可知,有侧面是一个长是35厘米,宽是30厘米的长方形,利用长方形的面积=长×宽,结合题中数据计算即可。
【解析】解:重新配的玻璃的面积是:35×30=1050(平方厘米)。
故选:B。
【点评】本题考查的是长方体的表面积的应用。
4.A
【分析】小时收割公顷小麦,求收割1公顷需要多少小时,就是用除以即可解答。
【解析】解:
(小时)
答:这台收割机收割1公顷需要小时。
故选:A。
【点评】这种类型的题目属于基本的分数除法应用题,利用基本数量关系解决问题。
5.D
【分析】根据三角形的三边关系可知:三角形的三边必须满足:任意两边之和大于第三边,才能围成三角形,由此只能选出1根4厘米和2根9厘米的小棒,根据三角形的周长定义即可解答。
【解析】解:选出围成一个等腰三角形的3根小棒的长度分别是:4厘米、9厘米、9厘米,
所以这个三角形的周长是:9+9+4=22(厘米)
答:围成的等腰三角形的周长是22厘米。
故选:D。
【点评】此题考查了三角形的三边关系以及三角形的周长的计算方法的灵活应用。
6.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解析】解:A.长方形面积=长×宽,长方形面积一定,是乘积一定,所以长和宽成反比例。
B.因为圆的面积S=πr2,(r为圆的半径),所以圆的面积÷半径的平方=π,π是一定的,即圆的半径的平方和面积成正比例关系,但圆的半径和面积不成比例。
C.订阅《小学生数学报》的总价÷数量=单价(一定),商一定,所以订阅《小学生数学报》的总价和数量成正比例关系。
D. ,xy=6×9,x和y的乘积一定,所以x和y成反比例。
故选:C。
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,还是对应的其它量一定,再作判断即可。
7.D
【分析】三角形的内角和为180°,进一步直接利用按比例分配求得份数最大的角,进而根据三角形的分类进行判断即可。
【解析】解:1+2+6=9
180120(度)
答:这个三角形一定是钝角三角形。
故选:D。
【点评】此题主要利用三角形的内角和与按比例分配来解答问题。
8.C
【分析】根据2 的倍数特征,B、C合适,再根据3的倍数特征,C合适。
【解析】解:根据2和3的倍数特征,只有132符合题意。
故选:C。
【点评】本题考查的是2和3的倍数特征,2的倍数特征:个位是0、2、4、6、8的;3的倍数特征:各位数字和是3的倍数。
9.C
【分析】正方体的体积等于棱长的立方,所以他们的体积比等于他们棱长的立方比。
【解析】解:因为正方体的棱长之比是1:3,
所以它们的体积之比是13:33,也就是1:27。
故选:C。
【点评】根据正方体的体积公式和比的知识解决此问题。
10.A
【分析】把一根铁丝看作单位“1”,平均分成3份,其中的2份表示剪去的,那么还剩下(3﹣2)份,据此比较即可。
【解析】解:根据分析可知,一根铁丝,剪去,还剩下1,,所以剪去的长。
故选:A。
【点评】本题考查了分数大小比较的应用。
二.填空题(共14小题,共24分)
11.3239680000,32。
【分析】根据整数的写法,从高位到低位,一级一级地写,哪一个数位上一个计数单位也没有,就在那个数位上写0,即可写出此数;
省略“亿”后面的尾数就是四舍五入到亿位,就是把亿位后的千万位上的数进行四舍五入,再在数的后面写上“亿”字。
【解析】解:三十二亿三千九百六十八万写作:3239680000,3239680000≈32亿。
故答案为:3239680000,32。
【点评】本题主要考查整数的写法和求近似数,分级写或借助数位表写数能较好地避免写错数的情况,求近似数时要注意带计数单位。
12.﹣1,。
【分析】根据图示,数轴上的0到﹣2之间平均分成4份,每份是1,结合正负数知识即可知道直线上的点x表示的数是﹣1;
数轴上的0到1之间平均分成5份,每份用分数表示是,据此解答即可。
【解析】解:直线上的点x表示的数是﹣1,点y表示的数写成分数是。
故答案为:﹣1,。
【点评】本题考查了数轴的认识,结合正负数知识解答即可。
13.1。
【分析】相邻的两个非0自然数互质,两个数互质,则最大公因数是1。
【解析】解:如果m﹣n=1(m和n是不为0的自然数),那么m和n的最大公因数是1。
故答案为:1。
【点评】本题主要考查求两个数的最大公因数的方法。
14.2:3。
【分析】根据长方形面积=长×宽,三角形面积=底×高÷2,分别求出它们的面积,再写出它们的比并化简,即可解答。
【解析】解:5×2=10
4×2÷2
=8÷2
=4
10﹣4=6
4:6=2:3
答:涂色部分面积与空白部分面积的最简整数比是2:3。
故答案为:2:3。
【点评】本题考查的是比的意义,理解和应用比的意义是解答关键。
15.8,113.04。
【分析】一个圆柱形木料底面直径是6厘米。如果沿着直径和高把它平均分成两块(如图1所示),那么表面积比原来增加两个长是圆柱底面直径,宽是圆柱的高的长方形面积,用96除以2,求出一个长方形面积,再除以6,求出长方形的宽,就是圆柱的高,如果把这个圆柱平均截成3段(如图2所示),那么表面积比原来增加4个圆柱底面面积,根据圆的面积=×半径×半径,求出一个圆柱底面面积,再乘4,即可解答。
【解析】解:96÷2÷6
=48÷6
=8(厘米)
3.14×(6÷2)×(6÷2)×4
=28.26×4
=113.04(平方厘米)
答:这个圆柱的高是8厘米;如果把这个圆柱平均截成3段(如图2所示),那么表面积比原来增加113.04平方厘米。
故答案为:8,113.04。
【点评】本题考查的是圆柱的底面积、侧面积、表面积,熟记公式是解答关键。
16.2060,0.08。
【分析】高级单位升化低级单位毫升乘进率1000。
低级单位平方米化高级单位公顷除以进率10000。
【解析】解:2.06升=2060毫升
800平方米=0.08公顷
故答案为:2060,0.08。
【点评】此题考查了体积(容积)的单位换算、面积的单位换算。单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率。
17.11111111。
【分析】观察题中算式可知:乘加算式中第一个因数是n个3,第二个因数是(n﹣1)个3和一共4,减数是1,结果等于2n个1。由此解答本题。
【解析】解:3333×3334﹣1111=11111111。
故答案为:11111111。
【点评】解决本题的关键是找出题中的规律,利用规律去解答。
18.白;再往袋子里放2个黑球(答案不唯一)。
【分析】根据白球和黑球的数量进行分析解答。
【解析】解:白球有4个,黑球有2个,所以摸到白球的可能性大;
如果要使摸到黑球和白球的可能性相等,则黑球和白球的数量应相等,可以再往袋子里放2个黑球(答案不唯一)。
故答案为:白;再往袋子里放2个黑球(答案不唯一)。
【点评】此题考查可能性的大小。
19.(8.5a+6.5b)。
【分析】苹果的单价是8.5元/千克,买了a千克苹果,根据单价×数量=总价,列式是8.5×a=8.5a买了a千克苹果,桃子的总价求法同苹果的总价。再把苹果和桃子的钱数加起来即可。
【解析】解:8.5×a+6.5×b=(8.5a+6.5b)元
答:一共要付(8.5a+6.5b)元。
故答案为:(8.5a+6.5b)。
【点评】本题考查了用字母表示单价、数量、总价的关系。
20.0.5。
【分析】依据题意可知,利用圆锥的体积=底面积×高÷3,长方体的体积=长×宽×高,结合题中数据计算即可。
【解析】解:30×1.5÷3÷(7.5×4)
=15÷30
=0.5(米)
答:沙坑里沙子的厚度是0.5米。
故答案为:0.5。
【点评】本题考查的是圆锥、长方体的体积公式的应用。
21.300。
【分析】商品打八八折,就是按照原价的88%出售,可以节省原价的(1﹣88%),用2500×(1﹣88%)计算。
【解析】解:2500×(1﹣88%)
=2500×12%
=300(元)
答:可以节省300元。
故答案为:300。
【点评】本题考查了百分数乘法的意义及折扣的知识。
22.见试题解答内容
【分析】用打折后的钱数除以原件即可求出打几折;先用成活的数量除以92%求出种树总数量;然后用总数量乘(1﹣92%)就是未成活数量。
【解析】解:4160÷5200×100%
=0.8×100%
=80%
80%=八折
46÷92%×(1﹣92%)
=50×8%
=4(棵)
故答案为:八;4。
【点评】此题应了解“折数”的概念,以及对简单的百分数应用题的掌握。
23.;11。
【分析】先根据分数单位的意义确定出的分数单位,然后根据假分数的意义先确定M的值,然后找出其中的质数即可。
【解析】解:的分数单位是。
是假分数,则M≥8;是假分数,则M≤12,所以8≤M≤12,M可以是8、9、10、11、12,如果M是一个质数,那么这里的M是11。
答:的分数单位是;如果M是一个质数,那么这里的M是 11。
故答案为:;11。
【点评】解答本题需熟练掌握假分数的意义,熟记20以内的质数,灵活解答。
24.12,(2a+2)。
【分析】单独一个正方形的周长是4厘米,每多一个正方形周长就增加2厘米,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,然后结合规律解答。
【解析】解:2个正方形拼成长方形的周长=4+(2﹣1)×2=6(厘米)
3个正方形拼成长方形的周长=4+(3﹣1)×2=8(厘米)
4个正方形拼成长方形的周长=4+(4﹣1)×2=10(厘米)
5个正方形拼成长方形的周长=4+(5﹣1)×2=12(厘米)
.......
由此得出规律:用a个正方形拼成长方形的周长=4+(a﹣1)×2=(2a+2)厘米
故答案为:12,(2a+2)。
【点评】此题属于数与形结合的规律,考查的目的是通过特例分析从而归纳总结出一般结论的能力,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,然后利用规律解决问题。
三.计算题(共3小题,共26分)
25.328,,1.52,,30,,,25。
【分析】根据整数减法,小数加法和除法,以及分数加减乘除法的计算方法求解;0.25×99+25%根据乘法分配律计算。
【解析】解:
726﹣398=328 0.72+0.8=1.52
5.7÷0.19=30 0.25×99+25%=25
【点评】本题考查了简单的计算,计算时要细心,注意平时积累经验,提高计算的水平。
26.x=2;x;x。
【分析】(1)先计算1.8×2,根据等式的基本性质,方程两边同时加上3.6;再同时除以3即可;
(2)先计算左面的算式,等式两边再同时除以;
(3)根据比例的基本性质,两个内项的积等于两个外项的积,化成普通方程,等式两边再同时除以即可。
【解析】解:3x﹣1.8×2=2.4
3x=6
x=2
x
x
x
x
【点评】此题主要考查了解比例问题,要熟练掌握,注意比例的基本性质的应用。
27.;34;3.048。
【分析】第一道题:先把小数化成分数,再根据分数连乘的计算方法计算即可;
第二道题:先算小括号里面的减法,再算中括号里面的除法,最后算括号外面的乘法;
第三道题:应用乘法分配律计算比较简便。
【解析】解:
[(1﹣90%)]
=34
=1.6+2﹣0.552
=3.048
【点评】熟练掌握乘法分配律和小数化成分数、分数连乘的计算方法以及四则混合运算的运算顺序,是解答本题的关键。
四.操作题(共1小题,共6分)
28.(以三角形ABC的AB边为底,再画出一个和三角形ABC面积相等的三角形,画法不唯一)。
【分析】(1)等底、等高的三角形面积相等,以AB为底,以点C所在行上的任意一点(或以AB下面2格的直线上任意一点)所画的三角形都与三角形ABC的面积相等(画法不唯一)。
(2)根据旋转的特征,三角形ABC绕点A逆时针旋转90°,点A的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(3)三角形ABC看作底为3格,高为2格三角形,根据图形放大的意义,把这个图形对应的底边、高均放大到原来的2倍,对应角大小不变,所得到的图形就是原图形按2:1放大后的图形。
【解析】解:根据题意画图如下:
(以三角形ABC的AB边为底,再画出一个和三角形ABC面积相等的三角形,画法不唯一)。
【点评】此题考查的知识点:三角形面积的计算、作旋转一定度数后的图形、图形的放大与缩小。
五.应用题(共6小题,共36分)
29.象棋有16副;跳棋有12副。
【分析】全是象棋时,少算了的人数与一副跳棋和一副象棋需要人数之差的商就是跳棋的副数,然后再进一步解答即可。
【解析】解:(104﹣2×28)÷(6﹣2)
=48÷4
=12(副)
28﹣12=16(副)
答:象棋有16副;跳棋有12副。
【点评】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
30.钢笔有8盒,铅笔有4盒。
【分析】假设全部是铅笔,则共有12×12=144(支),比实际的少算了144﹣128=16(支),因为把每盒钢笔当做铅笔多算了12﹣10=2(支),所以钢笔有16÷2=8(盒),则铅笔有12﹣8=4(盒),据此解答。
【解析】解:钢笔:(12×12﹣128)÷(12﹣10)
=16÷2
=8(盒)
铅笔:12﹣8=4(盒)
答:钢笔有8盒,铅笔有4盒。
【点评】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
31.44名学生购买学生票,8名老师正常购票。
【分析】根据总价=单价×数量,分别求出两种优惠政策下,购票需要的钱数各是多少,再比较大小,判断出选择哪种方案购票最合算即可。
【解析】解:(44+8)×20×60%
=52×20×0.6
=624(元)
20×8+44×20×50%
=160+440
=600(元)
600<624
答:44名学生购买学生票,8名老师正常购票更划算。
【点评】此题主要考查了最优化问题,解答此题的关键是熟练掌握单价、总价、数量的关系,分别求出两种优惠政策下,购票需要的钱数各是多少。
32.30人。
【分析】根据题干,设女生有x人,则男生就是(42﹣x)人,再利用等量关系:男生人数×2.5+女生人数×3=采集的标本总件数120,据此列出方程即可解答问题。
【解析】解:设女生有x人,则男生就是(42﹣x)人。
3x+2.5×(42﹣x)=120
3x+105﹣2.5x=120
0.5x=15
x=30
答:六年级3班女生有30人。
【点评】此题含有两个未知数,可以先设出其中一个为x,另一个用x来表示,再利用等量关系列出方程即可解决问题。
33.男教师有6人;女教师有2人。
【分析】假设都是男教师则共有学生6×8=48(人),比实际多了48﹣44=4(人),然后除以男、女老师负责的每组的人数差,求出女老师负责的组数,即女老师的人数,然后进一步解答即可。
【解析】解:(6×8﹣44)÷(6﹣4)
=4÷2
=2(人)
8﹣2=6(人)
答:男教师有6人;女教师有2人。
【点评】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
34.24页。
【分析】要想能准时归还而不交延时服务费,就必须10天看完这本书,所以要先求出这本书一共有多少页,就是求15个16页是多少,用乘法计算,即16×15;然后用总页数除以10天,就是她每天要看的页数,由此求解。
【解析】解:16×15÷10
=240÷10
=24(页)
答:李强每天至少要看24页。
【点评】本题主要考查了整数乘除法的意义和实际应用,要熟练掌握。
21世纪教育网(www.21cnjy.com)
同课章节目录
