(小升初择校分班考)小升初重点校入学分班考押题卷-2024-2025学年六年级下册数学苏教版(含答案解析)
文档属性
| 名称 | (小升初择校分班考)小升初重点校入学分班考押题卷-2024-2025学年六年级下册数学苏教版(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 286.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 05:32:10 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024-2025学年六年级下册数学小升初重点校入学分班考押题卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题(共10小题,共10分)
1.连云港到南京的距离约为320千米,在一张比例尺为1:2000000的江苏地图上,它们之间的距离大约相当于( )的长度。
A.一根火柴 B.一支铅笔 C.一把米尺 D.一根鱼竿
2.如图,农行在体育场的北偏东30°方向,它又在超市的( )方向。
A.北偏东60° B.北偏西60° C.北偏东30° D.北偏西30°
3.某房地产企业准备三种方案,计划分两次先后降价促销清盘。方案一:第一次降价5%,第二次降价10%;方案二:第一次降价8%,第二次降价7%;方案三:第一次降价12%,第二次降价3%。三种方案降价后的价格相比,( )
A.方案一低 B.方案二低 C.方案三低 D.价格相等
4.如图,将一个高为10厘米的圆柱体切拼成近似的长方体,表面积增加了80平方厘米,这个圆柱的半径是( )厘米。
A.4 B.5 C.8 D.10
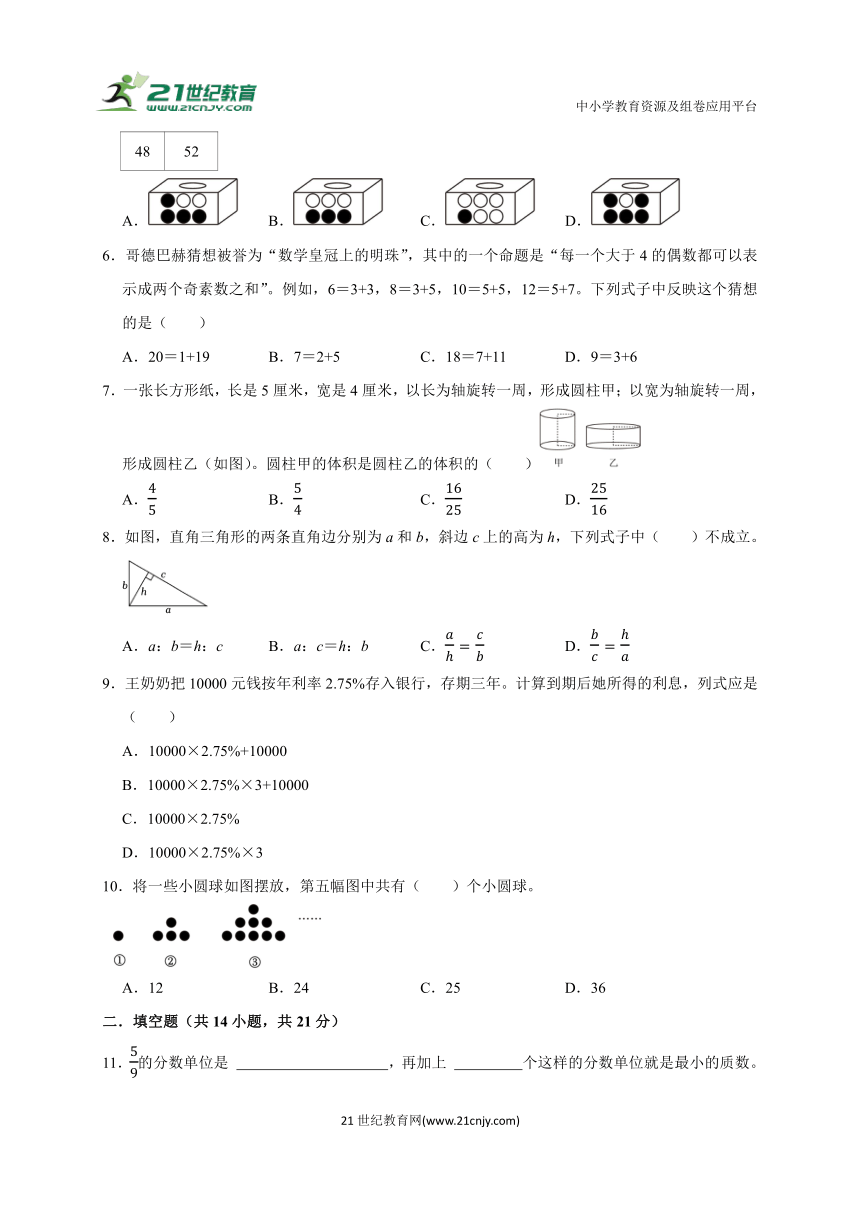
5.某儿童用品商店在六一儿童节期间开展促销活动,设计了一个摸球游戏领取活动纪念品。上午共有100名顾客参与摸球游戏,摸球的结果统计如表,根据统计的数据,此商店设计的摸球游戏盒子最有可能是( )
● 〇
48 52
A. B. C. D.
6.哥德巴赫猜想被誉为“数学皇冠上的明珠”,其中的一个命题是“每一个大于4的偶数都可以表示成两个奇素数之和”。例如,6=3+3,8=3+5,10=5+5,12=5+7。下列式子中反映这个猜想的是( )
A.20=1+19 B.7=2+5 C.18=7+11 D.9=3+6
7.一张长方形纸,长是5厘米,宽是4厘米,以长为轴旋转一周,形成圆柱甲;以宽为轴旋转一周,形成圆柱乙(如图)。圆柱甲的体积是圆柱乙的体积的( )
A. B. C. D.
8.如图,直角三角形的两条直角边分别为a和b,斜边c上的高为h,下列式子中( )不成立。
A.a:b=h:c B.a:c=h:b C. D.
9.王奶奶把10000元钱按年利率2.75%存入银行,存期三年。计算到期后她所得的利息,列式应是( )
A.10000×2.75%+10000
B.10000×2.75%×3+10000
C.10000×2.75%
D.10000×2.75%×3
将一些小圆球如图摆放,第五幅图中共有( )个小圆球。
A.12 B.24 C.25 D.36
二.填空题(共14小题,共21分)
11.的分数单位是 ,再加上 个这样的分数单位就是最小的质数。
12.如果a÷b(a、b为非0自然数),那么a和b的最大公因数是 ,最小公倍数是 。
13.甲数=2×3×5×A,乙数=2×3×7×A,已知甲、乙两数的最小公倍数是630,则A的取值为 .
14.一间舞蹈房在比例尺为1:300的平面图上,长3厘米,宽2.2厘米,舞蹈房的实际面积是 平方米。
15.一个半径是4厘米的圆,按2:1的比放大后,放大后的圆的面积是 ;如果按 的比缩小后,圆的面积是3.14平方厘米.
16.一项工程,甲每月完成它的,2个月完成这项工程的 ,还剩下这项工程的 .
17.如图,半圆中有一个直角三角形,其中直角边AB=12厘米,AC=16厘米,斜边BC=20厘米。阴影部分的面积是 平方厘米。
18.王老师买了3年期的国家建设债券1000元,如果年利率为2.9%,到期时他可获本金和利息共 元。
19.一个3mm长的零件画在图上是15cm,这幅图的比例尺是 。
20.如图,A点表示的数是 ,点C到0的距离与点B到0的距离相等,但方向相反,那么点C表示的数是 。
21.如图,一张方桌每面坐1人,可坐4人,2张方桌并在一起可坐6人,像这样6张桌并在一起可坐 人,n张方桌并在一起可坐 人。
22.鸡兔同笼是中国古代数学名题之一,在《孙子算经》中有记载。如果鸡兔同笼,上有35个头,下有94只脚,那么鸡有 只,兔有 只。
23.三角形三个角度数的比是2:4:3,最大的角是 .
24.一个长方形的长为x米,宽为y米;若宽增加5米,长不变,则面积比原来增加 平方米.
三.计算题(共3小题,共24分)
25.直接写出得数。(共8分)
45+37= 0.72÷0.8= 0.72=
12×0.5= 5÷9
26.求未知数x的值。(共4分)
x=30 12:x=0.4:
27.能简算的要简算。(共12分)
500﹣(350÷50+74) 36÷15+34÷3 3.752.25
1.9+1.99+1.999
四.操作题(共1小题,共9分)
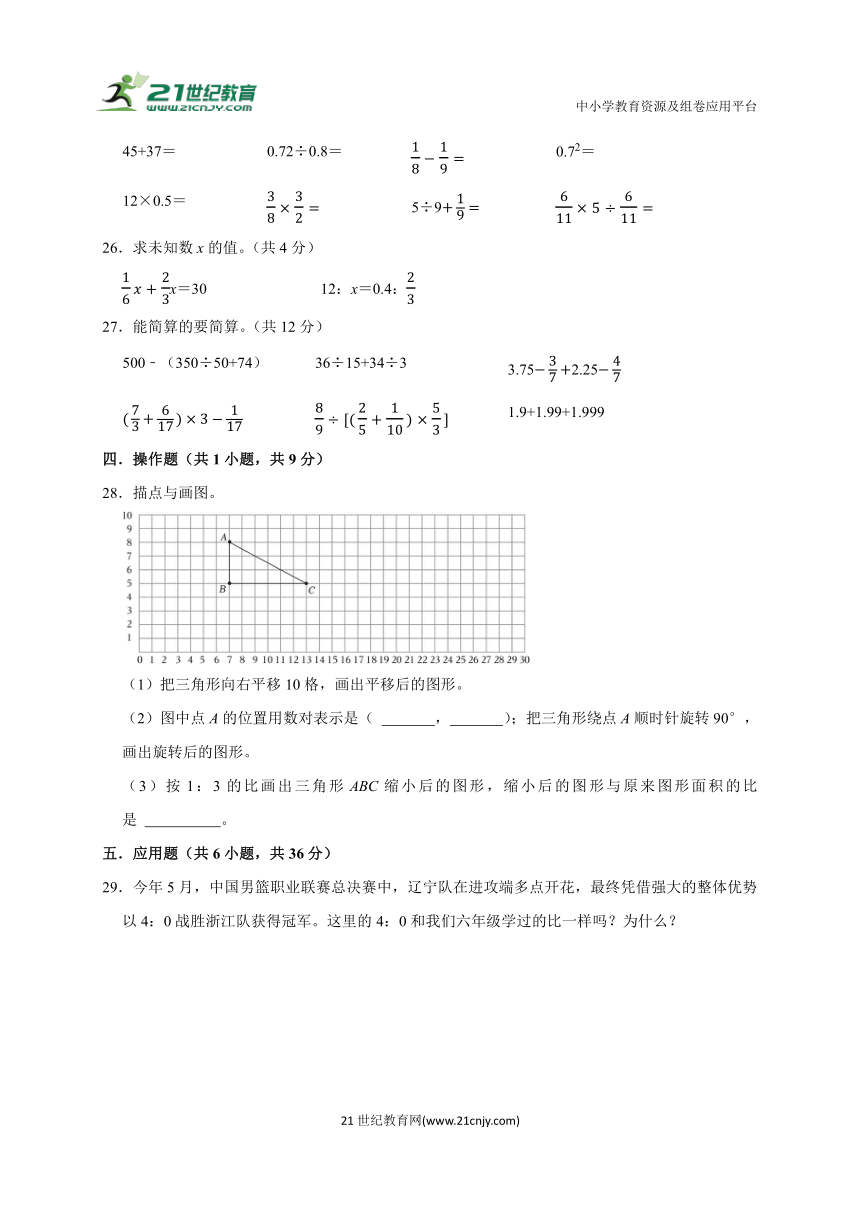
28.描点与画图。
(1)把三角形向右平移10格,画出平移后的图形。
(2)图中点A的位置用数对表示是( , );把三角形绕点A顺时针旋转90°,画出旋转后的图形。
(3)按1:3的比画出三角形ABC缩小后的图形,缩小后的图形与原来图形面积的比是 。
五.应用题(共6小题,共36分)
29.今年5月,中国男篮职业联赛总决赛中,辽宁队在进攻端多点开花,最终凭借强大的整体优势以4:0战胜浙江队获得冠军。这里的4:0和我们六年级学过的比一样吗?为什么?
30.王明看一本书,看了5天,还剩下82页。如果用同样的阅读速度看7天,就剩下全书的。这本书有多少页?
31.工地要运输一批水泥,原计划每天运输36吨,8天可以运完。由于工作效率提高,完成运输任务时,实际每天可以运输48吨水泥。
(1) 和 是两种相关联的量,它们成 比例关系。
因为:
(2)实际需要多少天可以运完?
32.在AB这条新铺的路上等距离安装路灯,但要求在C处及AC和BC的中点处都要安装一盏,问至少需要安装多少盏灯?
33.修路队修一条公路,4天完成了全长的48%,已知修路队平均每天修600米,这条路长多少千米?
34.一个笼子里有8条腿的蜘蛛和6条腿的蚱蜢共25只.如果它们的总腿数有170条,那么蜘蛛和蚱蜢各有多少只?
参考答案与试题解析
一.选择题(共10小题,共10分)
1.B
【分析】根据图上距离=实际距离×比例尺,解答此题即可。
【解析】解:320千米=32000000厘米
3200000016(厘米)
16厘米大约相当于一支铅笔的长度。
故选:B。
【点评】熟练掌握比例尺公式,是解答此题的关键。
2.B
【分析】根据三角形的内角和是180度,结合“上北下南左西右东”的图上方向,解答即可。
【解析】解:180°﹣90°﹣(90°﹣30°)
=90°﹣60°
=30°
90°﹣30°=60°
答:农行在体育场的北偏东30°方向,它又在超市的北偏西60°方向。
故选:B。
【点评】本题考查了方向与位置知识,结合三角形内角和知识解答即可。
3.C
【分析】采用赋值法计算,假设原楼盘单价是10000元/平方米,依次计算出三种方案降价后的价格比较即可。
【解析】解:假设原楼盘单价是10000元/平方米,则:
方案一:10000×(1﹣5%)×(1﹣10%)=8550(元)
方案二:10000×(1﹣8%)×(1﹣7%)=8556(元)
方案三:10000×(1﹣12%)×(1﹣3%)=8536(元)
8556>8550>8536,即方案三价格最低。
故选:C。
【点评】本题考查了百分数的实际应用。
4.A
【分析】根据题意,知道长方体表面积增加的80平方厘米,是2个以圆柱的底面半径为宽,高为长的长方形的面积,由此即可求出圆柱的底面半径。
【解析】解:80÷2÷10=4(厘米)
答:圆柱的底面半径是4厘米。
故选:A。
【点评】解答此题的关键是,知道切拼后的图形与圆柱之间的关系,再利用相应的公式解答。
5.B
【分析】根据摸球的结果来看●有48个,〇有52个,〇比●多几个,但差距不大,所以盒子里这两种球的数量差不多,但●的数量比〇的数量可能少一点,据此解答。
【解析】解:经分析和观察可看出:B选项中的盒子里球的数量最符合题意。
故选:B。
【点评】本题考查可能性的大小,可能性的大小与物体个数的多少有关,数量越多可能性越大,反之就越小。
6.C
【分析】1不是质数也不是合数,7不是偶数,9不是偶数。
【解析】解:哥德巴赫猜想被誉为“数学皇冠上的明珠”,其中的一个命题是“每一个大于4的偶数都可以表示成两个奇素数之和”。18=7+11反映了这个猜想。
故选:C。
【点评】本题考查的主要内容是奇数和偶数,质数和合数的应用问题。
7.A
【分析】根据圆柱的体积公式:V=πr2h,把数据代入公式求出两个圆柱的体积,然后进行比较。
【解析】解:甲的体积:
3.14×42×5
=3.14×16×5
=50.24×5
=251.2(立方厘米)
乙的体积:
3.14×52×4
=3.14×25×4
=3.14×100
=314(立方厘米)
252.1÷314
答:圆柱甲的体积是圆柱乙的体积的。
故选:A。
【点评】此题主要考查圆柱的体积公式的灵活运用,关键是熟记公式。
8.A
【分析】一个直角三角形,a、b分别是两条直角边,h是斜边c上的高,根据在直角三角形中两条直角边的乘积等于斜边与斜边上高的乘积,即ab=ch,选项中的比例外项积等于内项积,能化成ab=ch的形式,即为正确,反之错误。
【解析】解:A选项a:b=h:c,根据比例的基本性质,可转化为ac=bh,所以式子不成立;
B选项a:c=h:b,根据比例的基本性质,可转化为ab=ch,所以式子成立;
C选项,根据比例的基本性质,可转化为ab=ch,所以式子成立;
D选项,根据比例的基本性质,可转化为ab=ch,所以式子成立。
答:A选项中的a:b=h:c不成立。
故选:A。
【点评】本题的关键是掌握两点:一是在直角三角形中两条直角边的乘积等于斜边与斜边上高的乘积;二是比例的基本性质。
9.D
【分析】根据利息=本金×利率×存期,列式解答。
【解析】解:10000×2.75%×3
=10000×0.0275×3
=275×3
=825(元)
答:到期后她所得的利息是825元。
故选:D。
【点评】此题考查的目的是理解利息的意义,掌握利息的计算方法及应用。
10.C
【分析】看图可知,第一幅图有1个小圆球,第二幅图有(1+3)个,第三幅图有(1+3+5)个,第四幅图有(1+3+5+7)个。依此类推,那么第五幅图有(1+3+5+7+9)个小圆球。据此解题。
【解析】解:1+3+5+7+9=25(个)
答:第五幅图中共有25个小圆球。
故选:C。
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
二.填空题(共14小题,共21分)
11.,13。
【分析】表示把单位“1”平均分成9份,每份是,取其中的5份。根据分数单位的意义,把单位“1”平均分成若干份,表示其中1份的数叫分数单位。因此,这个分数的分数单位是,它有5个这样的分数单位。最小的质数是2,2,即18个这样的分数单位是最小的质数,需要再添上(18﹣5)个,即13个这样的分数单位就是最小的质数。
【解析】解:的分数单位是,再加上13个这样的分数单位就是最小的质数。
故答案为:,13。
【点评】此题考查的知识点:分数的意义、分数单位的意义、质数的意义。
12.a,b。
【分析】因为a÷b(a、b为非0自然数),根据“当两个数成倍数关系时,较小的那个数,是这两个数的最大公因数;较大的那个数,是这两个数的最小公倍数,进行解答即可。
【解析】解:因为a÷b(a、b为非0自然数),那么a和b的最大公因数是a,最小公倍数是b。
故答案为:a,b。
【点评】此题主要考查求两个数为倍数关系时的最大公约数和最小公倍数:两个数为倍数关系,最大公因数为较小的数,较大的那个数,是这两个数的最小公倍数。
13.见试题解答内容
【分析】求最小公倍数是公有质因数与独有质因数的连乘积,对于两个数来说,两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数,由此解决问题即可.
【解析】解:甲数=2×3×5×A,乙数=2×3×7×A,
甲、乙两数的最小公倍数是:
2×3×5×7×A=210A
210A=630
A=3
故答案为:3.
【点评】此题主要考查求两个数的最小公倍数的方法:两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数;数字大的可以用短除法解答.
14.59.4。
【分析】要求舞蹈房的实际面积,根据“图上距离÷比例尺=实际距离”,代入数值,分别计算出舞蹈房实际的长和宽,然后根据“长方形的面积=长×宽”,代入数值,计算即可。
【解析】解:3900(厘米)
900厘米=9米
2.2660(厘米)
660厘米=6.6米
9×6.6=59.4(平方米)
答:舞蹈房的实际面积是59.4平方米。
故答案为:59.4。
【点评】解答此题用到的知识点:(1)图上距离、实际距离和比例尺三者之间的关系;(2)长方形的面积计算方法。
15.见试题解答内容
【分析】(1)半径确定圆的半径大小,根据题干,放大后的圆的半径为:2×4=8厘米,利用圆的面积公式即可解答.
(2)根据圆的面积公式求出原来圆的面积,再求出原来的圆的面积与缩小后的圆的面积之比,面积之比等于半径平方之比,据此即可解答问题.
【解析】解:(1)2×4=8(厘米)
3.14×82=200.96(平方厘米)
答:放大后的圆的面积是200.96平方厘米.
(2)3.14:(3.14×42)=1:16
因为12:42=1:16,
答:按 1:4的比缩小后,圆的面积是3.14平方厘米.
故答案为:200.96平方厘米;1:4.
【点评】此题考查了图形的放大与缩小的性质以及圆的面积公式的应用,关键是明确放大与缩小后的面积之比等于半半径的平方比.
16.见试题解答内容
【分析】甲每月完成它的,2个月则完成这项工程的几分之几,直接乘以2即可;这项工程为单位“1”,减去2个月完成的几分之几,就是剩下的.
【解析】解:(1)2,
(2)1.
故答案为:,.
【点评】此题综合考查简单的分数乘法和分数加减法应用题.
17.61。
【分析】阴影部分的面积=半圆的面积﹣直角三角形的面积,半圆的面积πr2,三角形的面积=底×高÷2。代入公式计算即可求得阴影部分的面积。
【解析】解:12×16÷2
=12×8
=96(平方厘米)
3.14×(20÷2)2﹣96
=157﹣96
=61(平方厘米)
答:阴影部分的面积是61平方厘米。
故答案为:61。
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可。
18.1087。
【分析】利息=本金×年利率×时间,由此代入数据计算即可求出利息;最后拿到的钱是利息+本金,由此解决问题。
【解析】解:1000×2.9%×3
=29×3
=87(元)
1000+87=1087(元)
答:到期时他可获本金和利息共1087元。
故答案为:1087。
【点评】这种类型属于利息问题,有固定的计算方法,利息=本金×利率×时间(注意时间和利率的对应),本息=本金+利息,找清数据与问题,代入公式计算即可。
19.见试题解答内容
【分析】图上距离和实际距离已知,依据“比例尺”即可求得这幅图的比例尺.
【解析】解:因为3毫米=0.3厘米,
则15厘米:0.3厘米=50:1;
答:这幅图的比例尺是50:1.
故答案为:50:1.
【点评】此题主要考查比例尺的计算方法,解答时要注意单位的换算.
20.见试题解答内容
【分析】数轴是规定了原点(0点)、方向和单位长度的一条直线.原点的左边是负数,从原点向左的每个单位长度分别是﹣1、﹣2、﹣3......;右边是正数,从原点向右每个单位长度分别是1、2、3.......。把1﹣2这一段平均分成了5份,一份表示0.2,那么3份就表示0.6,0.6+1=1.6;点B到0的距离是3个格,点C到0的距离也是3格,且在0的左边,为负数﹣3,据此解答。
【解析】解:1+0.6=1.6
如图:
【点评】本题是考查数轴的认识.数轴是规定了原点(0点)、方向和单位长度的一条直线。
21.14;(2n+2)。
【分析】根据题意发现:一张方桌坐4人,每多1张方桌就多坐2人,则拼n张方桌,能坐(2n+2)个人;据此解答即可。
【解析】解:2×6+2
=12+2
=14(人)
n张方桌并在一起可坐(2n+2)人。
答:这样6张方桌并在一起可坐14人,n张方桌并在一起可坐(2n+2)人。
故答案为:14;(2n+2)。
【点评】本题主要考查数与形结合的规律,关键是根据图示发现这组图形的规律,利用规律做题。
22.23,12。
【分析】假设全是鸡,则脚有35×2=70(只)脚,则比已知少了94﹣70=24(只)脚,因为1只鸡比1只兔少2只脚,所以兔有24÷2=12(只),由此即可解答。
【解析】解:假设全是鸡,则兔有:
(94﹣35×2)÷(4﹣2)
=24÷2
=12(只)
35﹣12=23(只)
答:鸡有23只,兔有12只。
故答案为:23,12。
【点评】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
23.见试题解答内容
【分析】利用三角形的内角和是180°和这三个角的度数之比即可解决问题.
【解析】解:2+4+3=9,
180°80°,
答:最大的角是80°.
故答案为:80°.
【点评】此题考查了三角形的内角和是180°和按比例分配的应用.
24.见试题解答内容
【分析】根据长方形面积公式:长方形面积=长×宽,则原来长方形面积为xy平方米;宽增加5米后,则现在长方形面积为x(y+5)平方米.
【解析】解:x(y+5)﹣xy=5x(平方米)
答:面积比原来增加5x平方米.
故答案为:5x.
【点评】此题掌握长方形的面积公式和字母表示数的知识,即可解答.
三.计算题(共3小题,共24分)
25.82,0.9,,0.49,6,,,5。
【分析】根据100以内加法、小数乘法、小数除法、分数减法、分数乘法、分数四则混合运算的法则直接写出得数即可。
【解析】解:
45+37=82 0.72÷0.8=0.9 0.72=0.49
12×0.5=6 5÷9 5
【点评】本题主要考查了100以内加法、小数乘法、小数除法、分数减法、分数乘法、分数四则混合运算,属于基本的计算,在平时注意积累经验,逐步提高运算的速度和准确性。
26.x=36;x=20。
【分析】先化简,然后再根据等式的性质,方程两边同时求解;
根据比例的性质,写成0.4x=12,方程两边同时除以0.4,即可求出方程的解。
【解析】解:x=30
x=30
x30
x=36
12:x=0.4:
0.4x=12
0.4x=8
0.4x÷0.4=8÷0.4
x=20
【点评】本题考查了解方程和解比例,解题过程中要利用等式的性质,注意等号对齐。
27.419;;5;8;;5.889。
【分析】(1)先算括号里的除法,再算括号里的加法,最后算括号外的减法;
(2)先同时计算两步除法,再算加法;
(3)利用加法交换律和减法的性质计算;
(4)先利用乘法分配律去括号,再利用减法的性质计算;
(5)先利用乘法分配律去小括号,再算中括号里的加法,最后算中括号外的除法;
(6)将1.9化成(2﹣0.1),将1.99化成(2﹣0.01),将1.999化成(2﹣0.001),再利用加法交换律和减法的性质计算。
【解析】解:(1)500﹣(350÷50+74)
=500﹣(7+74)
=500﹣81
=419
(2)36÷15+34÷3
(3)3.752.25
=3.75+2.25﹣()
=6﹣1
=5
(4)()×3
33
=7
=7+()
=8
(5)[()]
[]
[]
(6)1.9+1.99+1.999
=(2﹣0.1)+(2﹣0.01)+(2﹣0.001)
=2﹣0.1+2﹣0.01+2﹣0.001
=2+2+2﹣(0.1+0.01+0.001)
=6﹣0.111
=5.889
【点评】解答本题需熟练掌握四则混合运算顺序,灵活使用运算律和运算性质。
四.操作题(共1小题,共9分)
28.(1)(2)7,8;(3)1:9。
【分析】(1)根据平移的方法,把三角形向右平移10格,画出平移后的图形即可。
(2)用数对表示位置时,先表示第几列,再表示第几行,图中点A的位置用数对表示是(7,8);根据旋转的方法,点A不动,把三角形绕点A顺时针旋转90°,画出旋转后的图形即可。
(3)根据图形缩小的方法,按1:3的比画出三角形ABC缩小到原来的后的图形,分别根据三角形的面积公式计算出缩小后的图形与原来图形的面积,解答即可。
【解析】解:(1)把三角形向右平移10格,画出平移后的图形。如图:
(2)图中点A的位置用数对表示是(7,8);把三角形绕点A顺时针旋转90°,画出旋转后的图形。如图:
(3)按1:3的比画出三角形ABC缩小后的图形,如图:
(2×1÷2):(6×3÷2)
=1:9
答:缩小后的图形与原来图形面积的比是1:9。
故答案为:7,8;1:9。
【点评】本题考查了数对表示位置知识,图形的平移、旋转以及图形的缩小知识,结合题意分析解答即可。
五.应用题(共6小题,共36分)
29.不一样;我们六年级学过的比是两个数相除,也叫两个数的比,这里的4:0是指辽宁队胜了4场,浙江队1场没胜。
【分析】这里的4:0和我们六年级学过的比不一样。我们六年级学过的比是两个数相除,也叫两个数的比,这里的4:0是指辽宁队胜了4场,浙江队1场没胜。
【解析】解:这里的4:0和我们六年级学过的比不一样。我们六年级学过的比是两个数相除,也叫两个数的比,这里的4:0是指辽宁队胜了4场,浙江队1场没胜。
【点评】本题考查了比的意义。
30.112页。
【分析】依据题意设这本书有x页,(总页数﹣剩下的页数):看的天数=[总页数×(1)]:看的天数,由此列方程计算,然后计算这本书的页数。
【解析】解:设这本书有x页,由题意得:
(x﹣82):5=[x×(1)]:7
7×(x﹣82)x
56x﹣4592=15x
41x=4592
x=112
答:这本书有112页。
【点评】本题考查的是列方程解决实际问题的应用。
31.(1)每天运输的水泥数量,运输的天数是两种相关联的量,反;每天运输的水泥数量×运输的天数=水泥的总量,每天运输的水泥数量与运输的天数的乘积一定,所以每天运输的水泥数量与运输的天数成反比例。 (2)6天。
【分析】(1)根据题意,每天运输的水泥数量和运输的天数是两种相关联的量,因为每天运输的水泥数量×运输的天数=水泥的总量,每天运输的水泥数量与运输的天数的乘积一定,所以每天运输的水泥数量与运输的天数成反比例。
(2)根据题意,先计算出水泥的总量,然后用水泥的总量÷每天运输的水泥数量=运输的天数,解答即可。
【解析】解:(1)每天运输的水泥数量和运输的天数是两种相关联的量,它们成反比例关系。因为:每天运输的水泥数量×运输的天数=水泥的总量,每天运输的水泥数量与运输的天数的乘积一定,所以每天运输的水泥数量与运输的天数成反比例。
(2)实际需要多少天可以运完?
36×8÷48
=288÷48
=6(天)
答:实际需要6天可以运完。
故答案为:每天运输的水泥数量,运输的天数是两种相关联的量,反;每天运输的水泥数量×运输的天数=水泥的总量,每天运输的水泥数量与运输的天数的乘积一定,所以每天运输的水泥数量与运输的天数成反比例。
【点评】本题考查反比例的识别及应用,结合题意分析解答即可。
32.见试题解答内容
【分析】假设因为在AC、BC的中点以及A、B、C的地方都分别安装一盏路灯,那么可得出两盏路灯之间的距离是(560÷2)和(630÷2)的公约数,题目要求安装路灯最少,那么需要我们求最大公约数,求出最大公约数可得出每段上分别需要的电灯数量,因为要求最少,再减去A、B处两盏路灯即可。
【解析】解:560÷2=280,
630÷2=315,
280=2×2×2×5×7,
315=3×3×5×7,
所以280和315的最大公约数是5×7=35,
共需要路灯:(560+630)÷35﹣1=33
所以共需路灯33(盏).
答:至少需要安装33盏灯.
【点评】此题属于应用类问题,解答本题的关键是明白两盏灯之间的距离是280和315的最大公约数,另外在求每一段路上的路灯时不要忘记加1.
33.见试题解答内容
【分析】先根据工作效率=工作总量÷工作时间,求出修路队的工作效率,也就是600米的分率,依据分数除法意义即可解答.
【解析】解:600÷(48%÷4),
=600÷12%,
=5000(米),
=5(千米),
答:这条路长5千米.
【点评】本题主要考查学生依据工作总量、工作时间以及工作效率之间数量关系解决问题的能力,关键是求出600米占的分率.
34.见试题解答内容
【分析】假设笼子里都是蚱蜢,那么就有25×6=150条腿,这样实际就比假设多170﹣150=20条腿;因为一只蜘蛛比一只蚱蜢多8﹣6=2条腿,所以就有20÷2=10只蜘蛛;进而求得蚱蜢的只数.
【解析】解:蜘蛛:(170﹣25×6)÷(8﹣6)
=20÷2
=10(只);
蚱蜢:25﹣10=15(只)
答:蜘蛛有10只,蚱蜢有15只.
【点评】此题属于典型的鸡兔同笼问题,解答此类题的关键是用假设法,也可以用方程进行解答.
21世纪教育网(www.21cnjy.com)
2024-2025学年六年级下册数学小升初重点校入学分班考押题卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题(共10小题,共10分)
1.连云港到南京的距离约为320千米,在一张比例尺为1:2000000的江苏地图上,它们之间的距离大约相当于( )的长度。
A.一根火柴 B.一支铅笔 C.一把米尺 D.一根鱼竿
2.如图,农行在体育场的北偏东30°方向,它又在超市的( )方向。
A.北偏东60° B.北偏西60° C.北偏东30° D.北偏西30°
3.某房地产企业准备三种方案,计划分两次先后降价促销清盘。方案一:第一次降价5%,第二次降价10%;方案二:第一次降价8%,第二次降价7%;方案三:第一次降价12%,第二次降价3%。三种方案降价后的价格相比,( )
A.方案一低 B.方案二低 C.方案三低 D.价格相等
4.如图,将一个高为10厘米的圆柱体切拼成近似的长方体,表面积增加了80平方厘米,这个圆柱的半径是( )厘米。
A.4 B.5 C.8 D.10
5.某儿童用品商店在六一儿童节期间开展促销活动,设计了一个摸球游戏领取活动纪念品。上午共有100名顾客参与摸球游戏,摸球的结果统计如表,根据统计的数据,此商店设计的摸球游戏盒子最有可能是( )
● 〇
48 52
A. B. C. D.
6.哥德巴赫猜想被誉为“数学皇冠上的明珠”,其中的一个命题是“每一个大于4的偶数都可以表示成两个奇素数之和”。例如,6=3+3,8=3+5,10=5+5,12=5+7。下列式子中反映这个猜想的是( )
A.20=1+19 B.7=2+5 C.18=7+11 D.9=3+6
7.一张长方形纸,长是5厘米,宽是4厘米,以长为轴旋转一周,形成圆柱甲;以宽为轴旋转一周,形成圆柱乙(如图)。圆柱甲的体积是圆柱乙的体积的( )
A. B. C. D.
8.如图,直角三角形的两条直角边分别为a和b,斜边c上的高为h,下列式子中( )不成立。
A.a:b=h:c B.a:c=h:b C. D.
9.王奶奶把10000元钱按年利率2.75%存入银行,存期三年。计算到期后她所得的利息,列式应是( )
A.10000×2.75%+10000
B.10000×2.75%×3+10000
C.10000×2.75%
D.10000×2.75%×3
将一些小圆球如图摆放,第五幅图中共有( )个小圆球。
A.12 B.24 C.25 D.36
二.填空题(共14小题,共21分)
11.的分数单位是 ,再加上 个这样的分数单位就是最小的质数。
12.如果a÷b(a、b为非0自然数),那么a和b的最大公因数是 ,最小公倍数是 。
13.甲数=2×3×5×A,乙数=2×3×7×A,已知甲、乙两数的最小公倍数是630,则A的取值为 .
14.一间舞蹈房在比例尺为1:300的平面图上,长3厘米,宽2.2厘米,舞蹈房的实际面积是 平方米。
15.一个半径是4厘米的圆,按2:1的比放大后,放大后的圆的面积是 ;如果按 的比缩小后,圆的面积是3.14平方厘米.
16.一项工程,甲每月完成它的,2个月完成这项工程的 ,还剩下这项工程的 .
17.如图,半圆中有一个直角三角形,其中直角边AB=12厘米,AC=16厘米,斜边BC=20厘米。阴影部分的面积是 平方厘米。
18.王老师买了3年期的国家建设债券1000元,如果年利率为2.9%,到期时他可获本金和利息共 元。
19.一个3mm长的零件画在图上是15cm,这幅图的比例尺是 。
20.如图,A点表示的数是 ,点C到0的距离与点B到0的距离相等,但方向相反,那么点C表示的数是 。
21.如图,一张方桌每面坐1人,可坐4人,2张方桌并在一起可坐6人,像这样6张桌并在一起可坐 人,n张方桌并在一起可坐 人。
22.鸡兔同笼是中国古代数学名题之一,在《孙子算经》中有记载。如果鸡兔同笼,上有35个头,下有94只脚,那么鸡有 只,兔有 只。
23.三角形三个角度数的比是2:4:3,最大的角是 .
24.一个长方形的长为x米,宽为y米;若宽增加5米,长不变,则面积比原来增加 平方米.
三.计算题(共3小题,共24分)
25.直接写出得数。(共8分)
45+37= 0.72÷0.8= 0.72=
12×0.5= 5÷9
26.求未知数x的值。(共4分)
x=30 12:x=0.4:
27.能简算的要简算。(共12分)
500﹣(350÷50+74) 36÷15+34÷3 3.752.25
1.9+1.99+1.999
四.操作题(共1小题,共9分)
28.描点与画图。
(1)把三角形向右平移10格,画出平移后的图形。
(2)图中点A的位置用数对表示是( , );把三角形绕点A顺时针旋转90°,画出旋转后的图形。
(3)按1:3的比画出三角形ABC缩小后的图形,缩小后的图形与原来图形面积的比是 。
五.应用题(共6小题,共36分)
29.今年5月,中国男篮职业联赛总决赛中,辽宁队在进攻端多点开花,最终凭借强大的整体优势以4:0战胜浙江队获得冠军。这里的4:0和我们六年级学过的比一样吗?为什么?
30.王明看一本书,看了5天,还剩下82页。如果用同样的阅读速度看7天,就剩下全书的。这本书有多少页?
31.工地要运输一批水泥,原计划每天运输36吨,8天可以运完。由于工作效率提高,完成运输任务时,实际每天可以运输48吨水泥。
(1) 和 是两种相关联的量,它们成 比例关系。
因为:
(2)实际需要多少天可以运完?
32.在AB这条新铺的路上等距离安装路灯,但要求在C处及AC和BC的中点处都要安装一盏,问至少需要安装多少盏灯?
33.修路队修一条公路,4天完成了全长的48%,已知修路队平均每天修600米,这条路长多少千米?
34.一个笼子里有8条腿的蜘蛛和6条腿的蚱蜢共25只.如果它们的总腿数有170条,那么蜘蛛和蚱蜢各有多少只?
参考答案与试题解析
一.选择题(共10小题,共10分)
1.B
【分析】根据图上距离=实际距离×比例尺,解答此题即可。
【解析】解:320千米=32000000厘米
3200000016(厘米)
16厘米大约相当于一支铅笔的长度。
故选:B。
【点评】熟练掌握比例尺公式,是解答此题的关键。
2.B
【分析】根据三角形的内角和是180度,结合“上北下南左西右东”的图上方向,解答即可。
【解析】解:180°﹣90°﹣(90°﹣30°)
=90°﹣60°
=30°
90°﹣30°=60°
答:农行在体育场的北偏东30°方向,它又在超市的北偏西60°方向。
故选:B。
【点评】本题考查了方向与位置知识,结合三角形内角和知识解答即可。
3.C
【分析】采用赋值法计算,假设原楼盘单价是10000元/平方米,依次计算出三种方案降价后的价格比较即可。
【解析】解:假设原楼盘单价是10000元/平方米,则:
方案一:10000×(1﹣5%)×(1﹣10%)=8550(元)
方案二:10000×(1﹣8%)×(1﹣7%)=8556(元)
方案三:10000×(1﹣12%)×(1﹣3%)=8536(元)
8556>8550>8536,即方案三价格最低。
故选:C。
【点评】本题考查了百分数的实际应用。
4.A
【分析】根据题意,知道长方体表面积增加的80平方厘米,是2个以圆柱的底面半径为宽,高为长的长方形的面积,由此即可求出圆柱的底面半径。
【解析】解:80÷2÷10=4(厘米)
答:圆柱的底面半径是4厘米。
故选:A。
【点评】解答此题的关键是,知道切拼后的图形与圆柱之间的关系,再利用相应的公式解答。
5.B
【分析】根据摸球的结果来看●有48个,〇有52个,〇比●多几个,但差距不大,所以盒子里这两种球的数量差不多,但●的数量比〇的数量可能少一点,据此解答。
【解析】解:经分析和观察可看出:B选项中的盒子里球的数量最符合题意。
故选:B。
【点评】本题考查可能性的大小,可能性的大小与物体个数的多少有关,数量越多可能性越大,反之就越小。
6.C
【分析】1不是质数也不是合数,7不是偶数,9不是偶数。
【解析】解:哥德巴赫猜想被誉为“数学皇冠上的明珠”,其中的一个命题是“每一个大于4的偶数都可以表示成两个奇素数之和”。18=7+11反映了这个猜想。
故选:C。
【点评】本题考查的主要内容是奇数和偶数,质数和合数的应用问题。
7.A
【分析】根据圆柱的体积公式:V=πr2h,把数据代入公式求出两个圆柱的体积,然后进行比较。
【解析】解:甲的体积:
3.14×42×5
=3.14×16×5
=50.24×5
=251.2(立方厘米)
乙的体积:
3.14×52×4
=3.14×25×4
=3.14×100
=314(立方厘米)
252.1÷314
答:圆柱甲的体积是圆柱乙的体积的。
故选:A。
【点评】此题主要考查圆柱的体积公式的灵活运用,关键是熟记公式。
8.A
【分析】一个直角三角形,a、b分别是两条直角边,h是斜边c上的高,根据在直角三角形中两条直角边的乘积等于斜边与斜边上高的乘积,即ab=ch,选项中的比例外项积等于内项积,能化成ab=ch的形式,即为正确,反之错误。
【解析】解:A选项a:b=h:c,根据比例的基本性质,可转化为ac=bh,所以式子不成立;
B选项a:c=h:b,根据比例的基本性质,可转化为ab=ch,所以式子成立;
C选项,根据比例的基本性质,可转化为ab=ch,所以式子成立;
D选项,根据比例的基本性质,可转化为ab=ch,所以式子成立。
答:A选项中的a:b=h:c不成立。
故选:A。
【点评】本题的关键是掌握两点:一是在直角三角形中两条直角边的乘积等于斜边与斜边上高的乘积;二是比例的基本性质。
9.D
【分析】根据利息=本金×利率×存期,列式解答。
【解析】解:10000×2.75%×3
=10000×0.0275×3
=275×3
=825(元)
答:到期后她所得的利息是825元。
故选:D。
【点评】此题考查的目的是理解利息的意义,掌握利息的计算方法及应用。
10.C
【分析】看图可知,第一幅图有1个小圆球,第二幅图有(1+3)个,第三幅图有(1+3+5)个,第四幅图有(1+3+5+7)个。依此类推,那么第五幅图有(1+3+5+7+9)个小圆球。据此解题。
【解析】解:1+3+5+7+9=25(个)
答:第五幅图中共有25个小圆球。
故选:C。
【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
二.填空题(共14小题,共21分)
11.,13。
【分析】表示把单位“1”平均分成9份,每份是,取其中的5份。根据分数单位的意义,把单位“1”平均分成若干份,表示其中1份的数叫分数单位。因此,这个分数的分数单位是,它有5个这样的分数单位。最小的质数是2,2,即18个这样的分数单位是最小的质数,需要再添上(18﹣5)个,即13个这样的分数单位就是最小的质数。
【解析】解:的分数单位是,再加上13个这样的分数单位就是最小的质数。
故答案为:,13。
【点评】此题考查的知识点:分数的意义、分数单位的意义、质数的意义。
12.a,b。
【分析】因为a÷b(a、b为非0自然数),根据“当两个数成倍数关系时,较小的那个数,是这两个数的最大公因数;较大的那个数,是这两个数的最小公倍数,进行解答即可。
【解析】解:因为a÷b(a、b为非0自然数),那么a和b的最大公因数是a,最小公倍数是b。
故答案为:a,b。
【点评】此题主要考查求两个数为倍数关系时的最大公约数和最小公倍数:两个数为倍数关系,最大公因数为较小的数,较大的那个数,是这两个数的最小公倍数。
13.见试题解答内容
【分析】求最小公倍数是公有质因数与独有质因数的连乘积,对于两个数来说,两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数,由此解决问题即可.
【解析】解:甲数=2×3×5×A,乙数=2×3×7×A,
甲、乙两数的最小公倍数是:
2×3×5×7×A=210A
210A=630
A=3
故答案为:3.
【点评】此题主要考查求两个数的最小公倍数的方法:两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数;数字大的可以用短除法解答.
14.59.4。
【分析】要求舞蹈房的实际面积,根据“图上距离÷比例尺=实际距离”,代入数值,分别计算出舞蹈房实际的长和宽,然后根据“长方形的面积=长×宽”,代入数值,计算即可。
【解析】解:3900(厘米)
900厘米=9米
2.2660(厘米)
660厘米=6.6米
9×6.6=59.4(平方米)
答:舞蹈房的实际面积是59.4平方米。
故答案为:59.4。
【点评】解答此题用到的知识点:(1)图上距离、实际距离和比例尺三者之间的关系;(2)长方形的面积计算方法。
15.见试题解答内容
【分析】(1)半径确定圆的半径大小,根据题干,放大后的圆的半径为:2×4=8厘米,利用圆的面积公式即可解答.
(2)根据圆的面积公式求出原来圆的面积,再求出原来的圆的面积与缩小后的圆的面积之比,面积之比等于半径平方之比,据此即可解答问题.
【解析】解:(1)2×4=8(厘米)
3.14×82=200.96(平方厘米)
答:放大后的圆的面积是200.96平方厘米.
(2)3.14:(3.14×42)=1:16
因为12:42=1:16,
答:按 1:4的比缩小后,圆的面积是3.14平方厘米.
故答案为:200.96平方厘米;1:4.
【点评】此题考查了图形的放大与缩小的性质以及圆的面积公式的应用,关键是明确放大与缩小后的面积之比等于半半径的平方比.
16.见试题解答内容
【分析】甲每月完成它的,2个月则完成这项工程的几分之几,直接乘以2即可;这项工程为单位“1”,减去2个月完成的几分之几,就是剩下的.
【解析】解:(1)2,
(2)1.
故答案为:,.
【点评】此题综合考查简单的分数乘法和分数加减法应用题.
17.61。
【分析】阴影部分的面积=半圆的面积﹣直角三角形的面积,半圆的面积πr2,三角形的面积=底×高÷2。代入公式计算即可求得阴影部分的面积。
【解析】解:12×16÷2
=12×8
=96(平方厘米)
3.14×(20÷2)2﹣96
=157﹣96
=61(平方厘米)
答:阴影部分的面积是61平方厘米。
故答案为:61。
【点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可。
18.1087。
【分析】利息=本金×年利率×时间,由此代入数据计算即可求出利息;最后拿到的钱是利息+本金,由此解决问题。
【解析】解:1000×2.9%×3
=29×3
=87(元)
1000+87=1087(元)
答:到期时他可获本金和利息共1087元。
故答案为:1087。
【点评】这种类型属于利息问题,有固定的计算方法,利息=本金×利率×时间(注意时间和利率的对应),本息=本金+利息,找清数据与问题,代入公式计算即可。
19.见试题解答内容
【分析】图上距离和实际距离已知,依据“比例尺”即可求得这幅图的比例尺.
【解析】解:因为3毫米=0.3厘米,
则15厘米:0.3厘米=50:1;
答:这幅图的比例尺是50:1.
故答案为:50:1.
【点评】此题主要考查比例尺的计算方法,解答时要注意单位的换算.
20.见试题解答内容
【分析】数轴是规定了原点(0点)、方向和单位长度的一条直线.原点的左边是负数,从原点向左的每个单位长度分别是﹣1、﹣2、﹣3......;右边是正数,从原点向右每个单位长度分别是1、2、3.......。把1﹣2这一段平均分成了5份,一份表示0.2,那么3份就表示0.6,0.6+1=1.6;点B到0的距离是3个格,点C到0的距离也是3格,且在0的左边,为负数﹣3,据此解答。
【解析】解:1+0.6=1.6
如图:
【点评】本题是考查数轴的认识.数轴是规定了原点(0点)、方向和单位长度的一条直线。
21.14;(2n+2)。
【分析】根据题意发现:一张方桌坐4人,每多1张方桌就多坐2人,则拼n张方桌,能坐(2n+2)个人;据此解答即可。
【解析】解:2×6+2
=12+2
=14(人)
n张方桌并在一起可坐(2n+2)人。
答:这样6张方桌并在一起可坐14人,n张方桌并在一起可坐(2n+2)人。
故答案为:14;(2n+2)。
【点评】本题主要考查数与形结合的规律,关键是根据图示发现这组图形的规律,利用规律做题。
22.23,12。
【分析】假设全是鸡,则脚有35×2=70(只)脚,则比已知少了94﹣70=24(只)脚,因为1只鸡比1只兔少2只脚,所以兔有24÷2=12(只),由此即可解答。
【解析】解:假设全是鸡,则兔有:
(94﹣35×2)÷(4﹣2)
=24÷2
=12(只)
35﹣12=23(只)
答:鸡有23只,兔有12只。
故答案为:23,12。
【点评】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
23.见试题解答内容
【分析】利用三角形的内角和是180°和这三个角的度数之比即可解决问题.
【解析】解:2+4+3=9,
180°80°,
答:最大的角是80°.
故答案为:80°.
【点评】此题考查了三角形的内角和是180°和按比例分配的应用.
24.见试题解答内容
【分析】根据长方形面积公式:长方形面积=长×宽,则原来长方形面积为xy平方米;宽增加5米后,则现在长方形面积为x(y+5)平方米.
【解析】解:x(y+5)﹣xy=5x(平方米)
答:面积比原来增加5x平方米.
故答案为:5x.
【点评】此题掌握长方形的面积公式和字母表示数的知识,即可解答.
三.计算题(共3小题,共24分)
25.82,0.9,,0.49,6,,,5。
【分析】根据100以内加法、小数乘法、小数除法、分数减法、分数乘法、分数四则混合运算的法则直接写出得数即可。
【解析】解:
45+37=82 0.72÷0.8=0.9 0.72=0.49
12×0.5=6 5÷9 5
【点评】本题主要考查了100以内加法、小数乘法、小数除法、分数减法、分数乘法、分数四则混合运算,属于基本的计算,在平时注意积累经验,逐步提高运算的速度和准确性。
26.x=36;x=20。
【分析】先化简,然后再根据等式的性质,方程两边同时求解;
根据比例的性质,写成0.4x=12,方程两边同时除以0.4,即可求出方程的解。
【解析】解:x=30
x=30
x30
x=36
12:x=0.4:
0.4x=12
0.4x=8
0.4x÷0.4=8÷0.4
x=20
【点评】本题考查了解方程和解比例,解题过程中要利用等式的性质,注意等号对齐。
27.419;;5;8;;5.889。
【分析】(1)先算括号里的除法,再算括号里的加法,最后算括号外的减法;
(2)先同时计算两步除法,再算加法;
(3)利用加法交换律和减法的性质计算;
(4)先利用乘法分配律去括号,再利用减法的性质计算;
(5)先利用乘法分配律去小括号,再算中括号里的加法,最后算中括号外的除法;
(6)将1.9化成(2﹣0.1),将1.99化成(2﹣0.01),将1.999化成(2﹣0.001),再利用加法交换律和减法的性质计算。
【解析】解:(1)500﹣(350÷50+74)
=500﹣(7+74)
=500﹣81
=419
(2)36÷15+34÷3
(3)3.752.25
=3.75+2.25﹣()
=6﹣1
=5
(4)()×3
33
=7
=7+()
=8
(5)[()]
[]
[]
(6)1.9+1.99+1.999
=(2﹣0.1)+(2﹣0.01)+(2﹣0.001)
=2﹣0.1+2﹣0.01+2﹣0.001
=2+2+2﹣(0.1+0.01+0.001)
=6﹣0.111
=5.889
【点评】解答本题需熟练掌握四则混合运算顺序,灵活使用运算律和运算性质。
四.操作题(共1小题,共9分)
28.(1)(2)7,8;(3)1:9。
【分析】(1)根据平移的方法,把三角形向右平移10格,画出平移后的图形即可。
(2)用数对表示位置时,先表示第几列,再表示第几行,图中点A的位置用数对表示是(7,8);根据旋转的方法,点A不动,把三角形绕点A顺时针旋转90°,画出旋转后的图形即可。
(3)根据图形缩小的方法,按1:3的比画出三角形ABC缩小到原来的后的图形,分别根据三角形的面积公式计算出缩小后的图形与原来图形的面积,解答即可。
【解析】解:(1)把三角形向右平移10格,画出平移后的图形。如图:
(2)图中点A的位置用数对表示是(7,8);把三角形绕点A顺时针旋转90°,画出旋转后的图形。如图:
(3)按1:3的比画出三角形ABC缩小后的图形,如图:
(2×1÷2):(6×3÷2)
=1:9
答:缩小后的图形与原来图形面积的比是1:9。
故答案为:7,8;1:9。
【点评】本题考查了数对表示位置知识,图形的平移、旋转以及图形的缩小知识,结合题意分析解答即可。
五.应用题(共6小题,共36分)
29.不一样;我们六年级学过的比是两个数相除,也叫两个数的比,这里的4:0是指辽宁队胜了4场,浙江队1场没胜。
【分析】这里的4:0和我们六年级学过的比不一样。我们六年级学过的比是两个数相除,也叫两个数的比,这里的4:0是指辽宁队胜了4场,浙江队1场没胜。
【解析】解:这里的4:0和我们六年级学过的比不一样。我们六年级学过的比是两个数相除,也叫两个数的比,这里的4:0是指辽宁队胜了4场,浙江队1场没胜。
【点评】本题考查了比的意义。
30.112页。
【分析】依据题意设这本书有x页,(总页数﹣剩下的页数):看的天数=[总页数×(1)]:看的天数,由此列方程计算,然后计算这本书的页数。
【解析】解:设这本书有x页,由题意得:
(x﹣82):5=[x×(1)]:7
7×(x﹣82)x
56x﹣4592=15x
41x=4592
x=112
答:这本书有112页。
【点评】本题考查的是列方程解决实际问题的应用。
31.(1)每天运输的水泥数量,运输的天数是两种相关联的量,反;每天运输的水泥数量×运输的天数=水泥的总量,每天运输的水泥数量与运输的天数的乘积一定,所以每天运输的水泥数量与运输的天数成反比例。 (2)6天。
【分析】(1)根据题意,每天运输的水泥数量和运输的天数是两种相关联的量,因为每天运输的水泥数量×运输的天数=水泥的总量,每天运输的水泥数量与运输的天数的乘积一定,所以每天运输的水泥数量与运输的天数成反比例。
(2)根据题意,先计算出水泥的总量,然后用水泥的总量÷每天运输的水泥数量=运输的天数,解答即可。
【解析】解:(1)每天运输的水泥数量和运输的天数是两种相关联的量,它们成反比例关系。因为:每天运输的水泥数量×运输的天数=水泥的总量,每天运输的水泥数量与运输的天数的乘积一定,所以每天运输的水泥数量与运输的天数成反比例。
(2)实际需要多少天可以运完?
36×8÷48
=288÷48
=6(天)
答:实际需要6天可以运完。
故答案为:每天运输的水泥数量,运输的天数是两种相关联的量,反;每天运输的水泥数量×运输的天数=水泥的总量,每天运输的水泥数量与运输的天数的乘积一定,所以每天运输的水泥数量与运输的天数成反比例。
【点评】本题考查反比例的识别及应用,结合题意分析解答即可。
32.见试题解答内容
【分析】假设因为在AC、BC的中点以及A、B、C的地方都分别安装一盏路灯,那么可得出两盏路灯之间的距离是(560÷2)和(630÷2)的公约数,题目要求安装路灯最少,那么需要我们求最大公约数,求出最大公约数可得出每段上分别需要的电灯数量,因为要求最少,再减去A、B处两盏路灯即可。
【解析】解:560÷2=280,
630÷2=315,
280=2×2×2×5×7,
315=3×3×5×7,
所以280和315的最大公约数是5×7=35,
共需要路灯:(560+630)÷35﹣1=33
所以共需路灯33(盏).
答:至少需要安装33盏灯.
【点评】此题属于应用类问题,解答本题的关键是明白两盏灯之间的距离是280和315的最大公约数,另外在求每一段路上的路灯时不要忘记加1.
33.见试题解答内容
【分析】先根据工作效率=工作总量÷工作时间,求出修路队的工作效率,也就是600米的分率,依据分数除法意义即可解答.
【解析】解:600÷(48%÷4),
=600÷12%,
=5000(米),
=5(千米),
答:这条路长5千米.
【点评】本题主要考查学生依据工作总量、工作时间以及工作效率之间数量关系解决问题的能力,关键是求出600米占的分率.
34.见试题解答内容
【分析】假设笼子里都是蚱蜢,那么就有25×6=150条腿,这样实际就比假设多170﹣150=20条腿;因为一只蜘蛛比一只蚱蜢多8﹣6=2条腿,所以就有20÷2=10只蜘蛛;进而求得蚱蜢的只数.
【解析】解:蜘蛛:(170﹣25×6)÷(8﹣6)
=20÷2
=10(只);
蚱蜢:25﹣10=15(只)
答:蜘蛛有10只,蚱蜢有15只.
【点评】此题属于典型的鸡兔同笼问题,解答此类题的关键是用假设法,也可以用方程进行解答.
21世纪教育网(www.21cnjy.com)
同课章节目录
