2024-2025学年浙江省温州市七年级(下)期末数学练习(含答案)
文档属性
| 名称 | 2024-2025学年浙江省温州市七年级(下)期末数学练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 377.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 00:00:00 | ||
图片预览



文档简介
2024-2025学年温州市七年级(下)期末数学练习
一、选择题(共10小题,每小题3分,共30分)
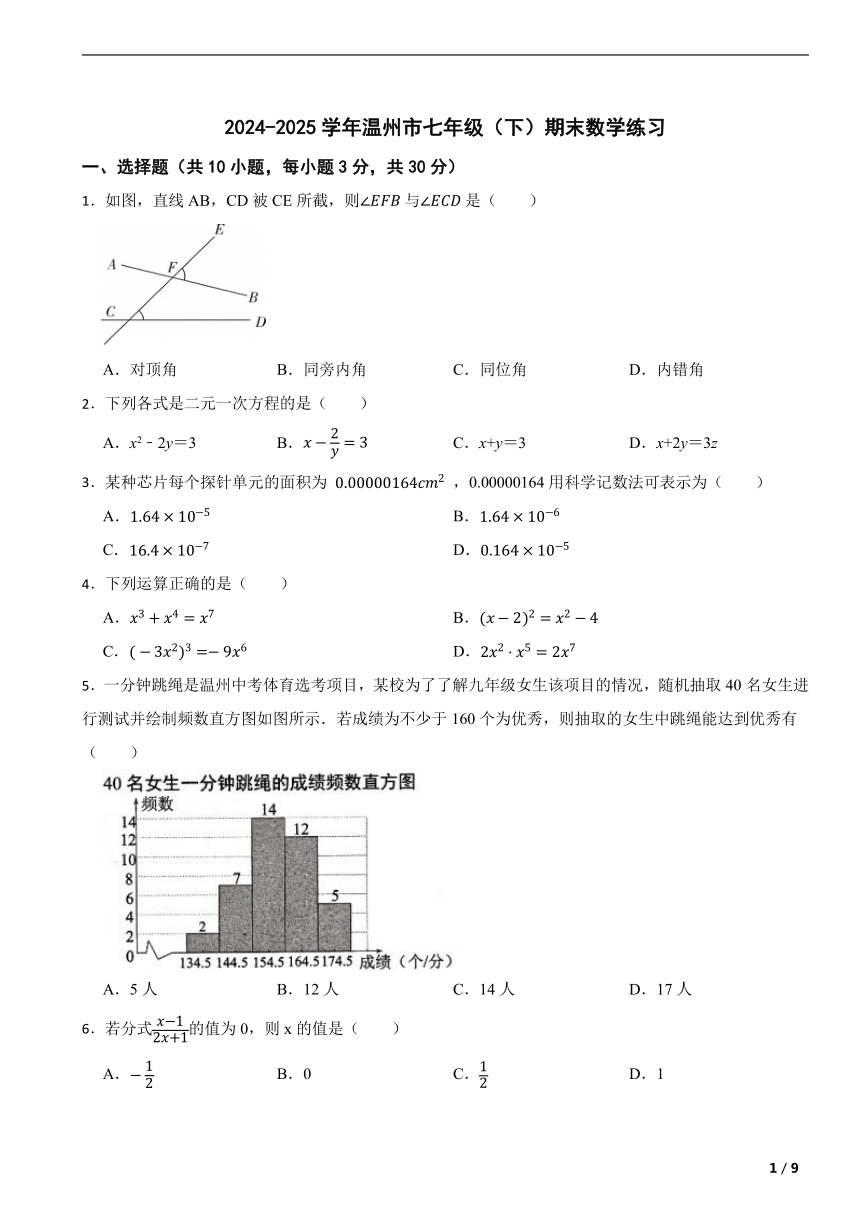
1.如图,直线AB,CD被CE所截,则与是( )
A.对顶角 B.同旁内角 C.同位角 D.内错角
2.下列各式是二元一次方程的是( )
A.x2﹣2y=3 B. C.x+y=3 D.x+2y=3z
3.某种芯片每个探针单元的面积为 ,0.00000164用科学记数法可表示为( )
A. B.
C. D.
4.下列运算正确的是( )
A. B.
C. D.
5.一分钟跳绳是温州中考体育选考项目,某校为了了解九年级女生该项目的情况,随机抽取40名女生进行测试并绘制频数直方图如图所示.若成绩为不少于160个为优秀,则抽取的女生中跳绳能达到优秀有( )
A.5人 B.12人 C.14人 D.17人
6.若分式的值为0,则x的值是( )
A. B.0 C. D.1
7.下列从左到右的变形属于因式分解且结果正确的是( )
A.a(2a+y)=2ax+ay B.y2﹣x2=(y+x)(y﹣x)
C.x2﹣4x+1=x(x﹣4)+1 D.x2+2xy+4y2=(x+2y)2
8.将一副三角尺(厚度不计)如图摆放,使AB边与CD边互相平行,则图中的大小为( )
A. B. C. D.
9.某新能源汽车制造厂采用高度自动化的机器人装配技术系统以提高生产效率,平均每小时比技术升级前多装配50辆汽车.现在装配1000辆汽车所需的时间与技术升级前装配800辆汽车所需的时间相同,设技术升级前每小时装配辆汽车,可列方程为( )
A. B.
C. D.
10.如图所示,将两个正方形并列放置,其中B、C、E三点在一条直线上,C、G、D三点在一条直线上,已知,,则阴影部分的面积是( )
A.10 B.20 C.30 D.40
二、填空题(共6小题,每小题3分,共18分)
11.因式分解:m2﹣m= .
12.计算: .
13.《义务教育劳动课程标准年版》首次把学生学会炒菜纳入劳动教育课程,并做出明确规定.某班有45名学生,其中学会炒菜的学生频率是,则该班学会炒菜的学生有 名.
14.已知是二元一次方程的一个解,则 ;
15.若x+=3,分式(x-)2= .
16.如图1是一盏可调节台灯,图2,图3为示意图.固定底座于点O,与是分别可绕点A和B旋转的调节杆.在调节过程中,灯体始终保持平行于,台灯最外侧光线组成的始终保持不变.如图2,调节台灯使光线,此时,且的延长线恰好是的角平分线,则 .
三、解答题(共8题,共52分)
17.(本题8分)计算:
(1); (2)
18.(本题8分)解下列方程(组):
(1) (2)
19.(本题6分)如图,把向上平移个单位,再向右平移个单位得到.
(1)在图中画出;
(2)请写出点,,的坐标;
(3)求出的面积.
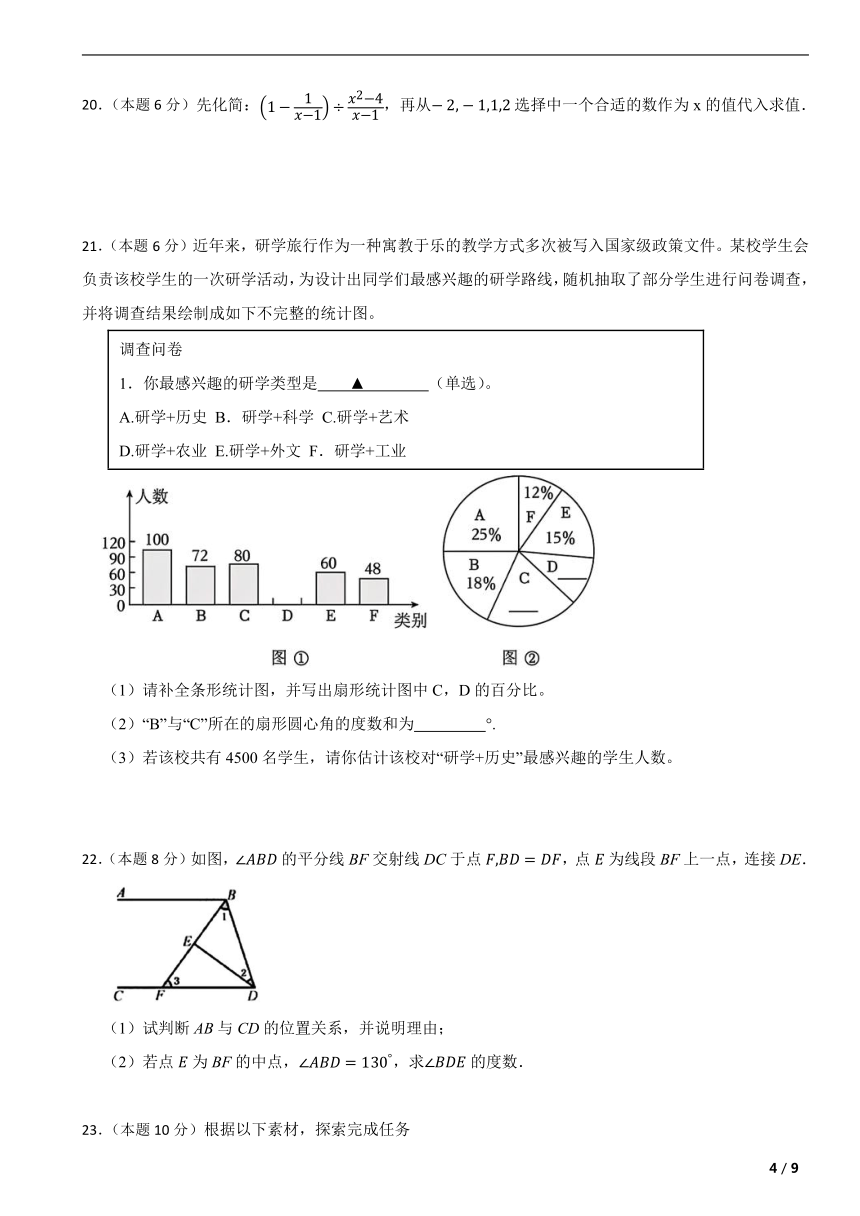
20.(本题6分)先化简:,再从选择中一个合适的数作为x的值代入求值.
21.(本题6分)近年来,研学旅行作为一种寓教于乐的教学方式多次被写入国家级政策文件。某校学生会负责该校学生的一次研学活动,为设计出同学们最感兴趣的研学路线,随机抽取了部分学生进行问卷调查,并将调查结果绘制成如下不完整的统计图。
调查问卷 1.你最感兴趣的研学类型是 ▲ (单选)。 A.研学+历史 B.研学+科学 C.研学+艺术 D.研学+农业 E.研学+外文 F.研学+工业
(1)请补全条形统计图,并写出扇形统计图中C,D的百分比。
(2)“B”与“C”所在的扇形圆心角的度数和为 °.
(3)若该校共有4500名学生,请你估计该校对“研学+历史”最感兴趣的学生人数。
22.(本题8分)如图,的平分线BF交射线DC于点,点为线段BF上一点,连接DE.
(1)试判断AB与CD的位置关系,并说明理由;
(2)若点为BF的中点,,求的度数.
23.(本题10分)根据以下素材,探索完成任务
素材1 某中学701班自制一款组合式的木质收纳架.如图所示,已知单个收纳架由2个横杆和5个竖杆组成,横杆长为60厘米,竖杆长为32厘米.
素材2 可提供的制作原料是每根长为160厘米的木条.考虑到所制作的收纳架的牢固性,规定单根杆件的用料不能拼接而成.
解决问题
任务(一) 拟定裁切方案 一根160厘米长的木条有以下裁剪方法.(余料作废) 方法①:当只裁剪32厘米的竖杆时,最多可裁剪_________根; 方法②:当先裁剪下1根60厘米长的横杆时,余下部分最多能裁剪32厘米长的竖杆_________根; 方法③:当先裁剪下2根60厘米长的横杆时,余下部分最多能裁剪32厘米长的竖杆_________根.
任务(二) 核算材料费用 班委会计划在教室墙壁上安装5个收纳架,若用任务(一)中的方法②和方法③进行裁剪,则裁剪多少根160厘米长的木条,才能刚好得到所需要的用料?
任务(三) 评价安装工效 同学们在安装过程中发现:单位时间内可以安装根竖杆或根横杆.任务(二)中的5个收纳架安装完毕时,发现安装竖杆所需的时间与安装横杆所需的时间相同,求的值.
参考答案
1.C
2.C
3.B
4.D
5.D
6.D
7.B
8.C
9.A
10.C
11.m(m﹣1)
12.
13.18
14.3
15.5
16.80°
17.(1)解:;
=2-(-1)+1
=2+1+1
=4
(2)解:4x(x-6)-(2x-1) (2x+1)
=4x2-24x- (4x2 -1)
=4x2-24x-4x2+1
=-24x+1.
18.(1)解:
(2)解:经检验x=-1是原方程的解
19.(1)解:如图所示,即为所求.
(2)解:,,
(3)解:的面积为.
20.解:
,
∵,,
∴把代入得:原式.
21.(1)解:样本容量为:100÷25%=400,
∴C所占百分比为:,
∴D所占百分比为:1-25%-18%-20%-15%-12%=10%,
D的人数为:400×10%=40,
补全条形统计图如下:
(2)136.8
(3)解:4500×25%=1125(人),
答:估计该校对“研学+历史”最感兴趣的学生人数约1125名.
22.(1)解:,理由如下:
平分,
,
,
,
,
.
(2)解:平分,
,
为BF中点,
,
在和中
,
,
,
,
,
.
23.任务一:5,3,1;
解:任务二:设按方法②需裁剪x根160厘米长的木条,
按方法③需裁剪y根160厘米长的木条,依据题意得:
,
解得:.
答:按方法②需裁剪8根160厘米长的木条,按方法③需裁剪1根160厘米长的木条,才能刚好得到所需要的相应数量的用料.
任务三:依据题意得,
解得:,
经检验,是该方程的解.
1 / 1
一、选择题(共10小题,每小题3分,共30分)
1.如图,直线AB,CD被CE所截,则与是( )
A.对顶角 B.同旁内角 C.同位角 D.内错角
2.下列各式是二元一次方程的是( )
A.x2﹣2y=3 B. C.x+y=3 D.x+2y=3z
3.某种芯片每个探针单元的面积为 ,0.00000164用科学记数法可表示为( )
A. B.
C. D.
4.下列运算正确的是( )
A. B.
C. D.
5.一分钟跳绳是温州中考体育选考项目,某校为了了解九年级女生该项目的情况,随机抽取40名女生进行测试并绘制频数直方图如图所示.若成绩为不少于160个为优秀,则抽取的女生中跳绳能达到优秀有( )
A.5人 B.12人 C.14人 D.17人
6.若分式的值为0,则x的值是( )
A. B.0 C. D.1
7.下列从左到右的变形属于因式分解且结果正确的是( )
A.a(2a+y)=2ax+ay B.y2﹣x2=(y+x)(y﹣x)
C.x2﹣4x+1=x(x﹣4)+1 D.x2+2xy+4y2=(x+2y)2
8.将一副三角尺(厚度不计)如图摆放,使AB边与CD边互相平行,则图中的大小为( )
A. B. C. D.
9.某新能源汽车制造厂采用高度自动化的机器人装配技术系统以提高生产效率,平均每小时比技术升级前多装配50辆汽车.现在装配1000辆汽车所需的时间与技术升级前装配800辆汽车所需的时间相同,设技术升级前每小时装配辆汽车,可列方程为( )
A. B.
C. D.
10.如图所示,将两个正方形并列放置,其中B、C、E三点在一条直线上,C、G、D三点在一条直线上,已知,,则阴影部分的面积是( )
A.10 B.20 C.30 D.40
二、填空题(共6小题,每小题3分,共18分)
11.因式分解:m2﹣m= .
12.计算: .
13.《义务教育劳动课程标准年版》首次把学生学会炒菜纳入劳动教育课程,并做出明确规定.某班有45名学生,其中学会炒菜的学生频率是,则该班学会炒菜的学生有 名.
14.已知是二元一次方程的一个解,则 ;
15.若x+=3,分式(x-)2= .
16.如图1是一盏可调节台灯,图2,图3为示意图.固定底座于点O,与是分别可绕点A和B旋转的调节杆.在调节过程中,灯体始终保持平行于,台灯最外侧光线组成的始终保持不变.如图2,调节台灯使光线,此时,且的延长线恰好是的角平分线,则 .
三、解答题(共8题,共52分)
17.(本题8分)计算:
(1); (2)
18.(本题8分)解下列方程(组):
(1) (2)
19.(本题6分)如图,把向上平移个单位,再向右平移个单位得到.
(1)在图中画出;
(2)请写出点,,的坐标;
(3)求出的面积.
20.(本题6分)先化简:,再从选择中一个合适的数作为x的值代入求值.
21.(本题6分)近年来,研学旅行作为一种寓教于乐的教学方式多次被写入国家级政策文件。某校学生会负责该校学生的一次研学活动,为设计出同学们最感兴趣的研学路线,随机抽取了部分学生进行问卷调查,并将调查结果绘制成如下不完整的统计图。
调查问卷 1.你最感兴趣的研学类型是 ▲ (单选)。 A.研学+历史 B.研学+科学 C.研学+艺术 D.研学+农业 E.研学+外文 F.研学+工业
(1)请补全条形统计图,并写出扇形统计图中C,D的百分比。
(2)“B”与“C”所在的扇形圆心角的度数和为 °.
(3)若该校共有4500名学生,请你估计该校对“研学+历史”最感兴趣的学生人数。
22.(本题8分)如图,的平分线BF交射线DC于点,点为线段BF上一点,连接DE.
(1)试判断AB与CD的位置关系,并说明理由;
(2)若点为BF的中点,,求的度数.
23.(本题10分)根据以下素材,探索完成任务
素材1 某中学701班自制一款组合式的木质收纳架.如图所示,已知单个收纳架由2个横杆和5个竖杆组成,横杆长为60厘米,竖杆长为32厘米.
素材2 可提供的制作原料是每根长为160厘米的木条.考虑到所制作的收纳架的牢固性,规定单根杆件的用料不能拼接而成.
解决问题
任务(一) 拟定裁切方案 一根160厘米长的木条有以下裁剪方法.(余料作废) 方法①:当只裁剪32厘米的竖杆时,最多可裁剪_________根; 方法②:当先裁剪下1根60厘米长的横杆时,余下部分最多能裁剪32厘米长的竖杆_________根; 方法③:当先裁剪下2根60厘米长的横杆时,余下部分最多能裁剪32厘米长的竖杆_________根.
任务(二) 核算材料费用 班委会计划在教室墙壁上安装5个收纳架,若用任务(一)中的方法②和方法③进行裁剪,则裁剪多少根160厘米长的木条,才能刚好得到所需要的用料?
任务(三) 评价安装工效 同学们在安装过程中发现:单位时间内可以安装根竖杆或根横杆.任务(二)中的5个收纳架安装完毕时,发现安装竖杆所需的时间与安装横杆所需的时间相同,求的值.
参考答案
1.C
2.C
3.B
4.D
5.D
6.D
7.B
8.C
9.A
10.C
11.m(m﹣1)
12.
13.18
14.3
15.5
16.80°
17.(1)解:;
=2-(-1)+1
=2+1+1
=4
(2)解:4x(x-6)-(2x-1) (2x+1)
=4x2-24x- (4x2 -1)
=4x2-24x-4x2+1
=-24x+1.
18.(1)解:
(2)解:经检验x=-1是原方程的解
19.(1)解:如图所示,即为所求.
(2)解:,,
(3)解:的面积为.
20.解:
,
∵,,
∴把代入得:原式.
21.(1)解:样本容量为:100÷25%=400,
∴C所占百分比为:,
∴D所占百分比为:1-25%-18%-20%-15%-12%=10%,
D的人数为:400×10%=40,
补全条形统计图如下:
(2)136.8
(3)解:4500×25%=1125(人),
答:估计该校对“研学+历史”最感兴趣的学生人数约1125名.
22.(1)解:,理由如下:
平分,
,
,
,
,
.
(2)解:平分,
,
为BF中点,
,
在和中
,
,
,
,
,
.
23.任务一:5,3,1;
解:任务二:设按方法②需裁剪x根160厘米长的木条,
按方法③需裁剪y根160厘米长的木条,依据题意得:
,
解得:.
答:按方法②需裁剪8根160厘米长的木条,按方法③需裁剪1根160厘米长的木条,才能刚好得到所需要的相应数量的用料.
任务三:依据题意得,
解得:,
经检验,是该方程的解.
1 / 1
同课章节目录
