2026届高三数学一轮复习-2年高考1年模拟-(七十六)“概率与统计”的综合问题(含解析)
文档属性
| 名称 | 2026届高三数学一轮复习-2年高考1年模拟-(七十六)“概率与统计”的综合问题(含解析) | 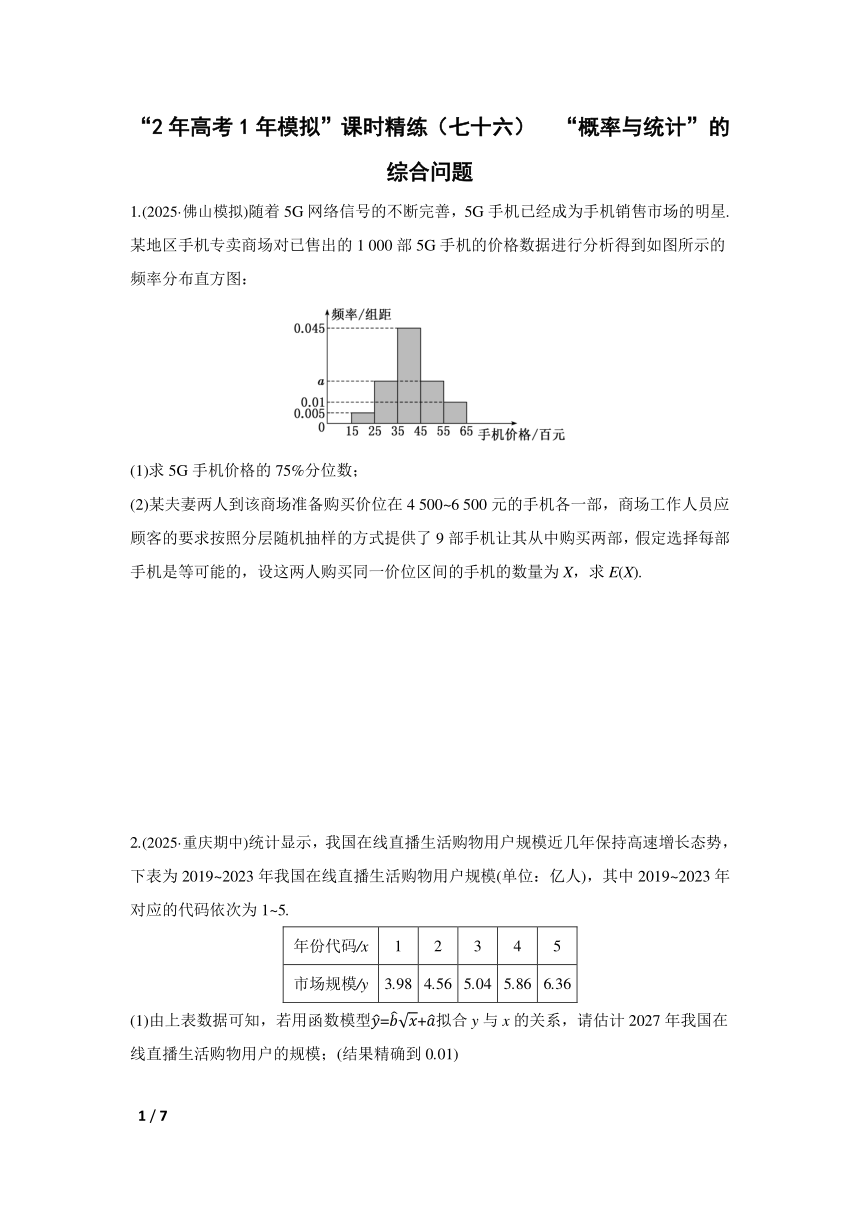 | |
| 格式 | docx | ||
| 文件大小 | 88.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 17:21:58 | ||
图片预览



文档简介
“2年高考1年模拟”课时精练(七十六) “概率与统计”的综合问题
1.(2025·佛山模拟)随着5G网络信号的不断完善,5G手机已经成为手机销售市场的明星.某地区手机专卖商场对已售出的1 000部5G手机的价格数据进行分析得到如图所示的频率分布直方图:
(1)求5G手机价格的75%分位数;
(2)某夫妻两人到该商场准备购买价位在4 500~6 500元的手机各一部,商场工作人员应顾客的要求按照分层随机抽样的方式提供了9部手机让其从中购买两部,假定选择每部手机是等可能的,设这两人购买同一价位区间的手机的数量为X,求E(X).
2.(2025·重庆期中)统计显示,我国在线直播生活购物用户规模近几年保持高速增长态势,下表为2019~2023年我国在线直播生活购物用户规模(单位:亿人),其中2019~2023年对应的代码依次为1~5.
年份代码/x 1 2 3 4 5
市场规模/y 3.98 4.56 5.04 5.86 6.36
(1)由上表数据可知,若用函数模型=+拟合y与x的关系,请估计2027年我国在线直播生活购物用户的规模;(结果精确到0.01)
(2)已知我国在线直播生活购物用户选择在品牌官方直播间购物的概率为p,现从我国在线直播购物用户中随机抽取5人,记这5人中选择在品牌官方直播间购物的人数为X,若P(X=5)=P(X=4),求X的均值和方差.
3.(2025·杭州一模)设随机变量X所有可能的取值为x1,x2,…,xn,P(X=xi)=pi>0(i=1,2,…,n),且p1+p2+…+pn=1.定义事件X=xi的信息量为Hi=-ln pi,称X的平均信息量H(X)=-(p1ln p1+p2ln p2+…+pnln pn)为信息熵.
(1)若n=3,pk+1=2pk(k=1,2),求此时的信息熵;
(2)最大熵原理:对一个随机事件的概率分布进行预测时,要使得信息熵最大.信息熵最大就是事物可能的状态数最多,复杂程度最大,概率分布最均匀,这才是风险最小(最合理)的决定.证明:H(X)≤ln n,并解释等号成立时的实际意义.
参考不等式:若f(x)=ln x,则pif(xi)≤f .
4.(2025·佛山模拟)某商场为促销设计了一项回馈客户的抽奖活动,抽奖规则是:有放回地从装有大小相同的6个红球和4个黑球的袋中任意抽取一个,若第一次抽到红球则奖励50元的奖券,抽到黑球则奖励25元的奖券;第二次开始,每一次抽到红球则奖券数额是上一次奖券数额的2倍,抽到黑球则奖励25元的奖券,记顾客甲第n次抽奖所得的奖券数额Xn(1≤n≤6)的数学期望为E(Xn).
(1)求E(X1)及X2的分布列;
(2)写出E(Xn)与E()(n≥2)的递推关系式,并证明{E(Xn)+50}为等比数列;
(3)若顾客甲一共有6次抽奖机会,求该顾客所得的所有奖券数额的期望值.(参考数据:1.26≈2.986)
(解析)精练(七十六) “概率与统计”的综合问题
1.(2025·佛山模拟)随着5G网络信号的不断完善,5G手机已经成为手机销售市场的明星.某地区手机专卖商场对已售出的1 000部5G手机的价格数据进行分析得到如图所示的频率分布直方图:
(1)求5G手机价格的75%分位数;
(2)某夫妻两人到该商场准备购买价位在4 500~6 500元的手机各一部,商场工作人员应顾客的要求按照分层随机抽样的方式提供了9部手机让其从中购买两部,假定选择每部手机是等可能的,设这两人购买同一价位区间的手机的数量为X,求E(X).
解:(1)由频率分布直方图可得(0.045+2a+0.01+0.005)×10=1,解得a=0.02.
因为5G手机的价格在1 500~4 500元的频率为(0.005+0.02+0.045)×10=0.7,
而价格在4 500~5 500元的频率为0.02×10=0.2,
故5G手机价格的75%分位数应该在4 500~5 500元这一组,且75%分位数为×100=4 750元.
(2)因为购买价位在4 500~5 500元和5 500~6 500元的手机占的比率分别为0.2和0.1,
故按照分层随机抽样的方式在4 500~5 500元这一价位选取了6部,在5 500~6 500元这一价位选取了3部,这两人购买同一价位的手机数量X的可能值有0,2.则P(X=0)==,
P(X=2)==,
X的分布列为
X 0 2
P
故E(X)=0×+2×=1.
2.(2025·重庆期中)统计显示,我国在线直播生活购物用户规模近几年保持高速增长态势,下表为2019~2023年我国在线直播生活购物用户规模(单位:亿人),其中2019~2023年对应的代码依次为1~5.
年份代码/x 1 2 3 4 5
市场规模/y 3.98 4.56 5.04 5.86 6.36
(1)由上表数据可知,若用函数模型=+拟合y与x的关系,请估计2027年我国在线直播生活购物用户的规模;(结果精确到0.01)
(2)已知我国在线直播生活购物用户选择在品牌官方直播间购物的概率为p,现从我国在线直播购物用户中随机抽取5人,记这5人中选择在品牌官方直播间购物的人数为X,若P(X=5)=P(X=4),求X的均值和方差.
参考数据:=5.16,≈1.68,viyi≈45.10,其中vi=.
参考公式:对于一组数据(v1,y1),(v2,y2),…,(vn,yn),其经验回归直线=v+的斜率和截距的最小二乘估计公式分别为==-.
解:(1)设v=,则=v+,
因为=5.16,≈1.68,=xi=15,
所以= ==≈1.98.
把(1.68,5.16)代入=-,
得=5.16-1.98×1.68≈1.83.
所以y关于x的回归方程为=1.98+1.83.
由题意知2027年对应的代码为9,
所以2027年我国在线直播生活购物用户的规模=1.98×3+1.83=7.77亿人.
(2)由题意知X~B(5,p),P(X=5)=p5(1-p)0=p5,P(X=4)=p4(1-p)1=5p4(1-p),
由p5=5p4(1-p),得p=,所以E(X)=5×=,D(X)=5××=.
3.(2025·杭州一模)设随机变量X所有可能的取值为x1,x2,…,xn,P(X=xi)=pi>0(i=1,2,…,n),且p1+p2+…+pn=1.定义事件X=xi的信息量为Hi=-ln pi,称X的平均信息量H(X)=-(p1ln p1+p2ln p2+…+pnln pn)为信息熵.
(1)若n=3,pk+1=2pk(k=1,2),求此时的信息熵;
(2)最大熵原理:对一个随机事件的概率分布进行预测时,要使得信息熵最大.信息熵最大就是事物可能的状态数最多,复杂程度最大,概率分布最均匀,这才是风险最小(最合理)的决定.证明:H(X)≤ln n,并解释等号成立时的实际意义.
参考不等式:若f(x)=ln x,则pif(xi)≤f .
解:(1)当n=3时,p1+p2+p3=1,且p2=2p1,p3=2p2,∴p1=,p2=,p3=,
∴H(X)=-(p1ln p1+p2ln p2+p3ln p3)
=-=-ln
=ln 7-ln 2.
(2)证明:根据参考不等式pif(xi)≤f(pixi),
H(X)=-(p1ln p1+p2ln p2+…+pnln pn)=- piln pi=piln ≤ln=ln n.
等号成立的实际意义:从数学角度理解,当p1=p2=…=pn=时,H(X)取得最大值;从现实生活理解,在没有任何已知信息时,对于未知信息,勿加主观臆断,对每一种可能性都有所估计,且等概率地分配是最保险的做法.
4.(2025·佛山模拟)某商场为促销设计了一项回馈客户的抽奖活动,抽奖规则是:有放回地从装有大小相同的6个红球和4个黑球的袋中任意抽取一个,若第一次抽到红球则奖励50元的奖券,抽到黑球则奖励25元的奖券;第二次开始,每一次抽到红球则奖券数额是上一次奖券数额的2倍,抽到黑球则奖励25元的奖券,记顾客甲第n次抽奖所得的奖券数额Xn(1≤n≤6)的数学期望为E(Xn).
(1)求E(X1)及X2的分布列;
(2)写出E(Xn)与E()(n≥2)的递推关系式,并证明{E(Xn)+50}为等比数列;
(3)若顾客甲一共有6次抽奖机会,求该顾客所得的所有奖券数额的期望值.(参考数据:1.26≈2.986)
解:(1)依题意,抽到一个红球的概率为0.6,抽到一个黑球的概率为0.4,
显然X1的值为25,50,则P(X1=25)=0.4,P(X1=50)=0.6,
所以E(X1)=25×0.4+50×0.6=40.
X2的值为25,50,100,则P(X2=25)=0.4,
P(X2=50)=0.4×0.6=0.24,P(X2=100)=0.6×0.6=0.36,
所以X2的分布列为
X2 25 50 100
P 0.4 0.24 0.36
(2)依题意,当n≥2时,甲第n次抽到红球所得的奖券数额为2E(Xn-1),对应概率为0.6,
抽到黑球所得的奖券数额为25元,对应概率为0.4,
因此当2≤n≤6时,E(Xn)=2E(Xn-1)×0.6+25×0.4=1.2E(Xn-1)+10,
E(Xn)+50=1.2E(Xn-1)+60,即E(Xn)+50=1.2[E(Xn-1)+50],又E(X1)+50=40+50=90,
所以数列{E(Xn)+50}为等比数列,公比为1.2,首项为90.
(3)由(2)得,E(Xn)+50=90×1.2n-1(1≤n≤6),即E(Xn)=90×1.2n-1-50,
所以顾客甲抽奖6次,所得奖券数额的期望为E(Xn)=-50×6≈-300=593.7(元).
4 / 4
1.(2025·佛山模拟)随着5G网络信号的不断完善,5G手机已经成为手机销售市场的明星.某地区手机专卖商场对已售出的1 000部5G手机的价格数据进行分析得到如图所示的频率分布直方图:
(1)求5G手机价格的75%分位数;
(2)某夫妻两人到该商场准备购买价位在4 500~6 500元的手机各一部,商场工作人员应顾客的要求按照分层随机抽样的方式提供了9部手机让其从中购买两部,假定选择每部手机是等可能的,设这两人购买同一价位区间的手机的数量为X,求E(X).
2.(2025·重庆期中)统计显示,我国在线直播生活购物用户规模近几年保持高速增长态势,下表为2019~2023年我国在线直播生活购物用户规模(单位:亿人),其中2019~2023年对应的代码依次为1~5.
年份代码/x 1 2 3 4 5
市场规模/y 3.98 4.56 5.04 5.86 6.36
(1)由上表数据可知,若用函数模型=+拟合y与x的关系,请估计2027年我国在线直播生活购物用户的规模;(结果精确到0.01)
(2)已知我国在线直播生活购物用户选择在品牌官方直播间购物的概率为p,现从我国在线直播购物用户中随机抽取5人,记这5人中选择在品牌官方直播间购物的人数为X,若P(X=5)=P(X=4),求X的均值和方差.
3.(2025·杭州一模)设随机变量X所有可能的取值为x1,x2,…,xn,P(X=xi)=pi>0(i=1,2,…,n),且p1+p2+…+pn=1.定义事件X=xi的信息量为Hi=-ln pi,称X的平均信息量H(X)=-(p1ln p1+p2ln p2+…+pnln pn)为信息熵.
(1)若n=3,pk+1=2pk(k=1,2),求此时的信息熵;
(2)最大熵原理:对一个随机事件的概率分布进行预测时,要使得信息熵最大.信息熵最大就是事物可能的状态数最多,复杂程度最大,概率分布最均匀,这才是风险最小(最合理)的决定.证明:H(X)≤ln n,并解释等号成立时的实际意义.
参考不等式:若f(x)=ln x,则pif(xi)≤f .
4.(2025·佛山模拟)某商场为促销设计了一项回馈客户的抽奖活动,抽奖规则是:有放回地从装有大小相同的6个红球和4个黑球的袋中任意抽取一个,若第一次抽到红球则奖励50元的奖券,抽到黑球则奖励25元的奖券;第二次开始,每一次抽到红球则奖券数额是上一次奖券数额的2倍,抽到黑球则奖励25元的奖券,记顾客甲第n次抽奖所得的奖券数额Xn(1≤n≤6)的数学期望为E(Xn).
(1)求E(X1)及X2的分布列;
(2)写出E(Xn)与E()(n≥2)的递推关系式,并证明{E(Xn)+50}为等比数列;
(3)若顾客甲一共有6次抽奖机会,求该顾客所得的所有奖券数额的期望值.(参考数据:1.26≈2.986)
(解析)精练(七十六) “概率与统计”的综合问题
1.(2025·佛山模拟)随着5G网络信号的不断完善,5G手机已经成为手机销售市场的明星.某地区手机专卖商场对已售出的1 000部5G手机的价格数据进行分析得到如图所示的频率分布直方图:
(1)求5G手机价格的75%分位数;
(2)某夫妻两人到该商场准备购买价位在4 500~6 500元的手机各一部,商场工作人员应顾客的要求按照分层随机抽样的方式提供了9部手机让其从中购买两部,假定选择每部手机是等可能的,设这两人购买同一价位区间的手机的数量为X,求E(X).
解:(1)由频率分布直方图可得(0.045+2a+0.01+0.005)×10=1,解得a=0.02.
因为5G手机的价格在1 500~4 500元的频率为(0.005+0.02+0.045)×10=0.7,
而价格在4 500~5 500元的频率为0.02×10=0.2,
故5G手机价格的75%分位数应该在4 500~5 500元这一组,且75%分位数为×100=4 750元.
(2)因为购买价位在4 500~5 500元和5 500~6 500元的手机占的比率分别为0.2和0.1,
故按照分层随机抽样的方式在4 500~5 500元这一价位选取了6部,在5 500~6 500元这一价位选取了3部,这两人购买同一价位的手机数量X的可能值有0,2.则P(X=0)==,
P(X=2)==,
X的分布列为
X 0 2
P
故E(X)=0×+2×=1.
2.(2025·重庆期中)统计显示,我国在线直播生活购物用户规模近几年保持高速增长态势,下表为2019~2023年我国在线直播生活购物用户规模(单位:亿人),其中2019~2023年对应的代码依次为1~5.
年份代码/x 1 2 3 4 5
市场规模/y 3.98 4.56 5.04 5.86 6.36
(1)由上表数据可知,若用函数模型=+拟合y与x的关系,请估计2027年我国在线直播生活购物用户的规模;(结果精确到0.01)
(2)已知我国在线直播生活购物用户选择在品牌官方直播间购物的概率为p,现从我国在线直播购物用户中随机抽取5人,记这5人中选择在品牌官方直播间购物的人数为X,若P(X=5)=P(X=4),求X的均值和方差.
参考数据:=5.16,≈1.68,viyi≈45.10,其中vi=.
参考公式:对于一组数据(v1,y1),(v2,y2),…,(vn,yn),其经验回归直线=v+的斜率和截距的最小二乘估计公式分别为==-.
解:(1)设v=,则=v+,
因为=5.16,≈1.68,=xi=15,
所以= ==≈1.98.
把(1.68,5.16)代入=-,
得=5.16-1.98×1.68≈1.83.
所以y关于x的回归方程为=1.98+1.83.
由题意知2027年对应的代码为9,
所以2027年我国在线直播生活购物用户的规模=1.98×3+1.83=7.77亿人.
(2)由题意知X~B(5,p),P(X=5)=p5(1-p)0=p5,P(X=4)=p4(1-p)1=5p4(1-p),
由p5=5p4(1-p),得p=,所以E(X)=5×=,D(X)=5××=.
3.(2025·杭州一模)设随机变量X所有可能的取值为x1,x2,…,xn,P(X=xi)=pi>0(i=1,2,…,n),且p1+p2+…+pn=1.定义事件X=xi的信息量为Hi=-ln pi,称X的平均信息量H(X)=-(p1ln p1+p2ln p2+…+pnln pn)为信息熵.
(1)若n=3,pk+1=2pk(k=1,2),求此时的信息熵;
(2)最大熵原理:对一个随机事件的概率分布进行预测时,要使得信息熵最大.信息熵最大就是事物可能的状态数最多,复杂程度最大,概率分布最均匀,这才是风险最小(最合理)的决定.证明:H(X)≤ln n,并解释等号成立时的实际意义.
参考不等式:若f(x)=ln x,则pif(xi)≤f .
解:(1)当n=3时,p1+p2+p3=1,且p2=2p1,p3=2p2,∴p1=,p2=,p3=,
∴H(X)=-(p1ln p1+p2ln p2+p3ln p3)
=-=-ln
=ln 7-ln 2.
(2)证明:根据参考不等式pif(xi)≤f(pixi),
H(X)=-(p1ln p1+p2ln p2+…+pnln pn)=- piln pi=piln ≤ln=ln n.
等号成立的实际意义:从数学角度理解,当p1=p2=…=pn=时,H(X)取得最大值;从现实生活理解,在没有任何已知信息时,对于未知信息,勿加主观臆断,对每一种可能性都有所估计,且等概率地分配是最保险的做法.
4.(2025·佛山模拟)某商场为促销设计了一项回馈客户的抽奖活动,抽奖规则是:有放回地从装有大小相同的6个红球和4个黑球的袋中任意抽取一个,若第一次抽到红球则奖励50元的奖券,抽到黑球则奖励25元的奖券;第二次开始,每一次抽到红球则奖券数额是上一次奖券数额的2倍,抽到黑球则奖励25元的奖券,记顾客甲第n次抽奖所得的奖券数额Xn(1≤n≤6)的数学期望为E(Xn).
(1)求E(X1)及X2的分布列;
(2)写出E(Xn)与E()(n≥2)的递推关系式,并证明{E(Xn)+50}为等比数列;
(3)若顾客甲一共有6次抽奖机会,求该顾客所得的所有奖券数额的期望值.(参考数据:1.26≈2.986)
解:(1)依题意,抽到一个红球的概率为0.6,抽到一个黑球的概率为0.4,
显然X1的值为25,50,则P(X1=25)=0.4,P(X1=50)=0.6,
所以E(X1)=25×0.4+50×0.6=40.
X2的值为25,50,100,则P(X2=25)=0.4,
P(X2=50)=0.4×0.6=0.24,P(X2=100)=0.6×0.6=0.36,
所以X2的分布列为
X2 25 50 100
P 0.4 0.24 0.36
(2)依题意,当n≥2时,甲第n次抽到红球所得的奖券数额为2E(Xn-1),对应概率为0.6,
抽到黑球所得的奖券数额为25元,对应概率为0.4,
因此当2≤n≤6时,E(Xn)=2E(Xn-1)×0.6+25×0.4=1.2E(Xn-1)+10,
E(Xn)+50=1.2E(Xn-1)+60,即E(Xn)+50=1.2[E(Xn-1)+50],又E(X1)+50=40+50=90,
所以数列{E(Xn)+50}为等比数列,公比为1.2,首项为90.
(3)由(2)得,E(Xn)+50=90×1.2n-1(1≤n≤6),即E(Xn)=90×1.2n-1-50,
所以顾客甲抽奖6次,所得奖券数额的期望为E(Xn)=-50×6≈-300=593.7(元).
4 / 4
同课章节目录
