2026届高三数学一轮复习-2年高考1年模拟-(六十七)成对数据的统计分析(含解析)
文档属性
| 名称 | 2026届高三数学一轮复习-2年高考1年模拟-(六十七)成对数据的统计分析(含解析) | 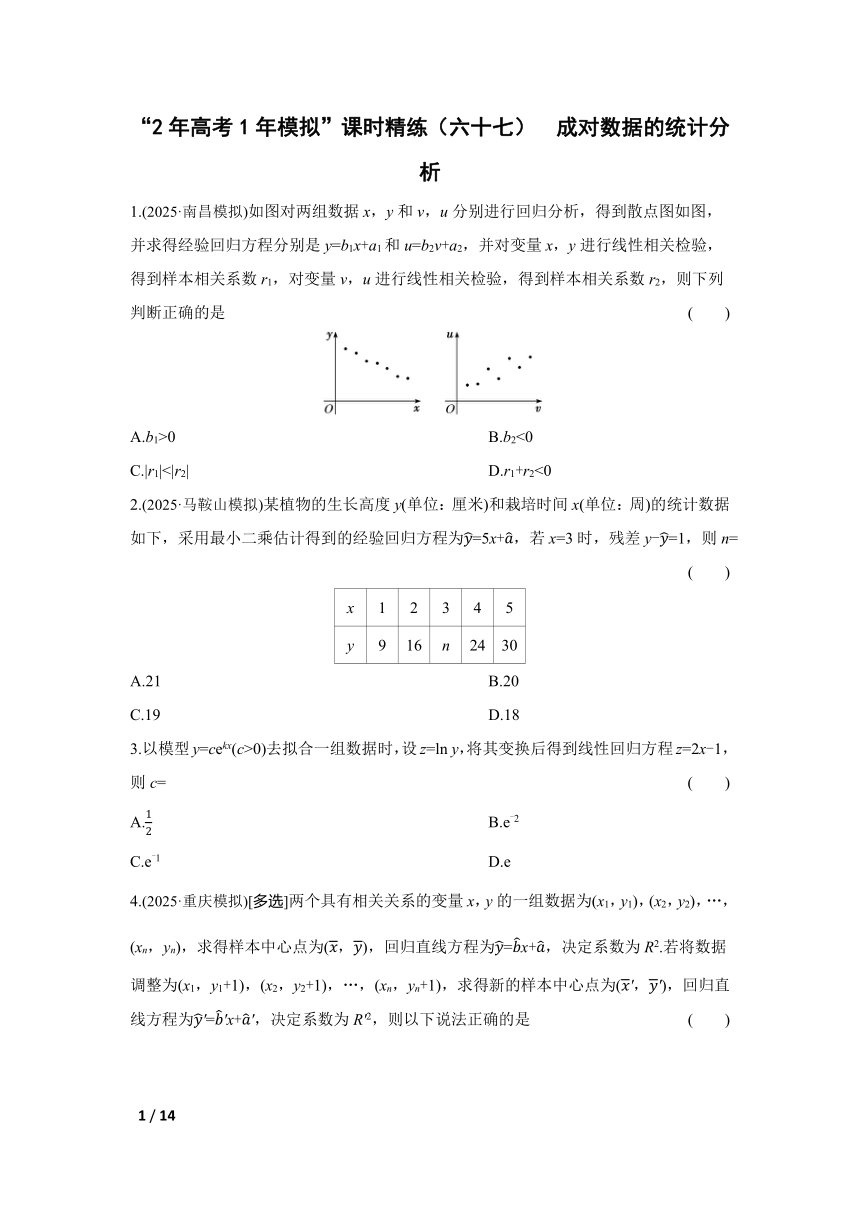 | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 17:26:34 | ||
图片预览




文档简介
“2年高考1年模拟”课时精练(六十七) 成对数据的统计分析
1.(2025·南昌模拟)如图对两组数据x,y和v,u分别进行回归分析,得到散点图如图,并求得经验回归方程分别是y=b1x+a1和u=b2v+a2,并对变量x,y进行线性相关检验,得到样本相关系数r1,对变量v,u进行线性相关检验,得到样本相关系数r2,则下列判断正确的是 ( )
A.b1>0 B.b2<0
C.|r1|<|r2| D.r1+r2<0
2.(2025·马鞍山模拟)某植物的生长高度y(单位:厘米)和栽培时间x(单位:周)的统计数据如下,采用最小二乘估计得到的经验回归方程为=5x+,若x=3时,残差y-=1,则n= ( )
x 1 2 3 4 5
y 9 16 n 24 30
A.21 B.20
C.19 D.18
3.以模型y=cekx(c>0)去拟合一组数据时,设z=ln y,将其变换后得到线性回归方程z=2x-1,则c= ( )
A. B.e-2
C.e-1 D.e
4.(2025·重庆模拟)[多选]两个具有相关关系的变量x,y的一组数据为(x1,y1),(x2,y2),…,(xn,yn),求得样本中心点为(),回归直线方程为=x+,决定系数为R2.若将数据调整为(x1,y1+1),(x2,y2+1),…,(xn,yn+1),求得新的样本中心点为(','),回归直线方程为'='x+',决定系数为R'2,则以下说法正确的是 ( )
附:==-,R2=1-.
A.=' B.='
C.<' D.R25.(2025·青岛模拟)现在很多人喜欢“自助游”,某调查机构为了了解赞成“自助游”是否与性别有关,在黄山旅游节期间,随机抽取了100人,得如下所示的列联表:
赞成“自助游” 不赞成“自助游” 合计
男性 30 15 45
女性 45 10 55
合计 75 25 100
附:
α 0.10 0.05 0.010 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
参照公式,得到的正确结论是 ( )
A.有99.5%以上的把握认为“赞成‘自助游’与性别无关”
B.有99.5%以上的把握认为“赞成‘自助游’与性别有关”
C.在犯错误的概率不超过0.1的前提下,认为“赞成‘自助游’与性别无关”
D.在犯错误的概率不超过0.1的前提下,认为“赞成‘自助游’与性别有关”
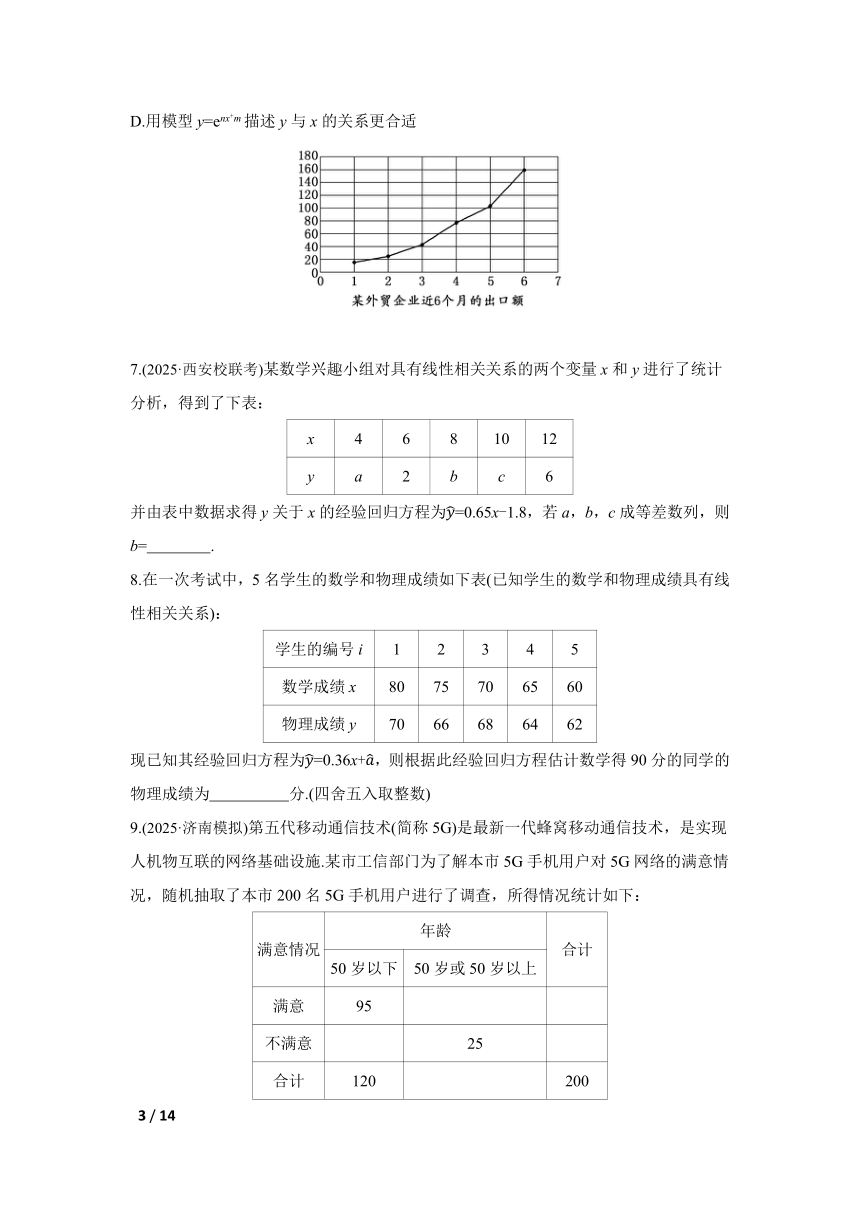
6.(2025·广州模拟)[多选]中欧班列是推进“一带一路”沿线国家道路联通、贸易畅通的重要举措.在中欧班列带动下,某外贸企业出口额逐年提升,以下为该企业近6个月的出口额情况统计,若已求得y关于x的经验回归方程为=28x+,则 ( )
月份编号x 1 2 3 4 5 6
出口额y/万元 16 25 43 77 102 159
A.y与x成正相关
B.样本数据y的第40百分位数为34
C.当x=3时,残差的绝对值最小
D.用模型y=enx+m描述y与x的关系更合适
7.(2025·西安校联考)某数学兴趣小组对具有线性相关关系的两个变量x和y进行了统计分析,得到了下表:
x 4 6 8 10 12
y a 2 b c 6
并由表中数据求得y关于x的经验回归方程为=0.65x-1.8,若a,b,c成等差数列,则b= .
8.在一次考试中,5名学生的数学和物理成绩如下表(已知学生的数学和物理成绩具有线性相关关系):
学生的编号i 1 2 3 4 5
数学成绩x 80 75 70 65 60
物理成绩y 70 66 68 64 62
现已知其经验回归方程为=0.36x+,则根据此经验回归方程估计数学得90分的同学的物理成绩为 分.(四舍五入取整数)
9.(2025·济南模拟)第五代移动通信技术(简称5G)是最新一代蜂窝移动通信技术,是实现人机物互联的网络基础设施.某市工信部门为了解本市5G手机用户对5G网络的满意情况,随机抽取了本市200名5G手机用户进行了调查,所得情况统计如下:
满意情况 年龄 合计
50岁以下 50岁或50岁以上
满意 95
不满意 25
合计 120 200
(1)完成上述2×2列联表,并估计本市5G手机用户对5G网络满意的概率;
(2)依据小概率值α=0.05的独立性检验,分析本市5G手机用户对5G网络满意与年龄在50岁以下是否有关.
满意情况 年龄 合计
50岁以下 50岁或50岁以上
满意 95 55 150
不满意 25 25 50
合计 120 80 200
10.为了解温度对物质A参与的某种化学反应的影响,研究小组在不同温度条件下做了四次实验,实验中测得的温度x(单位:℃)与A的转化率y% 的数据如下表所示:
x 45 55 65 75
y 23 38 65 74
(1)求y与x的样本相关系数(结果精确到0.01);
(2)该研究小组随后又进行了一次该实验,其中A的起始量为50 g,反应结束时还剩余2.5 g,若已知y关于x的线性回归方程为=x-58,估计这次实验是在多少摄氏度的温度条件下进行的.
11.某校为了弘扬中国诗词文化,现要求全校学生参加诗词大赛,随机抽取了100名学生的测试成绩(单位:分),将数据分成5组:[50,60),[60,70),[70,80),[80,90),[90,100]并整理得到如图的频率分布直方图.
(1)估计该校学生的测试成绩的中位数及平均数(同一组中的数据用该组区间的中点值作代表);
(2)若规定成绩不低于80分的记为“诗词达人”,已知被抽取的男生中的“诗词达人”人数占被抽取男生总数的一半,且本次调查得出“在犯错误的概率不超过5%的前提下认为是否为诗词达人与性别有关”的结论,则被调查的100名学生中男生至少有多少人
12.某企业生产一种热销产品,产品日产量为x(x≥1)吨,日销售额为y万元(每日生产的产品当日可销售完毕),且产品价格随着产量变化而有所变化.经过一段时间的产销,随机收集了某5天的日产量xi(i=1,2,…,5)(单位:吨)和日销售额yi(i=1,2,…,5)(单位:万元)的统计数据,并对这5组数据做了初步处理,得到统计数据如下表:
xi yi ui (xi-)2 (yi-)2 (ui-)2 (xi-)·(yi-) (ui-)·(yi-)
15 73 4.8 10 161.2 1.6 39 15.9
其中,ui=ln xi(i=1,2,…,5),分别为数据xi,yi,ui(i=1,2,…,5)的平均数.
(1)请从样本相关系数的角度,判断=x+与=ln x+哪一个模型更适合刻画日销售额y关于日产量x的关系
(2)根据(1)的结果解决下列问题:
①建立y关于x的经验回归方程(斜率的结果四舍五入保留整数);
②如果日产量x(单位:吨)与日生产总成本c(x)(单位:万元)满足关系c(x)=x+3,根据①中建立的经验回归方程估计日产量x为何值时,日利润r(x)最大
(解析)精练(六十七) 成对数据的统计分析
1.(2025·南昌模拟)如图对两组数据x,y和v,u分别进行回归分析,得到散点图如图,并求得经验回归方程分别是y=b1x+a1和u=b2v+a2,并对变量x,y进行线性相关检验,得到样本相关系数r1,对变量v,u进行线性相关检验,得到样本相关系数r2,则下列判断正确的是 ( )
A.b1>0 B.b2<0
C.|r1|<|r2| D.r1+r2<0
解析:选D 由散点图可知,x与y负相关,v与u正相关,则b1<0,b2>0,故A、B错误;且图形中点(x,y)比(v,u)更加集中在一条直线附近,则|r1|>|r2|,又r1<0,r2>0,得r1+r2<0,故C错误,D正确.
2.(2025·马鞍山模拟)某植物的生长高度y(单位:厘米)和栽培时间x(单位:周)的统计数据如下,采用最小二乘估计得到的经验回归方程为=5x+,若x=3时,残差y-=1,则n= ( )
x 1 2 3 4 5
y 9 16 n 24 30
A.21 B.20
C.19 D.18
解析:选A =×(1+2+3+4+5)=3,=×(9+16+n+24+30)=,又因为经验回归方程为=5x+,所以=15+,又残差y-等于1,所以n-15-=1,解得n=21.
3.以模型y=cekx(c>0)去拟合一组数据时,设z=ln y,将其变换后得到线性回归方程z=2x-1,则c= ( )
A. B.e-2
C.e-1 D.e
解析:选C 因为y=cekx(c>0),所以ln y=ln(cekx)=ln c+ln ekx=ln c+kx,令z=ln y,所以z=ln c+kx=2x-1,即c=e-1.故选C.
4.(2025·重庆模拟)[多选]两个具有相关关系的变量x,y的一组数据为(x1,y1),(x2,y2),…,(xn,yn),求得样本中心点为(),回归直线方程为=x+,决定系数为R2.若将数据调整为(x1,y1+1),(x2,y2+1),…,(xn,yn+1),求得新的样本中心点为(','),回归直线方程为'='x+',决定系数为R'2,则以下说法正确的是 ( )
附:==-,R2=1-.
A.=' B.='
C.<' D.R2解析:选BC '=×(y1+1+y2+1+y3+1+…+yn+1)=×(y1+y2+y3+…+yn)+1=+1,A错误;的计算中,xi数据不变,yi-=(yi+1)-'也不变,所以不变,B正确;'='-=+1-=+1>,C正确;由于R2=1-,yi变成了yi+1,'=+1,'='xi+'=xi++1=+1,从而yi-,yi-都不变,所以R2=R'2,D错误.故选BC.
5.(2025·青岛模拟)现在很多人喜欢“自助游”,某调查机构为了了解赞成“自助游”是否与性别有关,在黄山旅游节期间,随机抽取了100人,得如下所示的列联表:
赞成“自助游” 不赞成“自助游” 合计
男性 30 15 45
女性 45 10 55
合计 75 25 100
附:
α 0.10 0.05 0.010 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
参照公式,得到的正确结论是 ( )
A.有99.5%以上的把握认为“赞成‘自助游’与性别无关”
B.有99.5%以上的把握认为“赞成‘自助游’与性别有关”
C.在犯错误的概率不超过0.1的前提下,认为“赞成‘自助游’与性别无关”
D.在犯错误的概率不超过0.1的前提下,认为“赞成‘自助游’与性别有关”
解析:选D 由2×2列联表中的数据得χ2=≈3.030,∵2.706<3.030<3.841,∴在犯错误的概率不超过0.1的前提下,可以认为“赞成‘自助游’与性别有关”.
6.(2025·广州模拟)[多选]中欧班列是推进“一带一路”沿线国家道路联通、贸易畅通的重要举措.在中欧班列带动下,某外贸企业出口额逐年提升,以下为该企业近6个月的出口额情况统计,若已求得y关于x的经验回归方程为=28x+,则 ( )
月份编号x 1 2 3 4 5 6
出口额y/万元 16 25 43 77 102 159
A.y与x成正相关
B.样本数据y的第40百分位数为34
C.当x=3时,残差的绝对值最小
D.用模型y=enx+m描述y与x的关系更合适
解析:选AD 由题中表格数据可知,当x的值增加时,y的相应值也呈现增加的趋势,又由经验回归方程y=28x+中,x项的系数28>0,也可以看出y与x成正相关,故A正确;样本数据y的6个取值从小到大依次是16,25,43,77,102,159,由6×40%=2.4,则第40百分位数为第3个数据43,故B错误;=×(1+2+3+4+5+6)==×(16+25+43+77+102+159)=,将()代入=28x+,得=-,即=28x-,令x=3,得=84-,所以相应残差的绝对值为=,令x=2,得=56-,所以相应残差的绝对值为=<,故C错误;如图作出散点图,
可以看到相较“样本点分布在某一条直线模型y=bx+a的周围”,“样本点分布在某一条指数函数y=enx+m曲线的周围”这样的描述更贴切,所以用模型y=enx+m描述y与x的关系更合适些,故D正确.
7.(2025·西安校联考)某数学兴趣小组对具有线性相关关系的两个变量x和y进行了统计分析,得到了下表:
x 4 6 8 10 12
y a 2 b c 6
并由表中数据求得y关于x的经验回归方程为=0.65x-1.8,若a,b,c成等差数列,则b= .
解析:由题意得=×(4+6+8+10+12)=8,代入经验回归方程=0.65x-1.8得=3.4,则×(a+b+c+2+6)=3.4,所以a+b+c=9,又2b=a+c,所以b=3.
答案:3
8.在一次考试中,5名学生的数学和物理成绩如下表(已知学生的数学和物理成绩具有线性相关关系):
学生的编号i 1 2 3 4 5
数学成绩x 80 75 70 65 60
物理成绩y 70 66 68 64 62
现已知其经验回归方程为=0.36x+,则根据此经验回归方程估计数学得90分的同学的物理成绩为 分.(四舍五入取整数)
解析:=×(60+65+70+75+80)=70,=×(62+64+66+68+70)=66,所以66=0.36×70+,解得=40.8,即经验回归方程为=0.36x+40.8.当x=90时,=0.36×90+40.8=73.2≈73(分).
答案:73
9.(2025·济南模拟)第五代移动通信技术(简称5G)是最新一代蜂窝移动通信技术,是实现人机物互联的网络基础设施.某市工信部门为了解本市5G手机用户对5G网络的满意情况,随机抽取了本市200名5G手机用户进行了调查,所得情况统计如下:
满意情况 年龄 合计
50岁以下 50岁或50岁以上
满意 95
不满意 25
合计 120 200
(1)完成上述2×2列联表,并估计本市5G手机用户对5G网络满意的概率;
(2)依据小概率值α=0.05的独立性检验,分析本市5G手机用户对5G网络满意与年龄在50岁以下是否有关.
解:(1)2×2列联表如下:
满意情况 年龄 合计
50岁以下 50岁或50岁以上
满意 95 55 150
不满意 25 25 50
合计 120 80 200
所以本市5G手机用户对5G网络满意的概率约为=.
(2)零假设为H0:本市5G手机用户对5G网络满意与年龄在50岁以下无关.
根据列联表中的数据,计算可得χ2=≈2.778<3.841=x0.05.
根据小概率值α=0.05的χ2独立性检验原则,没有充分证据推断H0不成立,因此可以认为H0成立,即认为本市5G手机用户对5G网络满意与年龄在50岁以下无关.
10.为了解温度对物质A参与的某种化学反应的影响,研究小组在不同温度条件下做了四次实验,实验中测得的温度x(单位:℃)与A的转化率y% 的数据如下表所示:
x 45 55 65 75
y 23 38 65 74
(1)求y与x的样本相关系数(结果精确到0.01);
(2)该研究小组随后又进行了一次该实验,其中A的起始量为50 g,反应结束时还剩余2.5 g,若已知y关于x的线性回归方程为=x-58,估计这次实验是在多少摄氏度的温度条件下进行的.
参考数据: xiyi=12 900,=14 900,=11 674,≈91.5.
参考公式:样本相关系数r=.
解:(1)==60,
==50,
所以r=
=
==≈≈0.98.
(2)根据线性回归方程的性质,=-58,即50=60-58,得=1.8.
由条件可知=×100=95,
令1.8x-58=95,得x=85,因此估计这次实验是在85 ℃的温度条件下进行的.
11.某校为了弘扬中国诗词文化,现要求全校学生参加诗词大赛,随机抽取了100名学生的测试成绩(单位:分),将数据分成5组:[50,60),[60,70),[70,80),[80,90),[90,100]并整理得到如图的频率分布直方图.
(1)估计该校学生的测试成绩的中位数及平均数(同一组中的数据用该组区间的中点值作代表);
(2)若规定成绩不低于80分的记为“诗词达人”,已知被抽取的男生中的“诗词达人”人数占被抽取男生总数的一半,且本次调查得出“在犯错误的概率不超过5%的前提下认为是否为诗词达人与性别有关”的结论,则被调查的100名学生中男生至少有多少人
解:(1)由频率分布直方图得10(2a+3a+7a+6a+2a)=1,解得a=0.005.
设中位数和平均数分别为x0,,
因为前三个矩形的面积和为10(2a+3a+7a)=0.6,
前两个矩形的面积和为10(2a+3a)=0.25,故易知x0∈[70,80),
所以0.25+(x0-70)×7a=0.5,解得x0=.
所以=10(55×2a+65×3a+75×7a+85×6a+95×2a)=76.5.
(2)由题意知,诗词达人总数为10(2a+6a)×100=40,
设样本中男生人数为m,则列联表如下:
诗词达人 非诗词达人 合计
男生 m
女生 40- 60- 100-m
合计 40 60 100
所以χ2==≥3.841,解得m≥47.97.
又易知m为偶数,所以m的最小值为48,
即被调查的100名学生中男生至少有48人.
12.某企业生产一种热销产品,产品日产量为x(x≥1)吨,日销售额为y万元(每日生产的产品当日可销售完毕),且产品价格随着产量变化而有所变化.经过一段时间的产销,随机收集了某5天的日产量xi(i=1,2,…,5)(单位:吨)和日销售额yi(i=1,2,…,5)(单位:万元)的统计数据,并对这5组数据做了初步处理,得到统计数据如下表:
xi yi ui (xi-)2 (yi-)2 (ui-)2 (xi-)·(yi-) (ui-)·(yi-)
15 73 4.8 10 161.2 1.6 39 15.9
其中,ui=ln xi(i=1,2,…,5),分别为数据xi,yi,ui(i=1,2,…,5)的平均数.
(1)请从样本相关系数的角度,判断=x+与=ln x+哪一个模型更适合刻画日销售额y关于日产量x的关系
(2)根据(1)的结果解决下列问题:
①建立y关于x的经验回归方程(斜率的结果四舍五入保留整数);
②如果日产量x(单位:吨)与日生产总成本c(x)(单位:万元)满足关系c(x)=x+3,根据①中建立的经验回归方程估计日产量x为何值时,日利润r(x)最大
参考数据:≈40,≈16,≈25.
解:(1)设=x+模型的样本相关系数为r1,=ln x+模型的样本相关系数为r2,
所以r1==≈0.975,
r2==≈0.994,
由于0(2)①由(1)知y关于x的经验回归方程为=ln x+,由题可得===9.937 5≈10,=-=-10×=5,
所以=10 ln x+5.
②由题可得r(x)=10 ln x+5-x-3=10 ln x-x+2(x≥1),
所以r'(x)=-=,令r'(x)==0,解得x=20.
当1≤x<20时,r'(x)>0,当x>20时,r'(x)<0,则r(x)的单调递增区间为(1,20),单调递减区间为(20,+∞),所以当x=20时,日利润r(x)最大.
9 / 9
1.(2025·南昌模拟)如图对两组数据x,y和v,u分别进行回归分析,得到散点图如图,并求得经验回归方程分别是y=b1x+a1和u=b2v+a2,并对变量x,y进行线性相关检验,得到样本相关系数r1,对变量v,u进行线性相关检验,得到样本相关系数r2,则下列判断正确的是 ( )
A.b1>0 B.b2<0
C.|r1|<|r2| D.r1+r2<0
2.(2025·马鞍山模拟)某植物的生长高度y(单位:厘米)和栽培时间x(单位:周)的统计数据如下,采用最小二乘估计得到的经验回归方程为=5x+,若x=3时,残差y-=1,则n= ( )
x 1 2 3 4 5
y 9 16 n 24 30
A.21 B.20
C.19 D.18
3.以模型y=cekx(c>0)去拟合一组数据时,设z=ln y,将其变换后得到线性回归方程z=2x-1,则c= ( )
A. B.e-2
C.e-1 D.e
4.(2025·重庆模拟)[多选]两个具有相关关系的变量x,y的一组数据为(x1,y1),(x2,y2),…,(xn,yn),求得样本中心点为(),回归直线方程为=x+,决定系数为R2.若将数据调整为(x1,y1+1),(x2,y2+1),…,(xn,yn+1),求得新的样本中心点为(','),回归直线方程为'='x+',决定系数为R'2,则以下说法正确的是 ( )
附:==-,R2=1-.
A.=' B.='
C.<' D.R2
赞成“自助游” 不赞成“自助游” 合计
男性 30 15 45
女性 45 10 55
合计 75 25 100
附:
α 0.10 0.05 0.010 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
参照公式,得到的正确结论是 ( )
A.有99.5%以上的把握认为“赞成‘自助游’与性别无关”
B.有99.5%以上的把握认为“赞成‘自助游’与性别有关”
C.在犯错误的概率不超过0.1的前提下,认为“赞成‘自助游’与性别无关”
D.在犯错误的概率不超过0.1的前提下,认为“赞成‘自助游’与性别有关”
6.(2025·广州模拟)[多选]中欧班列是推进“一带一路”沿线国家道路联通、贸易畅通的重要举措.在中欧班列带动下,某外贸企业出口额逐年提升,以下为该企业近6个月的出口额情况统计,若已求得y关于x的经验回归方程为=28x+,则 ( )
月份编号x 1 2 3 4 5 6
出口额y/万元 16 25 43 77 102 159
A.y与x成正相关
B.样本数据y的第40百分位数为34
C.当x=3时,残差的绝对值最小
D.用模型y=enx+m描述y与x的关系更合适
7.(2025·西安校联考)某数学兴趣小组对具有线性相关关系的两个变量x和y进行了统计分析,得到了下表:
x 4 6 8 10 12
y a 2 b c 6
并由表中数据求得y关于x的经验回归方程为=0.65x-1.8,若a,b,c成等差数列,则b= .
8.在一次考试中,5名学生的数学和物理成绩如下表(已知学生的数学和物理成绩具有线性相关关系):
学生的编号i 1 2 3 4 5
数学成绩x 80 75 70 65 60
物理成绩y 70 66 68 64 62
现已知其经验回归方程为=0.36x+,则根据此经验回归方程估计数学得90分的同学的物理成绩为 分.(四舍五入取整数)
9.(2025·济南模拟)第五代移动通信技术(简称5G)是最新一代蜂窝移动通信技术,是实现人机物互联的网络基础设施.某市工信部门为了解本市5G手机用户对5G网络的满意情况,随机抽取了本市200名5G手机用户进行了调查,所得情况统计如下:
满意情况 年龄 合计
50岁以下 50岁或50岁以上
满意 95
不满意 25
合计 120 200
(1)完成上述2×2列联表,并估计本市5G手机用户对5G网络满意的概率;
(2)依据小概率值α=0.05的独立性检验,分析本市5G手机用户对5G网络满意与年龄在50岁以下是否有关.
满意情况 年龄 合计
50岁以下 50岁或50岁以上
满意 95 55 150
不满意 25 25 50
合计 120 80 200
10.为了解温度对物质A参与的某种化学反应的影响,研究小组在不同温度条件下做了四次实验,实验中测得的温度x(单位:℃)与A的转化率y% 的数据如下表所示:
x 45 55 65 75
y 23 38 65 74
(1)求y与x的样本相关系数(结果精确到0.01);
(2)该研究小组随后又进行了一次该实验,其中A的起始量为50 g,反应结束时还剩余2.5 g,若已知y关于x的线性回归方程为=x-58,估计这次实验是在多少摄氏度的温度条件下进行的.
11.某校为了弘扬中国诗词文化,现要求全校学生参加诗词大赛,随机抽取了100名学生的测试成绩(单位:分),将数据分成5组:[50,60),[60,70),[70,80),[80,90),[90,100]并整理得到如图的频率分布直方图.
(1)估计该校学生的测试成绩的中位数及平均数(同一组中的数据用该组区间的中点值作代表);
(2)若规定成绩不低于80分的记为“诗词达人”,已知被抽取的男生中的“诗词达人”人数占被抽取男生总数的一半,且本次调查得出“在犯错误的概率不超过5%的前提下认为是否为诗词达人与性别有关”的结论,则被调查的100名学生中男生至少有多少人
12.某企业生产一种热销产品,产品日产量为x(x≥1)吨,日销售额为y万元(每日生产的产品当日可销售完毕),且产品价格随着产量变化而有所变化.经过一段时间的产销,随机收集了某5天的日产量xi(i=1,2,…,5)(单位:吨)和日销售额yi(i=1,2,…,5)(单位:万元)的统计数据,并对这5组数据做了初步处理,得到统计数据如下表:
xi yi ui (xi-)2 (yi-)2 (ui-)2 (xi-)·(yi-) (ui-)·(yi-)
15 73 4.8 10 161.2 1.6 39 15.9
其中,ui=ln xi(i=1,2,…,5),分别为数据xi,yi,ui(i=1,2,…,5)的平均数.
(1)请从样本相关系数的角度,判断=x+与=ln x+哪一个模型更适合刻画日销售额y关于日产量x的关系
(2)根据(1)的结果解决下列问题:
①建立y关于x的经验回归方程(斜率的结果四舍五入保留整数);
②如果日产量x(单位:吨)与日生产总成本c(x)(单位:万元)满足关系c(x)=x+3,根据①中建立的经验回归方程估计日产量x为何值时,日利润r(x)最大
(解析)精练(六十七) 成对数据的统计分析
1.(2025·南昌模拟)如图对两组数据x,y和v,u分别进行回归分析,得到散点图如图,并求得经验回归方程分别是y=b1x+a1和u=b2v+a2,并对变量x,y进行线性相关检验,得到样本相关系数r1,对变量v,u进行线性相关检验,得到样本相关系数r2,则下列判断正确的是 ( )
A.b1>0 B.b2<0
C.|r1|<|r2| D.r1+r2<0
解析:选D 由散点图可知,x与y负相关,v与u正相关,则b1<0,b2>0,故A、B错误;且图形中点(x,y)比(v,u)更加集中在一条直线附近,则|r1|>|r2|,又r1<0,r2>0,得r1+r2<0,故C错误,D正确.
2.(2025·马鞍山模拟)某植物的生长高度y(单位:厘米)和栽培时间x(单位:周)的统计数据如下,采用最小二乘估计得到的经验回归方程为=5x+,若x=3时,残差y-=1,则n= ( )
x 1 2 3 4 5
y 9 16 n 24 30
A.21 B.20
C.19 D.18
解析:选A =×(1+2+3+4+5)=3,=×(9+16+n+24+30)=,又因为经验回归方程为=5x+,所以=15+,又残差y-等于1,所以n-15-=1,解得n=21.
3.以模型y=cekx(c>0)去拟合一组数据时,设z=ln y,将其变换后得到线性回归方程z=2x-1,则c= ( )
A. B.e-2
C.e-1 D.e
解析:选C 因为y=cekx(c>0),所以ln y=ln(cekx)=ln c+ln ekx=ln c+kx,令z=ln y,所以z=ln c+kx=2x-1,即c=e-1.故选C.
4.(2025·重庆模拟)[多选]两个具有相关关系的变量x,y的一组数据为(x1,y1),(x2,y2),…,(xn,yn),求得样本中心点为(),回归直线方程为=x+,决定系数为R2.若将数据调整为(x1,y1+1),(x2,y2+1),…,(xn,yn+1),求得新的样本中心点为(','),回归直线方程为'='x+',决定系数为R'2,则以下说法正确的是 ( )
附:==-,R2=1-.
A.=' B.='
C.<' D.R2
5.(2025·青岛模拟)现在很多人喜欢“自助游”,某调查机构为了了解赞成“自助游”是否与性别有关,在黄山旅游节期间,随机抽取了100人,得如下所示的列联表:
赞成“自助游” 不赞成“自助游” 合计
男性 30 15 45
女性 45 10 55
合计 75 25 100
附:
α 0.10 0.05 0.010 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
参照公式,得到的正确结论是 ( )
A.有99.5%以上的把握认为“赞成‘自助游’与性别无关”
B.有99.5%以上的把握认为“赞成‘自助游’与性别有关”
C.在犯错误的概率不超过0.1的前提下,认为“赞成‘自助游’与性别无关”
D.在犯错误的概率不超过0.1的前提下,认为“赞成‘自助游’与性别有关”
解析:选D 由2×2列联表中的数据得χ2=≈3.030,∵2.706<3.030<3.841,∴在犯错误的概率不超过0.1的前提下,可以认为“赞成‘自助游’与性别有关”.
6.(2025·广州模拟)[多选]中欧班列是推进“一带一路”沿线国家道路联通、贸易畅通的重要举措.在中欧班列带动下,某外贸企业出口额逐年提升,以下为该企业近6个月的出口额情况统计,若已求得y关于x的经验回归方程为=28x+,则 ( )
月份编号x 1 2 3 4 5 6
出口额y/万元 16 25 43 77 102 159
A.y与x成正相关
B.样本数据y的第40百分位数为34
C.当x=3时,残差的绝对值最小
D.用模型y=enx+m描述y与x的关系更合适
解析:选AD 由题中表格数据可知,当x的值增加时,y的相应值也呈现增加的趋势,又由经验回归方程y=28x+中,x项的系数28>0,也可以看出y与x成正相关,故A正确;样本数据y的6个取值从小到大依次是16,25,43,77,102,159,由6×40%=2.4,则第40百分位数为第3个数据43,故B错误;=×(1+2+3+4+5+6)==×(16+25+43+77+102+159)=,将()代入=28x+,得=-,即=28x-,令x=3,得=84-,所以相应残差的绝对值为=,令x=2,得=56-,所以相应残差的绝对值为=<,故C错误;如图作出散点图,
可以看到相较“样本点分布在某一条直线模型y=bx+a的周围”,“样本点分布在某一条指数函数y=enx+m曲线的周围”这样的描述更贴切,所以用模型y=enx+m描述y与x的关系更合适些,故D正确.
7.(2025·西安校联考)某数学兴趣小组对具有线性相关关系的两个变量x和y进行了统计分析,得到了下表:
x 4 6 8 10 12
y a 2 b c 6
并由表中数据求得y关于x的经验回归方程为=0.65x-1.8,若a,b,c成等差数列,则b= .
解析:由题意得=×(4+6+8+10+12)=8,代入经验回归方程=0.65x-1.8得=3.4,则×(a+b+c+2+6)=3.4,所以a+b+c=9,又2b=a+c,所以b=3.
答案:3
8.在一次考试中,5名学生的数学和物理成绩如下表(已知学生的数学和物理成绩具有线性相关关系):
学生的编号i 1 2 3 4 5
数学成绩x 80 75 70 65 60
物理成绩y 70 66 68 64 62
现已知其经验回归方程为=0.36x+,则根据此经验回归方程估计数学得90分的同学的物理成绩为 分.(四舍五入取整数)
解析:=×(60+65+70+75+80)=70,=×(62+64+66+68+70)=66,所以66=0.36×70+,解得=40.8,即经验回归方程为=0.36x+40.8.当x=90时,=0.36×90+40.8=73.2≈73(分).
答案:73
9.(2025·济南模拟)第五代移动通信技术(简称5G)是最新一代蜂窝移动通信技术,是实现人机物互联的网络基础设施.某市工信部门为了解本市5G手机用户对5G网络的满意情况,随机抽取了本市200名5G手机用户进行了调查,所得情况统计如下:
满意情况 年龄 合计
50岁以下 50岁或50岁以上
满意 95
不满意 25
合计 120 200
(1)完成上述2×2列联表,并估计本市5G手机用户对5G网络满意的概率;
(2)依据小概率值α=0.05的独立性检验,分析本市5G手机用户对5G网络满意与年龄在50岁以下是否有关.
解:(1)2×2列联表如下:
满意情况 年龄 合计
50岁以下 50岁或50岁以上
满意 95 55 150
不满意 25 25 50
合计 120 80 200
所以本市5G手机用户对5G网络满意的概率约为=.
(2)零假设为H0:本市5G手机用户对5G网络满意与年龄在50岁以下无关.
根据列联表中的数据,计算可得χ2=≈2.778<3.841=x0.05.
根据小概率值α=0.05的χ2独立性检验原则,没有充分证据推断H0不成立,因此可以认为H0成立,即认为本市5G手机用户对5G网络满意与年龄在50岁以下无关.
10.为了解温度对物质A参与的某种化学反应的影响,研究小组在不同温度条件下做了四次实验,实验中测得的温度x(单位:℃)与A的转化率y% 的数据如下表所示:
x 45 55 65 75
y 23 38 65 74
(1)求y与x的样本相关系数(结果精确到0.01);
(2)该研究小组随后又进行了一次该实验,其中A的起始量为50 g,反应结束时还剩余2.5 g,若已知y关于x的线性回归方程为=x-58,估计这次实验是在多少摄氏度的温度条件下进行的.
参考数据: xiyi=12 900,=14 900,=11 674,≈91.5.
参考公式:样本相关系数r=.
解:(1)==60,
==50,
所以r=
=
==≈≈0.98.
(2)根据线性回归方程的性质,=-58,即50=60-58,得=1.8.
由条件可知=×100=95,
令1.8x-58=95,得x=85,因此估计这次实验是在85 ℃的温度条件下进行的.
11.某校为了弘扬中国诗词文化,现要求全校学生参加诗词大赛,随机抽取了100名学生的测试成绩(单位:分),将数据分成5组:[50,60),[60,70),[70,80),[80,90),[90,100]并整理得到如图的频率分布直方图.
(1)估计该校学生的测试成绩的中位数及平均数(同一组中的数据用该组区间的中点值作代表);
(2)若规定成绩不低于80分的记为“诗词达人”,已知被抽取的男生中的“诗词达人”人数占被抽取男生总数的一半,且本次调查得出“在犯错误的概率不超过5%的前提下认为是否为诗词达人与性别有关”的结论,则被调查的100名学生中男生至少有多少人
解:(1)由频率分布直方图得10(2a+3a+7a+6a+2a)=1,解得a=0.005.
设中位数和平均数分别为x0,,
因为前三个矩形的面积和为10(2a+3a+7a)=0.6,
前两个矩形的面积和为10(2a+3a)=0.25,故易知x0∈[70,80),
所以0.25+(x0-70)×7a=0.5,解得x0=.
所以=10(55×2a+65×3a+75×7a+85×6a+95×2a)=76.5.
(2)由题意知,诗词达人总数为10(2a+6a)×100=40,
设样本中男生人数为m,则列联表如下:
诗词达人 非诗词达人 合计
男生 m
女生 40- 60- 100-m
合计 40 60 100
所以χ2==≥3.841,解得m≥47.97.
又易知m为偶数,所以m的最小值为48,
即被调查的100名学生中男生至少有48人.
12.某企业生产一种热销产品,产品日产量为x(x≥1)吨,日销售额为y万元(每日生产的产品当日可销售完毕),且产品价格随着产量变化而有所变化.经过一段时间的产销,随机收集了某5天的日产量xi(i=1,2,…,5)(单位:吨)和日销售额yi(i=1,2,…,5)(单位:万元)的统计数据,并对这5组数据做了初步处理,得到统计数据如下表:
xi yi ui (xi-)2 (yi-)2 (ui-)2 (xi-)·(yi-) (ui-)·(yi-)
15 73 4.8 10 161.2 1.6 39 15.9
其中,ui=ln xi(i=1,2,…,5),分别为数据xi,yi,ui(i=1,2,…,5)的平均数.
(1)请从样本相关系数的角度,判断=x+与=ln x+哪一个模型更适合刻画日销售额y关于日产量x的关系
(2)根据(1)的结果解决下列问题:
①建立y关于x的经验回归方程(斜率的结果四舍五入保留整数);
②如果日产量x(单位:吨)与日生产总成本c(x)(单位:万元)满足关系c(x)=x+3,根据①中建立的经验回归方程估计日产量x为何值时,日利润r(x)最大
参考数据:≈40,≈16,≈25.
解:(1)设=x+模型的样本相关系数为r1,=ln x+模型的样本相关系数为r2,
所以r1==≈0.975,
r2==≈0.994,
由于0
所以=10 ln x+5.
②由题可得r(x)=10 ln x+5-x-3=10 ln x-x+2(x≥1),
所以r'(x)=-=,令r'(x)==0,解得x=20.
当1≤x<20时,r'(x)>0,当x>20时,r'(x)<0,则r(x)的单调递增区间为(1,20),单调递减区间为(20,+∞),所以当x=20时,日利润r(x)最大.
9 / 9
同课章节目录
