2026届高三数学一轮复习-2年高考1年模拟-(六十六)用样本估计总体(含解析)
文档属性
| 名称 | 2026届高三数学一轮复习-2年高考1年模拟-(六十六)用样本估计总体(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-17 17:27:25 | ||
图片预览




文档简介
“2年高考1年模拟”课时精练(六十六) 用样本估计总体
1.为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别为x1,x2,…,xn,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是 ( )
A.x1,x2,…,xn的平均数
B.x1,x2,…,xn的标准差
C.x1,x2,…,xn的最大值
D.x1,x2,…,xn的中位数
2.(2025·牡丹江模拟)[多选]若2x1+1,2x2+1,…,2xn+1的平均数为3,方差为4,则x1,x2,…,xn的 ( )
A.平均数为1 B.方差为1
C.平均数为 D.方差为2
3.(2025·资阳模拟)某产品的标准质量是50克/袋,抽取8袋该产品,称出各袋的质量(单位:克)如下:48,49,50,50,50,50,51,52.这8袋产品中,质量在以平均数为中心,1倍标准差范围内的有 ( )
A.4袋 B.6袋
C.7袋 D.8袋
4.(2025·十堰模拟)为了解某地高三学生的期末数学考试成绩,研究人员随机抽取了100名学生对其进行调查,根据所得数据制成如图所示的频率分布直方图,则这100名学生期末数学成绩的中位数约为 ( )
A.92.5 B.95
C.97.5 D.100
5.(2025·合肥模拟)[多选]为了解中学生参与课外阅读的情况,某校一兴趣小组持续跟踪调查了该校某班全体同学10周课外阅读的时长,经过整理得到男生、女生这10周课外阅读的平均时长(单位:h)的数据如下表:
女生 7.0 7.3 7.5 7.8 8.4 8.6 8.9 9.0 9.2 9.3
男生 6.1 6.5 6.9 7.5 7.7 8.0 8.1 8.2 8.6 9.4
以下判断正确的是 ( )
A.该班男生每周课外阅读的平均时长的平均值为7.85
B.该班女生每周课外阅读的平均时长的80%分位数是9.0
C.该班女生每周课外阅读的平均时长波动性比男生小
D.由该班估计该校男生每周课外阅读的平均时长不低于8 h的概率为0.5
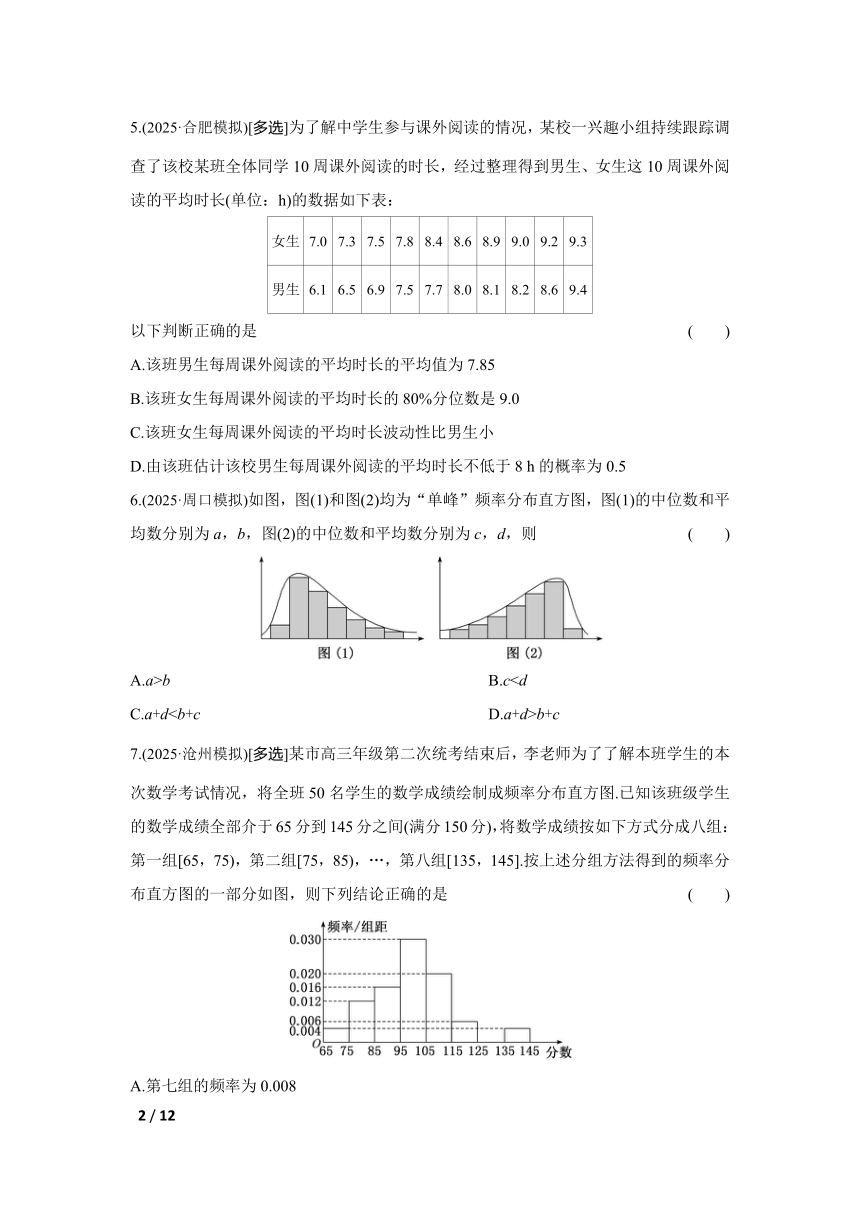
6.(2025·周口模拟)如图,图(1)和图(2)均为“单峰”频率分布直方图,图(1)的中位数和平均数分别为a,b,图(2)的中位数和平均数分别为c,d,则 ( )
A.a>b B.cC.a+db+c
7.(2025·沧州模拟)[多选]某市高三年级第二次统考结束后,李老师为了了解本班学生的本次数学考试情况,将全班50名学生的数学成绩绘制成频率分布直方图.已知该班级学生的数学成绩全部介于65分到145分之间(满分150分),将数学成绩按如下方式分成八组:第一组[65,75),第二组[75,85),…,第八组[135,145].按上述分组方法得到的频率分布直方图的一部分如图,则下列结论正确的是 ( )
A.第七组的频率为0.008
B.该班级数学成绩的中位数的估计值为101分
C.该班级数学成绩的平均分的估计值大于95分
D.该班级数学成绩的标准差的估计值大于6
8.[多选]某社区为优化数字化社区服务,问卷调查调研数字化社区服务的满意度,满意度采用计分制(满分100分),统计满意度绘制成如下频率分布直方图,图中b=3a.则下列结论正确的是 ( )
A.a=0.01
B.满意度计分的众数为80分
C.满意度计分的75%分位数是85分
D.满意度计分的平均分是76.5分
9.(2025·秦皇岛模拟)五名学生每人投篮15次,统计他们每人投中的次数,得到五个数据,若这五个数据的中位数是6,唯一的众数是7,则他们投中次数的总和最大是 .
10.(2025·云南师大附中模拟)某班级为了了解本班学生的身高情况,根据男、女学生的比例,采用样本量按比例分配的分层随机抽样分别抽取了男生5名和女生3名,测量他们的身高所得的数据(单位:cm)如下表所示,根据表中数据,可计算出该校高中学生身高的总样本平均数= ;总样本方差s2= .
性别 人数 平均数 方差
男生 5 172 18
女生 3 164 30
11.(2025·汉中模拟)粮食安全是国家安全的重要基础.从某实验农场种植的甲、乙两种玉米苗中各随机抽取5株,分别测量它们的株高如下(单位:cm):
甲:29,31,30,32,28;
乙:27,44,40,31,43.
请根据平均数和方差的相关知识,解答下列问题.
(1)哪种玉米苗长得高
(2)哪种玉米苗长得齐
12.某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用比例分配的分层随机抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:
(1)根据频率分布直方图估计分数的样本数据的70%分位数;
(2)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中女生的人数.
13.某电子产品制造企业为了提升生产质量,对现有的一条电子产品生产线进行技术升级改造,为了分析改造的效果,该企业质检人员从该条生产线所生产的电子产品中随机抽取了1 000件,检测产品的某项质量指标值,根据检测数据得到下表(单位:件).
质量 指标值 [25,35) [35,45) [45,55) [55,65) [65,75) [75,85) [85,95)
产品 60 100 160 300 200 100 80
(1)估计这组样本的质量指标值的平均数和方差s2(同一组中的数据用该组区间中点值作代表);
(2)设[x]表示不大于x的最大整数,{x}表示不小于x的最小整数,s精确到个位,an=5·,bn=5·,n∈N*,根据检验标准,技术升级改造后,若质量指标值有65%落在[a1,b1]内,则可以判断技术改造后的产品质量初级稳定;若有95%落在[a2,b2]内,则可以判断技术改造后的产品质量稳定,可认为生产线技术改造成功.请问:根据样本数据估计,是否可以判定生产线的技术改造是成功的
(解析)精练(六十六) 用样本估计总体
1.为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别为x1,x2,…,xn,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是 ( )
A.x1,x2,…,xn的平均数
B.x1,x2,…,xn的标准差
C.x1,x2,…,xn的最大值
D.x1,x2,…,xn的中位数
解析:选B 评估这种农作物亩产量稳定程度的指标是标准差.
2.(2025·牡丹江模拟)[多选]若2x1+1,2x2+1,…,2xn+1的平均数为3,方差为4,则x1,x2,…,xn的 ( )
A.平均数为1 B.方差为1
C.平均数为 D.方差为2
解析:选AB 若x1,x2,…,xn的平均数为,方差为s2,则2x1+1,2x2+1,…,2xn+1的平均数为2+1,方差为4s2,令2+1=3,4s2=4,解得=1,s2=1.故选AB.
3.(2025·资阳模拟)某产品的标准质量是50克/袋,抽取8袋该产品,称出各袋的质量(单位:克)如下:48,49,50,50,50,50,51,52.这8袋产品中,质量在以平均数为中心,1倍标准差范围内的有 ( )
A.4袋 B.6袋
C.7袋 D.8袋
解析:选B 这8袋产品的平均质量=×(48+49+50+50+50+50+51+52)=50,方差s2=×[(48-50)2+(49-50)2+4×(50-50)2+(51-50)2+(52-50)2]=1.25,标准差s=.质量在以平均数为中心,1倍标准差范围内,即在(50-,50+)内的产品有6袋.
4.(2025·十堰模拟)为了解某地高三学生的期末数学考试成绩,研究人员随机抽取了100名学生对其进行调查,根据所得数据制成如图所示的频率分布直方图,则这100名学生期末数学成绩的中位数约为 ( )
A.92.5 B.95
C.97.5 D.100
解析:选B 因为(0.006+0.014)×20=0.4<0.5,(0.006+0.014+0.02)×20=0.8>0.5,所以这100名学生期末数学成绩的中位数m∈[90,110),则(m-90)×0.02+0.4=0.5,得m=95.故选B.
5.(2025·合肥模拟)[多选]为了解中学生参与课外阅读的情况,某校一兴趣小组持续跟踪调查了该校某班全体同学10周课外阅读的时长,经过整理得到男生、女生这10周课外阅读的平均时长(单位:h)的数据如下表:
女生 7.0 7.3 7.5 7.8 8.4 8.6 8.9 9.0 9.2 9.3
男生 6.1 6.5 6.9 7.5 7.7 8.0 8.1 8.2 8.6 9.4
以下判断正确的是 ( )
A.该班男生每周课外阅读的平均时长的平均值为7.85
B.该班女生每周课外阅读的平均时长的80%分位数是9.0
C.该班女生每周课外阅读的平均时长波动性比男生小
D.由该班估计该校男生每周课外阅读的平均时长不低于8 h的概率为0.5
解析:选CD 由题表可知,该班男生每周课外阅读的平均时长的平均值为×(6.1+6.5+6.9+7.5+7.7+8.0+8.1+8.2+8.6+9.4)=7.7,故A错误;因为10×80%=8,则该班女生每周课外阅读的平均时长的80%分位数是=9.1,故B错误;由题表可知,该班女生每周课外阅读的平均时长的极差为9.3-7.0=2.3,该班男生每周课外阅读的平均时长的极差为9.4-6.1=3.3,所以该班女生每周课外阅读的平均时长波动性比男生小,故C正确;由题表可知,估计该校男生每周课外阅读的平均时长不低于8 h的概率为=0.5,故D正确.故选CD.
6.(2025·周口模拟)如图,图(1)和图(2)均为“单峰”频率分布直方图,图(1)的中位数和平均数分别为a,b,图(2)的中位数和平均数分别为c,d,则 ( )
A.a>b B.cC.a+db+c
解析:选C 对于A,图(1)中,众数靠近0这一侧,因此平均数会受到较大值的影响而表现为平均数在中位数的右侧,因此ad,故B错误;对于C、D,因为ad,由不等式的性质有a+d7.(2025·沧州模拟)[多选]某市高三年级第二次统考结束后,李老师为了了解本班学生的本次数学考试情况,将全班50名学生的数学成绩绘制成频率分布直方图.已知该班级学生的数学成绩全部介于65分到145分之间(满分150分),将数学成绩按如下方式分成八组:第一组[65,75),第二组[75,85),…,第八组[135,145].按上述分组方法得到的频率分布直方图的一部分如图,则下列结论正确的是 ( )
A.第七组的频率为0.008
B.该班级数学成绩的中位数的估计值为101分
C.该班级数学成绩的平均分的估计值大于95分
D.该班级数学成绩的标准差的估计值大于6
解析:选BCD 利用频率之和为1,可得第七组的频率为1-(0.004+0.012+0.016+0.030+0.020+0.006+0.004)×10=0.08,A错误;成绩在第一组到第八组的人数分别为2,6,8,15,10,3,4,2,所以中位数在第四组[95,105)内,设中位数为x,因为(0.004+0.012+0.016)×10=0.32<0.5,所以0.32+0.030×(x-95)=0.5,解得x=101,所以该班级数学成绩的中位数的估计值为101分,B正确;该班级数学成绩的平均分的估计值为70×0.04+80×0.12+90×0.16+100×0.3+110×0.2+120×0.06+130×0.08+140×0.04=102(分),C正确;×[2×(70-102)2+6×(80-102)2+…]>×2×(70-102)2=40.96>36,所以标准差的估计值大于6,D正确.故选BCD.
8.[多选]某社区为优化数字化社区服务,问卷调查调研数字化社区服务的满意度,满意度采用计分制(满分100分),统计满意度绘制成如下频率分布直方图,图中b=3a.则下列结论正确的是 ( )
A.a=0.01
B.满意度计分的众数为80分
C.满意度计分的75%分位数是85分
D.满意度计分的平均分是76.5分
解析:选ACD 由频率分布直方图可知(a+0.015+0.035+b+a)×10=1,即b+2a=0.05,又b=3a,所以a=0.01,A正确;满意度计分的众数为75分,B错误;前三组的频率之和为0.1+0.15+0.35=0.6<0.75,前四组的频率之和为0.6+0.3=0.9>0.75,则75%分位数m∈[80,90),故m=80+×10=85,满意度计分的75%分位数为85分,C正确;满意度计分的平均分为=55×0.1+65×0.15+75×0.35+85×0.3+95×0.1=76.5分,D正确.
9.(2025·秦皇岛模拟)五名学生每人投篮15次,统计他们每人投中的次数,得到五个数据,若这五个数据的中位数是6,唯一的众数是7,则他们投中次数的总和最大是 .
解析:假设五个数据按照由小到大排列为a,b,c,d,e,因为这五个数据的中位数是6,唯一的众数是7,所以c=6,d=e=7,所以最大的三个数的和为6+7+7=20.因为两个较小的数一定是小于6的非负整数,且不相等,最大为4和5,所以这五个数的和一定大于20且小于等于29,故答案为29.
答案:29
10.(2025·云南师大附中模拟)某班级为了了解本班学生的身高情况,根据男、女学生的比例,采用样本量按比例分配的分层随机抽样分别抽取了男生5名和女生3名,测量他们的身高所得的数据(单位:cm)如下表所示,根据表中数据,可计算出该校高中学生身高的总样本平均数= ;总样本方差s2= .
性别 人数 平均数 方差
男生 5 172 18
女生 3 164 30
解析:由题意知==169.
设男生的身高为x1,x2,x3,x4,x5,身高的平均数为,方差为,
设女生的身高为y1,y2,y3,身高的平均数为,方差为,
由=[++++],
得++++=5(+),同理++=3(+),
则s2=[++…++++]
=(++…+++++8-10-6 )
=[5+5+3+3(-)2]
=[5×18+5×(172-169)2+3×30+3×(164-169)2]=37.5.
答案:169 37.5
11.(2025·汉中模拟)粮食安全是国家安全的重要基础.从某实验农场种植的甲、乙两种玉米苗中各随机抽取5株,分别测量它们的株高如下(单位:cm):
甲:29,31,30,32,28;
乙:27,44,40,31,43.
请根据平均数和方差的相关知识,解答下列问题.
(1)哪种玉米苗长得高
(2)哪种玉米苗长得齐
解:(1)甲的平均值=×(29+31+30+32+28)=30(cm),
乙的平均值=×(27+44+40+31+43)=37(cm),
因为<,故乙种玉米苗长得高.
(2)甲的方差=×[(29-30)2+(31-30)2+(30-30)2+(32-30)2+(28-30)2]=2,
乙的方差=×[(27-37)2+(44-37)2+(40-37)2+(31-37)2+(43-37)2]=46,
因为<,故甲种玉米苗长得齐.
12.某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用比例分配的分层随机抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:
(1)根据频率分布直方图估计分数的样本数据的70%分位数;
(2)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中女生的人数.
解:(1)由频率分布直方图可知,样本中分数不小于70的频率为(0.02+0.04)×10=0.6,
则样本中分数小于70的频率为1-0.6=0.4.
又由频率分布直方图,得样本中分数小于80的频率为0.8,所以样本数据的70%分位数必定位于[70,80)之间.计算为70+10×=77.5,
所以其分数的样本数据的70%分位数估计值为77.5.
(2)由题知,样本中分数不小于70的学生人数为(0.02+0.04)×10×100=60,
则样本中分数不小于70的男生人数为60×=30,所以样本中的男生人数为30×2=60,女生人数为100-60=40,所以总体中女生人数为400×=160.
13.某电子产品制造企业为了提升生产质量,对现有的一条电子产品生产线进行技术升级改造,为了分析改造的效果,该企业质检人员从该条生产线所生产的电子产品中随机抽取了1 000件,检测产品的某项质量指标值,根据检测数据得到下表(单位:件).
质量 指标值 [25,35) [35,45) [45,55) [55,65) [65,75) [75,85) [85,95)
产品 60 100 160 300 200 100 80
(1)估计这组样本的质量指标值的平均数和方差s2(同一组中的数据用该组区间中点值作代表);
(2)设[x]表示不大于x的最大整数,{x}表示不小于x的最小整数,s精确到个位,an=5·,bn=5·,n∈N*,根据检验标准,技术升级改造后,若质量指标值有65%落在[a1,b1]内,则可以判断技术改造后的产品质量初级稳定;若有95%落在[a2,b2]内,则可以判断技术改造后的产品质量稳定,可认为生产线技术改造成功.请问:根据样本数据估计,是否可以判定生产线的技术改造是成功的
解:(1)由题可知,
=30×0.06+40×0.1+50×0.16+60×0.3+70×0.2+80×0.1+90×0.08=61.
s2=(30-61)2×0.06+(40-61)2×0.1+(50-61)2×0.16+(60-61)2×0.3+(70-61)2×0.2+(80-61)2×0.1+(90-61)2×0.08=241.
(2)由s2=241知,s≈16,
则a1=5×=45,b1=5×=75,
该抽样数据落在[45,75]内的频率约为
0.16+0.3+0.2=66%>65%;
又a2=5×=30,
b2=5×=90,
该抽样数据落在[30,90]内的频率约为1-0.03-0.04=0.93=93%<95%,
所以可以判断技术改造后的产品质量初级稳定,但不能判定生产线技术改造成功.
1 / 3
1.为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别为x1,x2,…,xn,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是 ( )
A.x1,x2,…,xn的平均数
B.x1,x2,…,xn的标准差
C.x1,x2,…,xn的最大值
D.x1,x2,…,xn的中位数
2.(2025·牡丹江模拟)[多选]若2x1+1,2x2+1,…,2xn+1的平均数为3,方差为4,则x1,x2,…,xn的 ( )
A.平均数为1 B.方差为1
C.平均数为 D.方差为2
3.(2025·资阳模拟)某产品的标准质量是50克/袋,抽取8袋该产品,称出各袋的质量(单位:克)如下:48,49,50,50,50,50,51,52.这8袋产品中,质量在以平均数为中心,1倍标准差范围内的有 ( )
A.4袋 B.6袋
C.7袋 D.8袋
4.(2025·十堰模拟)为了解某地高三学生的期末数学考试成绩,研究人员随机抽取了100名学生对其进行调查,根据所得数据制成如图所示的频率分布直方图,则这100名学生期末数学成绩的中位数约为 ( )
A.92.5 B.95
C.97.5 D.100
5.(2025·合肥模拟)[多选]为了解中学生参与课外阅读的情况,某校一兴趣小组持续跟踪调查了该校某班全体同学10周课外阅读的时长,经过整理得到男生、女生这10周课外阅读的平均时长(单位:h)的数据如下表:
女生 7.0 7.3 7.5 7.8 8.4 8.6 8.9 9.0 9.2 9.3
男生 6.1 6.5 6.9 7.5 7.7 8.0 8.1 8.2 8.6 9.4
以下判断正确的是 ( )
A.该班男生每周课外阅读的平均时长的平均值为7.85
B.该班女生每周课外阅读的平均时长的80%分位数是9.0
C.该班女生每周课外阅读的平均时长波动性比男生小
D.由该班估计该校男生每周课外阅读的平均时长不低于8 h的概率为0.5
6.(2025·周口模拟)如图,图(1)和图(2)均为“单峰”频率分布直方图,图(1)的中位数和平均数分别为a,b,图(2)的中位数和平均数分别为c,d,则 ( )
A.a>b B.c
7.(2025·沧州模拟)[多选]某市高三年级第二次统考结束后,李老师为了了解本班学生的本次数学考试情况,将全班50名学生的数学成绩绘制成频率分布直方图.已知该班级学生的数学成绩全部介于65分到145分之间(满分150分),将数学成绩按如下方式分成八组:第一组[65,75),第二组[75,85),…,第八组[135,145].按上述分组方法得到的频率分布直方图的一部分如图,则下列结论正确的是 ( )
A.第七组的频率为0.008
B.该班级数学成绩的中位数的估计值为101分
C.该班级数学成绩的平均分的估计值大于95分
D.该班级数学成绩的标准差的估计值大于6
8.[多选]某社区为优化数字化社区服务,问卷调查调研数字化社区服务的满意度,满意度采用计分制(满分100分),统计满意度绘制成如下频率分布直方图,图中b=3a.则下列结论正确的是 ( )
A.a=0.01
B.满意度计分的众数为80分
C.满意度计分的75%分位数是85分
D.满意度计分的平均分是76.5分
9.(2025·秦皇岛模拟)五名学生每人投篮15次,统计他们每人投中的次数,得到五个数据,若这五个数据的中位数是6,唯一的众数是7,则他们投中次数的总和最大是 .
10.(2025·云南师大附中模拟)某班级为了了解本班学生的身高情况,根据男、女学生的比例,采用样本量按比例分配的分层随机抽样分别抽取了男生5名和女生3名,测量他们的身高所得的数据(单位:cm)如下表所示,根据表中数据,可计算出该校高中学生身高的总样本平均数= ;总样本方差s2= .
性别 人数 平均数 方差
男生 5 172 18
女生 3 164 30
11.(2025·汉中模拟)粮食安全是国家安全的重要基础.从某实验农场种植的甲、乙两种玉米苗中各随机抽取5株,分别测量它们的株高如下(单位:cm):
甲:29,31,30,32,28;
乙:27,44,40,31,43.
请根据平均数和方差的相关知识,解答下列问题.
(1)哪种玉米苗长得高
(2)哪种玉米苗长得齐
12.某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用比例分配的分层随机抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:
(1)根据频率分布直方图估计分数的样本数据的70%分位数;
(2)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中女生的人数.
13.某电子产品制造企业为了提升生产质量,对现有的一条电子产品生产线进行技术升级改造,为了分析改造的效果,该企业质检人员从该条生产线所生产的电子产品中随机抽取了1 000件,检测产品的某项质量指标值,根据检测数据得到下表(单位:件).
质量 指标值 [25,35) [35,45) [45,55) [55,65) [65,75) [75,85) [85,95)
产品 60 100 160 300 200 100 80
(1)估计这组样本的质量指标值的平均数和方差s2(同一组中的数据用该组区间中点值作代表);
(2)设[x]表示不大于x的最大整数,{x}表示不小于x的最小整数,s精确到个位,an=5·,bn=5·,n∈N*,根据检验标准,技术升级改造后,若质量指标值有65%落在[a1,b1]内,则可以判断技术改造后的产品质量初级稳定;若有95%落在[a2,b2]内,则可以判断技术改造后的产品质量稳定,可认为生产线技术改造成功.请问:根据样本数据估计,是否可以判定生产线的技术改造是成功的
(解析)精练(六十六) 用样本估计总体
1.为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别为x1,x2,…,xn,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是 ( )
A.x1,x2,…,xn的平均数
B.x1,x2,…,xn的标准差
C.x1,x2,…,xn的最大值
D.x1,x2,…,xn的中位数
解析:选B 评估这种农作物亩产量稳定程度的指标是标准差.
2.(2025·牡丹江模拟)[多选]若2x1+1,2x2+1,…,2xn+1的平均数为3,方差为4,则x1,x2,…,xn的 ( )
A.平均数为1 B.方差为1
C.平均数为 D.方差为2
解析:选AB 若x1,x2,…,xn的平均数为,方差为s2,则2x1+1,2x2+1,…,2xn+1的平均数为2+1,方差为4s2,令2+1=3,4s2=4,解得=1,s2=1.故选AB.
3.(2025·资阳模拟)某产品的标准质量是50克/袋,抽取8袋该产品,称出各袋的质量(单位:克)如下:48,49,50,50,50,50,51,52.这8袋产品中,质量在以平均数为中心,1倍标准差范围内的有 ( )
A.4袋 B.6袋
C.7袋 D.8袋
解析:选B 这8袋产品的平均质量=×(48+49+50+50+50+50+51+52)=50,方差s2=×[(48-50)2+(49-50)2+4×(50-50)2+(51-50)2+(52-50)2]=1.25,标准差s=.质量在以平均数为中心,1倍标准差范围内,即在(50-,50+)内的产品有6袋.
4.(2025·十堰模拟)为了解某地高三学生的期末数学考试成绩,研究人员随机抽取了100名学生对其进行调查,根据所得数据制成如图所示的频率分布直方图,则这100名学生期末数学成绩的中位数约为 ( )
A.92.5 B.95
C.97.5 D.100
解析:选B 因为(0.006+0.014)×20=0.4<0.5,(0.006+0.014+0.02)×20=0.8>0.5,所以这100名学生期末数学成绩的中位数m∈[90,110),则(m-90)×0.02+0.4=0.5,得m=95.故选B.
5.(2025·合肥模拟)[多选]为了解中学生参与课外阅读的情况,某校一兴趣小组持续跟踪调查了该校某班全体同学10周课外阅读的时长,经过整理得到男生、女生这10周课外阅读的平均时长(单位:h)的数据如下表:
女生 7.0 7.3 7.5 7.8 8.4 8.6 8.9 9.0 9.2 9.3
男生 6.1 6.5 6.9 7.5 7.7 8.0 8.1 8.2 8.6 9.4
以下判断正确的是 ( )
A.该班男生每周课外阅读的平均时长的平均值为7.85
B.该班女生每周课外阅读的平均时长的80%分位数是9.0
C.该班女生每周课外阅读的平均时长波动性比男生小
D.由该班估计该校男生每周课外阅读的平均时长不低于8 h的概率为0.5
解析:选CD 由题表可知,该班男生每周课外阅读的平均时长的平均值为×(6.1+6.5+6.9+7.5+7.7+8.0+8.1+8.2+8.6+9.4)=7.7,故A错误;因为10×80%=8,则该班女生每周课外阅读的平均时长的80%分位数是=9.1,故B错误;由题表可知,该班女生每周课外阅读的平均时长的极差为9.3-7.0=2.3,该班男生每周课外阅读的平均时长的极差为9.4-6.1=3.3,所以该班女生每周课外阅读的平均时长波动性比男生小,故C正确;由题表可知,估计该校男生每周课外阅读的平均时长不低于8 h的概率为=0.5,故D正确.故选CD.
6.(2025·周口模拟)如图,图(1)和图(2)均为“单峰”频率分布直方图,图(1)的中位数和平均数分别为a,b,图(2)的中位数和平均数分别为c,d,则 ( )
A.a>b B.c
解析:选C 对于A,图(1)中,众数靠近0这一侧,因此平均数会受到较大值的影响而表现为平均数在中位数的右侧,因此a
A.第七组的频率为0.008
B.该班级数学成绩的中位数的估计值为101分
C.该班级数学成绩的平均分的估计值大于95分
D.该班级数学成绩的标准差的估计值大于6
解析:选BCD 利用频率之和为1,可得第七组的频率为1-(0.004+0.012+0.016+0.030+0.020+0.006+0.004)×10=0.08,A错误;成绩在第一组到第八组的人数分别为2,6,8,15,10,3,4,2,所以中位数在第四组[95,105)内,设中位数为x,因为(0.004+0.012+0.016)×10=0.32<0.5,所以0.32+0.030×(x-95)=0.5,解得x=101,所以该班级数学成绩的中位数的估计值为101分,B正确;该班级数学成绩的平均分的估计值为70×0.04+80×0.12+90×0.16+100×0.3+110×0.2+120×0.06+130×0.08+140×0.04=102(分),C正确;×[2×(70-102)2+6×(80-102)2+…]>×2×(70-102)2=40.96>36,所以标准差的估计值大于6,D正确.故选BCD.
8.[多选]某社区为优化数字化社区服务,问卷调查调研数字化社区服务的满意度,满意度采用计分制(满分100分),统计满意度绘制成如下频率分布直方图,图中b=3a.则下列结论正确的是 ( )
A.a=0.01
B.满意度计分的众数为80分
C.满意度计分的75%分位数是85分
D.满意度计分的平均分是76.5分
解析:选ACD 由频率分布直方图可知(a+0.015+0.035+b+a)×10=1,即b+2a=0.05,又b=3a,所以a=0.01,A正确;满意度计分的众数为75分,B错误;前三组的频率之和为0.1+0.15+0.35=0.6<0.75,前四组的频率之和为0.6+0.3=0.9>0.75,则75%分位数m∈[80,90),故m=80+×10=85,满意度计分的75%分位数为85分,C正确;满意度计分的平均分为=55×0.1+65×0.15+75×0.35+85×0.3+95×0.1=76.5分,D正确.
9.(2025·秦皇岛模拟)五名学生每人投篮15次,统计他们每人投中的次数,得到五个数据,若这五个数据的中位数是6,唯一的众数是7,则他们投中次数的总和最大是 .
解析:假设五个数据按照由小到大排列为a,b,c,d,e,因为这五个数据的中位数是6,唯一的众数是7,所以c=6,d=e=7,所以最大的三个数的和为6+7+7=20.因为两个较小的数一定是小于6的非负整数,且不相等,最大为4和5,所以这五个数的和一定大于20且小于等于29,故答案为29.
答案:29
10.(2025·云南师大附中模拟)某班级为了了解本班学生的身高情况,根据男、女学生的比例,采用样本量按比例分配的分层随机抽样分别抽取了男生5名和女生3名,测量他们的身高所得的数据(单位:cm)如下表所示,根据表中数据,可计算出该校高中学生身高的总样本平均数= ;总样本方差s2= .
性别 人数 平均数 方差
男生 5 172 18
女生 3 164 30
解析:由题意知==169.
设男生的身高为x1,x2,x3,x4,x5,身高的平均数为,方差为,
设女生的身高为y1,y2,y3,身高的平均数为,方差为,
由=[++++],
得++++=5(+),同理++=3(+),
则s2=[++…++++]
=(++…+++++8-10-6 )
=[5+5+3+3(-)2]
=[5×18+5×(172-169)2+3×30+3×(164-169)2]=37.5.
答案:169 37.5
11.(2025·汉中模拟)粮食安全是国家安全的重要基础.从某实验农场种植的甲、乙两种玉米苗中各随机抽取5株,分别测量它们的株高如下(单位:cm):
甲:29,31,30,32,28;
乙:27,44,40,31,43.
请根据平均数和方差的相关知识,解答下列问题.
(1)哪种玉米苗长得高
(2)哪种玉米苗长得齐
解:(1)甲的平均值=×(29+31+30+32+28)=30(cm),
乙的平均值=×(27+44+40+31+43)=37(cm),
因为<,故乙种玉米苗长得高.
(2)甲的方差=×[(29-30)2+(31-30)2+(30-30)2+(32-30)2+(28-30)2]=2,
乙的方差=×[(27-37)2+(44-37)2+(40-37)2+(31-37)2+(43-37)2]=46,
因为<,故甲种玉米苗长得齐.
12.某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用比例分配的分层随机抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:
(1)根据频率分布直方图估计分数的样本数据的70%分位数;
(2)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中女生的人数.
解:(1)由频率分布直方图可知,样本中分数不小于70的频率为(0.02+0.04)×10=0.6,
则样本中分数小于70的频率为1-0.6=0.4.
又由频率分布直方图,得样本中分数小于80的频率为0.8,所以样本数据的70%分位数必定位于[70,80)之间.计算为70+10×=77.5,
所以其分数的样本数据的70%分位数估计值为77.5.
(2)由题知,样本中分数不小于70的学生人数为(0.02+0.04)×10×100=60,
则样本中分数不小于70的男生人数为60×=30,所以样本中的男生人数为30×2=60,女生人数为100-60=40,所以总体中女生人数为400×=160.
13.某电子产品制造企业为了提升生产质量,对现有的一条电子产品生产线进行技术升级改造,为了分析改造的效果,该企业质检人员从该条生产线所生产的电子产品中随机抽取了1 000件,检测产品的某项质量指标值,根据检测数据得到下表(单位:件).
质量 指标值 [25,35) [35,45) [45,55) [55,65) [65,75) [75,85) [85,95)
产品 60 100 160 300 200 100 80
(1)估计这组样本的质量指标值的平均数和方差s2(同一组中的数据用该组区间中点值作代表);
(2)设[x]表示不大于x的最大整数,{x}表示不小于x的最小整数,s精确到个位,an=5·,bn=5·,n∈N*,根据检验标准,技术升级改造后,若质量指标值有65%落在[a1,b1]内,则可以判断技术改造后的产品质量初级稳定;若有95%落在[a2,b2]内,则可以判断技术改造后的产品质量稳定,可认为生产线技术改造成功.请问:根据样本数据估计,是否可以判定生产线的技术改造是成功的
解:(1)由题可知,
=30×0.06+40×0.1+50×0.16+60×0.3+70×0.2+80×0.1+90×0.08=61.
s2=(30-61)2×0.06+(40-61)2×0.1+(50-61)2×0.16+(60-61)2×0.3+(70-61)2×0.2+(80-61)2×0.1+(90-61)2×0.08=241.
(2)由s2=241知,s≈16,
则a1=5×=45,b1=5×=75,
该抽样数据落在[45,75]内的频率约为
0.16+0.3+0.2=66%>65%;
又a2=5×=30,
b2=5×=90,
该抽样数据落在[30,90]内的频率约为1-0.03-0.04=0.93=93%<95%,
所以可以判断技术改造后的产品质量初级稳定,但不能判定生产线技术改造成功.
1 / 3
同课章节目录
