【期末专项训练】第四单元测试(含解析)2024-2025学年四年级下册数学青岛版
文档属性
| 名称 | 【期末专项训练】第四单元测试(含解析)2024-2025学年四年级下册数学青岛版 |  | |
| 格式 | docx | ||
| 文件大小 | 387.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 06:23:46 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第四单元测试
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.以平行四边形的一条边为底,能作( )条高。
A.10 B.2 C.3 D.无数
2.这是一个四边形。( )
A.对 B.错
3.用4根木条钉成一个长方形框架,然后将它拉成一个平行四边形,平行四边形的周长与原长方形的周长相比,( )。
A.长方形的周长长一些 B.平行四边形的周长长一些 C.周长相等
4.在图中,梯形ABCD的高是( )。
A.12厘米 B.9厘米 C.11厘米 D.15厘米
5.把一个长方形沿着对角拉成平行四边形时,面积与原来相比( )
A.不变 B.变大 C.变小
6.一个等腰三角形的两条边长分别是3厘米和9厘米,这个三角形的周长是( )厘米。
A.15 B.21 C.15或21
7.认识了图形,老师和同学们玩一个“听指令做记号”的数学游戏,指令对就在图形上做一个记号,( )图形做的记号最多。
指令:
①四边形。
②两组对边分别平行。
③有钝角。
④邻边相等。
A. B. C. D.
8.一个等腰三角形其中两条边的长度分别是分米和分米,这个等腰三角形的周长是( )
A.分米 B.分米
C.1分米 D.分米或1分米
9.下列说法不正确的是( )。
A.等边三角形一定是等腰三角形。
B.有两个角是锐角的三角形一定是锐角三角形。
C.同一个平行四边形不同底边上的高不一定相等。
10.三角形中最小的一个角是50°,按角分类,这是一个( )三角形。
A.锐角 B.直角 C.钝角
二、填空题
11.三角形是由( )条线段围成的图形.
12.三角形具有( ),三角形任意( )之和大于第三边。
13.将一张长方形纸像图①一样折一折,展开后沿折痕剪下一个三角形(见图②),剪下的三角形是( )三角形(按边分)。
图① 图②
14.梯形里一组互相平行的对边分别叫作梯形的( )和( ),两个完全一样的梯形可以拼成一个( )。
15.如图,一个等腰三角形纸片破损后只剩一个底角,被撕去的顶角的度数是( )°。你推算的依据是( )。
16.猜一猜,被信封遮住的图形按角分可能是什么三角形?
( ) ( ) ( )
17.从长7厘米、4厘米、3厘米、3厘米的4根小棒中,任意选3根小棒围成三角形,这个三角形的周长是( )厘米,这是一个( )三角形。
18.一个等腰三角形的两条边分别是4.5厘米和11厘米。这个三角形的周长是( )厘米。
19.如下表,摆一个三角形需要3根小棒,摆2个、3个、4个呢?(填一填)
三角形个数 1 2 3 4 5 6 … n
火柴棒根数 3 …
(1)继续摆下去,我发现:每增加一个三角形,就增加( )根小棒。
(2)摆n个这样的三角形,要用( )根小棒。
(3)39根小棒可以摆成( )个三角形。
20.一个n边形的内角和是( )度。
三、判断题
21.内角和与的内角和一样大。( )
22.把一个锐角三角形中的55°的角剪下,剩下图形的内角和就变成了125°。( )
23.一个三角形既是直角三角形,又是等腰三角形,它一定有两个内角是45°。( )
24.四边形不可以密铺,而正五边形能密铺。( )
25.小明说他做了一个等腰三角形,这个等腰三角形的一个底角92°。( )
26.长方形可以单独密铺,正五边形也可以单独密铺。( )
四、计算题
27.计算下面图形的周长.
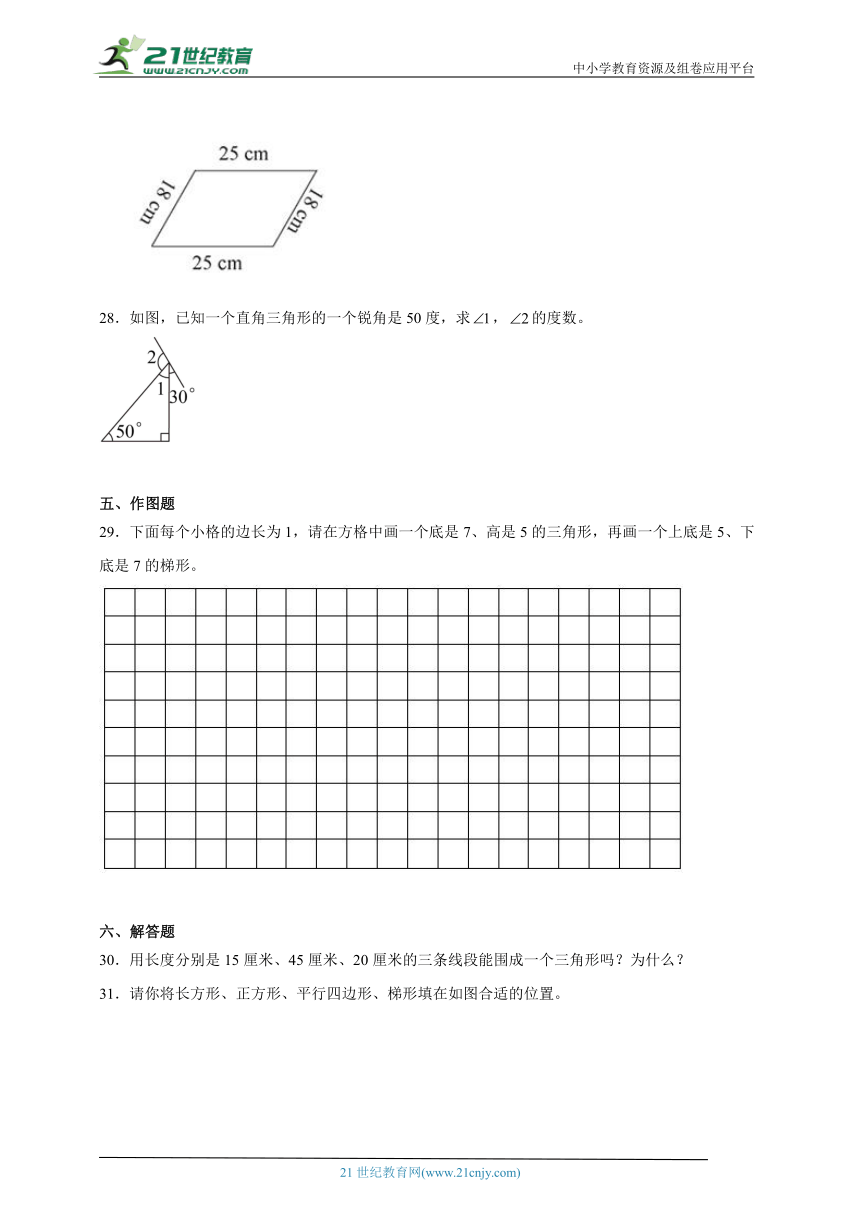
28.如图,已知一个直角三角形的一个锐角是50度,求,的度数。
五、作图题
29.下面每个小格的边长为1,请在方格中画一个底是7、高是5的三角形,再画一个上底是5、下底是7的梯形。
六、解答题
30.用长度分别是15厘米、45厘米、20厘米的三条线段能围成一个三角形吗?为什么?
31.请你将长方形、正方形、平行四边形、梯形填在如图合适的位置。
32.一个等腰三角形,它的一个底角是顶角的4倍,这个三角形的一个底角是多少度?
33.用一根绳子恰好可以围成一个边长是12分米的等边三角形,如果用这根绳子围成底边长是14分米的等腰三角形,这个三角形的一条腰长是多少分米?
34.(1)画出下面每个图形底边上的高。
(2)如果上面等腰三角形的一个底角是30度,顶角是( )度。平行四边行的∠1=75度,∠2=( )度。
《第四单元测试》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D A C C C B C C B A
1.D
【分析】从平行四边形的底边向对边的一点引一条垂线,这点和垂足之间的线段叫作平行四边形的高,从平行四边形的底边向对边能作出无数条高。据此解答即可。
【详解】以平行四边形的一条边为底,能作出无数条高。
故答案选:D
2.A
【详解】由四条边组成的封闭图形叫做四边形。
故答案为:A
3.C
【分析】长方形拉成一个平行四边形,周长不会改变,依此选择。
【详解】根据分析可知:平行四边形的周长与原长方形的周长相等。
故答案为:C
【点睛】此题考查的是对周长的认识,熟练掌握平行四边形易变形的特性是解答此题的关键。
4.C
【分析】只有一组对边平行的四边形叫做梯形;梯形上底到下底的距离是梯形的高;梯形ABCD的上底是BC,下底是AD,BC到AD之间的距离是11厘米,依此选择。
【详解】梯形ABCD的高是11厘米。
故答案为:C
5.C
【分析】把一个长方形活动框拉成一个平行四边形框架后,平行四边形的底是原长方形的长边,但是,拉动之后的高小于原长方形的宽,所以平行四边形的面积应小于原长方形的面积.
【详解】因为把长方形拉成平行四边形后,底不变,但高变短了,
所以面积比原来长方形的面积小了;
故选C.
6.B
【详解】三角形的腰长只能是9厘米,而不能是3 厘米,因为腰长如果是3厘米,3+3<9,不能围成三角形。9+9+3=21(厘米),所以这个三角形的周长是21厘米。
故答案为:B
7.C
【分析】根据平行四边形的特征,平行四边形是两组对边分别平行的四边形,结合选项逐一分析解答即可。
【详解】
A.符合①②,不符合③④。
B.符合③,不符合①②④。
C.符合①②③④。
D.符合①③,不符合②④。
做的记号最多。
故答案为:C
8.C
【详解】++=1(分米)
答:这个等腰三角形的周长是1分米.
故选C.
9.B
【分析】等边三角形三条边都相等,等腰三角形两腰相等;三角形一定有两个角是锐角;平行四边形的对边平行且相等,平行四边形的高连接两条对边并与两条对边互相垂直;据此解答。
【详解】根据分析:
A.等边三角形一定是等腰三角形,原题说法正确;
B.有两个角是锐角的三角形有可能是钝角三角形、直角三角形和锐角三角形,原题说法错误;
C.同一个平行四边形不同底边上的高不一定相等,原题说法正确。
故答案为:B
【点睛】本题主要考查的是三角形的分类,三角形的特征,以及平行四边形的特征。
10.A
【分析】由三角形的内角和求出另外两个角的和,再根据最小的内角是50°来判断其它两个角的情况。
【详解】180°-50°=130°;另外两个角的和是130°,最小的内角是50°,假设另外两个角中还有一个是50°,另一个就是:130°-50°=80°;最大的内角最大只能是80°,所以这个三角形的三个角都是锐角,这个三角形一定是锐角三角形。
故答案为:A
【点睛】解决本题首先要能根据三角形的内角和是180°,求出另外角的度数可能的情况,并由此求解。
11.三
【详解】略
12. 稳定性 两边
【详解】略
13.等腰
【分析】根据题意,因为是翻折,所以该三角形的两条边相等,等腰三角形的两条边相等,据此填空即可。
【详解】折完后形成一个正方形,正方形的四条边相等,所以沿折痕剪下的三角形是等腰三角形。
14. 上底 下底 平行四边形
【分析】只有一组对边互相平行的四边形叫梯形,在梯形里,互相平行的一组对边分别叫做梯形的上底和下底, 两个完全一样的梯形,将其中一个梯形翻转后与另一个梯形拼接,可以拼成一个平行四边形 。因为拼接后得到的四边形,它的两组对边分别平行且相等,符合平行四边形的特征。
【详解】由分析可知,梯形里一组互相平行的对边分别叫作梯形的上底和下底,两个完全一样的梯形可以拼成一个平行四边形。
15. 88 三角形内角和为180°
【分析】等腰三角形的特征:两腰相等,两底角也相等;再根据三角形内角和是180°和底角是46°,进而求得它的顶角的度数。
【详解】180°-46°×2
=180°-92°
=88°
被撕去的顶角的度数是88°。推算的依据是三角形内角和为180°。(答案不唯一)
【点睛】此题根据等腰三角形的特征和三角形的内角和进行解答即可。
16. 直角三角形 锐角三角形或钝角三角形或直角三角形 钝角三角形
【分析】按角分,三个角都是锐角的三角形是锐角三角形;有一个角是直角的三角形是直角三角形;有一个角是钝角的三角形是钝角三角形。第一个被信封遮住的三角形所露出的角是直角;第二个被信封遮住的三角形所露出的角是锐角,其它的两个角可能均为锐角,也可能有一个直角或钝角;第三个被信封遮住的三角形所露出的角是钝角,据此依次判断每个三角形是什么三角形即可。
【详解】第一个被信封遮住的三角形所露出的角是直角,因此第一个三角形是直角三角形;
第二个被信封遮住的三角形所露出的角是锐角,其它的两个角可能均为锐角,也可能有一个直角或钝角,因此第二个三角形是锐角三角形或钝角三角形或直角三角形;
第三个被信封遮住的三角形所露出的角是钝角,因此第三个三角形是钝角三角形。
17. 10 等腰
【详解】略
18.26.5
【分析】三角形三条边的总长度就是这个三角形的周长,等腰三角形的两腰相等,三角形任意两边的长度之和大于第三边,任意两边的长度之差小于第三边,此题依此解答即可。
【详解】假设腰长是4.5厘米,4.5+4.5=9(厘米),9厘米<11厘米,即腰长不能是4.5厘米;
则腰长是11厘米,4.5+11=15.5(厘米),15.5厘米>11厘米,11-4.5=6.5(厘米),6.5厘米<11厘米,即腰长11厘米满足。
11+11+4.5=26.5(厘米)
这个三角形的周长是26.5厘米。
19.6;9;12;15;18;3n
(1)3
(2)3n
(3)13
【分析】三角形有3条边,每摆一个三角形,需要3根小棒,摆一个三角形需要的小棒根数乘三角形个数,可以算出需要多少根小棒。据此填表。
(1)三角形有3条边,每增加一个三角形,就增加3根小棒。
(2)摆一个三角形需要的小棒根数乘三角形个数,可以算出摆n个这样的三角形要用(3n)根小棒。
(3)小棒根数除以每个三角形的小棒根数,即可算出39根小棒可以摆成(39÷3)个三角形。
【详解】
三角形个数 1 2 3 4 5 6 … n
火柴棒根数 3 6 9 12 15 18 … 3n
继续摆下去,我发现:(1)每增加一个三角形,就增加(3)根小棒。
(2)摆n个这样的三角形,要用(3n)根小棒。
(3)39÷3=13(个)
39根小棒可以摆成(13)个三角形。
20.(n-2)×180
【分析】从n边形的一个顶点出发与其它各个顶点的连线有(n-3)条,(这个点与它本身以及与它相邻的两个点不能连线),把n边形分成(n-2)个三角形,所以n边形的内角和是(n-2)×180度。
【详解】据分析知:把n边形分成(n-2)个三角形,所以n边形的内角和是(n-2)×180度。
【点睛】借助辅助线段,把n边形分成(n-2)个三角形,再计算n边形的内角和,这是解决此题的关键。
21.√
【分析】根据三角形内角和定理:任何三角形内角和都是180°据此解答即可。
【详解】
内角和与的内角和一样大,都是180°。原题说法正确。
故答案为:√
22.×
【分析】把一个锐角三角形中的55°的角剪下,剩下图形的是一个四边形,根据四边形的内角和,求出答案。
【详解】把一个锐角三角形中的55°的角剪下,剩下图形的内角和就变成了360°。
故答案为:×。
【点睛】本题主要考查的是四边形的内角和,解题关键在于求出剪下一个角之后,剩下的图形是四边形。
23.√
【分析】等腰三角形两个底角相等,三角形内角和是180°。据此解答。
【详解】(180°-90°)÷2
=90°÷2
=45° 所以它一定有两个内角是45°。
故答案为:√
24.×
【分析】平面图形的密铺是指用一种或几种相同的图形进行拼接,彼此之间不留空隙、不重叠地铺成一片;根据实验可知:三角形、四边形、正六边形能单独密铺,圆和正五边形不能单独密铺;据此解答。
【详解】根据分析可知:
四边形可以密铺,而正五边形不能密铺。原题说法错误。
故答案为:×
25.×
【分析】等腰三角形的两个底角度数相等;三角形的内角和等于180°,据此判断即可。
【详解】两个底角的度数和是92°×2=184°,与三角形的内角和等于180°矛盾。所以原题干说法错误。
故答案为:×
【点睛】本题考查三角形的内角和,明确等腰三角形的两个底角度数相等是解题的关键。
26.×
【分析】三角形的内角和是180°,能整除360°,可以单独密铺;四边形的内角和是360°,能整除360°,可以单独密铺;正五边形的内角和是540°,不能整除360°,不能单独密铺;因为正六边形的每个内角都是120°,正六边形的3个角拼在一起正好等于360°,可以单独密铺,据此即可解答。
【详解】根据分析可知,三角形、长方形、正六边形可以单独密铺,正五边形不能单独密铺,原说法错误。
故答案为:×
【点睛】本题考查了平面镶嵌,任意多边形能进行镶嵌,说明它的内角和应能整除360°。
27.86cm
【详解】平行四边形的周长为四边边长之和,所以其周长为:25+18+25+18=86(cm).
28.∠1=40°,∠2=110°
【分析】1直角是90°,三角形的内角和是180°,因此用180°减90°后,再减50°,即可得到∠1的度数;1平角是180°,因此用180°减30°后,再减∠1的度数,即可得到∠2的度数,依此解答。
【详解】∠1=180°-90°-50°=90°-50°=40°。
∠2=180°-30°-40°=150°-40°=110°。
∠1=40°,∠2=110°。
29.见详解
【分析】由三条边组成的封闭图形是三角形,从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底;因此先画一条长7个小格的线段作为三角形的底,在距离底边的5个小格处确定三角形的顶点,最后用线段将底边的两个端点和顶点连起来组成一个三角形即可。
只有一组对边平行的四边形叫做梯形;因此先画一条长7个小格的线段作为梯形的下底,然后在下底的上方,画一条与下底平行,且长度为5个小格的线段,最后将这两条线段左右两边的端点分别连起来组成一个梯形即可。
【详解】画图如下:
【点睛】此题考查的是画指定底长和高的三角形、画指定上底和下底的梯形,应熟练掌握三角形的特点,三角形的高及画法,以及梯形的特点。
30.不能;理由见详解
【分析】根据三角形的特征,两边之和大于第三边,三角形的两边的差一定小于第三边,进行解答即可。
【详解】15+20<45,两边之和小于第三边。
答:长度分别是15厘米、45厘米、20厘米的三条线段不能围成一个三角形。
【点睛】此题关键是根据三角形的特征进行分析。
31.见详解
【分析】据平行四边形、梯形、长方形和正方形的含义:两组对边都平行的四边形是平行四边形;一组对边平行而另一组对边不平行的四边形是梯形;有一个角是直角的平行四边形是长方形,一组邻边相等的长方形是正方形;可知:正方形是特殊的长方形,长方形是特殊的平行四边形;梯形和平行四边形都是四边形;据此解答即可。
【详解】
32.80°
【分析】等腰三角形的两个底角的度数相等,由于三角形的内角和为180°,且得知一个底角是顶角的4倍,则两个底角的度数加起来是顶角的8倍,三个角之和为180°,利用除法算式可以算出顶角的度数,据此解答即可。
【详解】4+4+1=9
顶角度数为:180°÷9=20°
则底角度数为:20°×4=80°
答:这个三角形的一个底角是80°。
【点睛】本题考查学生对等腰三角形特征的认识和应用。
33.11分米
【分析】两个三角形的周长相等,等边三角形的边长乘3等于等边三角形的周长,减去14分米等于等腰三角形两条腰的长度和,再除以2即等于一条腰的长度。
【详解】(12×3-14)÷2
=(36-14)÷2
=22÷2
=11(分米)
答:这个三角形的一条腰长是11分米。
【点睛】本题主要考查学生对三角形的周长和三角形分类知识的掌握。
34.(1)图见详解
(2)120;105
【分析】(1)从三角形的顶点向对边作垂线,顶点和垂足间的线段就是所画的指定底边上的高;从平行四边形一条边上的一点到对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,垂足所在的边叫做平行四边形的底。据此画图即可。
(2)三角形的内角和是180°,等腰三角形的两个底角相等,由此可以求出另一个角的度数;平行四边形的内角和为360°,平行四边形对角相等,邻角互补;据此即可解答。
【详解】(1)作图如下:
(2)180°-30°-30°
=150°-30°
=120°
即顶角是120°。
180°-75°=105°
即∠2=105°。
如果上面等腰三角形的一个底角是30度,顶角是120度。平行四边形的∠1=75度,∠2=105度。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四单元测试
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.以平行四边形的一条边为底,能作( )条高。
A.10 B.2 C.3 D.无数
2.这是一个四边形。( )
A.对 B.错
3.用4根木条钉成一个长方形框架,然后将它拉成一个平行四边形,平行四边形的周长与原长方形的周长相比,( )。
A.长方形的周长长一些 B.平行四边形的周长长一些 C.周长相等
4.在图中,梯形ABCD的高是( )。
A.12厘米 B.9厘米 C.11厘米 D.15厘米
5.把一个长方形沿着对角拉成平行四边形时,面积与原来相比( )
A.不变 B.变大 C.变小
6.一个等腰三角形的两条边长分别是3厘米和9厘米,这个三角形的周长是( )厘米。
A.15 B.21 C.15或21
7.认识了图形,老师和同学们玩一个“听指令做记号”的数学游戏,指令对就在图形上做一个记号,( )图形做的记号最多。
指令:
①四边形。
②两组对边分别平行。
③有钝角。
④邻边相等。
A. B. C. D.
8.一个等腰三角形其中两条边的长度分别是分米和分米,这个等腰三角形的周长是( )
A.分米 B.分米
C.1分米 D.分米或1分米
9.下列说法不正确的是( )。
A.等边三角形一定是等腰三角形。
B.有两个角是锐角的三角形一定是锐角三角形。
C.同一个平行四边形不同底边上的高不一定相等。
10.三角形中最小的一个角是50°,按角分类,这是一个( )三角形。
A.锐角 B.直角 C.钝角
二、填空题
11.三角形是由( )条线段围成的图形.
12.三角形具有( ),三角形任意( )之和大于第三边。
13.将一张长方形纸像图①一样折一折,展开后沿折痕剪下一个三角形(见图②),剪下的三角形是( )三角形(按边分)。
图① 图②
14.梯形里一组互相平行的对边分别叫作梯形的( )和( ),两个完全一样的梯形可以拼成一个( )。
15.如图,一个等腰三角形纸片破损后只剩一个底角,被撕去的顶角的度数是( )°。你推算的依据是( )。
16.猜一猜,被信封遮住的图形按角分可能是什么三角形?
( ) ( ) ( )
17.从长7厘米、4厘米、3厘米、3厘米的4根小棒中,任意选3根小棒围成三角形,这个三角形的周长是( )厘米,这是一个( )三角形。
18.一个等腰三角形的两条边分别是4.5厘米和11厘米。这个三角形的周长是( )厘米。
19.如下表,摆一个三角形需要3根小棒,摆2个、3个、4个呢?(填一填)
三角形个数 1 2 3 4 5 6 … n
火柴棒根数 3 …
(1)继续摆下去,我发现:每增加一个三角形,就增加( )根小棒。
(2)摆n个这样的三角形,要用( )根小棒。
(3)39根小棒可以摆成( )个三角形。
20.一个n边形的内角和是( )度。
三、判断题
21.内角和与的内角和一样大。( )
22.把一个锐角三角形中的55°的角剪下,剩下图形的内角和就变成了125°。( )
23.一个三角形既是直角三角形,又是等腰三角形,它一定有两个内角是45°。( )
24.四边形不可以密铺,而正五边形能密铺。( )
25.小明说他做了一个等腰三角形,这个等腰三角形的一个底角92°。( )
26.长方形可以单独密铺,正五边形也可以单独密铺。( )
四、计算题
27.计算下面图形的周长.
28.如图,已知一个直角三角形的一个锐角是50度,求,的度数。
五、作图题
29.下面每个小格的边长为1,请在方格中画一个底是7、高是5的三角形,再画一个上底是5、下底是7的梯形。
六、解答题
30.用长度分别是15厘米、45厘米、20厘米的三条线段能围成一个三角形吗?为什么?
31.请你将长方形、正方形、平行四边形、梯形填在如图合适的位置。
32.一个等腰三角形,它的一个底角是顶角的4倍,这个三角形的一个底角是多少度?
33.用一根绳子恰好可以围成一个边长是12分米的等边三角形,如果用这根绳子围成底边长是14分米的等腰三角形,这个三角形的一条腰长是多少分米?
34.(1)画出下面每个图形底边上的高。
(2)如果上面等腰三角形的一个底角是30度,顶角是( )度。平行四边行的∠1=75度,∠2=( )度。
《第四单元测试》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D A C C C B C C B A
1.D
【分析】从平行四边形的底边向对边的一点引一条垂线,这点和垂足之间的线段叫作平行四边形的高,从平行四边形的底边向对边能作出无数条高。据此解答即可。
【详解】以平行四边形的一条边为底,能作出无数条高。
故答案选:D
2.A
【详解】由四条边组成的封闭图形叫做四边形。
故答案为:A
3.C
【分析】长方形拉成一个平行四边形,周长不会改变,依此选择。
【详解】根据分析可知:平行四边形的周长与原长方形的周长相等。
故答案为:C
【点睛】此题考查的是对周长的认识,熟练掌握平行四边形易变形的特性是解答此题的关键。
4.C
【分析】只有一组对边平行的四边形叫做梯形;梯形上底到下底的距离是梯形的高;梯形ABCD的上底是BC,下底是AD,BC到AD之间的距离是11厘米,依此选择。
【详解】梯形ABCD的高是11厘米。
故答案为:C
5.C
【分析】把一个长方形活动框拉成一个平行四边形框架后,平行四边形的底是原长方形的长边,但是,拉动之后的高小于原长方形的宽,所以平行四边形的面积应小于原长方形的面积.
【详解】因为把长方形拉成平行四边形后,底不变,但高变短了,
所以面积比原来长方形的面积小了;
故选C.
6.B
【详解】三角形的腰长只能是9厘米,而不能是3 厘米,因为腰长如果是3厘米,3+3<9,不能围成三角形。9+9+3=21(厘米),所以这个三角形的周长是21厘米。
故答案为:B
7.C
【分析】根据平行四边形的特征,平行四边形是两组对边分别平行的四边形,结合选项逐一分析解答即可。
【详解】
A.符合①②,不符合③④。
B.符合③,不符合①②④。
C.符合①②③④。
D.符合①③,不符合②④。
做的记号最多。
故答案为:C
8.C
【详解】++=1(分米)
答:这个等腰三角形的周长是1分米.
故选C.
9.B
【分析】等边三角形三条边都相等,等腰三角形两腰相等;三角形一定有两个角是锐角;平行四边形的对边平行且相等,平行四边形的高连接两条对边并与两条对边互相垂直;据此解答。
【详解】根据分析:
A.等边三角形一定是等腰三角形,原题说法正确;
B.有两个角是锐角的三角形有可能是钝角三角形、直角三角形和锐角三角形,原题说法错误;
C.同一个平行四边形不同底边上的高不一定相等,原题说法正确。
故答案为:B
【点睛】本题主要考查的是三角形的分类,三角形的特征,以及平行四边形的特征。
10.A
【分析】由三角形的内角和求出另外两个角的和,再根据最小的内角是50°来判断其它两个角的情况。
【详解】180°-50°=130°;另外两个角的和是130°,最小的内角是50°,假设另外两个角中还有一个是50°,另一个就是:130°-50°=80°;最大的内角最大只能是80°,所以这个三角形的三个角都是锐角,这个三角形一定是锐角三角形。
故答案为:A
【点睛】解决本题首先要能根据三角形的内角和是180°,求出另外角的度数可能的情况,并由此求解。
11.三
【详解】略
12. 稳定性 两边
【详解】略
13.等腰
【分析】根据题意,因为是翻折,所以该三角形的两条边相等,等腰三角形的两条边相等,据此填空即可。
【详解】折完后形成一个正方形,正方形的四条边相等,所以沿折痕剪下的三角形是等腰三角形。
14. 上底 下底 平行四边形
【分析】只有一组对边互相平行的四边形叫梯形,在梯形里,互相平行的一组对边分别叫做梯形的上底和下底, 两个完全一样的梯形,将其中一个梯形翻转后与另一个梯形拼接,可以拼成一个平行四边形 。因为拼接后得到的四边形,它的两组对边分别平行且相等,符合平行四边形的特征。
【详解】由分析可知,梯形里一组互相平行的对边分别叫作梯形的上底和下底,两个完全一样的梯形可以拼成一个平行四边形。
15. 88 三角形内角和为180°
【分析】等腰三角形的特征:两腰相等,两底角也相等;再根据三角形内角和是180°和底角是46°,进而求得它的顶角的度数。
【详解】180°-46°×2
=180°-92°
=88°
被撕去的顶角的度数是88°。推算的依据是三角形内角和为180°。(答案不唯一)
【点睛】此题根据等腰三角形的特征和三角形的内角和进行解答即可。
16. 直角三角形 锐角三角形或钝角三角形或直角三角形 钝角三角形
【分析】按角分,三个角都是锐角的三角形是锐角三角形;有一个角是直角的三角形是直角三角形;有一个角是钝角的三角形是钝角三角形。第一个被信封遮住的三角形所露出的角是直角;第二个被信封遮住的三角形所露出的角是锐角,其它的两个角可能均为锐角,也可能有一个直角或钝角;第三个被信封遮住的三角形所露出的角是钝角,据此依次判断每个三角形是什么三角形即可。
【详解】第一个被信封遮住的三角形所露出的角是直角,因此第一个三角形是直角三角形;
第二个被信封遮住的三角形所露出的角是锐角,其它的两个角可能均为锐角,也可能有一个直角或钝角,因此第二个三角形是锐角三角形或钝角三角形或直角三角形;
第三个被信封遮住的三角形所露出的角是钝角,因此第三个三角形是钝角三角形。
17. 10 等腰
【详解】略
18.26.5
【分析】三角形三条边的总长度就是这个三角形的周长,等腰三角形的两腰相等,三角形任意两边的长度之和大于第三边,任意两边的长度之差小于第三边,此题依此解答即可。
【详解】假设腰长是4.5厘米,4.5+4.5=9(厘米),9厘米<11厘米,即腰长不能是4.5厘米;
则腰长是11厘米,4.5+11=15.5(厘米),15.5厘米>11厘米,11-4.5=6.5(厘米),6.5厘米<11厘米,即腰长11厘米满足。
11+11+4.5=26.5(厘米)
这个三角形的周长是26.5厘米。
19.6;9;12;15;18;3n
(1)3
(2)3n
(3)13
【分析】三角形有3条边,每摆一个三角形,需要3根小棒,摆一个三角形需要的小棒根数乘三角形个数,可以算出需要多少根小棒。据此填表。
(1)三角形有3条边,每增加一个三角形,就增加3根小棒。
(2)摆一个三角形需要的小棒根数乘三角形个数,可以算出摆n个这样的三角形要用(3n)根小棒。
(3)小棒根数除以每个三角形的小棒根数,即可算出39根小棒可以摆成(39÷3)个三角形。
【详解】
三角形个数 1 2 3 4 5 6 … n
火柴棒根数 3 6 9 12 15 18 … 3n
继续摆下去,我发现:(1)每增加一个三角形,就增加(3)根小棒。
(2)摆n个这样的三角形,要用(3n)根小棒。
(3)39÷3=13(个)
39根小棒可以摆成(13)个三角形。
20.(n-2)×180
【分析】从n边形的一个顶点出发与其它各个顶点的连线有(n-3)条,(这个点与它本身以及与它相邻的两个点不能连线),把n边形分成(n-2)个三角形,所以n边形的内角和是(n-2)×180度。
【详解】据分析知:把n边形分成(n-2)个三角形,所以n边形的内角和是(n-2)×180度。
【点睛】借助辅助线段,把n边形分成(n-2)个三角形,再计算n边形的内角和,这是解决此题的关键。
21.√
【分析】根据三角形内角和定理:任何三角形内角和都是180°据此解答即可。
【详解】
内角和与的内角和一样大,都是180°。原题说法正确。
故答案为:√
22.×
【分析】把一个锐角三角形中的55°的角剪下,剩下图形的是一个四边形,根据四边形的内角和,求出答案。
【详解】把一个锐角三角形中的55°的角剪下,剩下图形的内角和就变成了360°。
故答案为:×。
【点睛】本题主要考查的是四边形的内角和,解题关键在于求出剪下一个角之后,剩下的图形是四边形。
23.√
【分析】等腰三角形两个底角相等,三角形内角和是180°。据此解答。
【详解】(180°-90°)÷2
=90°÷2
=45° 所以它一定有两个内角是45°。
故答案为:√
24.×
【分析】平面图形的密铺是指用一种或几种相同的图形进行拼接,彼此之间不留空隙、不重叠地铺成一片;根据实验可知:三角形、四边形、正六边形能单独密铺,圆和正五边形不能单独密铺;据此解答。
【详解】根据分析可知:
四边形可以密铺,而正五边形不能密铺。原题说法错误。
故答案为:×
25.×
【分析】等腰三角形的两个底角度数相等;三角形的内角和等于180°,据此判断即可。
【详解】两个底角的度数和是92°×2=184°,与三角形的内角和等于180°矛盾。所以原题干说法错误。
故答案为:×
【点睛】本题考查三角形的内角和,明确等腰三角形的两个底角度数相等是解题的关键。
26.×
【分析】三角形的内角和是180°,能整除360°,可以单独密铺;四边形的内角和是360°,能整除360°,可以单独密铺;正五边形的内角和是540°,不能整除360°,不能单独密铺;因为正六边形的每个内角都是120°,正六边形的3个角拼在一起正好等于360°,可以单独密铺,据此即可解答。
【详解】根据分析可知,三角形、长方形、正六边形可以单独密铺,正五边形不能单独密铺,原说法错误。
故答案为:×
【点睛】本题考查了平面镶嵌,任意多边形能进行镶嵌,说明它的内角和应能整除360°。
27.86cm
【详解】平行四边形的周长为四边边长之和,所以其周长为:25+18+25+18=86(cm).
28.∠1=40°,∠2=110°
【分析】1直角是90°,三角形的内角和是180°,因此用180°减90°后,再减50°,即可得到∠1的度数;1平角是180°,因此用180°减30°后,再减∠1的度数,即可得到∠2的度数,依此解答。
【详解】∠1=180°-90°-50°=90°-50°=40°。
∠2=180°-30°-40°=150°-40°=110°。
∠1=40°,∠2=110°。
29.见详解
【分析】由三条边组成的封闭图形是三角形,从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底;因此先画一条长7个小格的线段作为三角形的底,在距离底边的5个小格处确定三角形的顶点,最后用线段将底边的两个端点和顶点连起来组成一个三角形即可。
只有一组对边平行的四边形叫做梯形;因此先画一条长7个小格的线段作为梯形的下底,然后在下底的上方,画一条与下底平行,且长度为5个小格的线段,最后将这两条线段左右两边的端点分别连起来组成一个梯形即可。
【详解】画图如下:
【点睛】此题考查的是画指定底长和高的三角形、画指定上底和下底的梯形,应熟练掌握三角形的特点,三角形的高及画法,以及梯形的特点。
30.不能;理由见详解
【分析】根据三角形的特征,两边之和大于第三边,三角形的两边的差一定小于第三边,进行解答即可。
【详解】15+20<45,两边之和小于第三边。
答:长度分别是15厘米、45厘米、20厘米的三条线段不能围成一个三角形。
【点睛】此题关键是根据三角形的特征进行分析。
31.见详解
【分析】据平行四边形、梯形、长方形和正方形的含义:两组对边都平行的四边形是平行四边形;一组对边平行而另一组对边不平行的四边形是梯形;有一个角是直角的平行四边形是长方形,一组邻边相等的长方形是正方形;可知:正方形是特殊的长方形,长方形是特殊的平行四边形;梯形和平行四边形都是四边形;据此解答即可。
【详解】
32.80°
【分析】等腰三角形的两个底角的度数相等,由于三角形的内角和为180°,且得知一个底角是顶角的4倍,则两个底角的度数加起来是顶角的8倍,三个角之和为180°,利用除法算式可以算出顶角的度数,据此解答即可。
【详解】4+4+1=9
顶角度数为:180°÷9=20°
则底角度数为:20°×4=80°
答:这个三角形的一个底角是80°。
【点睛】本题考查学生对等腰三角形特征的认识和应用。
33.11分米
【分析】两个三角形的周长相等,等边三角形的边长乘3等于等边三角形的周长,减去14分米等于等腰三角形两条腰的长度和,再除以2即等于一条腰的长度。
【详解】(12×3-14)÷2
=(36-14)÷2
=22÷2
=11(分米)
答:这个三角形的一条腰长是11分米。
【点睛】本题主要考查学生对三角形的周长和三角形分类知识的掌握。
34.(1)图见详解
(2)120;105
【分析】(1)从三角形的顶点向对边作垂线,顶点和垂足间的线段就是所画的指定底边上的高;从平行四边形一条边上的一点到对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,垂足所在的边叫做平行四边形的底。据此画图即可。
(2)三角形的内角和是180°,等腰三角形的两个底角相等,由此可以求出另一个角的度数;平行四边形的内角和为360°,平行四边形对角相等,邻角互补;据此即可解答。
【详解】(1)作图如下:
(2)180°-30°-30°
=150°-30°
=120°
即顶角是120°。
180°-75°=105°
即∠2=105°。
如果上面等腰三角形的一个底角是30度,顶角是120度。平行四边形的∠1=75度,∠2=105度。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
