期末应用题易错精选题(含解析)-2024-2025学年数学五年级下册苏教版
文档属性
| 名称 | 期末应用题易错精选题(含解析)-2024-2025学年数学五年级下册苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 807.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 09:40:09 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末应用题易错精选题-2024-2025学年数学五年级下册苏教版
1.沈艳爱好集邮,她用35.2元买了8角和2元的邮票共32枚。她买了多少枚2元的邮票?
2.小百灵合唱团中女生人数是男生的1.2倍,比男生多15人。合唱团中男女生各有多少人?(列方程解答)
3.某小学足球场是一个长方形,其长是105米,宽是65米,小睿和小芳绕着足球进行快走锻炼,他们同时从同一地点同向匀速行走,850秒后小睿从后面追上小芳。已知小睿的速度是1.5米/秒,则小芳的速度是多少?
4.有甲、乙两个仓库,甲仓库存粮是乙仓库的3倍,如果甲仓库调28吨到乙仓库,则甲仓库还比乙仓库多4吨,原来乙仓库存粮多少吨?
5.世界第一长河尼罗河比中国第一长河长江长307千米,尼罗河的长度比长江的3倍少12419千米。尼罗河和长江分别长多少千米?(列方程解答)
6.某汤包店今天共接到220个外卖订单,其中甲平台外卖订单数量是乙平台外卖订单数量的1.2倍。该店今天接到的甲平台外卖订单和乙平台外卖订单各有多少个?(列方程解答)
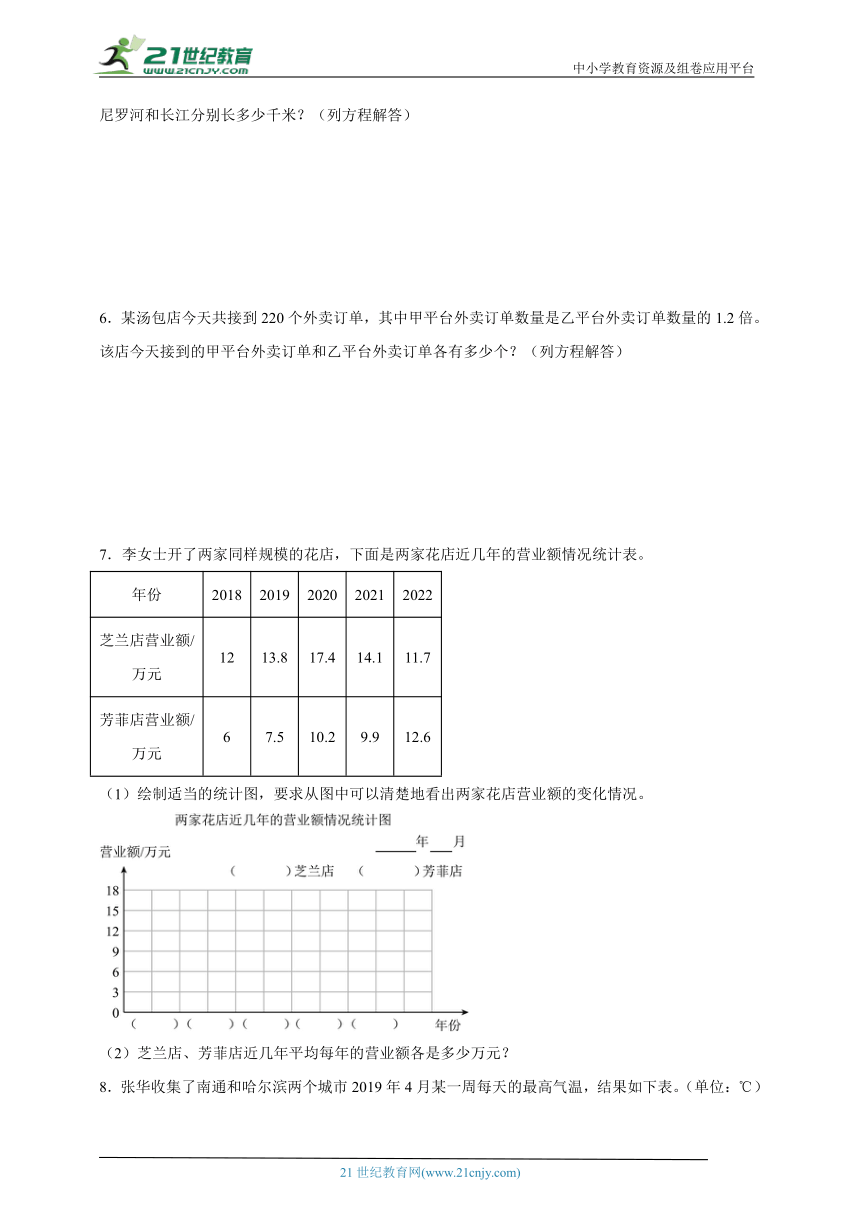
7.李女士开了两家同样规模的花店,下面是两家花店近几年的营业额情况统计表。
年份 2018 2019 2020 2021 2022
芝兰店营业额/万元 12 13.8 17.4 14.1 11.7
芳菲店营业额/万元 6 7.5 10.2 9.9 12.6
(1)绘制适当的统计图,要求从图中可以清楚地看出两家花店营业额的变化情况。
(2)芝兰店、芳菲店近几年平均每年的营业额各是多少万元?
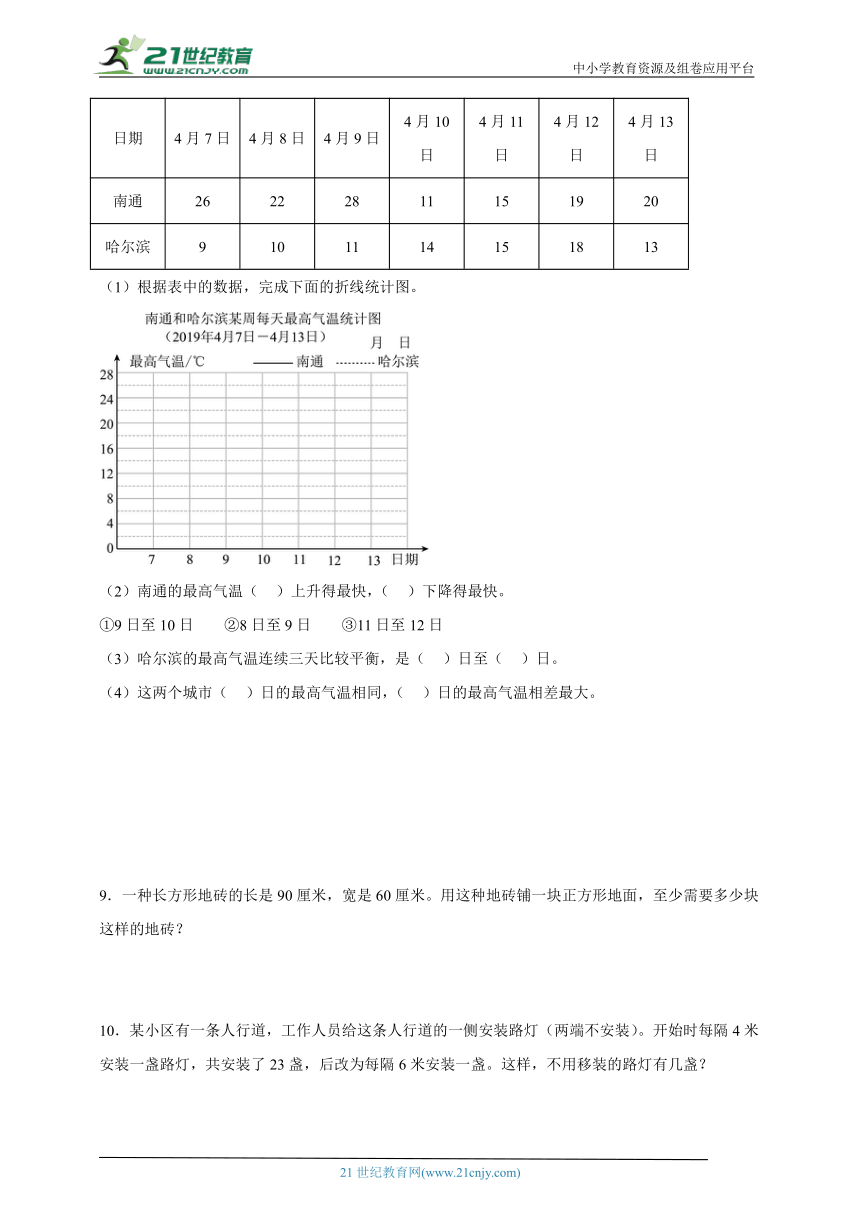
8.张华收集了南通和哈尔滨两个城市2019年4月某一周每天的最高气温,结果如下表。(单位:℃)
日期 4月7日 4月8日 4月9日 4月10日 4月11日 4月12日 4月13日
南通 26 22 28 11 15 19 20
哈尔滨 9 10 11 14 15 18 13
(1)根据表中的数据,完成下面的折线统计图。
(2)南通的最高气温( )上升得最快,( )下降得最快。
①9日至10日 ②8日至9日 ③11日至12日
(3)哈尔滨的最高气温连续三天比较平衡,是( )日至( )日。
(4)这两个城市( )日的最高气温相同,( )日的最高气温相差最大。
9.一种长方形地砖的长是90厘米,宽是60厘米。用这种地砖铺一块正方形地面,至少需要多少块这样的地砖?
10.某小区有一条人行道,工作人员给这条人行道的一侧安装路灯(两端不安装)。开始时每隔4米安装一盏路灯,共安装了23盏,后改为每隔6米安装一盏。这样,不用移装的路灯有几盏?
11.一台收割机5小时收割12公顷小麦,照这样计算,这台收割机1小时收割多少公顷小麦?收割1公顷小麦要多少小时?
12.一个兔兔杯中放了100克水,妈妈取出9克糖放入杯中。此时这杯糖水中糖占水的几分之几?糖占糖水的几分之几?
13.兴隆水果店新进香蕉、荔枝、苹果各300千克。卖了3天后,香蕉还剩,荔枝还剩,苹果还剩。照这样的销售情况,下次进货时,哪种水果要多进些?哪种水果要少进些?
14.一根铁丝长米,比另一根铁丝长米,两根铁丝一共长多少米?
15.爸爸买了千克的樱桃,妈妈吃了,楠楠吃了。还剩下这些樱桃的几分之几?
16.A、B两地相距千米。甲从A地到B地要10分钟,乙从B地到A地要8分钟。甲、乙两人同时分别从A、B两地出发,相向而行,3分钟后,两人间的距离占全程的几分之几?
17.一块菜地的面积是公顷,它的种番茄,种黄瓜,其余部分种白菜。白菜的种植面积占这块菜地的几分之几?
18.小亮对本班同学上学的交通方式进行了调查,结果显示:的同学乘公交车或地铁上学,的同学坐家长的自行车、摩托车或汽车上学,其余同学步行上学。这个班步行上学的同学占全班的几分之几?
19.小强买了一瓶饮料,第一次喝了升,第二次喝了升,第三次喝了升,正好喝完。这瓶饮料共有多少升?
20.用一块长180厘米、宽120厘米的长方形硬纸板,最多能裁出多少个半径30厘米的圆?
21.一个直角三角形的面积是12平方厘米,一条直角边长4厘米。以另一条直角边为直径画一个圆,这个圆的面积是多少平方厘米?
22.如图,用包装绳把4个底面直径都是8厘米的啤酒瓶捆扎在一起,打结处用了20厘米长的包装绳,一共需要包装绳多少厘米?
23.给缸口直径是0.95米的水缸做一个圆木盖,木盖的直径比缸口直径大5厘米。木盖的面积是多少平方米?如果在木盖的边沿钉一圈铁片,铁片长多少米?
24.图中大三角形的面积是30平方厘米,你能算出涂色部分的面积吗?
25.把一根长12.56分米的铁丝围成一个半圆弧(如图),还需配上一根长多少分米的铁丝,才能围成一个半圆?
26.如图所示,已知小正方形涂色部分的面积是大正方形涂色部分面积的,则小正方形空白部分的面积是大正方形空白部分面积的几分之几?
27.下图中正方形的边长是2厘米,四个相同圆的圆心分别是正方形的四个顶点。求涂色部分的面积。
《期末应用题易错精选题-2024-2025学年数学五年级下册苏教版》参考答案
1.8枚
【分析】根据1元=10角,把8角化成0.8元,设她买了2元的邮票x枚,则买了(32-x)枚8角的邮票,根据等量关系:“2元邮票的总价+8角邮票的总价=35.2元”列方程解答即可求出买2元邮票的数量。
【详解】解:设她买了2元的邮票x枚。
2x+0.8×(32-x)=35.2
2x+25.6-0.8x=35.2
1.2x+25.6=35.2
1.2x+25.6-25.6=35.2-25.6
1.2x=9.6
1.2x÷1.2=9.6÷1.2
x=8
答:她买了8枚2元的邮票。
2.男生75人;女生90人
【分析】设合唱团中男生有x人,因为女生人数是男生的1.2倍,所以女生人数为1.2x人,又已知女生比男生多15人,那么等量关系为:女生人数-男生人数=15,可列方程1.2x-x=15,先计算1.2x-x,等式两边同时除以0.2求出方程的解;再把x的值代入1.2x,可计算出女生人数。
【详解】解:设合唱团中男生有x人,则女生有1.2x人。
1.2x-x=15
0.2x=15
0.2x÷0.2=15÷0.2
x=75
1.2x=1.2×75=90
答:合唱团中男生有75人,女生有90人。
3.1.1米/秒
【分析】小睿和小芳同时同地同向行走,小睿从后面追上小芳时,小睿比小芳多走的路程就是足球场的周长;根据长方形周长公式可算出足球场周长;设小芳的速度是x米/秒,在850秒的时间里,小睿走的路程为850×1.5米,小芳走的路程为850x米,那么等量关系为:小睿走的路程-小芳走的路程=足球场的周长;根据上述等量关系可列方程:850×1.5-850x=(105+65)×2,先计算方程中1.5×850和(105+65)×2,原方程变为1275-850x = 340,方程两边同时加上850x,左右两边交换位置,再将方程两边同时减去340,最后方程两边同时除以850求解出x。
【详解】解:设小芳的速度是x米/秒。
850×1.5-850x=(105+65)×2
1275-850x=170×2
1275-850x=340
1275-850x+850x=340+850x
1275=340+850x
340+850x=1275
340+850x-340=1275-340
850x=935
850x÷850=935÷850
x=1.1
答:小芳的速度是1.1米/秒。
4.30吨
【分析】根据题意得:甲仓库存粮=乙仓库存粮×3,(甲仓库存粮-28)-(乙仓库存粮+28)=4,可设乙仓库存粮有x吨,甲仓库存粮3x吨,再运用等量关系列出方程,进而解答。
【详解】解:设乙仓库存粮有x吨,则甲仓库存粮3x吨。
答:原来乙仓库存粮30吨。
5.长江:6363千米;尼罗河6670千米
【分析】根据题意,可知数量关系:长江的长度×3-12419=尼罗河的长度,设长江的长度为x千米,那么尼罗河的长度为(x+307)千米,再根据数量关系列出方程,运用等式性质解方程即可。
【详解】解:设长江的长度为x千米,则尼罗河的长度为(x+307)千米。
3x-12419=x+307
3x-x-12419=x-x+307
2x-12419=307
2x-12419+12419=307+12419
2x=12726
2x÷2=12726÷2
x=6363
6363+307=6670(千米)
答:长江的长度为6363千米,尼罗河的长度为6670千米。
6.甲平台外卖订单有120个,乙平台外卖订单有100个。
【分析】先设乙平台外卖订单有个,则甲平台外卖订单有个,由题意可知等量关系式:甲平台外卖订单数量+乙平台外卖订单数量=220个,据此列方程解答即可。
【详解】 解:设乙平台外卖订单有个,则甲平台外卖订单有个
1.2×100=120(个)
答:甲平台外卖订单有120个,乙平台外卖订单有100个。
7.(1)见详解
(2)芝兰店13.8万元;芳菲店9.24万元
【分析】(1)根据统计表中的数据,先在图中分别描出两组数据的各点,并根据图例把各点用线段顺次连接起来,完成复式折线统计图的绘制。
(2)先用加法分别求出芝兰店、芳菲店近5年的总营业额,再除以5,求出芝兰店、芳菲店近几年平均每年的营业额。
【详解】(1)如图:
(2)芝兰店:
(12+13.8+17.4+14.1+11.7)÷5
=69÷5
=13.8(万元)
芳菲店:
(6+7.5+10.2+9.9+12.6)÷5
=46.2÷5
=9.24(万元)
答:芝兰店近几年平均每年的营业额是13.8万元,芳菲店近几年平均每年的营业额是9.24万元。
8.(1)图见详解
(2)②;①
(3)7;9
(4)11;9
【分析】(1)统计图的横轴表示日期,纵轴表示最高气温,结合数据的大小,分别描出两组数据的各点,并根据图例把各点用线段顺次连接起来,完成复式折线统计图的绘制。
(2)观察图中表示南通最高气温的折线,折线上升最快表示气温上升最快,折线下降最快表示气温下降最快,从图中找出对应的日期即可。
(3)观察图中表示哈尔滨最高气温的折线,找出折线连续平稳的三天即可。
(4)图中两条折线相交于一点时,表示两个城市这日的最高气温相同;当两条折线的叉口最大时,表示两个城市这日的最高气温相差最大。
【详解】(1)折线统计图如下:
(2)南通的最高气温8日至9日上升得最快,9日至10日下降得最快。
故答案为:②;①
(3)哈尔滨的最高气温连续三天比较平衡,是(7)日至(9)日。
(4)这两个城市(11)日的最高气温相同,(9)日的最高气温相差最大。
9.6块
【分析】要用长90厘米、宽60厘米的长方形地砖铺成正方形地面,正方形地面的边长应是90和60的公倍数,要求至少需要多少块地砖,就是求90和60的最小公倍数作为正方形地面的边长,用分解质因数法求出90和60的最小公倍数;在正方形地面的长的方向,所需地砖数量为180÷90=2(块) ,在正方形地面的宽的方向,所需地砖数量为180÷60=3(块);总共所需地砖数量为长方向所需地砖数乘宽方向所需地砖数,即2×3=6(块)。
【详解】90=2×3×3×5
60=2×2×3×5
60和90的最小公倍数是:
2×2×3×3×5
=4×3×3×5
=12×3×5
=36×5
=180
180÷90=2(块)
180÷60=3(块)
2×3=6(块)
答:至少需要6块这样的地砖。
10.7盏
【分析】因为两端都不安装路灯,根据“间隔数=灯的数量+1”,已知开始安装了23盏路灯,所以间隔数是23+1=24个;又因为每个间隔是4米,根据“距离=间隔数×间隔长度”,可得人行道长度为24×4=96米;分别对4和6分解质因数计算出4和6的最小公倍数是12,这意味着每隔12米处的路灯不用移栽;最后用总长度除以最小公倍数可得间隔数,由于两端都不安装路灯,根据“灯的数量=间隔数-1”计算出不用移栽的路灯数量。
【详解】4×(23+1)
=4×24
=96(米)
4=2×2
6=2×3
所以4和6的最小公倍数是:2×2×3=12
96÷12-1
=8-1
=7(盏)
答:不用移装的路灯有7盏。
11.2.4公顷;小时
【分析】求1小时收割公顷数:根据“工作效率=工作总量÷工作时间”的关系,已知工作总量(12公顷)和工作时间(5小时),用收割的小麦公顷数除以所用时间,就能得到这台收割机1小时收割小麦的公顷数。求收割1公顷所需时间:用所用的总时间除以收割的小麦总公顷数,得到收割1公顷小麦需要的时间。
【详解】计算1小时收割公顷数:12÷5=2.4(公顷)
计算收割1公顷所需时间:5÷12=(小时)
答:这台收割机1小时收割2.4公顷,收割1公顷小麦要小时。
12.;
【分析】已知糖的质量是9克,水的质量是100克,求一个数是另一个数的几分之几用除法计算,所以用糖的质量除以水的质量即可;
糖水质量=糖的质量+水的质量,即9+100=109克,糖的质量是9克,然后用糖的质量除以糖水的质量。
【详解】9÷100=
答:这杯糖水中糖占水的;
9+100=109(克)
9÷109=
答:糖占糖水的。
13.苹果多进;香蕉少进
【分析】因为香蕉、荔枝、苹果的总质量相等,比较卖了3天后,香蕉、荔枝、苹果还剩下的质量占总质量的分率大小,剩下最少的,卖出的就最多,这种水果要多进些;反之,剩下最多的,卖出的就最少,这种水果要少进些,据此解答。
分数大小的比较:分子相同时,分母越大,分数值反而越小。
【详解】
苹果剩下的最少,所以苹果卖出的最多;香蕉剩下的最多,所以香蕉卖出的最少。
答:下次进货时,苹果要多进些,香蕉要少进些。
14.米
【分析】根据题意,用减去可以求出另一根铁丝的长度,再加上第一根铁丝的长度,即可求出两根铁丝一共长多少米。
【详解】-+
=-+
=+
=
=(米)
答:两根铁丝一共长米。
15.
【分析】将爸爸买的樱桃看成单位“1”,减去妈妈吃和楠楠吃的几分之几,就是剩下的几分之几。在最后将分数约分成最简分数。
【详解】1-()
=1-
答:还剩下这些樱桃的。
16.
【分析】把甲、乙两地的距离看作单位“1”, 甲从A地到B地要10分钟,乙从B地到A地要8分钟,用3分别除以10和8,分别求出甲、乙3分钟各自行了全程的几分之几,再用1减去甲、乙3分钟各自行了全程的分率和即可解答。
【详解】3÷10=
3÷8=
1-(+)
=1-()
=1-
=
答:3分钟后,两人间的距离占全程的。
17.
【分析】求白菜的种植面积占这块菜地的几分之几?那么我们首先应该把这块菜地整体看作单位“1”,其中,番茄占,黄瓜占,那么剩余的就是白菜所占的分率,因此只需用1减去,再减去即可。
【详解】1--
=-
=
答:白菜的种植面积占这块菜地的。
18.
【分析】把全班同学看作单位“1”,根据减法的意义,用“1”减去乘公交车或地铁上学,再减去坐家长的自行车、摩托车或汽车上学的同学人数占全班同学的分率,即是步行上学的同学占全班的几分之几。
【详解】
答:这个班步行上学的同学占全班的。
19.升
【分析】本题可根据分数加法的意义来求解,即把三次喝的饮料量相加,其和就是这瓶饮料的总量;在计算分数加法时,分母不同,需要先通分,将它们化为分母相同的分数,再按照同分母分数加法的法则进行计算,同分母分数相加,分母不变,分子相加,最后将结果化为最简分数。
【详解】
=
=
=
=(升)
答:这瓶饮料共有升。
20.6个
【分析】求最多能裁几个半径是30厘米的圆,就是求直径是30×2=60厘米的圆,分别求出长方形的长和宽分别能裁几个圆,再相乘,即可解答。
【详解】30×2=60(厘米)
(180÷60)×(120÷60)
=3×2
=6(个)
答:最多能裁出6个半径30厘米的圆。
21.28.26平方厘米
【分析】直角三角形的两条直角边互为彼此的底和高,直角三角形的面积=一条直角边×另一条直角边÷2,另一条直角边=直角三角形的面积×2÷已知的直角边,另一条直角边等于圆的直径,利用“”求出这个圆的面积,据此解答。
【详解】12×2÷4
=24÷4
=6(厘米)
3.14×(6÷2)2
=3.14×32
=28.26(平方厘米)
答:这个圆的面积是28.26平方厘米。
22.77.12厘米
【分析】
如图所示,包装绳捆扎一周的长度由两部分组成,一部分是4条相等的线段,每条线段的长度等于圆的直径;另一部分是4条相同的曲线,它们合在一起的长度刚好等于圆的周长;最后加上打结处包装绳的长度,据此解答。
【详解】8×4+3.14×8+20
=32+25.12+20
=57.12+20
=77.12(厘米)
答:一共需要包装绳77.12厘米。
23.0.785平方米;3.14米
【分析】由题意可知,木盖的直径=缸口的直径+5厘米,利用“”求出木盖的面积;
求铁片的长度就是求木盖的周长,利用“”求出铁片的长度,据此解答。
【详解】5厘米=0.05米
0.95+0.05=1(米)
3.14×(1÷2)2
=3.14×0.52
=3.14×0.25
=0.785(平方米)
3.14×1=3.14(米)
答:木盖的面积是0.785平方米,铁片长3.14米。
24.17.1平方厘米
【分析】大三角形底为圆直径2r,高为半径r,由“三角形面积=底×高÷2”可得出大三角形面积S=2r×r÷2=r2,已知大三角形面积为30平方厘米,即确定r2=30平方厘米;
根据圆的面积公式,且半圆面积是圆面积一半,所以S半圆=πr2÷2,将r2=30代入可算出半圆面积;
因为涂色部分面积是半圆面积减去大三角形面积,算出半圆面积和已知大三角形面积后,两者作差就能得到涂色部分面积。
【详解】3.14×30÷2
=94.2÷2
=47.1(平方厘米)
47.1-30=17.1(平方厘米)
答:涂色部分的面积是17.1平方厘米。
25.8分米
【分析】由题意可知,半圆弧的长度等于圆周长的一半,则圆的周长为(12.56×2)分米,需要配的铁丝的长度等于圆的直径,利用“”求出圆的直径,据此解答。
【详解】12.56×2÷3.14
=25.12÷3.14
=8(分米)
答:还需配上一根长8分米的铁丝,才能围成一个半圆。
26.
【分析】观察图形可知,小正方形涂色部分和大正方形涂色部分是两个底相等的三角形,小正方形涂色部分的高等于小正方形的边长,大正方形涂色部分的高等于大正方形的边长。根据三角形的面积=底×高÷2,如果小正方形涂色部分的面积是大正方形涂色部分面积的,则小正方形的边长等于大正方形边长的。设小正方形的边长是1,则大正方形的边长是3。梯形的面积=(上底+下底)×高÷2,据此分别求出两个正方形空白部分的面积,再用小正方形空白部分的面积除以大正方形空白部分面积即可解答。
【详解】通过分析可得:小正方形的边长等于大正方形边长的,设小正方形的边长是1,则大正方形的边长是3。
小正方形空白部分的面积:1×1÷2=0.5
大正方形空白部分的面积:(3-1+3)×3÷2
=5×3÷2
=7.5
0.5÷7.5==
答:小正方形空白部分的面积是大正方形空白部分面积的。
27.9.42平方厘米
【分析】通过重新组合阴影部分得出阴影部分的面积就是3个圆的面积,根据题意,正方形的边长是2厘米,相当于圆的两个半径,即圆的半径就是1厘米,根据圆的面积=得出一个圆的面积,再乘3即可。
【详解】3.14×(2÷2)2×3
=3.14×12×3
=3.14×3
=9.42(平方厘米)
答:涂色部分的面积是9.42平方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末应用题易错精选题-2024-2025学年数学五年级下册苏教版
1.沈艳爱好集邮,她用35.2元买了8角和2元的邮票共32枚。她买了多少枚2元的邮票?
2.小百灵合唱团中女生人数是男生的1.2倍,比男生多15人。合唱团中男女生各有多少人?(列方程解答)
3.某小学足球场是一个长方形,其长是105米,宽是65米,小睿和小芳绕着足球进行快走锻炼,他们同时从同一地点同向匀速行走,850秒后小睿从后面追上小芳。已知小睿的速度是1.5米/秒,则小芳的速度是多少?
4.有甲、乙两个仓库,甲仓库存粮是乙仓库的3倍,如果甲仓库调28吨到乙仓库,则甲仓库还比乙仓库多4吨,原来乙仓库存粮多少吨?
5.世界第一长河尼罗河比中国第一长河长江长307千米,尼罗河的长度比长江的3倍少12419千米。尼罗河和长江分别长多少千米?(列方程解答)
6.某汤包店今天共接到220个外卖订单,其中甲平台外卖订单数量是乙平台外卖订单数量的1.2倍。该店今天接到的甲平台外卖订单和乙平台外卖订单各有多少个?(列方程解答)
7.李女士开了两家同样规模的花店,下面是两家花店近几年的营业额情况统计表。
年份 2018 2019 2020 2021 2022
芝兰店营业额/万元 12 13.8 17.4 14.1 11.7
芳菲店营业额/万元 6 7.5 10.2 9.9 12.6
(1)绘制适当的统计图,要求从图中可以清楚地看出两家花店营业额的变化情况。
(2)芝兰店、芳菲店近几年平均每年的营业额各是多少万元?
8.张华收集了南通和哈尔滨两个城市2019年4月某一周每天的最高气温,结果如下表。(单位:℃)
日期 4月7日 4月8日 4月9日 4月10日 4月11日 4月12日 4月13日
南通 26 22 28 11 15 19 20
哈尔滨 9 10 11 14 15 18 13
(1)根据表中的数据,完成下面的折线统计图。
(2)南通的最高气温( )上升得最快,( )下降得最快。
①9日至10日 ②8日至9日 ③11日至12日
(3)哈尔滨的最高气温连续三天比较平衡,是( )日至( )日。
(4)这两个城市( )日的最高气温相同,( )日的最高气温相差最大。
9.一种长方形地砖的长是90厘米,宽是60厘米。用这种地砖铺一块正方形地面,至少需要多少块这样的地砖?
10.某小区有一条人行道,工作人员给这条人行道的一侧安装路灯(两端不安装)。开始时每隔4米安装一盏路灯,共安装了23盏,后改为每隔6米安装一盏。这样,不用移装的路灯有几盏?
11.一台收割机5小时收割12公顷小麦,照这样计算,这台收割机1小时收割多少公顷小麦?收割1公顷小麦要多少小时?
12.一个兔兔杯中放了100克水,妈妈取出9克糖放入杯中。此时这杯糖水中糖占水的几分之几?糖占糖水的几分之几?
13.兴隆水果店新进香蕉、荔枝、苹果各300千克。卖了3天后,香蕉还剩,荔枝还剩,苹果还剩。照这样的销售情况,下次进货时,哪种水果要多进些?哪种水果要少进些?
14.一根铁丝长米,比另一根铁丝长米,两根铁丝一共长多少米?
15.爸爸买了千克的樱桃,妈妈吃了,楠楠吃了。还剩下这些樱桃的几分之几?
16.A、B两地相距千米。甲从A地到B地要10分钟,乙从B地到A地要8分钟。甲、乙两人同时分别从A、B两地出发,相向而行,3分钟后,两人间的距离占全程的几分之几?
17.一块菜地的面积是公顷,它的种番茄,种黄瓜,其余部分种白菜。白菜的种植面积占这块菜地的几分之几?
18.小亮对本班同学上学的交通方式进行了调查,结果显示:的同学乘公交车或地铁上学,的同学坐家长的自行车、摩托车或汽车上学,其余同学步行上学。这个班步行上学的同学占全班的几分之几?
19.小强买了一瓶饮料,第一次喝了升,第二次喝了升,第三次喝了升,正好喝完。这瓶饮料共有多少升?
20.用一块长180厘米、宽120厘米的长方形硬纸板,最多能裁出多少个半径30厘米的圆?
21.一个直角三角形的面积是12平方厘米,一条直角边长4厘米。以另一条直角边为直径画一个圆,这个圆的面积是多少平方厘米?
22.如图,用包装绳把4个底面直径都是8厘米的啤酒瓶捆扎在一起,打结处用了20厘米长的包装绳,一共需要包装绳多少厘米?
23.给缸口直径是0.95米的水缸做一个圆木盖,木盖的直径比缸口直径大5厘米。木盖的面积是多少平方米?如果在木盖的边沿钉一圈铁片,铁片长多少米?
24.图中大三角形的面积是30平方厘米,你能算出涂色部分的面积吗?
25.把一根长12.56分米的铁丝围成一个半圆弧(如图),还需配上一根长多少分米的铁丝,才能围成一个半圆?
26.如图所示,已知小正方形涂色部分的面积是大正方形涂色部分面积的,则小正方形空白部分的面积是大正方形空白部分面积的几分之几?
27.下图中正方形的边长是2厘米,四个相同圆的圆心分别是正方形的四个顶点。求涂色部分的面积。
《期末应用题易错精选题-2024-2025学年数学五年级下册苏教版》参考答案
1.8枚
【分析】根据1元=10角,把8角化成0.8元,设她买了2元的邮票x枚,则买了(32-x)枚8角的邮票,根据等量关系:“2元邮票的总价+8角邮票的总价=35.2元”列方程解答即可求出买2元邮票的数量。
【详解】解:设她买了2元的邮票x枚。
2x+0.8×(32-x)=35.2
2x+25.6-0.8x=35.2
1.2x+25.6=35.2
1.2x+25.6-25.6=35.2-25.6
1.2x=9.6
1.2x÷1.2=9.6÷1.2
x=8
答:她买了8枚2元的邮票。
2.男生75人;女生90人
【分析】设合唱团中男生有x人,因为女生人数是男生的1.2倍,所以女生人数为1.2x人,又已知女生比男生多15人,那么等量关系为:女生人数-男生人数=15,可列方程1.2x-x=15,先计算1.2x-x,等式两边同时除以0.2求出方程的解;再把x的值代入1.2x,可计算出女生人数。
【详解】解:设合唱团中男生有x人,则女生有1.2x人。
1.2x-x=15
0.2x=15
0.2x÷0.2=15÷0.2
x=75
1.2x=1.2×75=90
答:合唱团中男生有75人,女生有90人。
3.1.1米/秒
【分析】小睿和小芳同时同地同向行走,小睿从后面追上小芳时,小睿比小芳多走的路程就是足球场的周长;根据长方形周长公式可算出足球场周长;设小芳的速度是x米/秒,在850秒的时间里,小睿走的路程为850×1.5米,小芳走的路程为850x米,那么等量关系为:小睿走的路程-小芳走的路程=足球场的周长;根据上述等量关系可列方程:850×1.5-850x=(105+65)×2,先计算方程中1.5×850和(105+65)×2,原方程变为1275-850x = 340,方程两边同时加上850x,左右两边交换位置,再将方程两边同时减去340,最后方程两边同时除以850求解出x。
【详解】解:设小芳的速度是x米/秒。
850×1.5-850x=(105+65)×2
1275-850x=170×2
1275-850x=340
1275-850x+850x=340+850x
1275=340+850x
340+850x=1275
340+850x-340=1275-340
850x=935
850x÷850=935÷850
x=1.1
答:小芳的速度是1.1米/秒。
4.30吨
【分析】根据题意得:甲仓库存粮=乙仓库存粮×3,(甲仓库存粮-28)-(乙仓库存粮+28)=4,可设乙仓库存粮有x吨,甲仓库存粮3x吨,再运用等量关系列出方程,进而解答。
【详解】解:设乙仓库存粮有x吨,则甲仓库存粮3x吨。
答:原来乙仓库存粮30吨。
5.长江:6363千米;尼罗河6670千米
【分析】根据题意,可知数量关系:长江的长度×3-12419=尼罗河的长度,设长江的长度为x千米,那么尼罗河的长度为(x+307)千米,再根据数量关系列出方程,运用等式性质解方程即可。
【详解】解:设长江的长度为x千米,则尼罗河的长度为(x+307)千米。
3x-12419=x+307
3x-x-12419=x-x+307
2x-12419=307
2x-12419+12419=307+12419
2x=12726
2x÷2=12726÷2
x=6363
6363+307=6670(千米)
答:长江的长度为6363千米,尼罗河的长度为6670千米。
6.甲平台外卖订单有120个,乙平台外卖订单有100个。
【分析】先设乙平台外卖订单有个,则甲平台外卖订单有个,由题意可知等量关系式:甲平台外卖订单数量+乙平台外卖订单数量=220个,据此列方程解答即可。
【详解】 解:设乙平台外卖订单有个,则甲平台外卖订单有个
1.2×100=120(个)
答:甲平台外卖订单有120个,乙平台外卖订单有100个。
7.(1)见详解
(2)芝兰店13.8万元;芳菲店9.24万元
【分析】(1)根据统计表中的数据,先在图中分别描出两组数据的各点,并根据图例把各点用线段顺次连接起来,完成复式折线统计图的绘制。
(2)先用加法分别求出芝兰店、芳菲店近5年的总营业额,再除以5,求出芝兰店、芳菲店近几年平均每年的营业额。
【详解】(1)如图:
(2)芝兰店:
(12+13.8+17.4+14.1+11.7)÷5
=69÷5
=13.8(万元)
芳菲店:
(6+7.5+10.2+9.9+12.6)÷5
=46.2÷5
=9.24(万元)
答:芝兰店近几年平均每年的营业额是13.8万元,芳菲店近几年平均每年的营业额是9.24万元。
8.(1)图见详解
(2)②;①
(3)7;9
(4)11;9
【分析】(1)统计图的横轴表示日期,纵轴表示最高气温,结合数据的大小,分别描出两组数据的各点,并根据图例把各点用线段顺次连接起来,完成复式折线统计图的绘制。
(2)观察图中表示南通最高气温的折线,折线上升最快表示气温上升最快,折线下降最快表示气温下降最快,从图中找出对应的日期即可。
(3)观察图中表示哈尔滨最高气温的折线,找出折线连续平稳的三天即可。
(4)图中两条折线相交于一点时,表示两个城市这日的最高气温相同;当两条折线的叉口最大时,表示两个城市这日的最高气温相差最大。
【详解】(1)折线统计图如下:
(2)南通的最高气温8日至9日上升得最快,9日至10日下降得最快。
故答案为:②;①
(3)哈尔滨的最高气温连续三天比较平衡,是(7)日至(9)日。
(4)这两个城市(11)日的最高气温相同,(9)日的最高气温相差最大。
9.6块
【分析】要用长90厘米、宽60厘米的长方形地砖铺成正方形地面,正方形地面的边长应是90和60的公倍数,要求至少需要多少块地砖,就是求90和60的最小公倍数作为正方形地面的边长,用分解质因数法求出90和60的最小公倍数;在正方形地面的长的方向,所需地砖数量为180÷90=2(块) ,在正方形地面的宽的方向,所需地砖数量为180÷60=3(块);总共所需地砖数量为长方向所需地砖数乘宽方向所需地砖数,即2×3=6(块)。
【详解】90=2×3×3×5
60=2×2×3×5
60和90的最小公倍数是:
2×2×3×3×5
=4×3×3×5
=12×3×5
=36×5
=180
180÷90=2(块)
180÷60=3(块)
2×3=6(块)
答:至少需要6块这样的地砖。
10.7盏
【分析】因为两端都不安装路灯,根据“间隔数=灯的数量+1”,已知开始安装了23盏路灯,所以间隔数是23+1=24个;又因为每个间隔是4米,根据“距离=间隔数×间隔长度”,可得人行道长度为24×4=96米;分别对4和6分解质因数计算出4和6的最小公倍数是12,这意味着每隔12米处的路灯不用移栽;最后用总长度除以最小公倍数可得间隔数,由于两端都不安装路灯,根据“灯的数量=间隔数-1”计算出不用移栽的路灯数量。
【详解】4×(23+1)
=4×24
=96(米)
4=2×2
6=2×3
所以4和6的最小公倍数是:2×2×3=12
96÷12-1
=8-1
=7(盏)
答:不用移装的路灯有7盏。
11.2.4公顷;小时
【分析】求1小时收割公顷数:根据“工作效率=工作总量÷工作时间”的关系,已知工作总量(12公顷)和工作时间(5小时),用收割的小麦公顷数除以所用时间,就能得到这台收割机1小时收割小麦的公顷数。求收割1公顷所需时间:用所用的总时间除以收割的小麦总公顷数,得到收割1公顷小麦需要的时间。
【详解】计算1小时收割公顷数:12÷5=2.4(公顷)
计算收割1公顷所需时间:5÷12=(小时)
答:这台收割机1小时收割2.4公顷,收割1公顷小麦要小时。
12.;
【分析】已知糖的质量是9克,水的质量是100克,求一个数是另一个数的几分之几用除法计算,所以用糖的质量除以水的质量即可;
糖水质量=糖的质量+水的质量,即9+100=109克,糖的质量是9克,然后用糖的质量除以糖水的质量。
【详解】9÷100=
答:这杯糖水中糖占水的;
9+100=109(克)
9÷109=
答:糖占糖水的。
13.苹果多进;香蕉少进
【分析】因为香蕉、荔枝、苹果的总质量相等,比较卖了3天后,香蕉、荔枝、苹果还剩下的质量占总质量的分率大小,剩下最少的,卖出的就最多,这种水果要多进些;反之,剩下最多的,卖出的就最少,这种水果要少进些,据此解答。
分数大小的比较:分子相同时,分母越大,分数值反而越小。
【详解】
苹果剩下的最少,所以苹果卖出的最多;香蕉剩下的最多,所以香蕉卖出的最少。
答:下次进货时,苹果要多进些,香蕉要少进些。
14.米
【分析】根据题意,用减去可以求出另一根铁丝的长度,再加上第一根铁丝的长度,即可求出两根铁丝一共长多少米。
【详解】-+
=-+
=+
=
=(米)
答:两根铁丝一共长米。
15.
【分析】将爸爸买的樱桃看成单位“1”,减去妈妈吃和楠楠吃的几分之几,就是剩下的几分之几。在最后将分数约分成最简分数。
【详解】1-()
=1-
答:还剩下这些樱桃的。
16.
【分析】把甲、乙两地的距离看作单位“1”, 甲从A地到B地要10分钟,乙从B地到A地要8分钟,用3分别除以10和8,分别求出甲、乙3分钟各自行了全程的几分之几,再用1减去甲、乙3分钟各自行了全程的分率和即可解答。
【详解】3÷10=
3÷8=
1-(+)
=1-()
=1-
=
答:3分钟后,两人间的距离占全程的。
17.
【分析】求白菜的种植面积占这块菜地的几分之几?那么我们首先应该把这块菜地整体看作单位“1”,其中,番茄占,黄瓜占,那么剩余的就是白菜所占的分率,因此只需用1减去,再减去即可。
【详解】1--
=-
=
答:白菜的种植面积占这块菜地的。
18.
【分析】把全班同学看作单位“1”,根据减法的意义,用“1”减去乘公交车或地铁上学,再减去坐家长的自行车、摩托车或汽车上学的同学人数占全班同学的分率,即是步行上学的同学占全班的几分之几。
【详解】
答:这个班步行上学的同学占全班的。
19.升
【分析】本题可根据分数加法的意义来求解,即把三次喝的饮料量相加,其和就是这瓶饮料的总量;在计算分数加法时,分母不同,需要先通分,将它们化为分母相同的分数,再按照同分母分数加法的法则进行计算,同分母分数相加,分母不变,分子相加,最后将结果化为最简分数。
【详解】
=
=
=
=(升)
答:这瓶饮料共有升。
20.6个
【分析】求最多能裁几个半径是30厘米的圆,就是求直径是30×2=60厘米的圆,分别求出长方形的长和宽分别能裁几个圆,再相乘,即可解答。
【详解】30×2=60(厘米)
(180÷60)×(120÷60)
=3×2
=6(个)
答:最多能裁出6个半径30厘米的圆。
21.28.26平方厘米
【分析】直角三角形的两条直角边互为彼此的底和高,直角三角形的面积=一条直角边×另一条直角边÷2,另一条直角边=直角三角形的面积×2÷已知的直角边,另一条直角边等于圆的直径,利用“”求出这个圆的面积,据此解答。
【详解】12×2÷4
=24÷4
=6(厘米)
3.14×(6÷2)2
=3.14×32
=28.26(平方厘米)
答:这个圆的面积是28.26平方厘米。
22.77.12厘米
【分析】
如图所示,包装绳捆扎一周的长度由两部分组成,一部分是4条相等的线段,每条线段的长度等于圆的直径;另一部分是4条相同的曲线,它们合在一起的长度刚好等于圆的周长;最后加上打结处包装绳的长度,据此解答。
【详解】8×4+3.14×8+20
=32+25.12+20
=57.12+20
=77.12(厘米)
答:一共需要包装绳77.12厘米。
23.0.785平方米;3.14米
【分析】由题意可知,木盖的直径=缸口的直径+5厘米,利用“”求出木盖的面积;
求铁片的长度就是求木盖的周长,利用“”求出铁片的长度,据此解答。
【详解】5厘米=0.05米
0.95+0.05=1(米)
3.14×(1÷2)2
=3.14×0.52
=3.14×0.25
=0.785(平方米)
3.14×1=3.14(米)
答:木盖的面积是0.785平方米,铁片长3.14米。
24.17.1平方厘米
【分析】大三角形底为圆直径2r,高为半径r,由“三角形面积=底×高÷2”可得出大三角形面积S=2r×r÷2=r2,已知大三角形面积为30平方厘米,即确定r2=30平方厘米;
根据圆的面积公式,且半圆面积是圆面积一半,所以S半圆=πr2÷2,将r2=30代入可算出半圆面积;
因为涂色部分面积是半圆面积减去大三角形面积,算出半圆面积和已知大三角形面积后,两者作差就能得到涂色部分面积。
【详解】3.14×30÷2
=94.2÷2
=47.1(平方厘米)
47.1-30=17.1(平方厘米)
答:涂色部分的面积是17.1平方厘米。
25.8分米
【分析】由题意可知,半圆弧的长度等于圆周长的一半,则圆的周长为(12.56×2)分米,需要配的铁丝的长度等于圆的直径,利用“”求出圆的直径,据此解答。
【详解】12.56×2÷3.14
=25.12÷3.14
=8(分米)
答:还需配上一根长8分米的铁丝,才能围成一个半圆。
26.
【分析】观察图形可知,小正方形涂色部分和大正方形涂色部分是两个底相等的三角形,小正方形涂色部分的高等于小正方形的边长,大正方形涂色部分的高等于大正方形的边长。根据三角形的面积=底×高÷2,如果小正方形涂色部分的面积是大正方形涂色部分面积的,则小正方形的边长等于大正方形边长的。设小正方形的边长是1,则大正方形的边长是3。梯形的面积=(上底+下底)×高÷2,据此分别求出两个正方形空白部分的面积,再用小正方形空白部分的面积除以大正方形空白部分面积即可解答。
【详解】通过分析可得:小正方形的边长等于大正方形边长的,设小正方形的边长是1,则大正方形的边长是3。
小正方形空白部分的面积:1×1÷2=0.5
大正方形空白部分的面积:(3-1+3)×3÷2
=5×3÷2
=7.5
0.5÷7.5==
答:小正方形空白部分的面积是大正方形空白部分面积的。
27.9.42平方厘米
【分析】通过重新组合阴影部分得出阴影部分的面积就是3个圆的面积,根据题意,正方形的边长是2厘米,相当于圆的两个半径,即圆的半径就是1厘米,根据圆的面积=得出一个圆的面积,再乘3即可。
【详解】3.14×(2÷2)2×3
=3.14×12×3
=3.14×3
=9.42(平方厘米)
答:涂色部分的面积是9.42平方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
