2025新青岛版七年级数学下册期末数学综合检测试卷(含解析)
文档属性
| 名称 | 2025新青岛版七年级数学下册期末数学综合检测试卷(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 275.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-15 00:00:00 | ||
图片预览



文档简介
2025新青岛版七年级数学下册期末数学综合检测试卷
一、选择题
1.下列因式分解正确的是( )
A. B.
C. D.
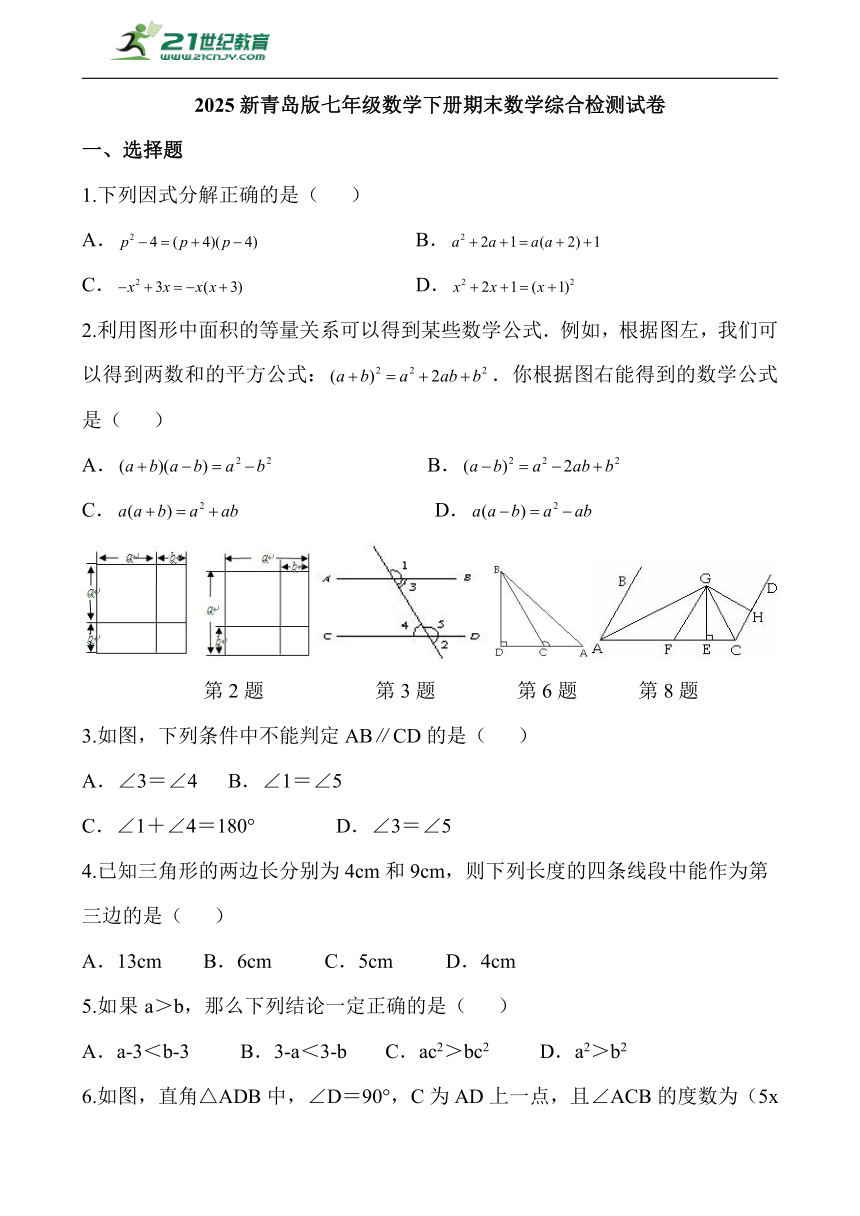
2.利用图形中面积的等量关系可以得到某些数学公式.例如,根据图左,我们可以得到两数和的平方公式:.你根据图右能得到的数学公式是( )
A. B.
C. D.
第2题 第3题 第6题 第8题
3.如图,下列条件中不能判定AB∥CD的是( )
A.∠3=∠4 B.∠1=∠5
C.∠1+∠4=180° D.∠3=∠5
4.已知三角形的两边长分别为4cm和9cm,则下列长度的四条线段中能作为第三边的是( )
A.13cm B.6cm C.5cm D.4cm
5.如果a>b,那么下列结论一定正确的是( )
A.a-3<b-3 B.3-a<3-b C.ac2>bc2 D.a2>b2
6.如图,直角△ADB中,∠D=90°,C为AD上一点,且∠ACB的度数为(5x-10)°,则x的值可能
是( )
A.10 B.20 C.30 D.40
7.玩具车间每天能生产甲种玩具零件24个或乙种玩具零件12个,若甲种玩具零件一个与乙种玩具零件2个能组成一个完整的玩具, 怎样安排生产才能在60 天内组装出最多的玩具?设生产甲种玩具零件x天 乙种玩具零件y天,则有( )
A. B. C. D.
8.如图,AB∥CD,∠BAC与∠DCA的平分线相交于点G,GE⊥AC于点E,F为AC上的一点,且
FA=FG=FC,GH⊥CD于H.下列说法:
①AG⊥CG;②∠BAG=∠CGE;③S△AFG=S△CFG;④若∠EGH:∠ECH=2:7,则∠EGF=50°.
其中正确的有( )
A.①②③④ B.②③④ C.①③④ D.①②④
二、填空题
9.将方程变形为用的代数式表示的形式是 .
10.用不等式表示“a与5的差不是正数”: .
11.如图,将△ABC沿CB边向右平移得到△DFE,DE交AB于点G.,已知∠A:∠C:∠ABC=1:2:3,AB=9cm,BF=5cm,AG=5cm,则图中阴影部分的面积为 cm2.
12.观察下列有规律的点的坐标:
A1(1,1),A2(2,-4),A3(3,4),A4(4,-2),A5(5,7),A6(6,),A7(7,10),A8(8,-1)……,
依此规律,A11的坐标为 ,A12的坐标为 .
三、解答题
13.解方程组
14.解不等式>x-1并把解集在数轴上表示出来.
15.如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.
16.如图,在平面直角坐标系中:
(1)写出点A的坐标;
(2)将线段OA向上平移两次,每次平移1个单位,再将线段向左平移2个单位,得到线段O′A′,写出点O,A的对应点O′,A′的坐标;
(3)在图中画出与线段OA相等的两条不同的线段.
17.如图,AD平分∠BAC,∠EAD=∠EDA.
(1)∠EAC与∠B相等吗?为什么?
(2)若∠B=50°,∠CAD:∠E=1:3,求∠E的度数.
18某帐篷厂生产的帐篷有两种规格,可供3人居住的小帐篷,价格每顶160元;可供10人居住的大帐篷,价格每顶400元.某公司用96000元采购这两种帐篷,正好可供2300人居住. 该公司准备租用甲、乙两种型号的卡车共20辆运输这批帐篷,已知甲型卡车每辆可同时装运4顶小帐篷和11顶大帐篷,乙型卡车每辆可同时装运12顶小帐篷和7顶大帐篷.
(1)求该公司采购了多少顶3人小帐篷,多少顶10人住的大帐篷;
(2)应如何安排甲、乙两种型号的卡车可一次性将这批帐篷全部运走?有几种方案?
19.已知:在△ABC和△DEF中,∠A=40°,∠E+∠F=95°,将△DEF如图摆放,使得∠D的两条边分别经过点B和点C.
(1)当将△DEF如图1摆放时,则∠ABD+∠ACD= 度.
(2)当将△DEF如图2摆放时,请求出∠ABD+∠ACD的度数,并说明理由.
(3)能否将△DEF摆放到某个位置时,使得BD,CD同时平分∠ABC和∠ACB?请直接写出你的结论: .
20.如图,A,B两点同时从原点O出发,点A以每秒x个单位长度沿x轴的负方向运动,点B以每秒y个单位长度沿y轴的正方向运动.
(1)若∣x+2y-5∣+∣2x-y∣=0,试分别求出1秒钟后,A,B两点的坐标.
(2)设∠BAO的邻补角和∠ABO的邻补角的平分线相交于点P,问:点A,B在运动的过程中,∠P的大小是否会发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
(3)如图,延长BA至E,在∠ABO的内部作射线BF交x轴于点C,若∠EAC,∠FCA,∠ABC的平分线相交于点G,过点G作BE的垂线,垂足为H,试问∠AGH和∠BGC的大小关系如何?请写出你的结论并说明理由.
参考答案
一、选择题
1.A 2.B 3.D 4.B 5.B 6.C 7.C 8.A
二、填空题
9.y= 10.a-5≤0 11. 12.(11,16),(12,-)
三、解答题
13.解:由①得 ③ .把③代入②得 ,.把代人③得
∴原方程组的解为 .
14.解: 1+2x>3x-3, 2x-3x>-3-1,-x>-4 ,x<4 .
15.证明: ∵∠A+∠ADE=180°,∴AB∥DE,∴∠CED=∠B=78°.又∠C=60°,∴∠EDC=180°-
∠CED-∠C=180°-78°-60°=42°.
16.(1)A(2,1) (2)O′(-2,2) 、A′(0,3) (3)略
17.解:(1)相等.理由如下:∵AD平分∠BAC,∴∠BAD=∠CAD.
又∠EAD=∠EDA,∴∠EAC=∠EAD-∠CAD=∠EDA-∠BAD=∠B.
(2)设∠CAD=x°,则∠E=3x°,由(1)有:∠EAC=∠B=50°,∴∠EAD=∠EDA=(x+50)°.
在△EAD中,∠E+∠EAD+∠EDA=180°,∴3 x+2(x+50)=180,解得:x=16,∴∠E=48°.
18.解:(1)设该校采购了x顶小帐篷,y顶大帐篷,
根据题意得 ,解这个方程组得 .
答:该公司采购了100顶3人小帐篷,200顶10人住的大帐篷.
(2)设甲型卡车安排了a辆,则乙型卡车安排了(20-a)辆,根据题意得,
解这个不等式组得15≤a≤17.5.∵车辆数为正整数,∴a=15或16或17.∴20-a =5或4或3.
答:学校可安排甲型卡车15辆,乙型卡车5辆或安排甲型卡车16辆,乙型卡车4辆或安排甲型卡车17辆,乙型卡车3辆,可一次性将这批帐篷全部运走.有3种方案.
19.解:(1)235.
(2)∠ABD+∠ACD=45°.理由如下: ∵∠E+∠F=95°,∴∠D=180°-(∠E+∠F)=85°,
∴∠ABD+∠ACD=180°-∠A-∠DBC-∠DCB=180°-40°-(180°-85°)=45°.
(3)不能.
20.解:(1)解方程组:,得:,∴A(-1,0),B(0,2).
(2)不发生变化.∠P=180°-∠PAB-∠PBA=180°-(∠EAB+∠FBA)=180°-(∠ABO+
90°+∠BAO+90°)=180°-(180°+180°-90°)=180°-135°=45°.
(3)作GM⊥BF于点M,由已知有:∠AGH=90°-∠EAC=90°-(180°-∠BAC)=∠BAC.
∠BGC=∠BGM-∠BGC=90°-∠ABC-(90°-∠ACF)=(∠ACF-∠ABC)=∠BAC.
∴∠AGH=∠BGC.
一、选择题
1.下列因式分解正确的是( )
A. B.
C. D.
2.利用图形中面积的等量关系可以得到某些数学公式.例如,根据图左,我们可以得到两数和的平方公式:.你根据图右能得到的数学公式是( )
A. B.
C. D.
第2题 第3题 第6题 第8题
3.如图,下列条件中不能判定AB∥CD的是( )
A.∠3=∠4 B.∠1=∠5
C.∠1+∠4=180° D.∠3=∠5
4.已知三角形的两边长分别为4cm和9cm,则下列长度的四条线段中能作为第三边的是( )
A.13cm B.6cm C.5cm D.4cm
5.如果a>b,那么下列结论一定正确的是( )
A.a-3<b-3 B.3-a<3-b C.ac2>bc2 D.a2>b2
6.如图,直角△ADB中,∠D=90°,C为AD上一点,且∠ACB的度数为(5x-10)°,则x的值可能
是( )
A.10 B.20 C.30 D.40
7.玩具车间每天能生产甲种玩具零件24个或乙种玩具零件12个,若甲种玩具零件一个与乙种玩具零件2个能组成一个完整的玩具, 怎样安排生产才能在60 天内组装出最多的玩具?设生产甲种玩具零件x天 乙种玩具零件y天,则有( )
A. B. C. D.
8.如图,AB∥CD,∠BAC与∠DCA的平分线相交于点G,GE⊥AC于点E,F为AC上的一点,且
FA=FG=FC,GH⊥CD于H.下列说法:
①AG⊥CG;②∠BAG=∠CGE;③S△AFG=S△CFG;④若∠EGH:∠ECH=2:7,则∠EGF=50°.
其中正确的有( )
A.①②③④ B.②③④ C.①③④ D.①②④
二、填空题
9.将方程变形为用的代数式表示的形式是 .
10.用不等式表示“a与5的差不是正数”: .
11.如图,将△ABC沿CB边向右平移得到△DFE,DE交AB于点G.,已知∠A:∠C:∠ABC=1:2:3,AB=9cm,BF=5cm,AG=5cm,则图中阴影部分的面积为 cm2.
12.观察下列有规律的点的坐标:
A1(1,1),A2(2,-4),A3(3,4),A4(4,-2),A5(5,7),A6(6,),A7(7,10),A8(8,-1)……,
依此规律,A11的坐标为 ,A12的坐标为 .
三、解答题
13.解方程组
14.解不等式>x-1并把解集在数轴上表示出来.
15.如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.
16.如图,在平面直角坐标系中:
(1)写出点A的坐标;
(2)将线段OA向上平移两次,每次平移1个单位,再将线段向左平移2个单位,得到线段O′A′,写出点O,A的对应点O′,A′的坐标;
(3)在图中画出与线段OA相等的两条不同的线段.
17.如图,AD平分∠BAC,∠EAD=∠EDA.
(1)∠EAC与∠B相等吗?为什么?
(2)若∠B=50°,∠CAD:∠E=1:3,求∠E的度数.
18某帐篷厂生产的帐篷有两种规格,可供3人居住的小帐篷,价格每顶160元;可供10人居住的大帐篷,价格每顶400元.某公司用96000元采购这两种帐篷,正好可供2300人居住. 该公司准备租用甲、乙两种型号的卡车共20辆运输这批帐篷,已知甲型卡车每辆可同时装运4顶小帐篷和11顶大帐篷,乙型卡车每辆可同时装运12顶小帐篷和7顶大帐篷.
(1)求该公司采购了多少顶3人小帐篷,多少顶10人住的大帐篷;
(2)应如何安排甲、乙两种型号的卡车可一次性将这批帐篷全部运走?有几种方案?
19.已知:在△ABC和△DEF中,∠A=40°,∠E+∠F=95°,将△DEF如图摆放,使得∠D的两条边分别经过点B和点C.
(1)当将△DEF如图1摆放时,则∠ABD+∠ACD= 度.
(2)当将△DEF如图2摆放时,请求出∠ABD+∠ACD的度数,并说明理由.
(3)能否将△DEF摆放到某个位置时,使得BD,CD同时平分∠ABC和∠ACB?请直接写出你的结论: .
20.如图,A,B两点同时从原点O出发,点A以每秒x个单位长度沿x轴的负方向运动,点B以每秒y个单位长度沿y轴的正方向运动.
(1)若∣x+2y-5∣+∣2x-y∣=0,试分别求出1秒钟后,A,B两点的坐标.
(2)设∠BAO的邻补角和∠ABO的邻补角的平分线相交于点P,问:点A,B在运动的过程中,∠P的大小是否会发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
(3)如图,延长BA至E,在∠ABO的内部作射线BF交x轴于点C,若∠EAC,∠FCA,∠ABC的平分线相交于点G,过点G作BE的垂线,垂足为H,试问∠AGH和∠BGC的大小关系如何?请写出你的结论并说明理由.
参考答案
一、选择题
1.A 2.B 3.D 4.B 5.B 6.C 7.C 8.A
二、填空题
9.y= 10.a-5≤0 11. 12.(11,16),(12,-)
三、解答题
13.解:由①得 ③ .把③代入②得 ,.把代人③得
∴原方程组的解为 .
14.解: 1+2x>3x-3, 2x-3x>-3-1,-x>-4 ,x<4 .
15.证明: ∵∠A+∠ADE=180°,∴AB∥DE,∴∠CED=∠B=78°.又∠C=60°,∴∠EDC=180°-
∠CED-∠C=180°-78°-60°=42°.
16.(1)A(2,1) (2)O′(-2,2) 、A′(0,3) (3)略
17.解:(1)相等.理由如下:∵AD平分∠BAC,∴∠BAD=∠CAD.
又∠EAD=∠EDA,∴∠EAC=∠EAD-∠CAD=∠EDA-∠BAD=∠B.
(2)设∠CAD=x°,则∠E=3x°,由(1)有:∠EAC=∠B=50°,∴∠EAD=∠EDA=(x+50)°.
在△EAD中,∠E+∠EAD+∠EDA=180°,∴3 x+2(x+50)=180,解得:x=16,∴∠E=48°.
18.解:(1)设该校采购了x顶小帐篷,y顶大帐篷,
根据题意得 ,解这个方程组得 .
答:该公司采购了100顶3人小帐篷,200顶10人住的大帐篷.
(2)设甲型卡车安排了a辆,则乙型卡车安排了(20-a)辆,根据题意得,
解这个不等式组得15≤a≤17.5.∵车辆数为正整数,∴a=15或16或17.∴20-a =5或4或3.
答:学校可安排甲型卡车15辆,乙型卡车5辆或安排甲型卡车16辆,乙型卡车4辆或安排甲型卡车17辆,乙型卡车3辆,可一次性将这批帐篷全部运走.有3种方案.
19.解:(1)235.
(2)∠ABD+∠ACD=45°.理由如下: ∵∠E+∠F=95°,∴∠D=180°-(∠E+∠F)=85°,
∴∠ABD+∠ACD=180°-∠A-∠DBC-∠DCB=180°-40°-(180°-85°)=45°.
(3)不能.
20.解:(1)解方程组:,得:,∴A(-1,0),B(0,2).
(2)不发生变化.∠P=180°-∠PAB-∠PBA=180°-(∠EAB+∠FBA)=180°-(∠ABO+
90°+∠BAO+90°)=180°-(180°+180°-90°)=180°-135°=45°.
(3)作GM⊥BF于点M,由已知有:∠AGH=90°-∠EAC=90°-(180°-∠BAC)=∠BAC.
∠BGC=∠BGM-∠BGC=90°-∠ABC-(90°-∠ACF)=(∠ACF-∠ABC)=∠BAC.
∴∠AGH=∠BGC.
同课章节目录
